Dual-Tunable Broadband Terahertz Absorber Based on a Hybrid Graphene-Dirac Semimetal Structure
Abstract
:1. Introduction
2. Materials and Design
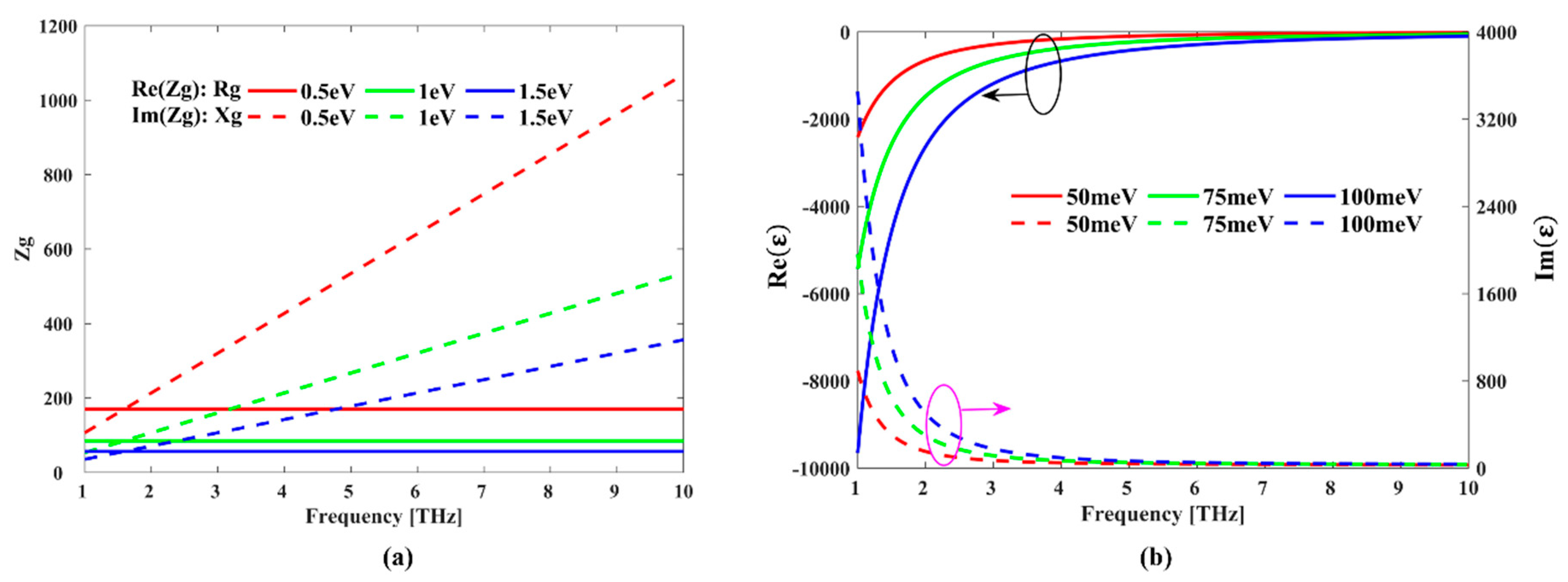
2.1. Graphene Material
2.2. BDS Material
2.3. Design Method
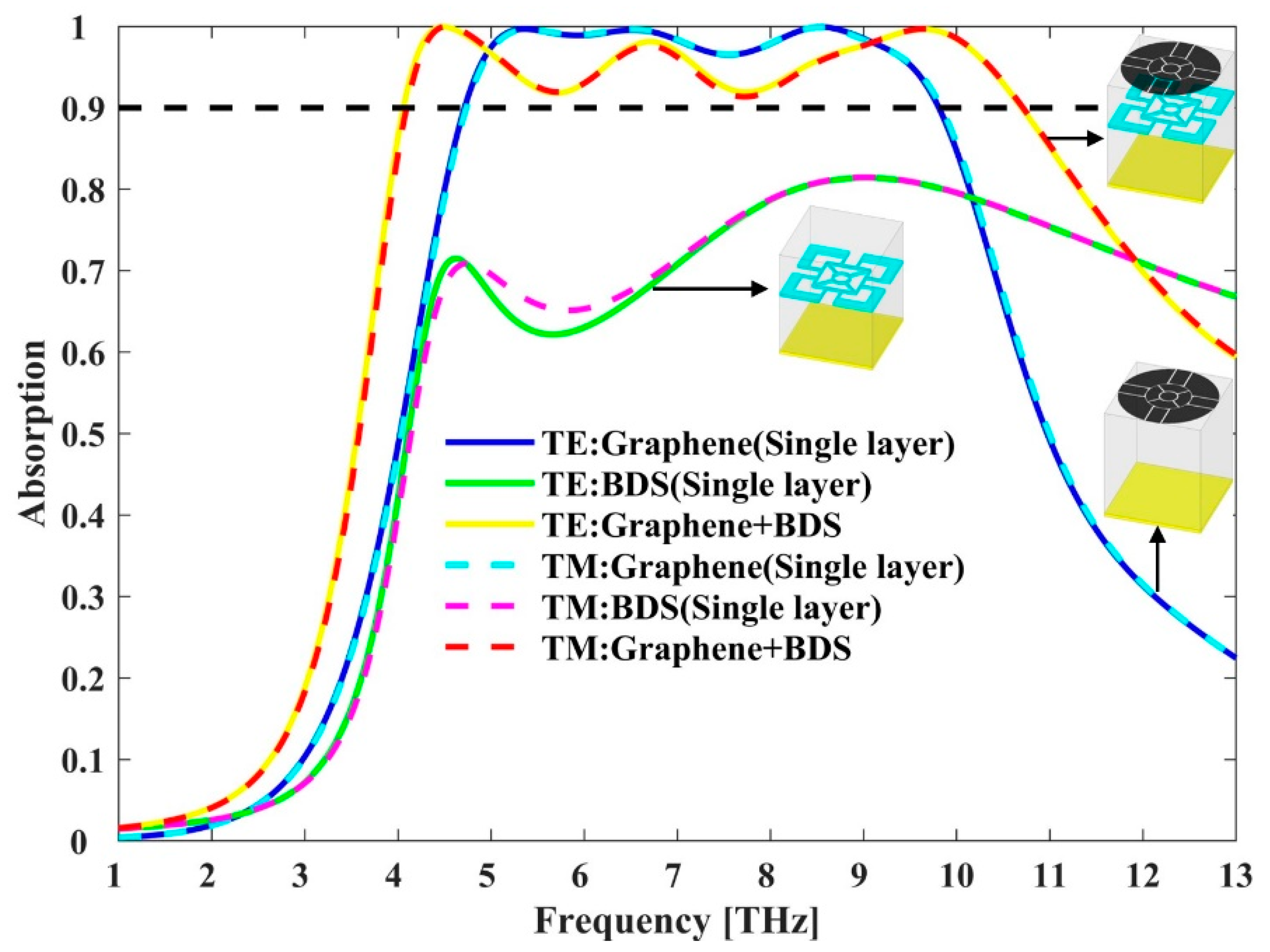
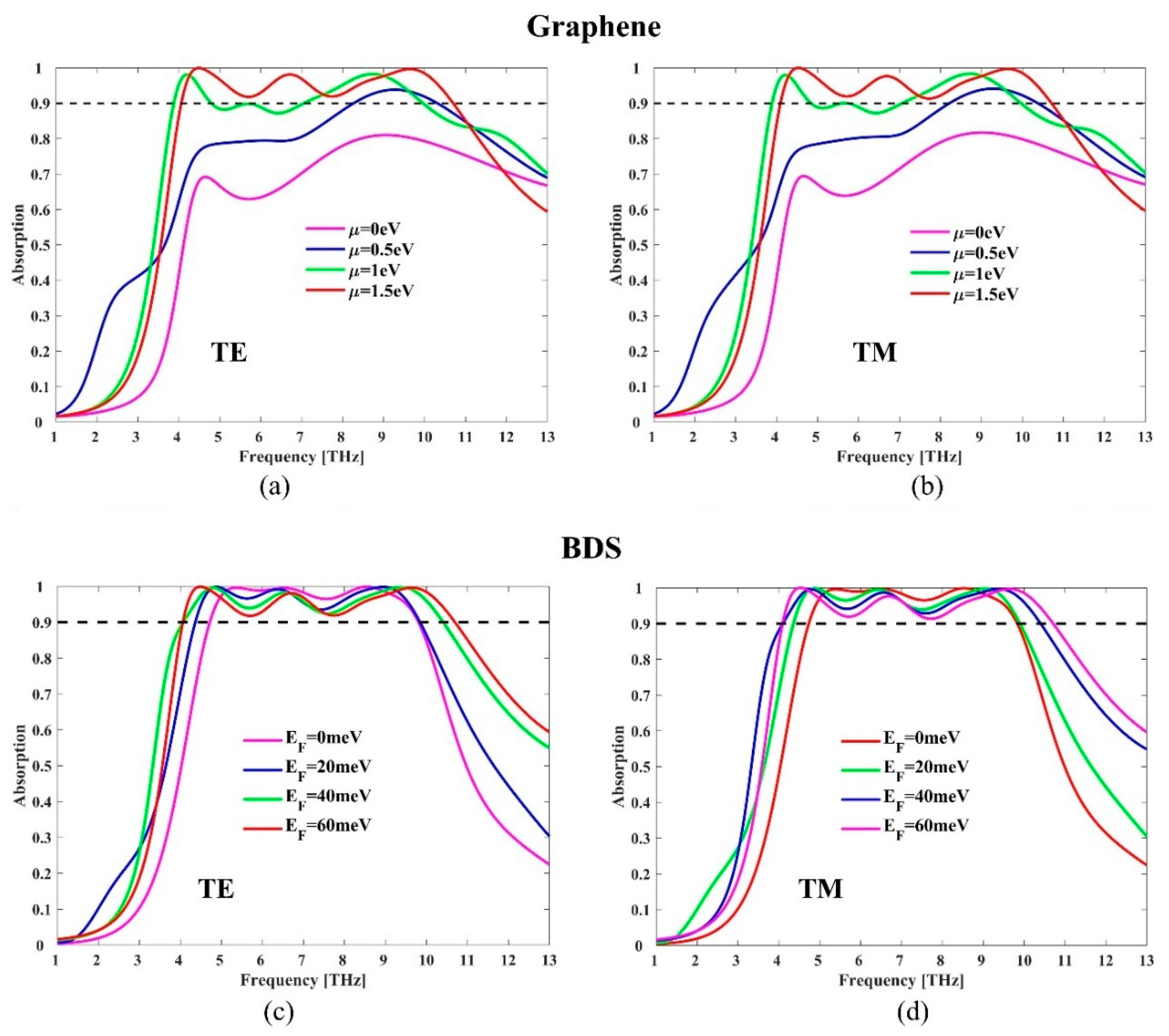
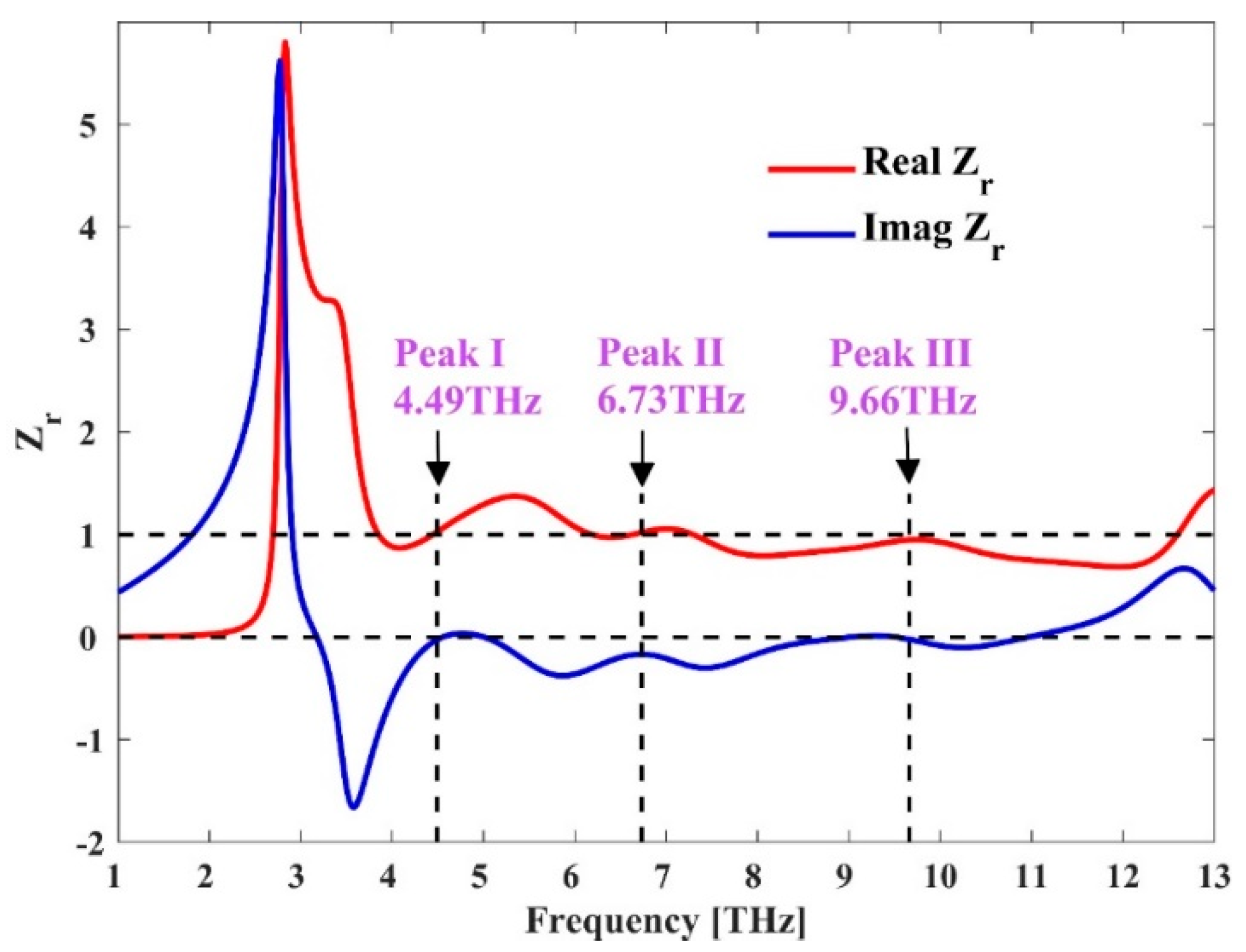
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Federici, J.; Moeller, L. Review of terahertz and subterahertz wireless communications. J. Appl. Phys. 2010, 107, 111101. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Zhang, J.; Xu, W.; Liu, K.; Yuan, X.; Qin, S.; Zhu, Z. Graphene-based perfect absorption structures in the visible to terahertz band and their optoelectronics applications. Nanomaterials 2018, 8, 1033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging-Modern techniques and applications. Laser Photonics Rev. 2011, 5, 125–159. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, D.; Liu, Y.; Liu, C.; Yu, Z.; Yu, L.; Ye, H. Design of a tunable ultra-broadband terahertz absorber based on multiple layers of graphene ribbons. Nanoscale Res. Lett. 2018, 13, 143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 2014, 22, 22743–22752. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.; Yang, F. Ultra-broadband and tunable saline water-based absorber in microwave regime. Opt. Express 2020, 28, 5306–5316. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiang, J.; Hu, S.; Lyu, M.; Zhu, W.; Ma, C.; Chen, Z.; Steglich, F.; Chen, G.; Sun, P. Large transverse thermoelectric figure of merit in a topological Dirac semimetal. Sci. China Phys. Mech. 2019, 63, 237011. [Google Scholar] [CrossRef] [Green Version]
- Wieder, B.J.; Wang, Z.; Cano, J.; Dai, X.; Schoop, L.M.; Bradlyn, B.; Bernevig, B.A. Strong and fragile topological Dirac semimetals with higher-order Fermi arcs. Nat. Commun. 2020, 11, 627. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Wan, X.; Wang, J.; Wang, J. Tunable terahertz absorber based on bulk-Dirac-semimetal metasurface. IEEE Photonics J. 2018, 10, 4600607. [Google Scholar] [CrossRef]
- Xiong, H.; Shen, Q.; Ji, Q. Broadband dynamically tunable terahertz absorber based on a Dirac semimetal. Appl. Opt. 2020, 59, 4970–4976. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Chen, Z.; Zhang, C.; Jian, R. A narrow dual-band monolayer unpatterned graphene-based perfect absorber with critical coupling in the near infrared. Micromachines 2020, 11, 58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raad, S.H.; Atlasbaf, Z. Broadband continuous/discrete spectrum optical absorber using graphene-wrapped fractal oligomers. Opt. Express 2020, 28, 18049–18058. [Google Scholar] [CrossRef] [PubMed]
- Yi, Z.; Chen, J.; Cen, C.; Chen, X.; Zhou, Z.; Tang, Y.; Ye, X.; Xiao, S.; Luo, W.; Wu, P. Tunable graphene-based plasmonic perfect metamaterial absorber in the THz region. Micromachines 2019, 10, 194. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Chen, C.; Deng, S.; Liu, H.; Teng, C.; Cheng, Y.; Yang, H.; Xu, R.; Deng, H.; Yuan, L. Dynamically tunable polarization-independent terahertz absorber based on bulk Dirac semimetals. OSA Contin. 2019, 2, 2477–2486. [Google Scholar] [CrossRef]
- Meng, H.; Shang, X.; Xue, X.; Tang, K.; Xia, X.; Zhai, X.; Liu, Z.; Chen, J.; Li, H.; Wang, L. Bidirectional and dynamically tunable THz absorber with Dirac semimetal. Opt. Express 2019, 27, 31062–31074. [Google Scholar] [CrossRef]
- Fang, P.; Shi, X.; Liu, C.; Zhai, X.; Li, H.; Wang, L. Single- and dual-band convertible terahertz absorber based on bulk Dirac semimetal. Opt. Commun. 2020, 462, 125333. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, X.; Xia, S.; Li, H.; Wang, L. Active control of narrowband total absorption based on terahertz hybrid Dirac semimetal-graphene metamaterials. J. Phys. D Appl. Phys. 2020, 53, 205106. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef] [Green Version]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef] [Green Version]
- Kotov, O.V.; Lozovik, Y.E. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 235417. [Google Scholar] [CrossRef] [Green Version]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Riemann%E2%80%93Siegel_theta_function (accessed on 20 August 2020).
- Fu, P.; Liu, F.; Ren, G.J.; Su, F.; Li, D.; Yao, J.Q. A broadband metamaterial absorber based on multi-layer graphene in the terahertz region. Opt. Commun. 2018, 417, 62–66. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Zhang, H.; Cao, M. Dual-controlled switchable broadband terahertz absorber based on a graphene-vanadium dioxide metamaterial. Opt. Mater. Express 2020, 10, 369–386. [Google Scholar] [CrossRef]





| Parameter | Size (μm) | Parameter | Size (μm) | Parameter | Size (μm) |
|---|---|---|---|---|---|
| 0.2 | 6 | 1.4 | |||
| 0.2 | 2.9 | (a – 2 × )/2 | |||
| 4 | 1.8 | 0.1 | |||
| 2.8 | 0.5 | 0.9 |
| References | Absorption Band (THz) | Fractional BW | Layers | Tunable Material | Polarization-Insensitivity | Angle-Insensitivity |
|---|---|---|---|---|---|---|
| [4] | 3–7.8 | 88.8% | 8 | Graphene | insensitive | 50° |
| [23] | 5.50–9.10 | 8.2% | 3 | Graphene | insensitive | 60° |
| [17] | <0.1 | <5% | 1 | BDS | insensitive | 60° |
| [24] | 1.05–1.6 | 42.5% | 2 | Graphene and vanadium dioxide | insensitive | 50° |
| This paper | 4.06–10.7 | 89.97% | 2 | Graphene and BDS | insensitive | 60° |
| Frequency (THz) | Real Part of Zr | Imaginary Part of Zr |
|---|---|---|
| Peak I 4.49 | 1.027 | −0.01 |
| Peak II 6.73 | 1.021 | −0.1673 |
| Peak III 9.66 | 0.9495 | −0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yuan, X.; Zhang, Y.; Yan, X.; Zhang, X. Dual-Tunable Broadband Terahertz Absorber Based on a Hybrid Graphene-Dirac Semimetal Structure. Micromachines 2020, 11, 1096. https://doi.org/10.3390/mi11121096
Wu J, Yuan X, Zhang Y, Yan X, Zhang X. Dual-Tunable Broadband Terahertz Absorber Based on a Hybrid Graphene-Dirac Semimetal Structure. Micromachines. 2020; 11(12):1096. https://doi.org/10.3390/mi11121096
Chicago/Turabian StyleWu, Jiali, Xueguang Yuan, Yangan Zhang, Xin Yan, and Xia Zhang. 2020. "Dual-Tunable Broadband Terahertz Absorber Based on a Hybrid Graphene-Dirac Semimetal Structure" Micromachines 11, no. 12: 1096. https://doi.org/10.3390/mi11121096





