Numerical Simulation and Experimental Validation of Liquid Metal Droplet Formation in a Co-Flowing Capillary Microfluidic Device
Abstract
:1. Introduction
2. Experiments
2.1. Materials
2.2. Experimental Setup
3. Numerical Simulation
3.1. Governing Equations
3.2. Numerical Method
4. Results and Discussion
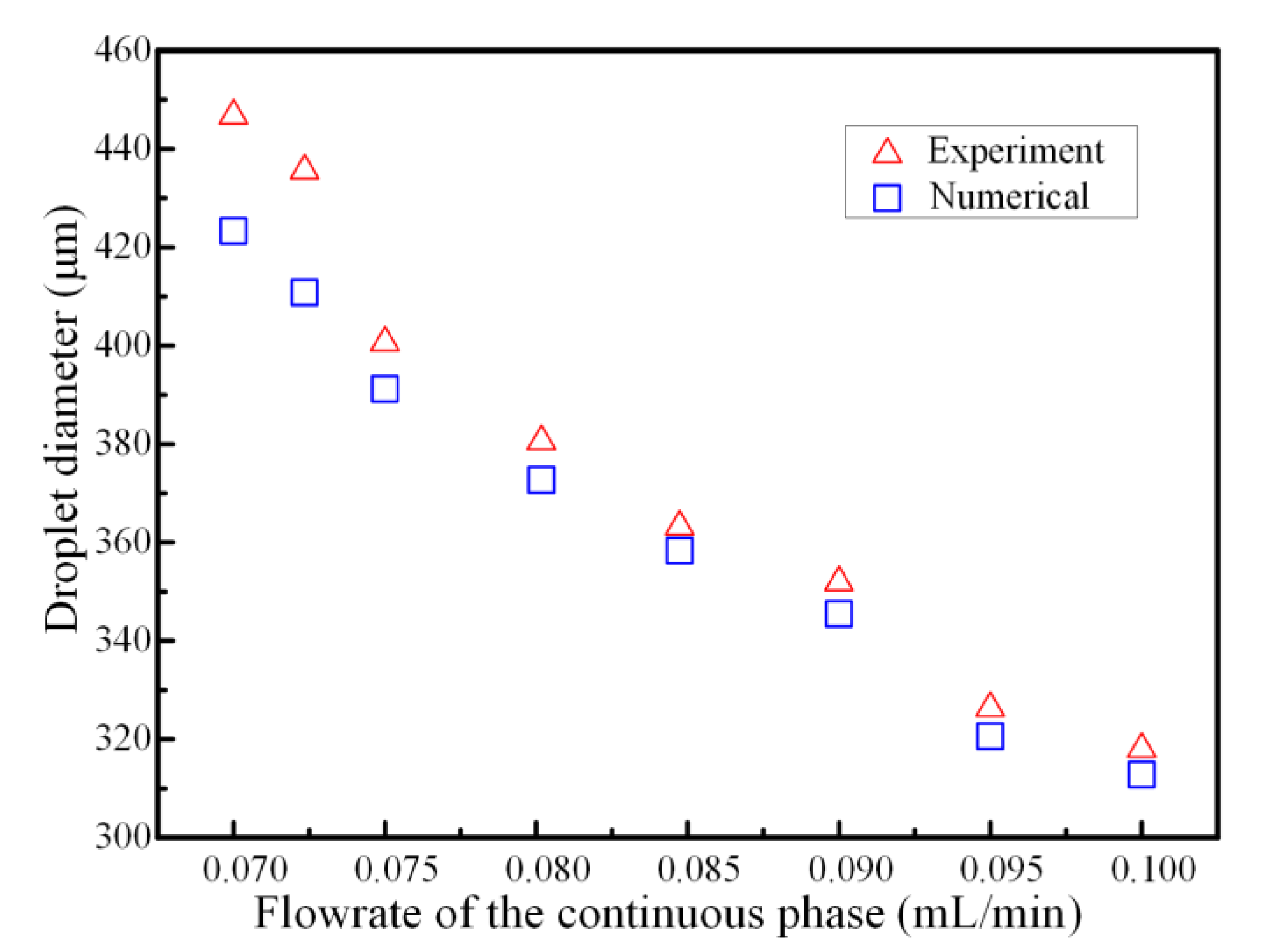
4.1. Model Validation of Simulation Results
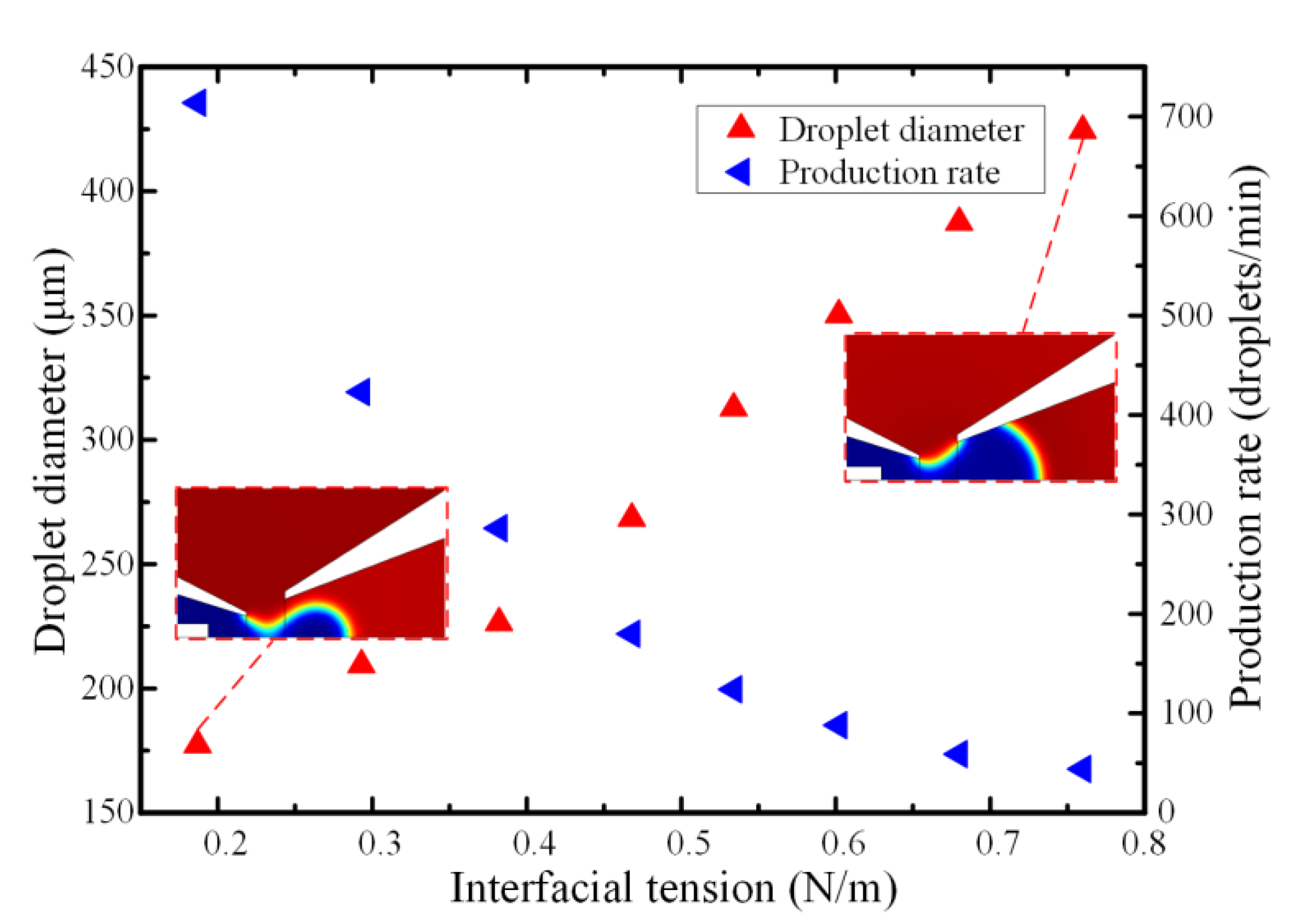
4.2. Effect of Interfacial Tension
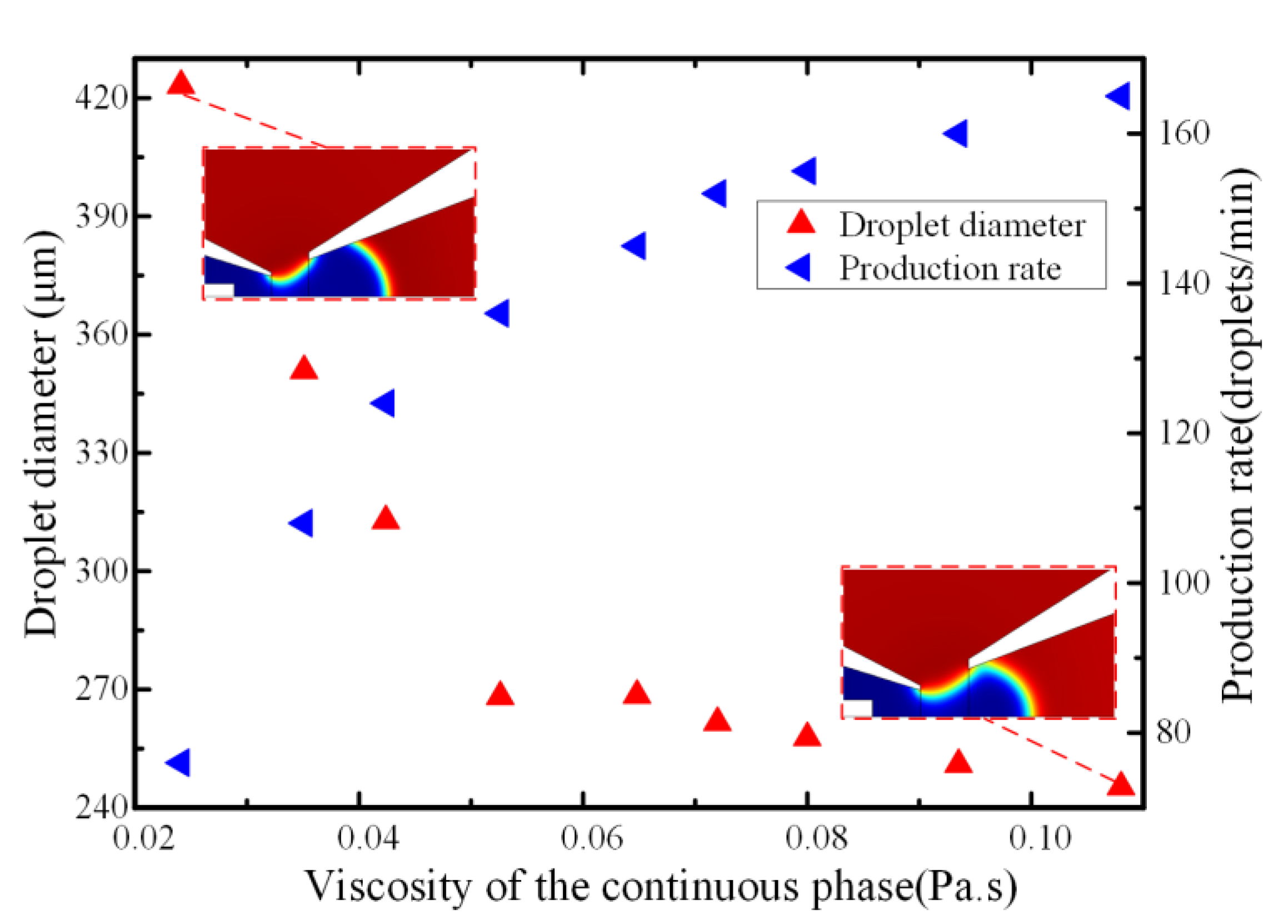
4.3. Effect of Viscosity of Continuous Phase Fluid
4.4. Effect of the Flowrates of Continuous Phase
4.5. Effect of the Wetting Property of the Micro-Needle
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dickey, M.D. Stretchable and Soft Electronics using Liquid Metals. Adv. Mater. 2017, 29, 1606425. [Google Scholar]
- Deng, Y.; Liu, J. A liquid metal cooling system for the thermal management of high power LEDs. Int. Commun. Heat Mass Transf. 2010, 37, 788–791. [Google Scholar]
- Chen, Y.; Zhou, T.; Li, Y.; Zhu, L.; Handschuh-Wang, S.; Zhu, D.; Zhou, X.; Liu, Z.; Gan, T.; Zhou, X. Robust Fabrication of Nonstick, Noncorrosive, Conductive Graphene-Coated Liquid Metal Droplets for Droplet-Based, Floating Electrodes. Adv. Funct. Mater. 2018, 28, 1706277. [Google Scholar]
- Shay, T.; Velev, O.D.; Dickey, M.D. Soft electrodes combining hydrogel and liquid metal. Soft Matter. 2018, 14, 3296–3303. [Google Scholar]
- Suarez, F.; Parekh, D.P.; Ladd, C.; Vashaee, D.; Dickey, M.D.; Öztürk, M.C. Flexible thermoelectric generator using bulk legs and liquid metal interconnects for wearable electronics. Appl. Energy 2017, 202, 736–745. [Google Scholar]
- Sheng, L.; Teo, S.; Liu, J. Liquid-Metal-Painted Stretchable Capacitor Sensors for Wearable Healthcare Electronics. J. Med. Biol. Eng. 2016, 36, 265–272. [Google Scholar]
- Wang, X.; Zhang, Y.; Guo, R.; Wang, H.; Yuan, B.; Liu, J. Conformable liquid metal printed epidermal electronics for smart physiological monitoring and simulation treatment. J. Micromech. Microeng. 2018, 28, 034003. [Google Scholar]
- Yu, Y.-Z.; Lu, J.-R.; Liu, J. 3D printing for functional electronics by injection and package of liquid metals into channels of mechanical structures. Mater. Des. 2017, 122, 80–89. [Google Scholar]
- Mailen, R.W.; Dickey, M.D.; Genzer, J.; Zikry, M. Effects of thermo-mechanical behavior and hinge geometry on folding response of shape memory polymer sheets. J. Appl. Phys. 2017, 122, 195103. [Google Scholar]
- Wissman, J.; Dickey, M.D.; Majidi, C. Field-Controlled Electrical Switch with Liquid Metal. Adv. Sci. 2017, 4, 1700169. [Google Scholar]
- Baek, S.; Park, U.; Choi, I.H.; Kim, J. Pneumatic RF MEMS switch using a liquid metal droplet. J. Micromech. Microeng. 2013, 23, 055006. [Google Scholar]
- McLanahan, A.R.; Richards, C.D.; Richards, R.F. A dielectric liquid contact thermal switch with electrowetting actuation. J. Micromech. Microeng. 2011, 21, 104009. [Google Scholar]
- Tang, S.-Y.; Khoshmanesh, K.; Sivan, V.; Petersen, P.; O’Mullane, A.P.; Abbott, D.; Mitchell, A.; Kalantar-zadeh, K. Liquid metal enabled pump. Proc. Natl. Acad. Sci. USA 2014, 111, 3304–3309. [Google Scholar] [PubMed] [Green Version]
- Tang, S.-Y.; Sivan, V.; Petersen, P.; Zhang, W.; Morrison, P.D.; Kalantar-zadeh, K.; Mitchell, A.; Khoshmanesh, K. Liquid Metal Actuator for Inducing Chaotic Advection. Adv. Funct. Mater. 2014, 24, 5851–5858. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Deng, W.; Jin, L.; Chun, F.; Pan, H.; Gu, B.; Zhang, H.; Lv, Z.; Yang, W.; et al. Self-Powered Acceleration Sensor Based on Liquid Metal Triboelectric Nanogenerator for Vibration Monitoring. ACS Nano 2017, 11, 7440–7446. [Google Scholar] [PubMed]
- Zou, L.; Withayachumnankul, W.; Shah, C.M.; Mitchell, A.; Bhaskaran, M.; Sriram, S.; Fumeaux, C. Dielectric resonator nanoantennas at visible frequencies. Opt. Express 2013, 21, 1344–1352. [Google Scholar]
- Hashimoto, M.; Mayers, B.; Garstecki, P.; Whitesides, G.M. Flowing Lattices of Bubbles as Tunable, Self-Assembled Diffraction Gratings. Small 2006, 2, 1292–1298. [Google Scholar]
- Yu, J.; Yang, Y.; Liu, A.; Chin, L.; Zhang, X. Microfluidic droplet grating for reconfigurable optical diffraction. Opt. Lett. 2010, 35, 1890–1892. [Google Scholar]
- Pollack, M.G.; Shenderov, A.D.; Fair, R.B. Electrowetting-based actuation of droplets for integrated microfluidics. Lab Chip 2002, 2, 96–101. [Google Scholar]
- Mohammed, M.; Xenakis, A.; Dickey, M. Production of Liquid Metal Spheres by Molding. Metals 2014, 4, 465–476. [Google Scholar]
- áO’Mullane, A.P. Generation of catalytically active materials from a liquid metal precursor. Chem. Commun. 2015, 51, 14026–14029. [Google Scholar]
- Tang, S.Y.; Ayan, B.; Nama, N.; Bian, Y.; Lata, J.P.; Guo, X.; Huang, T.J. On-Chip Production of Size-Controllable Liquid Metal Microdroplets Using Acoustic Waves. Small 2016, 12, 3861–3869. [Google Scholar] [PubMed]
- Zhu, P.; Wang, L. Passive and active droplet generation with microfluidics: A review. Lab Chip 2017, 17, 34–75. [Google Scholar]
- Adamo, A.; Sharei, A.; Adamo, L.; Lee, B.; Mao, S.; Jensen, K.F. Microfluidics-based assessment of cell deformability. Anal. Chem. 2012, 84, 6438–6443. [Google Scholar]
- Tan, Y.-C.; Cristini, V.; Lee, A.P. Monodispersed microfluidic droplet generation by shear focusing microfluidic device. Sens. Actuators B Chem. 2006, 114, 350–356. [Google Scholar]
- Tang, S.Y.; Joshipura, I.D.; Lin, Y.; Kalantar-Zadeh, K.; Mitchell, A.; Khoshmanesh, K.; Dickey, M.D. Liquid-Metal Microdroplets Formed Dynamically with Electrical Control of Size and Rate. Adv. Mater. 2016, 28, 604–609. [Google Scholar]
- Gol, B.; Kurdzinski, M.E.; Tovar-Lopez, F.J.; Petersen, P.; Mitchell, A.; Khoshmanesh, K. Hydrodynamic directional control of liquid metal droplets within a microfluidic flow focusing system. Appl. Phys. Lett. 2016, 108, 164101. [Google Scholar]
- Gol, B.; Tovar-Lopez, F.J.; Kurdzinski, M.E.; Tang, S.Y.; Petersen, P.; Mitchell, A.; Khoshmanesh, K. Continuous transfer of liquid metal droplets across a fluid-fluid interface within an integrated microfluidic chip. Lab Chip 2015, 15, 2476–2485. [Google Scholar]
- Hutter, T.; Bauer, W.-A.C.; Elliott, S.R.; Huck, W.T.S. Formation of Spherical and Non-Spherical Eutectic Gallium-Indium Liquid-Metal Microdroplets in Microfluidic Channels at Room Temperature. Adv. Funct. Mater. 2012, 22, 2624–2631. [Google Scholar]
- Thelen, J.; Dickey, M.D.; Ward, T. A study of the production and reversible stability of EGaIn liquid metal microspheres using flow focusing. Lab Chip 2012, 12, 3961–3967. [Google Scholar]
- Hu, Q.; Ren, Y.; Zheng, X.; Hou, L.; Jiang, T.; Liu, W.; Tao, Y.; Jiang, H. A micro-needle induced strategy for preparation of monodisperse liquid metal droplets in glass capillary microfluidics. Microfluid. Nanofluid. 2019, 23, 13. [Google Scholar]
- Lin, P.; Wei, Z.; Yan, Q.; Xie, J.; Fan, Y.; Wu, M.; Chen, Y.; Cheng, Z. Capillary-Based Microfluidic Fabrication of Liquid Metal Microspheres toward Functional Microelectrodes and Photothermal Medium. ACS Appl. Mater. Interfaces 2019, 11, 25295–25305. [Google Scholar] [PubMed]
- Zhang, K.; Ren, Y.; Tao, Y.; Deng, X.; Liu, W.; Jiang, T.; Jiang, H. Efficient particle and droplet manipulation utilizing the combined thermal buoyancy convection and temperature-enhanced rotating induced-charge electroosmotic flow. Anal. Chim. Acta 2020, 1096, 108–119. [Google Scholar] [PubMed]
- Lang, Q.; Wu, Y.; Ren, Y.; Tao, Y.; Lei, L.; Jiang, H. AC Electrothermal Circulatory Pumping Chip for Cell Culture. ACS Appl. Mater. Interfaces 2015, 7, 26792–26801. [Google Scholar]
- Bangjang, T.; Cherkasov, N.; Denissenko, P.; Jaree, A.; Rebrov, E.V. Enhanced Droplet Size Control in Liquid-Liquid Emulsions Obtained in a Wire-Guided X-Mixer. Chem. Eng. Technol. 2019, 42, 1053–1058. [Google Scholar]
- Si, T.; Feng, H.; Luo, X.; Xu, R.X. Formation of steady compound cone-jet modes and multilayered droplets in a tri-axial capillary flow focusing device. Microfluid. Nanofluid. 2014, 18, 967–977. [Google Scholar]
- Fang, J.; Davoudi, M.; Chase, G. Drop movement along a fiber axis due to pressure driven air flow in a thin slit. Sep. Purif. Technol. 2015, 140, 77–83. [Google Scholar]
- Lan, W.; Li, S.; Luo, G. Numerical and experimental investigation of dripping and jetting flow in a coaxial micro-channel. Chem. Eng. Sci. 2015, 134, 76–85. [Google Scholar]
- Deng, C.; Wang, H.; Huang, W.; Cheng, S. Numerical and experimental study of oil-in-water (O/W) droplet formation in a co-flowing capillary device. Colloids Surf. A Physicochem. Eng. Asp. 2017, 533, 1–8. [Google Scholar] [CrossRef]
- Nabavi, S.A.; Vladisavljević, G.T.; Gu, S.; Ekanem, E.E. Double emulsion production in glass capillary microfluidic device: Parametric investigation of droplet generation behaviour. Chem. Eng. Sci. 2015, 130, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Nabavi, S.A.; Gu, S.; Vladisavljevic, G.T.; Ekanem, E.E. Dynamics of double emulsion break-up in three phase glass capillary microfluidic devices. J. Colloid Interface Sci. 2015, 450, 279–287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soh, G.Y.; Yeoh, G.H.; Timchenko, V. Numerical investigation on the velocity fields during droplet formation in a microfluidic T-junction. Chem. Eng. Sci. 2016, 139, 99–108. [Google Scholar] [CrossRef]
- De Menech, M. Modeling of droplet breakup in a microfluidic T-shaped junction with a phase-field model. Phys. Rev. E 2006, 73, 031505. [Google Scholar] [CrossRef] [Green Version]
- Nabavi, S.A.; Vladisavljevic, G.T.; Bandulasena, M.V.; Arjmandi-Tash, O.; Manovic, V. Prediction and control of drop formation modes in microfluidic generation of double emulsions by single-step emulsification. J. Colloid Interface Sci. 2017, 505, 315–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smithwich, R.W. Contact-angle studies of microscopic mercury droplets on glass. J. Colloid Interface Sci. 1988, 123, 482–485. [Google Scholar] [CrossRef]
- Peng, L.; Yang, M.; Guo, S.S.; Liu, W.; Zhao, X.Z. The effect of interfacial tension on droplet formation in flow-focusing microfluidic device. Biomed. Microdevices 2011, 13, 559–564. [Google Scholar] [CrossRef]
- Tice, J.D.; Lyon, A.D.; Ismagilov, R.F. Effects of viscosity on droplet formation and mixing in microfluidic channels. Anal. Chim. Acta 2004, 507, 73–77. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Pastora, J.; Amiri Roodan, V.; Karampelas, I.H.; Alorabi, A.Q.; Tarn, M.D.; Iles, A.; Bringas, E.; Paunov, V.N.; Pamme, N.; Furlani, E.P.; et al. Two-Step Numerical Approach to Predict Ferrofluid Droplet Generation and Manipulation inside Multilaminar Flow Chambers. J. Phys. Chem. C 2019, 123, 10065–10080. [Google Scholar] [CrossRef]
- Manzo, G.M.; Wu, Y.; Chase, G.G.; Goux, A. Comparison of nonwoven glass and stainless steel microfiber media in aerosol coalescence filtration. Sep. Purif. Technol. 2016, 162, 14–19. [Google Scholar] [CrossRef]
- Jamali, M.; Tafreshi, H.V.; Pourdeyhimi, B. Droplet Mobility on Hydrophobic Fibrous Coatings Comprising Orthogonal Fibers. Langmuir 2018, 34, 12488–12499. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Jiang, T.; Jiang, H. Numerical Simulation and Experimental Validation of Liquid Metal Droplet Formation in a Co-Flowing Capillary Microfluidic Device. Micromachines 2020, 11, 169. https://doi.org/10.3390/mi11020169
Hu Q, Jiang T, Jiang H. Numerical Simulation and Experimental Validation of Liquid Metal Droplet Formation in a Co-Flowing Capillary Microfluidic Device. Micromachines. 2020; 11(2):169. https://doi.org/10.3390/mi11020169
Chicago/Turabian StyleHu, Qingming, Tianyi Jiang, and Hongyuan Jiang. 2020. "Numerical Simulation and Experimental Validation of Liquid Metal Droplet Formation in a Co-Flowing Capillary Microfluidic Device" Micromachines 11, no. 2: 169. https://doi.org/10.3390/mi11020169
APA StyleHu, Q., Jiang, T., & Jiang, H. (2020). Numerical Simulation and Experimental Validation of Liquid Metal Droplet Formation in a Co-Flowing Capillary Microfluidic Device. Micromachines, 11(2), 169. https://doi.org/10.3390/mi11020169



