A Microfluidic Concentration Gradient Maker with Tunable Concentration Profiles by Changing Feed Flow Rate Ratios
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chip Design and FFRR Strategy
2.2. Settings for Numerical Simulation
2.3. Experimental Setup
3. Results and Discussion
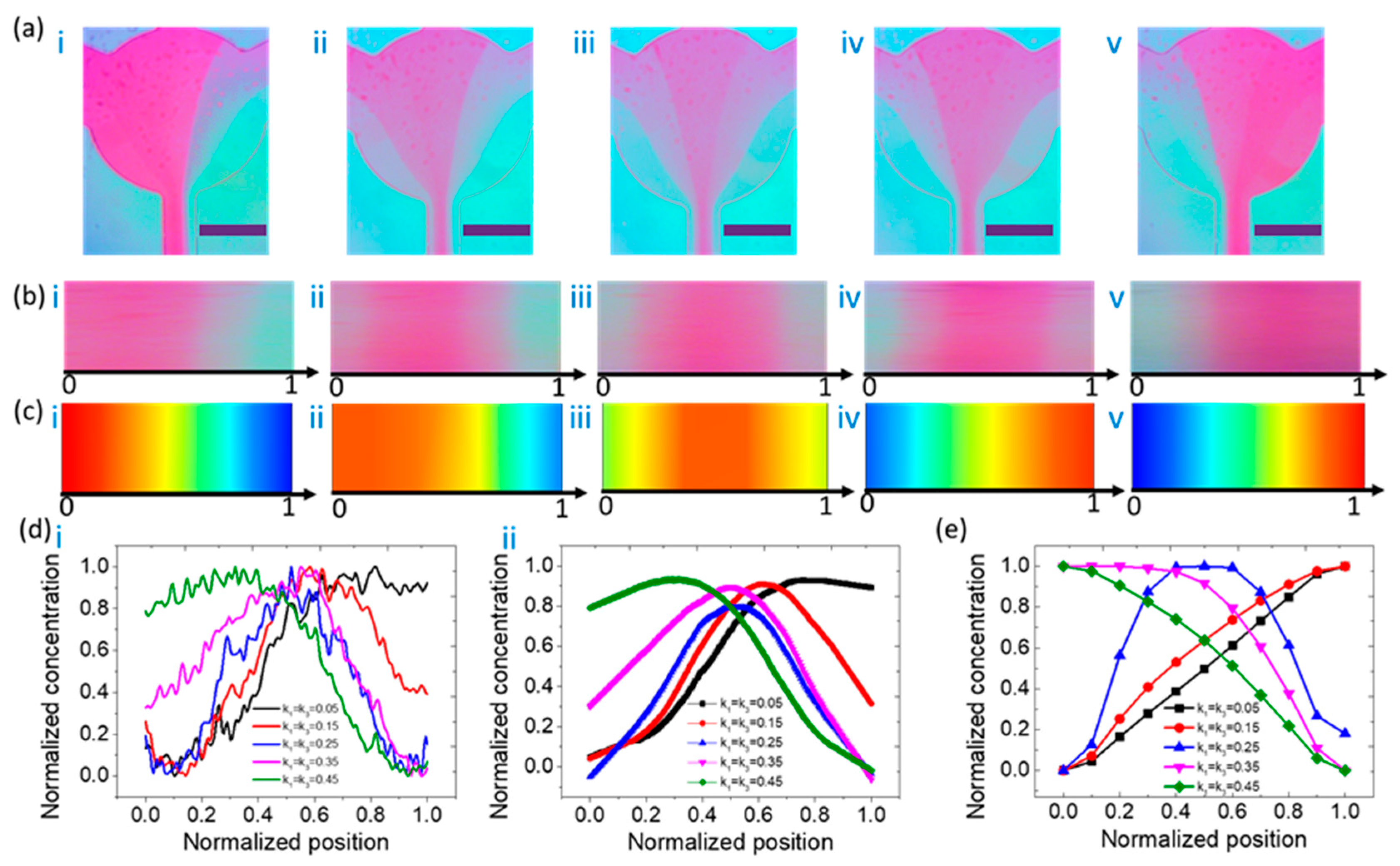
3.1. Concentration Distribution Profiles of the Type IV Mixer
3.2. Concentration Distribution Profiles of the Type V Mixer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sabourin, D.; Snakenborg, D.; Dufva, M. Interconnection blocks with minimal dead volumes permitting planar interconnection to thin microfluidic devices. Microfluid. Nanofluid. 2010, 9, 87–93. [Google Scholar] [CrossRef]
- Van den Berg, A.; Lammerink, T.S. Micro Total Analysis Systems: Microfluidic Aspects, Integration Concept and Applications. In Microsystem Technology in Chemistry and Life Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 21–49. [Google Scholar]
- Meng, J.; Li, S.; Li, J.; Yu, C.; Wei, C.; Dai, S. AC electrothermal mixing for high conductive biofluids by arc-electrodes. J. Micromech. Microeng. 2018, 28, 065004. [Google Scholar] [CrossRef]
- Moerland, C.; van IJzendoorn, L.; Prins, M. Rotating magnetic particles for lab-on-chip applications—A comprehensive review. Lab Chip 2019, 19, 919–933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Hellman, A.N.; Rau, K.R.; Yoon, H.H.; Bae, S.; Palmer, J.F.; Phillips, K.S.; Allbritton, N.L.; Venugopalan, V. Laser-induced mixing in microfluidic channels. Anal. Chem. 2007, 79, 4484–4492. [Google Scholar] [CrossRef] [Green Version]
- Jeon, H.; Lee, Y.; Jin, S.; Koo, S.; Lee, C.-S.; Yoo, J.Y. Quantitative analysis of single bacterial chemotaxis using a linear concentration gradient microchannel. Biomed. Microdevices 2009, 11, 1135. [Google Scholar] [CrossRef] [Green Version]
- Dertinger, S.K.; Chiu, D.T.; Jeon, N.L.; Whitesides, G.M. Generation of gradients having complex shapes using microfluidic networks. Anal. Chem. 2001, 73, 1240–1246. [Google Scholar] [CrossRef]
- Jeon, N.L.; Baskaran, H.; Dertinger, S.K.; Whitesides, G.M.; Van De Water, L.; Toner, M. Neutrophil chemotaxis in linear and complex gradients of interleukin-8 formed in a microfabricated device. Nat. Biotech. 2002, 20, 826–830. [Google Scholar] [CrossRef]
- Lin, F.; Saadi, W.; Rhee, S.W.; Wang, S.-J.; Mittal, S.; Jeon, N.L. Generation of dynamic temporal and spatial concentration gradients using microfluidic devices. Lab Chip 2004, 4, 164–167. [Google Scholar] [CrossRef] [Green Version]
- Sule, N.; Penarete-Acosta, D.; Englert, D.L.; Jayaraman, A. A Static Microfluidic Device for Investigating the Chemotaxis Response to Stable, Non-linear Gradients. In Bacterial Chemosensing; Springer, Humana Press: New York, NY, USA, 2018; pp. 47–59. [Google Scholar]
- Zhou, B.; Gao, Y.; Tian, J.; Tong, R.; Wu, J.; Wen, W. Preparation of orthogonal physicochemical gradients on PDMS surface using microfluidic concentration gradient generator. Appl. Surf. Sci. 2019, 471, 213–221. [Google Scholar] [CrossRef]
- Kim, J.; Taylor, D.; Agrawal, N.; Wang, H.; Kim, H.; Han, A.; Rege, K.; Jayaraman, A. A programmable microfluidic cell array for combinatorial drug screening. Lab Chip 2012, 12, 1813–1822. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Li, H.; Wang, N.; Lin, J.M. Evaluation of the absorption of methotrexate on cells and its cytotoxicity assay by using an integrated microfluidic device coupled to a mass spectrometer. Anal. Chem. 2012, 84, 9230–9237. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Weiss, T.L.; Thapa, H.R.; Devarenne, T.P.; Han, A. A microfluidic photobioreactor array demonstrating high-throughput screening for microalgal oil production. Lab Chip 2014, 14, 1415–1425. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Nie, K.; Dong, B.; Long, M.; Xu, H.; Liu, Z. Recent progress of microfluidic reactors for biomedical applications. Chem. Eng. J. 2019, 361, 635–650. [Google Scholar] [CrossRef]
- Wang, F. The signaling mechanisms underlying cell polarity and chemotaxis. Cold Spring Harb. Perspec. Biol. 2009, 1, a002980. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Chen, C.-H.; Xiang, Z.; Wang, M.; Lee, C. A convection-driven long-range linear gradient generator with dynamic control. Lab Chip 2015, 15, 1445–1450. [Google Scholar] [CrossRef]
- Tang, M.; Huang, X.; Chu, Q.; Ning, X.; Wang, Y.; Kong, S.-K.; Zhang, X.; Wang, G.; Ho, H.-P. A linear concentration gradient generator based on multi-layered centrifugal microfluidics and its application in antimicrobial susceptibility testing. Lab Chip 2018, 18, 1452–1460. [Google Scholar] [CrossRef] [PubMed]
- Ezra Tsur, E.; Zimerman, M.; Maor, I.; Elrich, A.; Nahmias, Y. Microfluidic concentric gradient generator design for high-throughput cell-based studies. Front. Bioeng. Biotech. 2017, 5, 21. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Liu, Z.; Pang, Y. Concentration gradient generation methods based on microfluidic systems. RSC Adv. 2017, 7, 29966–29984. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Wu, D.; Mei, X.; Zhou, Z.; Wang, L.; Zhao, Y.; Zheng, G.; Sun, D. 3D Printing Stereo Networks Microfluidic Concentration Gradient Chip. In Proceedings of the 2016 IEEE 10th International Conference on Nano/Molecular Medicine and Engineering (NANOMED), Macau, China, 30 October–2 November 2016; pp. 104–108. [Google Scholar]
- Irimia, D.; Geba, D.A.; Toner, M. Universal microfluidic gradient generator. Anal. Chem. 2006, 78, 3472–3477. [Google Scholar] [CrossRef] [Green Version]
- Li, C.-W.; Chen, R.; Yang, M. Generation of linear and non-linear concentration gradients along microfluidic channel by microtunnel controlled stepwise addition of sample solution. Lab Chip 2007, 7, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Meiners, J.-C. Topologic mixing on a microfluidic chip. Appl. Phys. Lett. 2004, 84, 2193–2195. [Google Scholar] [CrossRef]
- Zaidon, N.; Mansor, A.F.M.; Mak, W.C.; Ismail, A.F.; Nordin, A.N. Microfluidic Concentration Gradient for Toxicity Studies of Lung Carcinoma Cells. Procedia Technol. 2017, 27, 153–154. [Google Scholar] [CrossRef]
- Liu, Y. Microfluidic gradient device for simultaneously preparing four distinct types of microparticles. RSC Adv. 2019, 9, 17623–17630. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Roh, H.; Park, J.K. Finger-actuated microfluidic concentration gradient generator compatible with a microplate. Micromachines 2019, 10, 174. [Google Scholar] [CrossRef] [Green Version]
- Ebadi, M.; Moshksayan, K.; Kashaninejad, N.; Saidi, M.S.; Nguyen, N.T. A tool for designing tree-like concentration gradient generators for lab-on-a-chip applications. Chem. Eng. Sci. 2020, 212, 115339. [Google Scholar] [CrossRef]
- Cabaleiro, J.M. Flowrate independent 3D printed microfluidic concentration gradient generator. Chem. Eng. J. 2020, 382, 122742. [Google Scholar] [CrossRef]




| Type | C1 | C2 | C3 | C4 | C5 | Remarks |
|---|---|---|---|---|---|---|
| Type IV | buffer | dye | dye | buffer | Q1 = Q3, Q2 = Q4 | |
| buffer | dye | dye | buffer | Q1 = Q4, Q2 = Q3 | ||
| buffer | dye | buffer | dye | Q1 = Q3, Q2 = Q4 | ||
| buffer | dye | buffer | dye | Q1 = Q4, Q2 = Q3 | ||
| Type V | buffer | buffer | buffer | dye | dye | Q1,2 = Q3, Q4,5 |
| buffer | buffer | buffer | dye | dye | Q1,2 = Q4,5, Q3 | |
| buffer | buffer | dye | buffer | buffer | Q1,2 = Q3, Q4,5 | |
| buffer | buffer | dye | buffer | buffer | Q1,2 = Q4,5, Q3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Meng, J.; Li, S.; Yu, C.; Li, J.; Wei, C.; Dai, S. A Microfluidic Concentration Gradient Maker with Tunable Concentration Profiles by Changing Feed Flow Rate Ratios. Micromachines 2020, 11, 284. https://doi.org/10.3390/mi11030284
Zhang T, Meng J, Li S, Yu C, Li J, Wei C, Dai S. A Microfluidic Concentration Gradient Maker with Tunable Concentration Profiles by Changing Feed Flow Rate Ratios. Micromachines. 2020; 11(3):284. https://doi.org/10.3390/mi11030284
Chicago/Turabian StyleZhang, Tao, Jiyu Meng, Shanshan Li, Chengzhuang Yu, Junwei Li, Chunyang Wei, and Shijie Dai. 2020. "A Microfluidic Concentration Gradient Maker with Tunable Concentration Profiles by Changing Feed Flow Rate Ratios" Micromachines 11, no. 3: 284. https://doi.org/10.3390/mi11030284
APA StyleZhang, T., Meng, J., Li, S., Yu, C., Li, J., Wei, C., & Dai, S. (2020). A Microfluidic Concentration Gradient Maker with Tunable Concentration Profiles by Changing Feed Flow Rate Ratios. Micromachines, 11(3), 284. https://doi.org/10.3390/mi11030284





