Research on Asymmetric Hysteresis Modeling and Compensation of Piezoelectric Actuators with PMPI Model
Abstract
:1. Introduction
2. Polynomial-Modified Prandtl–Ishlinskii Model
2.1. Prandtl–Ishlinskii Model
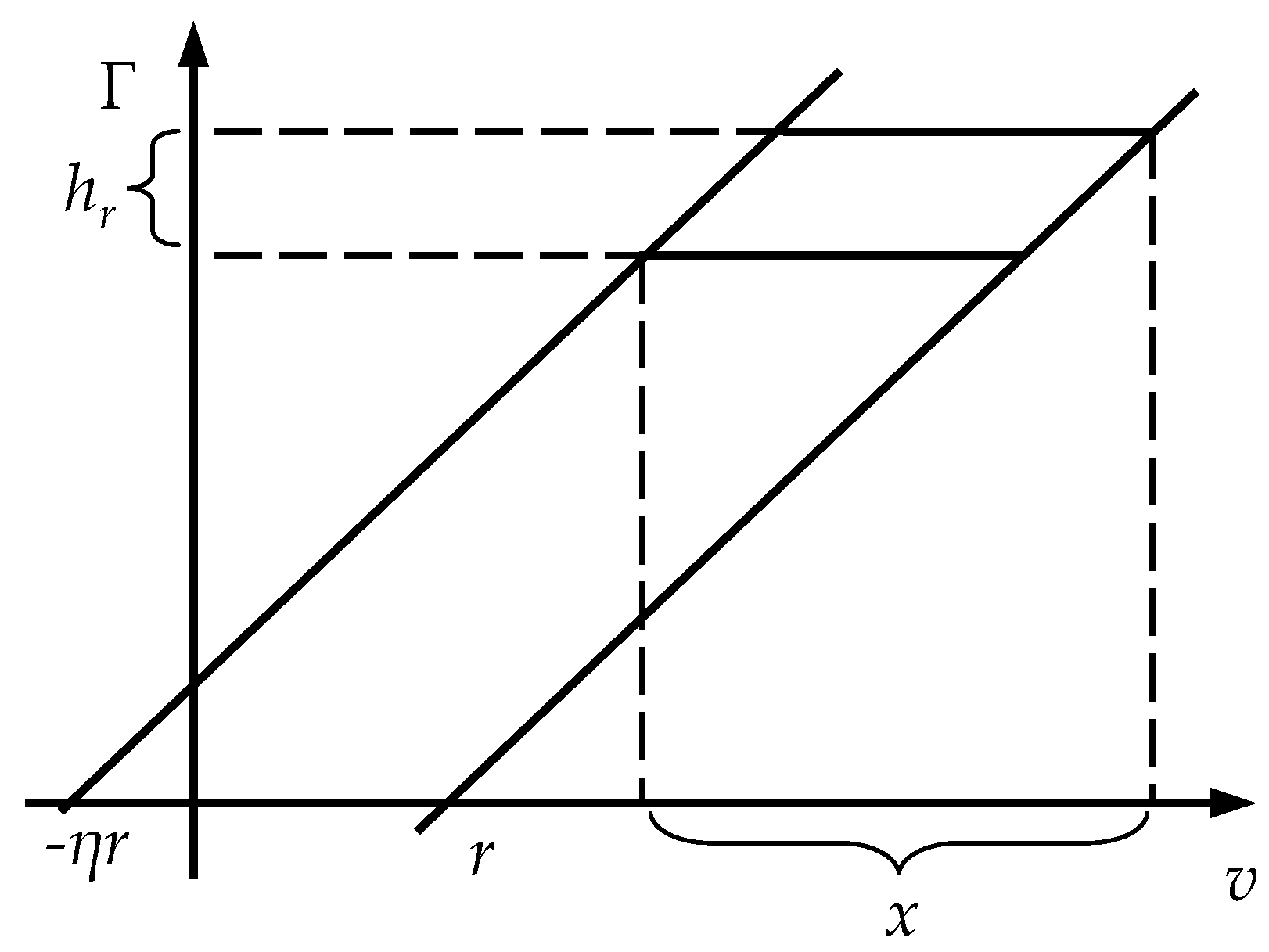
2.2. Polynomial-Modified Prandtl–Ishlinskii Model
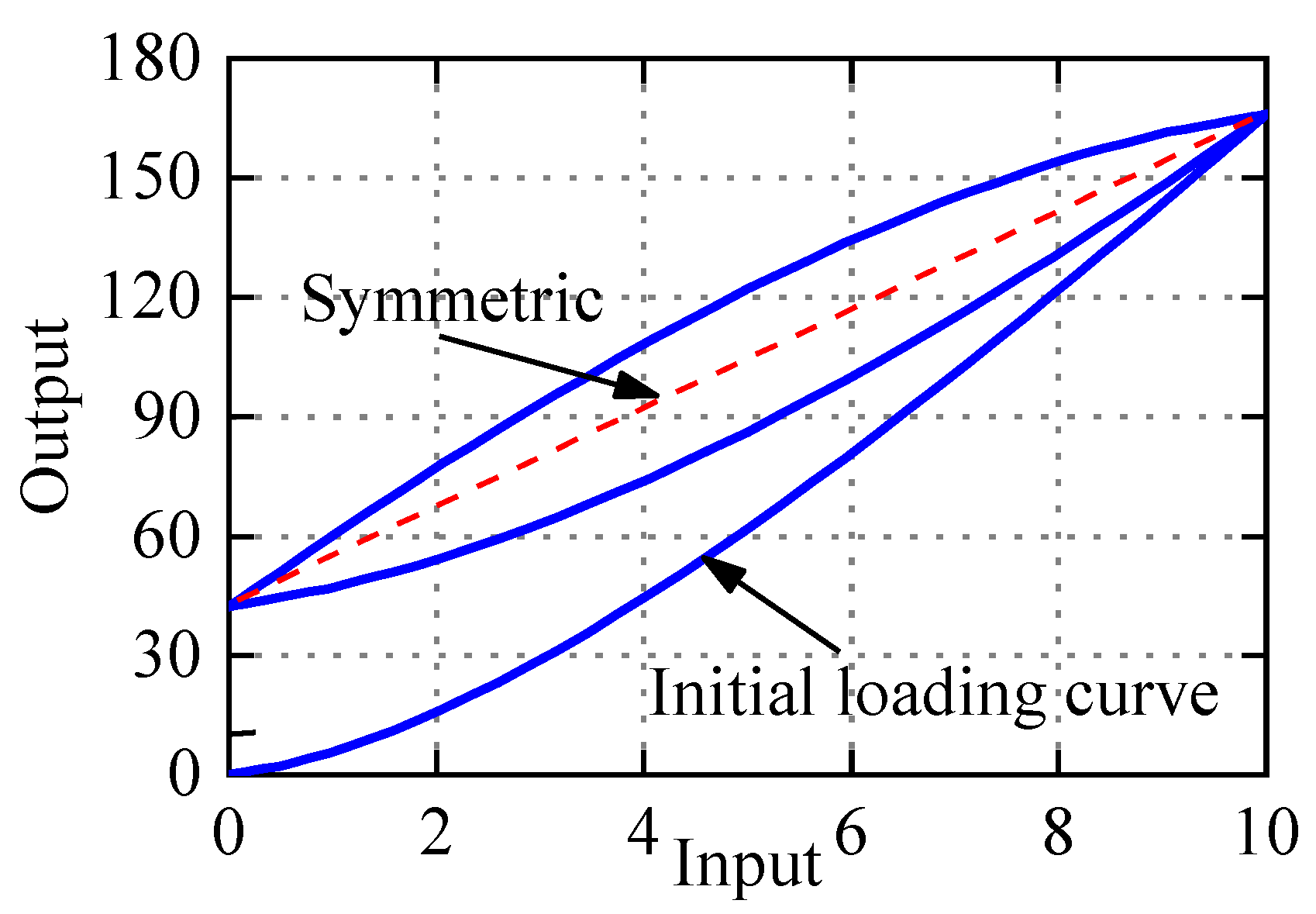
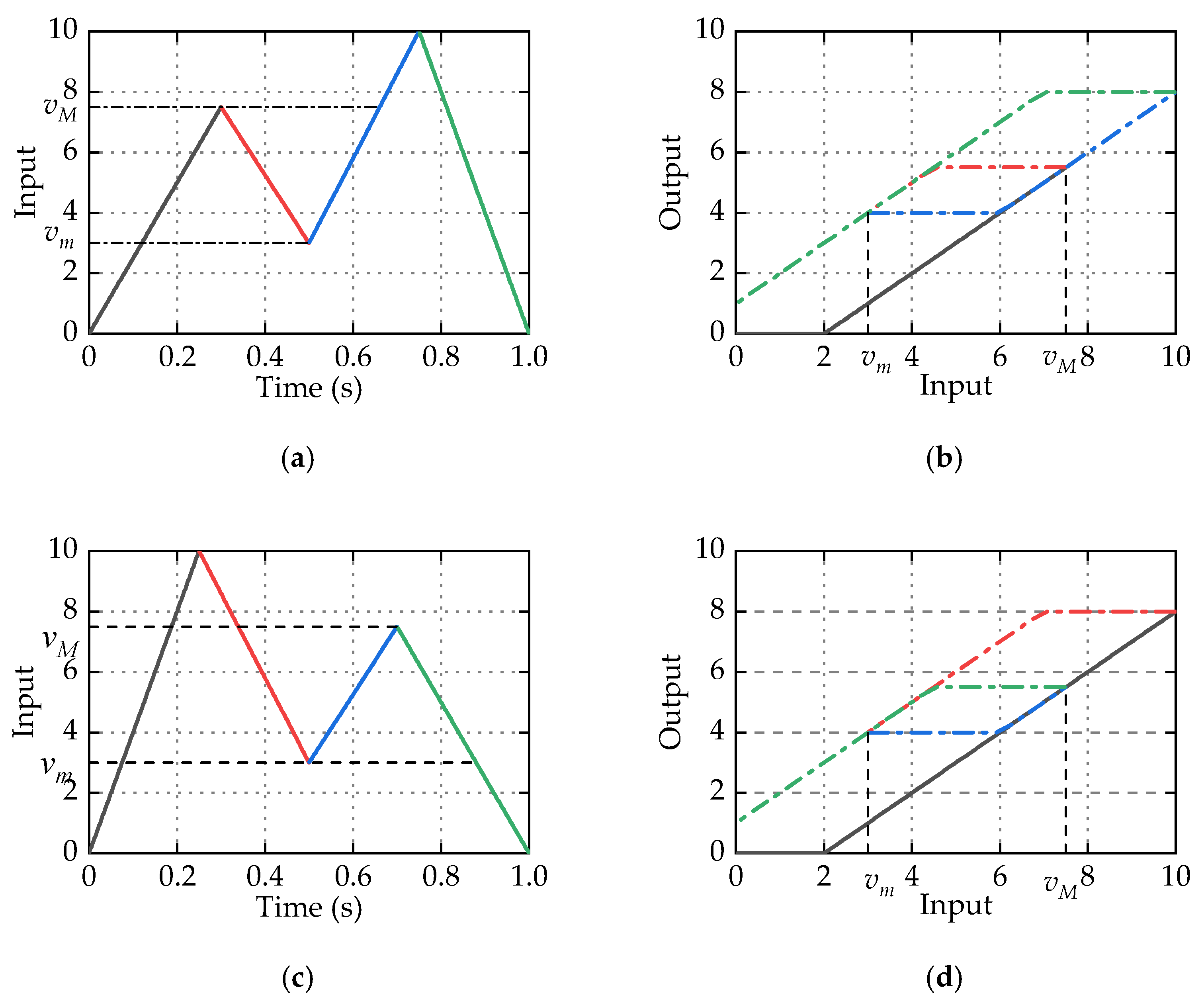
2.3. Congruency Property
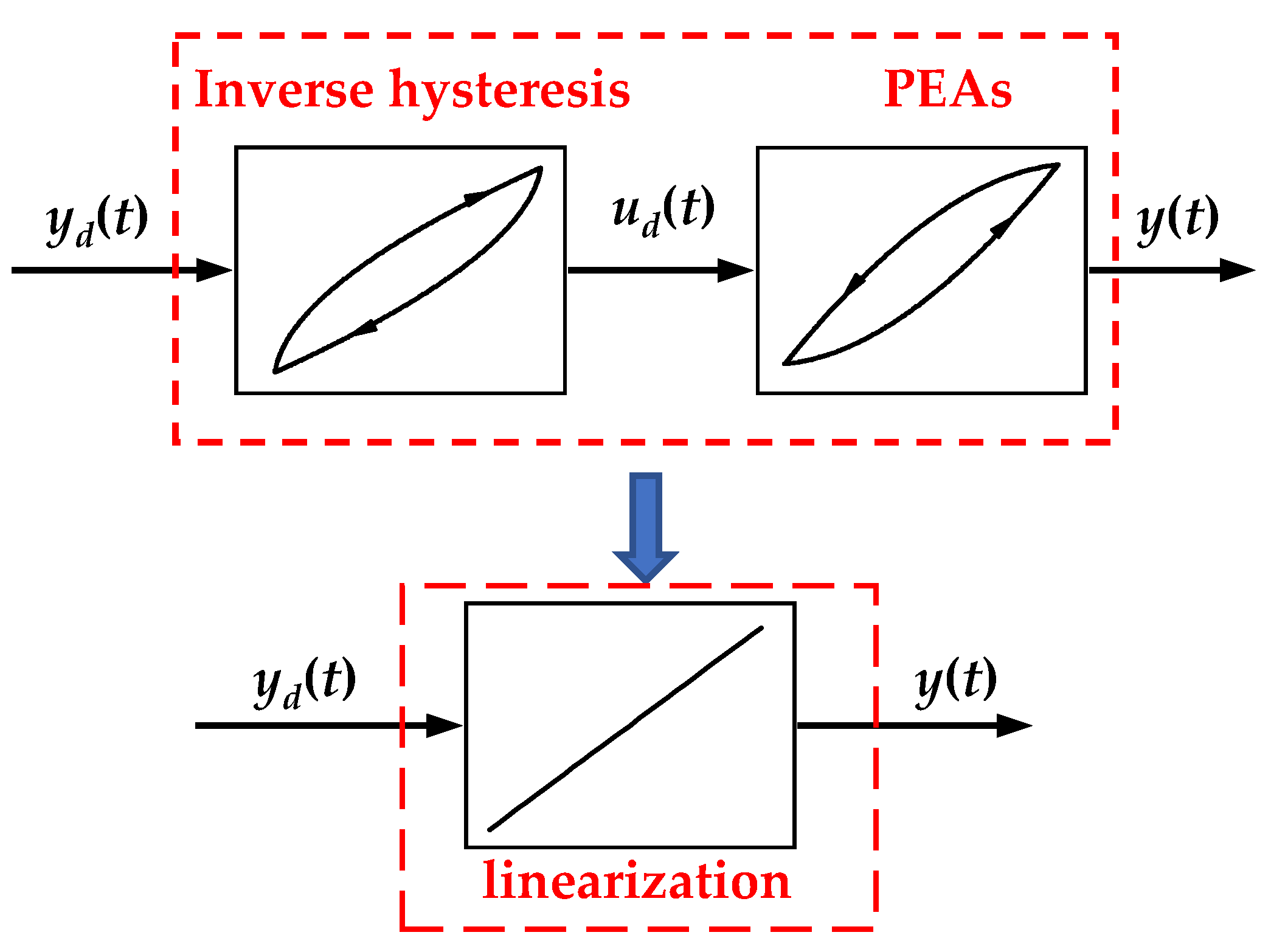
3. The Design and Analysis of the Inverse Model Compensator
3.1. Inverse model Compensator Design
3.2. Stability Analysis
4. Experimental Verification and Discussion
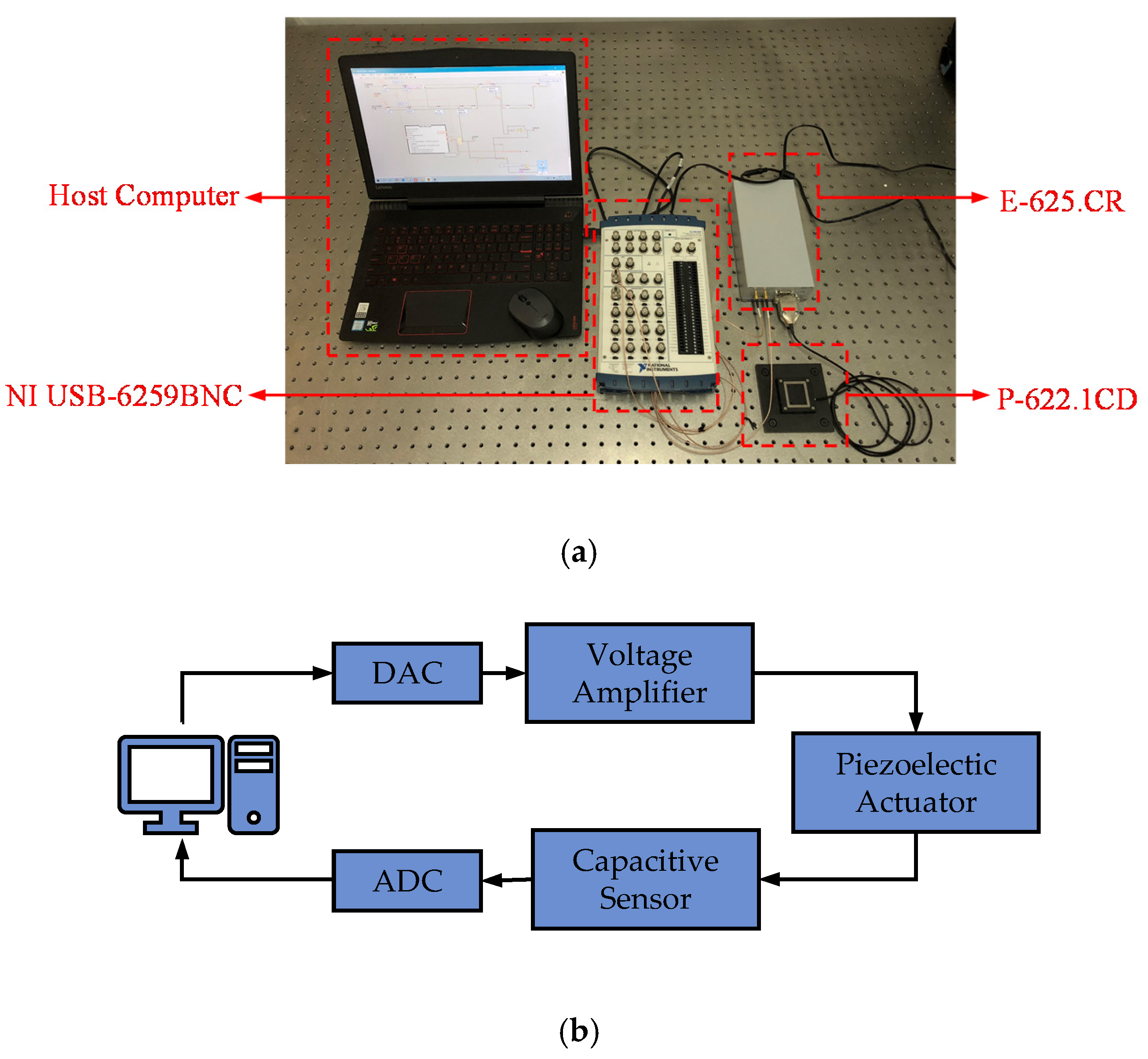
4.1. Experimental Setup
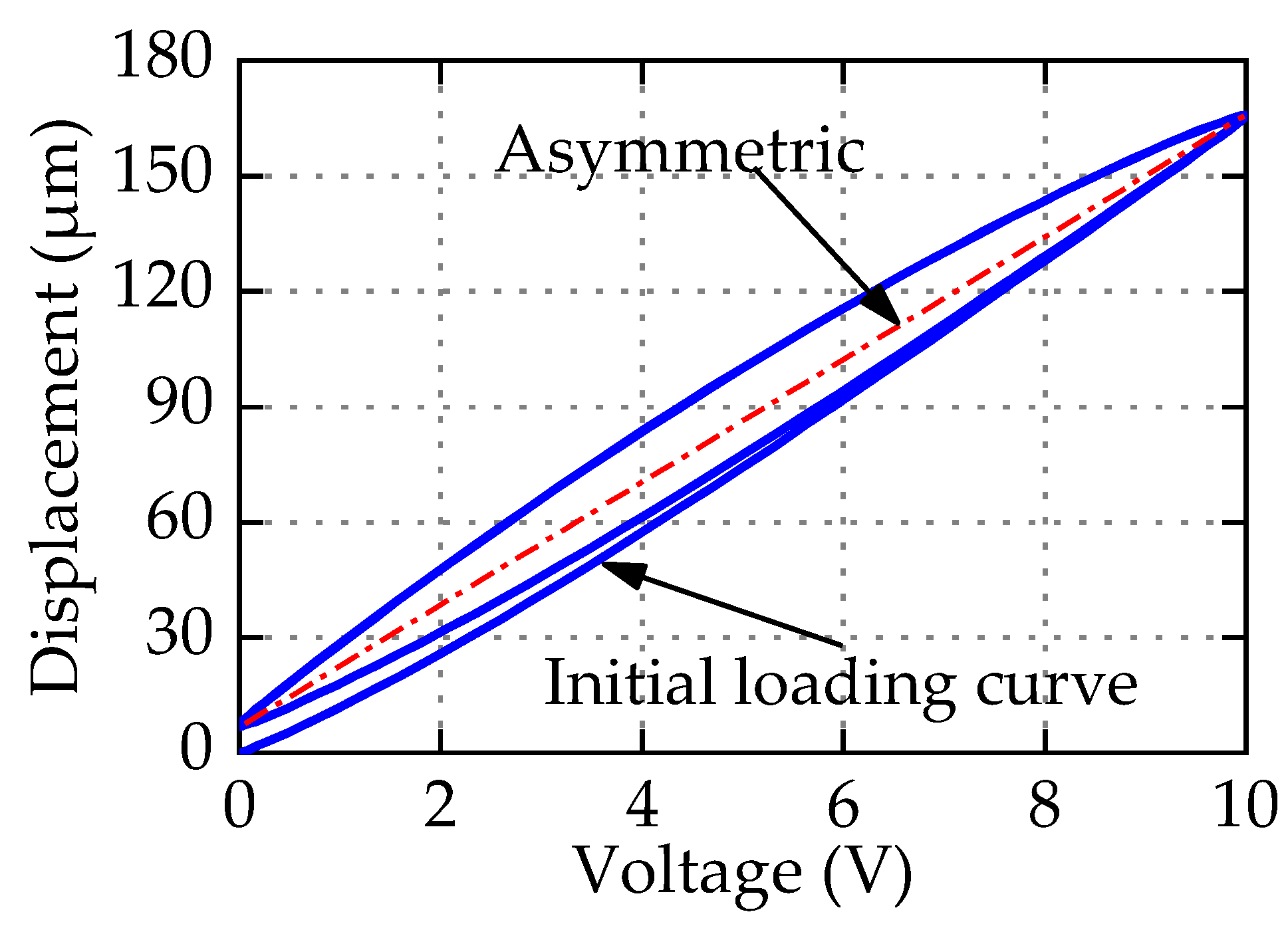
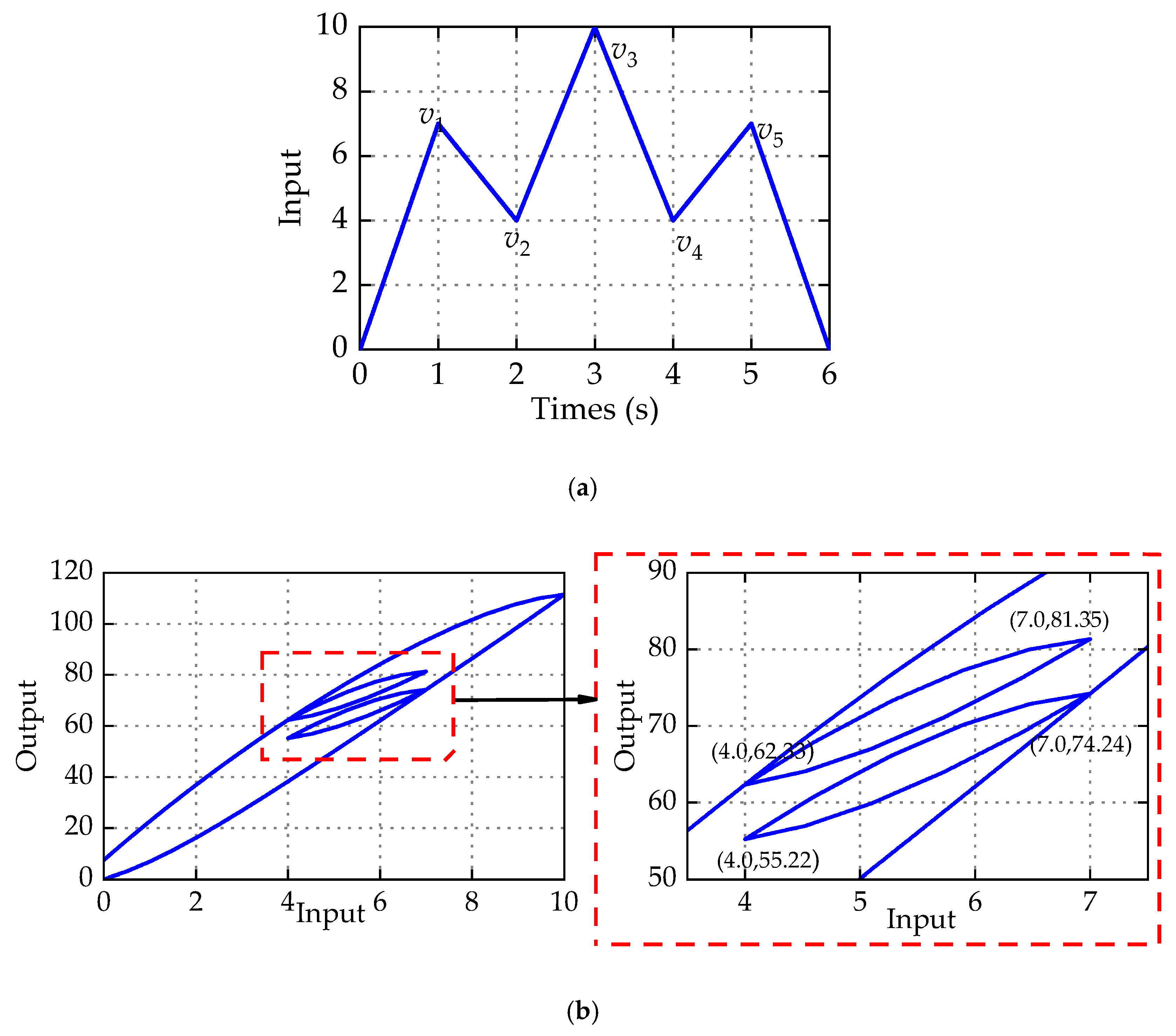
4.2. Asymmetric Hysteresis Description Results and Discussion
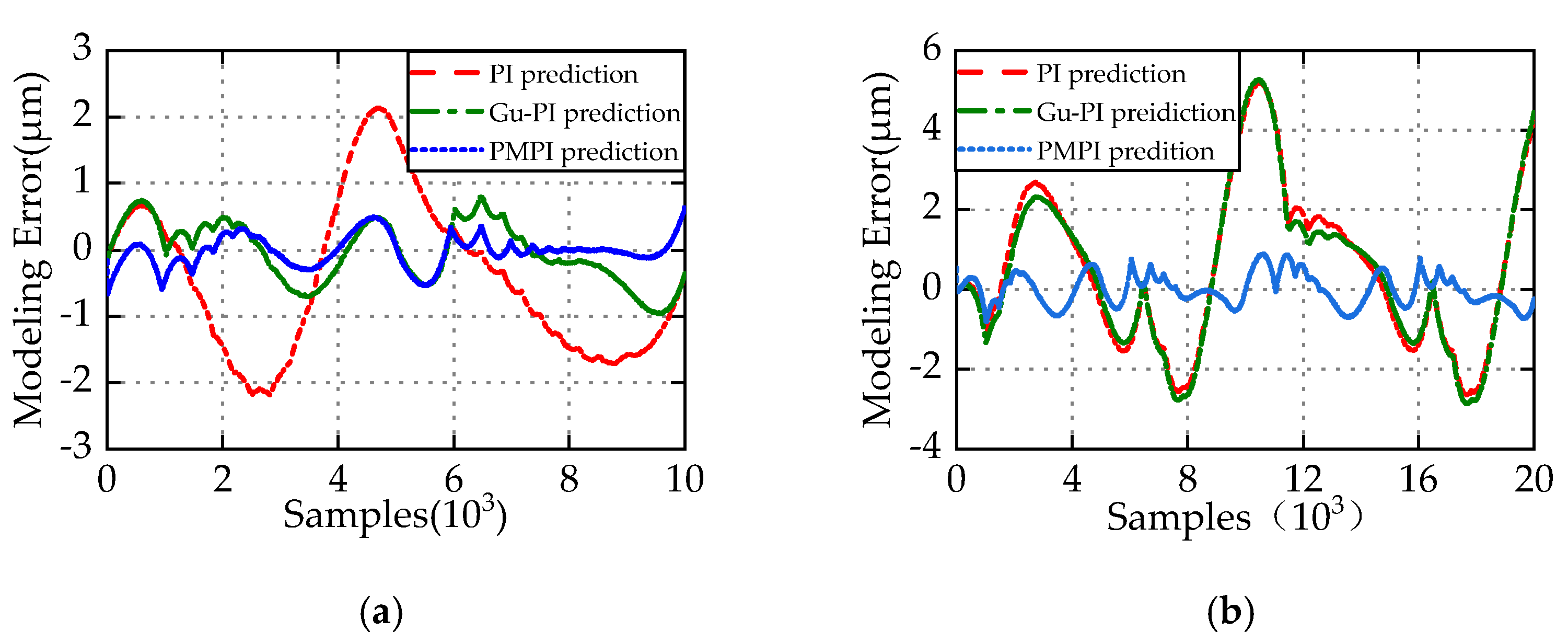
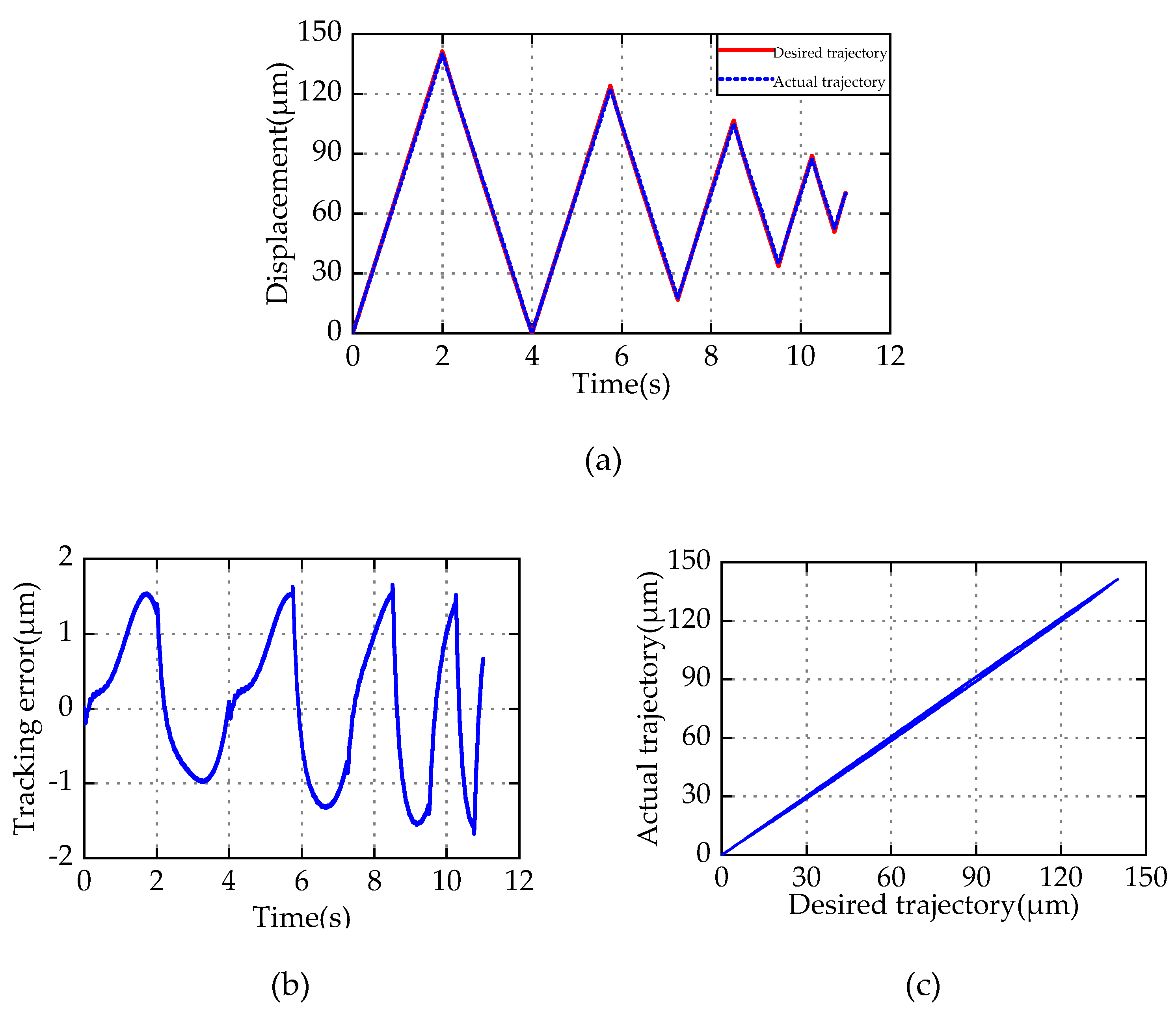
4.3. Hysteresis Compensation Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Devasia, S.; Eleftheriou, E.; Moheimani, S.O.R. A survey of control issues in nanopositioning. IEEE Trans. Control Syst. Technol. 2007, 15, 802–823. [Google Scholar] [CrossRef]
- Lu, H.J.; Shang, W.F.; Xi, H.; Shen, Y.J. Ultrahigh-Precision Rotational Positioning Under a Microscope: Nanorobotic System, Modeling, Control, and Applications. IEEE Trans. Robot. 2018, 34, 497–507. [Google Scholar] [CrossRef]
- Tanaka, Y. A Peristaltic Pump Integrated on a 100% Glass Microchip Using Computer Controlled Piezoelectric Actuators. Micromachines 2014, 5, 289–299. [Google Scholar] [CrossRef]
- Zainal, M.A.; Sahlan, S.; Mohamed Ali, M.S. Micromachined Shape-Memory-Alloy Microactuators and Their Application in Biomedical Devices. Micromachines 2015, 6, 879–901. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhang, X.Y.; Su, C.Y.; Chai, T.Y. Nonlinear Control of Systems Preceded by Preisach Hysteresis Description: A Prescribed Adaptive Control Approach. IEEE Trans. Control Syst. Technol. 2016, 24, 451–460. [Google Scholar] [CrossRef]
- Xu, Q.S.; Li, Y.M. Micro-/Nanopositioning Using Model Predictive Output Integral Discrete Sliding Mode Control. IEEE Trans. Ind. Electron. 2012, 59, 1161–1170. [Google Scholar] [CrossRef]
- Mehrabi, R.; Kadkhodaei, M. 3D phenomenological constitutive modeling of shape memory alloys based on microplane theory. Smart Mater. Struct. 2013, 22, 025017. [Google Scholar] [CrossRef]
- Hussain, S.; Lowther, D.A. Prediction of Iron Losses Using Jiles–Atherton Model With Interpolated Parameters Under the Conditions of Frequency and Compressive Stress. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Raghunathan, A.; Melikhov, Y.; Snyder, J.E.; Jiles, D.C. Modeling the Temperature Dependence of Hysteresis Based on Jiles-Atherton Theory. IEEE Trans. Magn. 2009, 45, 3954–3957. [Google Scholar] [CrossRef]
- Antonio, P.P.D.; de Campos, M.F.; Dias, F.M.D.; Campos, M.A.; Capo-Sanchez, J.; Padovese, L.R. Sharp Increase of Hysteresis Area Due to Small Plastic Deformation Studied With Magnetic Barkhausen Noise. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Tousignant, M.; Sirois, F.; Kedous-Lebouc, A. Identification of the Preisach Model parameters using only the major hysteresis loop and the initial magnetization curve. In Proceedings of the 2016 IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 13–16 November 2016; p. 1. [Google Scholar]
- Bi, S.S.; Wolf, F.; Lerch, R.; Sutor, A. An Inverted Preisach Model With Analytical Weight Function and Its Numerical Discrete Formulation. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Bashash, S.; Jalili, N. A polynomial-based linear mapping strategy for feedforward compensation of hysteresis in piezoelectric actuators. J. Dyn. Syst. Meas. Control 2008, 130, 031008. [Google Scholar] [CrossRef]
- Ru, C.; Sun, L. Improving positioning accuracy of piezoelectric actuators by feedforward hysteresis compensation based on a new mathematical model. Rev. Sci. Instrum. 2005, 76, 095111. [Google Scholar] [CrossRef]
- Qin, H.; Bu, N.; Chen, W.; Yin, Z. An Asymmetric Hysteresis Model and Parameter Identification Method for Piezoelectric Actuator. Math. Probl. Eng. 2014, 2014, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ding, B.X.; Li, Y.M. Hysteresis Compensation and Sliding Mode Control with Perturbation Estimation for Piezoelectric Actuators. Micromachines 2018, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Chen, G.Q. Identification of piezoelectric hysteresis by a novel Duhem model based neural network. Sens. Actuator A-Phys. 2017, 264, 282–288. [Google Scholar] [CrossRef]
- Lin, C.J.; Lin, P.T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef] [Green Version]
- Tai, N.T.; Ahn, K.K. A hysteresis functional link artificial neural network for identification and model predictive control of SMA actuator. J. Process Control 2012, 22, 766–777. [Google Scholar] [CrossRef]
- Nikdel, N.; Nikdel, P.; Badamchizadeh, M.A.; Hassanzadeh, I. Using Neural Network Model Predictive Control for Controlling Shape Memory Alloy-Based Manipulator. IEEE Trans. Ind. Electron. 2014, 61, 1394–1401. [Google Scholar] [CrossRef]
- Qin, Y.D.; Zhao, X.; Zhou, L. Modeling and Identification of the Rate-Dependent Hysteresis of Piezoelectric Actuator Using a Modified Prandtl-Ishlinskii Model. Micromachines 2017, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Song, B.; Xi, N.; Yang, R.; Hao, L.; Chen, L. Compensating asymmetric hysteresis for nanorobot motion control. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3501–3506. [Google Scholar]
- Li, Z.; Su, C.Y.; Chen, X. Modeling and inverse adaptive control of asymmetric hysteresis systems with applications to magnetostrictive actuator. Control Eng. Pract. 2014, 33, 148–160. [Google Scholar] [CrossRef]
- Kuhnen, K. Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Approach. Eur. J. Control 2003, 9, 407–418. [Google Scholar] [CrossRef]
- Janaideh, M.A.; Aljanaideh, O.; Rakheja, S. A Generalized Play Operator for Modeling and Compensation of Hysteresis Nonlinearities. In Proceedings of Intelligent Robotics and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 104–113. [Google Scholar]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y. Modeling and Compensation of Asymmetric Hysteresis Nonlinearity for Piezoceramic Actuators With a Modified Prandtl–Ishlinskii Model. IEEE Trans. Ind. Electron. 2014, 61, 1583–1595. [Google Scholar] [CrossRef]
- Sprekels, J.; Brokate, M. Hysteresis and Phase Transitions; Springer: Berlin/Heidelberg, Germany, 1996; Volume 121. [Google Scholar]
- Chan, C.-H.; Liu, G. Hysteresis identification and compensation using a genetic algorithm with adaptive search space. Mechatronics 2007, 17, 391–402. [Google Scholar] [CrossRef]
- Yang, M.; Gu, G.; Zhu, L.-M. Parameter Identification of the Generalized Prandtl-Ishlinskii Model for Piezoelectric Actuators Using Modified Particle Swarm Optimization. Sens. Actuators A Phys. 2012, 189. [Google Scholar] [CrossRef]
- Liu, L.; Tan, K.K.; Teo, C.S.; Chen, S.; Lee, T.H. Development of an Approach Toward Comprehensive Identification of Hysteretic Dynamics in Piezoelectric Actuators. IEEE Trans. Control Syst. Technol. 2013, 21, 1834–1845. [Google Scholar] [CrossRef]
- Lin, H. Hybridizing Differential Evolution and Nelder-Mead Simplex Algorithm for Global Optimization. In Proceedings of the 2016 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 198–202. [Google Scholar]






| Number of Operators n | Identification Error (μm) | Run Time (ms) |
|---|---|---|
| 5 | 1.503 | 48.93 |
| 10 | 0.884 | 53.30 |
| 20 | 0.831 | 69.49 |
| 30 | 0.848 | 87.50 |
| Model | MAE (μm) | MRE (%) | MAD (μm) | RMSE (μm) |
|---|---|---|---|---|
| PI | 2.186 | 1.37 | 1.058 | 1.243 |
| Gu-PI | 0.968 | 0.61 | 0.397 | 0.463 |
| PMPI | 0.698 | 0.44 | 0.172 | 0.232 |
| Model | MAE (μm) | MRE (%) | MAD (μm) | RMSE (μm) |
|---|---|---|---|---|
| PI | 5.193 | 3.14 | 1.654 | 2.049 |
| Gu-PI | 5.280 | 3.19 | 1.627 | 2.038 |
| PMPI | 0.905 | 0.55 | 0.334 | 0.397 |
| i | ri | αi | ηi | ai |
|---|---|---|---|---|
| 1 | 0 | 6.904 | 0.849 | 0.037 |
| 2 | 1 | 0.517 | 0.043 | −0.647 |
| 3 | 2 | - | 0.276 | 0 |
| 4 | 3 | 0.376 | - | |
| 5 | 4 | 0.336 | ||
| 6 | 5 | 0.443 | ||
| 7 | 6 | 0.561 | ||
| 8 | 7 | 0.335 | ||
| 9 | 8 | 0.158 | ||
| 10 | 9 | 0.040 | ||
| p0 | 4.770 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, J.; Chen, Z.; Wang, R.; Lu, K.; Sang, Z.; Ju, B. Research on Asymmetric Hysteresis Modeling and Compensation of Piezoelectric Actuators with PMPI Model. Micromachines 2020, 11, 357. https://doi.org/10.3390/mi11040357
Wang W, Wang J, Chen Z, Wang R, Lu K, Sang Z, Ju B. Research on Asymmetric Hysteresis Modeling and Compensation of Piezoelectric Actuators with PMPI Model. Micromachines. 2020; 11(4):357. https://doi.org/10.3390/mi11040357
Chicago/Turabian StyleWang, Wen, Jian Wang, Zhanfeng Chen, Ruijin Wang, Keqing Lu, Zhiqian Sang, and Bingfeng Ju. 2020. "Research on Asymmetric Hysteresis Modeling and Compensation of Piezoelectric Actuators with PMPI Model" Micromachines 11, no. 4: 357. https://doi.org/10.3390/mi11040357





