Correlated Time-0 and Hot-Carrier Stress Induced FinFET Parameter Variabilities: Modeling Approach
Abstract
:1. Introduction
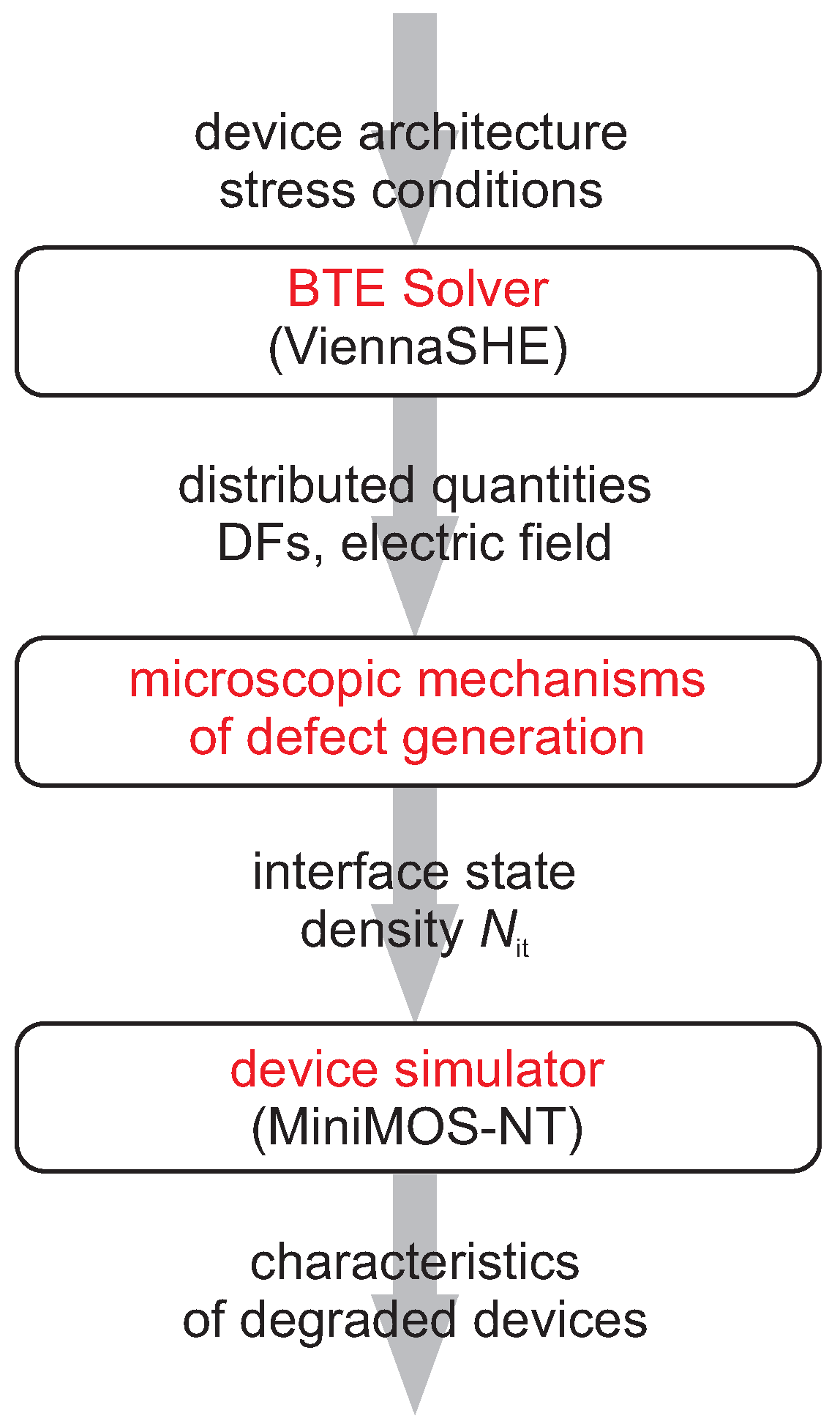
2. The Modeling Framework
2.1. Carrier Transport Modeling
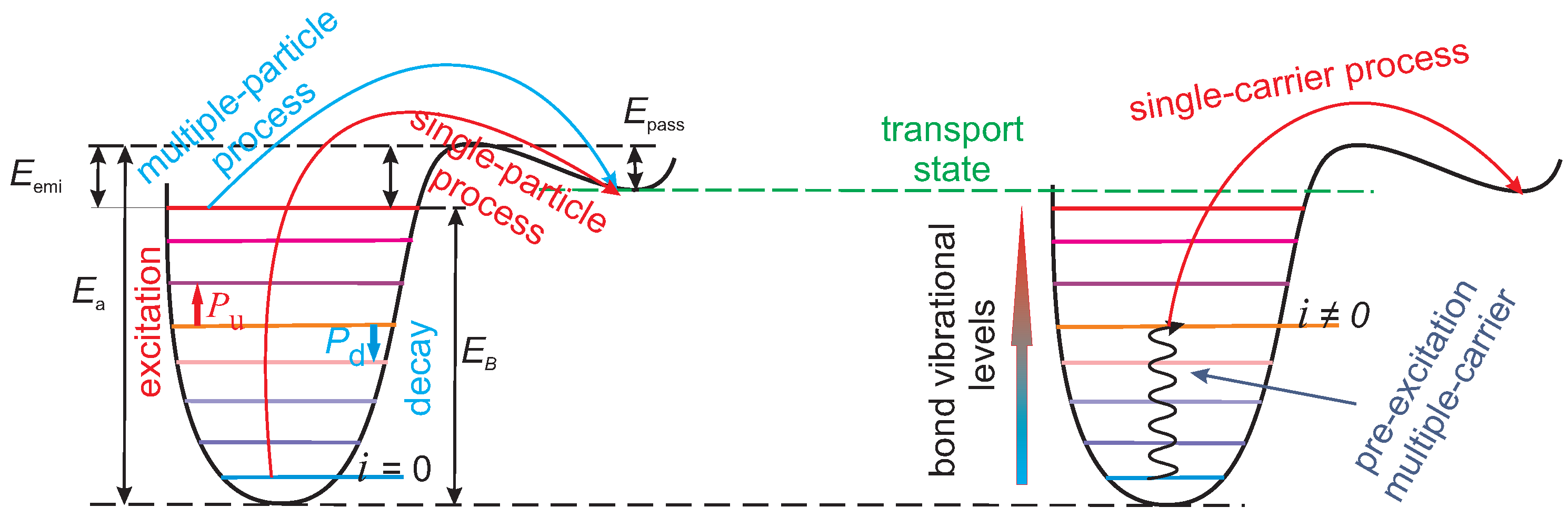
2.2. Defect Generation
2.3. Modeling of the Degraded Devices
2.4. Calibration of the Deterministic Model for HCD
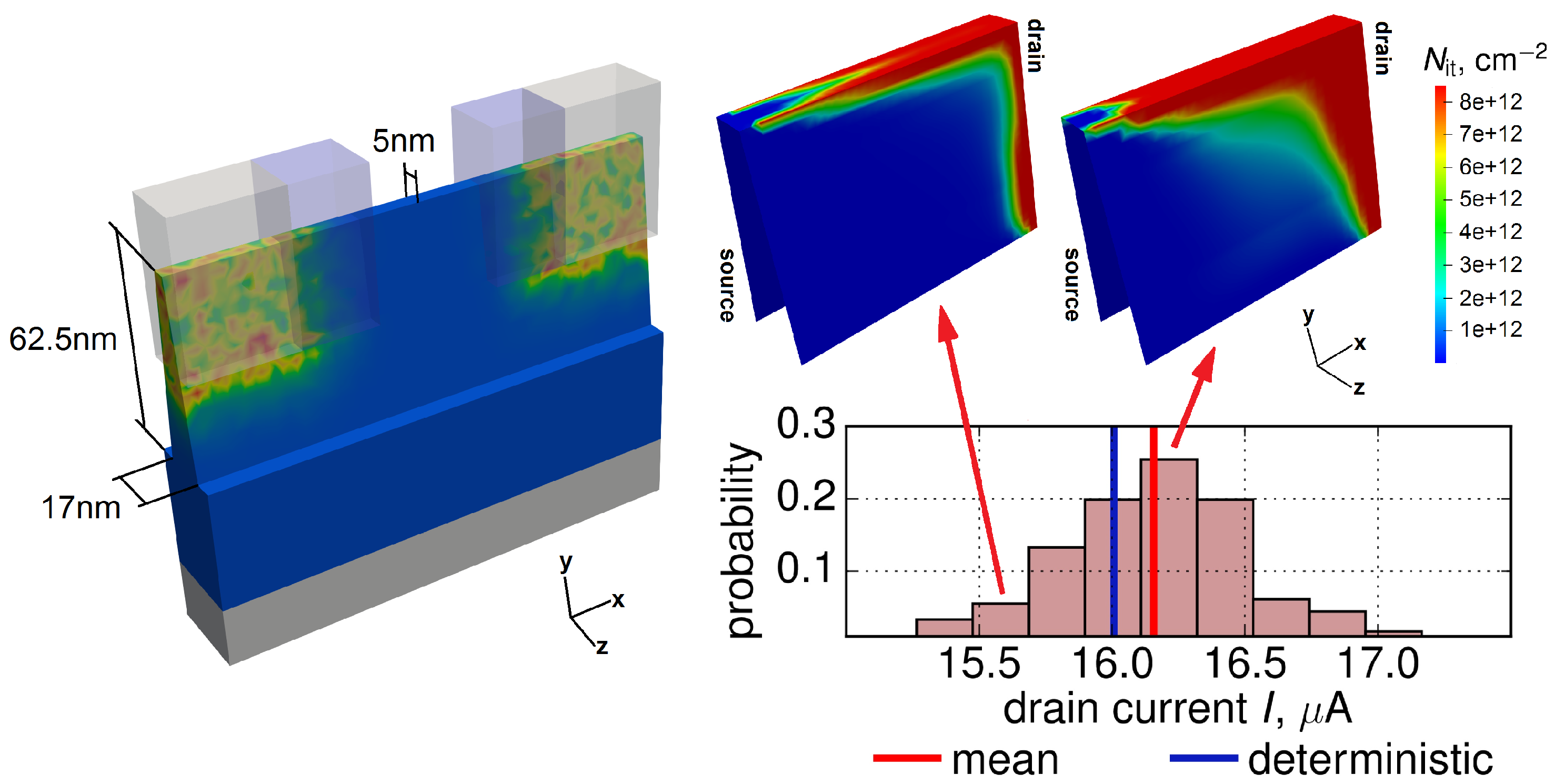
2.5. The Stochastic Model for HCD
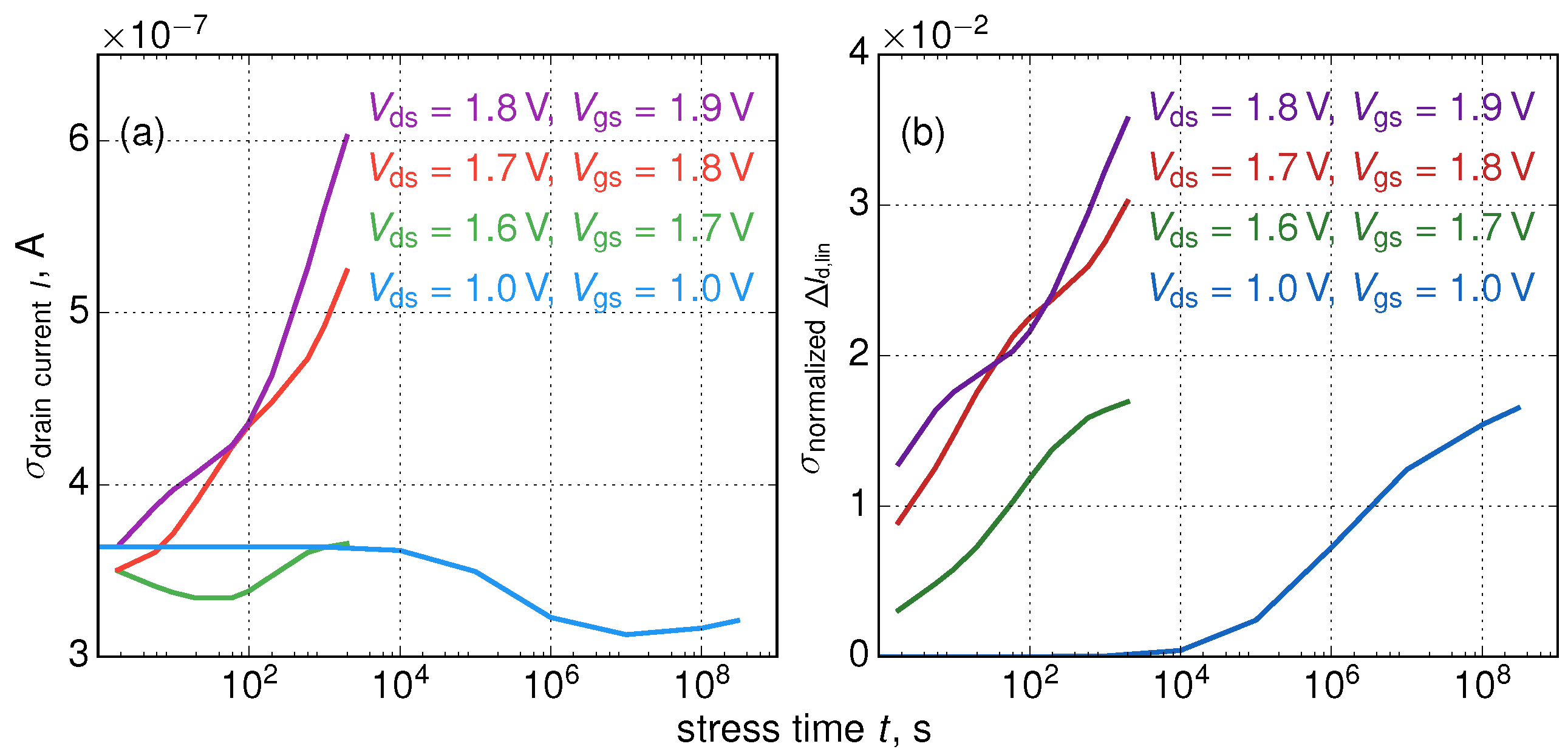
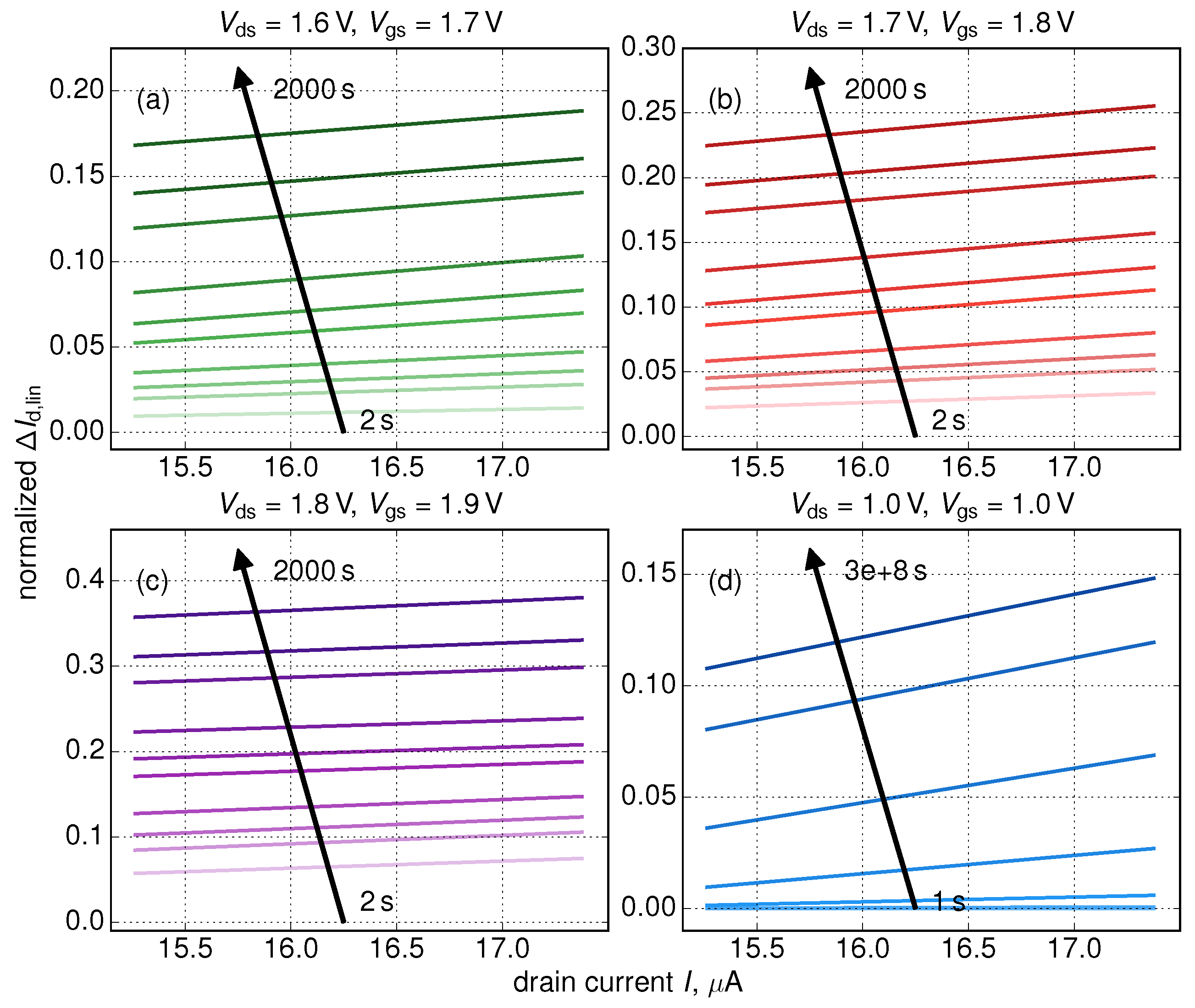
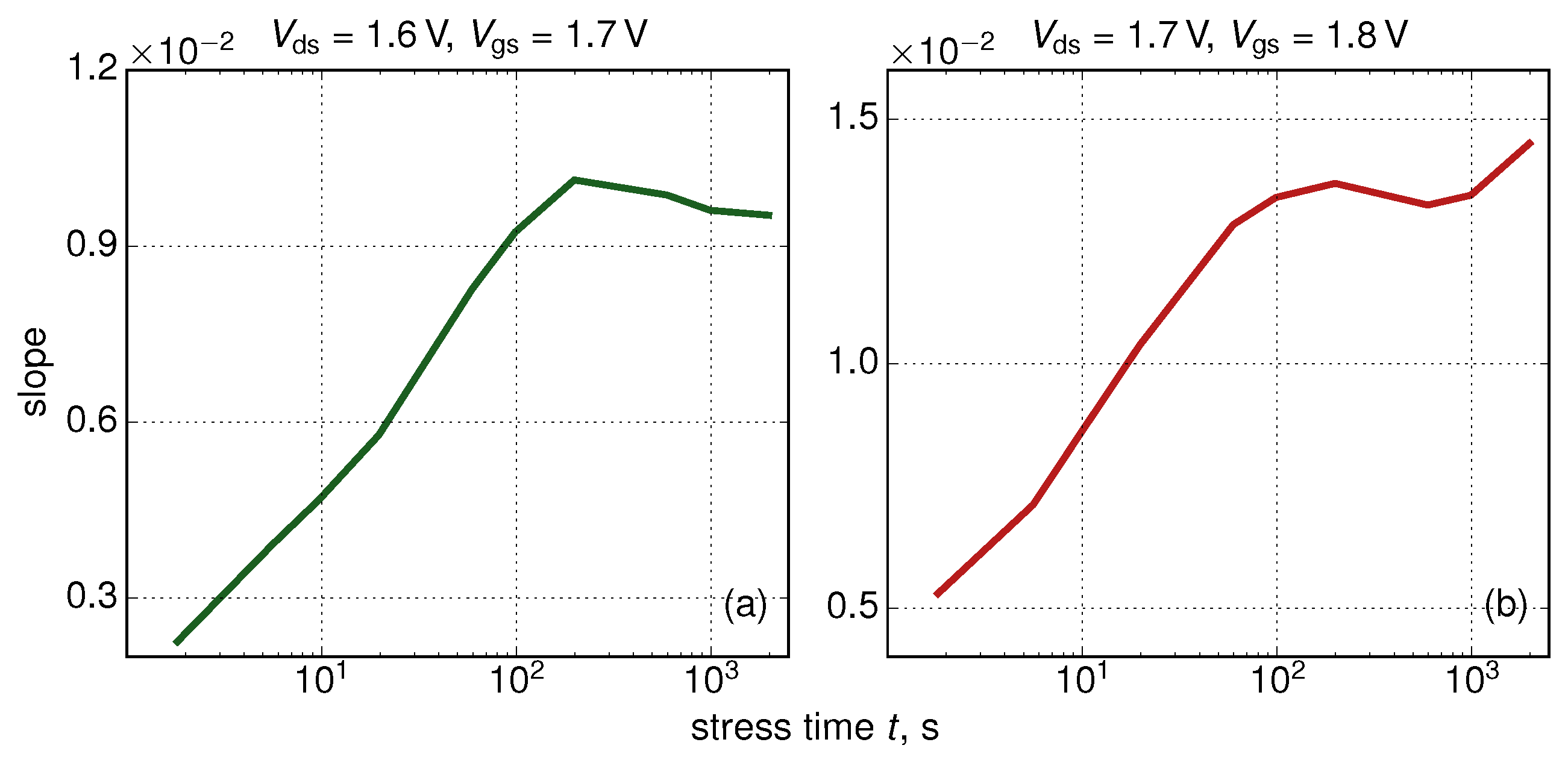
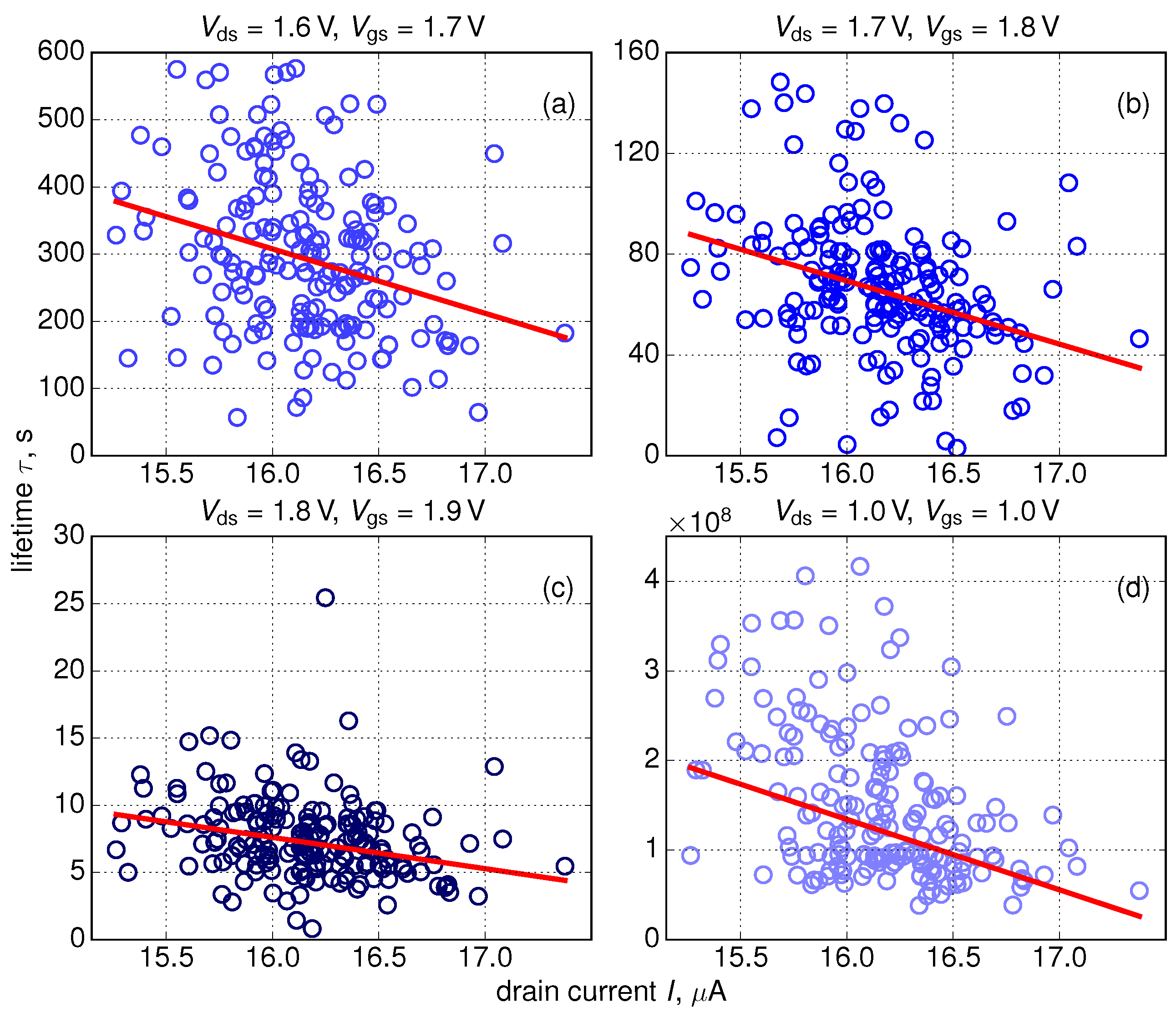
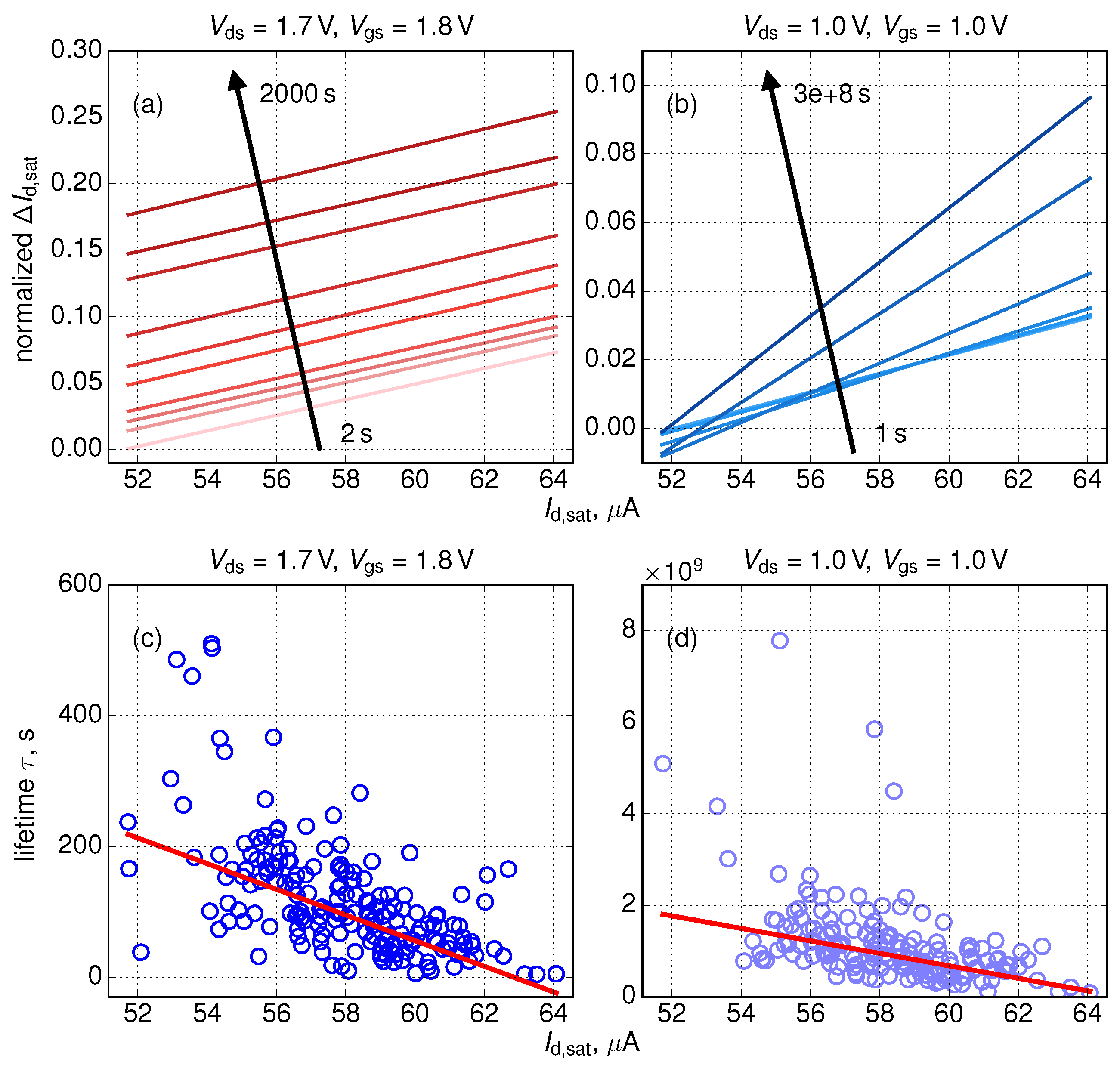
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BTE | Boltzmann transport equation |
| DFs | distribution functions |
| FET | field-effect transistor |
| HCD | hot-carrier degradation |
| MC | multiple-carrier (machanism of bond rupture) |
| RDs | random dopants |
| RTs | random traps |
| SC | single-carrier (mechanism of bond rupture) |
References
- Asenov, A. Random Dopant Induced Threshold Voltage Lowering and Fluctuations in sub-0.1 μm MOSFET’s: A 3-D Atomistic Simulation Study. IEEE Trans. Electron Devices 1998, 45, 2505–2513. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.R.; Watling, J.R.; Asenov, A.; Bersuker, G.; Zeitzoff, P. Intrinsic Parameter Fluctuations in MOSFETs due to Structural Non-uniformity of High-κ Gate Stack Materials. In Proceedings of the 2005 International Conference On Simulation of Semiconductor Processes and Devices, Tokyo, Japan, 1–3 September 2005; pp. 27–30. [Google Scholar] [CrossRef]
- Brown, A.R.; Watling, J.R.; Asenov, A. Intrinsic Parameter Fluctuations due to Random Grain Orientations in High-κ Gate Stacks. J. Comput. Electron. 2006, 5, 333–336. [Google Scholar] [CrossRef]
- Asenov, A.; Kaya, S.; Davies, J.H. Intrinsic Threshold Voltage fluctuations in Decanano MOSFETs due to Local Oxide Thickness Variations. IEEE Trans. Electron Devices 2002, 49, 112–119. [Google Scholar] [CrossRef] [Green Version]
- Tyaginov, S.; Vexler, M.; Shulekin, A.; Grekhov, I. Statistical Analysis of Tunnel Currents in Scaled MOS Structures with a Non-uniform Oxide Thickness Distribution. Solid State Electron. 2005, 49, 1192–1197. [Google Scholar] [CrossRef]
- Kaczer, B.; Franco, J.; Weckx, P.; Roussel, P.; Simicic, M.; Putcha, V.; Bury, E.; Cho, M.; Degraeve, R.; Linten, D.; et al. The Defect-Centric Perspective of Device and Circuit Reliability—From Gate Oxide Defects to Circuits. Solid-State Electron. 2016, 125, 52–62. [Google Scholar] [CrossRef]
- Kerber, A.; Nigam, T. Correlation of BTI induced device parameter degradation and variation in scaled Metal Gate/High-k CMOS technologies. In Proceedings of the 2014 IEEE International Reliability Physics Symposium, Waikoloa, HI, USA, 1–5 June 2014; pp. 6A.6.1–6A.6.6. [Google Scholar] [CrossRef]
- Kerber, A.; Srinivasan, P. Impact of Stress Mode on Stochastic BTI in Scaled MG/HK CMOS Devices. IEEE Electron Device Lett. 2014, 35, 431–433. [Google Scholar] [CrossRef]
- Angot, D.; Huard, V.; Rahhal, L.; Cros, A.; Federspiel, X.; Bajolet, A.; Carminati, Y.; Saliva, M.; Pion, E.; Cacho, F.; et al. BTI Variability Fundamental Understandings and Impact on Digital Logic by the Use of Extensive Dataset. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 15.4.1–15.4.4. [Google Scholar] [CrossRef]
- Hussin, R.; Amoroso, S.M.; Gerrer, L.; Kaczer, B.; Weckx, P.; Franco, J.; Vanderheyden, A.; Vanhaeren, D.; Horiguchi, N.; Asenov, A. Interplay Between Statistical Variability and Reliability in Contemporary pMOSFETs: Measurements Versus Simulations. IEEE Trans. Electron Devices 2014, 61, 3265–3273. [Google Scholar] [CrossRef]
- Wang, L.; Brown, A.R.; Nedjalkov, M.; Alexander, C.; Cheng, B.; Millar, C.; Asenov, A. Impact of Self-Heating on the Statistical Variability in Bulk and SOI FinFETs. IEEE Trans. Electron Devices 2015, 62, 2106–2112. [Google Scholar] [CrossRef] [Green Version]
- Gerrer, L.; Hussin, R.; Amoroso, S.M.; Franco, J.; Weckx, P.; Simicic, M.; Horiguchi, N.; Kaczer, B.; Grasser, T.; Asenov, A. Experimental Evidences and Simulations of Trap Generation along a Percolation Path. In Proceedings of the 2015 45th European Solid State Device Research Conference (ESSDERC), Graz, Austria, 14–18 September 2015; pp. 226–229. [Google Scholar] [CrossRef]
- Novak, S.; Parker, C.; Becher, D.; Liu, M.; Agostinelli, M.; Chahal, M.; Packan, P.; Nayak, P.; Ramey, S.; Natarajan, S. Transistor Aging and Reliability in 14nm Tri-gate Technology. In Proceedings of the 2015 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015; pp. 2F.2.1–2F.2.5. [Google Scholar] [CrossRef]
- Rahman, A.; Dacuna, J.; Nayak, P.; Leatherman, G.; Ramey, S. Reliability Studies of a 10nm High-performance and Low-power CMOS Technology Featuring 3rd Generation FinFET and 5th Generation HK/MG. In Proceedings of the 2018 IEEE International Reliability Physics Symposium (IRPS), Burlingame, CA, USA, 11–15 March 2018; pp. 6F.4-1–6F.4-6. [Google Scholar] [CrossRef]
- Tu, C.H.; Chen, S.Y.; Chuang, A.E.; Huang, H.S.; Jhou, Z.W.; Chang, C.J.; Chou, S.; Ko, J. Transistor Variability after CHC and NBTI Stress in 90 nm pMOSFET Technology. Electron. Lett. 2009, 45, 854–856. [Google Scholar] [CrossRef]
- Hsieh, E.R.; Chung, S.S.; Tsai, C.H.; Huang, R.M.; Tsai, C.T.; Liang, C.W. New Observations on the Physical Mechanism of Vth-variation in Nanoscale CMOS Devices after Long Term Stress. In Proceedings of the 2011 International Reliability Physics Symposium, Monterey, CA, USA, 10–14 April 2011; pp. XT.9.1–XT.9.2. [Google Scholar] [CrossRef]
- Magnone, P.; Crupi, F.; Wils, N.; Tuinhout, H.P.; Fiegna, C. Characterization and Modeling of Hot Carrier-Induced Variability in Subthreshold Region. IEEE Trans. Electron Devices 2012, 59, 2093–2099. [Google Scholar] [CrossRef]
- Chung, S.S. The Process and Stress-induced Variability Issues of Trigate CMOS Devices. In Proceedings of the 2013 IEEE International Conference of Electron Devices and Solid-state Circuits, Hong Kong, China, 3–5 June 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Kaczer, B.; Franco, J.; Cho, M.; Grasser, T.; Roussel, P.J.; Tyaginov, S.; Bina, M.; Wimmer, Y.; Procel, L.M.; Trojman, L.; et al. Origins and Implications of Increased Channel hot Carrier Variability in nFinFETs. In Proceedings of the 2015 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015; pp. 3B.5.1–3B.5.6. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Lee, K.T.; Pae, S.; Park, J. New Observations on Hot Carrier Induced Dynamic Variation in Nano-scaled SiON/poly, HK/MG and FinFET Devices Based on On-the-fly HCI Technique: The Role of Single Trap Induced Degradation. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 34.6.1–34.6.4. [Google Scholar] [CrossRef]
- Huard, V.; Cacho, F.; Federspiel, X.; Arfaoui, W.; Saliva, M.; Angot, D. Technology scaling and reliability: Challenges and opportunities. In Proceedings of the 2015 IEEE International Electron Devices Meeting, Washington, DC, USA, 7–9 December 2015; pp. 20.5.1–20.5.6. [Google Scholar] [CrossRef]
- Bottini, R.; Ghetti, A.; Vigano, S.; Valentini, M.G.; Murali, P.; Mouli, C. Non-Poissonian Behavior of Hot Carrier Degradation Induced Variability in MOSFETs. In Proceedings of the 2018 IEEE International Reliability Physics Symposium, Burlingame, CA, USA, 11–15 March 2018; pp. 6E.7-1–6E.7-6. [Google Scholar] [CrossRef]
- Makarov, A.; Kaczer, B.; Roussel, P.; Chasin, A.; Grill, A.; Vandemaele, M.; Hellings, G.; El-Sayed, E.M.; Grasser, T.; Linten, D.; et al. Modeling the Effect of Random Dopants on Hot-Carrier Degradation in FinFETs. In Proceedings of the 2019 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 31 March–4 April 2019; pp. 6C.3.1–6C.3.6. [Google Scholar] [CrossRef]
- Makarov, A.; Kaczer, B.; Roussel, P.; Chasin, A.; Vandemaele, M.; Hellings, G.; El-Sayed, A.; Jech, M.; Grasser, T.; Linten, D.; et al. Stochastic Modeling of Hot-Carrier Degradation in nFinFETs Considering the Impact of Random Traps and Random Dopants. In Proceedings of the ESSDERC 2019 - 49th European Solid-State Device Research Conference (ESSDERC), Cracow, Poland, 23–26 September 2019; pp. 262–265. [Google Scholar] [CrossRef]
- Makarov, A.; Kaczer, B.; Roussel, P.; Chasin, A.; Grill, A.; Vandemaele, M.; Hellings, G.; El-Sayed, A.; Grasser, T.; Linten, D.; et al. Stochastic Modeling of the Impact of Random Dopants on Hot-Carrier Degradation in n-FinFETs. IEEE Electron Device Lett. 2019, 40, 870–873. [Google Scholar] [CrossRef]
- Makarov, A.; Kaczer, B.; Chasin, A.; Vandemaele, M.; Bury, E.; Jech, M.; Grill, A.; Hellings, G.; El-Sayed, A.; Grasser, T.; et al. Bi-Modal Variability of nFinFET Characteristics During Hot-Carrier Stress: A Modeling Approach. IEEE Electron Device Lett. 2019, 40, 1579–1582. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Z.; Sun, Z.; Wang, R.; Huang, R. On the Trap Locations in Bulk FinFETs After Hot Carrier Degradation (HCD). IEEE Trans. Electron Devices 2020, 67, 3005–3009. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, Z.; Wang, R.; Zhang, J.; Huang, R. Hot Carrier Degradation-Induced Dynamic Variability in FinFETs: Experiments and Modeling. IEEE Trans. Electron Devices 2020, 67, 1517–1522. [Google Scholar] [CrossRef]
- Schlünder, C.; Berthold, J.; Proebster, F.; Martin, A.; Gustin, W.; Reisinger, H. On the Influence of BTI and HCI on Parameter Variability. In Proceedings of the 2017 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 2–6 April 2017; pp. 2E-4.1–2E-4.8. [Google Scholar] [CrossRef]
- Ramey, S.; Chahal, M.; Nayak, P.; Novak, S.; Prasad, C.; Hicks, J. Transistor Reliability Variation Correlation to Threshold Voltage. In Proceedings of the 2015 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 19–23 April 2015; pp. 3B.2.1–3B.2.6. [Google Scholar] [CrossRef]
- Federspiel, X.; Diouf, C.; Cacho, F.; Vincent, E. Comparison of Variability of HCI Induced Drift for SiON and HKMG Devices. In Proceedings of the International Reliability Physics Symposium, Dallas, TX, USA, 28 April–30 May 2020; pp. 5A.5.1–5A.5.5. [Google Scholar]
- Tyaginov, S.; Bina, M.; Franco, J.; Wimmer, Y.; Osintsev, D.; Kaczer, B.; Grasser, T. A Predictive Physical Model for Hot-Carrier Degradation in Ultra-Scaled MOSFETs. In Proceedings of the Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, Japan, 9–11 September 2014; pp. 89–92. [Google Scholar] [CrossRef]
- Tyaginov, S.; Jech, M.; Franco, J.; Sharma, P.; Kaczer, B.; Grasser, T. Understanding and Modeling the Temperature Behavior of Hot-Carrier Degradation in SiON nMOSFETs. IEEE Electron Device Lett. 2016, 37, 84–87. [Google Scholar] [CrossRef]
- Sharma, P.; Tyaginov, S.; Wimmer, Y.; Rudolf, F.; Rupp, K.; Bina, M.; Enichlmair, H.; Park, J.M.; Minixhofer, R.; Ceric, H.; et al. Modeling of Hot-Carrier Degradation in nLDMOS Devices: Different Approaches to the Solution of the Boltzmann Transport Equation. IEEE Trans. Electron Devices 2015, 62, 1811–1818. [Google Scholar] [CrossRef]
- Sharma, P.; Tyaginov, S.; Jech, M.; Wimmer, Y.; Rudolf, F.; Enichlmair, H.; Park, J.M.; Ceric, H.; Grasser, T. The role of cold carriers and the multiple-carrier process of Si–H bond dissociation for hot-carrier degradation in n- and p-channel LDMOS devices. Solid-State Electron. 2016, 115 Pt B, 185–191. [Google Scholar] [CrossRef]
- Makarov, A.; Tyaginov, S.E.; Kaczer, B.; Jech, M.; Chasin, A.; Grill, A.; Hellings, G.; Vexler, M.I.; Linten, D.; Grasser, T. Hot-Carrier Degradation in FinFETs: Modeling, Peculiarities, and Impact of Device Topology. In Proceedings of the 2017 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 2–6 December 2017; pp. 13.1.1–13.1.4. [Google Scholar] [CrossRef]
- Vandemaele, M.; Kaczer, B.; Tyaginov, S.; Stanojević, Z.; Makarov, A.; Chasin, A.; Bury, E.; Mertens, H.; Linten, D.; Groeseneken, G. Full (Vg,Vd) Bias Space Modeling of Hot-Carrier Degradation in Nanowire FETs. In Proceedings of the 2019 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 31 March–4 April 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Rupp, K.; Grasser, T.; Jüngel, A. On the Feasibility of Spherical Harmonics Expansions of the Boltzmann Transport Equation for Three-Dimensional Device Geometries. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 34.1.1–34.1.4. [Google Scholar] [CrossRef]
- Rupp, K.; Grasser, T.; Jüngel, A. Adaptive variable-order spherical harmonics expansion of the Boltzmann Transport Equation. In Proceedings of the 2011 International Conference on Simulation of Semiconductor Processes and Devices, Osaka, Japan, 8–10 September 2011; pp. 151–154. [Google Scholar] [CrossRef]
- Bina, M.; Rupp, K.; Tyaginov, S.; Triebl, O.; Grasser, T. Modeling of Hot Carrier Degradation Using a Spherical Harmonics Expansion of the Bipolar Boltzmann Transport Equation. In Proceedings of the International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012; pp. 713–716. [Google Scholar] [CrossRef]
- ViennaSHE. 2014. Available online: http://viennashe.sourceforge.net/ (accessed on 1 June 2020).
- Tyaginov, S.; Makarov, A.; Jech, M.; Franco, J.; Sharma, P.; Kaczer, B.; Grasser, T. On the Effect of Interface Traps on the Carrier Distribution Function During Hot-Carrier Degradation. In Proceedings of the 2015 IEEE International Integrated Reliability Workshop Final Report, South Lake Tahoe, CA, USA, 9–13 October 2016; pp. 95–98. [Google Scholar] [CrossRef]
- Tyaginov, S.; Starkov, I.; Triebl, O.; Cervenka, J.; Jungemann, C.; Carniello, S.; Park, J.; Enichlmail, H.; Kernstock, C.; Seebacher, E.; et al. Interface Traps Density-of-states as a Vital Component for Hot-carrier Degradation Modeling. Microelectron. Reliab. 2010, 50, 1267–1272. [Google Scholar] [CrossRef]
- Starkov, I.; Tyaginov, S.; Enichlmair, H.; Cervenka, J.; Jungemann, C.; Carniello, S.; Park, J.; Ceric, H.; Grasser, T. Hot-Carrier degradation caused interface state profile - simulations vs. experiment. J. Vac. Sci. Technol. B 2011, 29, 01AB09-1–01AB09-8. [Google Scholar] [CrossRef]
- Jungemann, C.; Meinerzhagen, B. Hierarchical Device Simulation; Springer: Berlin, Germany, 2003. [Google Scholar]
- Brower, K. Dissociation Kinetics of Hydrogen-Passivated (111)Si-Si02 Interface Defects. Phy. Rev. B 1990, 42, 3444–3454. [Google Scholar] [CrossRef]
- Stesmans, A. Dissociation kinetics of hydrogen-passivated Pb defects at the (111)Si/SiO2 interface. Phys. Rev. B 2000, 61, 8393–8403. [Google Scholar] [CrossRef]
- Jech, M.; El-Sayed, A.M.; Tyaginov, S.; Shluger, A.L.; Grasser, T. Ab initio treatment of silicon-hydrogen bond rupture at Si/SiO2 interfaces. Phys. Rev. B 2019, 100, 195302. [Google Scholar] [CrossRef]
- Rauch, S.; Rosa, G.L. CMOS Hot Carrier: From Physics to End Of Life Projections, and Qualification. In Proceedings of the International Reliability Physics Symposium, tutorial, 23–25 April 2010. [Google Scholar]
- Bravaix, A.; Huard, V. Hot-Carrier Degradation Issues in Advanced CMOS Nodes. In Proceedings of the European Symposium on Reliability of Electron Devices Failure Physics and Analysis (ESREF), Gaeta, Italy, 11–15 October 2010; pp. 1267–1272. [Google Scholar]
- Tyaginov, S.; Starkov, I.; Enichlmair, H.; Park, J.; Jungemann, C.; Grasser, T. Physics-Based Hot-Carrier Degradation Models (invited). ECS Transact. 2011, 35, 321–352. [Google Scholar] [CrossRef] [Green Version]
- McMahon, W.; Matsuda, K.; Lee, J.; Hess, K.; Lyding, J. The Effects of a Multiple Carrier Model of Interface States Generation of Lifetime Extraction for MOSFETs. In Proceedings of the International Conference on Modeling and Simulation of Microsystem, San Juan, Puerto Rico, 21–25 April 2002; Volume 1, pp. 576–579. [Google Scholar]
- McMahon, W.; Hess, K. A Multi-Carrier Model for Interface Trap Generation. J. Comput. Electron. 2002, 1, 395–398. [Google Scholar] [CrossRef]
- Bravaix, A.; Goguenheim, D.; Revil, N.; Vincent, E.; Varrot, M.; Mortini, P. Analysis of High Temperatures Effects on Performance and Hot-Carrier Degradation in DC/AC Stressed 0.35 μm n-MOSFETs. Microel. Reliab. 1999, 39, 35–44. [Google Scholar] [CrossRef]
- Guerin, C.; Huard, V.; Bravaix, A. General Framework about Defect Creation at the Si/SiO2 Interface. J. Appl. Phy. 2009, 105, 114513-1–114513-12. [Google Scholar] [CrossRef]
- Randriamihaja, Y.; Federspiel, X.; Huard, V.; Bravaix, A.; Palestri, P. New Hot Carrier Degradation Modeling Reconsidering the Role of EES in Ultra Short n-channel MOSFETs. In Proceedings of the International Reliability Physics Symposium, Anaheim, CA, USA, 14–18 April 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Bina, M.; Tyaginov, S.; Franco, J.; Rupp, K.; Wimmer, Y.; Osinstev, D.; Kaczer, B.; Grasser, T. Predictive Hot-Carrier Modeling of n-channel MOSFETs. IEEE Trans. Electron Devices 2014, 61, 3103–3110. [Google Scholar] [CrossRef]
- Tyaginov, S.; Bina, M.; Franco, J.; Osintsev, D.; Triebl, O.; Kaczer, B.; Grasser, T. Physical Modeling of Hot-Carrier Degradation for Short- and Long-Channel MOSFETs. In Proceedings of the International Reliability Physics Symposium, Waikoloa, HI, USA, 1–5 June 2014; pp. 16-1–16-8. [Google Scholar]
- Andrianov, I.; Saalfrank, P. Theoretical Study of Vibration-Phonon Coupling of H Adsorbed on a Si(100) Surface. J. Chem. Phys. 2006, 124, 1–10. [Google Scholar] [CrossRef]
- Stesmans, A. Revision of H2 Passivation of Pb Interface Defects in Standard (111)Si/SiO2. Appl. Phys. Lett. 1996, 68, 2723–2725. [Google Scholar] [CrossRef]
- Stesmans, A. Passivation of Pb0 and Pb1 Interface Defects in Thermal (100) Si/SiO2 with Molecular Hydrogen. Appl. Phys. Lett. 1996, 68, 2076–2078. [Google Scholar] [CrossRef]
- Pobegen, G.; Tyaginov, S.; Nelhiebel, M.; Grasser, T. Observation of Normally Distributed Activation Energies for the Recovery from Hot Carrier Damage. IEEE Electron Dev. Lett. 2013, 34, 939–941. [Google Scholar] [CrossRef]
- Stockinger, T.B.; Dragosits, K.; Grasser, T.; Klima, R.; Knaipp, M.; Kosina, H.; Mlekus, R.; Palankovski, V.; Rottinger, M.; Schrom, G.; et al. MINIMOS-NT User’s Guide; Institut für Mikroelektronik: Stuttgart, Germany, 1998. [Google Scholar]
- Wong, H.S.; White, M.; Krutsick, J.; Booth, R. Modeling of transconductance degradation and extraction of threshold voltage in thin oxide MOSFET’s. Solid State Electron. 1987, 30, 953–958. [Google Scholar] [CrossRef]
- Prakash, A.G.; Ke, S.; Siddappa, K. High-energy radiation effects on subthreshold characteristics, transconductance and mobility of n-channel MOSFETs. Semicond. Sci. Technol. 2003, 18, 1037–1042. [Google Scholar] [CrossRef]
- Sentaurus Process User Guide, O-2018.06; Synopsys: Mountain View, CA, USA, 2018.
- Next-Generation TCAD Software. Available online: http://www.globaltcad.com/en/products/minimos-nt.html (accessed on 2 June 2020).
- Hess, K.; Haggag, A.; McMahon, W.; Fischer, B.; Cheng, K.; Lee, J.; Lyding, L. Simulation of Si-SiO2 Defect Generation in CMOS Chips: From Atomistic Structure to Chip Failure Rates. In Proceedings of the International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2000; pp. 93–96. [Google Scholar] [CrossRef]
- Bravaix, A.; Huard, V.; Goguenheim, D.; Vincent, E. Hot-Carrier to Cold-Carrier Device Lifetime Modeling with Temperature for Low power 40nm Si-Bulk NMOS and PMOS FETs. In Proceedings of the International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 622–625. [Google Scholar] [CrossRef]
- Reggiani, S.; Poli, S.; Denison, M.; Gnani, E.; Gnudi, A.; Baccarani, G.; Pendharkar, S.; Wise, R. Physics-Based Analytical Model for HCS Degradation in STI-LDMOS Transistors. IEEE Trans. Electron Devices 2011, 58, 3072–3080. [Google Scholar] [CrossRef]
- Reggiani, S.; Barone, G.; Gnani, E.; Gnudi, A.; Baccarani, G.; Poli, S.; Wise, R.; Chuang, M.Y.; Tian, W.; Pendharkar, S.; et al. Characterization and Modeling of Electrical Stress Degradation in STI-based Integrated Power Devices. Solid State Electron. 2014, 102, 25–41. [Google Scholar] [CrossRef]
- Varghese, D.; Alam, M.A.; Weir, B. A generalized, IB-independent, physical HCI lifetime projection methodology based on universality of hot-carrier degradation. In Proceedings of the 2010 IEEE International Reliability Physics Symposium, Anaheim, CA, USA, 2–6 May 2010; pp. 1091–1094. [Google Scholar] [CrossRef]
- Lee, J.; Chen, J.; Wu, K.M.; Liu, C.; Hsu, S. Effect of hot-carrier-induced interface states distribution on linear drain current degradation in 0.35 μm n-type lateral diffused metal-oxide-semiconductor transistors. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Chen, J.; Chen, S.Y.; Wu, K.M.; Liu, C. Investigation of hot-carrier-induced degradation mechanisms in p-type high-voltage drain extended metal-oxide-semiconductor transistors. Jpn. J. Appl. Phy. 2009, 48, 04C039. [Google Scholar] [CrossRef]
- Ang, D.S.; Phua, T.W.H.; Liao, H.; Ling, C.H. High-energy tail electrons as the mechanism for the worst-case hot-carrier stress degradation of the deep submicrometer N-MOSFET. IEEE Electron Device Lett. 2003, 24, 469–471. [Google Scholar] [CrossRef]
- Manzini, S.; Gallerano, A. Avalanche Injection of Hot Holes in the Gate Oxide of LDMOS. Solid State Electron. 2000, 44, 1325–1330. [Google Scholar] [CrossRef]
- Tyaginov, S.; Makarov, A.; Chasin, A.; Bury, E.; Vandemaele, M.; Jech, M.; Grill, A.; Keersgieter, A.D.; Linten, D.; Kaczer, B. Physical Modeling the Impact of Self-Heating Carrier on-Hot Degradation in pNWFETs. 2020; in press. [Google Scholar]
- Makarov, A.; Roussel, P.J.; Bury, E.; Vandemaele, M.; Spessot, A.; Linten, D.; Kaczer, B.; Tyaginov, S. On Correlation Between Hot-Carrier Stress Induced Device Parameter Degradation and Time-Zero Variability. In Proceedings of the IEEE International Integrated Reliability Workshop, South Lake Tahoe, CA, USA, 13–17 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- McMahon, W.; Mamy-Randriamihaja, Y.; Vaidyanathan, B.; Nigam, T.; Pimparkar, N. From Atoms to Circuits: Theoretical and Empirical Modeling of Hot Carrier Degradation. In Hot Carrier Degradation in Semiconductor Devices; Springer: Berlin, Germany, 2015; pp. 3–25. [Google Scholar]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarov, A.; Roussel, P.; Bury, E.; Vandemaele, M.; Spessot, A.; Linten, D.; Kaczer, B.; Tyaginov, S. Correlated Time-0 and Hot-Carrier Stress Induced FinFET Parameter Variabilities: Modeling Approach. Micromachines 2020, 11, 657. https://doi.org/10.3390/mi11070657
Makarov A, Roussel P, Bury E, Vandemaele M, Spessot A, Linten D, Kaczer B, Tyaginov S. Correlated Time-0 and Hot-Carrier Stress Induced FinFET Parameter Variabilities: Modeling Approach. Micromachines. 2020; 11(7):657. https://doi.org/10.3390/mi11070657
Chicago/Turabian StyleMakarov, Alexander, Philippe Roussel, Erik Bury, Michiel Vandemaele, Alessio Spessot, Dimitri Linten, Ben Kaczer, and Stanislav Tyaginov. 2020. "Correlated Time-0 and Hot-Carrier Stress Induced FinFET Parameter Variabilities: Modeling Approach" Micromachines 11, no. 7: 657. https://doi.org/10.3390/mi11070657
APA StyleMakarov, A., Roussel, P., Bury, E., Vandemaele, M., Spessot, A., Linten, D., Kaczer, B., & Tyaginov, S. (2020). Correlated Time-0 and Hot-Carrier Stress Induced FinFET Parameter Variabilities: Modeling Approach. Micromachines, 11(7), 657. https://doi.org/10.3390/mi11070657






