Force Prediction and Cutting-Parameter Optimization in Micro-Milling Al7075-T6 Based on Response Surface Method
Abstract
:1. Introduction
2. Experimental
2.1. Micro-Milling Experiment Setup
2.2. Experimental Design
- (1)
- A series of center points (the center point of rectangle in Figure 2) provide information on whether there is a curved surface in the model or information about pure errors: including groups 1–7 experiments in the central point (0,0,0,0);
- (2)
- The factor points (the vertices of the cube in Figure 2) are mainly used to estimate the linear and interactive terms: the 8–23 groups experiment with 2 full-factor part experiment points;
- (3)
- The axial point parts (the star point in Figure 2) are used to estimate the quadratic term: the 24–31 groups are experiments of the axial point part and the axial point of each factor is −2 or 2. There were 8 groups of experiments in which 4 factors were combined.
3. Experimental Results
4. Discussion
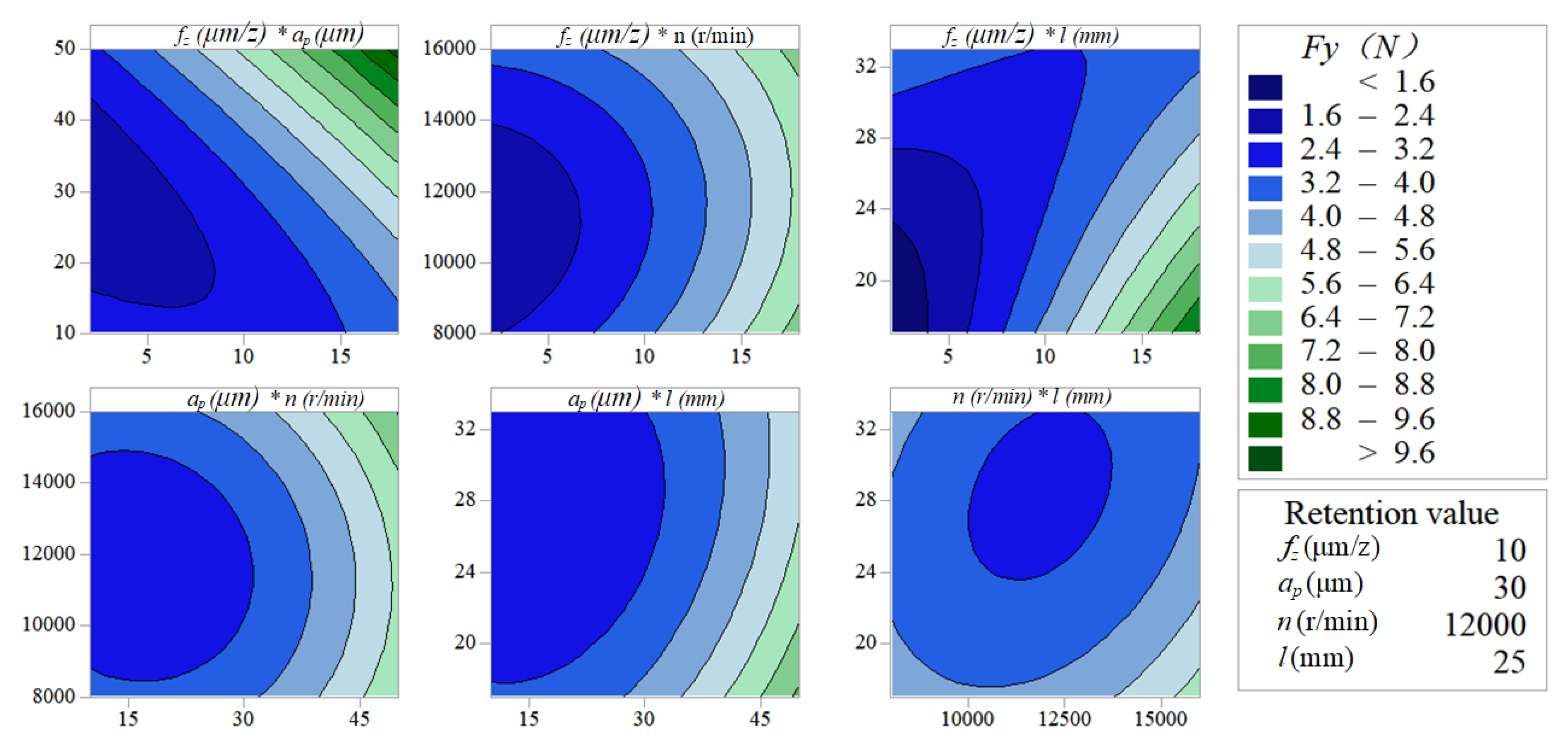
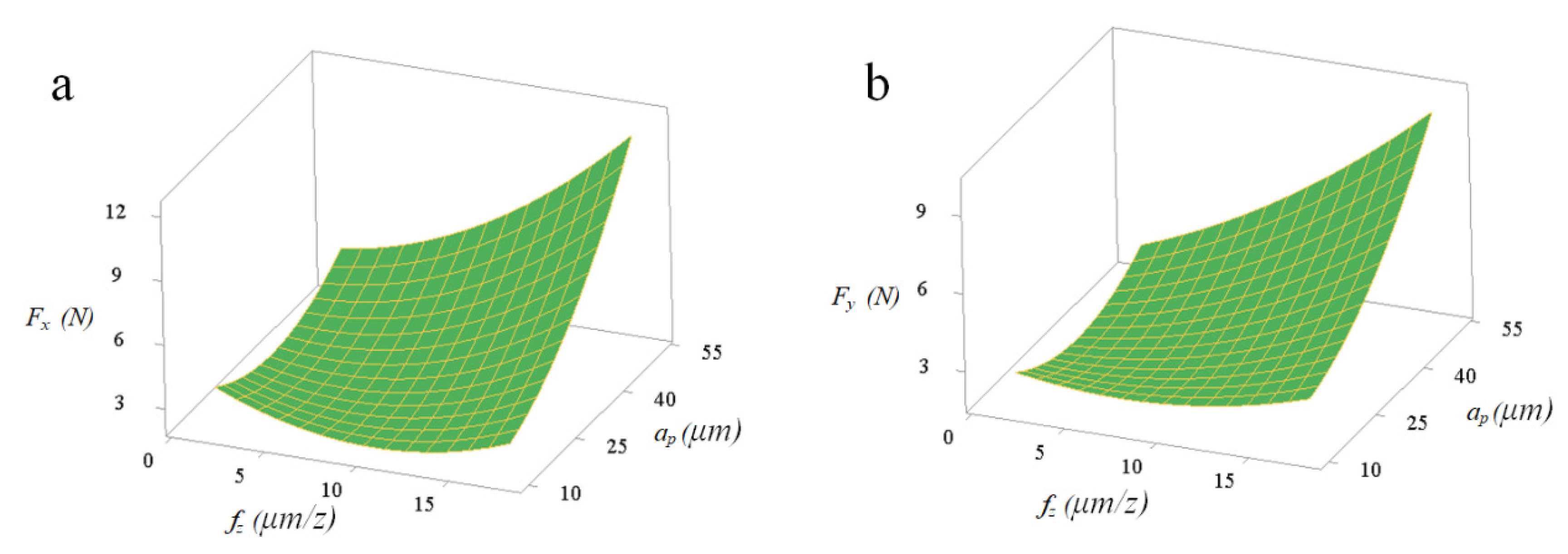
4.1. Micro-Milling Force Analysis
- (1)
- Individual effect: ap > fz > l > n;
- (2)
- Interaction effect: fz*l > fz*ap > fz*n > ap*l > n*l > ap*n;
- (3)
- Quadratic effect: n2 > fz2 > ap2 > l2.
- (1)
- Individual effect: fz > ap > l > n;
- (2)
- Interaction effect: fz*l > fz*ap > n*l > ap*l > fz*n > ap*n;
- (3)
- Quadratic effect: ap2 > n2 > fz2 > l2.
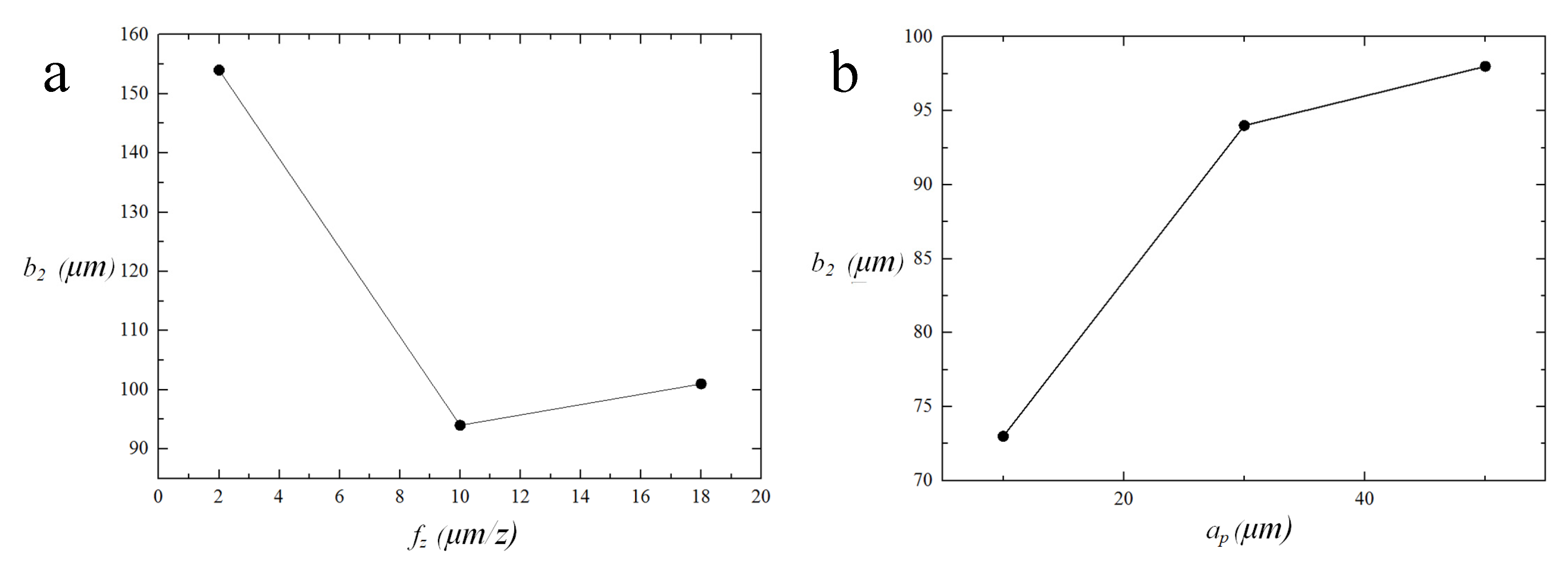
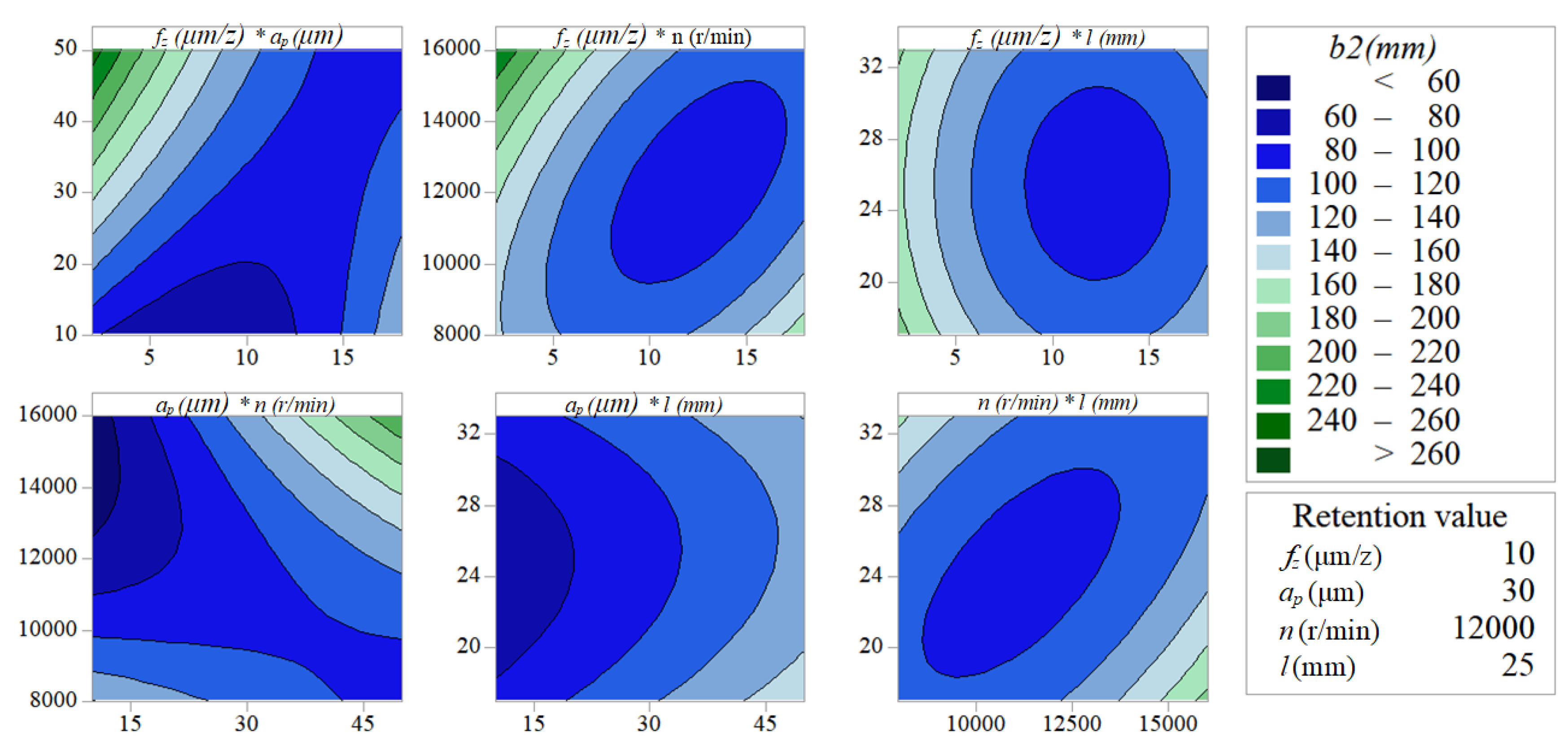
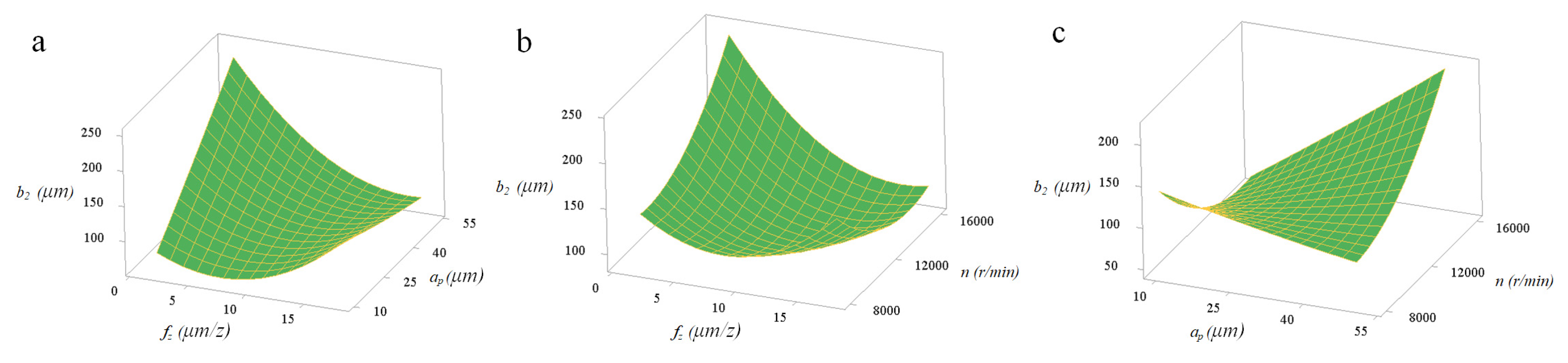
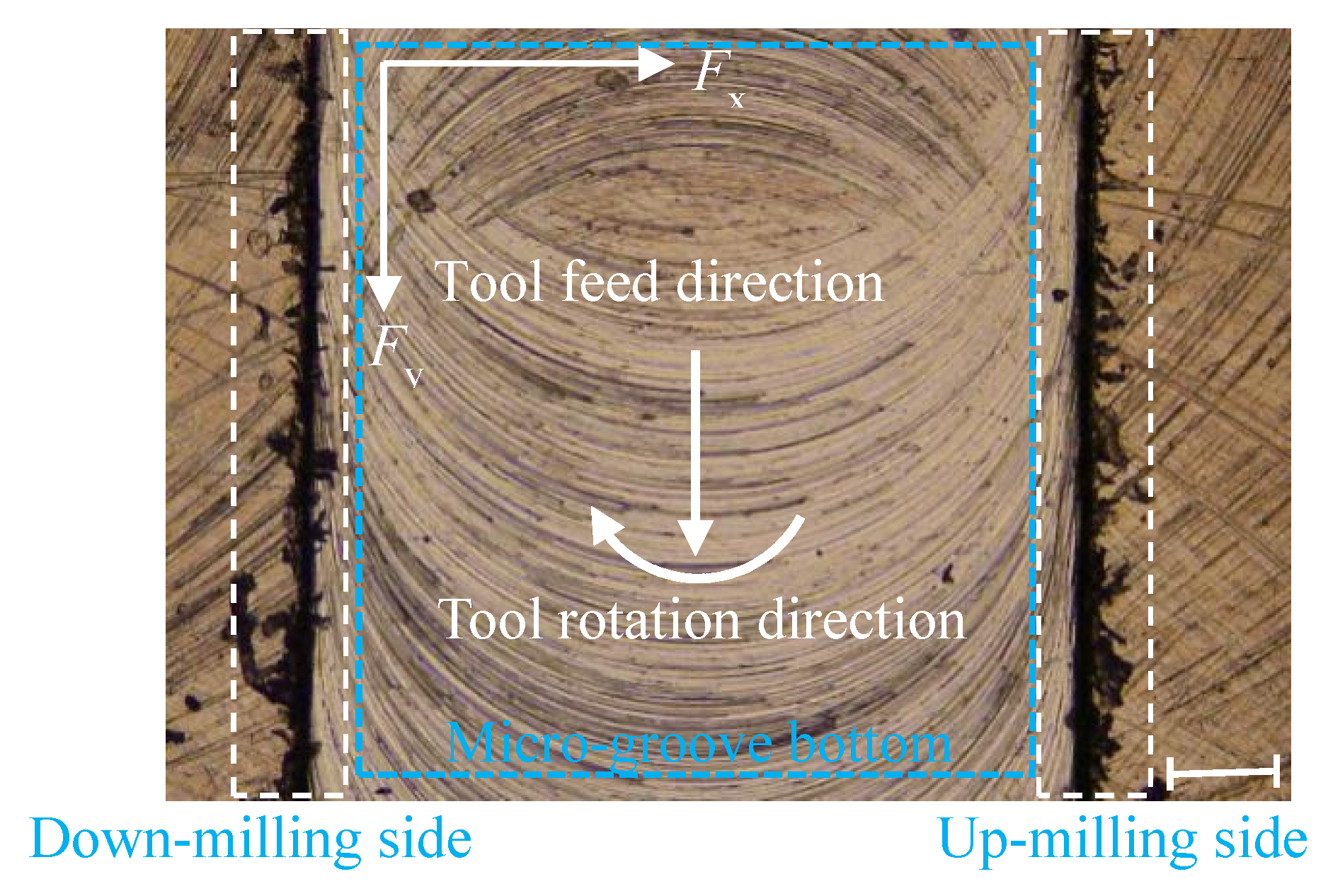
4.2. The Top Burrs Morphology Analysis
4.3. Cutting-Parameter Optimization
5. Conclusions
- (1)
- The change of cutting parameters had a significant effect on the micro-milling force and the width of up-milling side top burrs. The prediction model of the quadratic response surface around micro-milling force (Fx and Fy) and the width of burrs on the up-milling side (b2) was in a significant state. The experimental measured value and the predicted value had a high fitting degree;
- (2)
- During micro-milling workpiece material Al7075-T6, ap and fz show a significant linear effect on force and width of top burrs. The response values (Fx, Fy, b1 and b2) were mainly affected by ap, followed by was fz, but n and l had few significant effects;
- (3)
- In addition, mainly considering the linear effects of ap and fz, the optimization of cutting parameters also needs to consider the interaction effects and secondary effects between each cutting parameter. Simultaneously reducing fz and ap or simultaneously reducing fz and l could actively reduce the micro-milling force, while reducing ap and increasing n or simultaneously increasing fz and ap could effectively reduce the top burrs;
- (4)
- The reasonable setting of cutting parameters could improve the quality of machined surface. According to the quadratic response surface model, the optimal response value could be obtained by optimizing combination of cutting parameters: n = 11,394 r/min, fz = 5.8 µm/z, ap = 11.6 µm and l = 20.9 mm.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, T.; Wu, X.Y.; Zhang, G.Q.; Xu, B.; Chen, Y.H.; Ruan, S.C. Experimental Study on Machinability of Zr-Based Bulk Metallic Glass during Micro Milling. Micromachines 2020, 11, 86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subramanian, M.; Sakthivel, M.; Sooryaprakash, K.; Sudhakaran, R. Optimization of Cutting Parameters for Cutting Force in Shoulder Milling of Al7075-T6 Using Response Surface Methodology and Genetic Algorithm. In International Conference on Design and Manufacturing; Sreekumar, M., Zoppi, M., Nithiarasu, P., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2013; Volume 64, pp. 690–700. [Google Scholar]
- Rahman, M.A.; Rahman, M.; Kumar, A.S. Material perspective on the evolution of micro- and nano-scale cutting of metal alloys. J. Micromanuf. 2018, 1, 97–114. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; He, N.; Zhao, G.L.; Shen, J.Y. Experimental Investigation on Direct Micro Milling of Cemented Carbide. Micromachines 2019, 10, 147. [Google Scholar] [CrossRef] [Green Version]
- Chern, G.L. Experimental observation and analysis of burr formation mechanisms in face milling of aluminum alloys. Int. J. Mach. Tools Manuf. 2006, 46, 1517–1525. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Huo, D. Investigation on the Tool Wear Suppression Mechanism in Non-Resonant Vibration-Assisted Micro Milling. Micromachines 2020, 11, 380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afazov, S.M.; Ratchev, S.M.; Segal, J. Modelling and simulation of micro-milling cutting forces. J. Mater. Process. Technol. 2010, 210, 2154–2162. [Google Scholar] [CrossRef]
- Asad, A.; Masaki, T.; Rahman, M.; Lim, H.S.; Wong, Y. Tool-based micro-machining. J. Mater. Process. Technol. 2007, 192, 204–211. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, H.; Zhang, G.Q.; Chen, Y.B.; Ma, J.; Mo, R.D. Machinability and Surface Generation of Pd40Ni10Cu30P20 Bulk Metallic Glass in Single-Point Diamond Turning. Micromachines 2020, 11, 4. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Li, L.; He, N. Investigation on the burr formation mechanism in micro cutting. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2017, 47, 191–196. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhu, K.P. Generic instantaneous force modeling and comprehensive real engagement identification in micro-milling. Int. J. Mech. Sci. 2020, 176, 17. [Google Scholar] [CrossRef]
- Bao, W.Y.; Tansel, I.N. Modeling micro-end-milling operations. Part I: Analytical cutting force model. Int. J. Mach. Tools Manuf. 2000, 40, 2155–2173. [Google Scholar] [CrossRef]
- Jing, X.B.; Lv, R.Y.; Chen, Y.; Tian, Y.L.; Li, H.Z. Modelling and experimental analysis of the effects of run out, minimum chip thickness and elastic recovery on the cutting force in micro-end-milling. Int. J. Mech. Sci. 2020, 176, 11. [Google Scholar] [CrossRef]
- Wang, T.; Wu, X.Y.; Zhang, G.Q.; Chen, Y.H.; Xu, B.; Ruan, S.C. Study on surface roughness and top burr of micro-milled Zr-based bulk metallic glass in shear dominant zone. Int. J. Adv. Manuf. Technol. 2020, 107, 4287–4299. [Google Scholar] [CrossRef]
- Rahman, M.A.; Woon, K.S.; Venkatesh, V.C.; Rahman, M. Modelling of the combined microstructural and cutting edge effects in ultraprecision machining. CIRP Ann. Manuf. Technol. 2018, 67, 129–132. [Google Scholar] [CrossRef]
- Camara, M.A.; Rubio, J.C.C.; Abrao, A.M.; Davim, J.P. State of the Art on Micromilling of Materials, a Review. J. Mater. Sci. Technol. 2012, 28, 673–685. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rahman, M.; Kumar, A.S. Chip perforation and ‘burnishing-like’ finishing of Al alloy in precision machining. Precis. Eng. J. Int. Soc. Precis. Eng. Nanotechnol. 2017, 50, 393–409. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rahman, M.; Mia, M.; Asad, A.; Fardin, A. Manufacturing of Al Alloy Microrods by Micro Cutting in a Micromachining Center. Micromachines 2019, 10, 831. [Google Scholar] [CrossRef] [Green Version]
- Fredj, N.B.; Amamou, R.; Rezgui, M.A. Surface roughness prediction based upon experimental design and neural network models. In Proceedings of the 2002 IEEE International Conference on Systems, Man and Cybernetics, Yasmine Hammamet, Tunisia, 6–9 October 2002; Cat. No.02CH37349. Volume 5, p. 6. [Google Scholar] [CrossRef]
- Lu, X.H.; Jia, Z.Y.; Wang, H.; Feng, Y.X.; Liang, S.Y. The effect of cutting parameters on micro-hardness and the prediction of Vickers hardness based on a response surface methodology for micro-milling Inconel 718. Measurement 2019, 140, 56–62. [Google Scholar] [CrossRef]
- Campatelli, G.; Lorenzini, L.; Scippa, A. Optimization of process parameters using a Response Surface Method for minimizing power consumption in the milling of carbon steel. J. Clean. Prod. 2014, 66, 309–316. [Google Scholar] [CrossRef]
- Kant, G.; Sangwan, K.S. Predictive Modelling and Optimization of Machining Parameters to Minimize Surface Roughness using Artificial Neural Network Coupled with Genetic Algorithm. In 15th Cirp Conference on Modelling of Machining Operations; Schulze, V., Ed.; Elsevier Science Bv: Amsterdam, The Netherlands, 2015; Volume 31, pp. 453–458. [Google Scholar]
- Cus, F.; Zuperl, U. Approach to optimization of cutting conditions by using artificial neural networks. J. Mater. Process. Technol. 2006, 173, 281–290. [Google Scholar] [CrossRef]
- Koklu, U. Optimisation of machining parameters in interrupted cylindrical grinding using the Grey-based Taguchi method. Int. J. Comput. Integr. Manuf. 2013, 26, 696–702. [Google Scholar] [CrossRef]
- Lin, C.L. Use of the Taguchi method and grey relational analysis to optimize turning operations with multiple performance characteristics. Mater. Manuf. Process. 2004, 19, 209–220. [Google Scholar] [CrossRef]
- Bouacha, K.; Yallese, M.A.; Mabrouki, T.; Rigal, J.F. Statistical analysis of surface roughness and cutting forces using response surface methodology in hard turning of AISI 52100 bearing steel with CBN tool. Int. J. Refract. Met. Hard Mater. 2010, 28, 349–361. [Google Scholar] [CrossRef]
- Kumar, S.P.L. Experimental investigations and empirical modeling for optimization of surface roughness and machining time parameters in micro end milling using Genetic Algorithm. Measurement 2018, 124, 386–394. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, T.; Zhang, G.Q. Research on Parameter Optimization of Micro-Milling Al7075 Based on Edge-Size-Effect. Micromachines 2020, 11, 197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Oliveira, F.B.; Rodrigues, A.R.; Coelho, R.T.; de Souza, A.F. Size effect and minimum chip thickness in micromilling. Int. J. Mach. Tools Manuf. 2015, 89, 39–54. [Google Scholar] [CrossRef]
- Lai, X.M.; Li, H.T.; Li, C.F.; Lin, Z.Q.; Ni, J. Modelling and analysis of micro scale milling considering size effect, micro cutter edge radius and minimum chip thickness. Int. J. Mach. Tools Manuf. 2008, 48, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.F.; Feng, C.; Wang, H.; Gong, Y.D. Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling. Micromachines 2019, 10, 582. [Google Scholar] [CrossRef] [Green Version]
- Mamedov, A.; Layegh, S.E.; Lazoglu, I. Instantaneous tool deflection model for micro milling. Int. J. Adv. Manuf. Technol. 2015, 79, 769–777. [Google Scholar] [CrossRef]


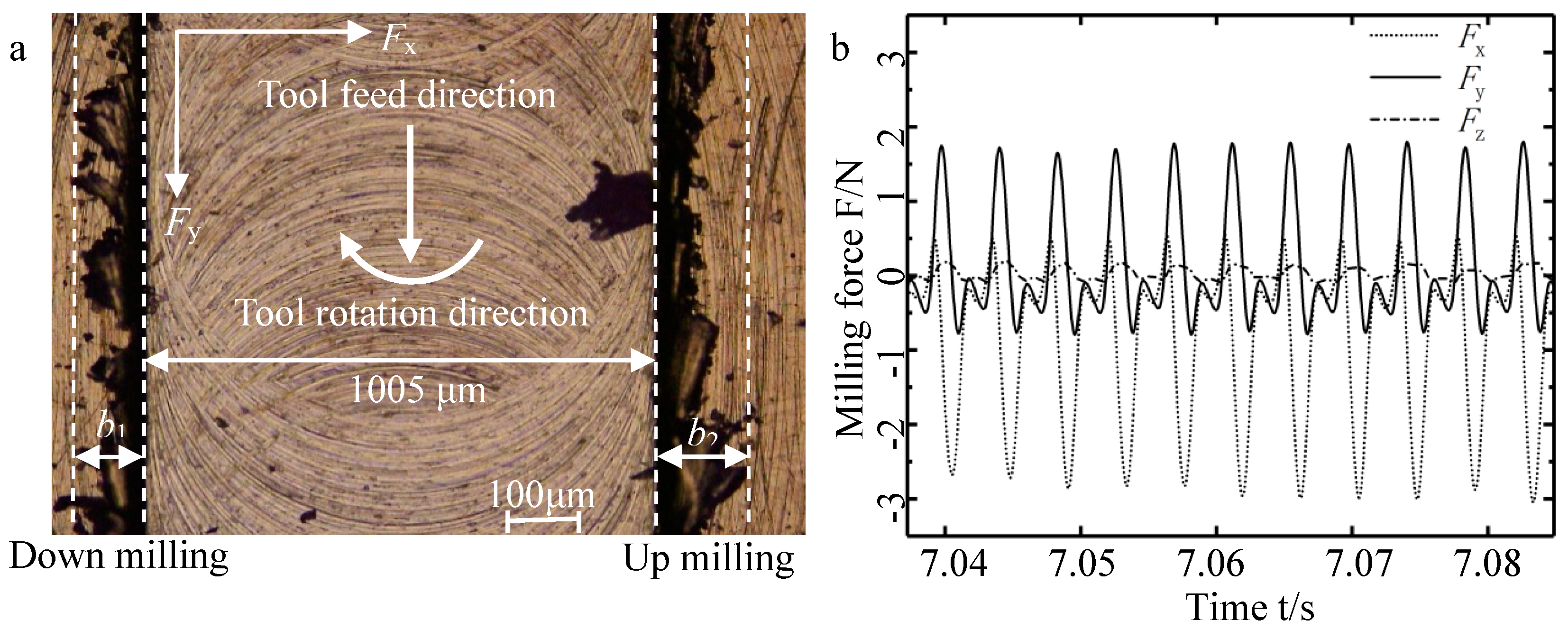
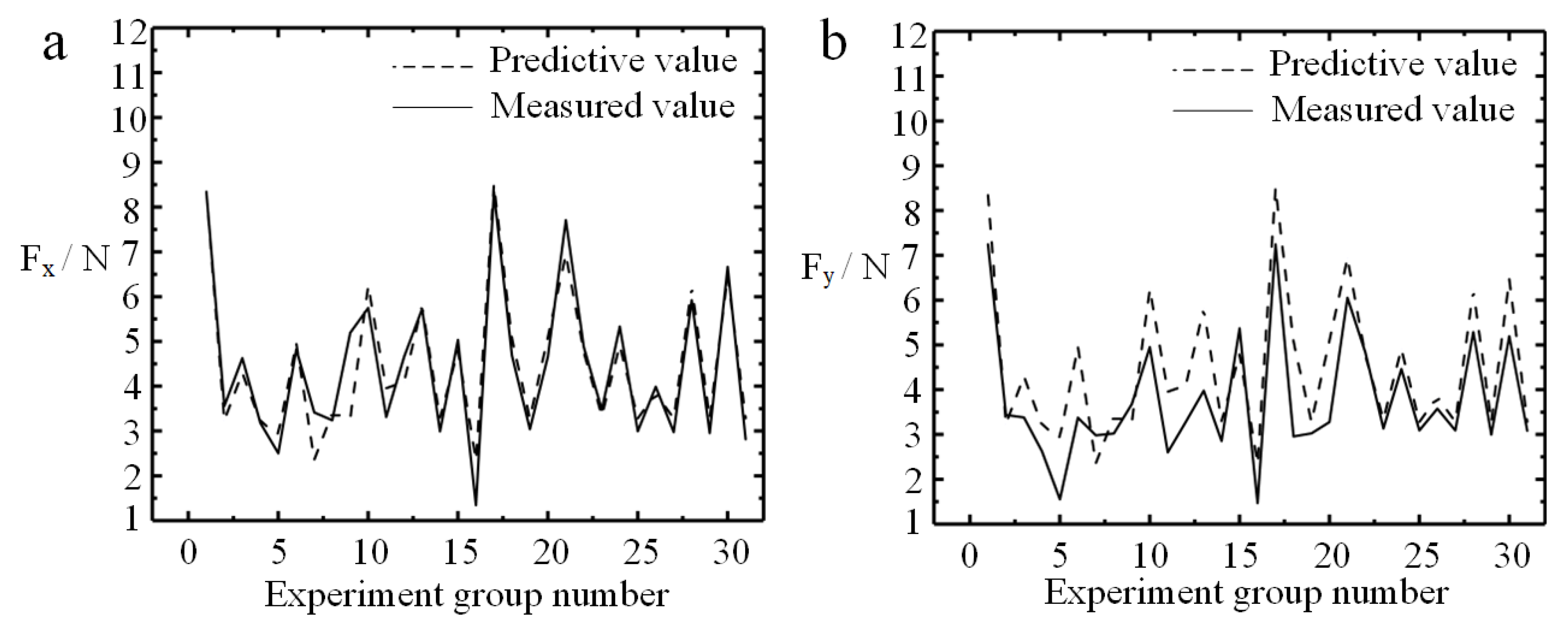





| No. | Variables | Response Value | ||||||
|---|---|---|---|---|---|---|---|---|
| b1 (μm) | b2(μm) | Fx (N) | Fy (N) | |||||
| 1 | 0 | 0 | 0 | 0 | 94 | 104 | 5.193 | 3.681 |
| 2 | 0 | 0 | 0 | 0 | 60 | 103 | 2.992 | 2.854 |
| 3 | 0 | 0 | 0 | 0 | 88 | 103 | 3.042 | 3.027 |
| 4 | 0 | 0 | 0 | 0 | 64 | 94 | 2.994 | 3.091 |
| 5 | 0 | 0 | 0 | 0 | 60 | 82 | 2.975 | 3.091 |
| 6 | 0 | 0 | 0 | 0 | 64 | 94 | 2.954 | 2.998 |
| 7 | 0 | 0 | 0 | 0 | 73 | 77 | 2.818 | 3.084 |
| 8 | −1 | −1 | 1 | −1 | 79 | 109 | 3.182 | 2.628 |
| 9 | −1 | 1 | 1 | −1 | 122 | 207 | 5.332 | 4.46 |
| 10 | 1 | 1 | −1 | −1 | 91 | 104 | 8.338 | 7.246 |
| 11 | −1 | −1 | 1 | 1 | 84 | 92 | 5.033 | 5.37 |
| 12 | 1 | 1 | 1 | −1 | 73 | 143 | 8.338 | 7.246 |
| 13 | 1 | −1 | 1 | −1 | 75 | 91 | 4.66 | 3.28 |
| 14 | 1 | −1 | 1 | 1 | 60 | 88 | 3.562 | 3.437 |
| 15 | −1 | 1 | 1 | 1 | 102 | 194 | 4.66 | 3.278 |
| 16 | −1 | −1 | −1 | −1 | 77 | 106 | 3.415 | 2.983 |
| 17 | 1 | −1 | −1 | −1 | 68 | 115 | 4.871 | 4.825 |
| 18 | −1 | 1 | −1 | −1 | 100 | 131 | 3.312 | 2.604 |
| 19 | 1 | −1 | −1 | 1 | 64 | 126 | 3.476 | 3.136 |
| 20 | −1 | 1 | −1 | 1 | 110 | 143 | 4.626 | 3.382 |
| 21 | −1 | −1 | −1 | 1 | 79 | 109 | 3.242 | 3.024 |
| 22 | 1 | 1 | 1 | 1 | 70 | 97 | 5.751 | 4.95 |
| 23 | 1 | 1 | −1 | 1 | 82 | 124 | 5.925 | 5.286 |
| 24 | 0 | 0 | −2 | 0 | 88 | 101 | 4.824 | 3.375 |
| 25 | 0 | 0 | 0 | −2 | 60 | 103 | 4.688 | 2.958 |
| 26 | 0 | 2 | 0 | 0 | 70 | 98 | 7.712 | 6.056 |
| 27 | 0 | −2 | 0 | 0 | 63 | 73 | 1.345 | 1.471 |
| 28 | 0 | 0 | 2 | 0 | 86 | 122 | 5.729 | 3.978 |
| 29 | 2 | 0 | 0 | 0 | 82 | 101 | 6.668 | 5.192 |
| 30 | 0 | 0 | 0 | 2 | 60 | 106 | 3.988 | 3.577 |
| 31 | −2 | 0 | 0 | 0 | 87 | 154 | 2.503 | 1.555 |
| Parameter | Notation | Unit | Levels | ||||
|---|---|---|---|---|---|---|---|
| −2 | −1 | 0 | 1 | 2 | |||
| Per-feed tooth (fz) | μm/z | 2 | 6 | 10 | 14 | 18 | |
| Axial cutting depth (ap) | μm | 10 | 20 | 30 | 40 | 50 | |
| Spindle speed (n) | r/min | 8000 | 10,000 | 12,000 | 14,000 | 16,000 | |
| Tool extended length (l) | mm | 17 | 21 | 25 | 29 | 33 | |
| Coefficient | fz | ap | n | l | fz2 | ap2 | n2 | l2 | fz*ap | fz*n | fz*l | ap*n | ap*l | n*l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-value | 0 | 0 | 0.187 | 0.006 | 0.032 | 0.029 | 0.002 | 0.055 | 0.018 | 0.312 | 0.005 | 0.885 | 0.37 | 0.85 |
| F value | 32.52 | 55.04 | 1.90 | 3.88 | 6.27 | 5.78 | 13.86 | 4.28 | 6.91 | 1.09 | 10.46 | 0.02 | 0.85 | 0.04 |
| Significance level | 2 | 1 | 10 | 9 | 6 | 7 | 3 | 8 | 5 | 11 | 4 | 14 | 12 | 13 |
| Coefficient | fz | ap | n | l | fz2 | ap2 | n2 | l2 | fz*ap | fz*n | fz*l | ap*n | ap*l | n*l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-value | 0 | 0 | 0.345 | 0.085 | 0.200 | 0.054 | 0.074 | 0.273 | 0.045 | 0.691 | 0.011 | 0.816 | 0.549 | 0.504 |
| F value | 77.71 | 29.98 | 0.95 | 3.37 | 1.79 | 4.31 | 3.65 | 1.29 | 4.74 | 0.16 | 8.36 | 0.06 | 0.38 | 0.47 |
| Significance level | 1 | 2 | 10 | 7 | 8 | 5 | 6 | 9 | 4 | 13 | 3 | 14 | 12 | 11 |
| Coefficient | fz | ap | n | l | fz2 | ap2 | n2 | l2 | fz*ap | fz*n | fz*l | ap*n | ap*l | n*l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-value | 0.024 | 0.015 | 0.88 | 0.436 | 0.079 | 0.949 | 0.049 | 0.564 | 0.134 | 0.58 | 0.606 | 0.631 | 0.882 | 0.361 |
| F value | 6.19 | 7.47 | 0.02 | 0.64 | 3.52 | 0 | 4.52 | 0.35 | 2.5 | 0.32 | 0.28 | 0.24 | 0.02 | 0.8 |
| Significance level | 2 | 1 | 12 | 7 | 4 | 14 | 3 | 8 | 5 | 9 | 10 | 11 | 12 | 6 |
| Coefficient | fz | ap | n | l | fz2 | ap2 | n2 | l2 | fz*ap | fz*n | fz*l | ap*n | ap*l | n*l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-value | 0.001 | 0 | 0.19 | 0.71 | 0.002 | 0.827 | 0.027 | 0.084 | 0.004 | 0.021 | 0.962 | 0.003 | 0.766 | 0.06 |
| F value | 16.01 | 21.64 | 1.87 | 0.14 | 14.49 | 0.05 | 5.96 | 3.4 | 11.56 | 6.6 | 0 | 11.78 | 0.09 | 4.11 |
| Significance level | 2 | 1 | 10 | 11 | 3 | 13 | 7 | 9 | 5 | 6 | 14 | 4 | 12 | 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Chen, Y.; Zhang, G. Force Prediction and Cutting-Parameter Optimization in Micro-Milling Al7075-T6 Based on Response Surface Method. Micromachines 2020, 11, 766. https://doi.org/10.3390/mi11080766
Zhou M, Chen Y, Zhang G. Force Prediction and Cutting-Parameter Optimization in Micro-Milling Al7075-T6 Based on Response Surface Method. Micromachines. 2020; 11(8):766. https://doi.org/10.3390/mi11080766
Chicago/Turabian StyleZhou, Menghua, Yinghua Chen, and Guoqing Zhang. 2020. "Force Prediction and Cutting-Parameter Optimization in Micro-Milling Al7075-T6 Based on Response Surface Method" Micromachines 11, no. 8: 766. https://doi.org/10.3390/mi11080766
APA StyleZhou, M., Chen, Y., & Zhang, G. (2020). Force Prediction and Cutting-Parameter Optimization in Micro-Milling Al7075-T6 Based on Response Surface Method. Micromachines, 11(8), 766. https://doi.org/10.3390/mi11080766





