Design and Implementation of Multiband Noncontact Temperature-Measuring Microwave Radiometer
Abstract
:1. Introduction
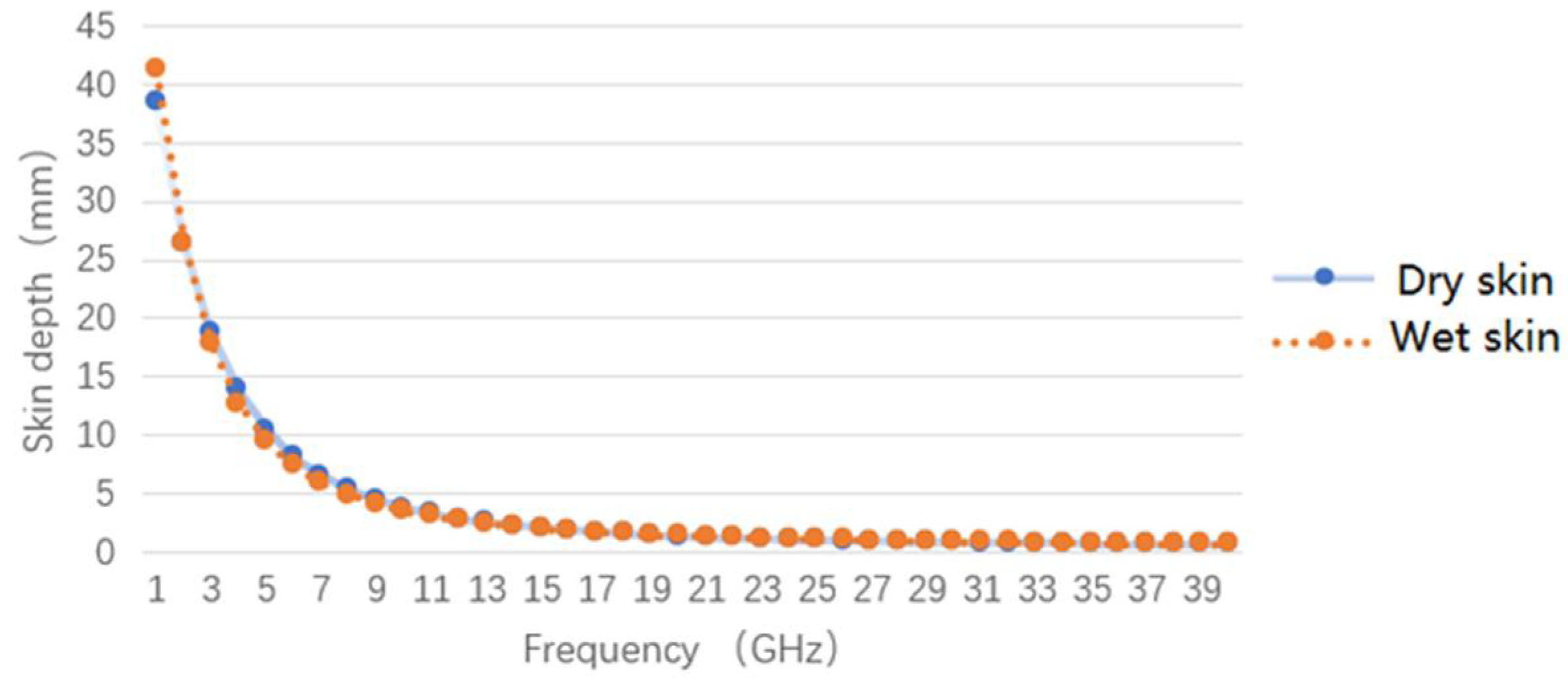
2. Relationship between Multilayer Tissue Measurement and Microwave Frequency Band
3. Hardware Circuit Design of Multiband Microwave Temperature-Measuring Radiometer
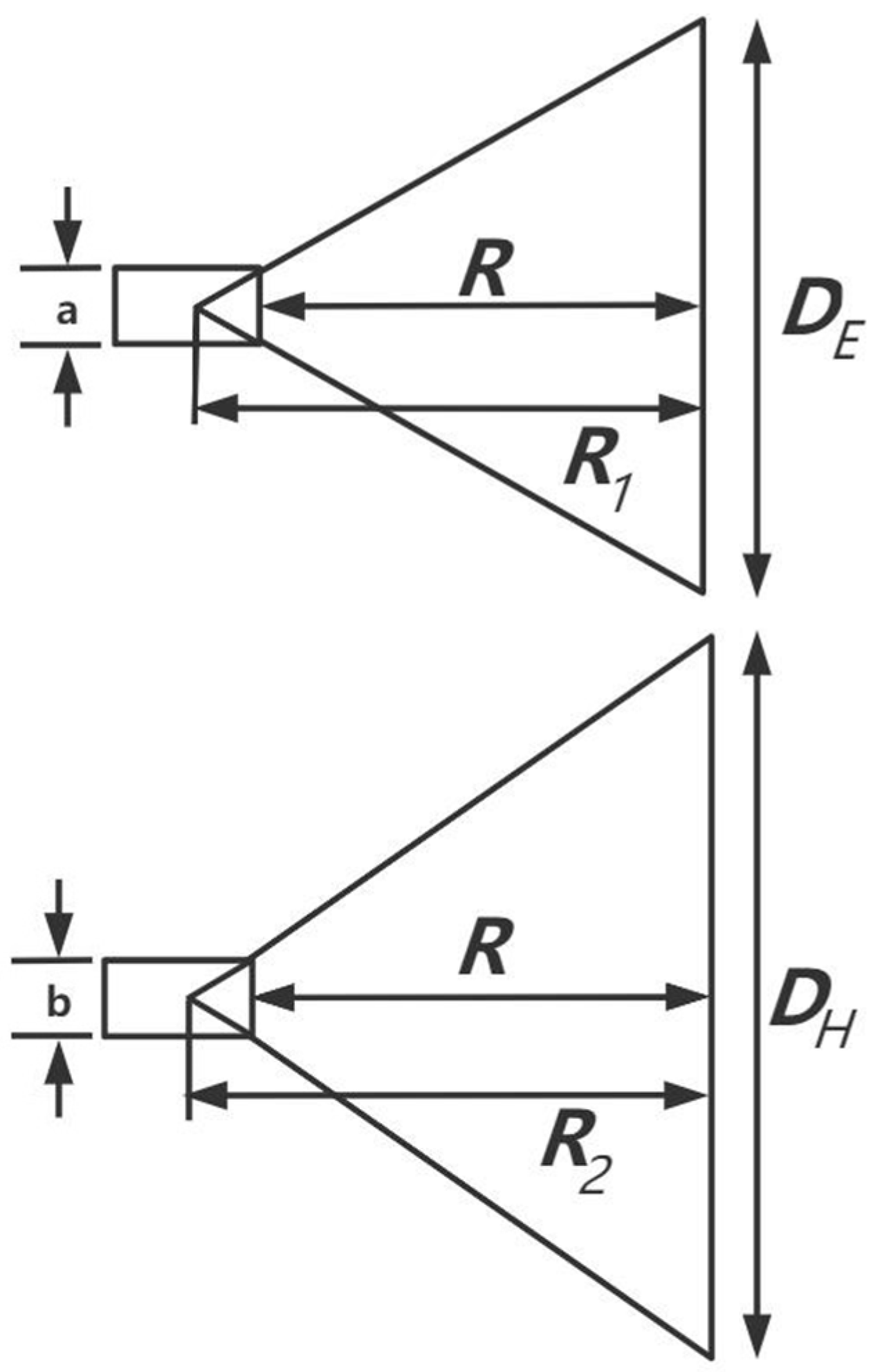
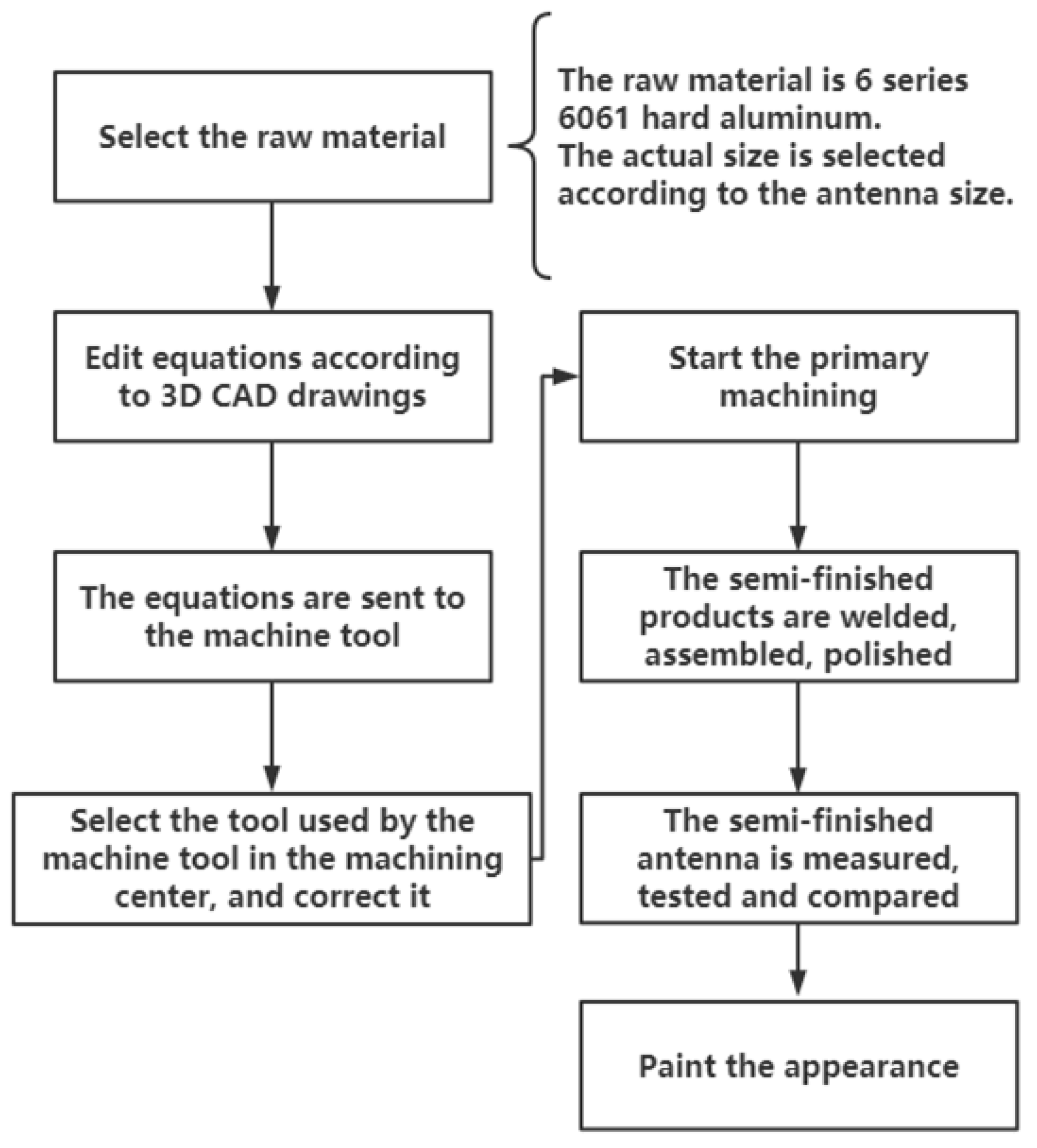
3.1. Design of Multi-Band Pyramidal Horn Antenna
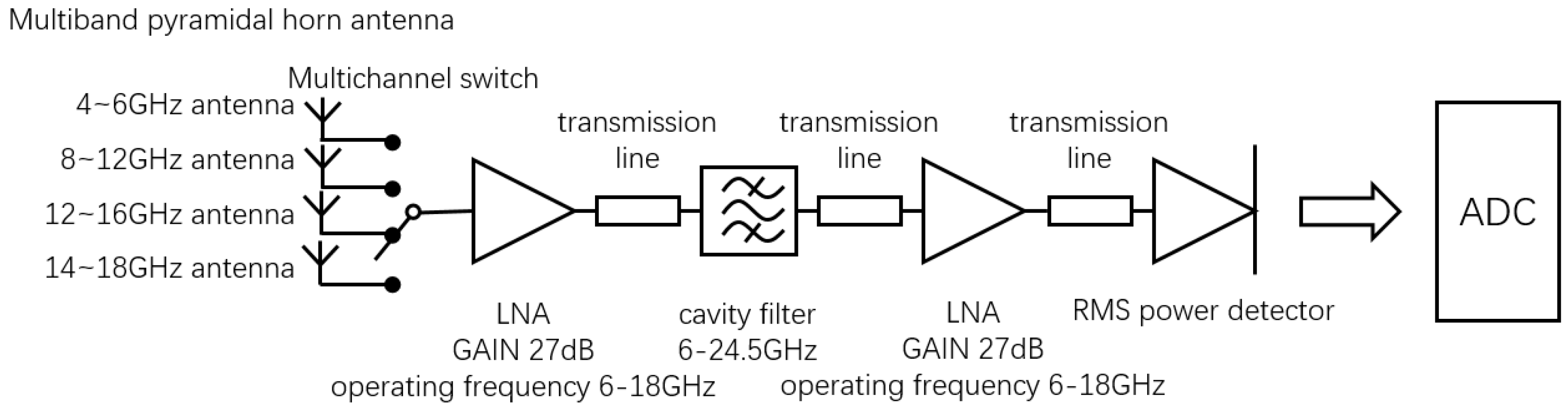
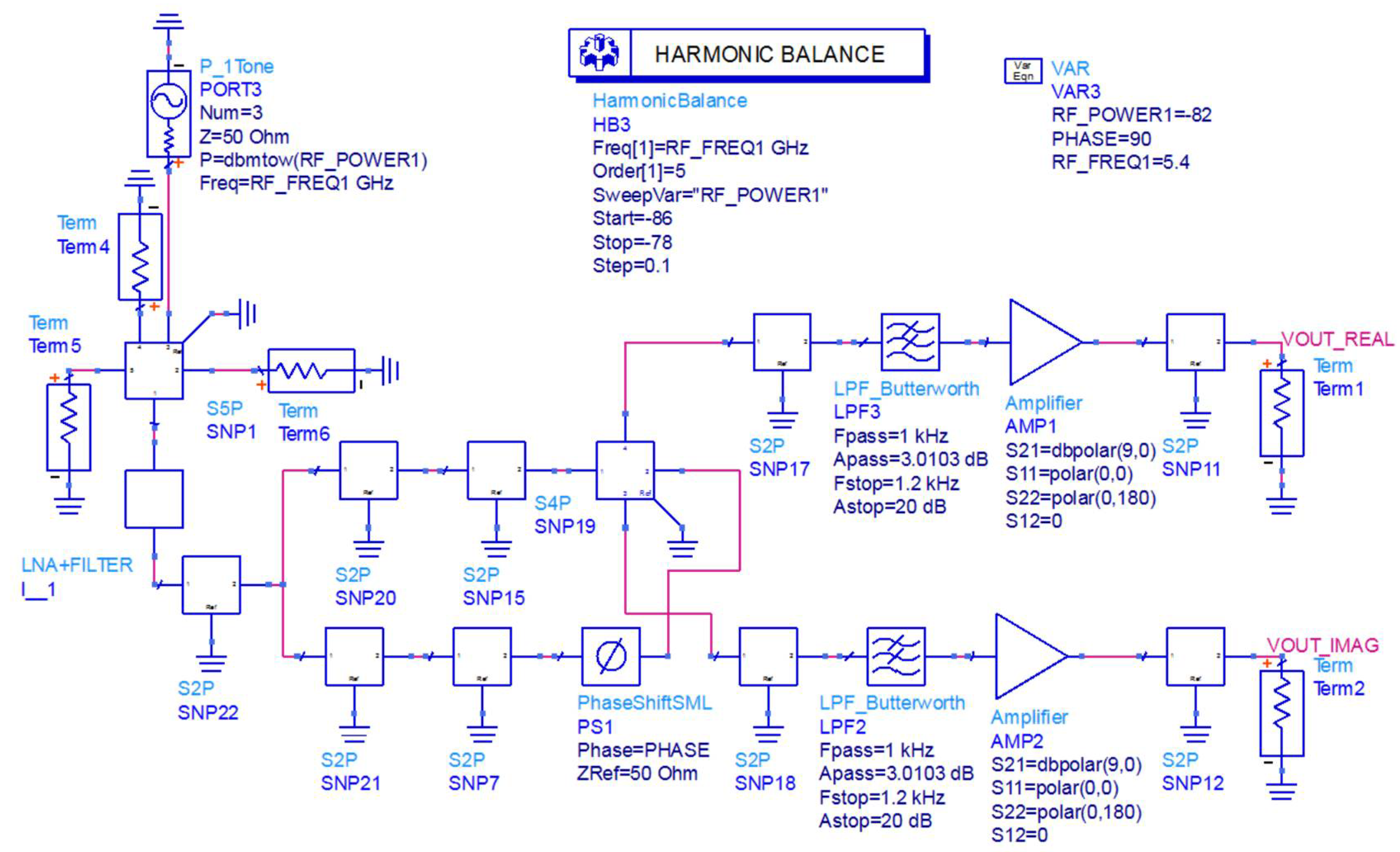
3.2. Circuit Design of Full-Power Microwave Temperature Measurement Radiometer
3.3. Influence of Different Types of Radiation Sources on Full-Power Microwave Radiometer
3.4. Influence of Wide-Band Thermal Radiation Source on Interferometric Microwave Radiometer
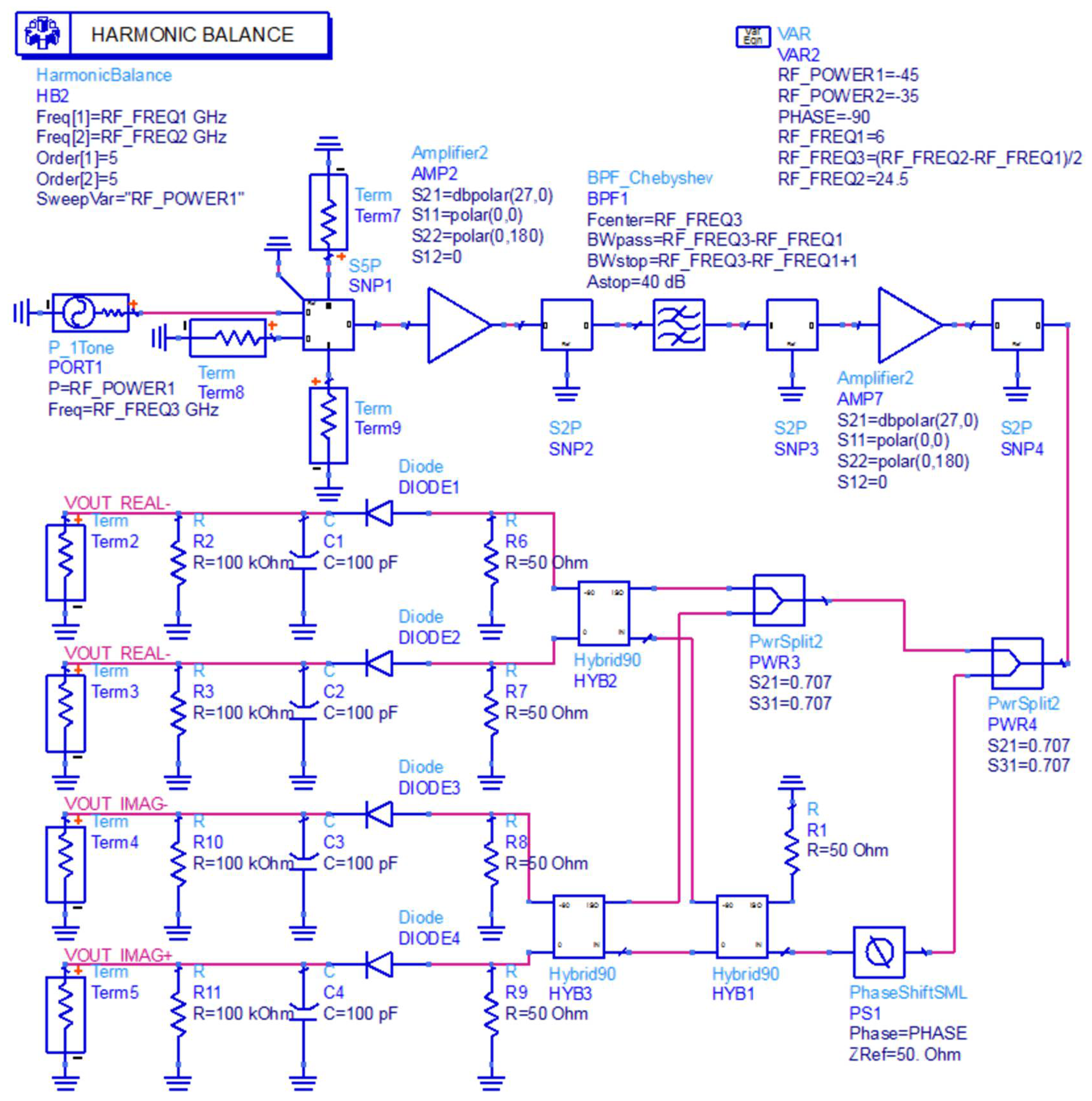
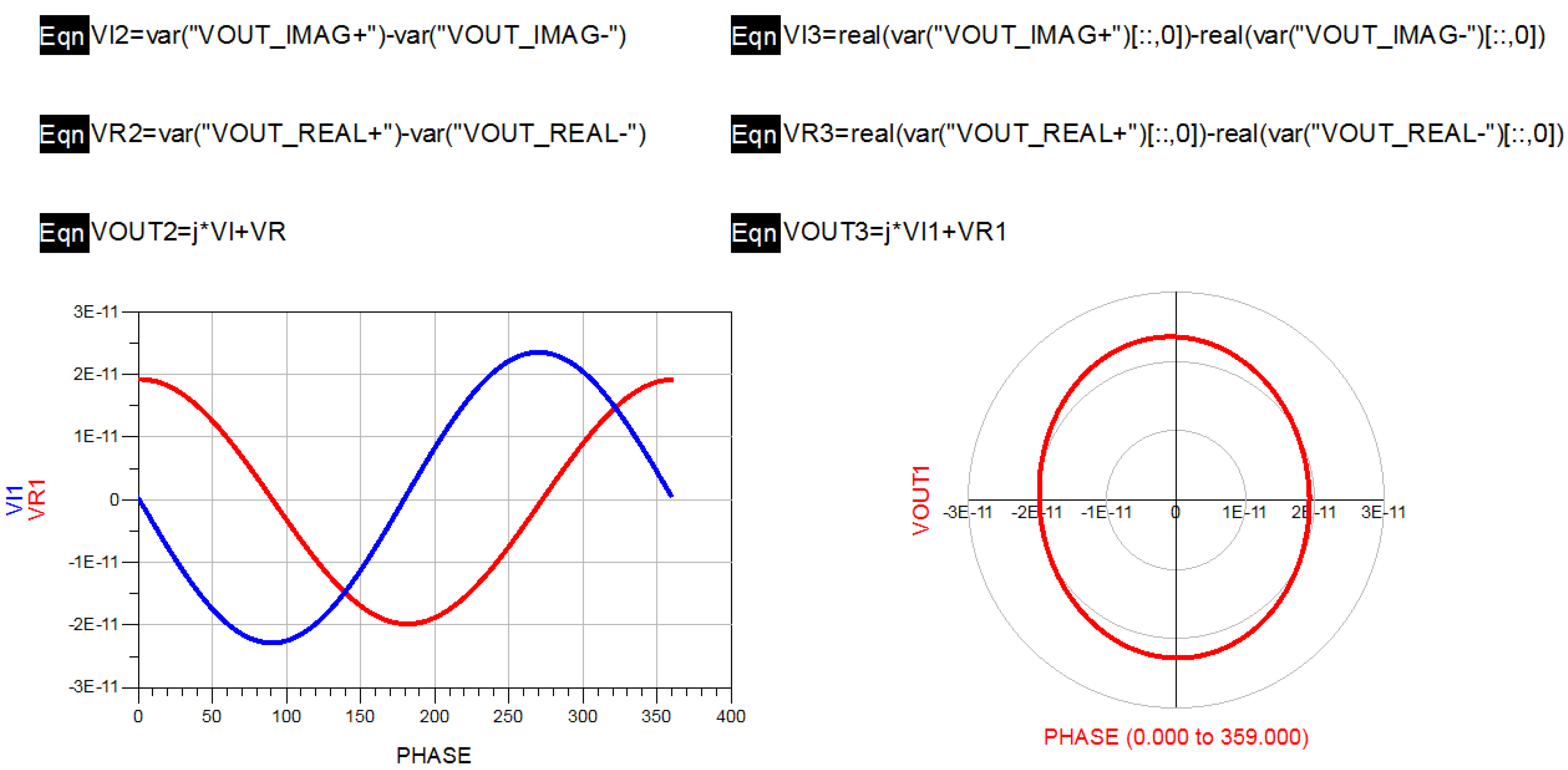
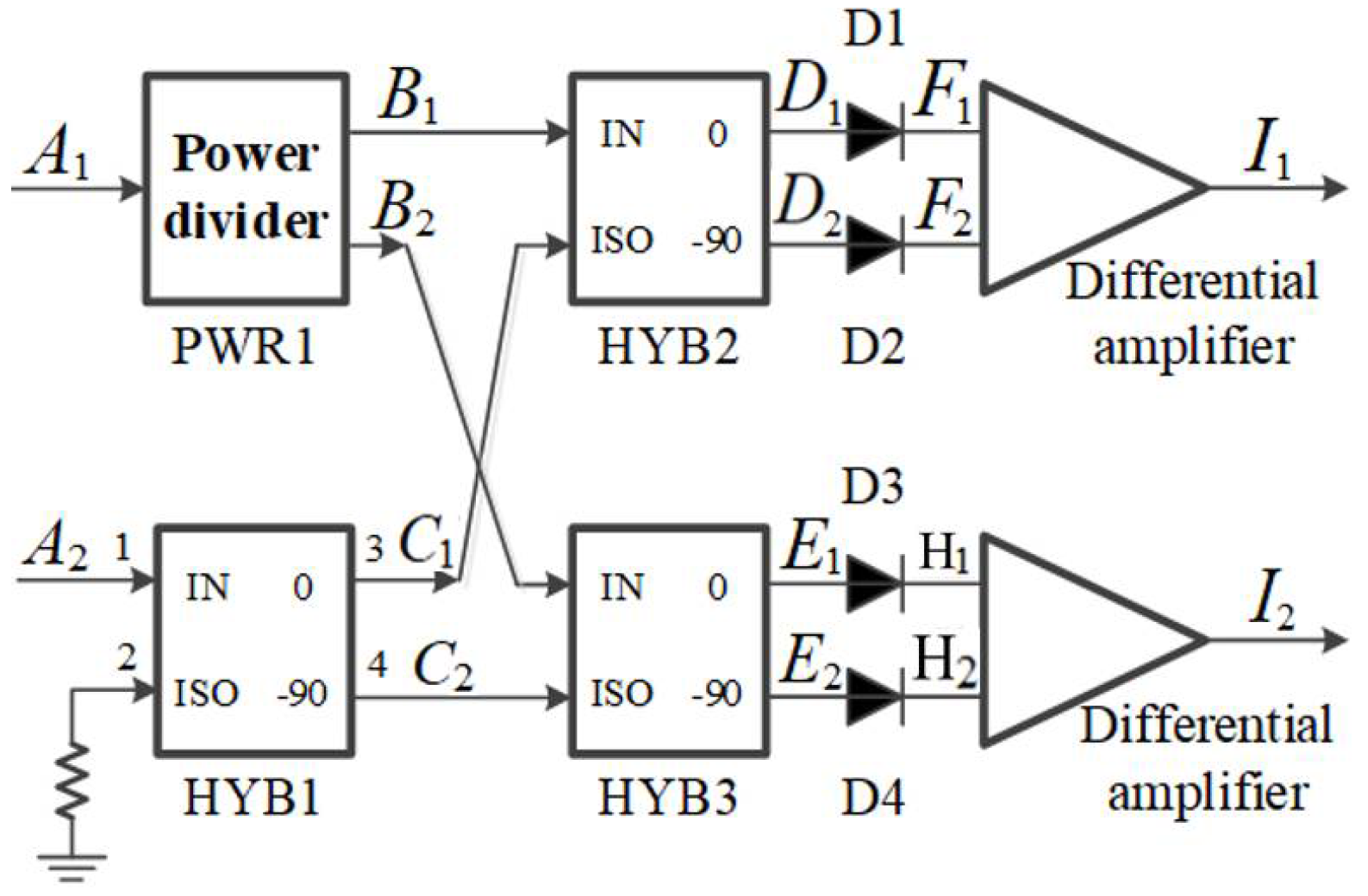
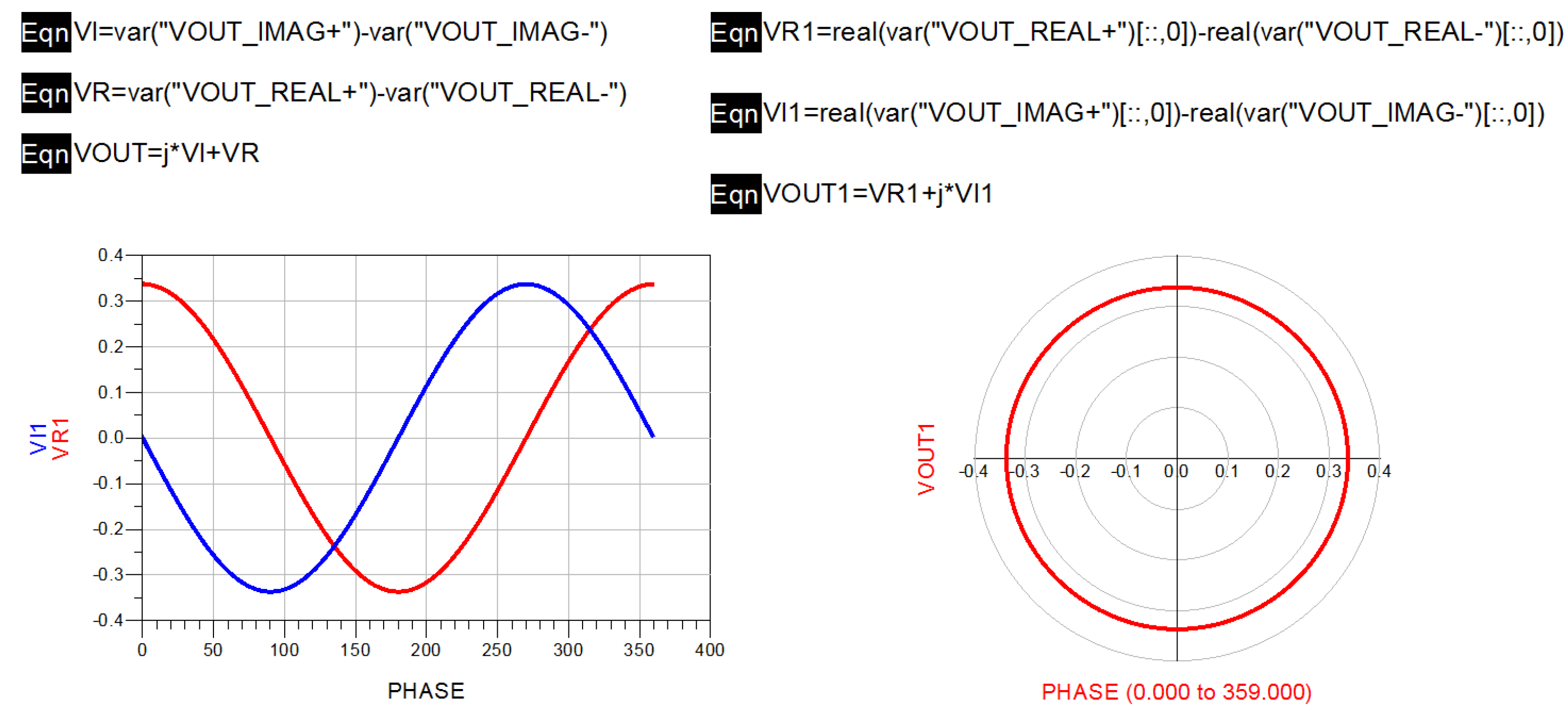
3.5. Design of Novel Interferometric Microwave Temperature Radiometer
4. Performance Tests of Two Microwave Temperature-Measuring Radiometer Systems
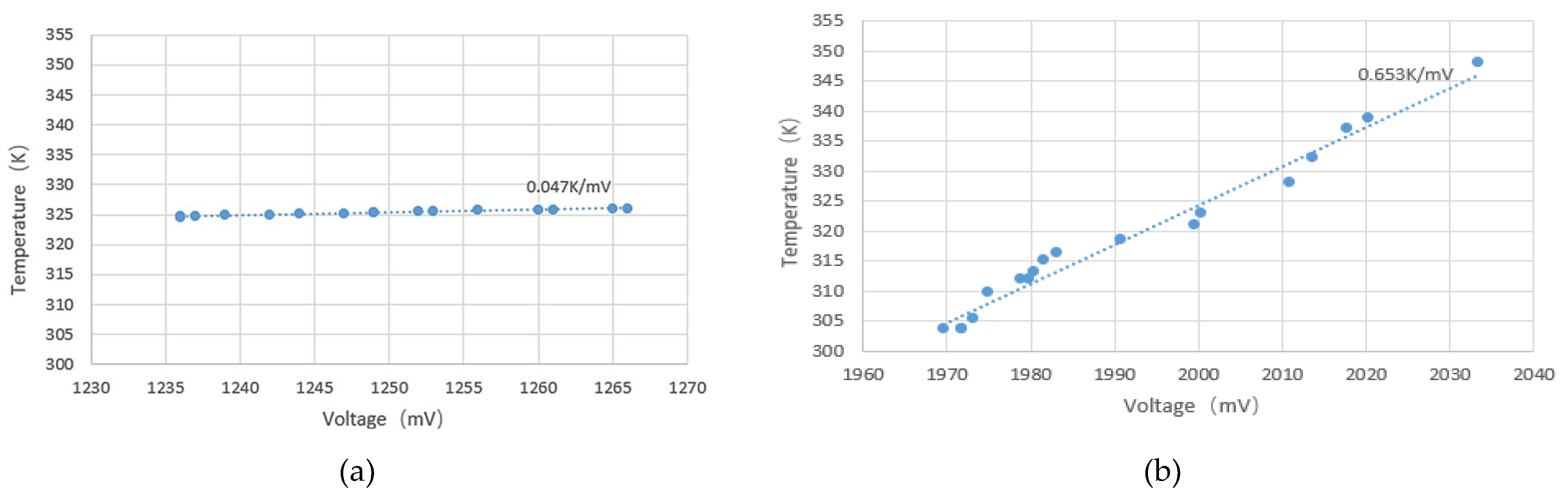
4.1. Temperature Sensitivity of Microwave Temperature Radiometer
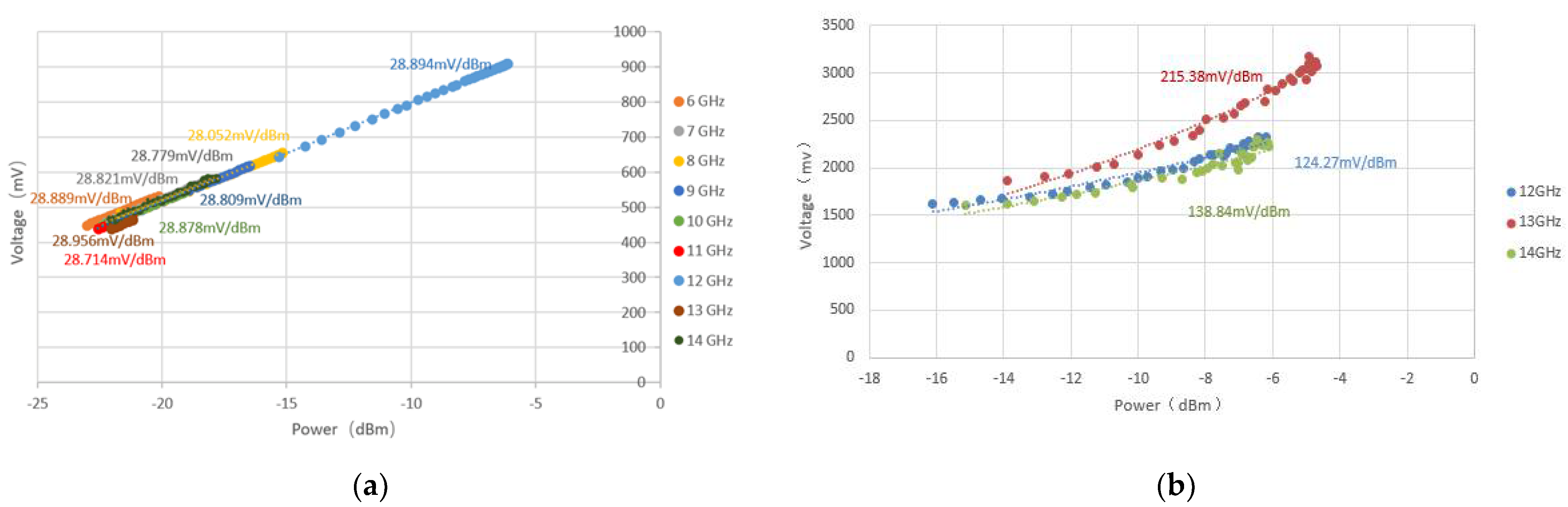
4.2. Detection Sensitivity of Microwave Temperature Radiometer
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.; Jin, H. Clinical application of infrared electronic thermometer to replace mercury thermometer. China Contin. Med. Educ. 2019, 11, 175–177. [Google Scholar]
- Vanggaard, L.; Paulev, P.-E.; Zubieta-Calleja, G. Chapter 21: Thermo-regulation, temperature and radiation. In New Human Physiology, 2nd ed.; Available online: http://www.zuniv.net/physiology/book/chapter21.html (accessed on 25 August 2021).
- Popovic, Z.; Momenroodaki, P.; Scheeler, R. Toward wearable wireless thermometers for internal body temperature measurements. IEEE Commun. Mag. 2014, 52, 118–125. [Google Scholar] [CrossRef]
- Yashar, E.; Vivian, N.; Ivan, P.-S.; Van Albert, D.; Mark, B.; Thomas, S.; Sessler, D.I. An evaluation of a zero-heat-flux cutaneous thermometer in cardiac surgical patients. Anesth. Analg. 2014, 119, 543–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carr, K.L. Microwave radiometry: Its importance to the detection of cancer. IEEE Trans. Microw. Theory Tech. 1989, 37, 1862–1869. [Google Scholar] [CrossRef]
- Garcia-Collado, A.J.; Molina-Cuberos, G.J.; Marti, J.; Nunez, M.J. Transference of electromagnetic energy to superficial human skin tissue. IEEE Lat. Am. Trans. 2009, 7, 170–175. [Google Scholar] [CrossRef]
- Park, W.; Jeong, J. Total Power Radiometer for Medical Sensor Applications Using Matched and Mismatched Noise Sources. Sensors 2017, 17, 2105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Livanos, N.-A.; Hammal, S.; Nikolopoulos, C.D.; Baklezos, A.T.; Capsalis, C.N.; Koulouras, G.E.; Charamis, P.I.; Vardiambasis, I.O.; Nassiopoulos, A.; Kostopoulos, S.A.; et al. Design and Interdisciplinary Simulations of a Hand-Held Device for Internal-Body Temperature Sensing Using Microwave Radiometry. IEEE Sens. J. 2018, 18, 2421–2433. [Google Scholar] [CrossRef]
- Momenroodaki, P.; Haines, W.; Fromandi, M.; Popovic, Z. Noninvasive Internal Body Temperature Tracking with Near-Field Microwave Radiometry. IEEE Trans. Microw. Theory Tech. 2018, 66, 2535–2545. [Google Scholar] [CrossRef]
- Ravi, V.M.; Akki, R.S.; Sugumar, S.; Venkata, K.C.; Arunachalam, K. Design and evaluation of medical microwave radiometer for measuring tissue temperature. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Momenroodaki, P.; Haines, W.; Popović, Z. Non-invasive microwave thermometry of multilayer human tissues. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium, Honololu, HI, USA, 4–9 June 2017; pp. 1387–1390. [Google Scholar] [CrossRef]
- Momenroodaki, P.; Popovic, Z.; Scheeler, R. 1.4-GHz Radiometer for Internal Body Temperature Measurements. In Proceedings of the 45th European Microwave Conference, Paris, France, 7–10 September 2015. [Google Scholar]
- Zhaofeng, P.I. Research on Microwave Radiometer Antenna for Human Body Temperature Measurement; Huazhong University of Science and Technology: Wuhan, China, 2015. [Google Scholar]
- Hao, M.; Ye, C.; Sun, L. Research on 89 GHz dual-polarization direct detection radiometer. In Proceedings of the 2016 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Chennai, India, 15–17 December 2016. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, J.; Wang, M.; Wang, M.; Chen, Z. A High Sensitivity Full W-Band Radiometer with Temperature-Compensation Function. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shanghai, China, 17–20 May 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Kai, F. System Design and Temperature Measurement Accuracy Analysis of Full-Polarization Microwave Radiometer; Xidian University: Xi’an, China, 2019. [Google Scholar]
- Holler, C.M.; Kaneko, T.; Jones, M.E.; Grainge, K.; Scott, P. A 6–12 GHz analogue lag-correlator for radio interferometry. Astron. Astrophys. 2007, 464, 795–806. [Google Scholar] [CrossRef] [Green Version]
- Maruyma, K.; Mizushina, S.; Sugiura, T.; van Leeuwen, G.M.J.; Hand, J.W.; Marrocco, G.; Bardati, F.; Edwards, A.D.; Azzopardi, D.; Land, D. Feasibility of noninvasive measurement of deep brain temperature in newborn infants by multifrequency microwave radiometry. IEEE Trans. Microw. Theory Tech. 2000, 48, 2141–2147. [Google Scholar]
- Hand, J.W.; van Leeuwen, G.M.J.; Mizushina, S.; van de Kamer, J.B.; Maruyama, K.; Sugiura, T.; Azzopardi, D.V.; Edwards, A.D. Monitoring of deep brain temperature in infants using multi-frequency microwave radiometry and thermal modelling. Phys. Med. Biol. 2001, 46, 1885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugiura, T.; Kouno, Y.; Hashizume, A.; Hirata, H.; Hand, J.W.; Okita, Y.; Mizushina, S. Five-band microwave radiometer system for non-invasive measurement of brain temperature in new-born infants: System calibration and its feasibility. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; pp. 2292–2295. [Google Scholar] [CrossRef]
- Fan, H. Study on Inversion Method of Microwave Nondestructive Measurement of Human Body Internal Temperature. Master’s Thesis, Engineering Huazhong University of Science and Technology, Wuhan, China, 2015. [Google Scholar]
- Bin, W. Calibration of AC Radiometer System; Huazhong University of Science and Technology: Wuhan, China, 2013. [Google Scholar]
- Zhiyong, Z. Microwave Radiometer front End and Its Wide if superheterodyne Model and Application; University of Electronic Science and Technology of China: Chengdu, China, 2019. [Google Scholar]
- Ubaichin, A.V.; Zhuk, G.G.; Uulu, T.A. High Stability Microwave Radiometer. In Proceedings of the 19th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 29 June–3 July 2018; pp. 104–109. [Google Scholar] [CrossRef]
- Quenton, B. A Microwave Radiometer for Close Proximity Core Body Temperature Monitoring: Design, Development, and Experimentation; University of South Florida: Tampa, FL, USA, 2010. [Google Scholar]
- Zhang, X.; Chen, Y.; Xie, Y.; Zhan, A. Research on a Pyramidal Horn Antenna in W-Band. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Lahore, Pakistan, 22–23 February 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Xianghua, Y. Design of Square Circular-polarized Horn Antenna. Ann. Sci. Technol. China Acad. Eng. Phys. 2003, 1, 294–295. [Google Scholar]
- Kordas, G.; Baltzis, K.B.; Miaris, G.S.; Sahalos, J.N. Pyramidal-horn design under constraints on half-power beamwidth. IEEE Antennas Propag. Mag. 2002, 44, 102–108. [Google Scholar] [CrossRef]
- Nanzer, J.A. Microwave and Millimeter-Wave Remote Sensing for Security Applications; Artech House: Norwood, MA, USA, 2012; p. 372. ISBN 978-1-60807-172-2. [Google Scholar]
- Jinzhan, G. Detection of Weak Signals, 2nd ed.; Tsinghua University Press: Beijing, China, 2011; 360p. [Google Scholar]
- Kashif, M.; Hu, A.; Miao, J. Design and implementation of an analog complex correlator for passive millimeter wave imaging system. In Proceedings of the 13th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 12–16 January 2016; pp. 611–616. [Google Scholar] [CrossRef]
- Vaks, V.L.; Gaikovich, K.P.; Reznik, A.N. Thermal near field and the possibilities of its use for in-depth temperature diagnostics of media. Radiophys. Quantum Electron. 2002, 45, 7–22. [Google Scholar] [CrossRef]








| Microwave Frequency | 4–6 GHz | 8–12 GHz | 12–16 GHz | 14–18 GHz |
|---|---|---|---|---|
| Skin depth of dry skin (mm) | 8.2–13.9 | 2.9–5.3 | 1.9–2.9 | 1.5–23 |
| Skin depth of wet skin (mm) | 7.4–12.7 | 2.7–4.9 | 1.8–2.7 | 1.5–2.2 |
| Human tissue | Subcutaneous tissue | Corium layer and subcutaneous tissue | Corium layer | Epidermal layer and corium layer |
| Antenna Frequency | |||
|---|---|---|---|
| 4–6 GHz | 88.04 mm | 89.05 mm | 49.08 mm |
| 8–12 GHz | 46.63 mm | 46.23 mm | 29.01 mm |
| 12–16 GHz | 34.47 mm | 34.18 mm | 21.14 mm |
| 14–18 GHz | 30.16 mm | 29.91 mm | 17.70 mm |
| Antenna Frequency | VSWR | Far-Field Radiation Model | Pre/Post Suppression Ratio | Far-Field Gain | 3 dB Beam Angle |
|---|---|---|---|---|---|
| 4–6 GHz | ≤1.98 | 38.1 V/m | 18.65 | 15.88 dB | 38.5° |
| 8–12 GHz | ≤1.48 | 34.9 V/m | 17.46 | 14.90 dB | 29.4° |
| 12–16 GHz | ≤1.44 | 34.7 V/m | 16.44 | 14.36 dB | 30.2° |
| 14–18 GHz | ≤1.41 | 35.0 V/m | 19.68 | 14.45 dB | 30.9° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Liu, J.; Ma, J.; Zhang, K.; Sun, Z.; Wu, Q.; Wang, H.; Liu, Y. Design and Implementation of Multiband Noncontact Temperature-Measuring Microwave Radiometer. Micromachines 2021, 12, 1202. https://doi.org/10.3390/mi12101202
Sun G, Liu J, Ma J, Zhang K, Sun Z, Wu Q, Wang H, Liu Y. Design and Implementation of Multiband Noncontact Temperature-Measuring Microwave Radiometer. Micromachines. 2021; 12(10):1202. https://doi.org/10.3390/mi12101202
Chicago/Turabian StyleSun, Guangmin, Jie Liu, Jingyan Ma, Kai Zhang, Zhenlin Sun, Qiang Wu, Hao Wang, and Yiming Liu. 2021. "Design and Implementation of Multiband Noncontact Temperature-Measuring Microwave Radiometer" Micromachines 12, no. 10: 1202. https://doi.org/10.3390/mi12101202
APA StyleSun, G., Liu, J., Ma, J., Zhang, K., Sun, Z., Wu, Q., Wang, H., & Liu, Y. (2021). Design and Implementation of Multiband Noncontact Temperature-Measuring Microwave Radiometer. Micromachines, 12(10), 1202. https://doi.org/10.3390/mi12101202







