Modeling and Analysis of Micro Surface Topography from Ball-End Milling in a Trochoidal Milling Mode
Abstract
:1. Introduction
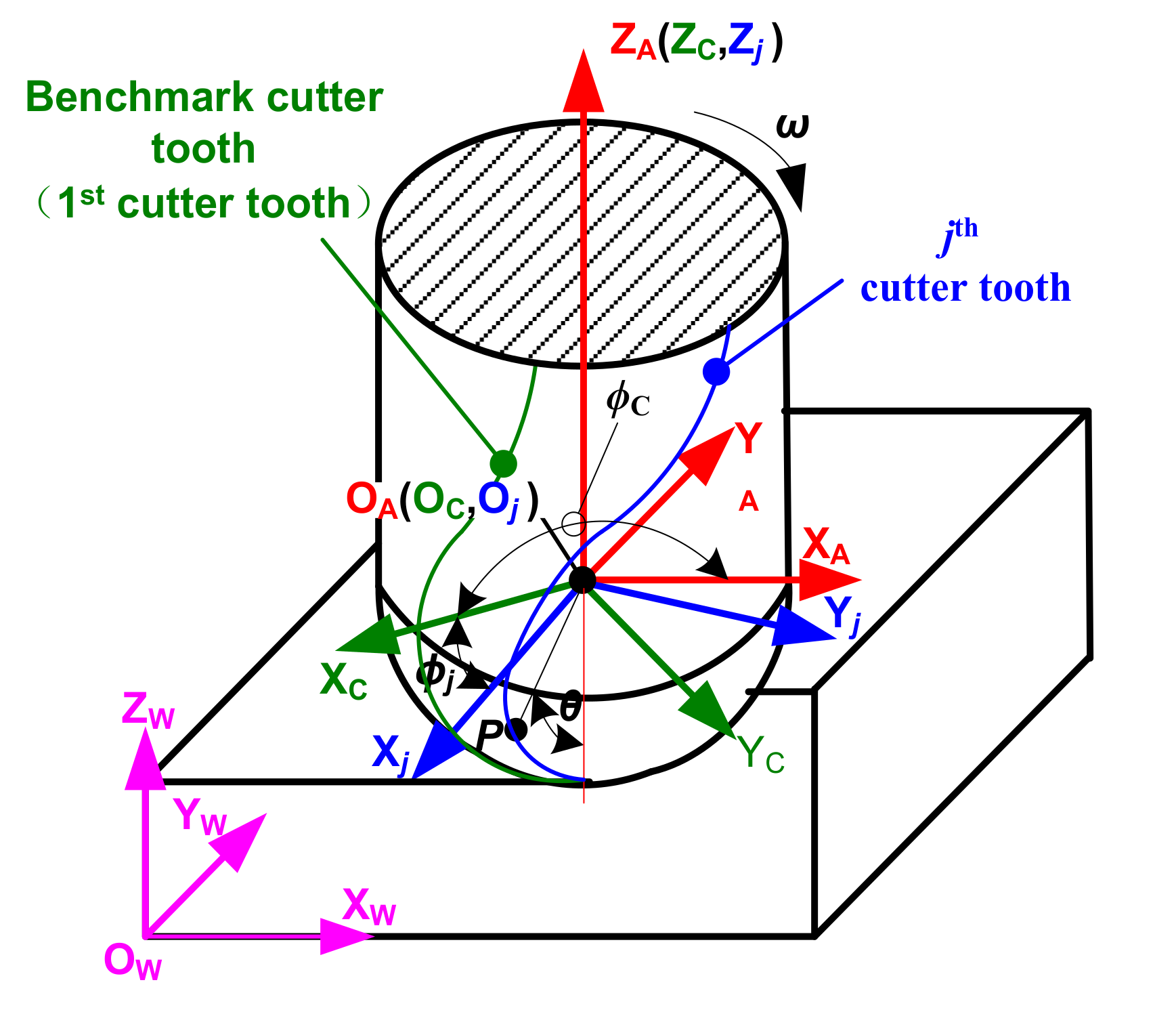
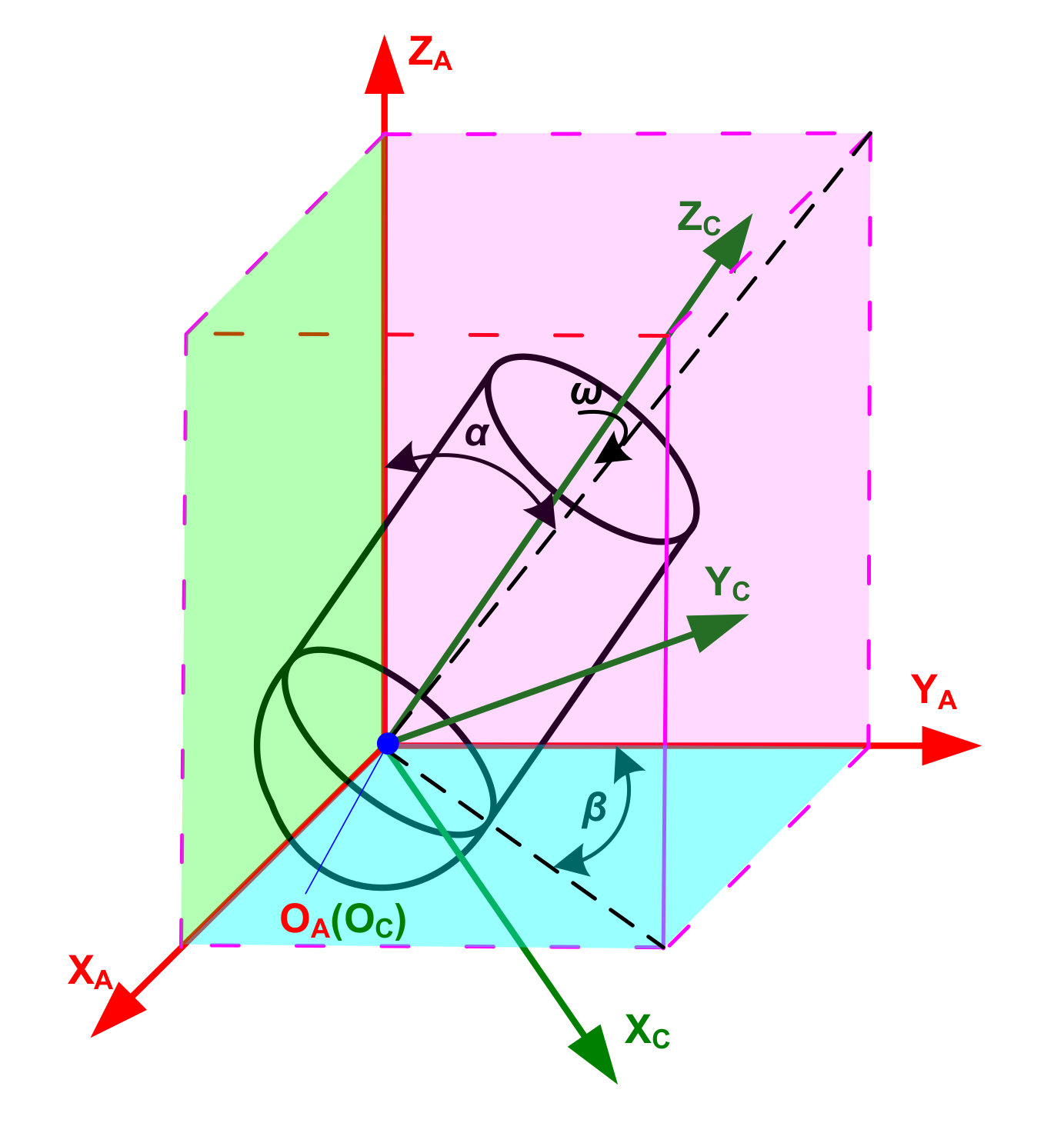
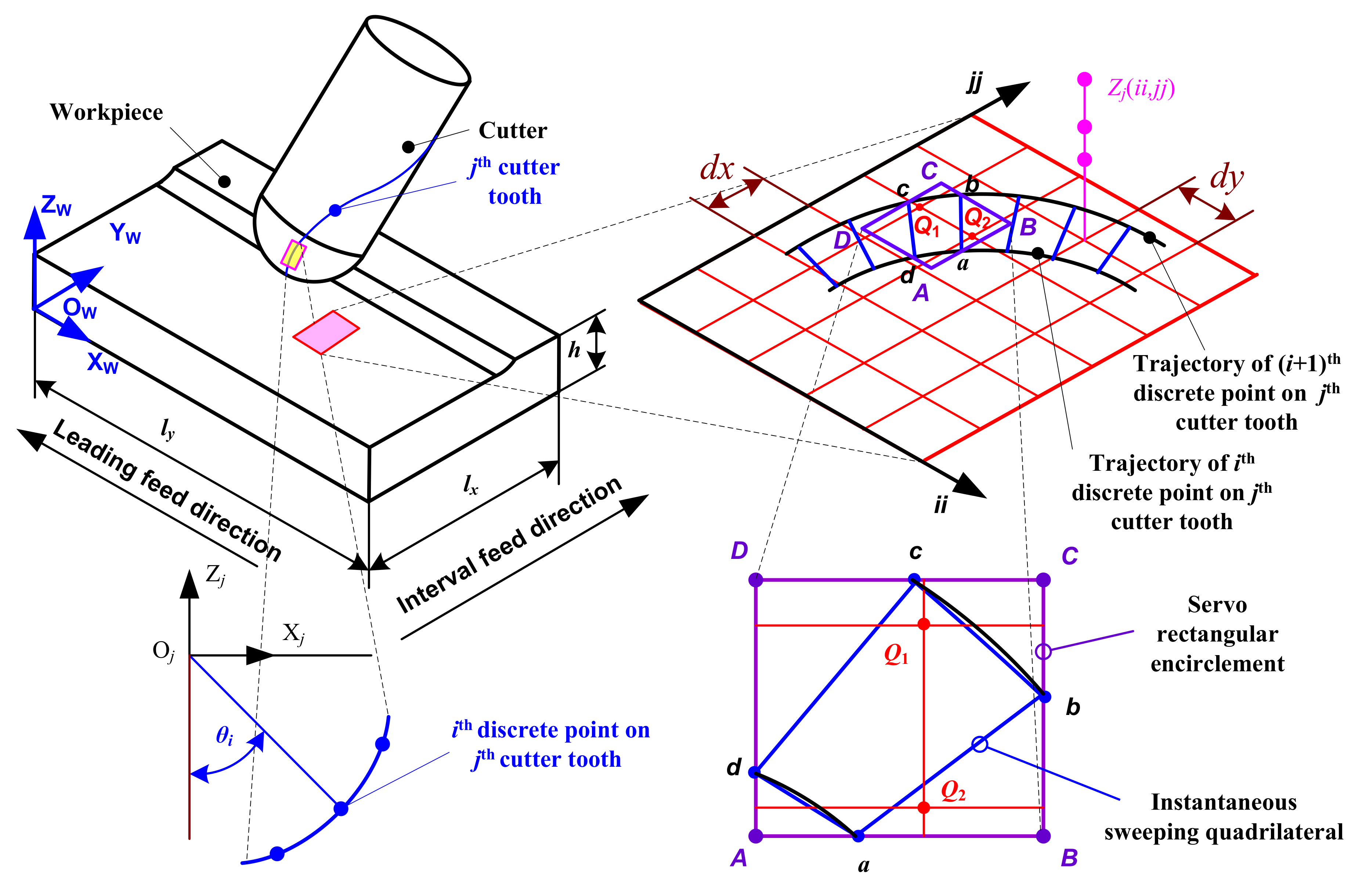
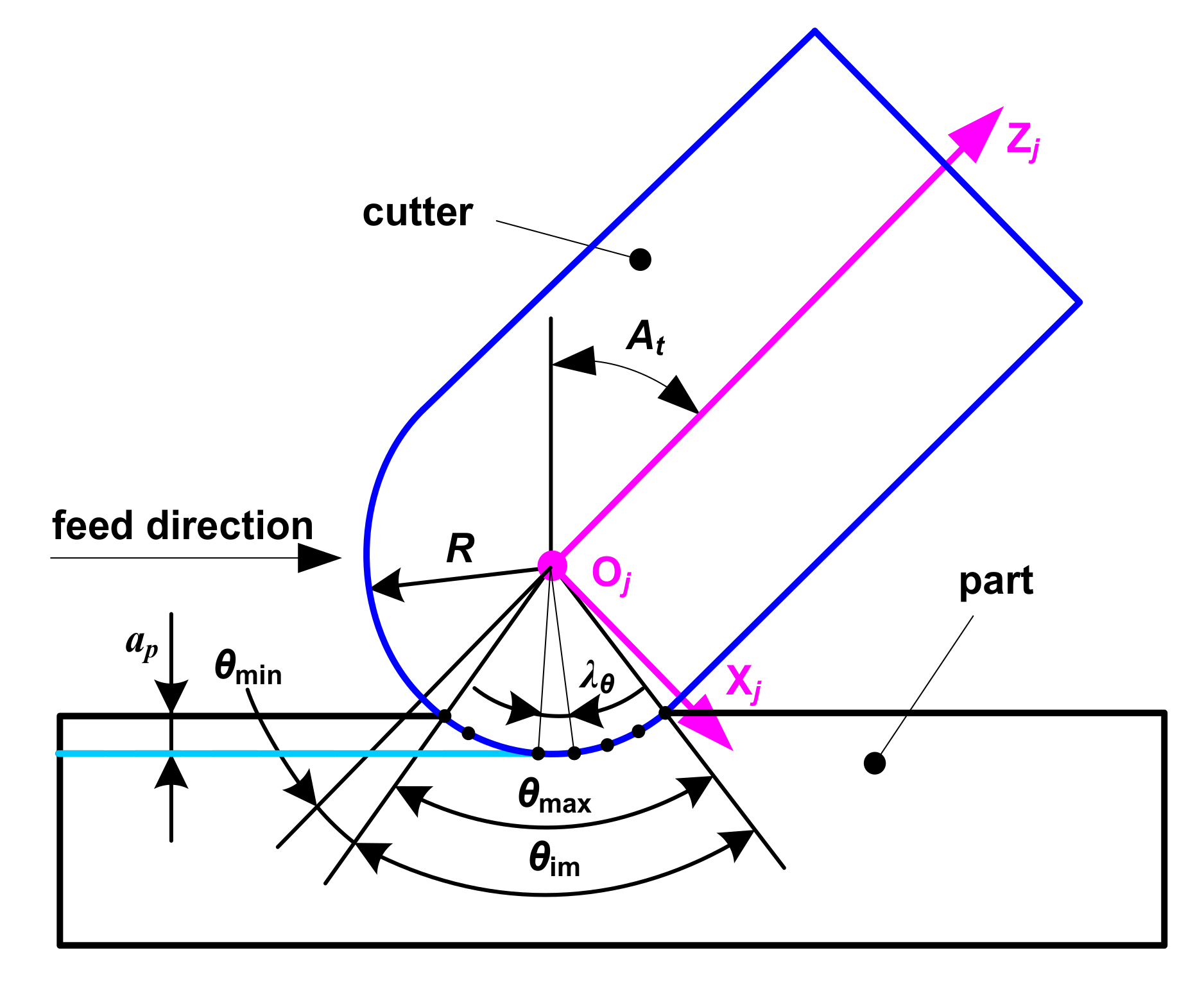
2. Motion Trajectory Equation of a Ball-End Milling Cutter Tooth
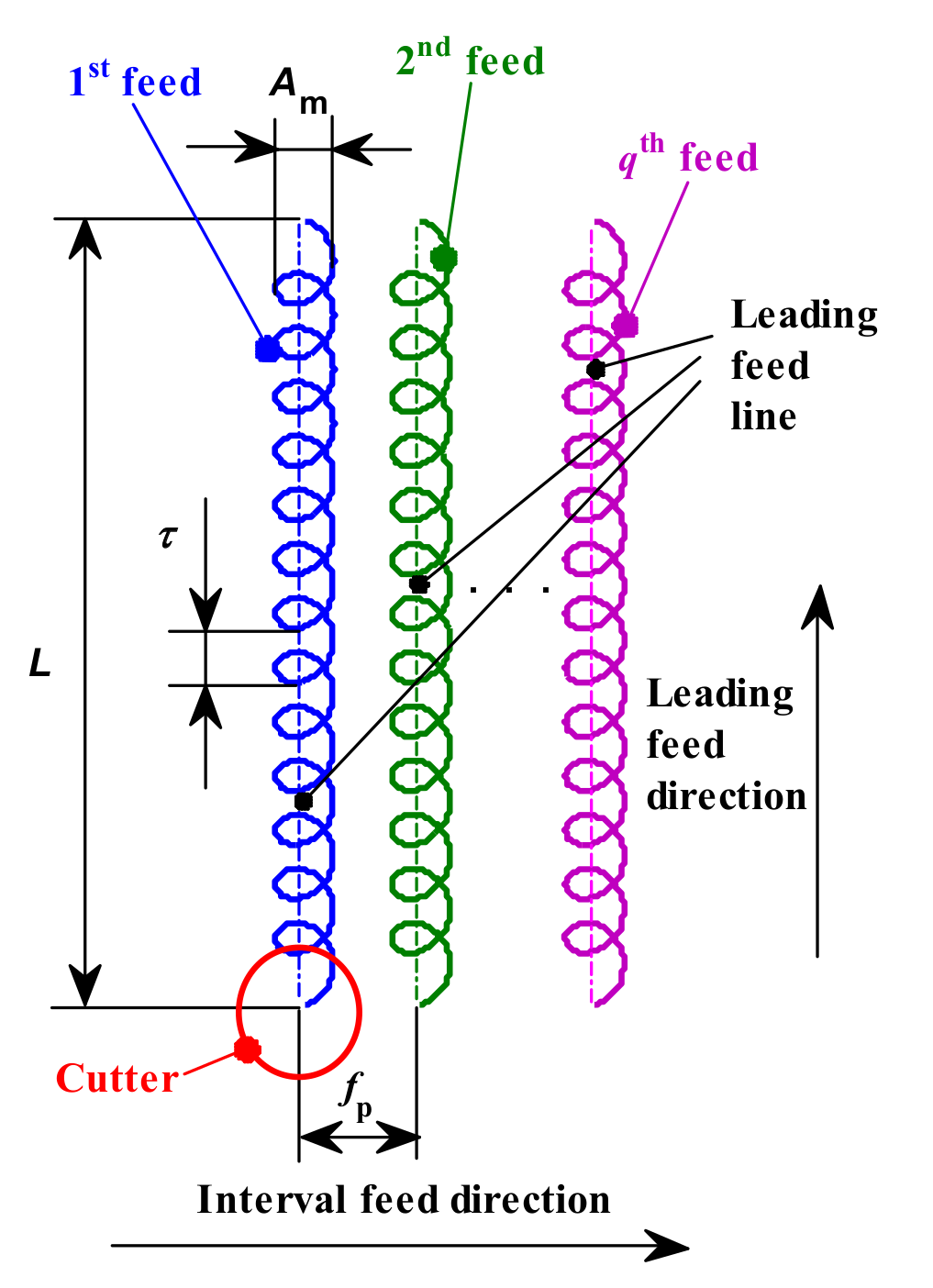
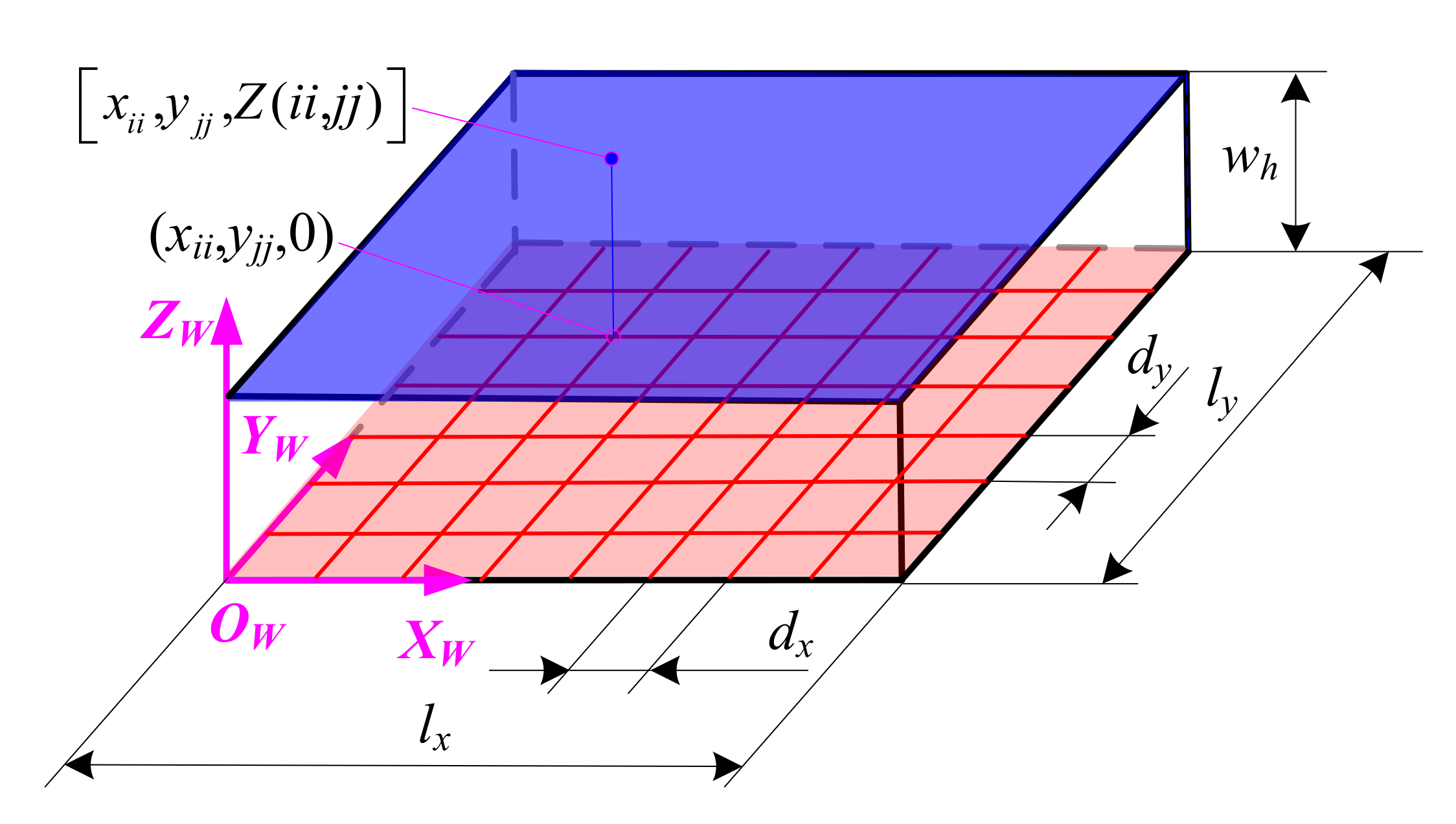
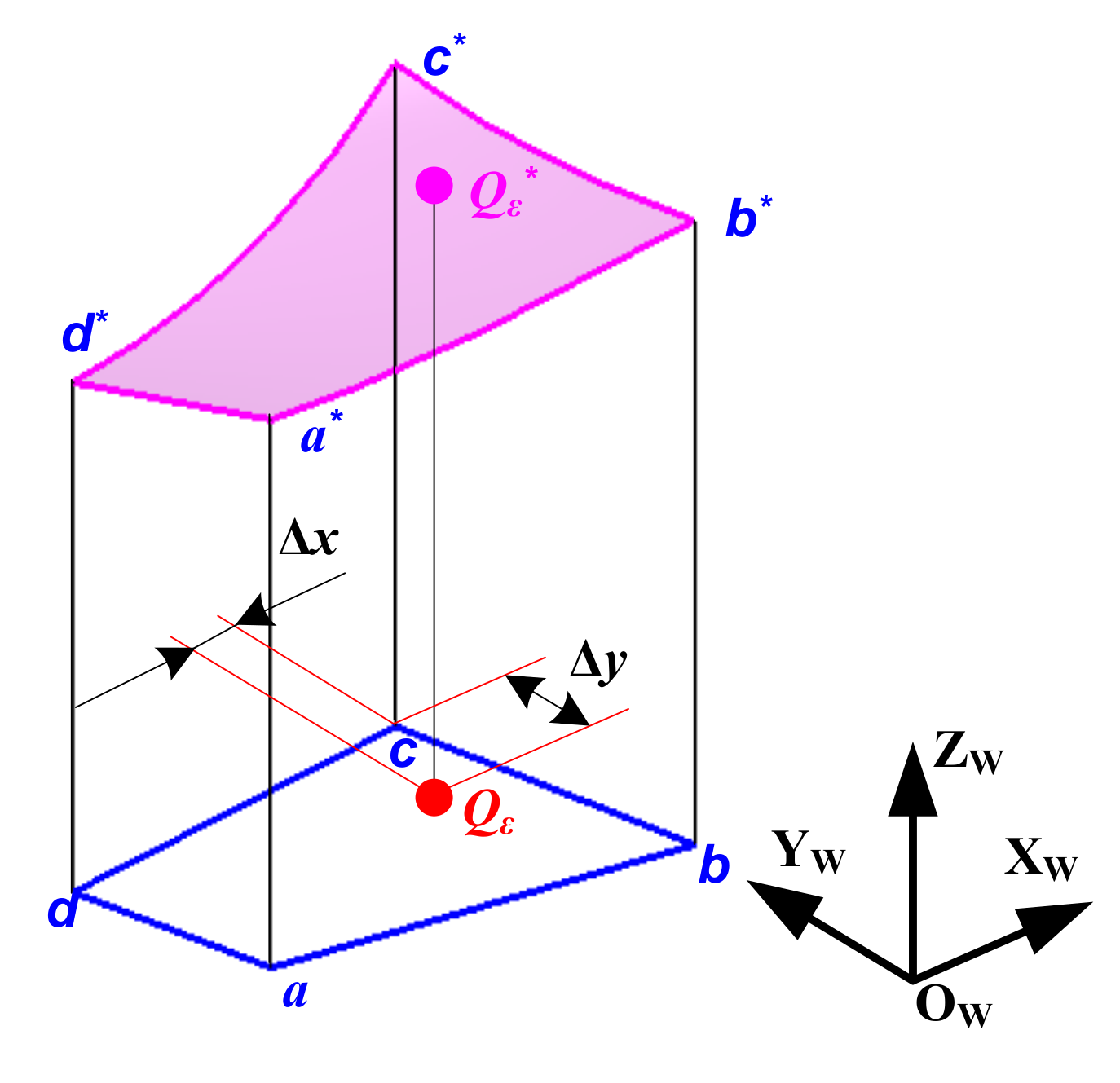
3. Simulation Method for Ball-End Trochoidal Milling Micro Surface Topography
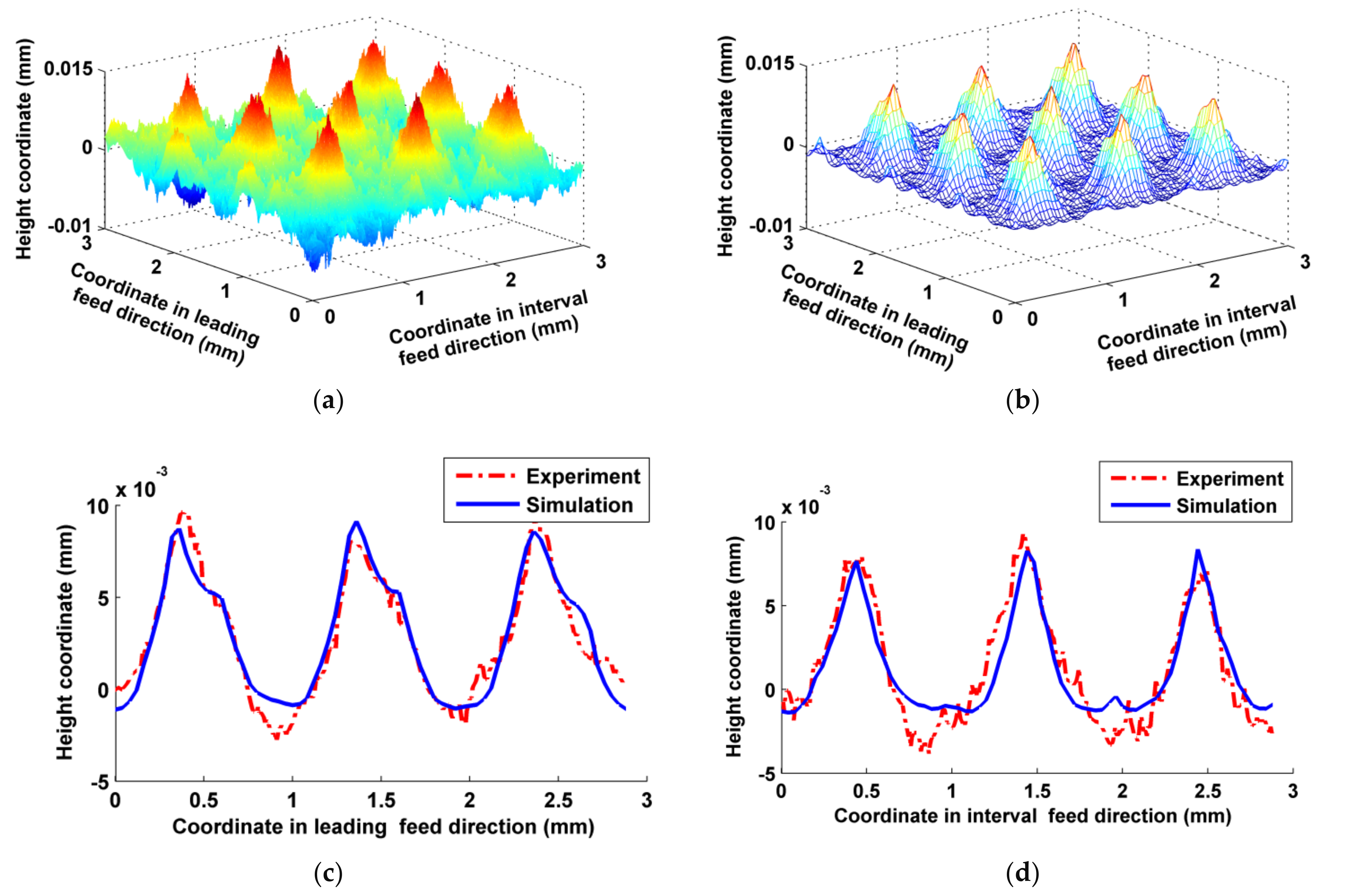
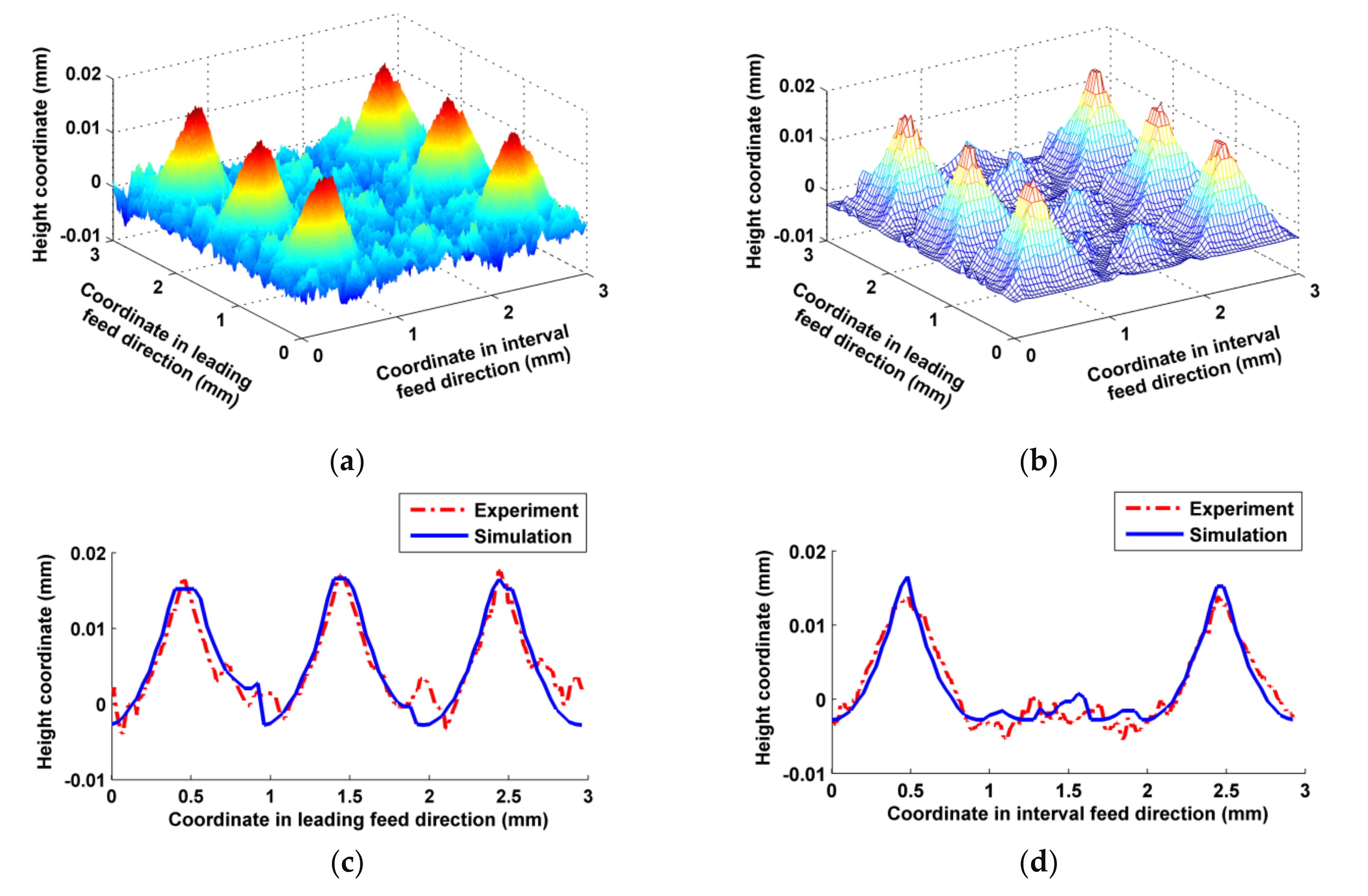
4. Experimental Validation
5. Simulation Analysis
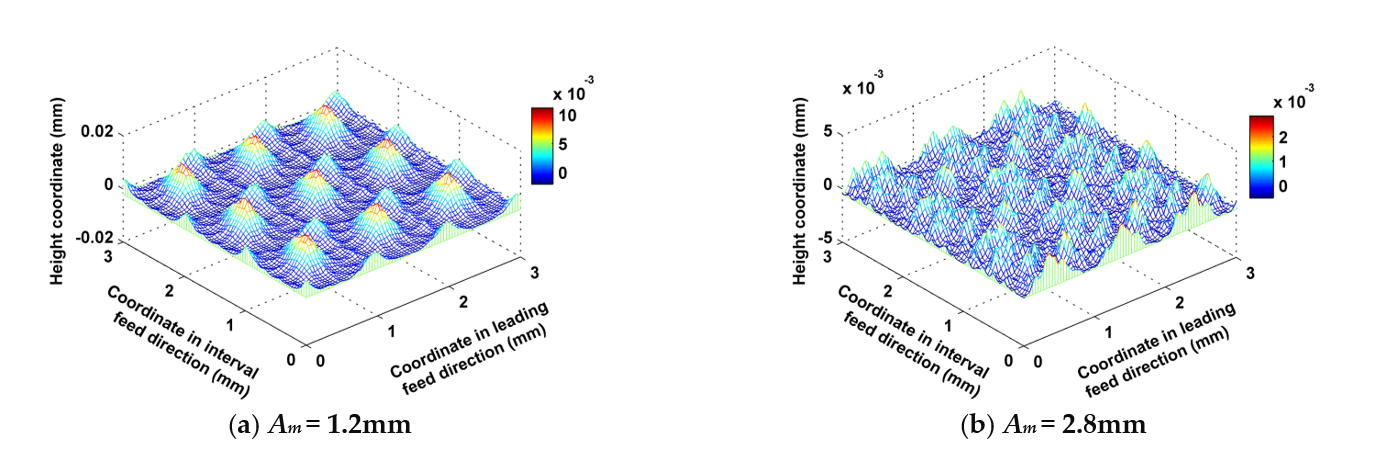
5.1. Influence of the Amplitude of the Trochoid on the Micro Surface Topography
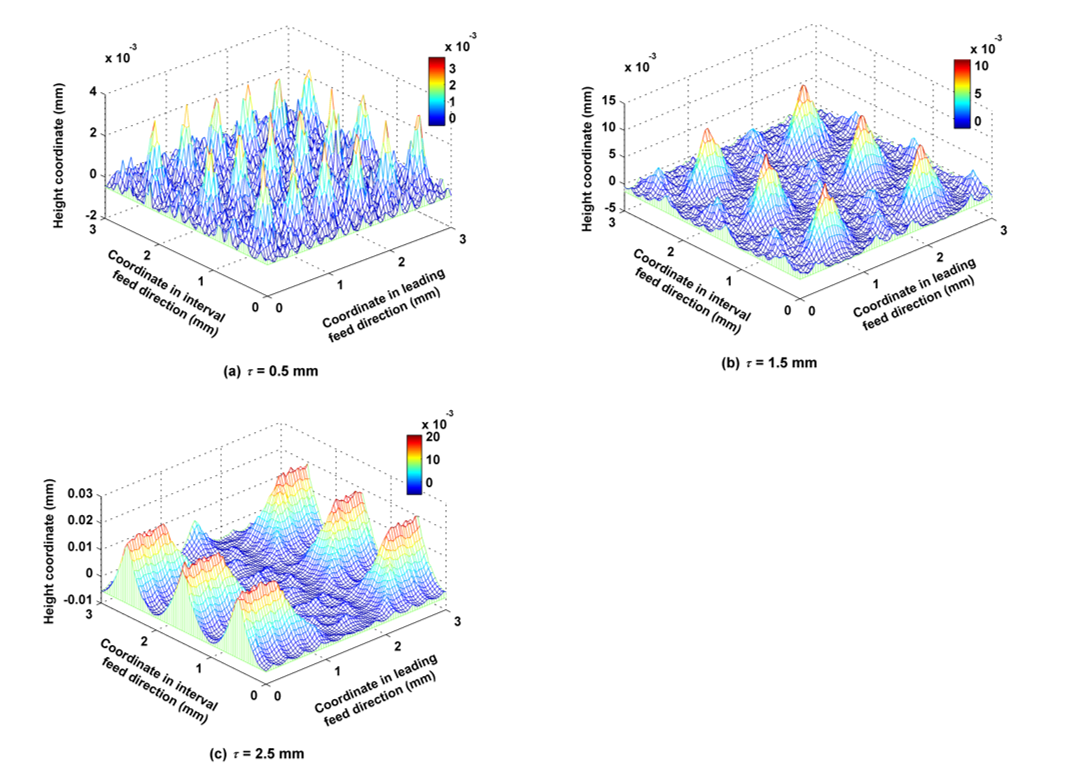
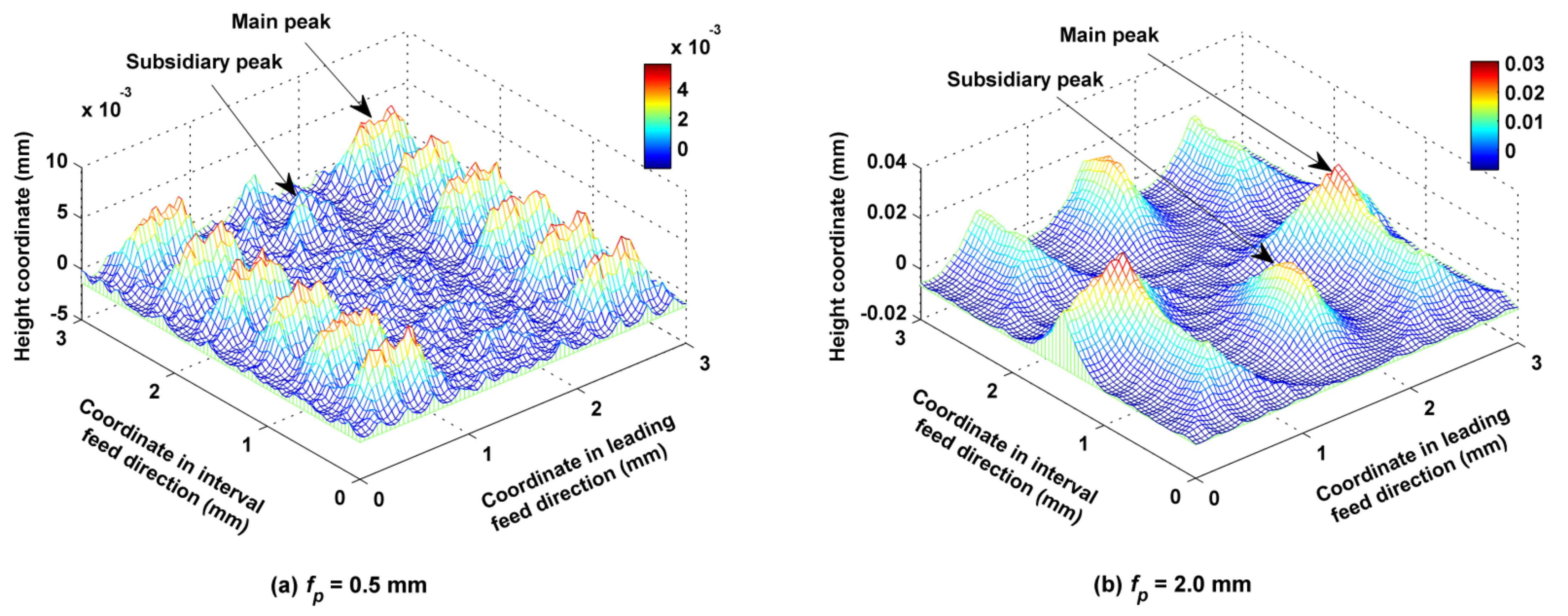
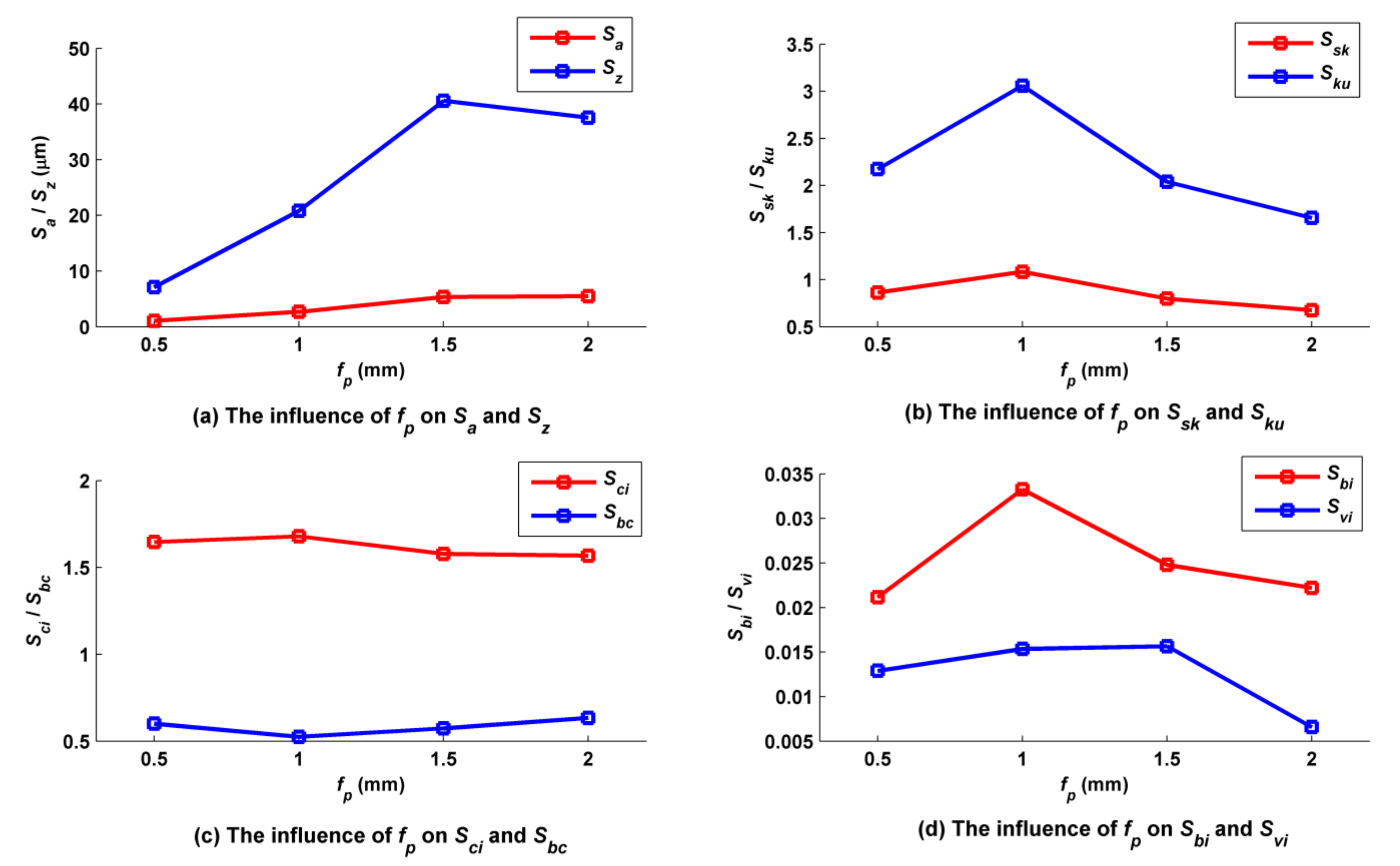
5.2. Influence of the Pitch of the Trochoid on the Micro Surface Topography
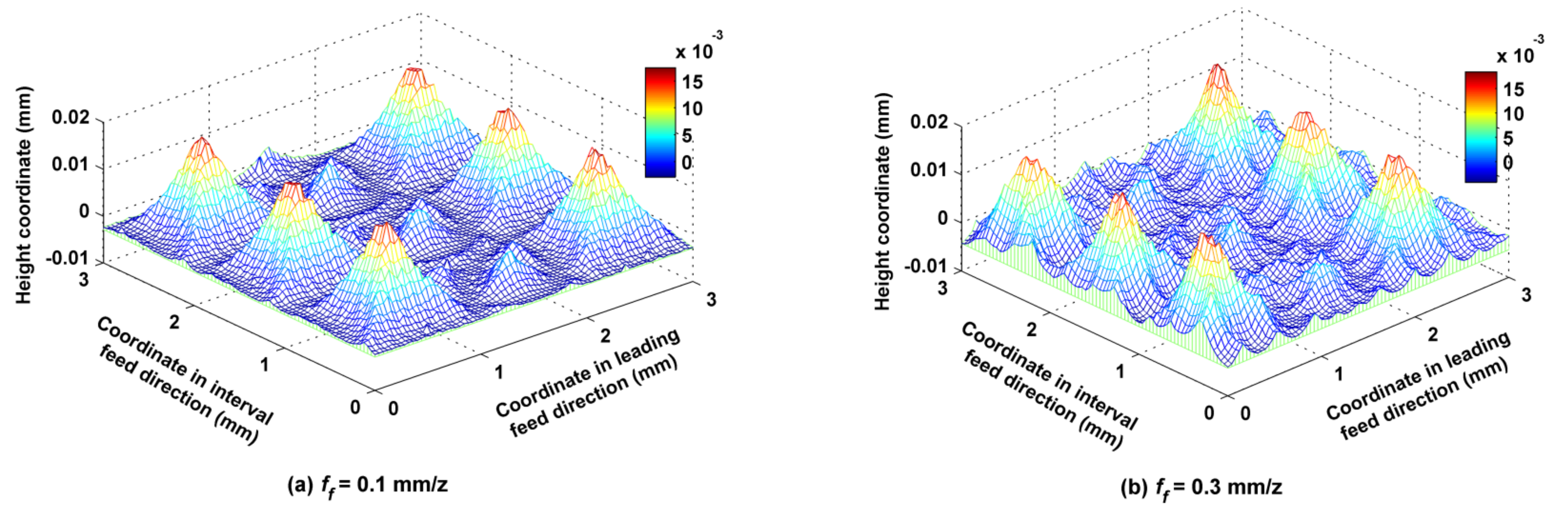
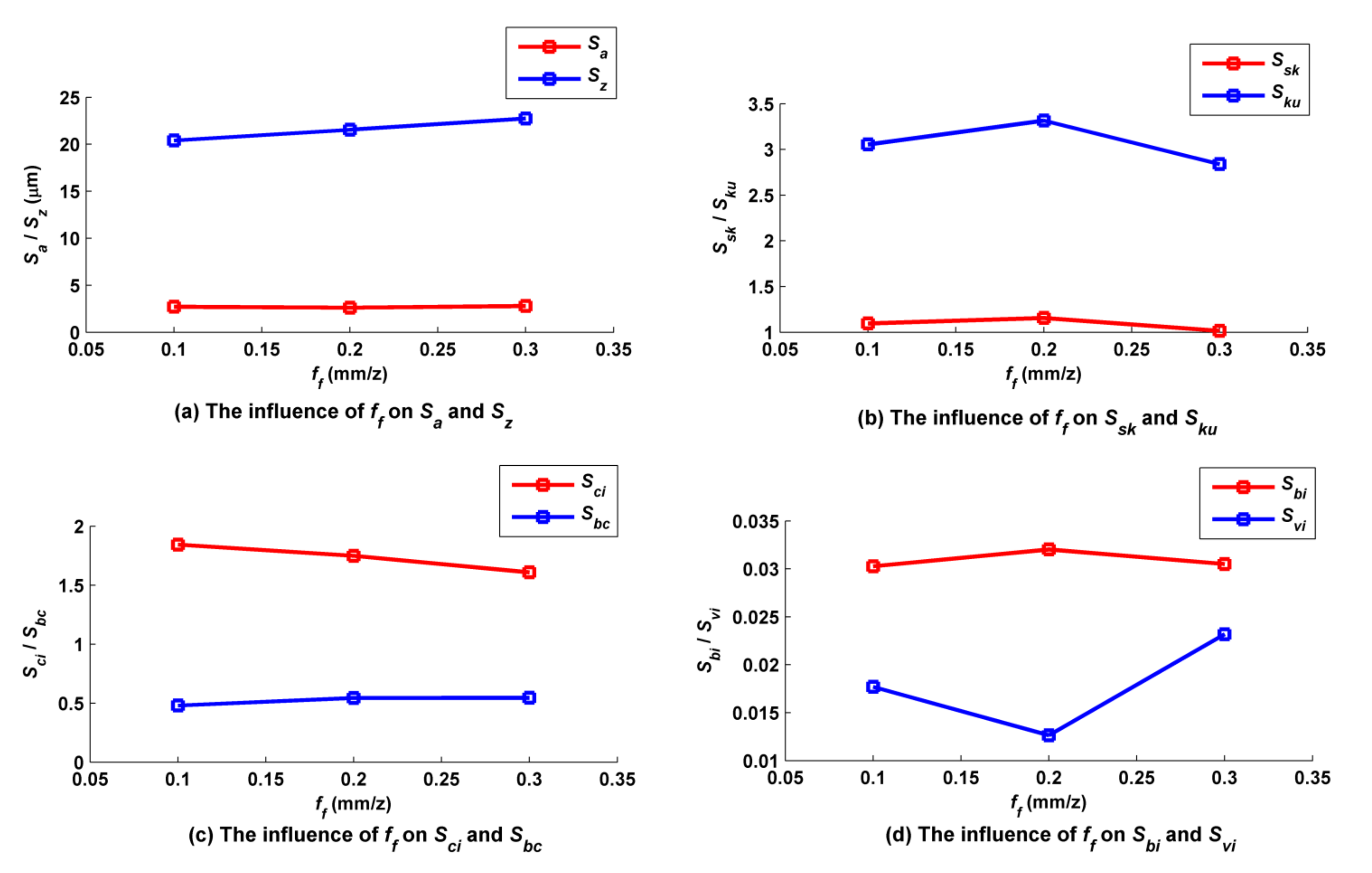
5.3. Influence of Feed per Tooth on the Micro Surface Topography
5.4. Influence of Stepover on the Micro Surface Topography
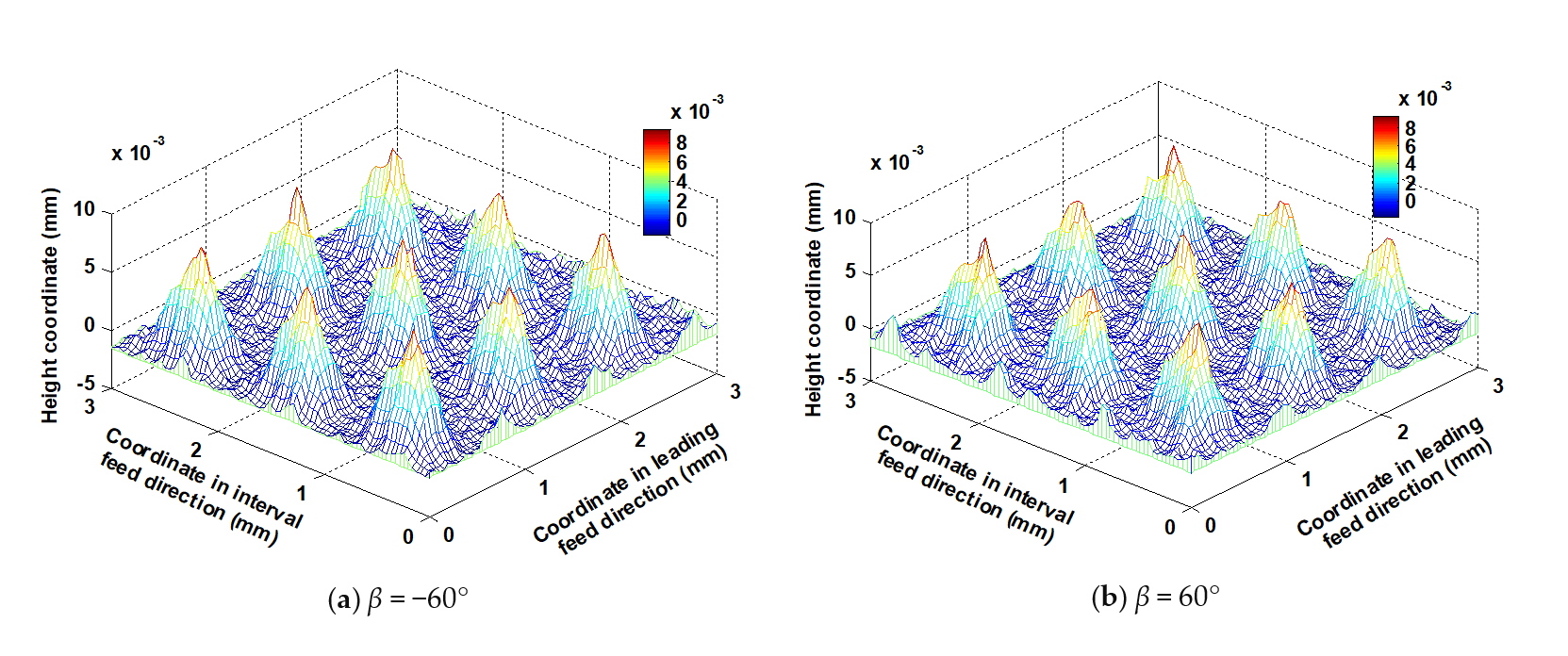
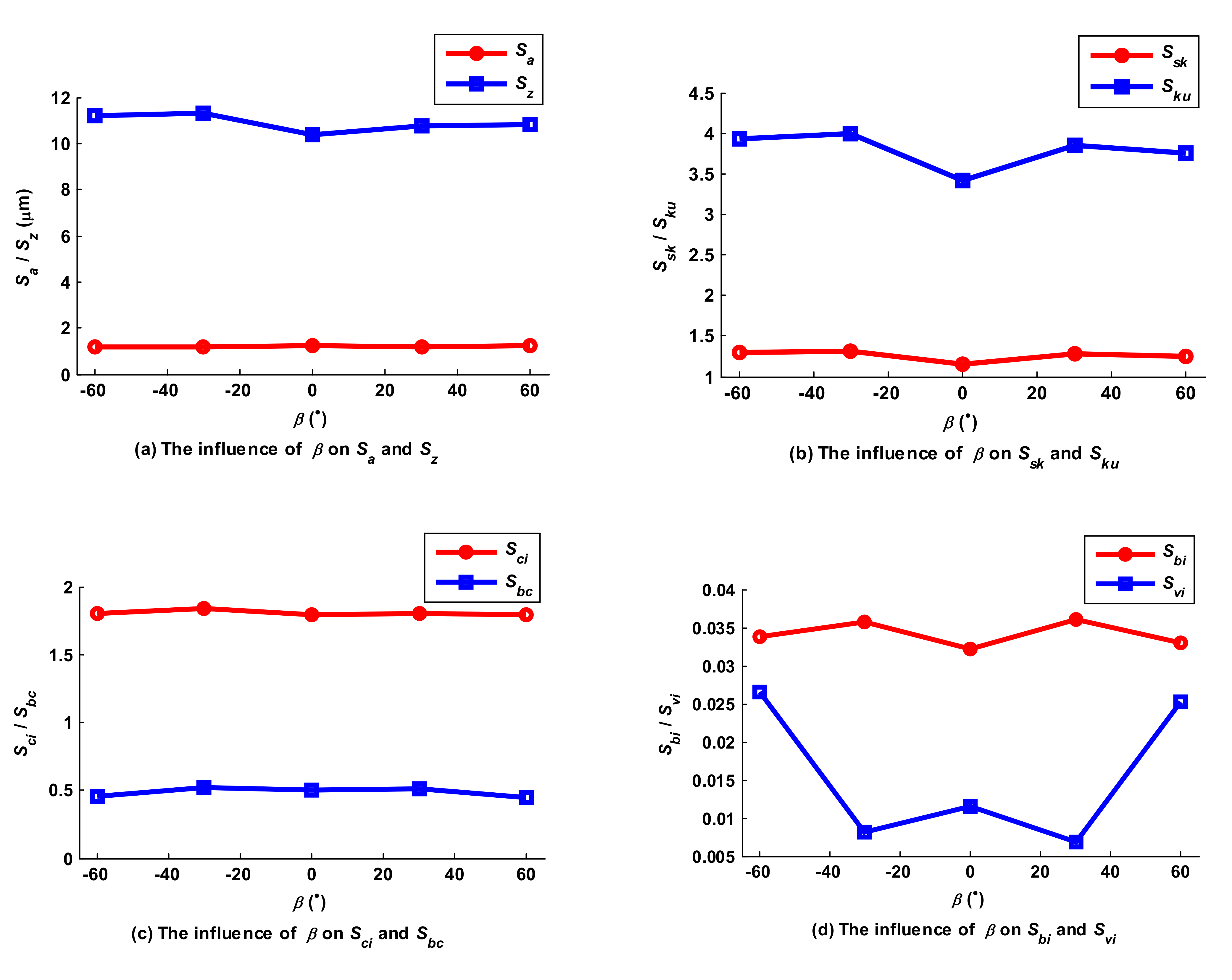
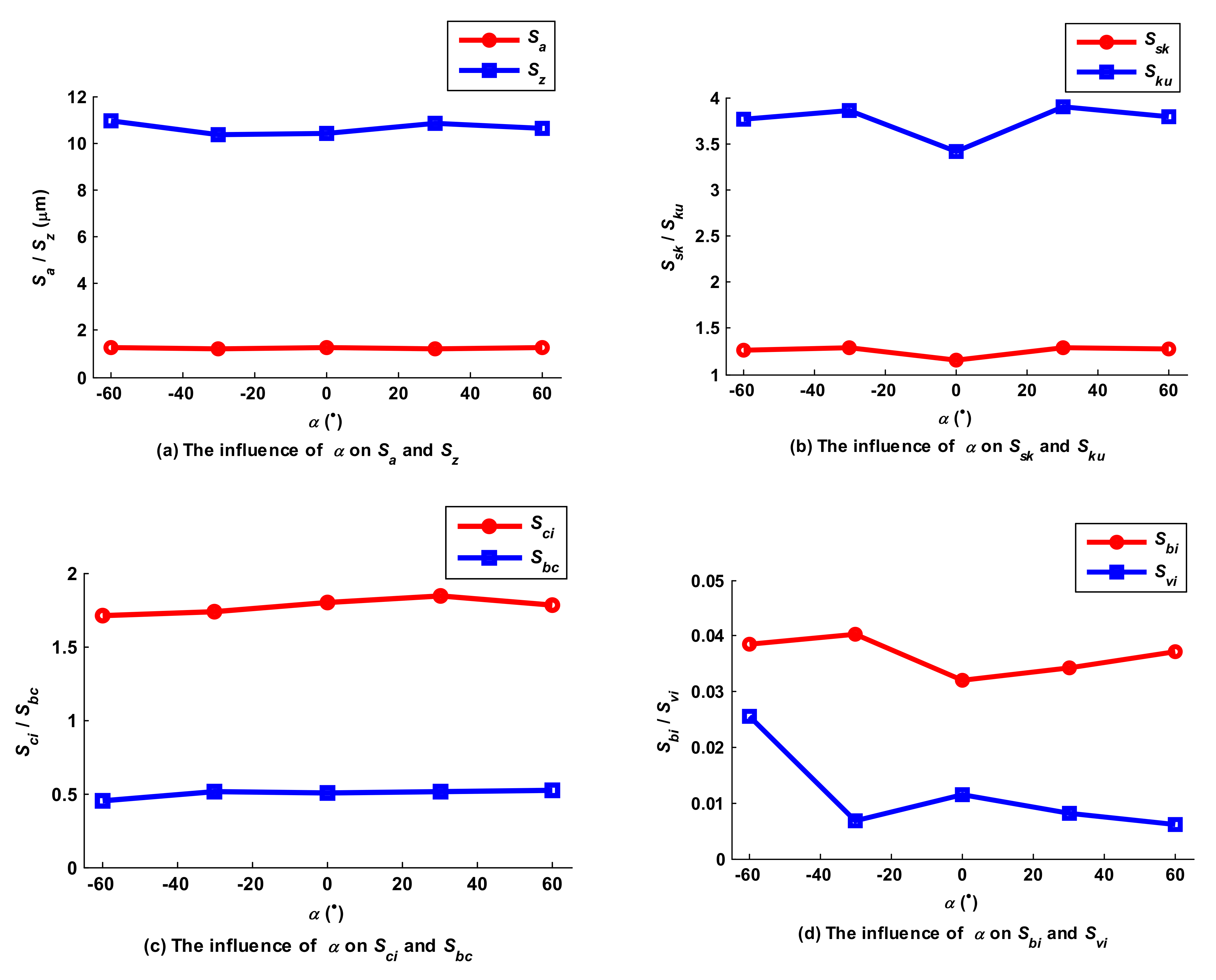
5.5. Influence of Lead Angle on the Micro Surface Topography
5.6. Influence of Tilt Angle on the Micro Surface Topography
6. Conclusions
- The modeling of ball-end trochoidal milling micro surface topography is based on the following assumptions: the trajectory of the cutter tooth can be established by homogeneous coordinate matrix transformation; the part, cutter and milling time are reasonably discrete; the fall-in points of the part are detected through follow-up matrix encirclement and the angle accumulation method; and the height coordinates of the fall-in points are calculated by a Taylor formula-based interpolation method. The simulation and experiment results had good agreement on three-dimensional micro surface topographies, and the differences in Ra in the sectional profiles were less than 10% in both vertical milling and inclined milling. The t-test values of these sectional profiles all satisfied |t| < 1.667, which means there were no significant differences between the simulation and experiment. Hence, this model can be used to substitute for experiments to research ball-end trochoidal milling micro surface topography.
- The rules governing the influence of cutting parameters, such as amplitude and pitch of the trochoid, feed per tooth, stepover, cutter lead angle and tilt angle, on the amplitude and functional parameters of micro surface topography were derived from the simulated data. Unlike in common milling modes, amplitude and pitch of the trochoid and stepover were the main factors which influenced the resulting surface characteristics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, X.H.; Wang, J.J.; Wang, X.C. Ultrasonic vibration-assisted milling of aluminum alloy. Int. J. Adv. Manuf. Technol. 2012, 63, 41–49. [Google Scholar] [CrossRef]
- Tao, G.; Ma, C.; Bai, L.; Shen, X.; Zhang, J. Feed-direction ultrasonic vibration–assisted milling surface texture formation. Adv. Manuf. Process. 2016, 32, 193–198. [Google Scholar] [CrossRef]
- Suárez, A.; Veiga, F.; Lacalle, L.N.; Polvorosa, R.; Lutze, S.; Wretland, A. Effects of Ultrasonics-Assisted Face Milling on Surface Integrity and Fatigue Life of Ni-Alloy 718. J. Mater. Eng. Perform. 2016, 25, 5076–5086. [Google Scholar] [CrossRef]
- Otkur, M.; Lazoglu, I. Trochoidal milling. Int. J. Mach. Tools Manuf. 2007, 47, 1324–1332. [Google Scholar] [CrossRef]
- Wu, S.; Ma, W.; Li, B.; Wang, C. Trochoidal machining for the high-speed milling of pockets. J. Mater. Process. Technol. 2016, 233, 29–43. [Google Scholar]
- Uhlmann, E.; Fürstmann, P.; Rosenau, B.; Gebhard, S.; Gerstenberger, R.; Müller, G. The Potential of Reducing the Energy Consumption for Machining TiAl6V4 by Using Innovative Metal Cutting Processes. Glob. Conf. Sustain. Manuf. 2013, 646–651. [Google Scholar]
- Polishetty, A.; Goldberg, M.; Littlefair, G.; Puttaraju, M.; Patil, P.; Kalra, A. A Preliminary Assessment of Machinability of Titanium Alloy Ti 6AL 4V During thin Wall Machining Using Trochoidal Milling. Procedia Eng. 2014, 97, 357–364. [Google Scholar] [CrossRef] [Green Version]
- Pleta, A. Investigation of Trochoidal Milling in Nickel-Based Superalloy Inconel 738 and Comparison With End Milling. J. Vet. Behav. Clin. Appl. Res. 2014, 8, 36–37. [Google Scholar]
- Wu, S.; Zhao, Z.; Wang, C.Y.; Xie, Y.; Ma, W. Optimization of toolpath with circular cycle transition for sharp corners in pocket milling. Int. J. Adv. Manuf. Technol. 2016, 1, 1–11. [Google Scholar] [CrossRef]
- Ferreira, J.C.E.; Ochoa, D.M. A Method for Generating Trochoidal Tool Paths for 2½D Pocket Milling Process Planning with Multiple Tools. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1287–1298. [Google Scholar] [CrossRef]
- Zhang, X.H.; Peng, F.Y.; Qiu, F.; Yan, R.; Li, B. Prediction of Cutting Force in Trochoidal Milling Based on Radial Depth of Cut. Adv. Mater. Res. 2014, 852, 457–462. [Google Scholar] [CrossRef]
- Wang, H.X.; Zong, W.J.; Sun, T.; Liu, Q. Modification of three dimensional topography of the machined KDP crystal surface using wavelet analysis method. Appl. Surf. Sci. 2010, 256, 5061–5068. [Google Scholar] [CrossRef]
- Zhang, Y. Recent Patents on the Design of Surface Topography for Improving the Performance of a Lubricated Sliding Contact. Recent Pat. Mech. Eng. 2015, 8, 59–63. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, J. A study on the effects of surface dimple geometry on fretting fatigue performance. Int. J. Precis. Eng. Manuf. 2015, 16, 707–713. [Google Scholar] [CrossRef]
- Ait-Sadi, H.; Hemmouche, L.; Hattali, L.; Britah, M.; Iost, A.; Mesrati, N. Effect of nanosilica additive particles on both friction and wear performance of mild steel/CuSn/SnBi multimaterial system. Tribol. Int. 2015, 90, 372–385. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.P.; Zhang, J.J.; Xu, G.Y.; Liu, J.H. Simulation of Micro Geomatrical Texture of Surface Milled by Face Milling Cutter. J. Syst. Simul. 2009, 21, 2496–2499. (In China) [Google Scholar]
- Liu, L.J.; Lü, M.; Wu, W.G.; Zhu, X.J. Experimental Study on the Chip Morpholgy in High Speed Milling Ti-6Al-4V Alloy. Chin. J. Mech. Eng. 2015, 51, 196–205. (In China) [Google Scholar] [CrossRef]
- Liang, X.G.; Yao, Z.Q. Dynamic-based Simulation for Machined Surface Topography in 5-axis Ball-end Milling. Chin. J. Mech. Eng. 2013, 49, 171–178. (In China) [Google Scholar] [CrossRef]
- Liu, N.; Loftus, M.; Whitten, A. Surface finish visualisation in high speed, ball nose milling applications. Int. J. Mach. Tools Manuf. 2005, 45, 1152–1161. [Google Scholar] [CrossRef]
- Sadeghi, M.H.; Haghighat, H.; Elbestawi, M.A. A solid modeler based ball-end milling process simulation. Int. J. Adv. Manuf. Technol. 2003, 22, 775–785. [Google Scholar] [CrossRef]
- Imani, B.M.; Elbestawi, M.A. Geometric Simulation of Ball-End Milling Operations. J. Manuf. Sci. Eng. 2001, 123, 177. [Google Scholar] [CrossRef] [Green Version]
- Jung, T.-S.; Yang, M.-Y.; Lee, K.-J. A new approach to analysing machined surfaces by ball-end milling, part II. Int. J. Adv. Manuf. Technol. 2004, 25, 841–849. [Google Scholar] [CrossRef]
- Jung, T.-S.; Yang, M.-Y.; Lee, K.-J. A new approach to analysing machined surfaces by ball-end milling, part I. Int. J. Adv. Manuf. Technol. 2004, 25, 833–840. [Google Scholar] [CrossRef]
- Yang, J.X.; Guan, J.Y.; Xue-Feng, Y.E.; Bo, L.I.; Cao, Y.L. Effects of geometric and spindle errors on the quality of end turning surface. J. Zhejiang Univ. A 2015, 16, 371–386. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.Y.; Liang, Z.Q.; Wang, X.B.; Zhou, T.F.; Zhao, W.X.; Wu, Y.B.; Jiao, L. Research on Modeling and Simulation of Surface Microtopography in Ultrasonic Vibration Spiral Grinding. Chin. J. Mech. Eng. 2017, 53, 83–89. (In China) [Google Scholar] [CrossRef]
- Hu, W.; Guan, J.; Li, B.; Cao, Y.; Yang, J. Influence of Tool Assembly Error on Machined Surface in Peripheral Milling Process. Procedia CIRP 2015, 27, 137–142. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.Q.; Liu, Q.; Zheng, M.; Wang, X. Z-map based surface machining accuracy in high speed peripherial milling of flexiable system. J. HuaZhong Univ. Sci. Technol. 2012, 40, 52–55. (In China) [Google Scholar]
- Dang, J.W.; Zhang, W.H.; Wan, M.; Yang, J.; Wang, Y.T. A Novel Model for Predicting Machining Error in Peripheral Milling Process. Chin. J. Mech. Eng. 2011, 17, 150–155. (In China) [Google Scholar] [CrossRef]
- Arizmendi, M.; Campa, F.J.; Fernández, J.; López de Lacalle, L.N.; Gil, A.; Bilbao, E.; Veiga, F.; Lamikiz, A. Model for surface topography prediction in peripheral milling considering tool vibration. CIRP Ann.-Manuf. Technol. 2009, 58, 93–96. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Couey, J.; Marsh, E.; Mauntler, N.; Hughes, D. Runout effects in milling: Surface finish, surface location error, and stability. Int. J. Mach. Tools Manuf. 2007, 47, 841–851. [Google Scholar] [CrossRef]
- Omar, O.E.E.K.; El-Wardany, T.; Ng, E.; Elbestawi, M.A. An improved cutting force and surface topography prediction model in end milling. Int. J. Mach. Tools Manuf. 2007, 47, 1263–1275. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, W.; Qiu, K.; Wan, M. Numerical Simulation of Machined Surface Topography and Roughness in Milling Process. J. Manuf. Sci. Eng. 2006, 128, 96–103. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, W.H.; Qiu, K.P.; Wan, M. A new algorithm of simulation on peripherial milling surface topography. J. North West. Polytech. Univ. 2004, 22, 221–224. (In China) [Google Scholar]
- Franco, P.; Estrems, M.; Faura, F. A study of back cutting surface finish from tool errors and machine tool deviations during face milling. Int. J. Mach. Tools Manuf. 2008, 48, 112–123. [Google Scholar] [CrossRef]
- Lavernhe, S.; Quinsat, Y.; Lartigue, C. Model for the prediction of 3D surface topography in 5-axis milling. Int. J. Adv. Manuf. Technol. 2010, 51, 915–924. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Soshi, M.; Sahasrabudhe, A.; Yamazaki, K.; Mori, M. A Geometrical Simulation System of Ball End Finish Milling Process and Its Application for the Prediction of Surface Micro Features. J. Manuf. Sci. Eng. 2006, 128, 74–85. [Google Scholar] [CrossRef]
- Yan, B.; Zhang, D.W. Modeling and Simulation of Ball End Milling Surface Topology. J. Comput. Aided Des. Graph. 2001, 13, 135–140. (In China) [Google Scholar]
- Zhao, X.M.; Hu, D.J.; Zhao, G.W. Simulation of Workpiece Surface Texture in 5-Axis Control Machining. J. Shanghai Jiaotong Univ. 2003, 37, 690–694. (In China) [Google Scholar]
- Zhang, C.; Zhang, H.; Li, Y.; Zhou, L. Modeling and on-line simulation of surface topography considering tool wear in multi-axis milling process. Int. J. Adv. Manuf. Technol. 2014, 77, 735–749. [Google Scholar] [CrossRef]
- Bouzakis, K.D.; Aichouh, P.; Efstathiou, K. Determination of the chip geometry, cutting force and roughness in free form surfaces finishing milling, with ball end tools. Int. J. Mach. Tools Manuf. 2003, 43, 499–514. [Google Scholar] [CrossRef]
- Antoniadis, A.; Savakis, C.; Bilalis, N.; Balouktsis, A. Prediction of Surface Topomorphy and Roughness in Ball-End Milling. Int. J. Adv. Manuf. Technol. 2003, 21, 965–971. [Google Scholar] [CrossRef]
- Chen, J.-S.; Huang, Y.-K.; Chen, M.-S. A study of the surface scallop generating mechanism in the ball-end milling process. Int. J. Mach. Tools Manuf. 2005, 45, 1077–1084. [Google Scholar] [CrossRef]
- Wang, M.; Gao, L.; Zheng, Y. An examination of the fundamental mechanics of cutting force coefficients. Int. J. Mach. Tools Manuf. 2014, 78, 1–7. [Google Scholar] [CrossRef]
- Berestovskyi, D.; Hung, W.N.P.; Lomeli, P. Surface Finish of Ball-End Milled Microchannels. J. Micro Nano-Manuf. 2014, 2, 041005. [Google Scholar] [CrossRef]
- Dong, W.P.; Sullivan, P.J.; Stout, K.J. Comprehensive study of parameters for characterising three dimensional surface topography IV_ Parameters for characterising spatial and hybrid properties. Wear 1994, 178, 29–43. [Google Scholar] [CrossRef]





| Material | E (GPa) | μ | ρ (kg/m3) | c (J/(kg∙m)) | λ (W/(m∙K)) | δl (10−6/K) |
|---|---|---|---|---|---|---|
| 7050-T6 | 69 | 0.30 | 2850 | 526 | 114 | 20.8 |
| Milling Parameters | N (rpm) | ff (mm/z) | fp (mm) | ap (mm) | Am (mm) | τ (mm) | α (º) | β (º) |
|---|---|---|---|---|---|---|---|---|
| Setting in inclining milling | 6000 | 0.2 | 1 | 0.5 | 2 | 1 | 0 | 30 |
| Setting in vertical milling | 6000 | 0.2 | 1 | 0.5 | 2 | 2 | 0 | 0 |
| Sectional Profile | Ra of the Experiment (µm) | Ra of the Simulation (µm) | Relative Error (%) |
|---|---|---|---|
| In leading feed direction | 2.78 | 2.94 | 5.75 |
| In interval feed direction | 2.52 | 2.41 | 4.37 |
| Sectional Profile | Ra of the Experiment (µm) | Ra of the Simulation (µm) | Relative Error (%) |
|---|---|---|---|
| In leading feed direction | 4.69 | 5.11 | 8.96 |
| In interval feed direction | 4.76 | 4.43 | 6.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Li, S.; Zhang, Q.; Li, P.; Jia, Z.; Li, Y. Modeling and Analysis of Micro Surface Topography from Ball-End Milling in a Trochoidal Milling Mode. Micromachines 2021, 12, 1203. https://doi.org/10.3390/mi12101203
Dong Y, Li S, Zhang Q, Li P, Jia Z, Li Y. Modeling and Analysis of Micro Surface Topography from Ball-End Milling in a Trochoidal Milling Mode. Micromachines. 2021; 12(10):1203. https://doi.org/10.3390/mi12101203
Chicago/Turabian StyleDong, Yongheng, Shujuan Li, Qian Zhang, Pengyang Li, Zhen Jia, and Yan Li. 2021. "Modeling and Analysis of Micro Surface Topography from Ball-End Milling in a Trochoidal Milling Mode" Micromachines 12, no. 10: 1203. https://doi.org/10.3390/mi12101203
APA StyleDong, Y., Li, S., Zhang, Q., Li, P., Jia, Z., & Li, Y. (2021). Modeling and Analysis of Micro Surface Topography from Ball-End Milling in a Trochoidal Milling Mode. Micromachines, 12(10), 1203. https://doi.org/10.3390/mi12101203





