Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber
Abstract
:1. Introduction
2. Sensor Fabrication and Principle
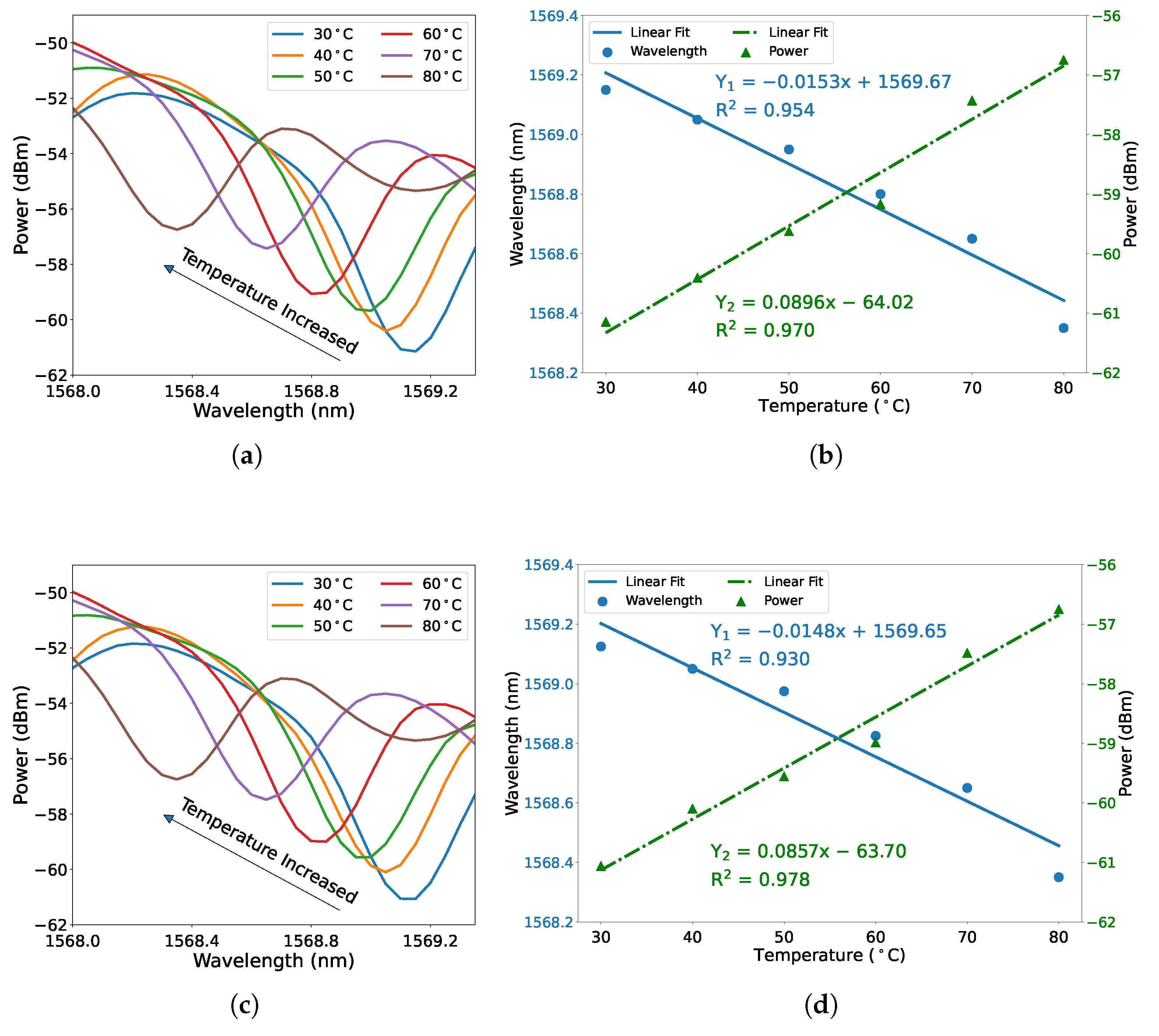
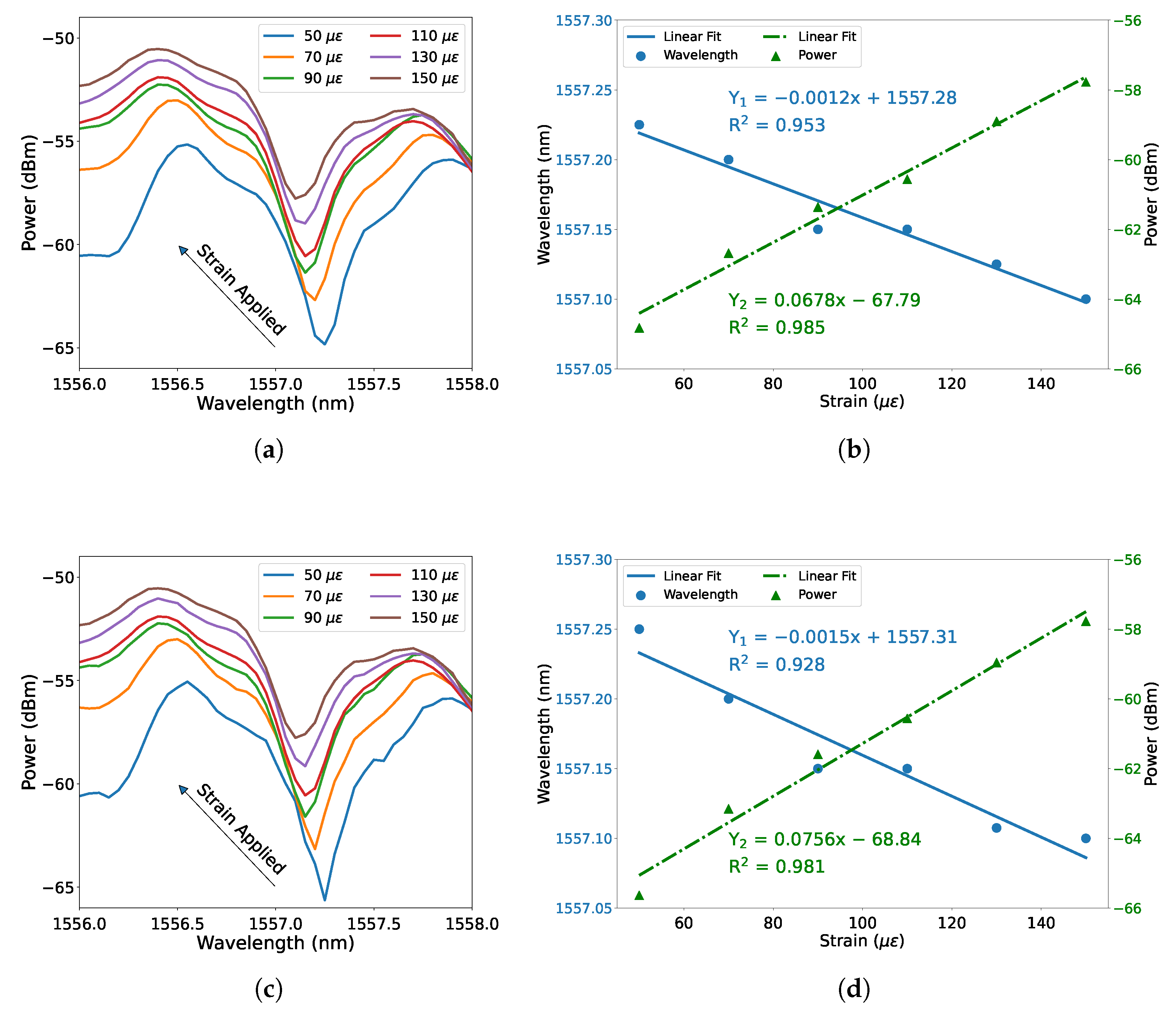
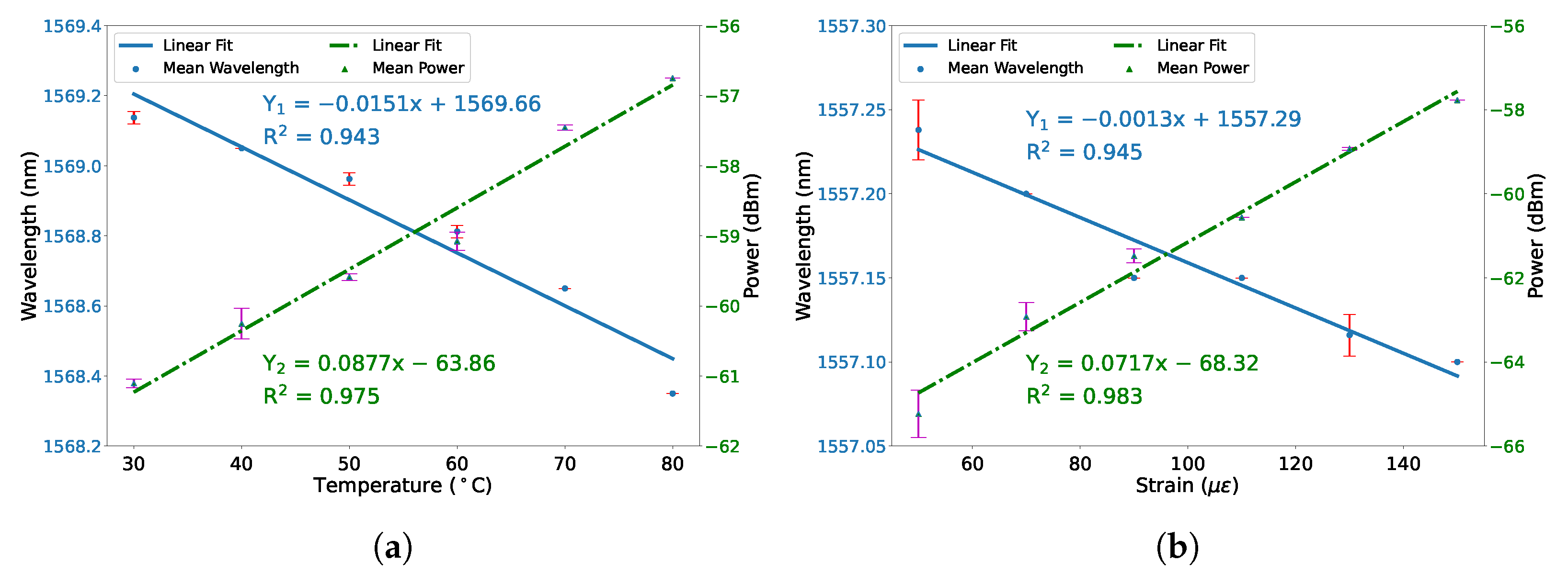
3. Experiment and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.-D.; Wolfbeis, O.S. Fiber-Optic Chemical Sensors and Biosensors (2015–2019). Anal. Chem. 2020, 92, 397–430. [Google Scholar] [CrossRef]
- Wang, X.; Tian, K.; Yuan, L.; Lewis, E.; Farrell, G.; Wang, P. A High-Temperature Humidity Sensor Based on a Singlemode-Side Polished Multimode-Singlemode Fiber Structure. J. Light. Technol. 2018, 36, 2730–2736. [Google Scholar] [CrossRef]
- Mizuno, Y.; Numata, G.; Kawa, T.; Lee, H.; Hayashi, N.; Nakamura, K. Multimodal Interference in Perfluorinated Polymer Optical Fibers: Application to Ultrasensitive Strain and Temperature Sensing. IEICE Trans. Electron. 2018, 101-C, 602–610. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Dong, X.; Köhler, M.H.; Kienle, P.; Bian, Q.; Jakobi, M.; Koch, A.W. Advances in Optical Fiber Sensors Based on Multimode Interference (MMI): A Review. IEEE Sens. J. 2021, 21, 132–142. [Google Scholar] [CrossRef]
- Hill, K.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. Review of long period fiber gratings written by CO2 laser. J. Appl. Phys. 2010, 108, 081101. [Google Scholar] [CrossRef]
- Alahbabi, M.N.; Cho, Y.T.; Newson, T.P. Simultaneous temperature and strain measurement with combined spontaneous Raman and Brillouin scattering. Opt. Lett. 2005, 30, 1276–1278. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, Y.; Hayashi, N.; Fukuda, H.; Song, K.Y.; Nakamura, K. Ultrahigh-speed distributed Brillouin reflectometry. Light. Sci. Appl. 2016, 5, e16184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehta, A.; Mohammed, W.; Johnson, E. Multimode interference-based fiber-optic displacement sensor. IEEE Photonics Technol. Lett. 2003, 15, 1129–1131. [Google Scholar] [CrossRef]
- Zhao, Y.; Cai, L.; Li, X.G. High Sensitive Modal Interferometer for Temperature and Refractive Index Measurement. IEEE Photonics Technol. Lett. 2015, 27, 1341–1344. [Google Scholar] [CrossRef]
- Olivero, M.; Vallan, A.; Orta, R.; Perrone, G. Single-Mode–Multimode–Single-Mode Optical Fiber Sensing Structure With Quasi-Two-Mode Fibers. IEEE Trans. Instrum. Meas. 2018, 67, 1223–1229. [Google Scholar] [CrossRef]
- Zhao, Y.; Cai, L.; Li, X.G.; Meng, F.C. Liquid concentration measurement based on SMS fiber sensor with temperature compensation using an FBG. Sens. Actuators B Chem. 2014, 196, 518–524. [Google Scholar] [CrossRef]
- Chai, Q.; Liu, Y.; Zhang, J.; Yang, J.; Chen, Y.; Yuan, L.; Peng, G.D. Asymmetric transmission and reflection spectra of FBG in single-multi-single mode fiber structure. Opt. Express 2015, 23, 11665–11673. [Google Scholar] [CrossRef]
- Lu, C.; Su, J.; Dong, X.; Sun, T.; Grattan, K.T.V. Simultaneous Measurement of Strain and Temperature with a Few-Mode Fiber-Based Sensor. J. Light. Technol. 2018, 36, 2796–2802. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, T.; Rao, Y.J.; Wu, Y. All-Fiber Curvature Sensor Based on Multimode Interference. IEEE Photonics Technol. Lett. 2011, 23, 679–681. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Yan, X.; Zhang, X.; Wang, F.; Suzuki, T.; Ohishi, Y.; Cheng, T. A Refractive Index Sensitive Liquid Level Monitoring Sensor Based on Multimode Interference. Photonics 2020, 7, 89. [Google Scholar] [CrossRef]
- Tong, Z.; Su, J.; Cao, Y.; Zhang, W. Simultaneous Measurement Based on Composite Interference Structure. IEEE Photonics Technol. Lett. 2014, 26, 1310–1313. [Google Scholar] [CrossRef]
- Wang, X.; Farrell, G.; Lewis, E.; Tian, K.; Yuan, L.; Wang, P. A Humidity Sensor Based on a Singlemode-Side Polished Multimode–Singlemode Optical Fibre Structure Coated with Gelatin. J. Light. Technol. 2017, 35, 4087–4094. [Google Scholar] [CrossRef]
- Sun, K.; Ding, Z.; Zhang, Z. Fiber directional position sensor based on multimode interference imaging and machine learning. Appl. Opt. 2020, 59, 5745–5751. [Google Scholar] [CrossRef]
- Tian, K.; Farrell, G.; Wang, X.; Yang, W.; Xin, Y.; Liang, H.; Lewis, E.; Wang, P. Strain sensor based on gourd-shaped single-mode-multimode-single-mode hybrid optical fibre structure. Opt. Express 2017, 25, 18885–18896. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Socorro, A.B.; Santamaría, E.; Fernández-Irigoyen, J.; Villar, I.D.; Corres, J.M.; Arregui, F.J.; Matias, I.R. Fiber-Optic Immunosensor Based on an Etched SMS Structure. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 314–321. [Google Scholar] [CrossRef]
- Wang, P.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. High-sensitivity, evanescent field refractometric sensor based on a tapered, multimode fiber interference. Opt. Lett. 2011, 36, 2233–2235. [Google Scholar] [CrossRef] [PubMed]
- Cardona-Maya, Y.; Del Villar, I.; Socorro, A.B.; Corres, J.M.; Matias, I.R.; Botero-Cadavid, J.F. Wavelength and Phase Detection Based SMS Fiber Sensors Optimized With Etching and Nanodeposition. J. Light. Technol. 2017, 35, 3743–3749. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Zhou, J.; Guan, J.; Long, S.; Yu, J.; Guan, H.; Lu, H.; Luo, Y.; Zhang, J.; Chen, Z. Fabrication of Side-Polished Single Mode-Multimode-Single Mode Fiber and Its Characteristics of Refractive Index Sensing. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 238–245. [Google Scholar] [CrossRef]
- Zhao, Y.; Cai, L.; Li, X.G. In-fiber modal interferometer for simultaneous measurement of curvature and temperature based on hollow core fiber. Opt. Laser Technol. 2017, 92, 138–141. [Google Scholar] [CrossRef]
- Yang, F.; Wang, Z.; Wang, D. A highly sensitive optical fiber strain sensor based on cascaded multimode fiber and photonic crystal fiber. Opt. Fiber Technol. 2019, 47, 102–106. [Google Scholar] [CrossRef]
- Velsink, M.C.; Lyu, Z.; Pinkse, P.W.H.; Amitonova, L.V. Comparison of round- and square-core fibers for sensing, imaging, and spectroscopy. Opt. Express 2021, 29, 6523–6531. [Google Scholar] [CrossRef]
- Matias, I.R.; Ikezawa, S.; Corres, J. Fiber Optic Sensors: Current Status and Future Possibilities; Springer: Berlin/Heidelberg, Germany, 2016; Volume 21. [Google Scholar]
- Kumar, A.; Varshney, R.K.; Siny Antony, C.; Sharma, P. Transmission characteristics of SMS fiber optic sensor structures. Opt. Commun. 2003, 219, 215–219. [Google Scholar] [CrossRef]
- Tripathi, S.M.; Kumar, A.; Varshney, R.K.; Kumar, Y.B.P.; Marin, E.; Meunier, J.P. Strain and temperature sensing characteristics of single-mode–multimode–single-mode structures. J. Light. Technol. 2009, 27, 2348–2356. [Google Scholar] [CrossRef]
- Li, E. Temperature compensation of multimode-interference-based fiber devices. Opt. Lett. 2007, 32, 2064–2066. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, L.; Wang, T.; Yang, L.; Zhu, B.; Zhang, Q. High Performance Temperature Sensing of Single Mode-Multimode-Single Mode Fiber With Thermo-Optic Polymer as Cladding of Multimode Fiber Segment. IEEE Sens. J. 2014, 14, 1143–1147. [Google Scholar] [CrossRef]
- Wang, K.; Dong, X.; Köhler, M.H.; Kienle, P.; Bian, Q.; Fink, M.; Jakobi, M.; Koch, A.W. Optical fiber sensors based on multimode interference using square-core fiber for temperature measurement. In Photonic Instrumentation Engineering VIII; Soskind, Y., Busse, L.E., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11693, pp. 120–126. [Google Scholar]
- Chen, Y.; Wang, Y.; Chen, R.; Yang, W.; Liu, H.; Liu, T.; Han, Q. A hybrid multimode interference structure-based refractive index and temperature fiber sensor. IEEE Sens. J. 2015, 16, 331–335. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, C.; Liu, J.; Yang, J. Single modal interference-based fiber-optic sensor for simultaneous measurement of curvature and strain with dual-differential temperature compensation. IEEE Sens. J. 2018, 18, 8375–8380. [Google Scholar] [CrossRef]
- Andre, R.M.; Biazoli, C.R.; Silva, S.O.; Marques, M.B.; Cordeiro, C.M.B.; Frazao, O. Strain-Temperature Discrimination Using Multimode Interference in Tapered Fiber. IEEE Photonics Technol. Lett. 2013, 25, 155–158. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Ning, T.; Wen, X.; Li, J.; Zheng, J.; You, H.; Chen, H.; Zhang, C.; Jian, W. Strain and temperature discrimination using a fiber Bragg grating and multimode interference effects. Opt. Commun. 2015, 343, 6–9. [Google Scholar] [CrossRef]
- Sun, Q.; Luo, H.; Luo, H.; Lai, M.; Liu, D.; Zhang, L. Multimode microfiber interferometer for dual-parameters sensing assisted by Fresnel reflection. Opt. Express 2015, 23, 12777–12783. [Google Scholar] [CrossRef] [PubMed]


| Optical Fiber Sensor Structure | Measurement Range | Sensitivity (max.) | Reference |
|---|---|---|---|
| SMF-HCF-SMF (with abrupt taper joints) | 18–50 C | 12.3 pm/C | [25] |
| SMF-No-Core Fiber (NCF)- SMF-MMF-SMF | 30–90 C | 9.2 pm/C | [34] |
| SMF-Tapered NCF-SMF | 0–280 C | 16.56 pm/C | [36] |
| SMF-NCF-SMF (with FBG) | 0–50 C | 12.8 pm/C | [37] |
| Tapered SMF-Micro MMF- Tapered SMF | 35–60 C | 0.028 dB/C | [38] |
| SMF-Square-Core Fiber-SMF | 30–80 C | −15.3 pm/C 0.0896 dBm/C | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Dong, X.; Kienle, P.; Fink, M.; Kurz, W.; Köhler, M.H.; Jakobi, M.; Koch, A.W. Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber. Micromachines 2021, 12, 1239. https://doi.org/10.3390/mi12101239
Wang K, Dong X, Kienle P, Fink M, Kurz W, Köhler MH, Jakobi M, Koch AW. Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber. Micromachines. 2021; 12(10):1239. https://doi.org/10.3390/mi12101239
Chicago/Turabian StyleWang, Kun, Xingchen Dong, Patrick Kienle, Maximilian Fink, Wolfgang Kurz, Michael H. Köhler, Martin Jakobi, and Alexander W. Koch. 2021. "Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber" Micromachines 12, no. 10: 1239. https://doi.org/10.3390/mi12101239
APA StyleWang, K., Dong, X., Kienle, P., Fink, M., Kurz, W., Köhler, M. H., Jakobi, M., & Koch, A. W. (2021). Optical Fiber Sensor for Temperature and Strain Measurement Based on Multimode Interference and Square-Core Fiber. Micromachines, 12(10), 1239. https://doi.org/10.3390/mi12101239







