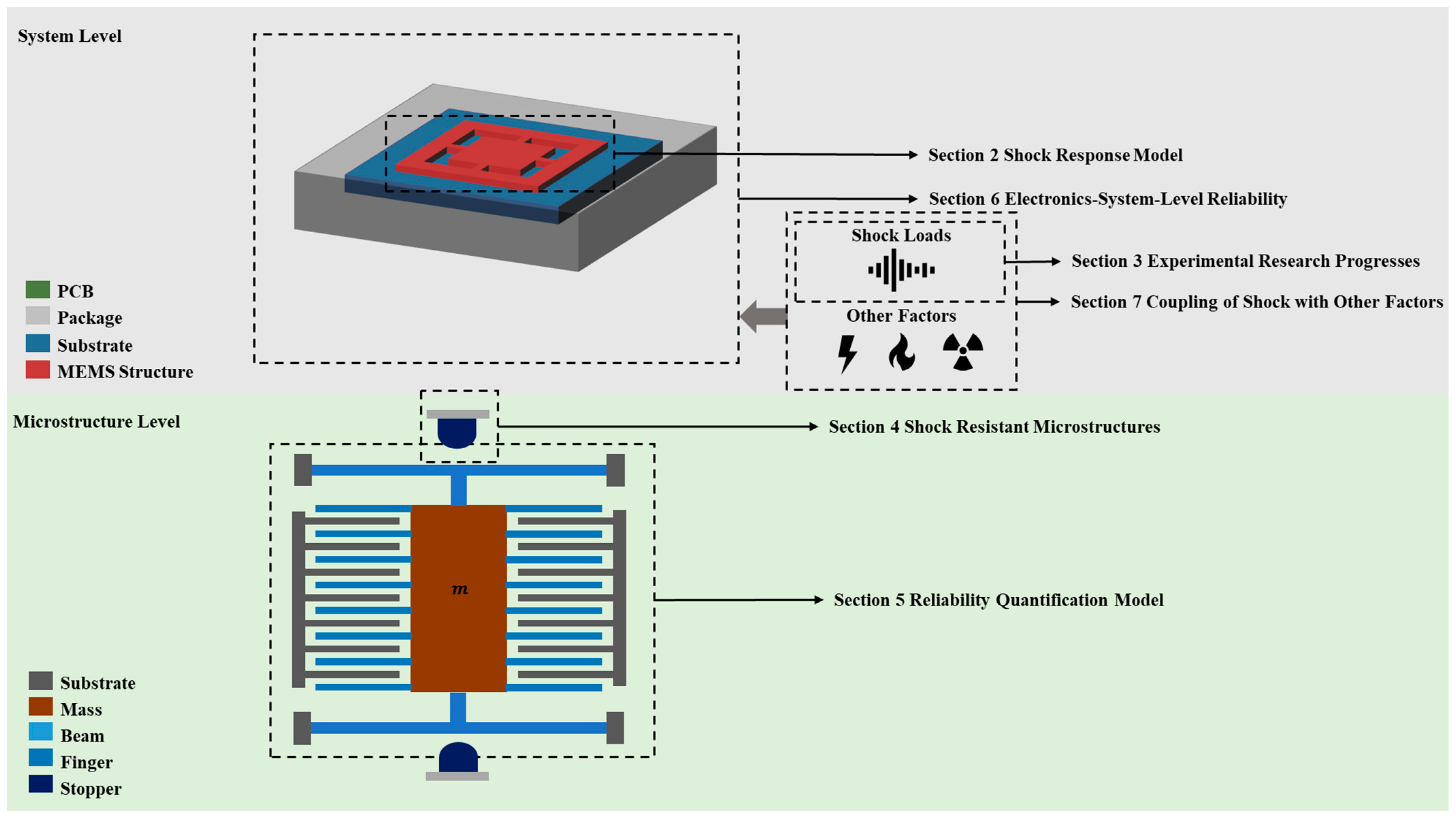
Reliability of MEMS in Shock Environments: 2000–2020
Abstract
:1. Introduction
2. Shock Response Model
2.1. Analytical Model
2.2. Numerical Research
3. Experimental Research Progresses
3.1. Experimental Research on MEMS Products
| Class | Products | Shock Resistance | Ref. |
|---|---|---|---|
| Class I | Accelerometer | 104~105 g | [48,51,52] |
| Microphone | >6.5 × 104 g | [53,54,55] | |
| MEMS Inductor | >6.0 × 104 g | [56] | |
| Class II | Gyroscope | ~103 g | [57,58,59] |
| Resonator | 103~104 g | [60,61,62] | |
| Energy Harvester | ~102 g | [63] | |
| Comb Driver | ~103 g | [45,46,47] | |
| Class III | Inertial Switch | 103~105 g | [64] |
| RF Switch | 103~104 g | [65] | |
| Class IV | Micromirror | ~102 g | [49] |
| Gear | <2 × 104 g | [46,47] |
3.2. Shock Experimental Method
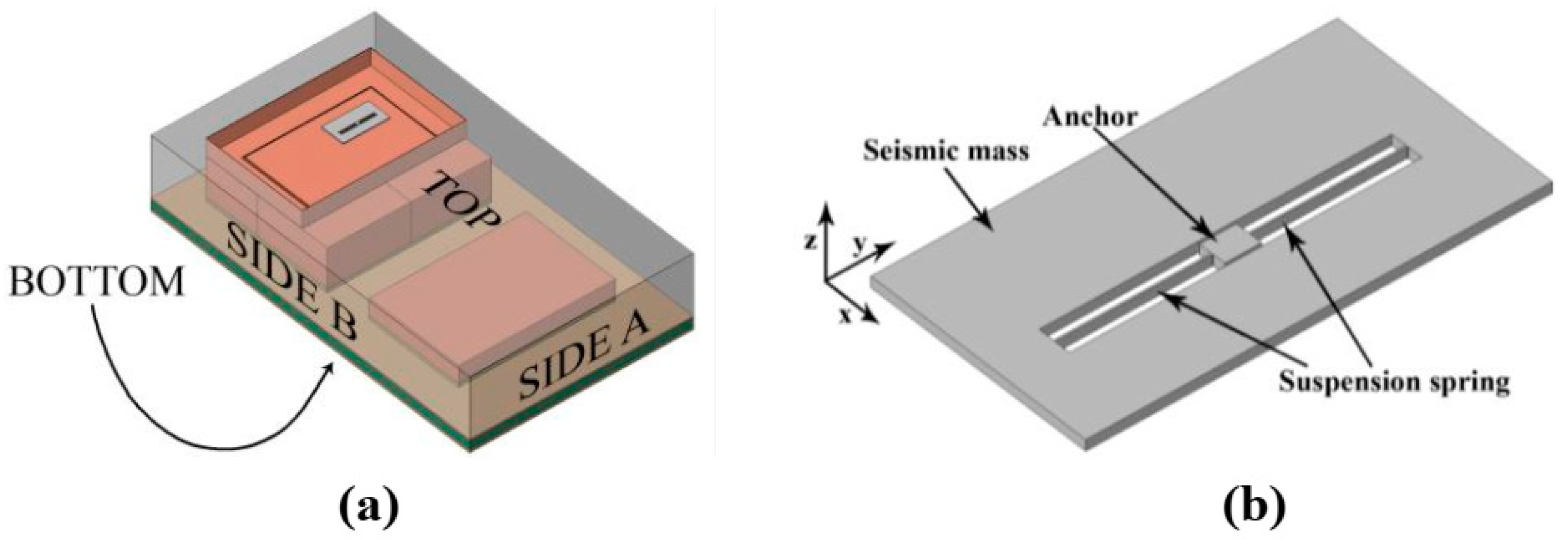
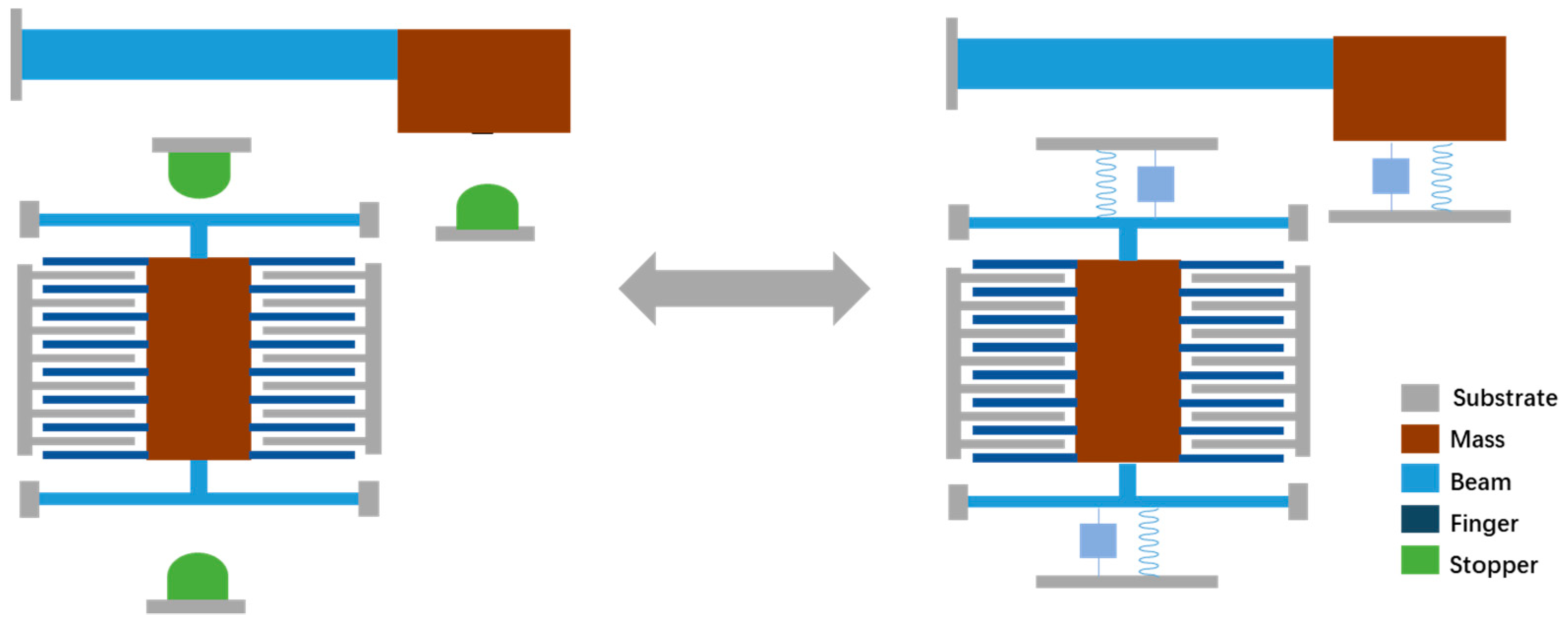
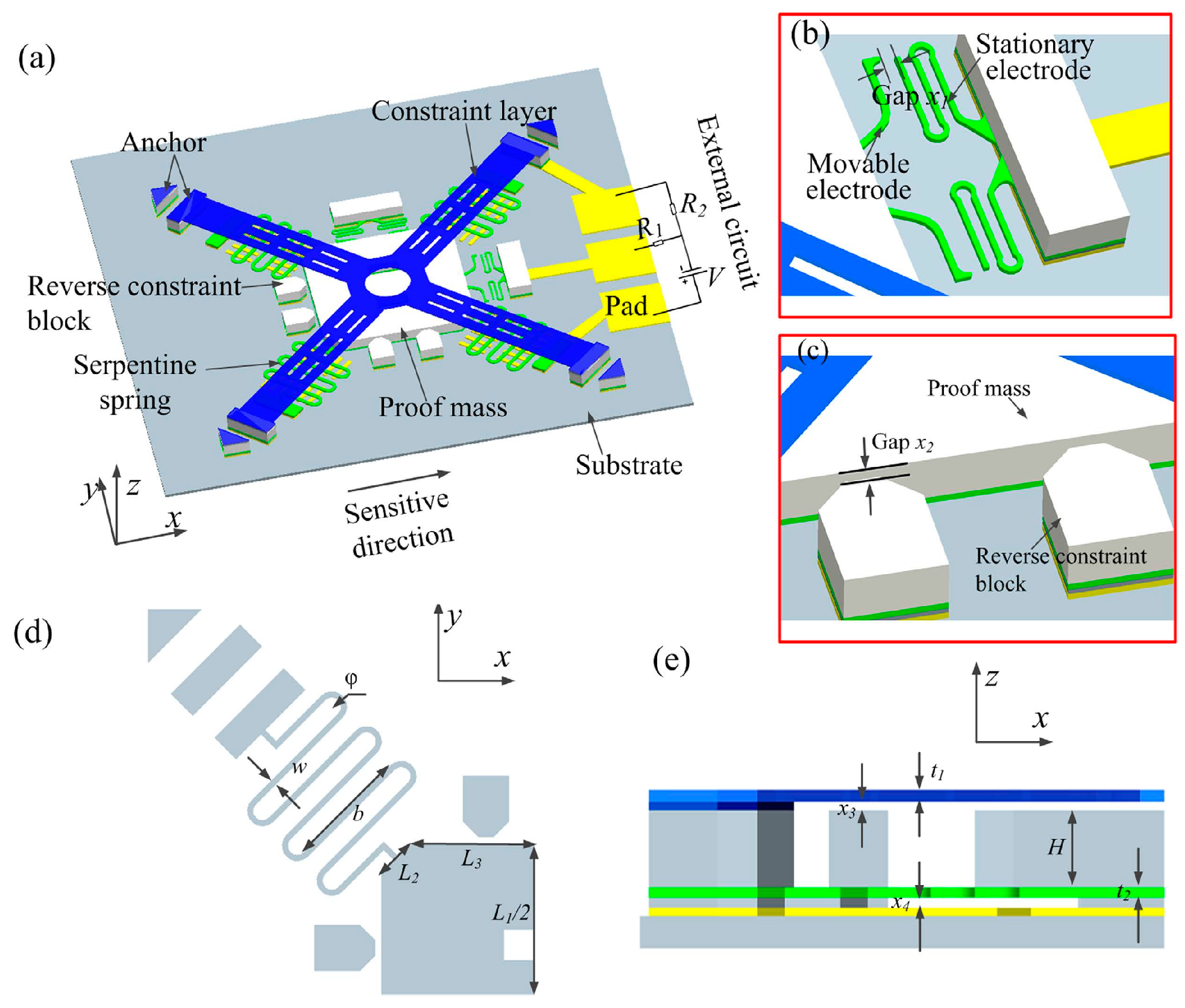
4. Shock Resistant Microstructures
4.1. Stoppers
4.2. Latch Mechanisms
4.3. Specific Anti-Shock Structures
5. Reliability Quantification Model
5.1. Strength Model of Brittle Materials
5.2. Reliability Quantification Model
| Reliability Model | Key Equations | Ref. |
|---|---|---|
| Reliability Quantification for General Structures | [119,120,121] | |
| Weibull Distribution Model | [124,125,126,127] | |
| The Weakest-link Model | [128] | |
| [129] | ||
| [130] |
6. Electronics-System-Level Reliability
6.1. System-Level Experimental Research
6.2. System-Level Modeling and Optimization
6.3. Key Factors of Shock Load Transmission
7. Coupling of Shock with Other Factors
7.1. Electrical-Shock Coupling
7.2. Thermal-Shock Coupling
7.3. Multi-Factor Reliability Models
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harris, M.C.; Piersol, A.G. Harris’ Shock and Vibration Handbook; McGraw-Hill: New York, NY, USA, 2002; Volume 5. [Google Scholar]
- van Spengen, W.M.; Modliński, R.; Puers, R.; Jourdain, A. Failure Mechanisms in MEMS/NEMS Devices. In Springer Handbook of Nanotechnology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1761–1782. [Google Scholar]
- Tabata, O.; Tsuchija, T. Reliability of MEMS: Testing of Materials and Devices; WILEY-VCH: Weinheim, Germany, 2008; Volume 6. [Google Scholar]
- Hartzell, A.L.; Da Silva, M.G.; Shea, H.R. MEMS Reliability; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Tiwari, A.; Raj, B. (Eds.) Materials and Failures in MEMS and NEMS; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Jones, N. Structural Impact; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Broek, D. The Practical Use of Fracture Mechanics; Springer Science & Business Media: Dordrecht, The Netherland, 2012. [Google Scholar]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Elsayed, E.A. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Hartley, F.T.; Arney, S.; Sexton, F. Microsystems Reliability, Test and Metrology; ITRS: London, UK, 2001. [Google Scholar]
- Fonseca, D.J.; Sequera, M. On MEMS reliability and failure mechanisms. J. Qual. Reliab. Eng. 2011, 2011, 820243. [Google Scholar] [CrossRef]
- Skogström, L.; Li, J.; Mattila, T.T.; Vuorinen, V. MEMS reliability. In Handbook of Silicon Based MEMS Materials and Technologies; Elsevier: Amsterdam, The Netherlands, 2020; pp. 851–876. [Google Scholar]
- Van Spengen, W.M. MEMS reliability from a failure mechanisms perspective. Microelectron. Reliab. 2003, 43, 1049–1060. [Google Scholar] [CrossRef]
- Huang, Y.; Vasan, A.S.S.; Doraiswami, R.; Osterman, M.; Pecht, M. MEMS reliability review. IEEE Trans. Device Mater. Reliab. 2012, 12, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Somà, A. A survey of Mechanical failure and design for Reliability of MEMS. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Cluj-Napoca, Romania, 2020; Volume 724. [Google Scholar]
- Tanner, D.M. MEMS reliability: Where are we now? Microelectron. Reliab. 2009, 49, 937–940. [Google Scholar] [CrossRef]
- Tanner, D.M.; Parson, T.B.; Corwin, A.D.; Walraven, J.A.; Wittwer, J.W.; Boyce, B.L.; Winzer, S.R. Science-based MEMS reliability methodology. Microelectron. Reliab. 2007, 47, 1806–1811. [Google Scholar] [CrossRef]
- Iannacci, J. Reliability of MEMS: A perspective on failure mechanisms, improvement solutions and best practices at development level. Displays 2015, 37, 62–71. [Google Scholar] [CrossRef]
- Hu, Y.; Shen, X.; Zhang, Y.; Wang, Z.; Chen, X. Research reviews and prospects of MEMS reliability. Integr. Ferroelectr. 2014, 152, 8–21. [Google Scholar] [CrossRef]
- Tariq Jan, M.; Hisham Bin Hamid, N.; Md Khir, M.H.; Ashraf, K.; Shoaib, M. Reliability and fatigue analysis in cantilever-based MEMS devices operating in harsh environments. J. Qual. Reliab. Eng. 2014, 2014, 987847. [Google Scholar] [CrossRef] [Green Version]
- Rafiee, P.; Khatibi, G.; Zehetbauer, M. A Review of the Most Important Failure, Reliability and Nonlinearity Aspects in the Development of Microelectromechanical Systems (MEMS); Microelectronics International: London, UK, 2017. [Google Scholar]
- Băjenescu, T.M.I. MEMS Manufacturing and Reliability; Journal of Engineering Science: Asyut, Egypt, 2019. [Google Scholar]
- Tan, Q.-M. Dimensional Analysis: With Case Studies in Mechanics; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Darrin, M.; Garrison, A.; Barth, J.L. (Eds.) Systems Engineering for Microscale and Nanoscale Technologies; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Développement, Y. Status of the MEMS Industry 2020–Market and Technology Report; Tech. Rep. Yole. Develop.: Villeurbanne, France, 2020. [Google Scholar]
- Bishop, R.E.D.; Johnson, D.C. The Mechanics of Vibration; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wodek, G. Advanced Structural Dynamics and Active Control of Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- James, S.W. Impact Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Jan, A. Wave Propagation in Elastic Solids; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Srikar, V.T.; Senturia, S.D. The reliability of microelectromechanical systems (MEMS) in shock environments. J. Microelectromechanical Syst. 2002, 11, 206–214. [Google Scholar] [CrossRef]
- Fang, X.W.; Huang, Q.A.; Tang, J.Y. Modeling of MEMS reliability in shock environments. In Proceedings of the 7th International Conference on Solid-State and Integrated Circuits Technology, Beijing, China, 18–21 October 2004; Volume 2. [Google Scholar]
- Younis, M.I.; Miles, R. Response of MEMS devices under shock loads. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition. Design Engineering, Parts A and B, Orlando, FL, USA, 5–11 November 2005. [Google Scholar]
- Younis, M.I.; Jordy, D.; Pitarresi, J.M. Computationally efficient approaches to characterize the dynamic response of microstructures under mechanical shock. J. Microelectromechanical Syst. 2007, 16, 628–638. [Google Scholar] [CrossRef]
- Younis, M.I.; Alsaleem, F.; Jordy, D. The response of clamped–clamped microbeams under mechanical shock. Int. J. Non-Linear Mech. 2007, 42, 643–657. [Google Scholar] [CrossRef]
- Yagubizade, H.; Younis, M.I.; Rezazadeh, G. The effect of squeeze-film damping on suppressing the shock response of MEMS. In Proceedings of the ASME 2009 International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009. [Google Scholar]
- Sundaram, S.; Tormen, M.; Timotijevic, B.; Lockhart, R.; Overstolz, T.; Stanley, R.P.; Shea, H.R. Vibration and shock reliability of MEMS: Modeling and experimental validation. J. Micromech. Microeng. 2011, 21, 045022. [Google Scholar] [CrossRef]
- Ouakad, H.M. The response of a micro-electro-mechanical system (MEMS) cantilever-paddle gas sensor to mechanical shock loads. J. Vib. Control 2015, 21, 2739–2754. [Google Scholar] [CrossRef]
- Xu, K.; Zhu, N.; Jiang, F.; Zhang, W.; Hao, Y. A Transfer Function Approach to Shock Duration Compensation for Laboratory Evaluation of Ultra-High-G Vacuum-Packaged MEMS Accelerometers. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Korea, 27–31 January 2019. [Google Scholar]
- Jordy, D.; Younis, M.I. Characterization of the dynamical response of a micromachined g-sensor to mechanical shock loading. J. Dyn. Syst. Meas. Control 2008, 130, 041003. [Google Scholar] [CrossRef]
- Mariani, S.; Ghisi, A.; Fachin, F.; Cacchione, F.; Corigliano, A.; Zerbini, S. A three-scale FE approach to reliability analysis of MEMS sensors subject to impacts. Meccanica 2008, 43, 469–483. [Google Scholar] [CrossRef]
- Mariani, S.; Ghisi, A.; Corigliano, A.; Zerbini, S. Multi-scale analysis of MEMS sensors subject to drop impacts. Sensors 2007, 7, 1817–1833. [Google Scholar] [CrossRef] [Green Version]
- Mariani, S.; Ghisi, A.; Corigliano, A.; Martini, R.; Simoni, B. Two-scale simulation of drop-induced failure of polysilicon MEMS sensors. Sensors 2011, 11, 4972–4989. [Google Scholar] [CrossRef] [Green Version]
- Ghisi, A.; Fachin, F.; Mariani, S.; Zerbini, S. Multi-scale analysis of polysilicon MEMS sensors subject to accidental drops: Effect of packaging. Microelectron. Reliab. 2009, 49, 340–349. [Google Scholar] [CrossRef]
- Caruso, H.; Szymkowiak, E. A Clarification of the Shock/Vibration Equivalence in MIL-STD-810D/E. J. Environ. Sci. 1989, 32, 28–31. [Google Scholar]
- Tanner, D.M.; Walraven, J.A.; Helgesen, K.S.; Irwin, L.W.; Gregory, D.L.; Stake, J.R.; Smith, N.F. MEMS reliability in a vibration environment. In Proceedings of the 2000 IEEE International Reliability Physics Symposium Proceedings. 38th Annual (Cat. No. 00CH37059), San Jose, CA, USA, 10–13 April 2000. [Google Scholar]
- Tanner, D.M.; Walraven, J.A.; Helgesen, K.; Irwin, L.W.; Brown, F.; Smith, N.F.; Masters, N. MEMS reliability in shock environments. In Proceedings of the 2000 IEEE International Reliability Physics Symposium Proceedings 38th Annual (Cat. No. 00CH37059), San Jose, CA, USA, 10–13 April 2000. [Google Scholar]
- Tanner, D.M.; Smith, N.F.; Irwin, L.W.; Eaton, W.P.; Helgesen, K.S.; Clement, J.J.; Peterson, K.A. Mems Reliability: Infrastructure, Test Structures, Experiments, and Failure Modes; No. SAND2000-0091; Sandia National Labs.: Albuquerque, NM, USA; Livermore, CA, USA, 2000.
- Fan, M.S. Dynamic Response Assessment for the Mems Accelerometer Under Severe Shock Loads; NASA: Washington, DC, USA, 2001. [Google Scholar]
- Sontheimer, A.B. Digital micromirror device (DMD) hinge memory lifetime reliability modeling. In Proceedings of the 2002 IEEE International Reliability Physics Symposium, Dallas, TX, USA, 7–11 April 2002; pp. 118–121. [Google Scholar]
- Narasimhan, V.; Li, H.; Jianmin, M. Micromachined high-g accelerometers: A review. J. Micromechanics Microengineering 2015, 25, 033001. [Google Scholar] [CrossRef]
- Kim, J.W.; Park, H.W.; Choi, M.K.; Jeung, W.K.; Lee, J.W. Drop impact reliability of MEMS inertial sensors with membrane suspensions for mobile phones. In Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2012. [Google Scholar]
- Lall, P.; Kothari, N.; Glover, J. Mechanical shock reliability analysis and multiphysics modeling of MEMS accelerometers in harsh environments. In Proceedings of the ASME 2015 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems collocated with the ASME 2015 13th International Conference on Nanochannels, Microchannels, and Minichannels. American Society of Mechanical Engineers Digital Collection, San Francisco, CA, USA, 6–9 July 2015. [Google Scholar]
- Li, J.; Makkonen, J.; Broas, M.; Hokka, J.; Mattila, T.T.; Paulasto-Kröckel, M.; Dasgupta, A. Reliability assessment of a MEMS microphone under shock impact loading. In Proceedings of the 2013 14th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Wroclaw, Poland, 14–17 April 2013. [Google Scholar]
- Li, J.; Broas, M.; Raami, J.; Mattila, T.T.; Paulasto-Kröckel, M. Reliability assessment of a MEMS microphone under mixed flowing gas environment and shock impact loading. Microelectron. Reliab. 2014, 54, 1228–1234. [Google Scholar] [CrossRef]
- Lu, C.-L.; Ni, P.; Yeh, M. Stress analysis of CMOS-MEMS microphone under shock loading by Taguchi method. Microelectron. Reliab. 2018, 88, 824–828. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Li, J. Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock. Micromachines 2020, 11, 957. [Google Scholar] [CrossRef]
- Li, J.; Broas, M.; Makkonen, J.; Mattila, T.T.; Hokka, J.; Paulasto-Kröckel, M. Shock impact reliability and failure analysis of a three-axis MEMS gyroscope. J. Microelectromechanical Syst. 2013, 23, 347–355. [Google Scholar] [CrossRef]
- Nekrasov, Y.A.; Moiseev, N.V.; Belyaev, Y.V.; Pavlova, S.V.; Lyukshonkov, R.G. Influence of translational vibrations, shocks and acoustic noise on MEMS gyro performance. Gyroscopy Navig. 2017, 8, 31–37. [Google Scholar] [CrossRef]
- Lian, J.; Li, Y.; Tang, Y.; Li, J.; Xu, L. Analysis of the vulnerability of MEMS tuning fork gyroscope during the gun launch. Microelectron. Reliab. 2020, 107, 113619. [Google Scholar] [CrossRef]
- Linxi, D.; Quan, Y.; Jinyan, B.; Jiaping, T. Analysis of reliability factors of MEMS disk resonator under the strong inertial impact. J. Semicond. 2014, 35, 074014. [Google Scholar]
- Lall, P.; Abrol, A.S.; Simpson, L.; Glover, J. A study on damage progression in MEMS based Silicon oscillators subjected to high-g harsh environments. In Proceedings of the 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 31 May–3 June 2016. [Google Scholar]
- Heinz, D.B.; Hong, V.A.; Yang, Y.; Ahn, C.H.; Kenny, T.W. High-G (>20,000 g) inertial shock survivability of epitaxially encapsulated silicon MEMS devices. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Fujita, T.; Renaud, M.; Goedbloed, M.; de Nooijer, C.; Altena, G.; Elfrink, R.; van Schaijk, R. Reliability improvement of vibration energy harvester with shock absorbing structures. Procedia Eng. 2014, 87, 1206–1209. [Google Scholar] [CrossRef] [Green Version]
- Renaud, M.; Fujita, T.; Goedbloed, M.; de Nooijer, C.; van Schaijk, R. Shock reliability analysis and improvement of MEMS electret-based vibration energy harvesters. J. Micromechanics Microengineering 2015, 25, 104010. [Google Scholar] [CrossRef]
- Ying, W.; Wenzhong, L.; Yue, Z.; Fufu, W. High impact-induced failure of a novel solid MEMS switch. In Proceedings of the 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Suzhou, China, 7–10 April 2013. [Google Scholar]
- De Pasquale, G.; Soma, A.; Barbato, M.; Meneghesso, G. Impact wear and other contact effects on the electro-mechanical reliability of MEMS. In Proceedings of the 2014 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), Cannes, France, 1–4 April 2014. [Google Scholar]
- Eitzen, I.; Renberg, J.; Færevik, H. The Use of Wearable Sensor Technology to Detect Shock Impacts in Sports and Occupational Settings: A Scoping Review. Sensors 2021, 21, 4962. [Google Scholar] [CrossRef]
- Lall, P.; Panchagade, D.; Iyengar, D.; Shantaram, S.; Suhling, J.; Schrier, H. High speed digital image correlation for transient-shock reliability of electronics. In Proceedings of the 2007 Proceedings 57th Electronic Components and Technology Conference, Sparks, NV, USA, 29 May–1 June 2007. [Google Scholar]
- Lall, P.; Choudhary, P.; Gupte, S.; Gupta, P.; Suhling, J.; Hofmeister, J. Transient-Response Spectral Analysis Based Feature Extraction for Built-In Reliability Test of Electronics Under Shock Loads. In Proceedings of the ASME 2007 InterPACK Conference collocated with the ASME/JSME 2007 Thermal Engineering Heat Transfer Summer Conference, Vancouver, BC, Canada, 8–12 July 2007. [Google Scholar]
- Lall, P.; Lowe, R.; Goebel, K. Resistance spectroscopy-based condition monitoring for prognostication of high reliability electronics under shock-impact. In Proceedings of the 2009 59th Electronic Components and Technology Conference, San Diego, CA, USA, 26–29 May 2009. [Google Scholar]
- Yang, C.; Zhang, B.; Chen, D.; Lin, L. Drop-shock dynamic analysis of MEMS/package system. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010. [Google Scholar]
- Zhang, L.; Yang, F.; Li, R.; Guan, T.; He, J.; Fu, F.S.; Zhang, D. A novel impact tester for in situ evaluating the shock reliability of micro-structures. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar]
- She, D.; Yang, Y.; Wei, Z.; Li, K.; Yu, Z.; Ding, F. Novel shock wave excitation method for dynamic characterization of microstructures. Microsyst. Technol. 2017, 23, 125–133. [Google Scholar] [CrossRef]
- Cao, Y.; Xi, Z.; Yu, P.; Wang, J.; Nie, W. Optical measurement of the dynamic contact process of a MEMS inertial switch under high shock loads. IEEE Trans. Ind. Electron. 2016, 64, 701–709. [Google Scholar] [CrossRef]
- Feng, H.; Lou, W.; Wang, D.; Zheng, F. Design, test and analysis of a threshold-value judging mechanism in silicon-based MEMS safety and arming device. J. Micromechanics Microengineering 2019, 29, 065006. [Google Scholar] [CrossRef]
- Gdoutos, E.E. Fracture Mechanics: An Introduction; Springer Nature: Cham, Switzerland, 2020; Volume 263. [Google Scholar]
- Naumann, M.; Mehner, J.; Lin, D.; Miller, T.F. Design and application of flexible stops for MEMS devices. In Proceedings of the SENSORS, 2010 IEEE, Waikoloa, HI, USA, 1–4 November 2010. [Google Scholar]
- Jiang, T.; Zhou, J.; Feng, F. Study on designs of stoppers for MEMS devices in shock environment. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2012; Volume 184. [Google Scholar]
- Jiang, T.; Wei, Y.; Yao, S.; Zhou, J. Study on shock resistance of MEMS Devices with different Stoppers. In Key Engineering Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2014; Volume 609. [Google Scholar]
- Jiang, T.; Ma, N. Stopper Parameters Design for Micro-elastic Beam Under High Shock Environment. In DEStech Transactions on Computer Science and Engineering; Iciti: Guangzhou, China, 2018. [Google Scholar]
- Lehée, G.; Calvar-Mimica, A.; Chantrait, T.; Charles, A.; Jeanroy, A.; Onfroy, P.; Berthelot, A. MEMS reliability study in shock environments through numerical and experimental investigations. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017. [Google Scholar]
- Tao, Y.-K.; Liu, Yu.; Dong, Ji. Flexible stop and double-cascaded stop to improve shock reliability of MEMS accelerometer. Microelectron. Reliab. 2014, 54, 1328–1337. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, Z.; Sun, Y.; Lai, L.; Jin, Z.; Ding, G.; Wang, J. Shock-resistibility of mems-based inertial microswitch under reverse directional ultra-high g acceleration for IoT applications. Sci. Rep. 2017, 7, 1–12. [Google Scholar]
- Delahunty, A.K.; Pike, W.T. Metal-armouring for shock protection of MEMS. Sens. Actuators A Phys. 2014, 215, 36–43. [Google Scholar] [CrossRef]
- Yamane, D.; Konishi, T.; Safu, T.; Toshiyoshi, H.; Sone, M.; Masu, K.; Machida, K. Evaluation and modeling of adhesion layer in shock-protection structure for MEMS accelerometer. Microelectronics Reliability 2016, 66, 78–84. [Google Scholar] [CrossRef]
- Chen, S.T.; Du, S.; Arroyo, E.; Jia, Y.; Seshia, A. Shock reliability enhancement for MEMS vibration energy harvesters with nonlinear air damping as a soft stopper. J. Micromechanics Microengineering 2017, 27, 104003. [Google Scholar] [CrossRef]
- Lani, S.; Chandran, O.; Auchlin, M.; Marozau, I.; Dunan, B. 3d Printing on MEMS: Integration of 3d Shock Stopper on a Micro Mirror. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019. [Google Scholar]
- Xu, K.; Zhu, N.; Zhang, X.; Su, W.; Zhang, W.; Hao, Y. A novel shock protection method based on MEMS compliant latching stopper. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar]
- Xu, K.; Zhang, W.; Hao, Y. Mechanical latching stops for reliability improvement of MEMS in shock environments. Microsyst. Technol. 2018, 24, 3399–3407. [Google Scholar] [CrossRef]
- Lee, Y.; Sim, S.M.; Kim, H.; Kim, Y.K.; Kim, J.M. Silicon MEMS acceleration switch with high reliability using hooked latch. Microelectron. Eng. 2016, 152, 10–19. [Google Scholar] [CrossRef]
- Tu, H.; Lou, W.; Sun, Z.; Qian, Y. Structural reliability simulation for the latching mechanism in MEMS-based Safety and Arming device. Adv. Eng. Softw. 2017, 108, 48–56. [Google Scholar] [CrossRef]
- Singh, V.; Kumar, V.; Saini, A.; Khosla, P.K.; Mishra, S. Response analysis of MEMS based high-g acceleration threshold switch under mechanical shock. Int. J. Mech. Mater. Des. 2021, 17, 137–151. [Google Scholar] [CrossRef]
- Zhou, J.; Jiang, T.; Jiao, J.W.; Wu, M. Design and fabrication of a micromachined gyroscope with high shock resistance. Microsyst. Technol. 2014, 20, 137–144. [Google Scholar] [CrossRef]
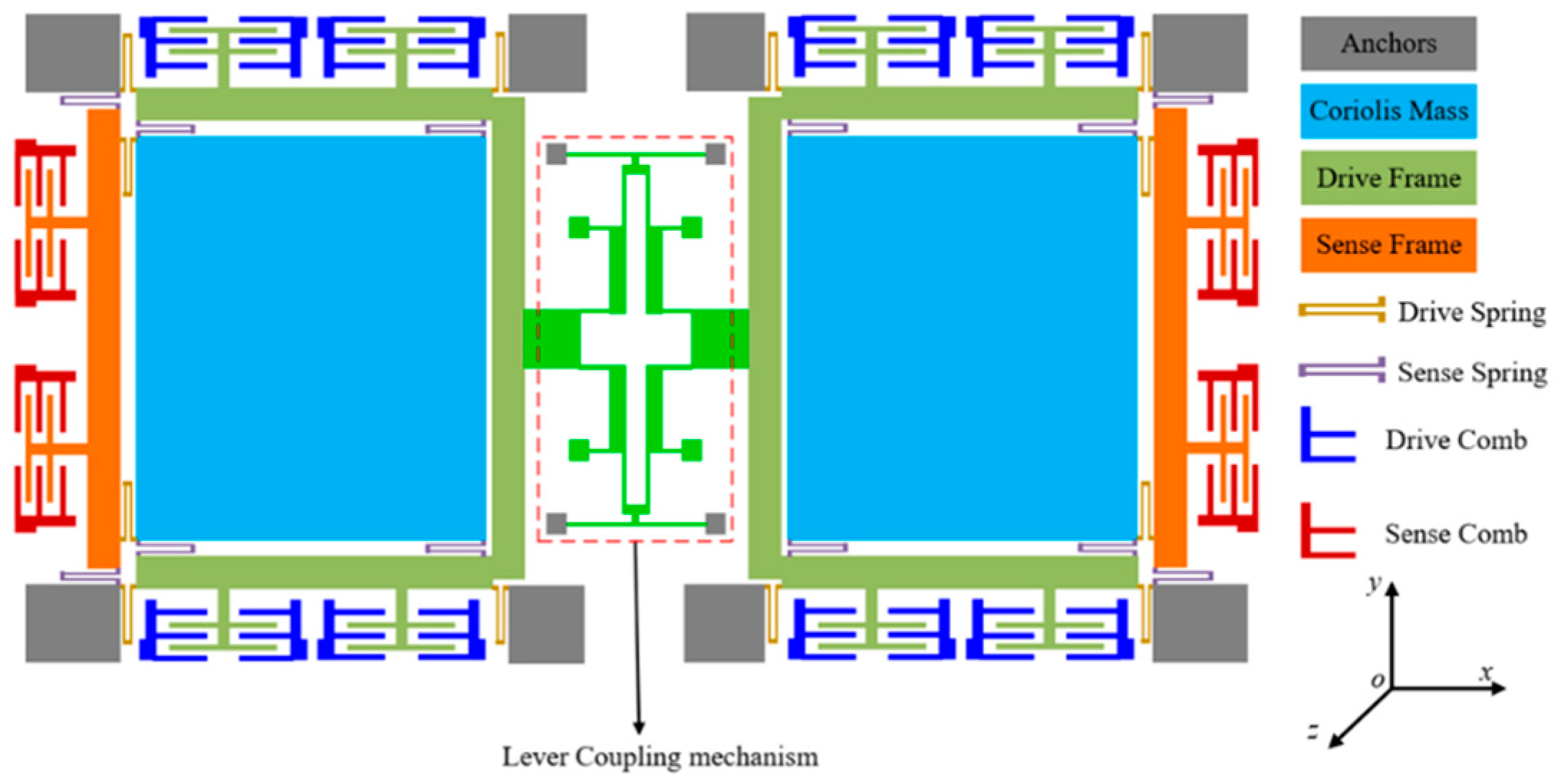
- Gao, Y.; Li, H.; Huang, L.; Sun, H. A lever coupling mechanism in dual-mass micro-gyroscopes for improving the shock resistance along the driving direction. Sensors 2017, 17, 995. [Google Scholar] [CrossRef] [Green Version]
- Fathalilou, M.; Soltani, K.; Rezazadeh, G.; Cigeroglu, E. Enhancement of the reliability of MEMS shock sensors by adopting a dual-mass model. Measurement 2020, 153, 107428. [Google Scholar] [CrossRef]
- Yoon, S.; Park, U.; Rhim, J.; Yang, S.S. Tactical grade MEMS vibrating ring gyroscope with high shock reliability. Microelectronic Engineering 2015, 142, 22–29. [Google Scholar] [CrossRef]
- Bai, B.; Ren, Z.; Ding, J.; Xu, W.; Zhang, G.; Liu, J.; Zhang, W.; Xue, C.; Zhang, B.; Wang, R. Cross-supported planar MEMS vector hydrophone for high impact resistance. Sens. Actuators A Phys. 2017, 263, 563–570. [Google Scholar] [CrossRef]
- Liu, F.; Gao, S.; Niu, S.; Zhang, Y.; Guan, Y.; Gao, C.; Li, P. Optimal design of high-g MEMS piezoresistive accelerometer based on Timoshenko beam theory. Microsyst. Technol. 2018, 24, 855–867. [Google Scholar] [CrossRef]
- Hauch, J.A.; Holland, D.; Marder, M.P.; Swinney, H.L. Dynamic fracture in single crystal silicon. Phys. Rev. Lett. 1999, 82, 3823. [Google Scholar] [CrossRef] [Green Version]
- Namazu, T.; Isono, Y.; Tanaka, T. Evaluation of size effect on mechanical properties of single crystal silicon by nanoscale bending test using AFM. J. Microelectromechanical Syst. 2000, 9, 450–459. [Google Scholar] [CrossRef]
- Cho, S.W.; Chasiotis, I. Elastic properties and representative volume element of polycrystalline silicon for MEMS. Exp. Mech. 2007, 47, 37–49. [Google Scholar] [CrossRef]
- Miller, D.C.; Boyce, B.L.; Dugger, M.T.; Buchheit, T.E.; Gall, K. Characteristics of a commercially available silicon-on-insulator MEMS material. Sens. Actuators A Phys. 2007, 138, 130–144. [Google Scholar] [CrossRef]
- Boyce, B.L.; Grazier, J.M.; Buchheit, T.E.; Shaw, M.J. Strength distributions in polycrystalline silicon MEMS. J. Microelectromechanical Syst. 2007, 16, 179–190. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromechanical Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef] [Green Version]
- Masolin, A.; Bouchard, P.O.; Martini, R.; Bernacki, M. Thermo-mechanical and fracture properties in single-crystal silicon. J. Mater. Sci. 2013, 48, 979–988. [Google Scholar] [CrossRef] [Green Version]
- Tilli, M.; Paulasto-Krockel, M.; Petzold, M.; Theuss, H.; Motooka, T.; Lindroos, V. (Eds.) Handbook of Silicon Based MEMS Materials and Technologies; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Chen, M.; Pethö, L.; Sologubenko, A.S.; Ma, H.; Michler, J.; Spolenak, R.; Wheeler, J.M. Achieving micron-scale plasticity and theoretical strength in Silicon. Nat. Commun. 2020, 11, 1–10. [Google Scholar]
- Fitzgerald, A.M.; Iyer, R.S.; Dauskardt, R.H.; Kenny, T.W. Subcritical crack growth in single-crystal silicon using micromachined specimens. J. Mater. Res. 2002, 17, 683–692. [Google Scholar] [CrossRef]
- Saleh, M.E.; Beuth, J.L.; de Boer, M.P. Validated Prediction of the Strength Size Effect in Polycrystalline Silicon Using the Three-Parameter Weibull Function. J. Am. Ceram. Soc. 2014, 97, 3982–3990. [Google Scholar] [CrossRef]
- DelRio, F.W.; Cook, R.F.; Boyce, B.L. Fracture strength of micro-and nano-scale silicon components. Appl. Phys. Rev. 2015, 2, 021303. [Google Scholar] [CrossRef] [Green Version]
- Cook, R.F.; DelRio, F.W. Determination of ceramic flaw populations from component strengths. J. Am. Ceram. Soc. 2019, 102, 4794–4808. [Google Scholar] [CrossRef]
- Cook, R.F.; DelRio, F.W. Material flaw populations and component strength distributions in the context of the Weibull function. Exp. Mech. 2019, 59, 279–293. [Google Scholar] [CrossRef] [PubMed]
- Vayrette, R.; Galceran, M.; Coulombier, M.; Godet, S.; Raskin, J.P.; Pardoen, T. Size dependent fracture strength and cracking mechanisms in freestanding polycrystalline silicon films with nanoscale thickness. Eng. Fract. Mech. 2016, 168, 190–203. [Google Scholar] [CrossRef]
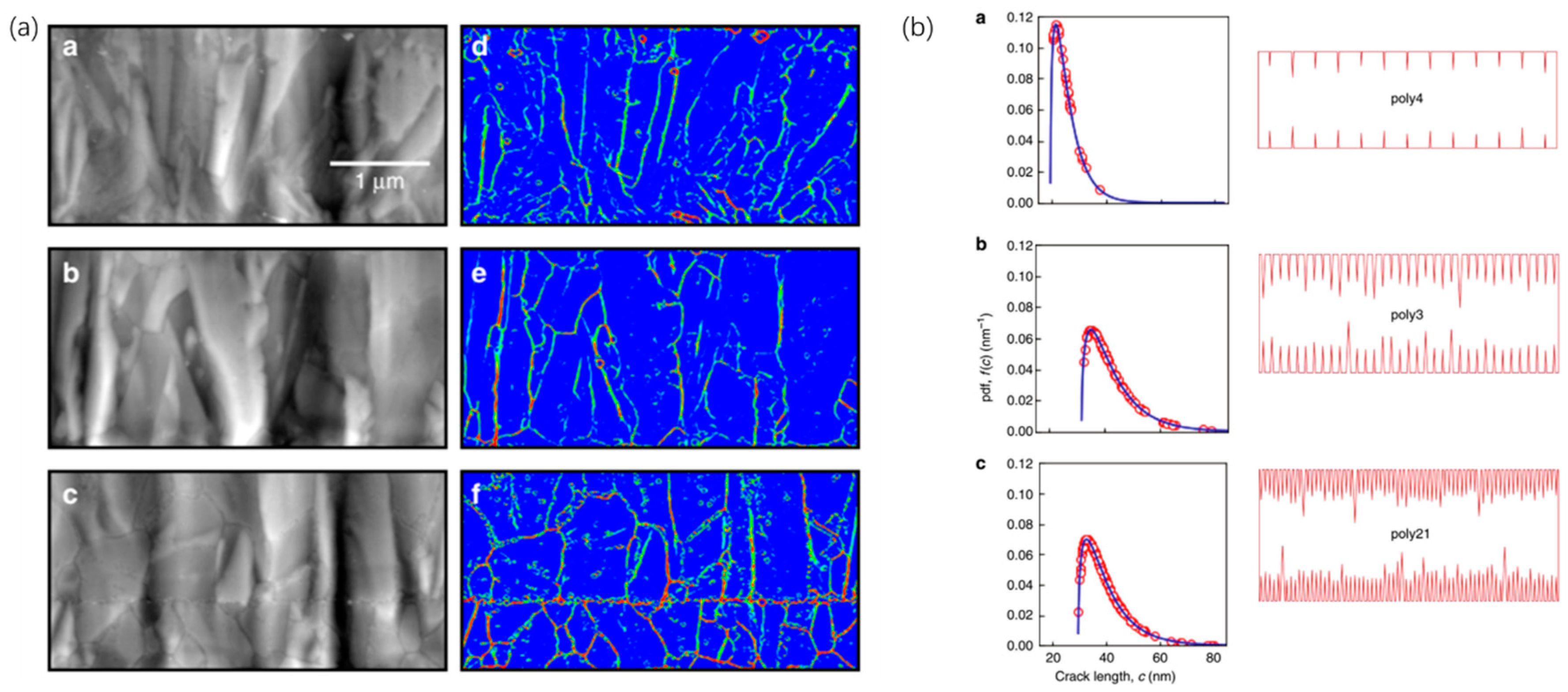
- Mariani, S.; Martini, R.; Ghisi, A.; Corigliano, A.; Simoni, B. Monte Carlo simulation of micro-cracking in polysilicon MEMS exposed to shocks. Int. J. Fract. 2011, 167, 83–101. [Google Scholar] [CrossRef]
- Molina, J.P.Q.; Rosafalco, L.; Mariani, S. Stochastic Mechanical Characterization of Polysilicon MEMS: A Deep Learning Approach. Multidiscip. Digit. Publ. Inst. Proc. 2019, 42, 8. [Google Scholar] [CrossRef] [Green Version]
- Molina, J.P.Q.; Rosafalco, L.; Mariani, S. Mechanical Characterization of Polysilicon MEMS Devices: A Stochastic, Deep Learning-based Approach. In Proceedings of the 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Cracow, Poland, 5–8 July 2020. [Google Scholar]
- Millet, O.; Collard, D.; Buchaillot, L. Reliability of packaged MEMS in shock environment: Crack and striction modeling. In Design, Test, Integration, and Packaging of MEMS/MOEMS; International Society for Optics and Photonics: Mandelieu, France, 2002; Volume 4755, pp. 696–703. [Google Scholar]
- Chen, K.-S.; Ou, K. Equivalent strengths for reliability assessment of MEMS structures. Sens. Actuators A Phys. 2004, 112, 163–174. [Google Scholar] [CrossRef]
- Fitzgerald, A.M.; Pierce, D.M.; Huigens, B.M.; White, C.D. A general methodology to predict the reliability of single-crystal silicon MEMS devices. J. Microelectromechanical Syst. 2009, 18, 962–970. [Google Scholar] [CrossRef]
- Fitzgerald, A.M.; Pierce, D.M.; Zeyen, B. Predicting reliability of silicon MEMS. In Reliability, Packaging, Testing, and Characterization of MEMS/MOEMS and Nanodevices IX; International Society for Optics and Photonics: San Francisco, CA, USA, 2010; Volume 7592, p. 759208. [Google Scholar]
- Pierce, D.M.; Zeyen, B.; Huigens, B.M.; Fitzgerald, A.M. Predicting the failure probability of device features in MEMS. IEEE Trans. Device Mater. Reliab. 2011, 11, 433–441. [Google Scholar] [CrossRef]
- Nagayoshi, K.; Gaspar, J.; Paul, O.; Izumi, H.; Kamiya, S. A study of prediction of static fracture strength of MEMS structure for strength design scheme. Procedia Eng. 2010, 5, 1292–1295. [Google Scholar] [CrossRef] [Green Version]
- Sharon, G.; Oberc, R.; Barker, D. Assessing the dynamic failure response of MEMS structures. Int. J. Struct. Integr. 2013, 4, 191–205. [Google Scholar] [CrossRef]
- Reedy, E.D.; Foulk, J.W.; Field, R.V.; de Boer, M.P.; Hazra, S.S. Predicting Fracture in Micron-Scale Polycrystalline Silicon MEMS Structures; No. SAND2011-3665P; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA; Sandia National Lab. (SNL-CA): Livermore, CA, USA, 2011.
- Reedy, E.D.; Boyce, B.L.; Foulk, J.W.; Field, R.V.; de Boer, M.P.; Hazra, S.S. Predicting fracture in micrometer-scale polycrystalline silicon MEMS structures. J. Microelectromechanical Syst. 2011, 20, 922–932. [Google Scholar] [CrossRef]
- Cook, R.F.; DelRio, F.W.; Boyce, B.L. Predicting strength distributions of MEMS structures using flaw size and spatial density. Microsyst. Nanoeng. 2019, 5, 1–12. [Google Scholar] [CrossRef]
- Borrero-Lopez, O.; Hoffman, M. Measurement of fracture strength in brittle thin films. Surf. Coat. Technol. 2014, 254, 1–10. [Google Scholar] [CrossRef]
- Le, J.; Ballarini, R.; Zhu, Z. Modeling of probabilistic failure of polycrystalline silicon MEMS structures. J. Am. Ceram. Soc. 2015, 98, 1685–1697. [Google Scholar] [CrossRef]
- Xu, Z.; Le, J. A first passage based model for probabilistic fracture of polycrystalline silicon MEMS structures. J. Mech. Phys. Solids 2017, 99, 225–241. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Ballarini, R.; Le, J. A renewal weakest-link model of strength distribution of polycrystalline silicon MEMS structures. J. Appl. Mech. 2019, 86, 081005. [Google Scholar] [CrossRef]
- Xu, Z. Probabilistic Modeling of Brittle and Quasi-Brittle Fracture: First-Passage and Weakest-Link Analyses. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2019. [Google Scholar]
- Lall, P.; Panchagade, D.R.; Choudhary, P.; Gupte, S.; Suhling, J.C. Failure-envelope approach to modeling shock and vibration survivability of electronic and MEMS packaging. IEEE Trans. Compon. Packag. Technol. 2008, 31, 104–113. [Google Scholar] [CrossRef]
- Lall, P.; Dornala, K.; Lowe, R.; Foley, J. Survivability assessment of electronics subjected to mechanical shocks up to 25,000 g. In Proceedings of the 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 31 May–3 June 2016. [Google Scholar]
- Lall, P.; Dornala, K.; Lowe, R.; Deep, J. Explicit FE Failure Prediction of Interfaces and Interconnect in Potted Electronics Assemblies Subject to High-g Acceleration Loads. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019. [Google Scholar]
- Lall, P.; Pandurangan, A.R.R.; Dornala, K.; Suhling, J.; Deep, J. Effect of Shock Angle on Solder-Joint Reliability of Potted Assemblies Under High-G Shock. In Proceedings of the 2020 19th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 26–29 May 2020. [Google Scholar]
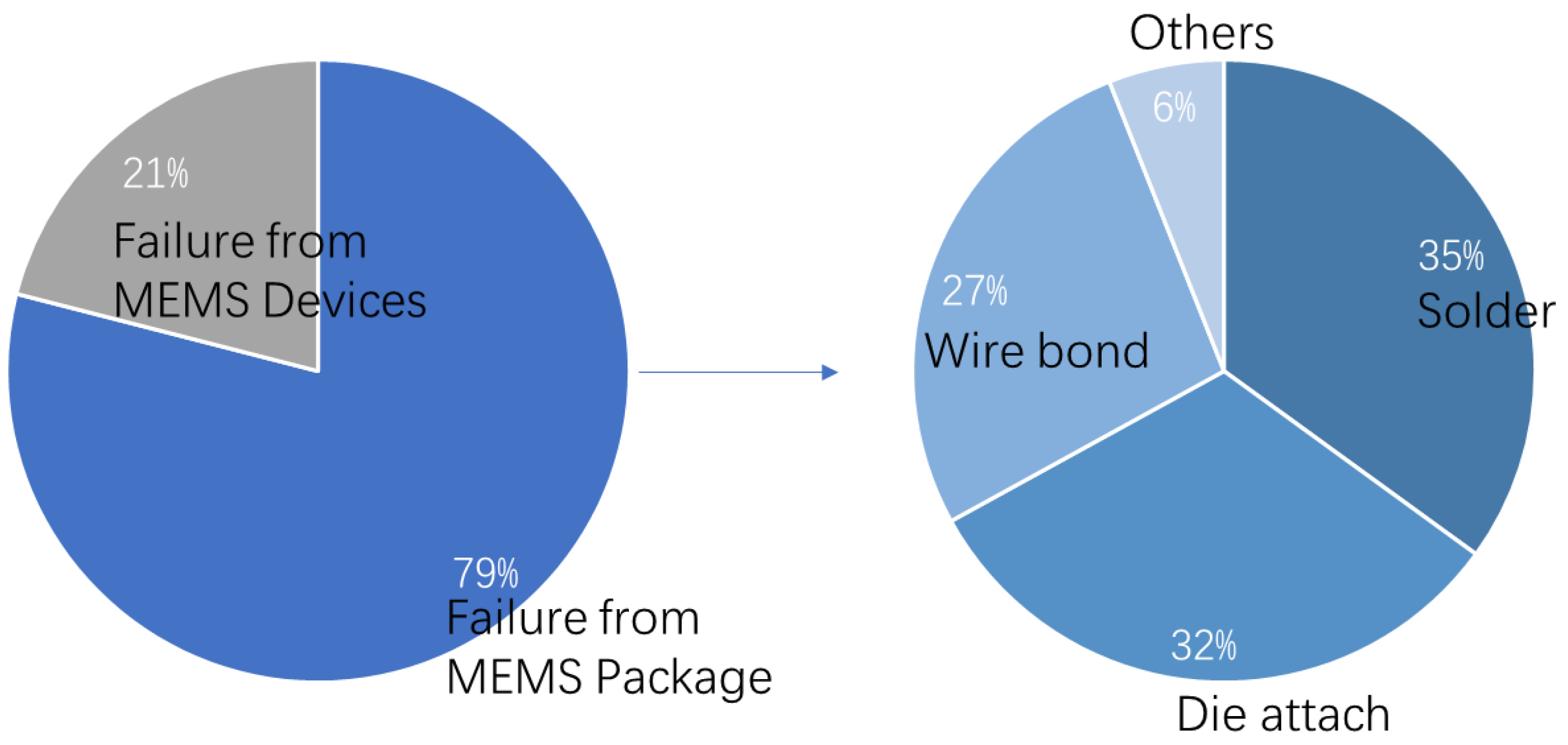
- Meng, J.; Douglas, S.T.; Dasgupta, A. Mems packaging reliability in board-level drop tests under severe shock and impact loading conditions—Part I: Experiment. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 1595–1603. [Google Scholar] [CrossRef]
- Meng, J.; Dasgupta, A. MEMS packaging reliability in board-level drop tests under severe shock and impact loading conditions—Part II: Fatigue damage modeling. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 1604–1614. [Google Scholar] [CrossRef]
- Chai, T.C.; Quek, S.; Hnin, W.Y.; Wong, E.H.; Chia, J.; Wang, Y.Y.; Lim, C.T. Board level drop test reliability of IC packages. In Proceedings of the Proceedings Electronic Components and Technology, 2005. ECTC’05, Lake Buena Vista, FL, USA, 31 May–3 June 2005. [Google Scholar]
- Alsaleem, F.; Younis, M.I.; Miles, R. An investigation into the effect of the PCB motion on the dynamic response of MEMS devices under mechanical shock loads. J. Electron. Packag. 2008, 130, 031002. [Google Scholar] [CrossRef]
- Cui, J.; Sun, B.; Feng, Q.; Zeng, S. Study on MEMS board-level package reliability under high-G impact. Annu. Conf. PHM Society. 2011, 3, 1. [Google Scholar]
- Zhou, C.Y.; Yu, T.X. Analytical models for shock isolation of typical components in portable electronics. Int. J. Impact Eng. 2009, 36, 1377–1384. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.-W.; Lu, L.-X.; Zhu, Y.; Wang, Y.-G. Three-dimensional shock spectrum of critical component for nonlinear packaging system. Shock. Vib. 2011, 18, 437–445. [Google Scholar] [CrossRef]
- Baranyai, T.; Várkonyi, P.L. Optimal Mechanical Design of Electronic Devices for Shock Protection. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1533–1543. [Google Scholar] [CrossRef]
- Shi, Y.; Wen, X.; Zhao, Y.; Zhao, R.; Cao, H.; Liu, J. Investigation and Experiment of High Shock Packaging Technology for High-G MEMS Accelerometer. IEEE Sens. J. 2020, 20, 9029–9037. [Google Scholar] [CrossRef]
- Perkins, A.E.; Sitaraman, S.K. Solder Joint Reliability Prediction for Multiple Environments; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Tamin, M.N.; Shaffiar, N.M. Solder joint reliability assessment. In Finite Element Simulation Methodology; Springer Series: Cham, Switzerland, 2014. [Google Scholar]
- Lau, J.H.; Lee, N.-C. Assembly and Reliability of Lead-Free Solder Joints; Springer Nature: Singapore, 2020. [Google Scholar]
- Shao, J.; Zhang, H.; Chen, B. Experimental study on the reliability of PBGA electronic packaging under shock loading. Electronics 2019, 8, 279. [Google Scholar] [CrossRef] [Green Version]
- Lall, P.; Dornala, K.; Deep, J.; Lowe, R. Measurement and Prediction of Interface Crack Growth at the PCB-Epoxy Interfaces Under High-G Mechanical Shock. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May–1 June 2018. [Google Scholar]
- Meguid, S.A.; Zhuo, C.; Yang, F. Effective mitigation of shock loads in embedded electronic packaging using bilayered potting materials. J. Electron. Packag. 2014, 136, 041010. [Google Scholar] [CrossRef]
- Chao, N.H.; Cordes, J.A.; Carlucci, D.; DeAngelis, M.E.; Lee, J. The use of potting materials for electronic-packaging survivability in smart munitions. J. Electron. Packag. 2011, 133, 041003. [Google Scholar] [CrossRef]
- Reinhardt, L.E.; Cordes, J.A.; Haynes, A.S.; Metz, J.D. Assessment of need for solder in modeling potted electronics during gun-shot. J. Appl. Mech. 2013, 80, 031502. [Google Scholar] [CrossRef]
- Chao, N.-H.; Dispenza, J.A.; DeAngelis, M. Advanced Methodologies for Developing Improved Potted Smart Munitions for High-G Applications. J. Electron. Packag. 2013, 135, 031002. [Google Scholar] [CrossRef]
- Chao, N.H.; DeAngelis, M.E.; Lee, J.; Kleinbach, K.S.; Cheng, R.B. Advanced Modeling for Miniaturized Potted Smart Munitions Development. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
- Younis, M.I.; Miles, R.; Jordy, D. Investigation of the response of microstructures under the combined effect of mechanical shock and electrostatic forces. J. Micromechanics Microengineering 2006, 16, 2463. [Google Scholar] [CrossRef] [Green Version]
- Younis, M.I.; Alsaleem, F.M.; Miles, R.; Su, Q. Characterization of the performance of capacitive switches activated by mechanical shock. J. Micromechanics Microengineering 2007, 17, 1360. [Google Scholar] [CrossRef] [Green Version]
- Ouakad, H.; Younis, M.I.; Alsaleem, F.; Levo, T.; Pitarresi, J. Response of an electrostatically actuated microbeam to drop-table test. In 2010 11th International Thermal, Mechanical & Multi-Physics Simulation, and Experiments in Microelectronics and Microsystems (EuroSimE); IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Alqasimi, J.E.; Ouakad, H.M. Exploration of the Response of Electrically Actuated MEMS Arches Under the Effect of Mechanical Shock Loads. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: Tampa, FL, USA, 2017; Volume 58387. [Google Scholar]
- Alqasimi, J.E.; Ouakad, H.M. Vibrational response of initially deformed bistable microbeams under the combined effect of mechanical shock loads and electrostatic forces. J. Vib. Acoust. 2018, 140, 021013. [Google Scholar] [CrossRef]
- Ouakad, H.M.; AlQasimi, J.E. Reliability of MEMS shallow arches based actuator under the combined effect of mechanical shock and electric loads. Microelectron. Reliab. 2017, 79, 352–359. [Google Scholar] [CrossRef]
- Kevin, L.; Hunter, A.; Abdelkefi, A. Comparative investigations of multi-fidelity modeling on performance of electrostatically-actuated cracked micro-beams. Int. J. Mech. Sci. 2021, 192, 106139. [Google Scholar]
- Haynes, A.S.; Cordes, J.A.; Krug, J. Thermomechanical Impact of Polyurethane Potting on Gun Launched Electronics. J. Eng. 2013, 2013, 148362. [Google Scholar] [CrossRef] [Green Version]
- Lall, P.; Abrol, A.S.; Simpson, L.; Glover, J. Reliability of MEMS devices under multiple environments. In Proceedings of the Fourteenth Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 27–30 May 2014. [Google Scholar]
- Li, Y.; Jiang, Z. An overview of reliability and failure mode analysis of microelectromechanical systems (MEMS). In Handbook of Performability Engineering; Springer: London, UK, 2008; pp. 953–966. [Google Scholar]
- Feng, Q.; Coit, D.W. Reliability analysis for multiple dependent failure processes: An MEMS application. Int. J. Perform. Eng. 2010, 6, 100. [Google Scholar]
- Zhang, Z.; Yang, X.; Oseledets, I.V.; Karniadakis, G.E.; Daniel, L. Enabling high-dimensional hierarchical uncertainty quantification by ANOVA and tensor-train decomposition. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 34, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Sun, Y.; Hu, W.; Wang, Z. A novel correlative model of failure mechanisms for evaluating MEMS devices reliability. Microelectron. Reliab. 2016, 64, 669–675. [Google Scholar] [CrossRef]







| Scenarios | Shock Load |
|---|---|
| Ships | 120~150 g, 25 Hz |
| Vehicles | 0.1~1 g, 5~50 Hz |
| Industry | 0.1 g, 5~100 Hz |
| Earthquake | 0.1~0.5 g, 2~90 Hz |
| Drop | 10 g, 50~200 Hz |
| Plane Crash | 15~30 g, ~100 Hz |
| Gun Shot | 103~104 g, 102~103 Hz |
| Hard Target Penetration | 104~105 g, 103~104 Hz |
| Class | Features | Products |
|---|---|---|
| Class I | No movable/active structure | Accelerometer, pressure sensor, micro injection pin |
| Class II | Active structure, no contacts or frictions | Gyroscope, resonator, filter, comb driver |
| Class III | Active structure with contacts but no frictions | RF switch, micro valve |
| Class IV | Active structure with contacts and frictions | Optical switch, micromirror |
| Class | Features | Failure |
|---|---|---|
| Class I | Accelerometer | wear, fatigue, fracture, electrical failure |
| Pressure sensor | fracture, fatigue, shock, vibration | |
| Class II | Gyroscope | shock, vibration, electrical failure |
| Class III | Heat Actuator | wear, shock, vibration |
| Micro Valve | wear, fracture, fatigue, shock, vibration | |
| RF Switch | wear, fracture, fatigue, shock, vibration, electrical failure | |
| Class IV | Electrostatic actuator | wear, fracture, fatigue, shock, vibration, friction |
| Optical switch | wear, fracture, fatigue, shock, vibration | |
| Micromirror | wear, fracture, fatigue, shock, vibration, optical performance degradation | |
| Micro gears | wear, fracture, fatigue, shock, vibration, friction | |
| Micro turbines | wear, fracture, shock, vibration, friction |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, T.; You, Z. Reliability of MEMS in Shock Environments: 2000–2020. Micromachines 2021, 12, 1275. https://doi.org/10.3390/mi12111275
Peng T, You Z. Reliability of MEMS in Shock Environments: 2000–2020. Micromachines. 2021; 12(11):1275. https://doi.org/10.3390/mi12111275
Chicago/Turabian StylePeng, Tianfang, and Zheng You. 2021. "Reliability of MEMS in Shock Environments: 2000–2020" Micromachines 12, no. 11: 1275. https://doi.org/10.3390/mi12111275
APA StylePeng, T., & You, Z. (2021). Reliability of MEMS in Shock Environments: 2000–2020. Micromachines, 12(11), 1275. https://doi.org/10.3390/mi12111275







