Topological Design of Multi-Material Compliant Mechanisms with Global Stress Constraints
Abstract
:1. Introduction
2. Optimization Problem
2.1. Material Interpolation Method
2.2. Global Stress Constraints
2.3. The Topology Optimization Formulation
3. Sensitivity Analysis
4. Numerical Examples
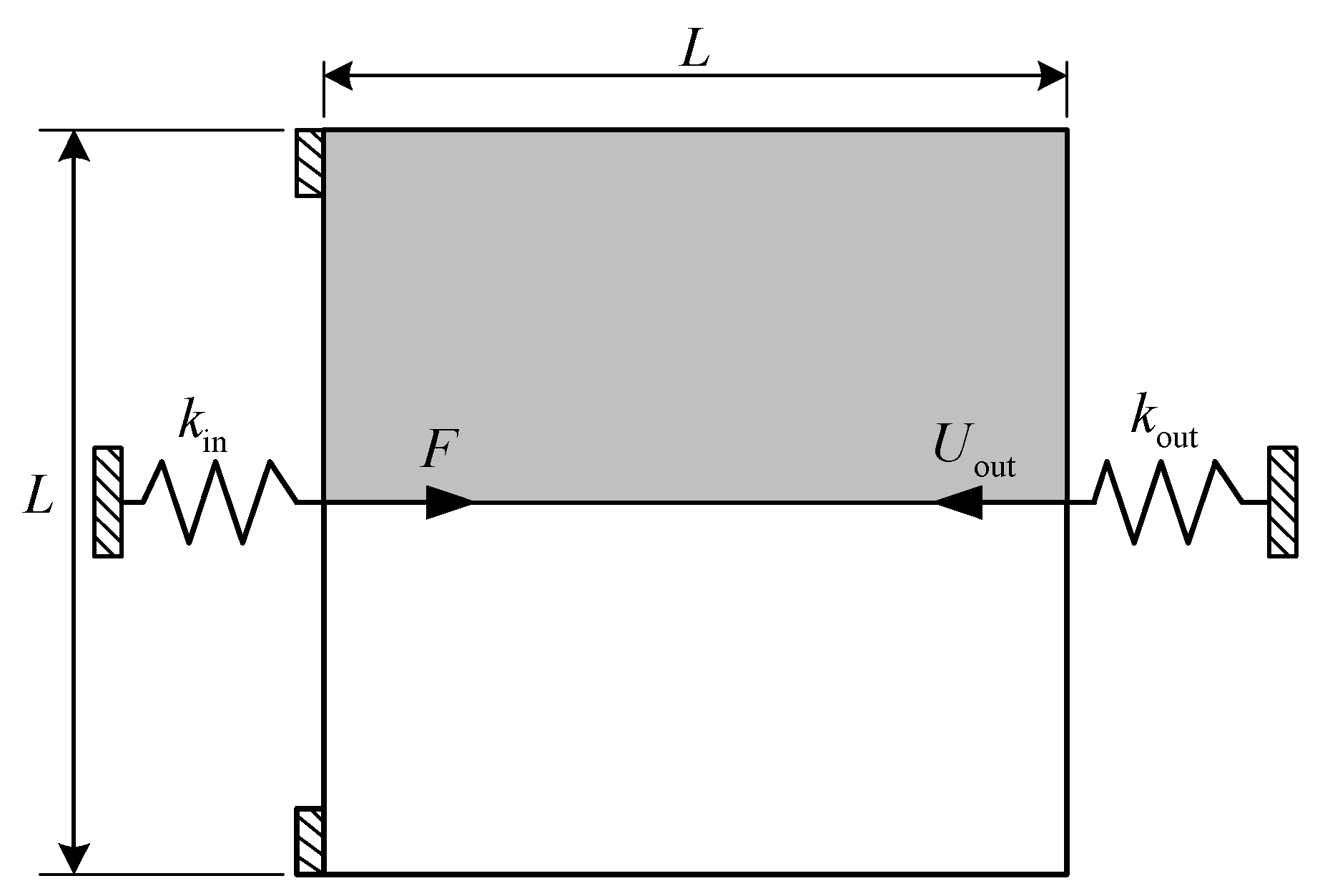
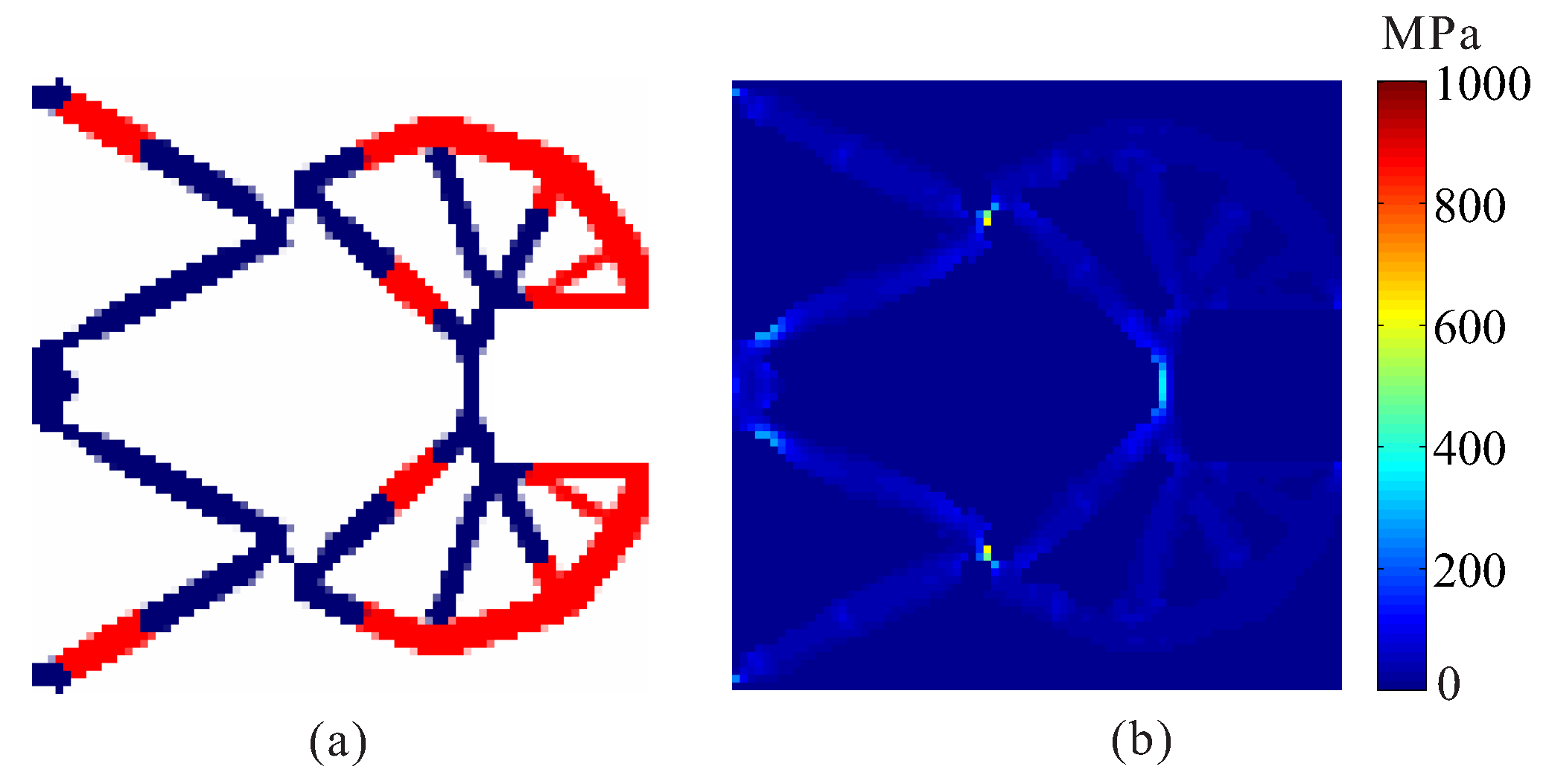
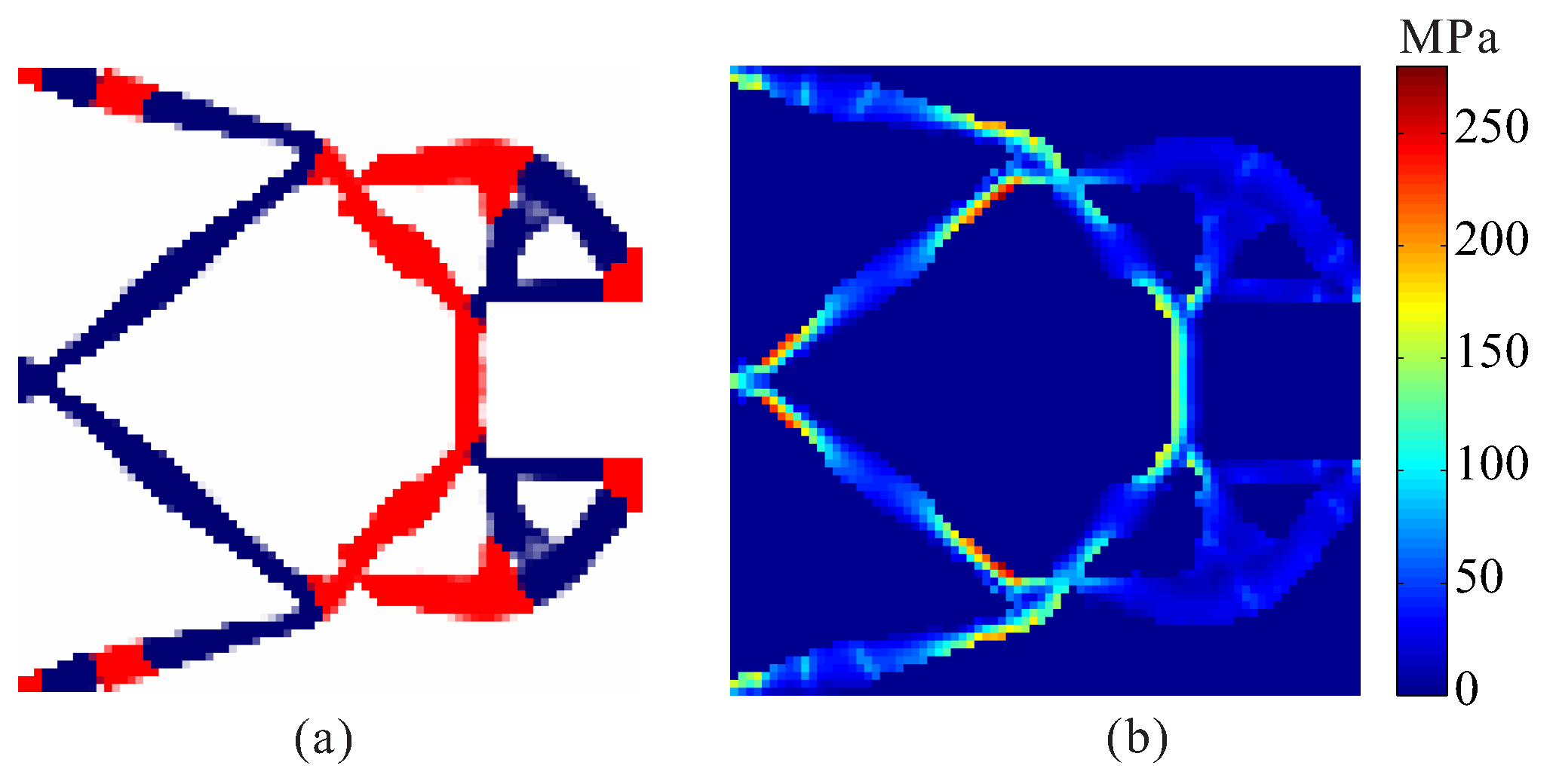
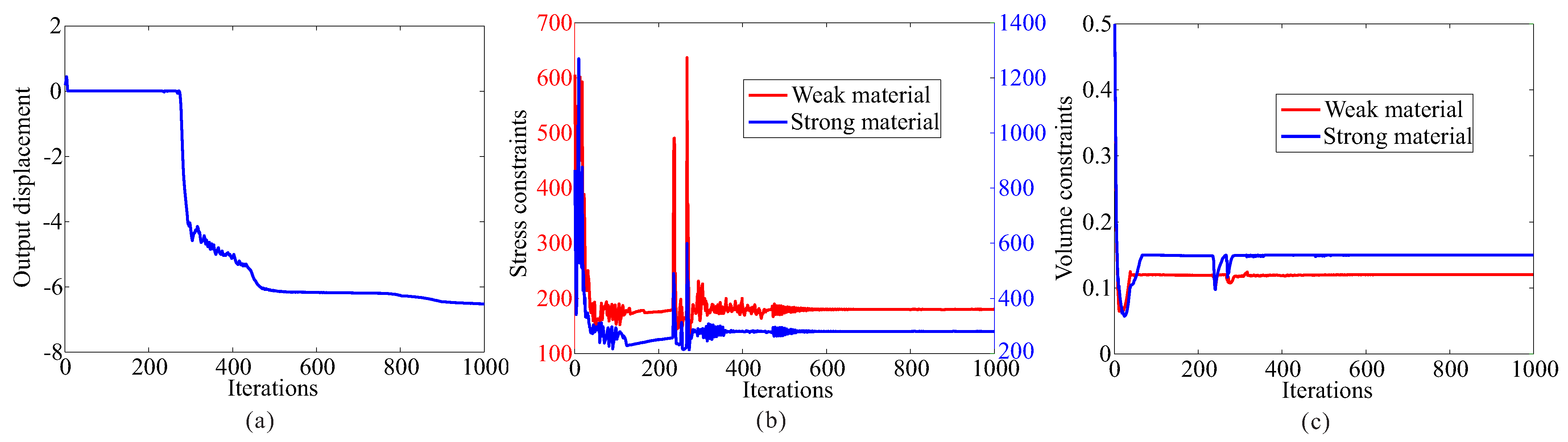
4.1. Displacement Inverter
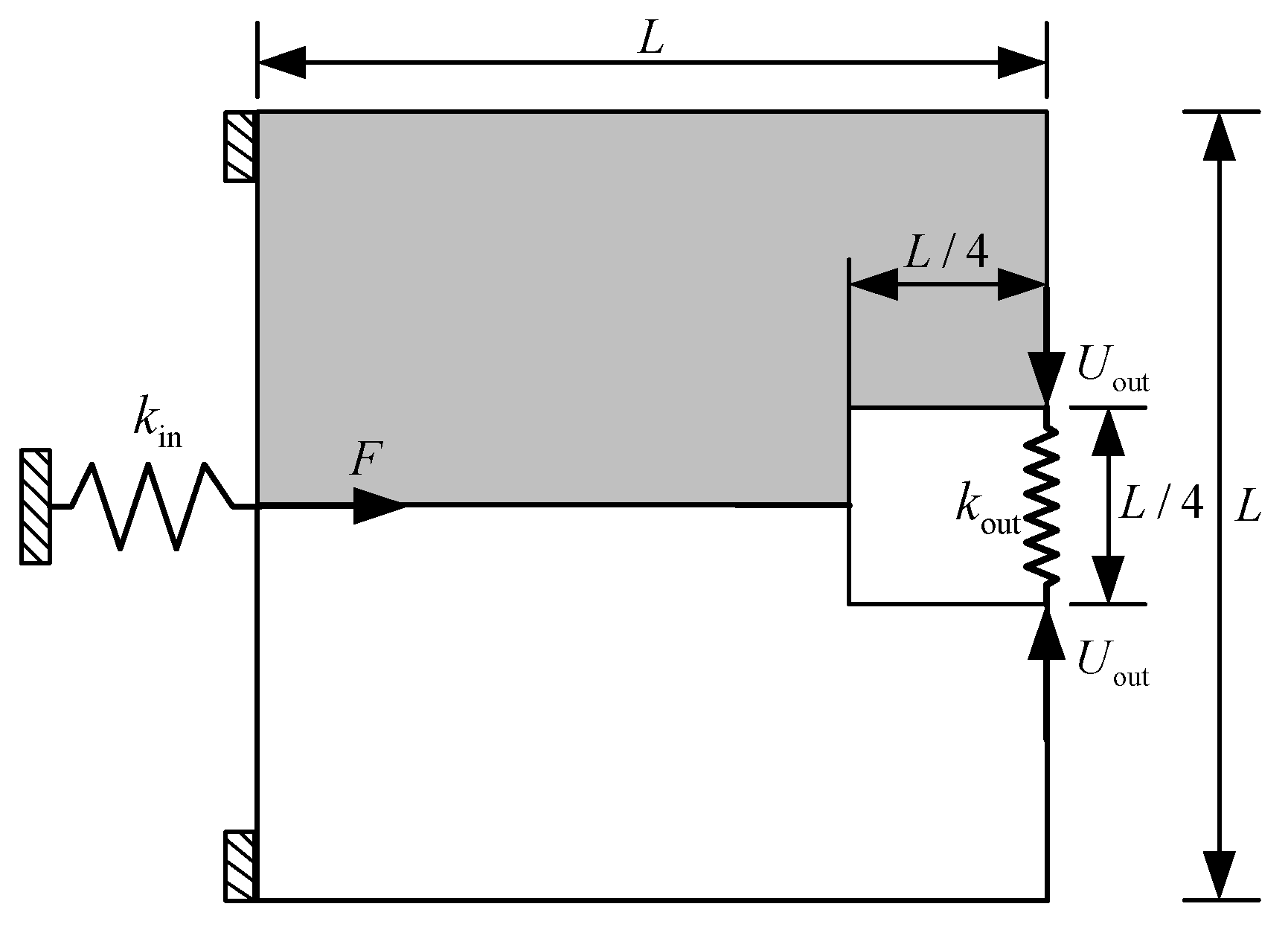
4.2. Compliant Gripper
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Howell, L.L. Compliant Mechanisms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Li, H.; Hao, G. Position-Space-Based Design of a Symmetric Spatial Translational Compliant Mechanism for Micro-/Nano-Manipulation. Micromachines 2018, 9, 189. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of Compliant Mechanisms Using Continuum Topology Optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Zhu, D.; Zhan, W.; Wu, F.; Simeone, A. Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator. Micromachines 2018, 9, 184. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Zhan, J.; Zhu, B.; Zhang, X. Topology Optimization of Compliant Mechanism Considering Actual Output Displacement Using Adaptive Output Spring Stiffness. Mech. Mach. Theory 2020, 143, 103728. [Google Scholar] [CrossRef]
- Chen, G.; Howell, L.L. Symmetric Equations for Evaluating Maximum Torsion Stress of Rectangular Beams in Compliant Mechanisms. Chin. J. Mech. Eng. 2018, 31, 14. [Google Scholar] [CrossRef] [Green Version]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Ananthasuresh, G.K.; Kota, S.; Kikuchi, N. Strategies for systematic synthesis of compliant MEMS. In Proceedings of the ASME Winter Annual Meeting, Chicago, IL, USA, 6–10 November 1994; pp. 677–686. [Google Scholar]
- Zhan, J.; Zhang, X. Topology Optimization of Compliant Mechanisms with Geometrical Nonlinearities Using the Ground Structure Approach. Chin. J. Mech. Eng. 2011, 24, 257–263. [Google Scholar] [CrossRef]
- Liu, M.; Zhan, J.; Zhu, B.; Zhang, X. Topology optimization of distributed flexure hinges with desired performance. Eng. Optim. 2020, 52, 405–425. [Google Scholar] [CrossRef]
- Zhang, W.; Zhong, W.; Guo, X. An explicit length scale control approach in SIMP-based topology optimization. Comput. Methods Appl. Mech. Eng. 2014, 282, 71–86. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Luo, Z.; Tong, L.; Wang, M.Y.; Wang, S. Shape and topology optimization of compliant mechanisms using a parameterization level set method. J. Comput. Phys. 2007, 227, 680–705. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. A further review of ESO type methods for topology optimization. Struct. Multidiscip. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y.M. Bi-directional Evolutionary Structural Optimization on Advanced Structures and Materials: A Comprehensive Review. Arch. Comput. Methods Eng. 2016, 25, 437–478. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing topology optimization explicitly and geometrically—A new moving morphable components based framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Yin, L.; Ananthasuresh, G. Topology optimization of compliant mechanisms with multiple materials using a peak function material interpolation scheme. Struct. Multidisc. Optim. 2001, 23, 49–62. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization—Part II: Two-material structures. Comput. Methods Appl. Mech. Eng. 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
- Saxena, A. Topology design of large displacement compliant mechanisms with multiple materials and multiple output ports. Struct. Multidisc. Optim. 2005, 30, 477–490. [Google Scholar] [CrossRef]
- Wang, M.Y.; Chen, S.; Wang, X.; Mei, Y. Design of Multimaterial Compliant Mechanisms Using Level-Set Methods. J. Mech. Des. 2005, 127, 941–956. [Google Scholar] [CrossRef]
- Alonso, C.; Ansola, R.; Querin, O.M. Topology synthesis of multi-material compliant mechanisms with a Sequential Element Rejection and Admission method. Finite Elem. Anal. Des. 2014, 85, 11–19. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Meisel, N.A.; Williams, C.B.; Guest, J.K. Multiple-Material Topology Optimization of Compliant Mechanisms Created Via PolyJet Three-Dimensional Printing. J. Manuf. Sci. E-T ASME 2014, 136, 061015. [Google Scholar] [CrossRef] [Green Version]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Wang, N.; Hu, K.; Zhang, X. Hierarchical optimization for topology design of multi-material compliant mechanisms. Eng. Optim. 2017, 49, 2013–2035. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]
- Poulsen, T.A. A new scheme for imposing a minimum length scale in topology optimization. Int. J. Numer. Methods Eng. 2003, 57, 741–760. [Google Scholar] [CrossRef]
- Yin, L.; Ananthasuresh, G.K. Design of Distributed Compliant Mechanisms. Mech. Based Des. Struc. 2003, 31, 151–179. [Google Scholar] [CrossRef]
- Zhou, H. Topology optimization of compliant mechanisms using hybrid discretization model. J. Mech. Des. 2010, 132, 111003. [Google Scholar] [CrossRef]
- Luo, J.; Luo, Z.; Chen, S.; Tong, L.; Wang, M.Y. A new level set method for systematic design of hinge-free compliant mechanisms. Comput. Methods Appl. Mech. Eng. 2008, 198, 318–331. [Google Scholar] [CrossRef]
- Wang, M.Y.; Chen, S. Compliant mechanism optimization: Analysis and design with intrinsic characteristic stiffness. Mech. Based Des. Struc. 2009, 37, 183–200. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Fatikow, S. Level set-based topology optimization of hinge-free compliant mechanisms using a two-step elastic modeling method. J. Mech. Des. 2014, 136, 031007. [Google Scholar] [CrossRef]
- Leon, D.M.D.; Alexandersen, J.; Fonseca, J.S.O.; Sigmund, O. Stress-constrained topology optimization for compliant mechanism design. Struct. Multidiscip. Optim. 2015, 52, 1–15. [Google Scholar]
- Lopes, C.G.; Novotny, A.A. Topology design of compliant mechanisms with stress constraints based on the topological derivative concept. Struct. Multidiscip. Optim. 2016, 54, 737–746. [Google Scholar] [CrossRef]
- Chu, S.; Gao, L.; Xiao, M.; Luo, Z.; Li, H. Stress-based multi-material topology optimization of compliant mechanisms. Int. J. Numer. Methods Eng. 2018, 113, 1021–1044. [Google Scholar] [CrossRef]
- Yoon, G.H.; Park, Y.K.; Kim, Y.Y. Element stacking method for topology optimization with material-dependent boundary and loading conditions. J. Mech. Mater. Struct. 2007, 2, 883–895. [Google Scholar] [CrossRef]
- Jeong, S.H.; Choi, D.; Yoon, G.H. Separable stress interpolation scheme for stress-based topology optimization with multiple homogenous materials. Finite Elem. Anal. Des. 2014, 82, 16–31. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Zhou, J.; Du, Z.; Li, B.; Guo, X. A moving morphable void (MMV)-based explicit approach for topology optimization considering stress constraints. Comput. Methods Appl. Mech. Eng. 2018, 334, 381–413. [Google Scholar] [CrossRef]
- Le, C.; Norato, J.; Bruns, T.; Ha, C.; Tortorelli, D. Stress-based topology optimization for continua. Struct. Multidiscip. Optim. 2010, 41, 605–620. [Google Scholar] [CrossRef]
- Holmberg, E.; Bo, T.; Klarbring, A. Stress constrained topology optimization. Struct. Multidiscip. Optim. 2013, 48, 33–47. [Google Scholar] [CrossRef] [Green Version]
- Oest, J.; Lund, E. Topology optimization with finite-life fatigue constraints. Struct. Multidiscip. Optim. 2017, 56, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Andreassen, E.; Clausen, A.T.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Svanberg, K. The Method of Moving Asymptotes—A New Method for Structural Optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Sigmund, O. On the design of compliant mechanisms using topology optimization. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]

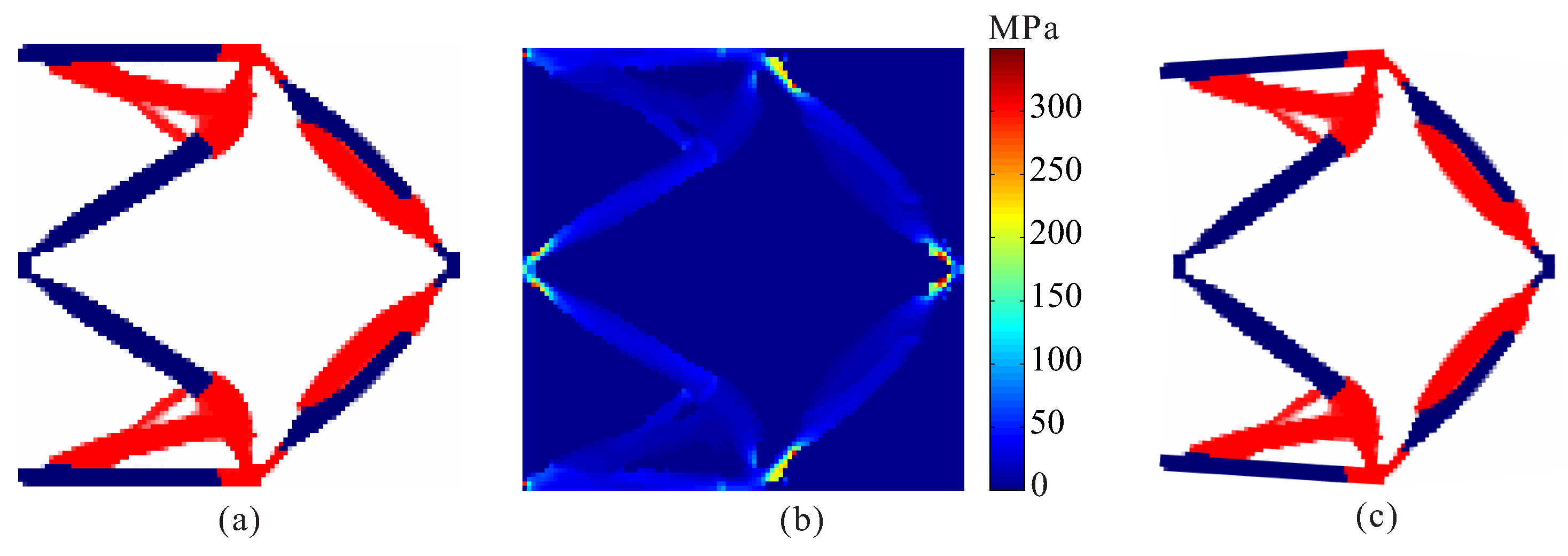

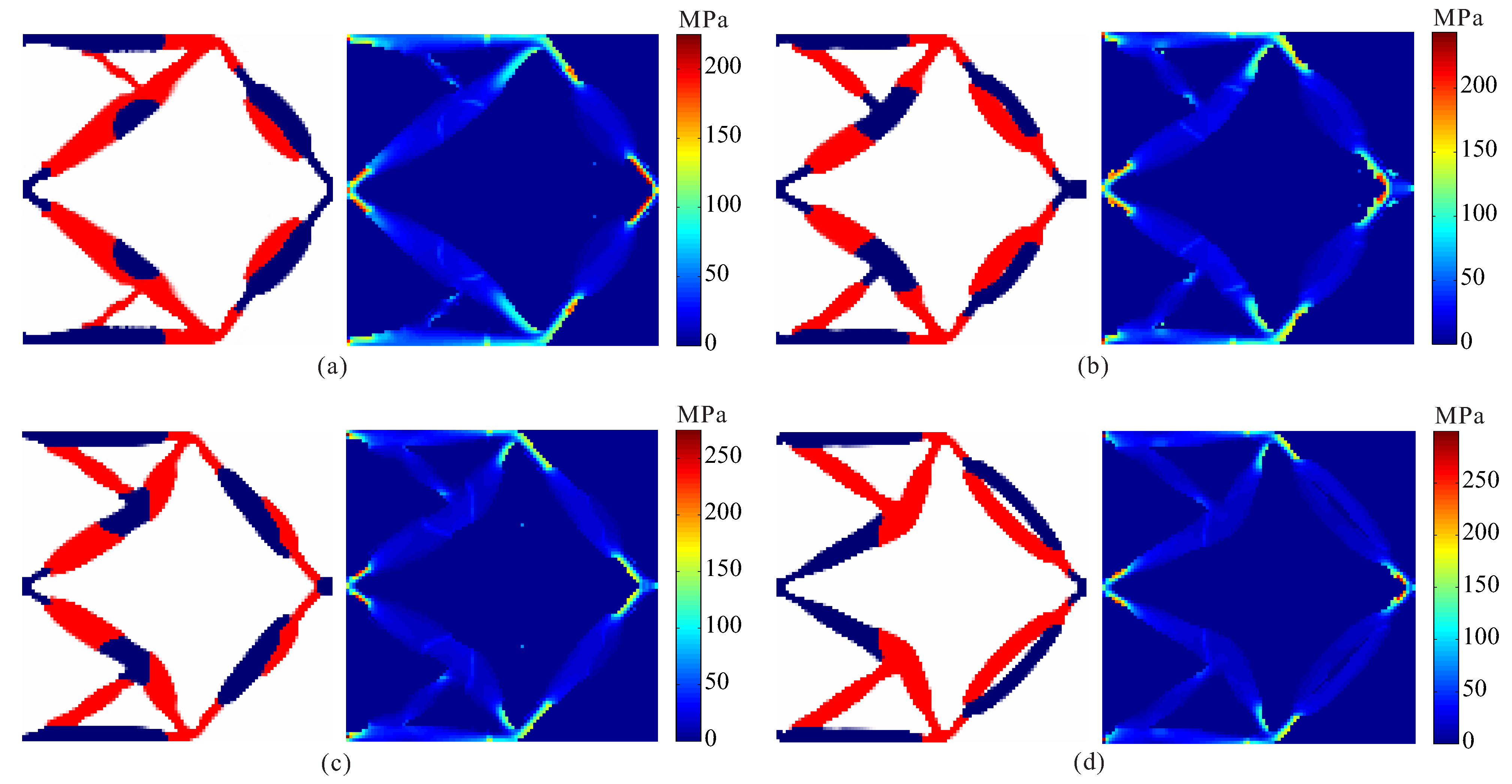

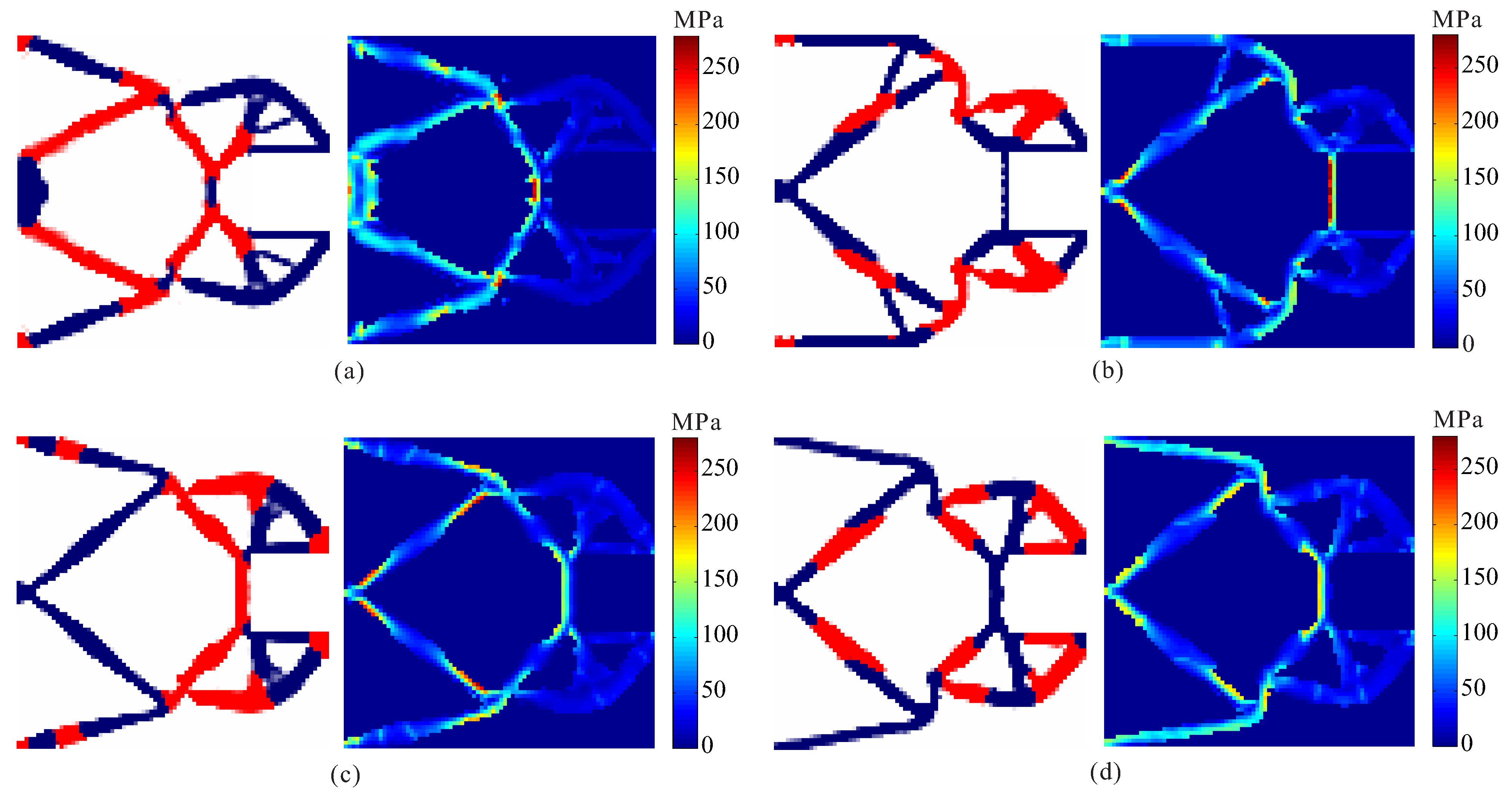
| Stress Constraints | Output Displacement (μm) | Maximum Stress (MPa) | ||
|---|---|---|---|---|
| Weak Material | Strong Material | |||
| 150 | 225 | 13.361 | 149.538 | 224.976 |
| 175 | 250 | 13.941 | 172.011 | 243.847 |
| 200 | 275 | 14.376 | 200.065 | 275.011 |
| 225 | 300 | 14.587 | 224.986 | 299.837 |
| Stress Constraints | Output Displacement (μm) | Maximum Stress (MPa) | ||
|---|---|---|---|---|
| Weak Material | Strong Material | |||
| 150 | 250 | 5.199 | 151.192 | 250.275 |
| 170 | 270 | 5.914 | 169.814 | 269.678 |
| 190 | 290 | 7.055 | 191.839 | 290.063 |
| 210 | 310 | 7.125 | 202.027 | 310.068 |
| Output Spring Stiffness (N/m) | Output Displacement (μm) | Maximum Stress (MPa) | |
|---|---|---|---|
| Weak Material | Strong Material | ||
| 1 × 103 | 9.168 | 180.064 | 280.571 |
| 2 × 103 | 7.579 | 179.894 | 279.709 |
| 3 × 103 | 6.526 | 180.234 | 279.946 |
| 4 × 103 | 5.239 | 177.928 | 280.065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, J.; Li, Y.; Luo, Z.; Liu, M. Topological Design of Multi-Material Compliant Mechanisms with Global Stress Constraints. Micromachines 2021, 12, 1379. https://doi.org/10.3390/mi12111379
Zhan J, Li Y, Luo Z, Liu M. Topological Design of Multi-Material Compliant Mechanisms with Global Stress Constraints. Micromachines. 2021; 12(11):1379. https://doi.org/10.3390/mi12111379
Chicago/Turabian StyleZhan, Jinqing, Yifeng Li, Zhen Luo, and Min Liu. 2021. "Topological Design of Multi-Material Compliant Mechanisms with Global Stress Constraints" Micromachines 12, no. 11: 1379. https://doi.org/10.3390/mi12111379
APA StyleZhan, J., Li, Y., Luo, Z., & Liu, M. (2021). Topological Design of Multi-Material Compliant Mechanisms with Global Stress Constraints. Micromachines, 12(11), 1379. https://doi.org/10.3390/mi12111379







