A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser
Abstract
:1. Introduction
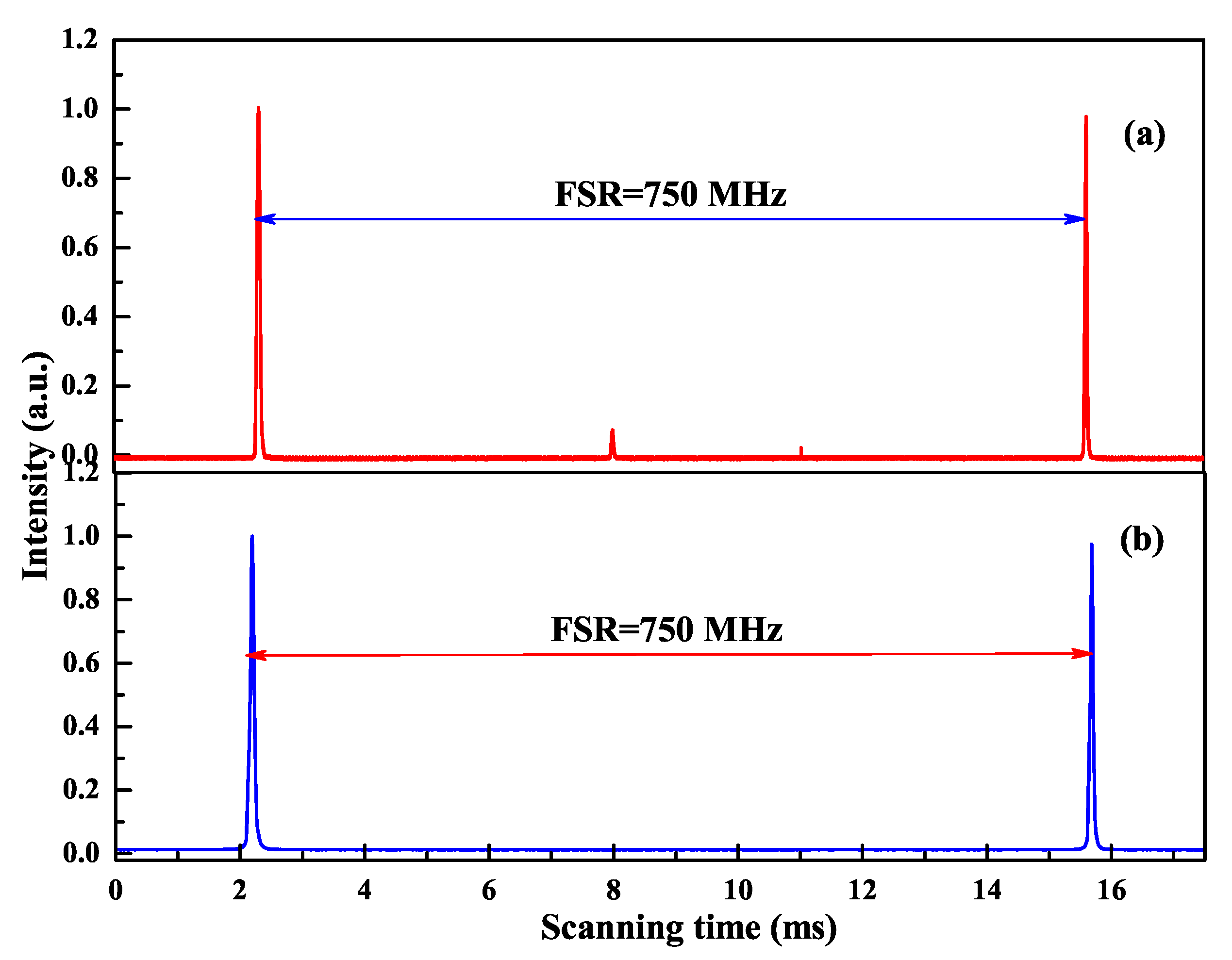
2. High-Power All-Solid-State Single-Frequency CW 1064 nm Lasers
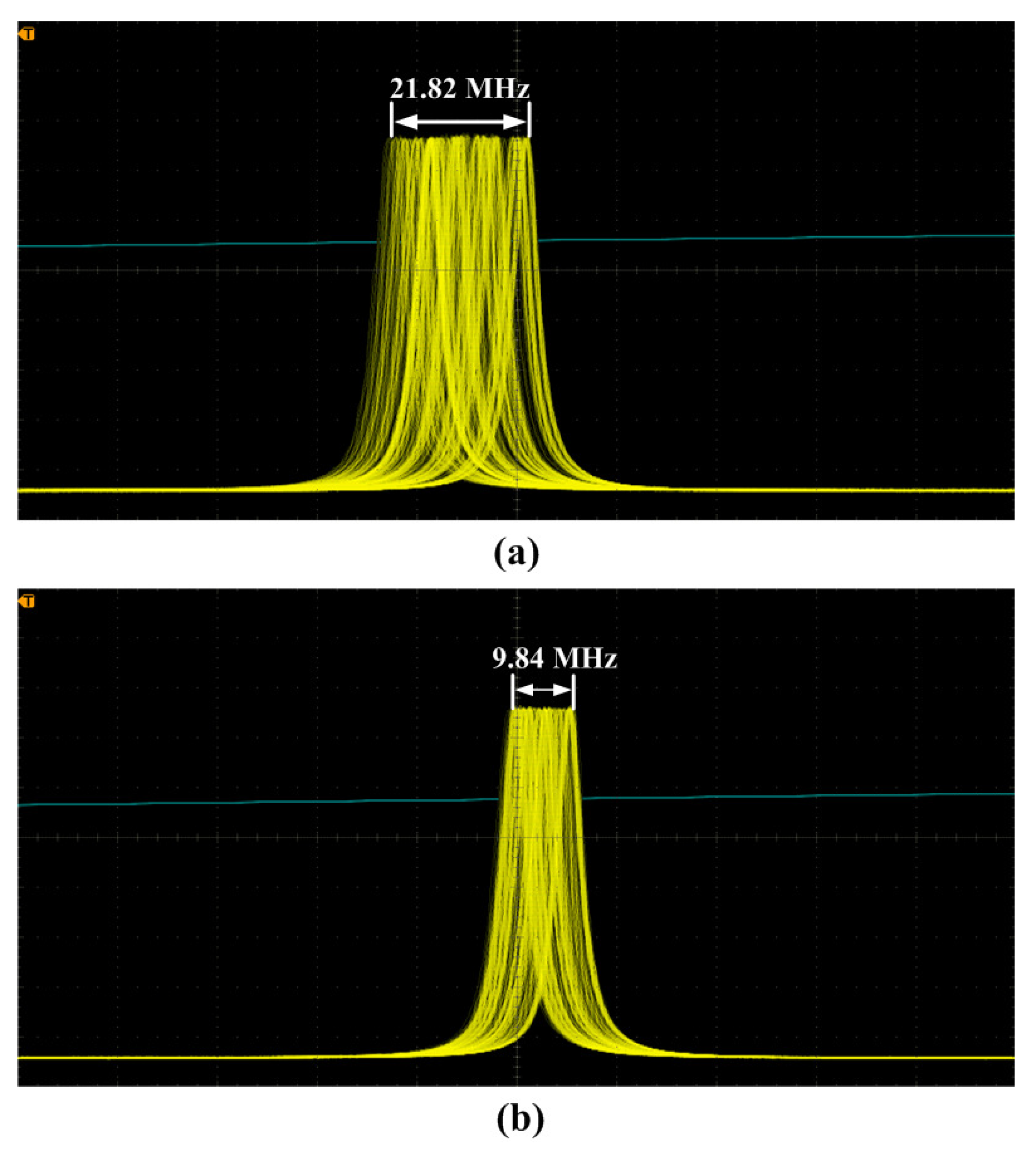
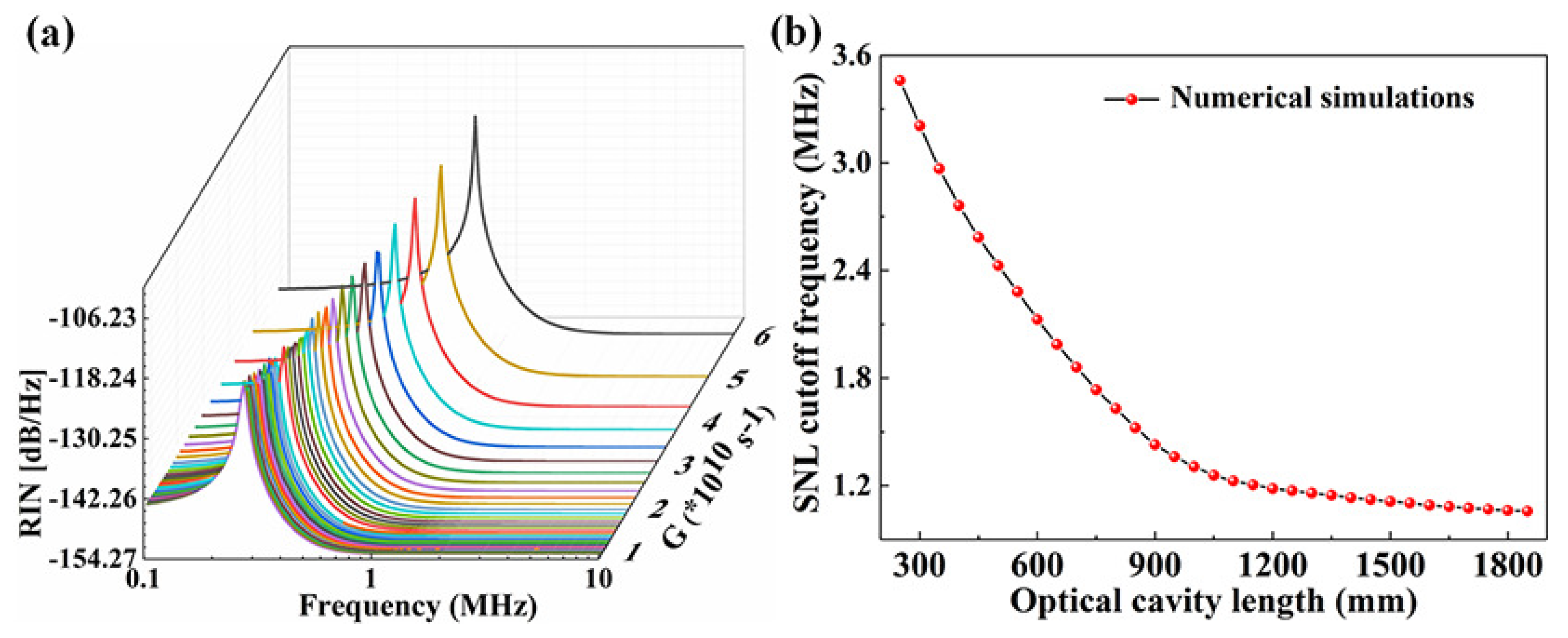
2.1. Physical Conditions of SLM Operation
2.2. Employing Nonlinear Loss to Accurately Measure the Intracavity Loss of the Laser
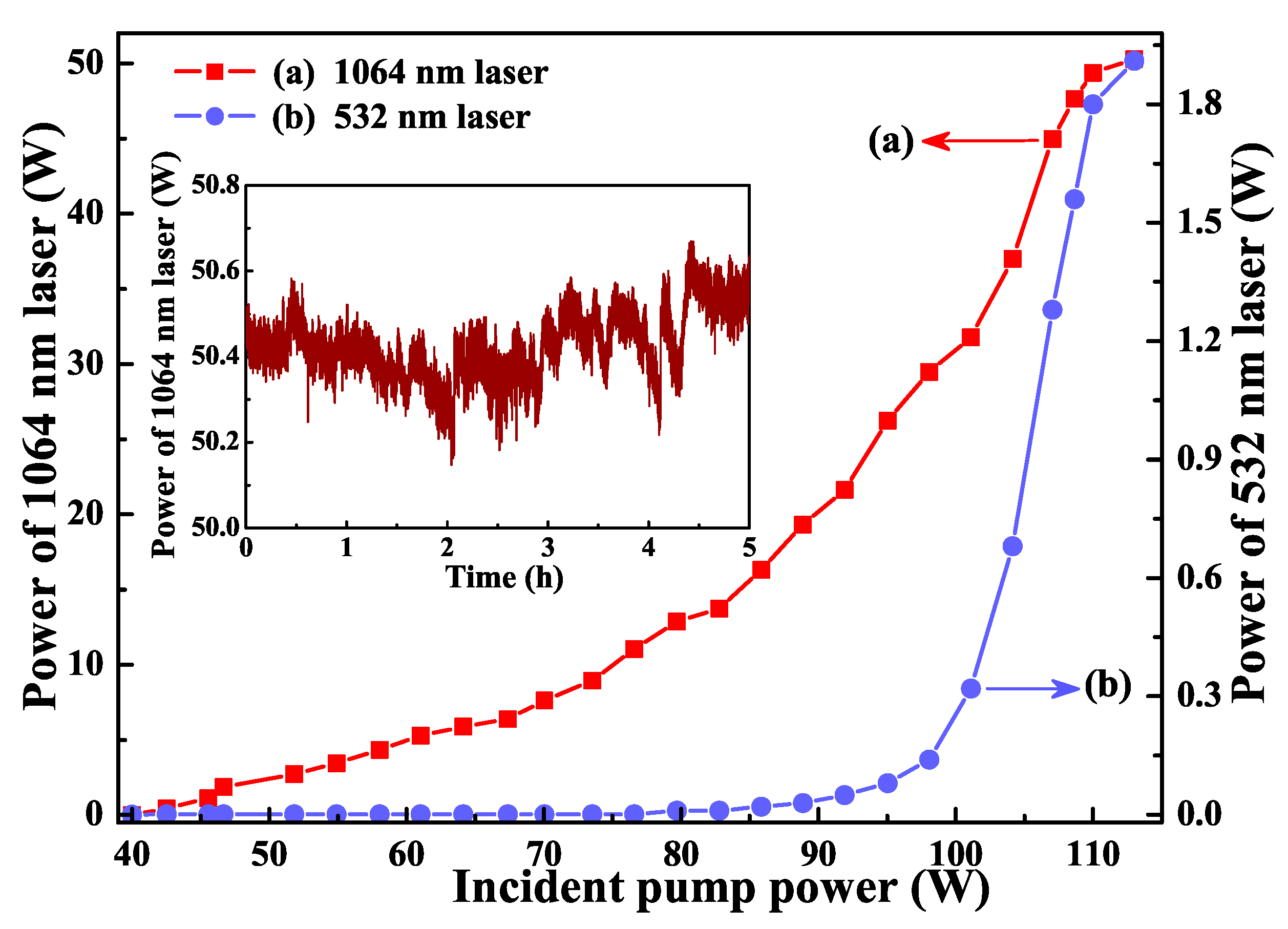
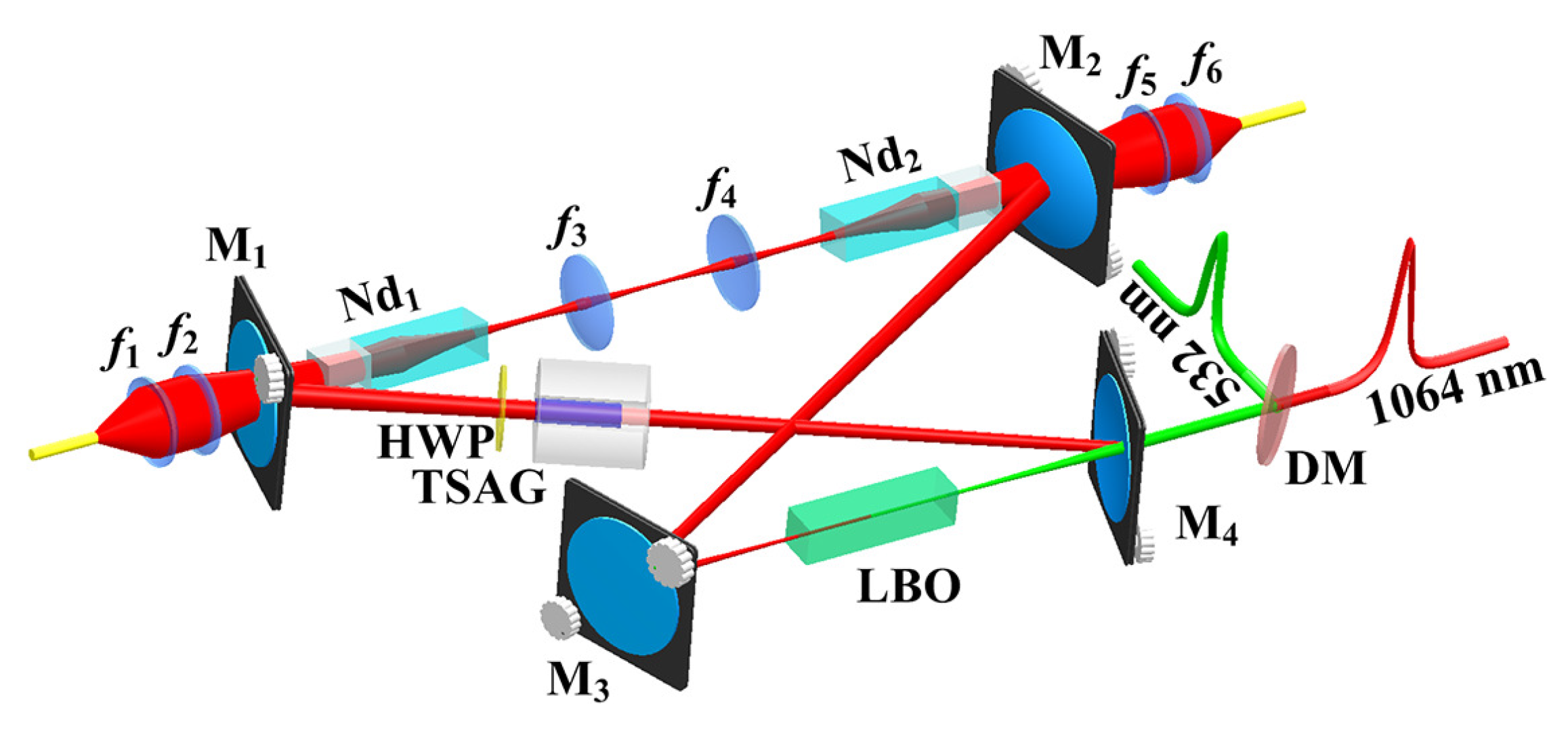
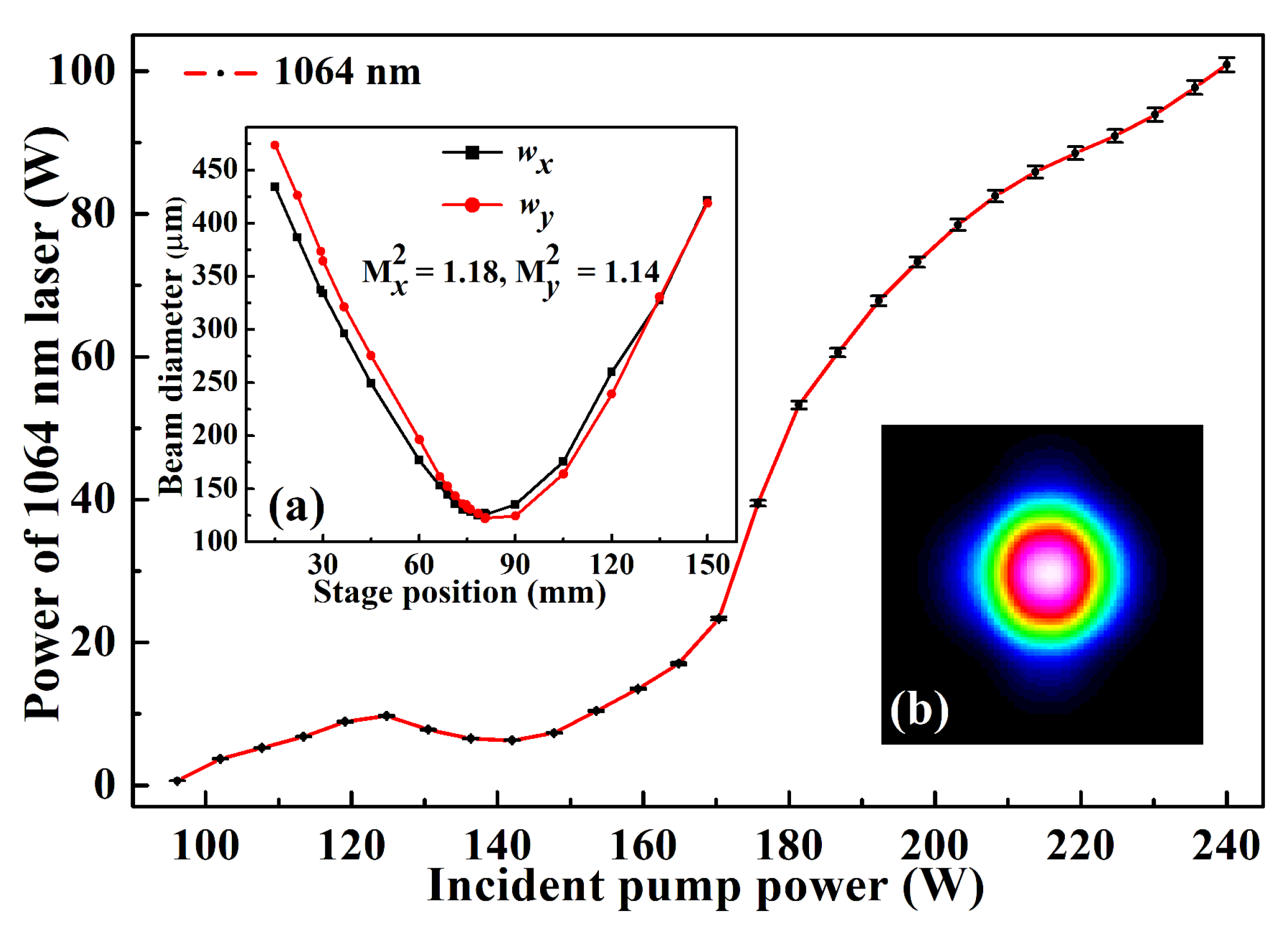
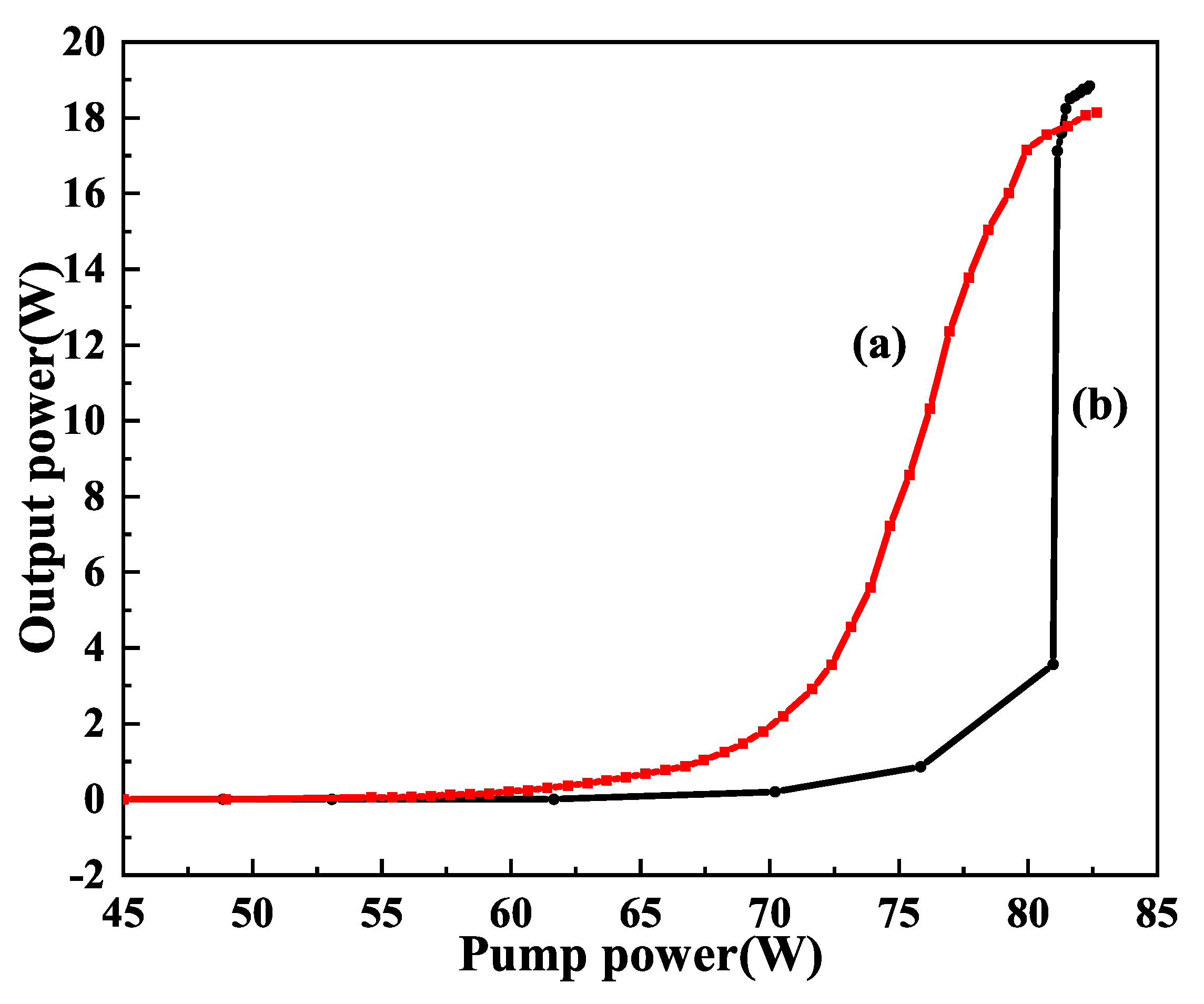
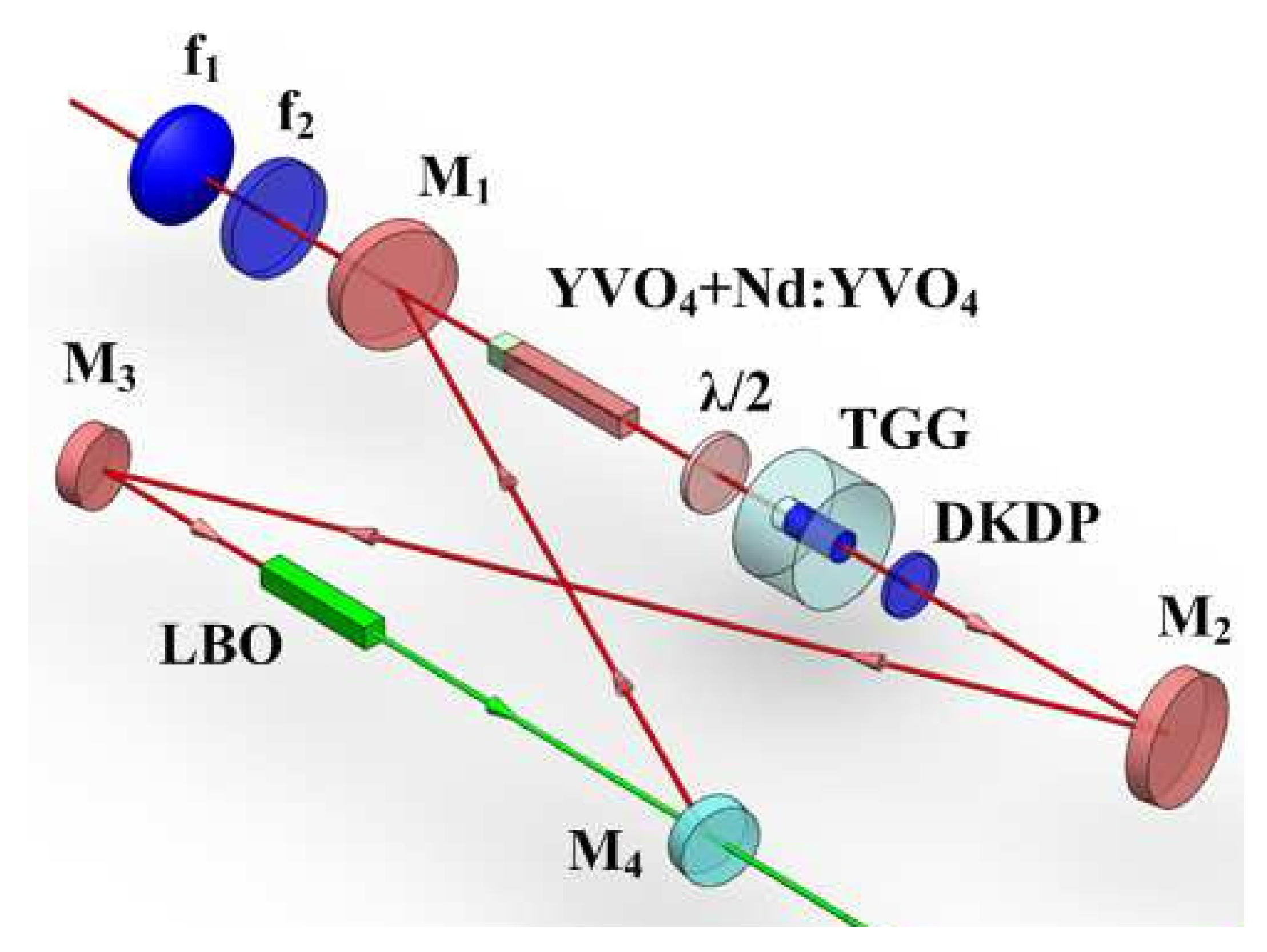
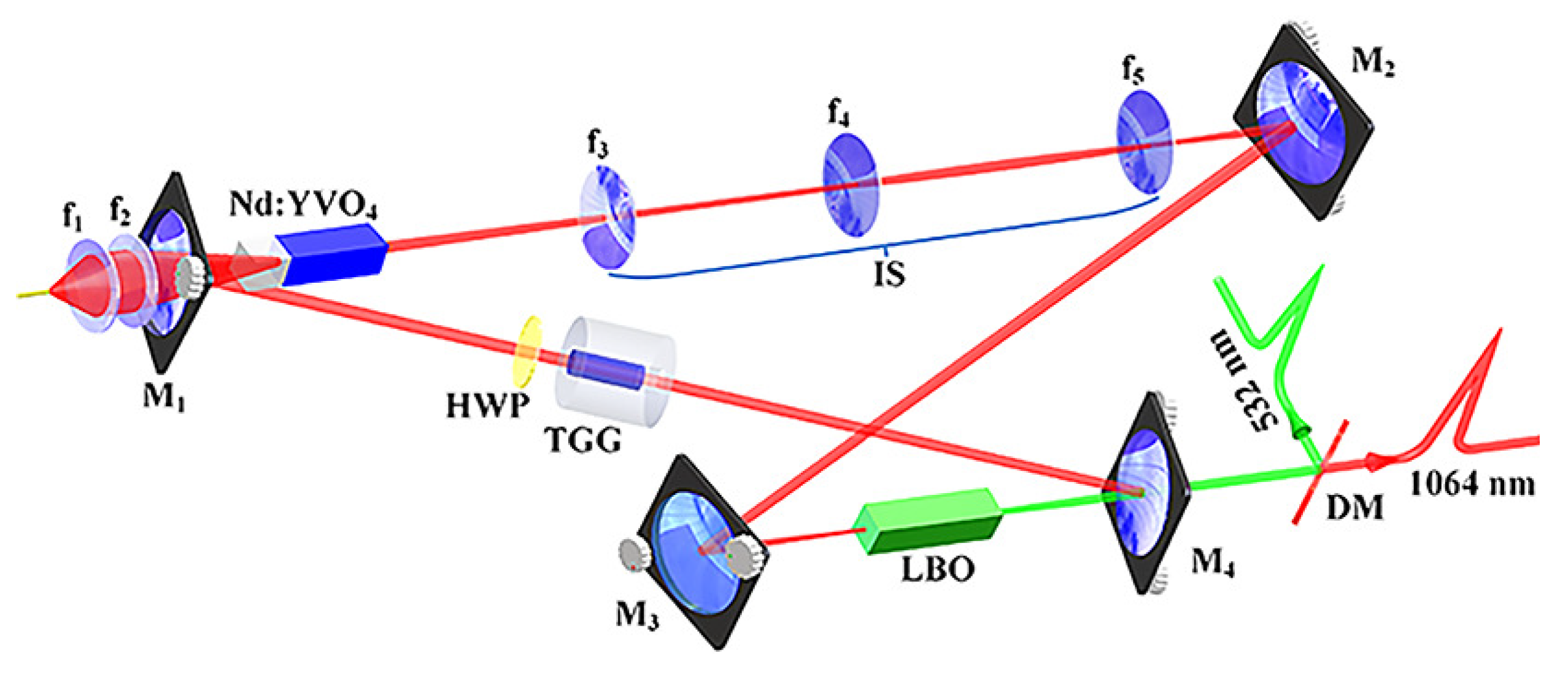
2.3. 101 W Single-Frequency CW 1064 nm Laser
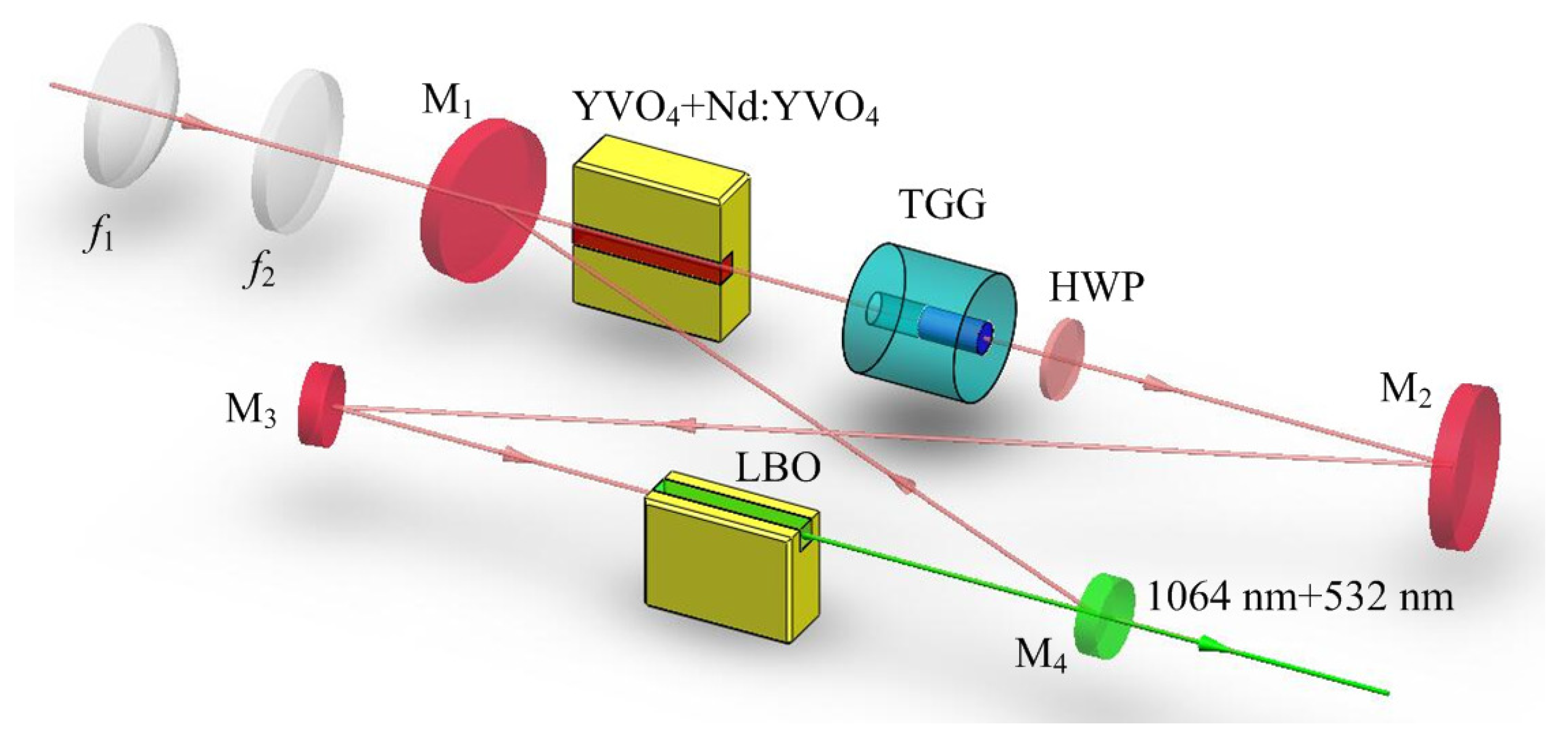
3. High-Power All-Solid-State Single-Frequency and Frequency-Doubling CW Lasers
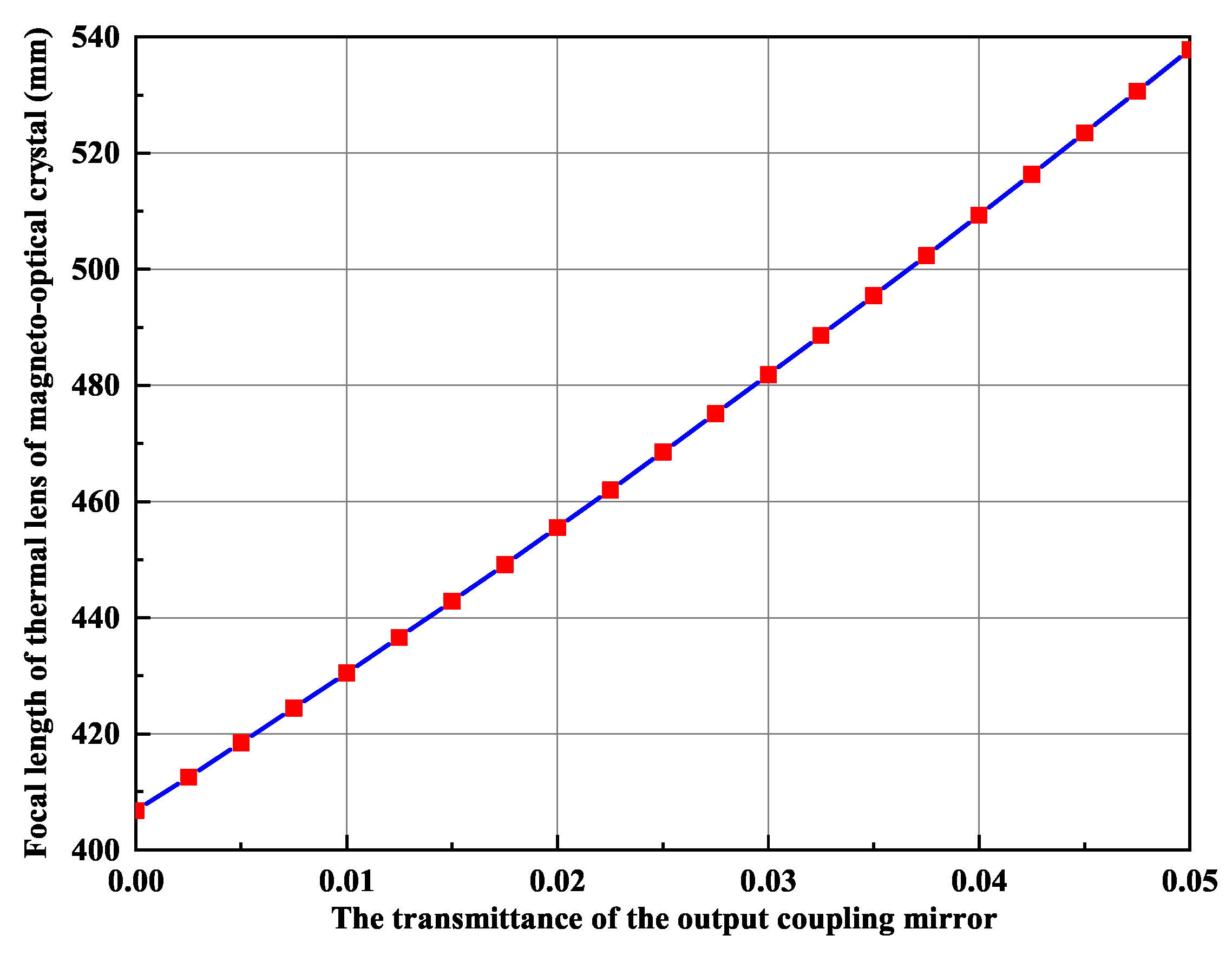
3.1. Thermal Lens Effect of the Magneto-Optical Crystal
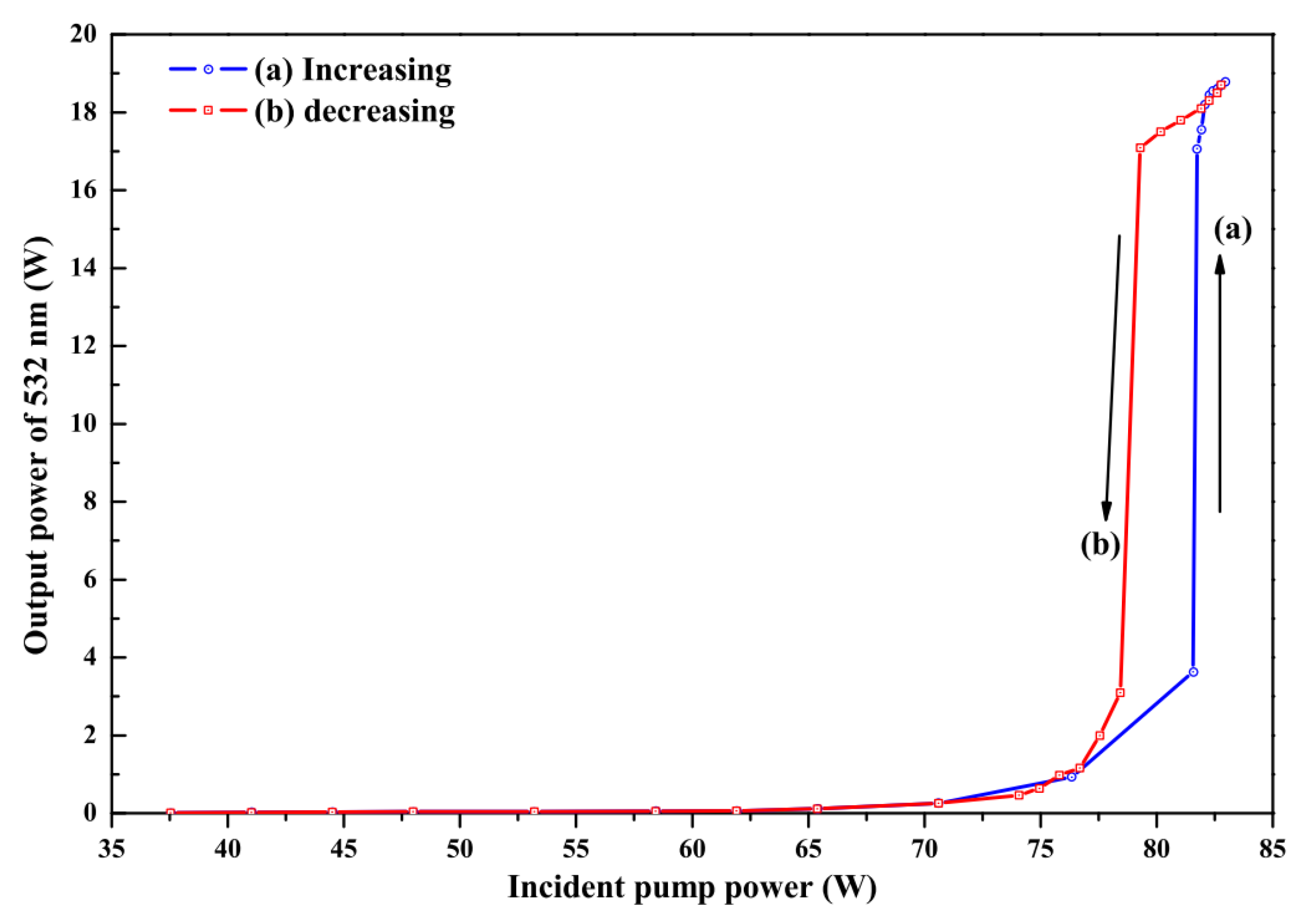
3.2. Employing the Crystal with a Negative Thermo-Optic Coefficient to Actively and Dynamically Compensate for the Positive Thermal Lens Effect of the Magneto-Optical Crystal in Real Time
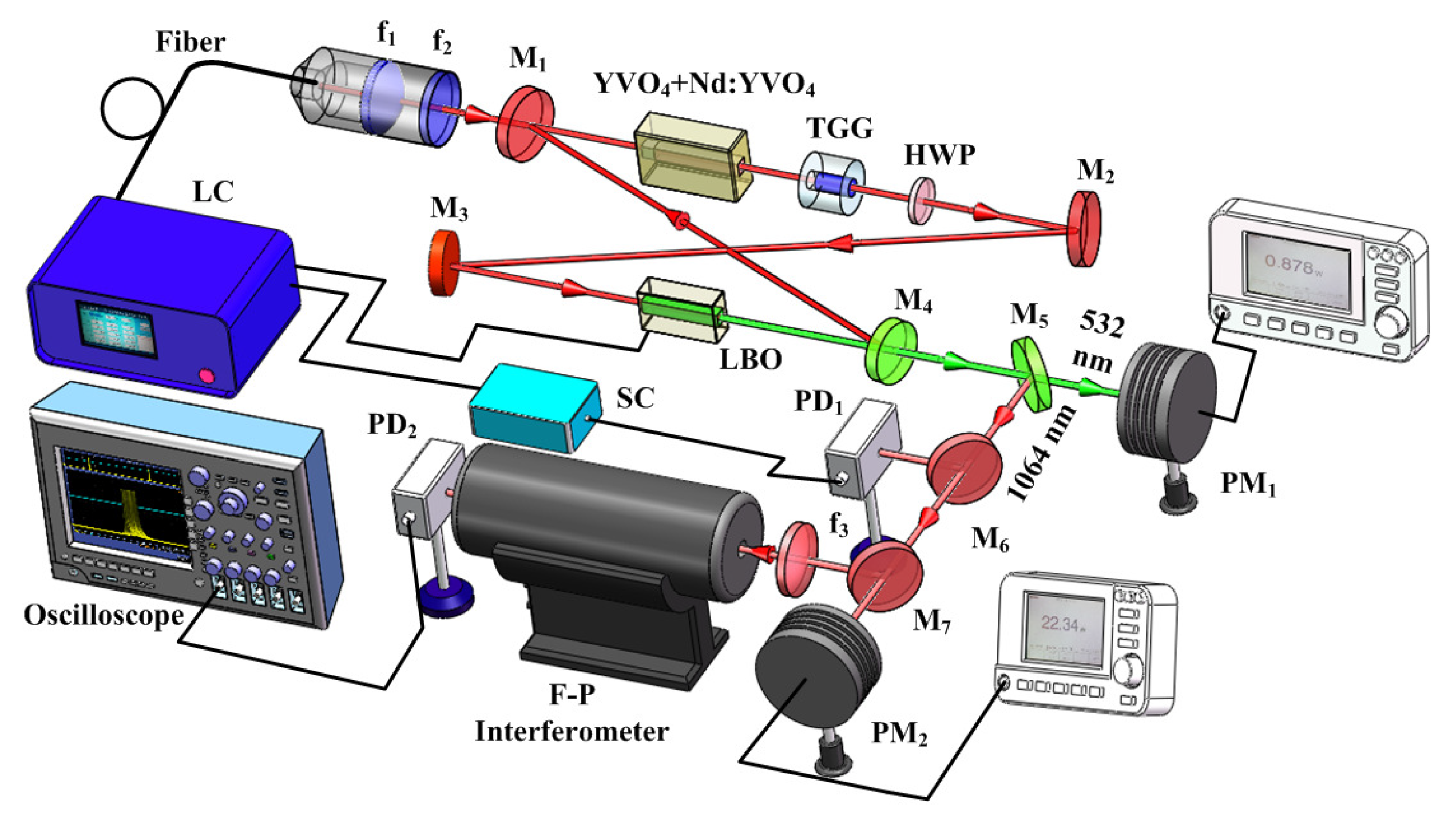
4. Improvement of the Power and Frequency Stabilities
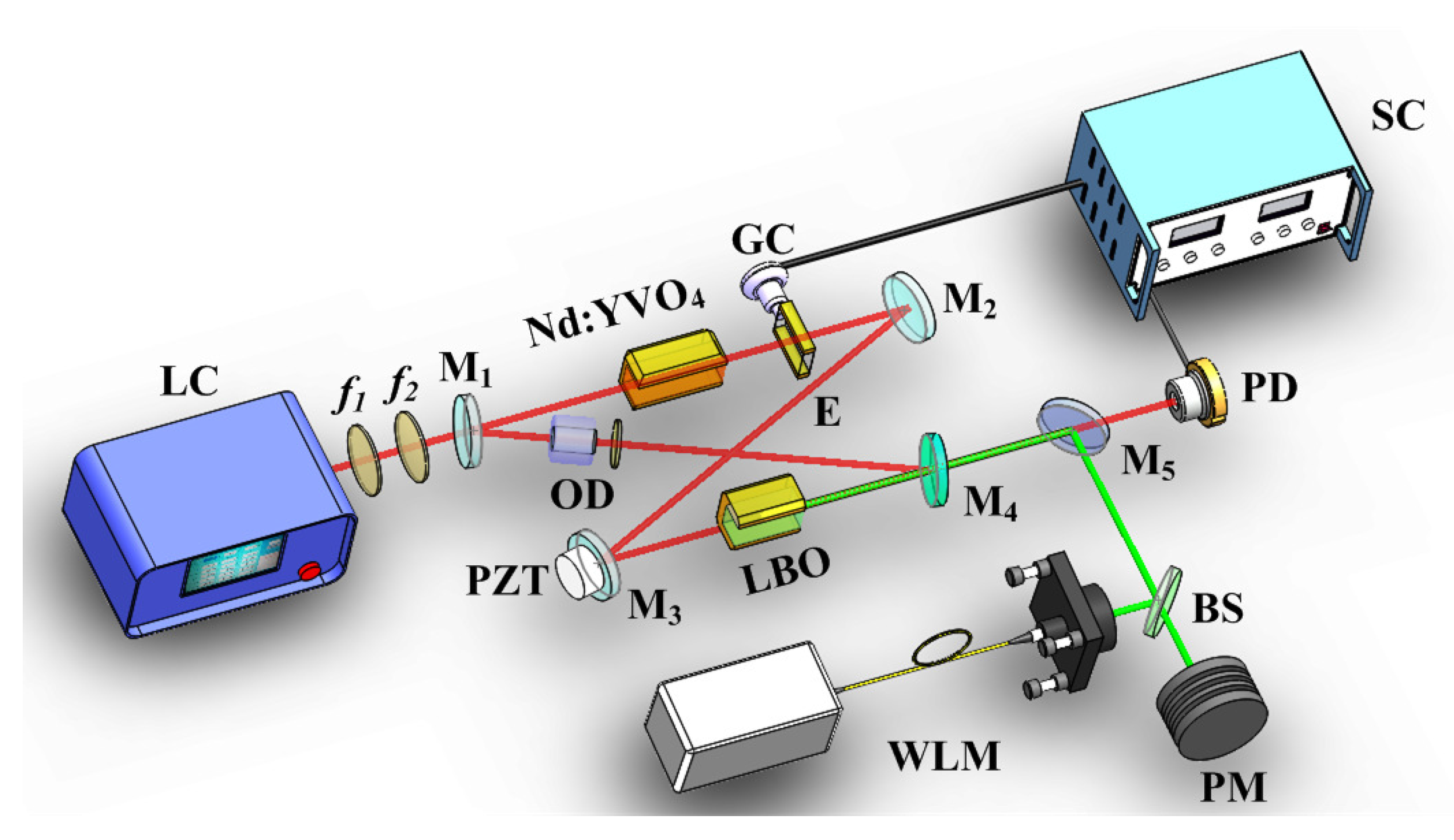
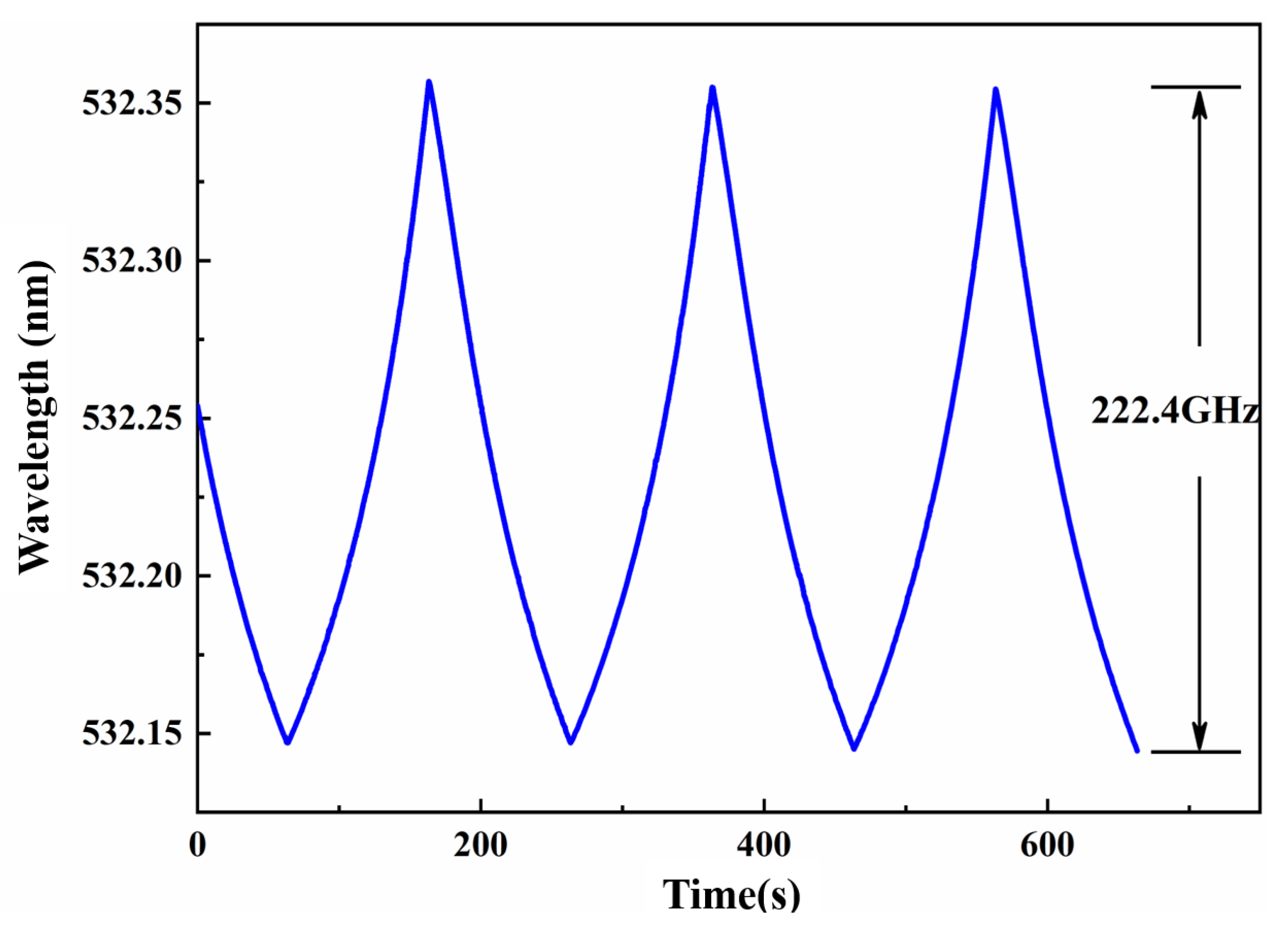
5. Extension of the Continuous Frequency-Tuning Range
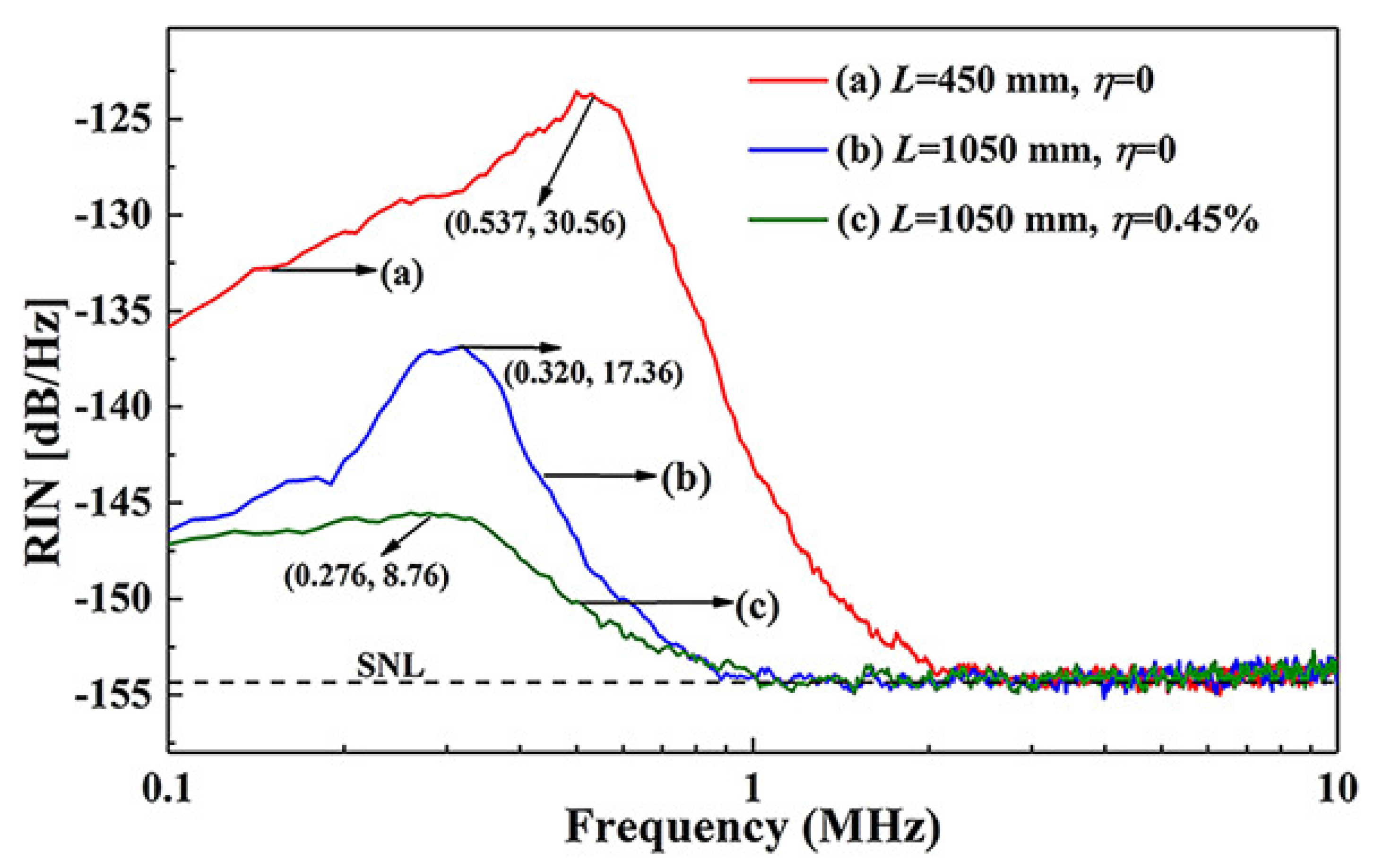
6. Suppression of the Intensity Noise of the High-Power All-Solid-State Single-Frequency CW Laser
6.1. Controlling the Nonlinear Loss to Suppress the Intensity Noise of the Fundamental Wave or Second Harmonic Wave
6.2. Influence of the Pump Scheme on the Intensity Noise of a Single-Frequency CW Lasers
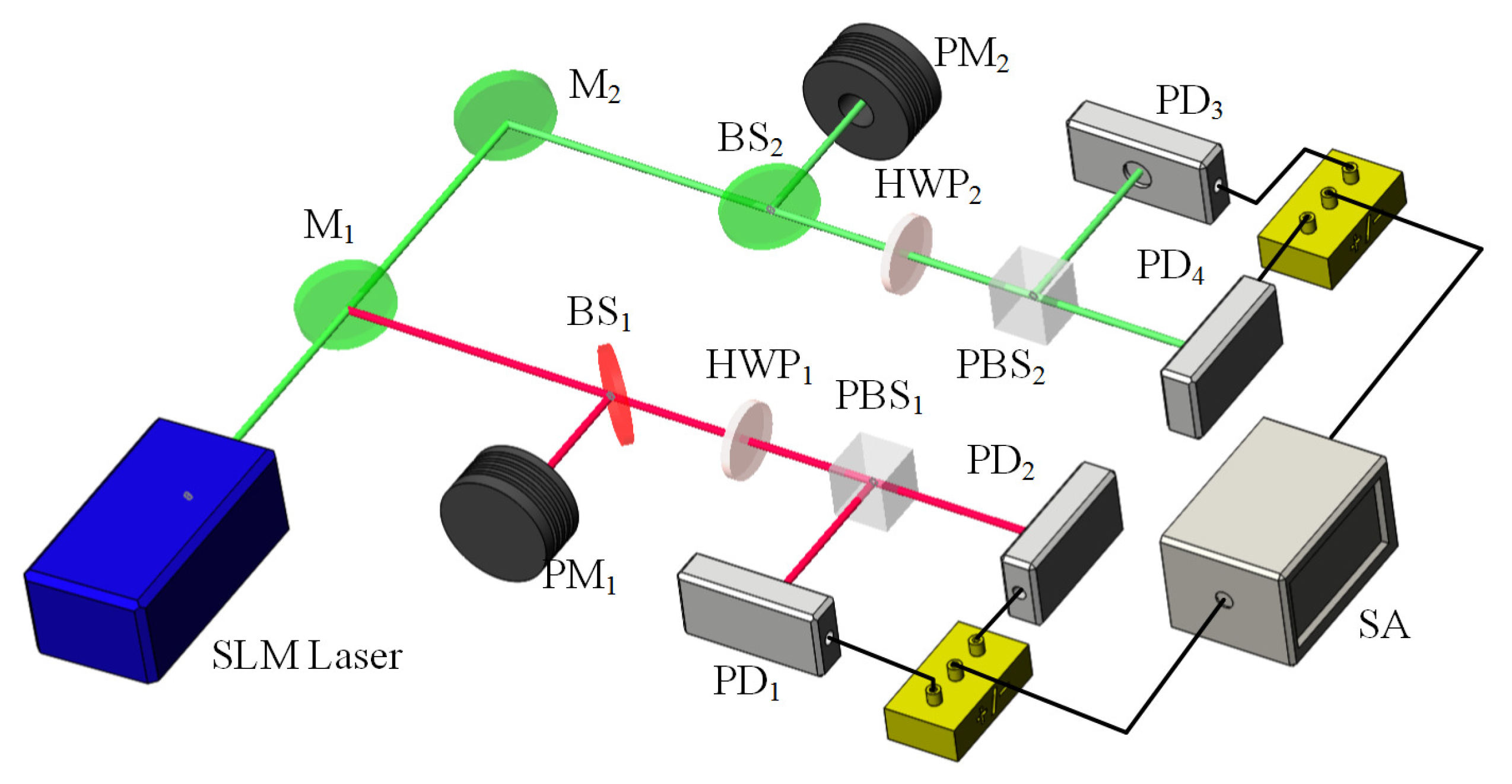
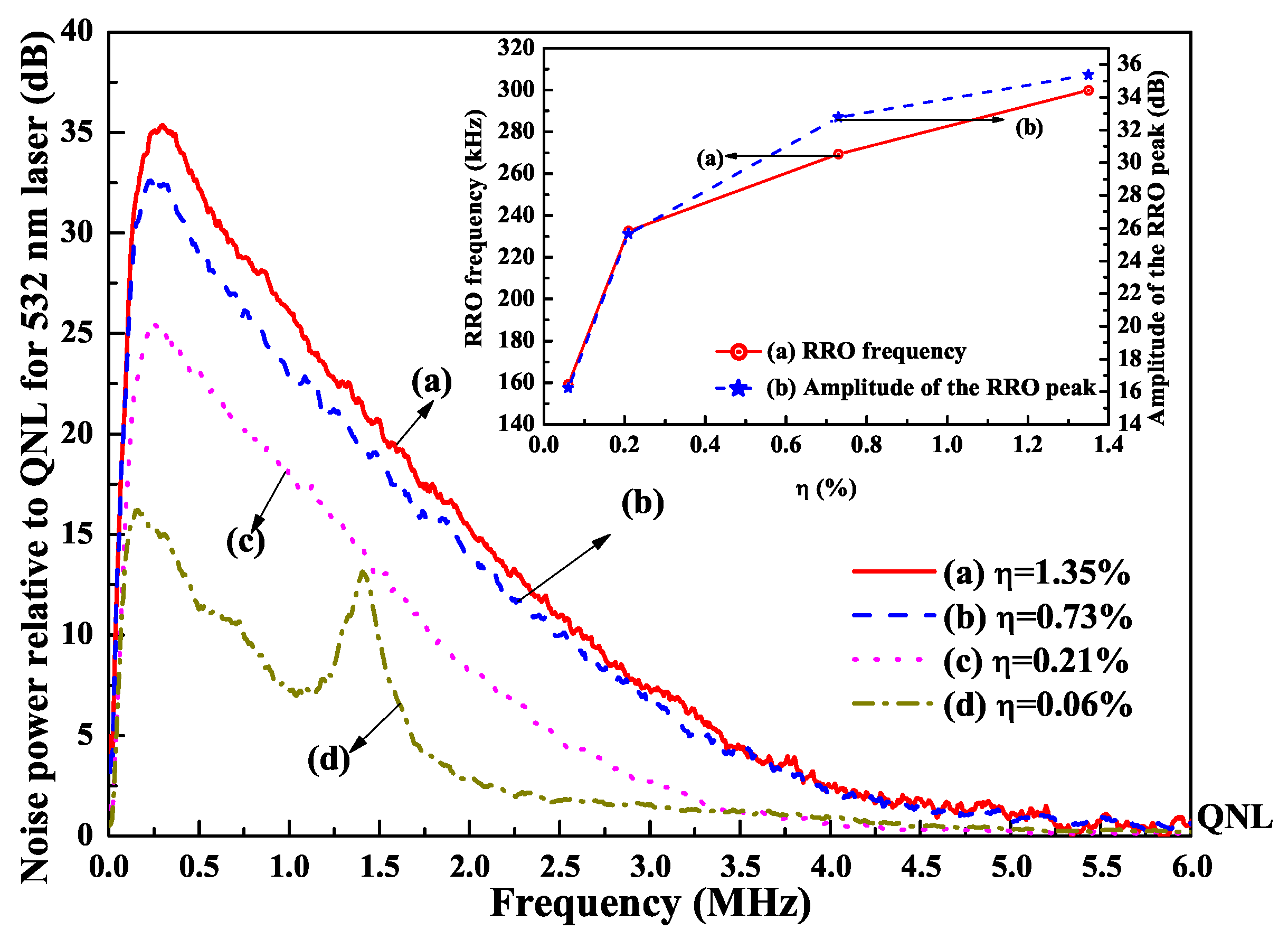
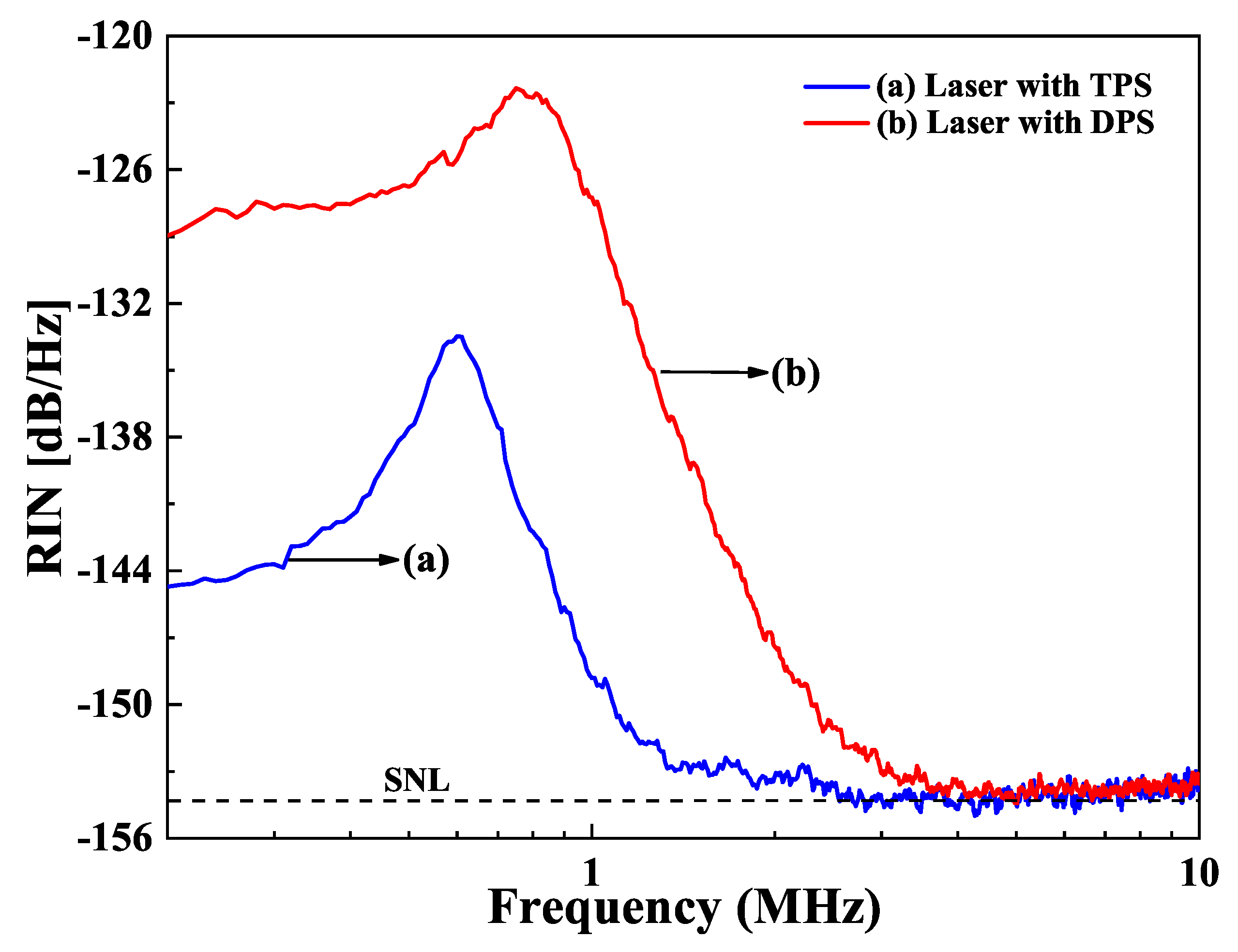
6.3. Suppression of the Intensity Noise by Controlling the SER
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Jiang, Y.; Fang, S.; Bi, Z.; Ma, L. Frequency stabilization of Nd:YAG lasers with a most probable linewidth of 0.6 Hz. J. Opt. Soc. Am. B 2013, 30, 1546–1550. [Google Scholar] [CrossRef]
- Huo, M.; Qin, J.; Cheng, J.; Yan, Z.; Qin, Z.; Su, X.; Jia, X.; Xie, C.; Peng, K. Deterministic quantum teleportation through fiber channels. Sci. Adv. 2018, 4, eaas9401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eismann, U.; Bergschneider, A.; Sievers, F.; Kretzschmar, N.; Salomon, C.; Chevy, F. 2.1-watts intracavity-frequency-doubled all-solid-state light source at 671 nm for laser cooling of lithium. Opt. Express 2013, 21, 9091–9102. [Google Scholar] [CrossRef] [Green Version]
- LIGO Scientific Collaboration and Virgo Collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Dietz, T.; Bauer, D.; Scharun, M.; Hock, H.; Sutter, D.; Killi, A.; Leitenstorfer, A. Monolithic multi-pass thin-disk laser amplifier providing near fundamental mode 2.3 mJ pulse energy at 1.4 kW average output power and 950 fs pulse duration. In Laser Congress 2018 (ASSL); Optical Society of America: Washington, DC, USA, 2018; p. AM2A.4. [Google Scholar] [CrossRef]
- Stolzenburg, C.; Larionov, M.; Giesen, A.; Butze, F. Power scalable single-frequency thin disk oscillator. In Advanced Solid-State Photonics; Optical Society of America: Washington, DC, USA, 2005; p. TuB40. [Google Scholar] [CrossRef]
- Ning, J.; Han, K.; He, J.; Wang, Y.; Nie, H.; Zhang, H.; Zhang, B.; Yang, K.; Wang, R. 83.4 W, 17.69 kHz spectral bandwidth, continuous-wave, beam densely folded Innoslab amplifier. Opt. Lett. 2017, 42, 1109–1112. [Google Scholar] [CrossRef]
- Dergachev, A.; Flint, J.H.; Isyanova, Y.; Pati, B.; Slobodtchikov, E.V.; Wall, K.F.; Moulton, P.F. Review of multipass slab laser systems. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 647–660. [Google Scholar] [CrossRef]
- Wellmann, F.; Steinke, M.; Meylahn, F.; Bode, N.; Willke, B.; Overmeyer, L.; Neumann, J.; Kracht, D. High power, single-frequency, monolithic fiber amplifier for the next generation of gravitational wave detectors. Opt. Express 2019, 27, 28523–28533. [Google Scholar] [CrossRef]
- Liem, A.; Limpert, J.; Zellmer, H.; Tünnermann, A. 100-W single-frequency master-oscillator fiber power amplifier. Opt. Lett. 2003, 28, 1537–1539. [Google Scholar] [CrossRef]
- Robin, C.; Dajani, I.; Pulford, B. Modal instability-suppressing, single-frequency photonic crystal fiber amplifier with 811 W output power. Opt. Lett. 2014, 39, 666–669. [Google Scholar] [CrossRef]
- Palma-Vega, G.; Walbaum, T.; Heinzig, M.; Kuhn, S.; Hupel, C.; Hein, S.; Feldkamp, G.; Sattler, B.; Nold, J.; Haarlammert, N.; et al. Ring-up-doped fiber for the generation of more than 600 W single-mode narrow-band output at 1018 nm. Opt. Lett. 2019, 44, 2502–2505. [Google Scholar] [CrossRef] [PubMed]
- Buikema, A.; Jose, F.; Augst, S.J.; Fritschel, P.; Mavalvala, N. Narrow-linewidth fiber amplifier for gravitational-wave detectors. Opt. Lett. 2019, 44, 3833–3836. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, Y.; Cong, Z.; Zhao, Z.; Jia, Z.; Li, C.; Qin, G.; Wang, S.; Gao, X.; Shao, X.; et al. 110 mW single-frequency Yb:YAG crystal-derived silica fiber laser at 1064 nm. Opt. Lett. 2019, 44, 4307–4310. [Google Scholar] [CrossRef]
- Saraf, S.; Sinha, S.; Sridharan, A.K.; Byer, R.L. 100 W, single frequency, low-noise, diffraction-limited beam from an Nd:YAG end-pumped slab MOPA for LIGO. In Advanced Solid-State Photonics; Optical Society of America: Washington, DC, USA, 2004; p. PDP15. [Google Scholar] [CrossRef]
- Frede, M.; Wilhelm, R.; Kracht, D.; Fallnich, C.; Seifert, F.; Willke, B. 195 W Injection-locked single-frequency laser system. In Conference on Lasers and Electro-Optics/Quantum Electronics and Laser Science and Photonic Applications Systems Technologies; Optical Society of America: Washington, DC, USA, 2005; p. CMA1. Available online: https://www.osapublishing.org/abstract.cfm?URI=CLEO-2005-CMA1 (accessed on 30 September 2021).
- Frede, M.; Schulz, B.; Wilhelm, R.; Kwee, P.; Seifert, F.; Willke, B.; Kracht, D. Fundamental mode, single-frequency laser amplifier for gravitational wave detectors. Opt. Express 2007, 15, 459–465. [Google Scholar] [CrossRef]
- Winkelmann, L.; Puncken, O.; Kluzik, R.; Veltkamp, C.; Kwee, P.; Poeld, J.; Bogan, C.; Willke, B.; Frede, M.; Neumann, J.; et al. Injection-locked single-frequency laser with an output power of 220 W. Appl. Phys. B 2011, 102, 529–538. [Google Scholar] [CrossRef]
- Martin, K.I.; Clarkson, W.A.; Hanna, D.C. Self-suppression of axial mode hopping by intracavity second-harmonic generation. Opt. Lett. 1997, 22, 375–377. [Google Scholar] [CrossRef] [PubMed]
- Greenstein, S.; Rosenbluh, M. The influence of nonlinear spectral bandwidth on single longitudinal mode intra-cavity second harmonic generation. Opt. Commun. 2005, 248, 241–248. [Google Scholar] [CrossRef]
- Lu, H.; Su, J.; Zheng, Y.; Peng, K. Physical conditions of single-longitudinal-mode operation for high-power all-solid-state lasers. Opt. Lett. 2014, 39, 1117–1120. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, H.; Yin, Q.; Su, J. Continuous-wave single-frequency laser with dual wavelength at 1064 and 532 nm. Appl. Opt. 2014, 53, 6371–6374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Lu, H.; Yin, Q.; Su, J. Intra-cavity round-trip loss measurement of all-solid-state single-frequency laser by introducing extra nonlinear loss. Chin. Opt. Lett. 2017, 15, 021402. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Lu, H.; Xu, M.; Su, J.; Peng, K. Investigation about the influence of longitudinal-mode structure of the laser on the relative intensity noise properties. Opt. Express 2018, 26, 21108–21118. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Xu, M.; Peng, W.; Su, J.; Lu, H.; Peng, K. Realization of a 101W single-frequency continuous wave all-solid-state 1064nm laser by means of mode self-reproduction. Opt. Lett. 2018, 43, 6017–6020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, Q.; Lu, H.; Peng, K. Investigation of the thermal lens effect of the TGG crystal in high-power frequency-doubled laser with single frequency operation. Opt. Express 2015, 23, 4981–4990. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Lu, H.; Su, J.; Peng, K. High power single-frequency and frequency-doubled laser with active compensation for the thermal lens effect of terbium gallium garnet crystal. Opt. Lett. 2016, 41, 2033–2036. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Peng, K. Realization of the single-frequency and high power as well as frequency-tuning of the laser by manipulating the nonlinear loss. J. Quantum Opt. 2015, 21, 171–176. [Google Scholar] [CrossRef]
- Jin, P.; Lu, H.; Su, J.; Peng, K. Scheme for improving laser stability via feedback control of intracavity nonlinear loss. Appl. Opt. 2016, 55, 3478–3482. [Google Scholar] [CrossRef]
- Jin, P.; Lu, H.; Yin, Q.; Su, J.; Peng, K. Expanding continuous tuning range of a CW single-frequency laser by combining an intracavity etalon with a nonlinear loss. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1600505. [Google Scholar] [CrossRef]
- Lu, H.; Guo, Y.; Peng, K. Intensity noise manipulation of a single-frequency laser with high output power by intracavity nonlinear loss. Opt. Lett. 2015, 40, 5196–5199. [Google Scholar] [CrossRef]
- Guo, Y.; Peng, W.; Su, J.; Lu, H.; Peng, K. Influence of the pump scheme on the output power and the intensity noise of a single-frequency continuous-wave laser. Opt. Express 2020, 28, 5866–5874. [Google Scholar] [CrossRef]
- Harb, C.C.; Ralph, T.C.; Huntington, E.H.; McClelland, D.E.; Bachor, H.A.; Freitag, I. Intensity-noise dependence of Nd:YAG lasers on their diode-laser pump source. J. Opt. Soc. Am. B 1997, 14, 2936–2945. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, K.; Chen, Y.; Zhang, T.; Xie, C.; Peng, K. Intensity noise properties of LD pumped single-frequency ring lasers. Acta Opt. Sin. 2000, 20, 1311–1316. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, H.; Peng, W.; Su, J.; Peng, K. Intensity noise suppression of a high-power single-frequency CW laser by controlling the stimulated emission rate. Opt. Lett. 2019, 44, 6033–6036. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Bai, Z.; Chen, D.; Chen, W.; Feng, Y.; Mildren, R.P. Widely-tunable single-frequency diamond Raman laser. Opt. Express 2021, 29, 29449–29457. [Google Scholar] [CrossRef] [PubMed]
- Bereczki, A.; Ferreira, A.A.; Wetter, N.U. Dynamically stable single frequency ring resonator from diode pumped Nd:YAG modules with 55.6 W of output power. Opt. Express 2021, 29, 23167–23181. [Google Scholar] [CrossRef] [PubMed]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Jin, P.; Li, F.; Su, J.; Lu, H.; Peng, K. A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser. Micromachines 2021, 12, 1426. https://doi.org/10.3390/mi12111426
Peng W, Jin P, Li F, Su J, Lu H, Peng K. A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser. Micromachines. 2021; 12(11):1426. https://doi.org/10.3390/mi12111426
Chicago/Turabian StylePeng, Weina, Pixian Jin, Fengqin Li, Jing Su, Huadong Lu, and Kunchi Peng. 2021. "A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser" Micromachines 12, no. 11: 1426. https://doi.org/10.3390/mi12111426
APA StylePeng, W., Jin, P., Li, F., Su, J., Lu, H., & Peng, K. (2021). A Review of the High-Power All-Solid-State Single-Frequency Continuous-Wave Laser. Micromachines, 12(11), 1426. https://doi.org/10.3390/mi12111426