A Novel Frequency Stabilization Approach for Mass Detection in Nonlinear Mechanically Coupled Resonant Sensors
Abstract
:1. Introduction
2. Problem Formulation
3. Nonlinear Dynamic Behavior
3.1. Perturbation Analysis
3.2. Coupled-Mode Vibration
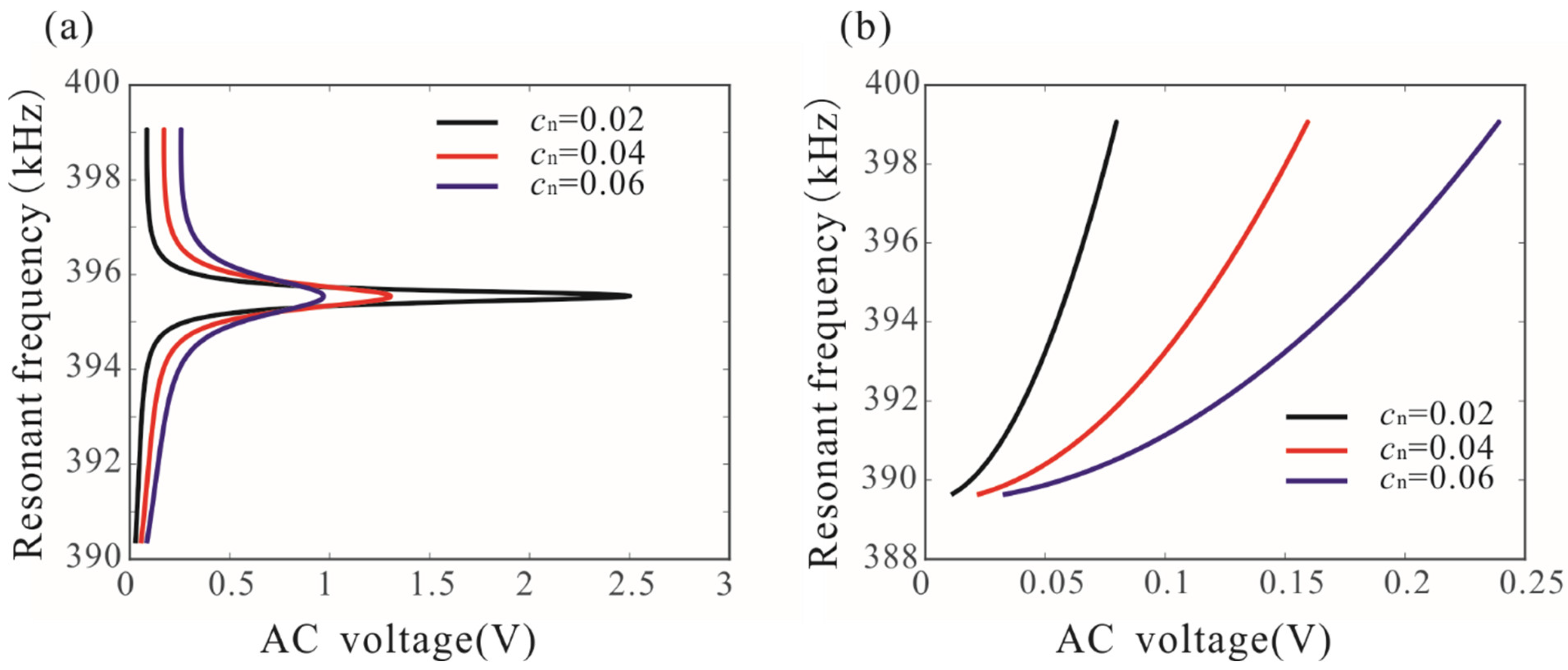
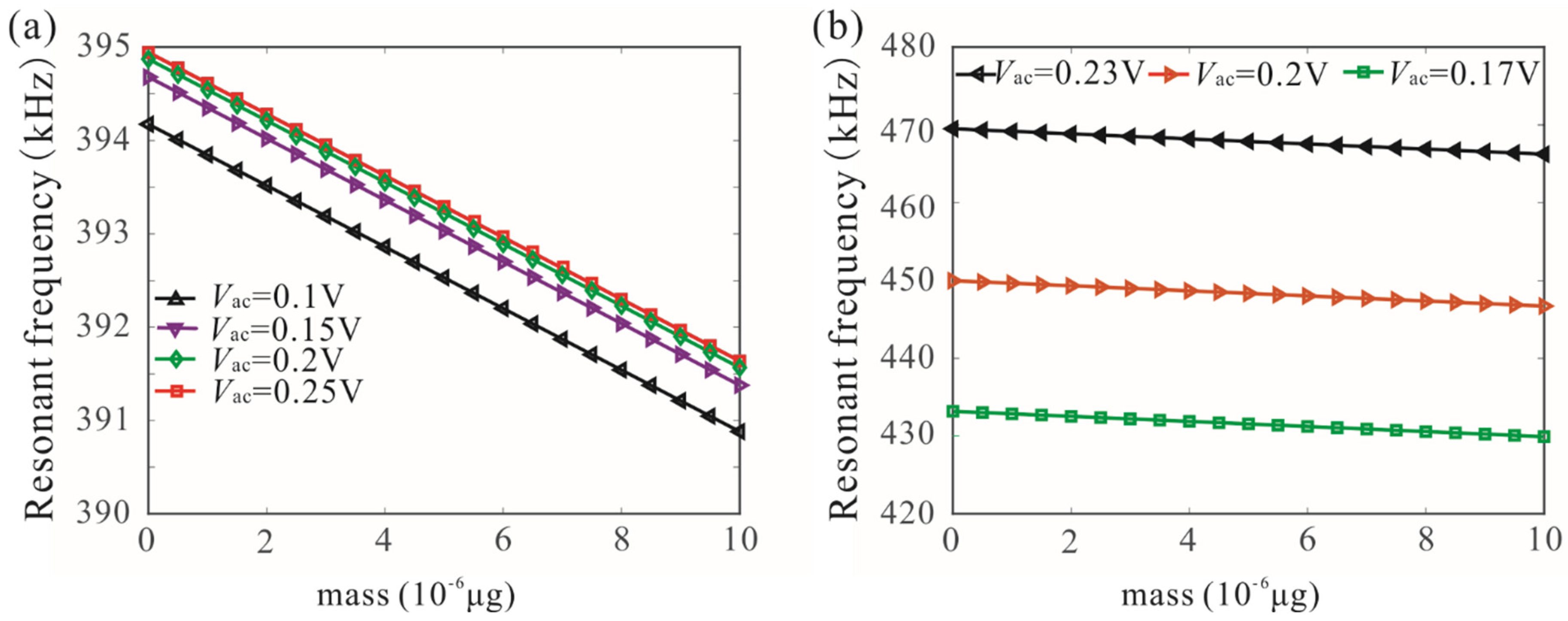
3.3. Frequency Stabilization
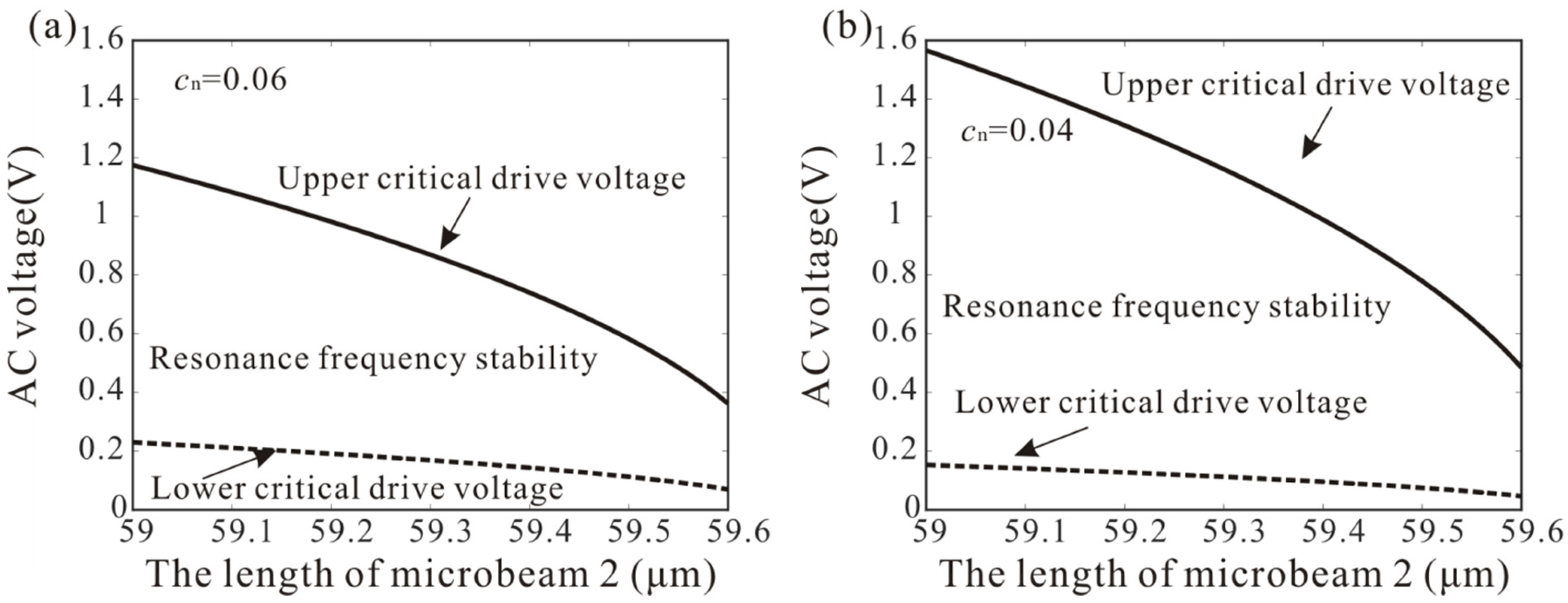
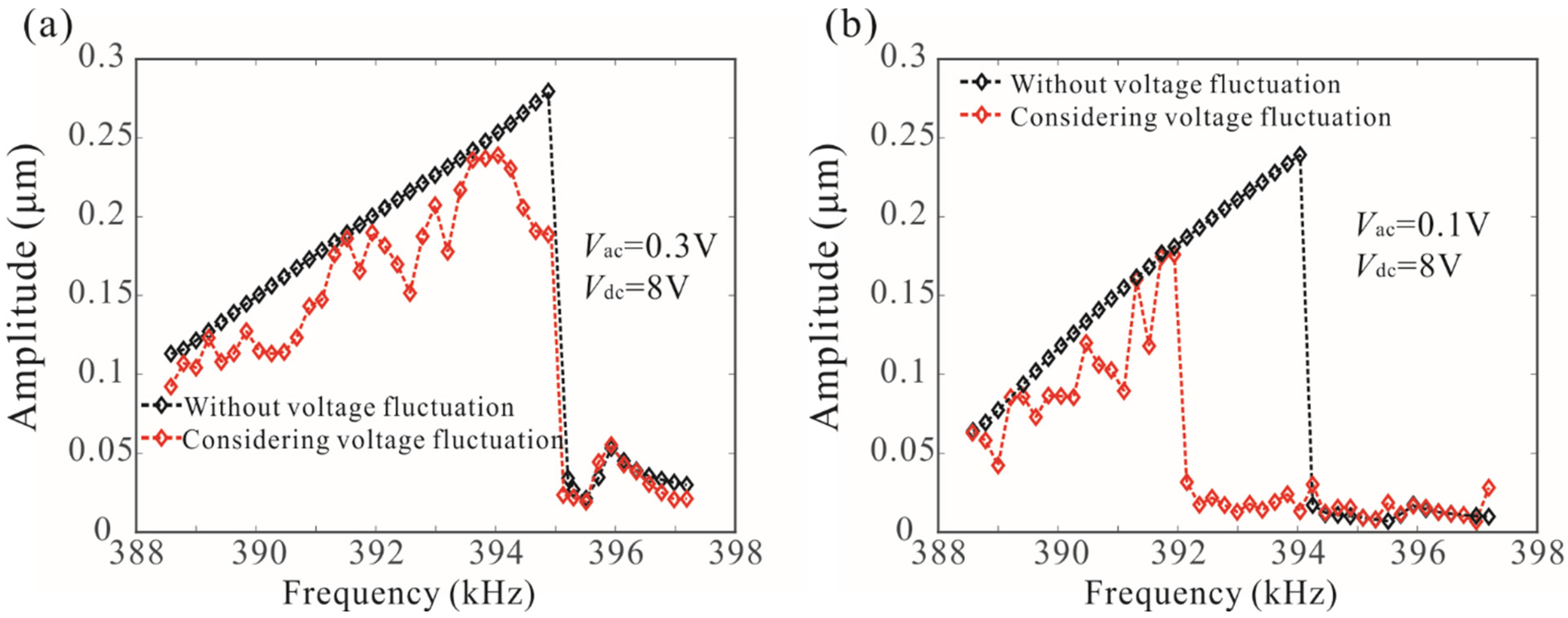
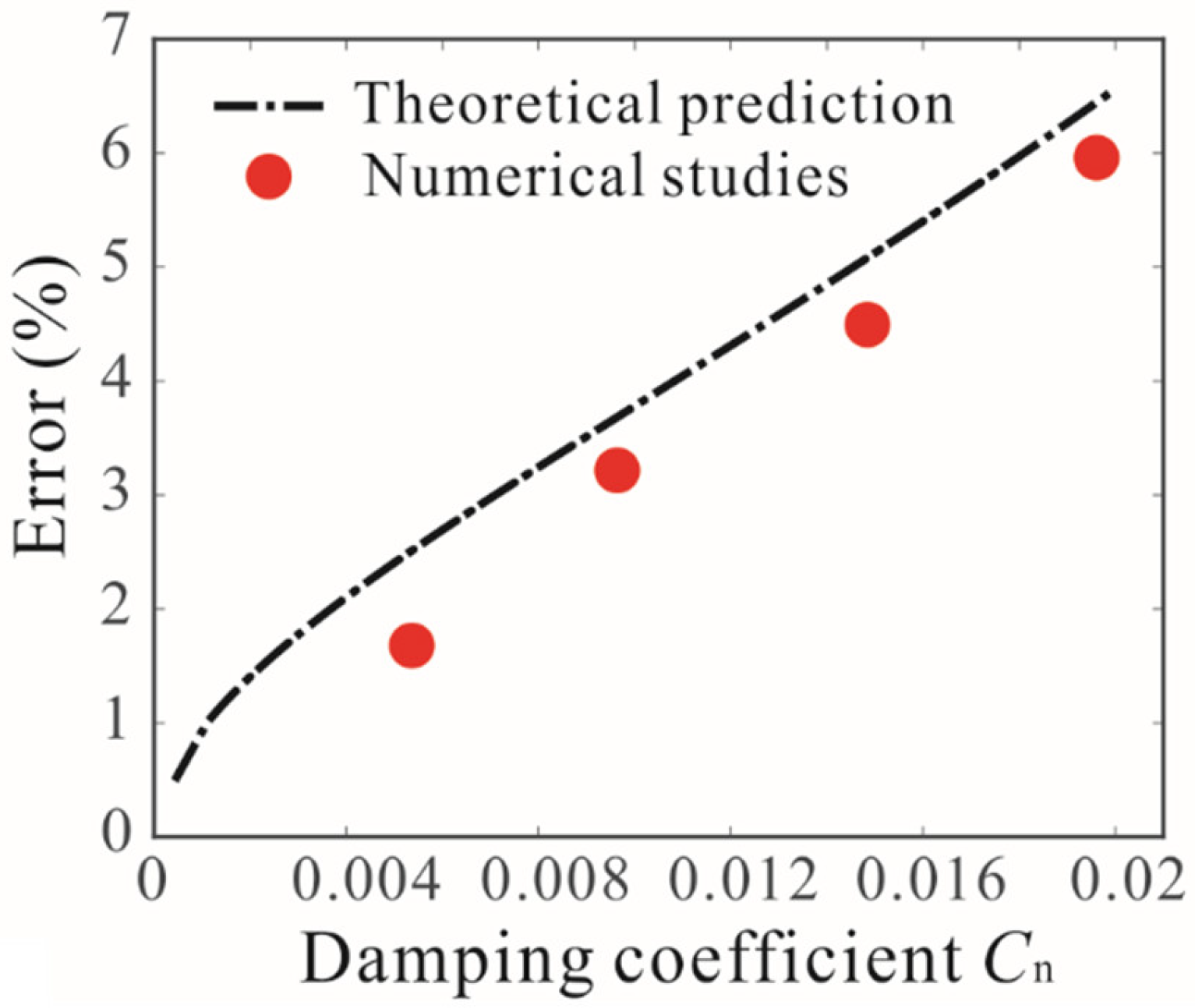
4. Robust Analysis
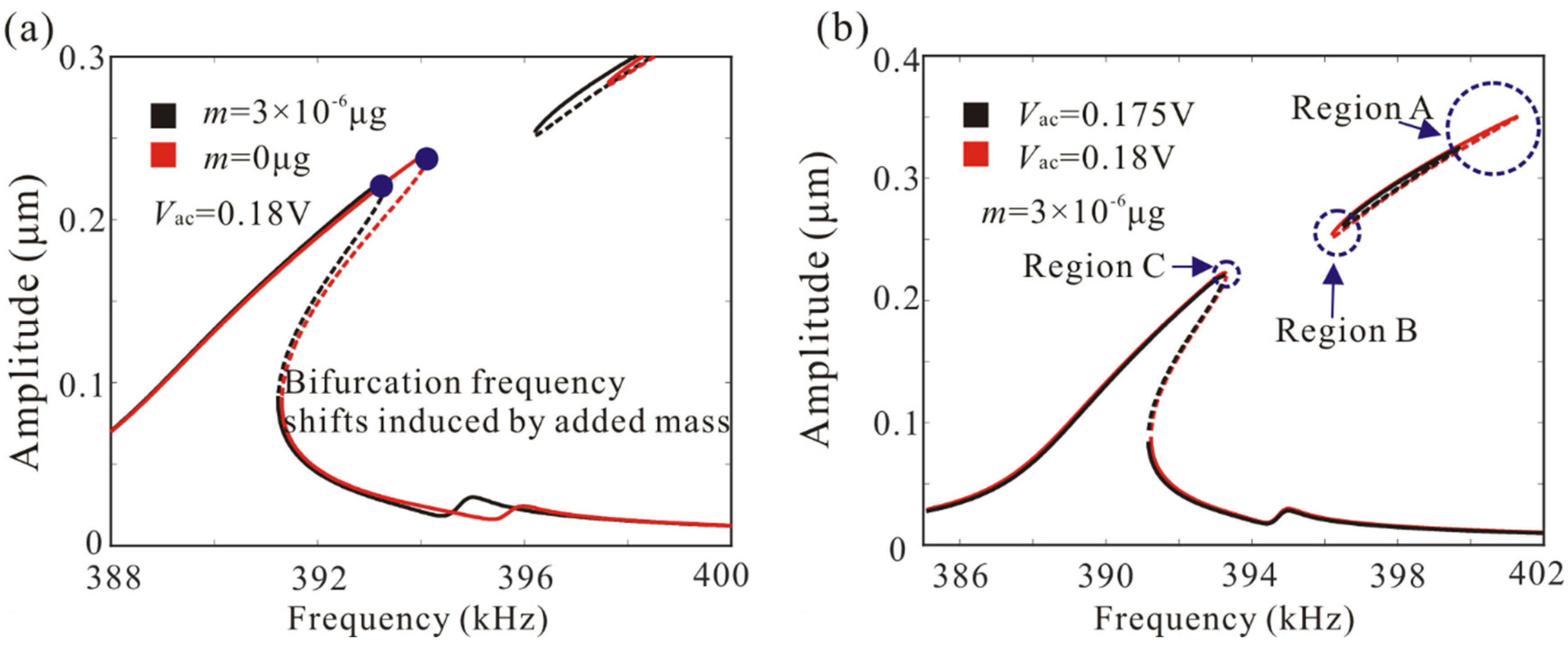
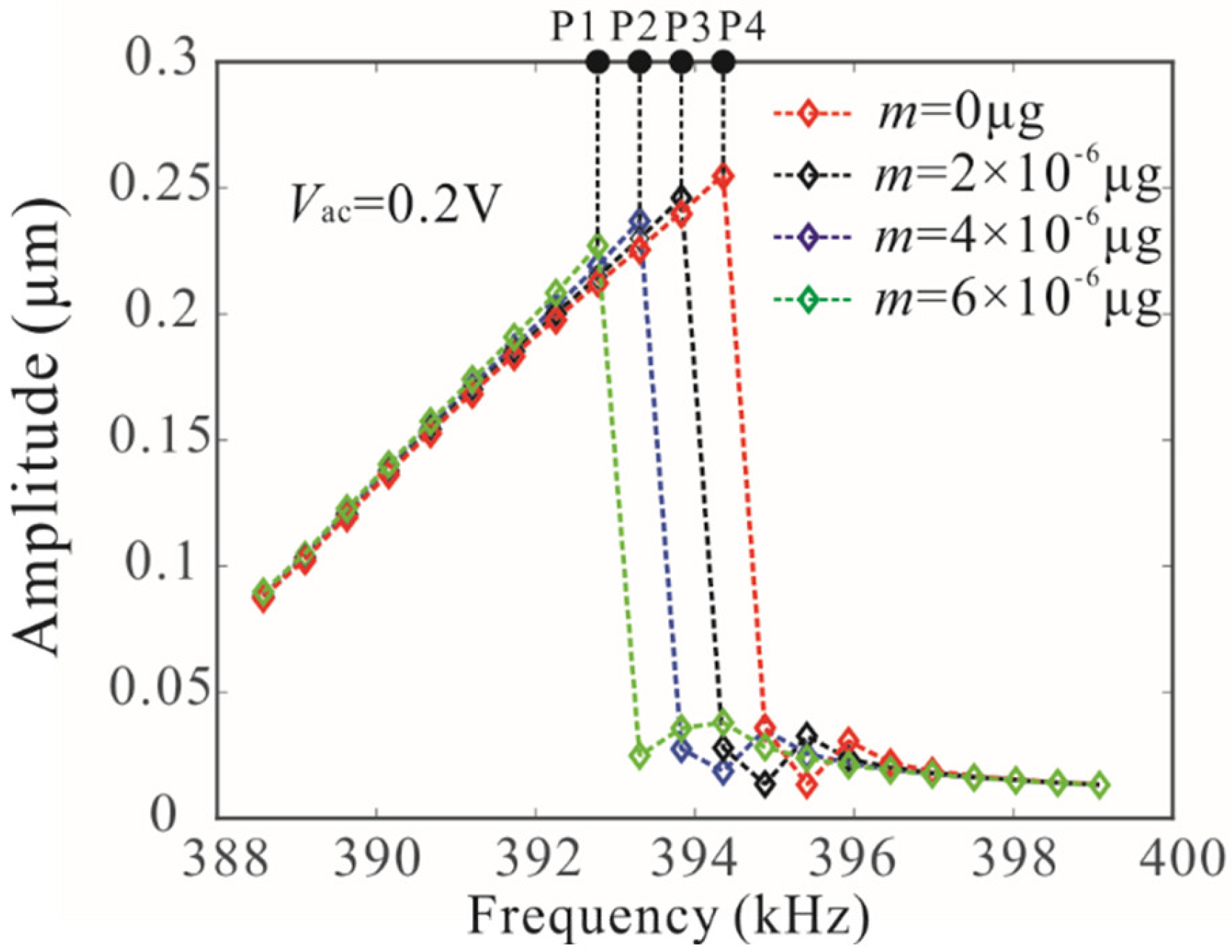
5. Parameter Identification Based on Frequency Stabilization and Bifurcation Jumping Behavior
6. Conclusions
- (1)
- The physical conditions for frequency stabilization were presented when operating a MEMS in a nonlinear regime. It was found that improving quality factor is the key to achieving frequency stabilization. When the quality factor of the system is high enough, the effect of the driving voltage on the peak frequency can be ignored.
- (2)
- Considering the voltage fluctuation, we analyzed the stochastic dynamic behavior of the coupled resonator under different driving voltages, and it was proven that the coupled resonator can overcome the influence of voltage noise on resonance frequency in the nonlinear regime and improve the robustness of the sensor.
- (3)
- A very simple parameter identification formula was proposed to establish the relationship between resonance frequency and detection mass. Bifurcation and frequency stabilization were introduced to improve the accuracy and sensitivity of the sensor. The numerical results show that the mass identification method based on bifurcation frequency stabilization can make mass sensors work in a nonlinear vibration range and avoid resonance frequency shifts caused by driving voltage. The detection error function is presented to explain the difference between the detection results and the real results. It was noted that the mass detection method requires the MEMS resonator to have a high enough quality factor.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Baguet, S.; Nguyen, V.N.; Grenat, C.; Lamarque, C.H.; Dufour, R. Nonlinear dynamics of micromechanical resonator arrays for mass sensing. Nonlin. Dynam. 2019, 95, 1203–1220. [Google Scholar] [CrossRef] [Green Version]
- Park, K.; Kim, N.; Morisette, D.T.; Aluru, N.R.; Bashir, R. Resonant mems mass sensors for measurement of microdroplet evaporation. J. Microelectromech. Syst. 2012, 21, 702–711. [Google Scholar] [CrossRef]
- Potekin, R.; Kim, S.; Mcfarland, D.M.; Bergman, L.A.; Cho, H.; Vakakis, A.F. A micromechanical mass sensing method based on amplitude tracking within an ultra-wide broadband resonance. Nonlin. Dynam. 2018, 92, 287–302. [Google Scholar] [CrossRef]
- Burg, T.P.; Mirza, A.R.; Milovic, N.; Tsau, C.H.; Popescu, G.A.; Foster, J.S.; Manalis, S.R. Vacuum-Packaged Suspended Microchannel Resonant Mass Sensor for Biomolecular Detection. J. Microelectromech. Syst. 2007, 15, 1466–1476. [Google Scholar] [CrossRef]
- Gupta, A.; Akin, D.; Bashir, R. Single Virus Particle Mass Detection Using Microresonators With Nanoscale Thickness. Appl. Phys. Lett. 2004, 84, 1976–1978. [Google Scholar] [CrossRef]
- Daichi, E.; Hiroshi, Y.; Yasuyuki, Y.; Sohei, M. Mass Sensing in a Liquid Environment Using Nonlinear Self-Excited Coupled-Microcantilevers. J. Microelectromech. Syst. 2018, 27, 774–779. [Google Scholar]
- Bouchaala, A.; Nayfeh, A.H.; Younis, M.I. Frequency shifts of micro and nano cantilever beam resonators due to added masses. J. Dyn. Syst. Meas. Control 2016, 138, 091002. [Google Scholar] [CrossRef]
- Jensen, K.; Kim, K.; Zettl, A. An atomic-resolution nanomechanical mass sensor. Nat. Nanotechnol. 2008, 3, 533–537. [Google Scholar] [CrossRef]
- Seshia, A.; Palaniapan, M.; Roessig, T.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef] [Green Version]
- Sabater, A.B.; Rhoads, J.F. Parametric system identification of resonant micro/nanosystems operating in a nonlinear response regime. Mech. Syst. Signal Pr. 2008, 84, 241–264. [Google Scholar] [CrossRef] [Green Version]
- Farokhi, H.; Païdoussis, M.P.; Misra, A.K. Nonlinear behaviour and mass detection sensitivity of geometrically imperfect cantilevered carbon nanotube resonators. Commun. Nonlin. Sci. Numer. Simul. 2018, 65, 272–298. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhang, L.; Zheng, W.; Wang, K.; Wu, C. A bistable vibration isolator with nonlinear electromagnetic shunt damping. Mech. Syst. Signal Pr. 2020, 136, 106504. [Google Scholar] [CrossRef]
- Kumar, V.; Yang, Y.; Boley, J.W.; Chiu, T.C.; Rhoads, J.F. Modeling analysis and experimental validation of a bifurcation-based microsensor. J. Microelectromech. Syst. 2012, 21, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Farokhi, H.; Ghayesh, M.H. Electrically actuated MEMS resonators: Effects of fringing field and nonlinear viscoelasticity. Mech. Syst. Signal Pr. 2017, 95, 345–362. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Wang, W.; Han, J. Nonlinear coupled vibration of electrostatically actuated clamped–clamped microbeams under higher-order modes excitation. Nonlin. Dynam. 2017, 90, 1593–1606. [Google Scholar] [CrossRef]
- Zanette, D.H. Stability of two-mode internal resonance in a nonlinear oscillator. Eur. Phys. J. B 2018, 91, 89. [Google Scholar] [CrossRef]
- Matheny, M.; Villanueva, L.; Karabalin, R.; Sader, J.E.; Roukes, M. Nonlinear mode-coupling in nanomechanical systems. Nano Lett. 2013, 13, 1622–1626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajjaj, A.Z.; Jaber, N.; Ilyas, S.; Alfosail, F.K.; Younis, M.I. Linear and nonlinear dynamics of micro and nano-resonators: Review of recent advances. Int. J. Non Lin. Mech. 2020, 119, 103328. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Pu, D.; Huan, R. Single-electron detection utilizing coupled nonlinear microresonators. Microsyst. Nanoeng. 2020, 6, 78. [Google Scholar] [CrossRef]
- Kilinc, Y.; Karakan, M.A.; Leblebici, Y.; Hanay, M.S.; Alaca, B.E. Observation of coupled mechanical resonance modes within suspended 3d nanowire arrays. Nanoscale 2020, 12, 22042. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.P.; Ma, C.C.; Liu, C.C.; Peng, B. Anti-symmetric mode vibration of electrostatically actuated clamped–clamped microbeams for mass sensing. Micromachines 2020, 11, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Du, S.; Zou, X.; Seshia, A. Utilizing Energy Localization in Weakly Coupled Nonlinear Resonators for Sensing Applications. J. Microelectromech. Syst. 2019, 28, 182–188. [Google Scholar] [CrossRef]
- Antonio, D.; Zanette, D.H.; López, D. Frequency stabilization in nonlinear micromechanical oscillators. Nat. Commun. 2012, 3, 806. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Ren, J.; Wei, X.; Jiang, Z.; Huan, R. Nonlinear coupling of flexural mode and extensional bulk mode in micromechanical resonators. Appl. Phys. Lett. 2016, 109, 224102. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, T.; Jiang, Z.; Ren, J.; Huan, R. Frequency latching in nonlinear micromechanical resonators. Appl. Phys. Lett. 2017, 110, 143506. [Google Scholar] [CrossRef]
- Zanette, D.H. Frequency stabilization by synchronization of Duffing oscillators. Europhys. Lett. 2016, 115, 20009. [Google Scholar] [CrossRef] [Green Version]
- Ghayesh, M.H.; Farokhi, H. Bistable nonlinear response of MEMS resonators. Nonlin. Dynam. 2017, 90, 1627–1645. [Google Scholar] [CrossRef]
- Tchakui, M.V.; Fondjo, V.Y.T.; Woafo, P. Bifurcation structures in three unidirectionally coupled electromechanical systems with no external signal and with regenerative process. Nonlin. Dynam. 2016, 84, 1961–1972. [Google Scholar] [CrossRef]
- Dick, A.J.; Balachandran, B.; Mote, C.D. Intrinsic localized modes in microresonator arrays and their relationship to nonlinear vibration modes. Nonlin. Dynam. 2008, 54, 13–29. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Balachandran, B. Energy localization and white noise-induced enhancement of Response in a Micro-scale Oscillator Array. Nonlin. Dynam. 2010, 62, 1–16. [Google Scholar] [CrossRef]
- Perkins, E.; Kimura, M.; Hikihara, T.; Balachandran, B. Effects of Noise on Symmetric Intrinsic Localized Modes. Nonlin. Dynam. 2016, 85, 333–341. [Google Scholar] [CrossRef]
- Dick, A.J.; Balachandran, B.; Mote, C.D. Localization in Microresonator Arrays: Influence of Natural Frequency Tuning. J.Comp. Nonlin. Dynam. 2010, 5, 011002. [Google Scholar] [CrossRef]
- Labadze, G.; Dukalski, M.; Blanter, Y.M. Dynamics of coupled vibration modes in a quantum non-linear mechanical resonator. Physica E Low Dimens. Syst. Nanostruc. 2016, 76, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Ilyas, S.; Chappanda, K.N.; Younis, M.I. Exploiting nonlinearities of micro-machined resonators for filtering applications. Appl. Phys. Lett. 2017, 110, 253508. [Google Scholar] [CrossRef] [Green Version]
- Kudo, K.; Suto, H.; Nagasawa, T. Frequency stabilization of spin-torque-driven oscillations by coupling with a magnetic nonlinear resonator. J. Appl. Phys. 2014, 116, 163911. [Google Scholar] [CrossRef]
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on mems coupled resonators for sensing applications utilizing mode localization. Sens. Actuators. A: Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Mei, J.; Li, L. Frequency self-tuning of carbon nanotube resonator with application in mass sensors. Sens. Actuators B Chem. 2013, 188, 661–668. [Google Scholar] [CrossRef]
- Zhang, Y. Detecting the stiffness and mass of biochemical adsorbates by a resonator sensor. Sens. Actuators B Chem. 2014, 202, 286–293. [Google Scholar] [CrossRef]
- Spletzer, M.; Raman, A.; Wu, A.Q.; Xu, X.; Reifenberger, R. Ultrasensitive mass sensing using mode localization in coupled microcantilevers. Appl. Phys. Lett. 2006, 88, 254102. [Google Scholar] [CrossRef] [Green Version]
- Bouchaala, A.; Nayfeh, A.H.; Younis, M.I. Analytical study of the frequency shifts of micro and nano clamped-clamped beam resonators due to an added mass. Meccanica 2017, 52, 333–348. [Google Scholar] [CrossRef]
- Younis, M.I.; Nayfeh, A.H. A Study of the Nonlinear Response of a Resonant Microbeam to an Electric Actuation. Nonlinear Dynam. 2002, 31, 91–117. [Google Scholar] [CrossRef]
- Younis, M.I.; Alsaleem, F. Exploration of new concepts for mass detection in electrostatically-actuated structures based on nonlinear phenomena. J. Comput. Nonlin. Dyn. 2009, 4, 021010. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A bifurcation-based coupled linear-bistable system for microscale mass sensing. J. Sound Vib. 2014, 333, 2241–2252. [Google Scholar] [CrossRef]
- Nguyen, V.-N.; Baguet, S.; Lamarque, C.-H.; Dufour, R. Bifurcation-based micro-/nano electromechanical mass detection. Nonlin. Dynam. 2015, 79, 647–662. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.H.; Alsaleem, F.M.; Ouakad, H.M. Novel threshold pressure sensors based on nonlinear dynamics of MEMS resonators. J. Micromech. Microeng. 2018, 28, 065007. [Google Scholar] [CrossRef]
- Alghamdi, M.; Khater, M.; Stewart, K.; Alneamy, A.; Abdel-Rahman, E.M.; Penlidis, A. Dynamic bifurcation mems gas sensors. J. Micromech. Microeng. 2019, 29, 015005. [Google Scholar] [CrossRef]
- Azizi, S.; Kivi, A.R.; Marzbanrad, J. Mass detection based on pure parametric excitation of a micro beam actuated by piezoelectric layers. Microsyst. Technol. 2017, 23, 991–998. [Google Scholar] [CrossRef]
- Li, L.; Han, J.; Zhang, Q.; Liu, C.; Guo, Z. Nonlinear dynamics and parameter identification of electrostatically coupled resonators. Int. J. Nonlin. Mech. 2019, 110, 104–114. [Google Scholar] [CrossRef]
- COMSOL. Available online: http://www.comsol.com/ (accessed on 11 February 2021).
- Ekinci, K.; Huang, X.; Roukes, M. Ultrasensitive nanoelectromechanical mass detection. Appl. Phys. Lett. 2004, 84, 4469–4471. [Google Scholar]
- Peng, B.; Hu, K.M.; Shao, L.; Yan, H.; Zhang, W.M. A sensitivity tunable accelerometer based on series-parallel electromechanically coupled resonators using mode localization. J. Microelectromech. Syst. 2020, 29, 3–13. [Google Scholar] [CrossRef]
- Alsaleem, F.M.; Younis, M.I. Stabilization of electrostatic MEMS resonators using a delayed feedback controller. Smart Mater. Struct. 2010, 19, 035016. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. The dynamic behavior of MEMS arch resonators actuated electrically. Int. J. Nonlin. Mech. 2010, 45, 704–713. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Nonlinear Interactions; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]


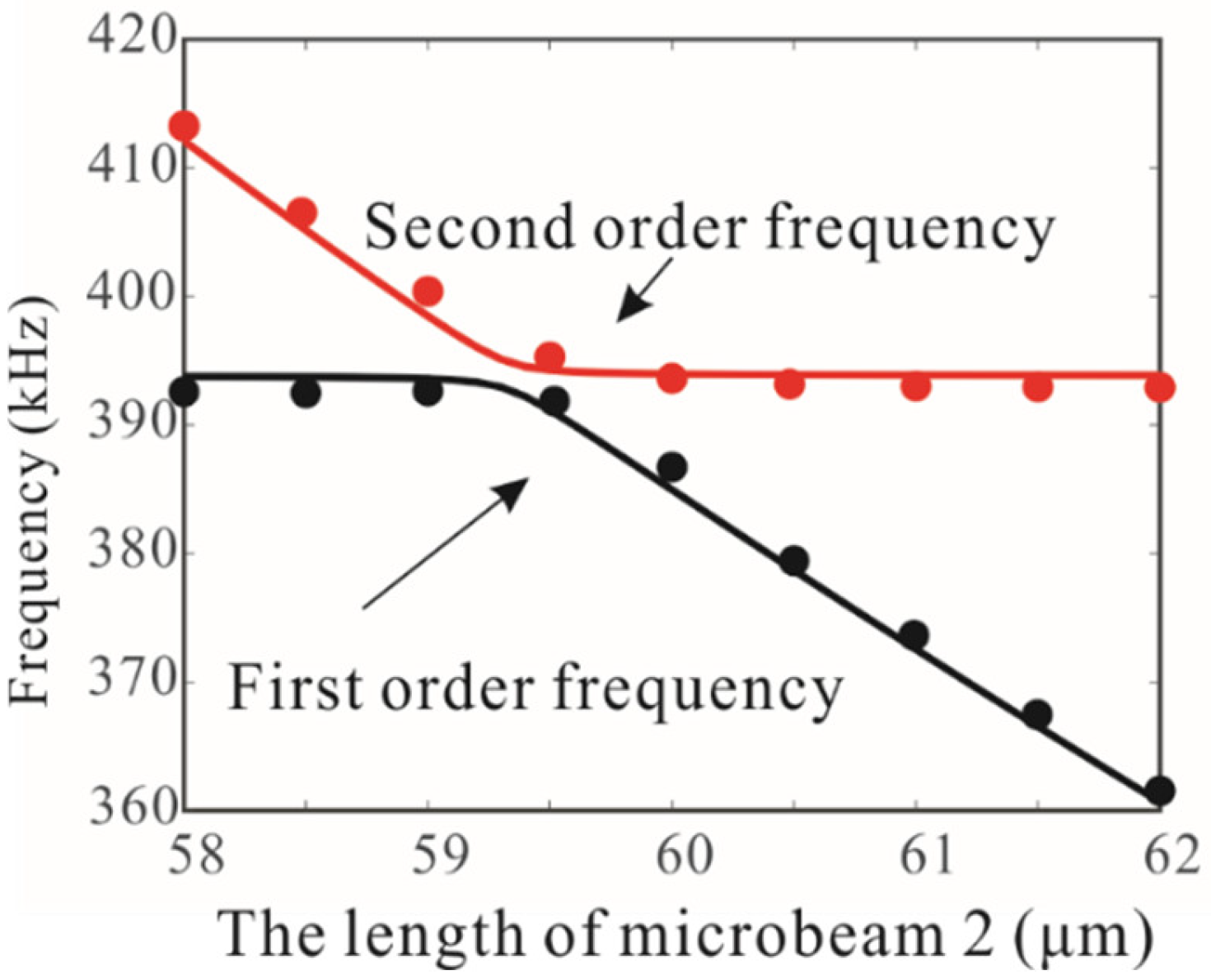
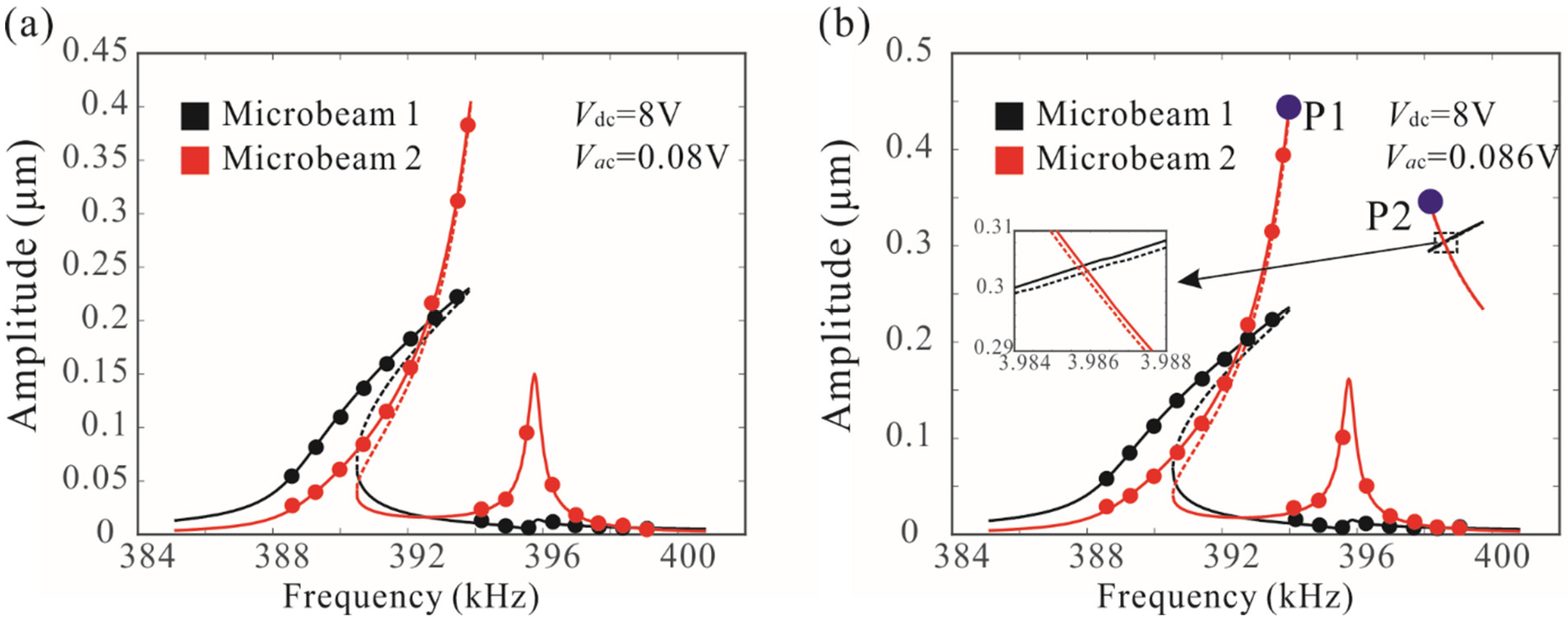
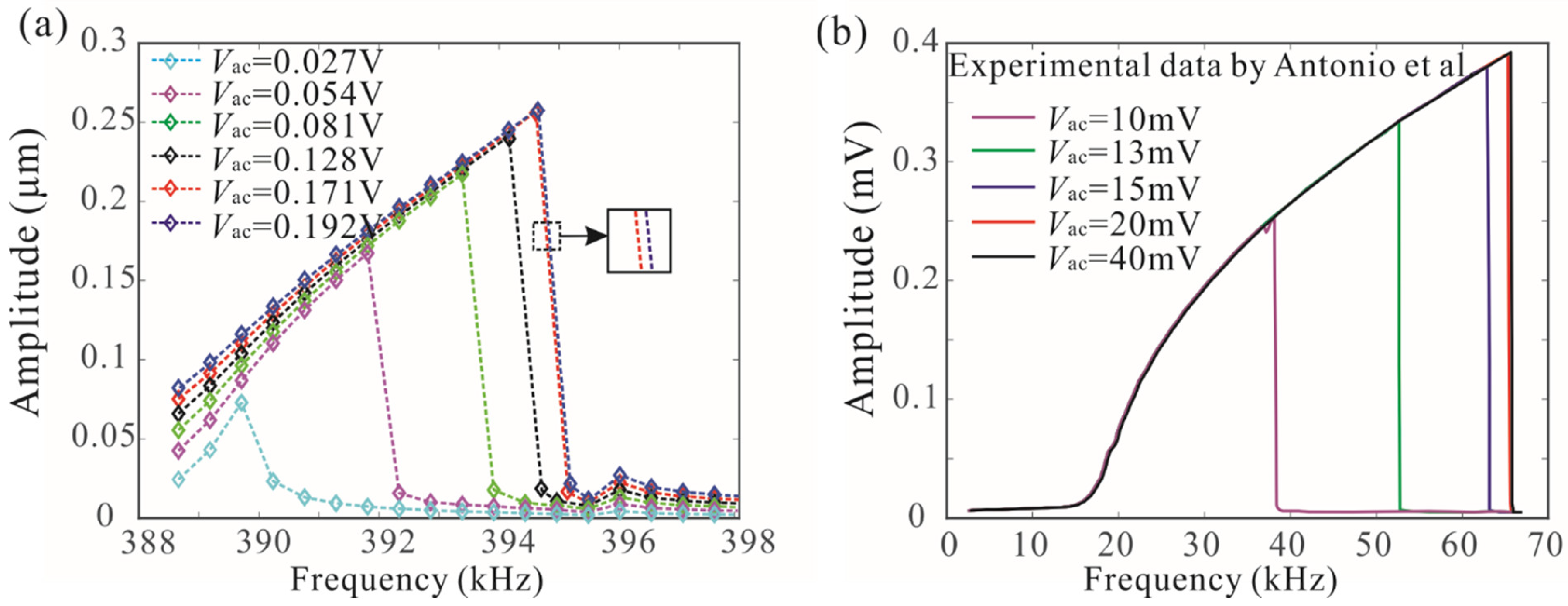
| Physical Parameter (Units) | Value |
|---|---|
| Length of microbeam 1, L (µm) | 150 |
| Length of microbeam 3, R (µm) | 10 |
| Thickness of all microbeams, h (µm) | 1 |
| Widths of microbeams 1 and 2, b (µm) | 10 |
| Width of microbeam 3, (µm) | 1 |
| Position of the coupling beam, L1 (µm) | 5 |
| Mass adsorption position, L2 (µm) | 50 |
| Gap between the electrodes, d (µm) | 1.5 |
| Density of the electrode material, ρ (kg/m3) | 2300 |
| Young’s Modulus, E (GPa) | 169 |
| Dielectric constant of the medium, | 8.85 × 10−12 |
| Number | The True Mass m (10−6 μg) | Damping Coefficient cn | Identification Results m (10−6 μg) | The Ratio between the Analyte and the Sensor Mass | Error |
|---|---|---|---|---|---|
| 1 | 2 | 0.02 | 1.884 | 0.04% | 5.8% |
| 2 | 4 | 0.02 | 3.768 | 0.08% | 5.81% |
| 3 | 6 | 0.02 | 5.647 | 0.12% | 5.89% |
| 4 | 2 | 0.01 | 1.939 | 0.04% | 3.05% |
| 5 | 4 | 0.01 | 3.876 | 0.08% | 3.1% |
| 6 | 6 | 0.01 | 5.813 | 0.12% | 3.12% |
| 7 | 2 | 0.005 | 1.976 | 0.04% | 1.22% |
| 8 | 4 | 0.005 | 3.95 | 0.08% | 1.24% |
| 9 | 6 | 0.005 | 5.922 | 0.12% | 1.3% |
| Sensor | Detection Principle | Nonlinear Factor | Advantages | Disadvantages |
|---|---|---|---|---|
| Mass sensor reported by Ekinci et al. [50] | The resonance frequency shifts induced by the added mass | Ignoring nonlinearity | The operation is simple | The influence of nonlinear factors is not considered |
| Accelerometer sensor reported by Peng et al. [51] | A change of modal amplitude ratio due to the mode localization | Ignoring nonlinearity | The sensitivity of the sensor is improved | The influence of nonlinear factors is not considered |
| Mass sensor reported by Nguyen et al. [44] | The bifurcation jumping induced by the added mass | Utilizing nonlinearity | Nonlinear jump can improve the sensitivity and resolution | Nonlinearity results in dependence of bifurcation frequency on amplitude |
| This work | The bifurcation frequency shifts induced by the added mass | Utilizing nonlinear coupled mode vibration | The dependence of bifurcation frequency on driving voltage is solved | High quality factors are needed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Liu, H.; Shao, M.; Ma, C. A Novel Frequency Stabilization Approach for Mass Detection in Nonlinear Mechanically Coupled Resonant Sensors. Micromachines 2021, 12, 178. https://doi.org/10.3390/mi12020178
Li L, Liu H, Shao M, Ma C. A Novel Frequency Stabilization Approach for Mass Detection in Nonlinear Mechanically Coupled Resonant Sensors. Micromachines. 2021; 12(2):178. https://doi.org/10.3390/mi12020178
Chicago/Turabian StyleLi, Lei, Hanbiao Liu, Mingyu Shao, and Chicheng Ma. 2021. "A Novel Frequency Stabilization Approach for Mass Detection in Nonlinear Mechanically Coupled Resonant Sensors" Micromachines 12, no. 2: 178. https://doi.org/10.3390/mi12020178






