1. Introduction
A hot runner system (HRS) is widely adopted in modern injection molding processes. The HRS allows higher productivity, easier quality control, and apparent resin cost saving. Rapid product cycle demands the lead time be shorter and shorter while the reliability of mold tooling is always important. As a result, the design process should be quick as well as systematic. In an HRS design, there are two important functions that should be guaranteed. The first one is to maintain the target temperature within a tolerable range. Second, the runner system has to deliver melt in an efficient as well as balanced fashion. This work is focused on the second part. The dimensions of the manifold and the nozzles should be optimally determined considering both the allowable pressure drop and the necessary flow rate [
1].
The pressure drop is especially important in microsystem. Injection molding of a micro-device requires a high pressure at the gate to drive the filling flow in the micro-cavity [
2,
3,
4,
5]. To maintain the required pressure at the gate, the pressure drop through the runner should be suppressed. The diameter of the runner should be increased while the length should be shortened. However, the length is very difficult to shorten since it is supposed to set by the delivery requirement. In the meantime, the increase of the diameter causes serious problems which negatively impacts the molding process. The increased diameter adds volume to the runner. The pressure drops linearly along with the diameter while the volume increases quadratically. The increased volume per se is the situation that should be avoided. The melt retained in the runner will degrade while the stagnant phases. Moreover, the temperature can be non-uniform and fluctuating for wider runners. Thus, the runner diameter should not be bigger than required.
Technologies and studies of numerical filling simulations for conventional injection molding process have matured [
2,
3,
6,
7,
8,
9]. In other processes, molding optimization is an important issue [
10]. It has been widely used for design of molds and products as well as for troubleshooting in the processes [
11,
12,
13,
14,
15,
16]. There are several CAE (computer aided engineering) packages, such as MoldFlow, Modex3D, and 3D Timon, which are commercially successful in industry and also widely accepted as research tools [
2,
9,
17,
18]. Especially, CAE has been utilized for cooling line design of injection molds [
15,
19]. It is also proven that it can handle fairly complicated HRs [
20,
21].
In an HR design, it is desirable to maintain sufficient flow conductance with limited pressure [
1]. The pressure drop is always an important matter of concern in HR both in the sequential and conventional gating methods [
20,
22,
23]. Given a flow rate, the pressure drop can be obtained by a numerical simulation, which can be conducted in many commercial CAE programs.
However, there are several difficulties in calculating the pressure drops for design purpose using such programs. First of all, it is necessary to train the design engineers to let them learn the entire CAE process from three-dimensional drawing to simulation. Second, whenever the dimensional parameters are changed, the mesh should be regenerated repeatedly. It is thought that the HR design engineers would not be willing to repeat the meshing. Rather, they would reuse existing design dimensions or change the dimensions by a rule of thumb without a scientific analysis. Third, the simulation itself takes a quite long time for each case. Even when the mesh is ready, one simulation run takes quite a long time to be used while designing a hot runner. Fourth, such simulation programs are expensive to purchase and costly to operate. To allow all the in-house design engineers to access the simulation program, multiple licenses should be purchased. This is impracticable to most HR providers.
As a result, the pressure drop is suggested to be calculated based on analytical methods in the design phase [
24,
25]. The analytical approach cannot consider the pressure drops due to directional changes and flow distributions. Moreover, the viscosity approximation, which is conducted by the power law or other shear thinning models, can induce additional errors. Once the dimensions are set, a runner designer can move onto numerical simulation for verification. However, this can cause laborious trial and errors.
Thus, a computer tool dedicated to flow design of HRS would help the design process. However, such a tool can hardly be found in the literature. To expedite the design process of HRS, this work proposes a rapid numerical method for calculating the pressure drop while melt flows through the hot runner. This work focuses on calculation of the melt flow in HR for HR field designers. The whole flow field will be sectioned into several subdomains, and then the pressure drop will be calculated for each subdomain. Afterwards, the total pressure drop can be estimated by summing up the pressure drops in the subdomains. Given the melt flow rate and geometric setup, the proposed system will yield the pressure drop in affordable time. The method will be implemented using a spread sheet computer software and a publicly available CFD (computational fluid dynamics) computer program. A CFD computer program usually numerically solves the Navier–Stokes problem by the finite volume (FV) or finite element (FE) methods. A public FV-based CFD program, OpenFOAM, was employed to allow other engineers or researchers to easily reproduce our work. It is expected that this work would contribute to reduction of the HRS design time.
2. Numerical Methods
2.1. Overall Approach
The hot runners include two major parts, which are the manifold and nozzles. They have several typical forms especially depending on the number of nozzles. The HR providers have their own product lines, which are internally standardized and presented in their catalogues. Most of the orders fall into the standards. Therefore, a flow simulation tool that is dedicated to flow through the manifold and the nozzle can be developed taking the standard geometries into account. The basic approach here is to divide the entire flow path into a number of subdomains followed by assessing the pressure drop in each subdomain during a saturated flow of a generalized Newtonian fluid (GNF). The GNF models can well represent rheological behaviors of molten polymers that can be assumed as inelastic non-Newtonian fluids. Then, the whole pressure drop is estimated by adding up the pressure drop in all the subdomains. This kind of method has been widely exploited in many pipe network designs [
26].
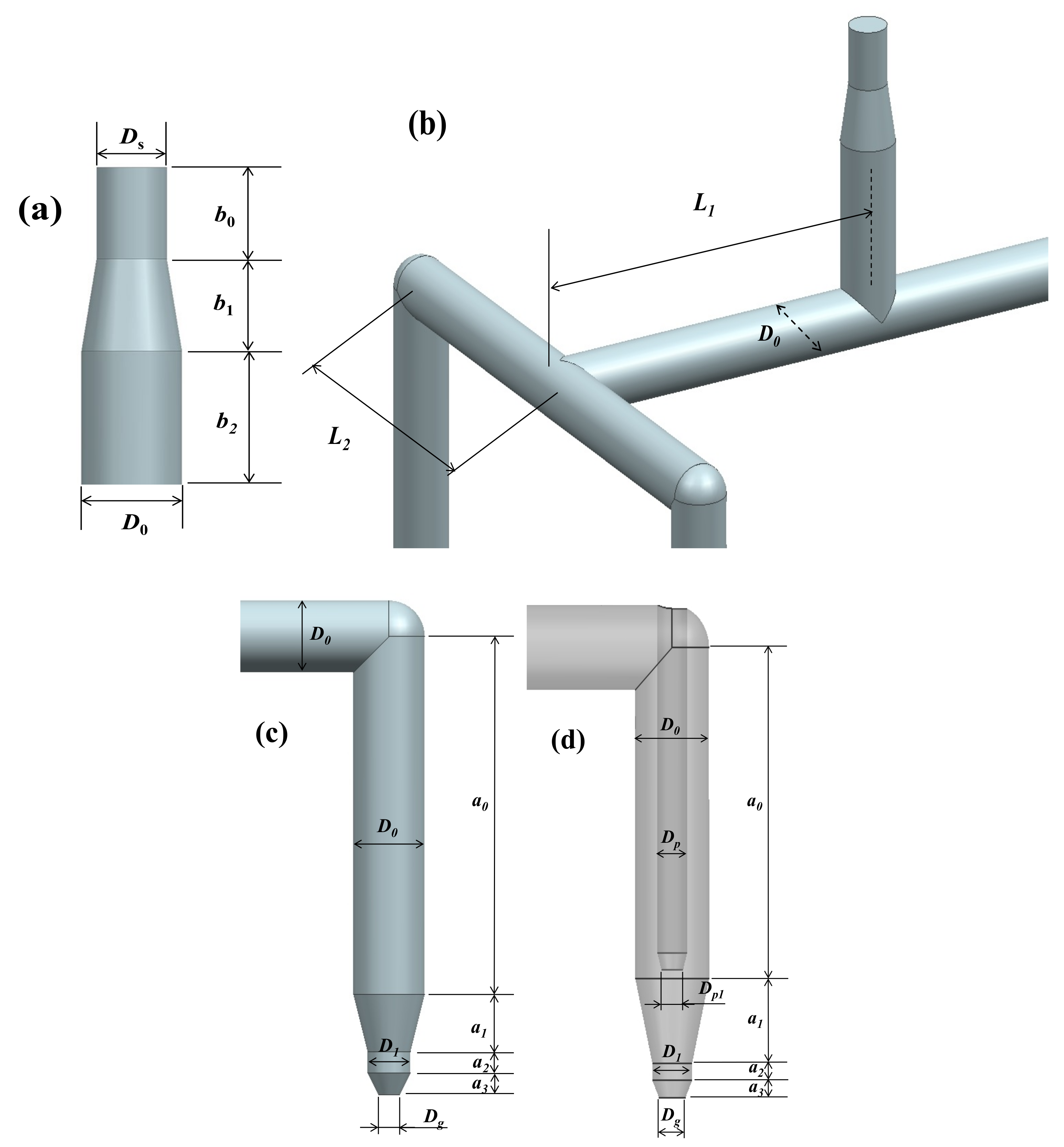
Figure 1 shows a typical hot runner layout with four drops. There are four straight sections with a sprue section, two intersections, one elbow, and the nozzle. In most parts of the flow path, the cross-section is circular. For a fairly long circular pipe section, the pressure drop can be analytically calculated assuming fully developed flow of power-law fluid (PLF), which will be utilized here. In the proposed method, the pressure drop in each section is calculated separately and added up to assess the pressure drop throughout the whole runner. Several different kinds of HRS will be treated including the one shown in
Figure 1.
Consider design parameters that determine the geometry shown in
Figure 1. A set of design parameters are predefined as
In a subdomain indexed
i, the pressure drop will be
and the total pressure drop is represented as
The purpose of this work is to calculate the total pressure drop, , under a given set of design parameters, g. An HR designer will be able to check the change in due to the change in any design variable, .
2.2. Assumptions
This work argues that the total pressure loss for driving the HR flow can be assessed by solving a steady saturated flow of each subdomain followed by adding up the pressure drops. Let us first discuss the assumption of a saturated steady flow. The flow between the sprue to the gate in HR can be considered steady if the flow rate is constant since the downstream cavity flow normally cannot affect the upstream HR flow. In an injection molding process, the melt flow is inherently unsaturated and the melt front poses a moving boundary inside a mold cavity. A hot runner needs to be flow-conductive enough to reserve the pressure head for filling the cavity and for transmitting sufficient packing pressure during the post-filling phase. Regardless of the degree of filling, the pressure drop from the sprue to the gate does not significantly vary while injection rate is maintained constant.
Figure 2 shows the pressure drop during filling of a sample cavity. It was obtained by Autodesk MoldFlow Insight 2012, which will be referred to as MoldFlow in the rest of this paper. The geometric model is shown in the inset of
Figure 1. The pressure drop in HRS is maintained almost constant during filling until the switch-over. Thus, it is reasonable to estimate the pressure drop throughout a hot runner during mold filling based on a saturated steady flow model. As a design method for HRS, it will be a viable and effective method. Moreover, it should be noted that the pressure drop before the switch-over is likely to be the highest since that begins to decrease from the switch-over point.
The next matter is to justify division of the whole domain into several subdomains. The benefits from this include faster computation, facilitation of parallel computation, easier mesh handling, and two-dimensional approximation for axisymmetric subdomains. Here, two approximations are required. First, in each subdomain, a fully-developed velocity profile of the PLF will be imposed on the inlet boundary with some additional length as shown in
Figure 3. In the first subdomain of the inlet, as long as the flow in the injection molding machine is not analyzed, a fully-developed profile is the best condition imposable here. In the middle subdomains, the velocity of the adjacent upstream outlet can be possibly imposed. However, that way is not chosen in this work since it requires sequential computation and prevents connection between axisymmetric and three-dimensional subdomains. As a result of this approximation, any secondary flows, which are perpendicular to the primary flow, cannot be relayed on the interface between the subdomains. Especially when one of the adjacent subdomains is curved, there should be a secondary flow and it is known to contribute to the pressure drop. However, the effect of the secondary flow on the interface will be negligible since most of the pressure drop due to the secondary flow will be taken into account in calculation within the curved sections and the interfaces will be far downstream from the curved section. Second, the absolute pressure cannot be accurately obtained by this method. Thus, dependency of the viscosity and the density on pressure cannot be considered. This is assumed in many Newtonian incompressible flows. However, in injection molding simulation, the pressure effects have been taken into consideration, although it is not significant in the filling phase. The validity of these assumptions will be checked out by comparing the pressure drops with those of fully three-dimensional analyses.
2.3. Governing Equations
A typical formalism for momentum transport of a generalized Newtonian fluid (GNF) is reproduced here. This work adopts an isothermal three-dimensional steady model. This work ignores viscous heating although it is important in HR to reduce the computational time, which will be discussed later. Consider the velocity vector
u, pressure
p, and density
ρ. Neglecting body force, a steady-state momentum equation for a GNF is
Here, for a given temperature
T, the shear stress tensor
is expressed as
where
is the rate of deformation tensor, which is of the form
The shear rate, , which is the second invariant of , is given by .
2.4. Viscosity Model
In this work, the power law model and the cross model are employed to represent the viscosity. The power law model is expressed as
where
n and
K are the power-law index and the consistency, respectively.
The most widely employed viscosity model for simulation of injection molding is the Cross-WLF model, which will more realistically represent the viscosity especially near the first Newtonian plateau. To utilize the existing viscosity data in that form, the hot runner pressure drop calculator (HRPDC) will also allow input of the Cross model, which takes the form of
where
τ is a curve-fitted constant for a specific polymer and
is the zero-shear viscosity. This study does not solve energy equation. However, the HR temperature significantly affects the pressure drop by changing the viscosity. Thus, it will be an important input value to the hot runner pressure drop calculator (HRPDC). Sometimes, the high pressure of the melt resident in the hot runner noticeably increases the viscosity. The WLF model is employed to represent
as a function of pressure and temperature, which is of the form
Here, D1, D2, A1, and A2 are constant values that should be determined from experimental measurements for a specific polymer.
In the circular straight section, an analytical solution is available in a simple closed form for PLF but not for CLF (Cross law fluid). Note that the aforementioned CFD computer program, OpenFOAM, will solve Equation (3) with Equation (7).
2.5. Boundary Conditions
The boundary conditions are quite simple since there is no free boundary in this model. The boundary conditions are the same for all subdomains. First, a no-slip condition is imposed on the walls.
Second, a Neumann condition is imposed on the outlet.
where
n is the coordinate variable normal to the wall along the normal vector
n. Moreover, a reference cell for pressure field is chosen on this boundary and a gauge pressure of zero is imposed. Thus,
in
Figure 3 is set as zero. As a result, the pressure at the inlet will be the pressure difference. Third, a velocity profile should be imposed in the inlet. In every subdomain, the flow starts again with an inlet velocity.
The easiest way is to simply impose a uniform velocity throughout the boundary.
where the uniform velocity is of the form
where
Q and
D are the flow rate and the diameter, respectively.
The velocity field between the subdomains should be fully developed. Thus, it is necessary to add more length to the beginning part of each subdomain. For a laminar flow, the entry length is roughly
The calculated value of
cannot be larger than
D in HR melt flow of any thermoplastics however fast the melt flow is. Hence, the additional length, ahead of the actual interval for pressure calculation is set as
Although this would probably be enough, to guarantee the fully developed flow at the point of the inlet pressure measurement, a fully developed velocity profile of a PLF is imposed instead of a flat profile of
, which is
where
R is the radius of the runner.
By doing so, for a PLF,
can be set equal to 0, and for a CLF, the velocity will rapidly develop to a fully developed profile of a CLF while flowing the additional length. It is assumed that any velocity components other than normal to the inlet surface do not significantly contribute to the pressure drop near the connecting boundary, which will be examined in test cases. Moreover, given a flow rate and length, the pressure drop in a linear runner flowing PLF is obtained simply as
5. Conclusions
This work has presented a method for rapid calculation of pressure drip in hot runners. Assuming steady-state and isothermality, a steady Navier–Stokes equation has been solved to obtain the pressure drop in the subdomains, which are defined by dividing the whole domain along the flow path. A computer method that can estimate pressure drops according to the hot runner dimensions are established. We have verified that the pressure drop can be accurately estimated by adding up those calculated in all the subdomains based on comparisons with MoldFlow. The computer utility has been built using two existing computer tools, Excel and OpenFOAM. The communication structure between these two tools has been implemented by the Excel VBA. It has also been shown that the developed tool, the HRPDC, can be employed for practical design of hot runner dimensions.
Although the model has a couple of assumptions, the proposed method is not a rough tool with big approximations. The method has utilized the standardized characteristics of hot runner manifolds and runners in contrast to those of mold cavities. For a given hot runner product line, the geometric models can be reused for different orders. The developed tool has been adopted for real-world design processes of hot runner systems.