Interfacial Tension Measurements in Microfluidic Quasi-Static Extensional Flows
Abstract
:1. Introduction
2. Theoretical Background
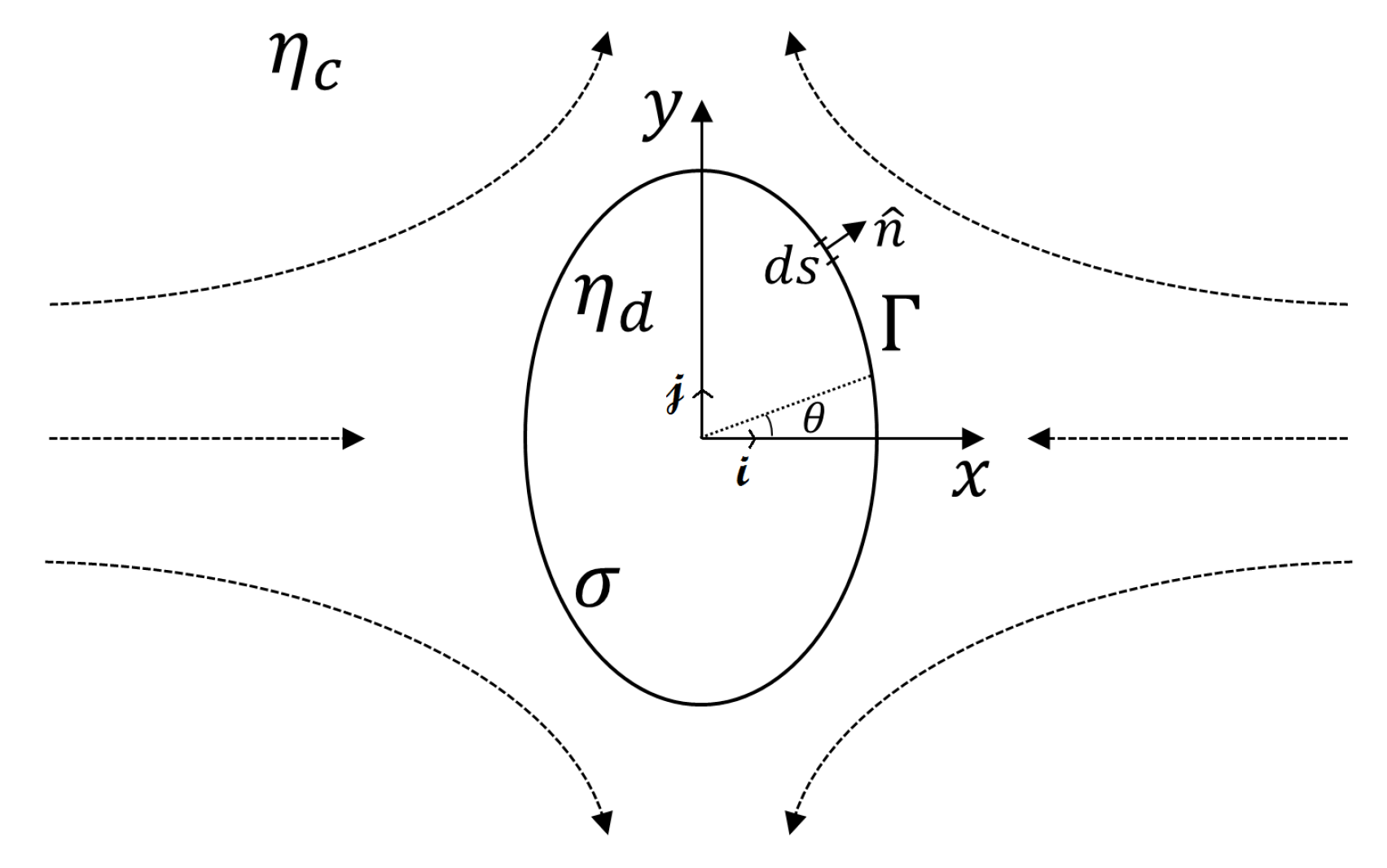
2.1. 2D Darcy Approximation Model for a Confined Droplet
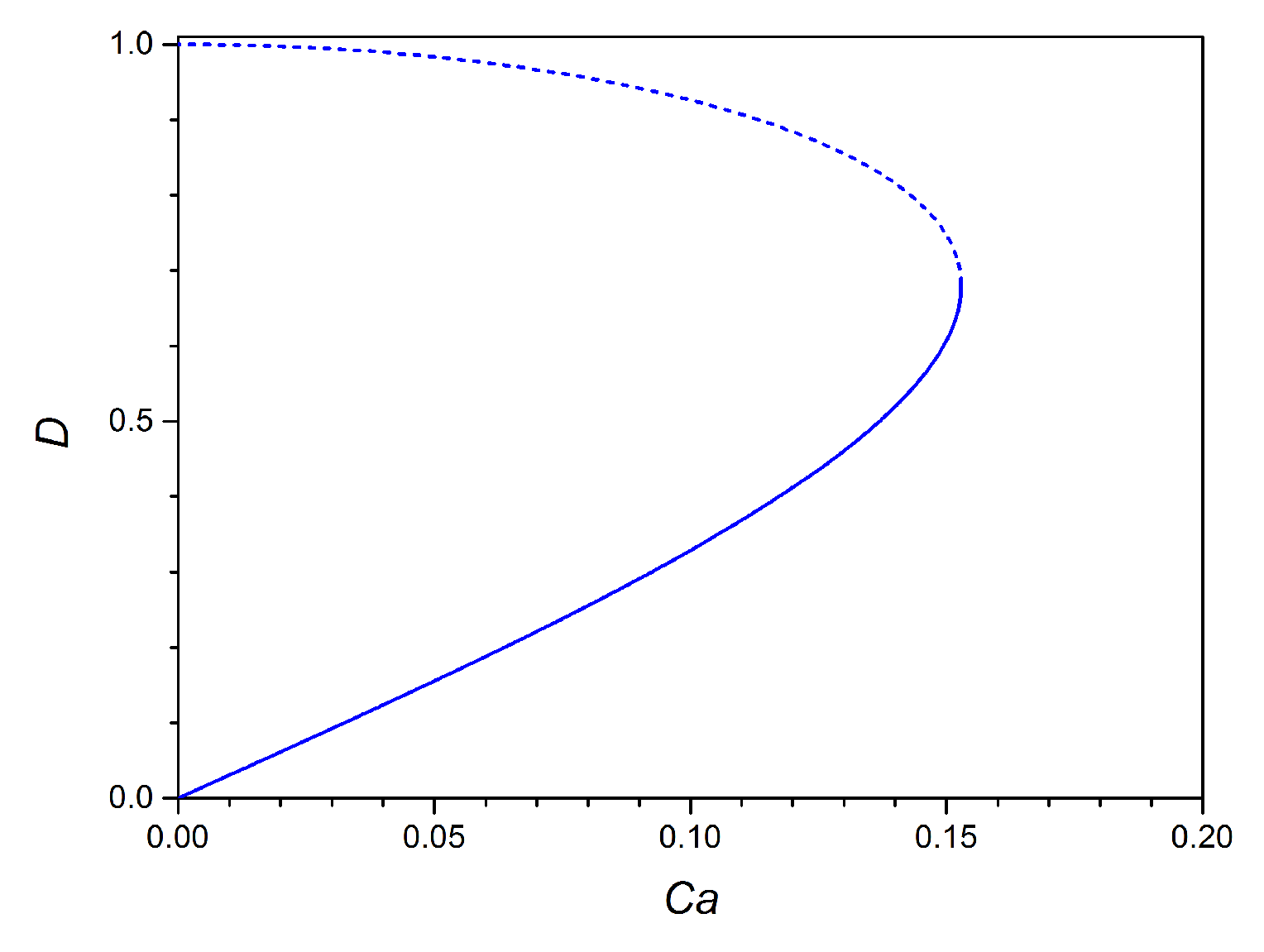
2.2. 3D Small Deformation Model for an Unconfined Droplet
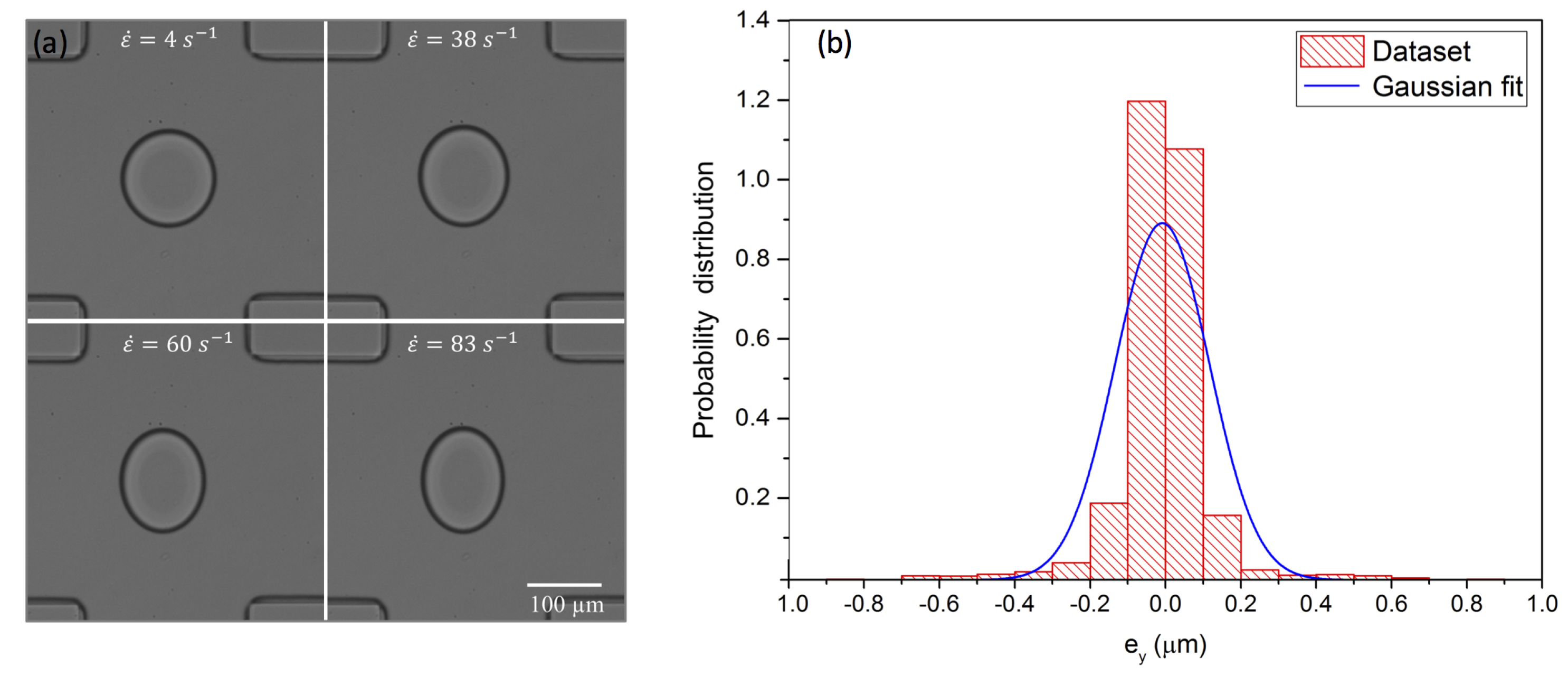
3. Experimental Methods
4. Results and Discussion
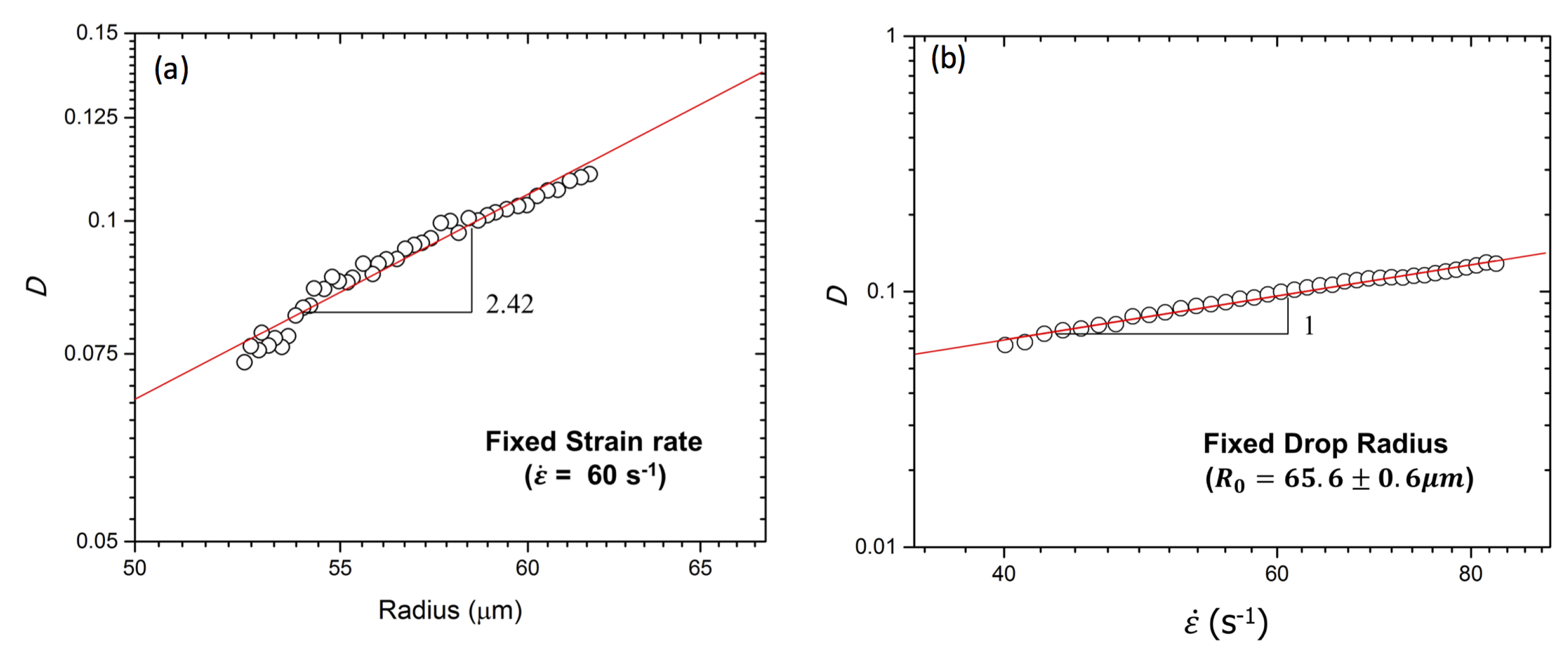
4.1. 2D Darcy Approximation Model for Confined Droplet
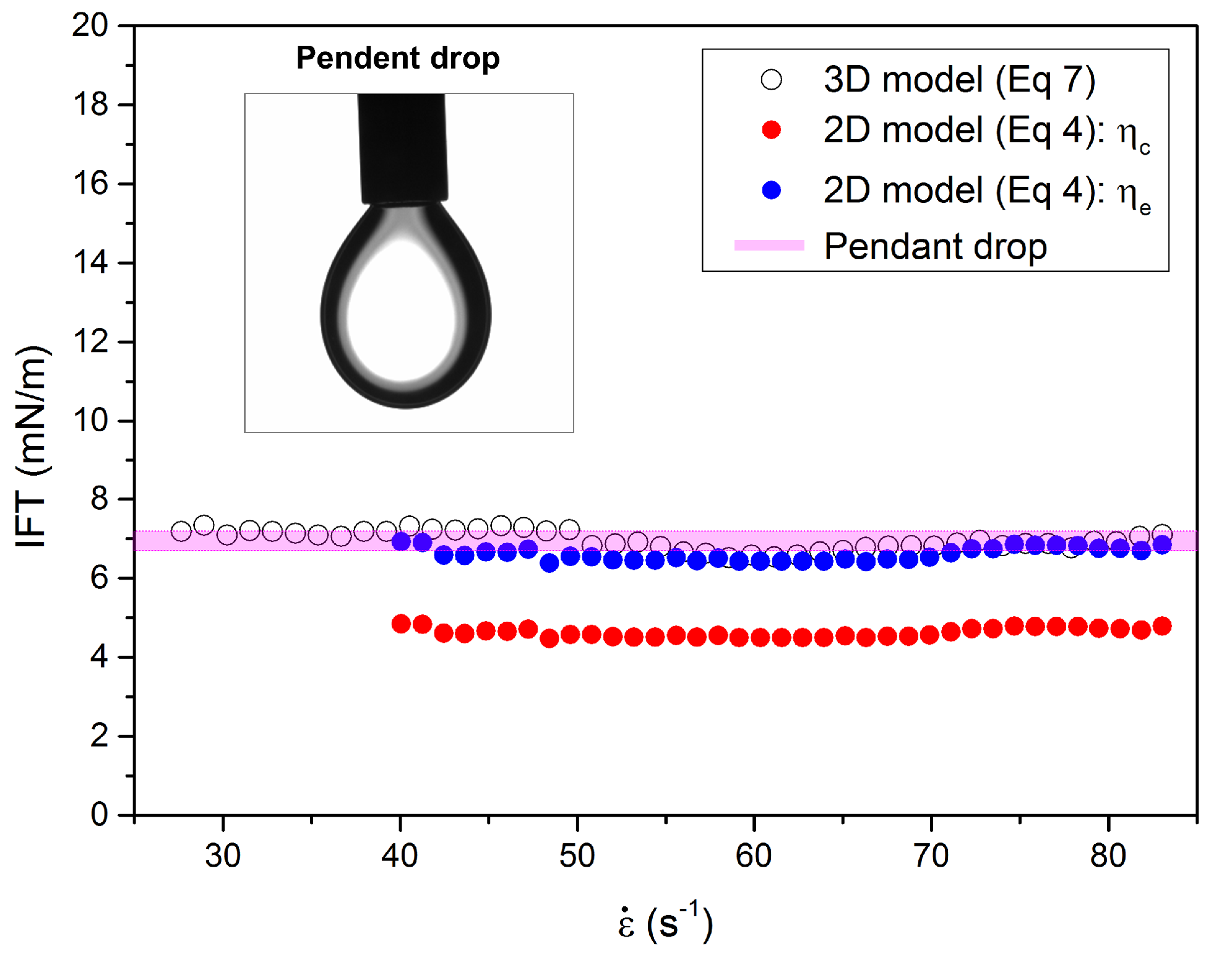
4.2. IFT Measurements in Microfluidics with 2D and 3D Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Teh, S.Y.; Lin, R.; Hung, L.H.; Lee, A.P. Droplet microfluidics. Lab Chip 2008, 8, 198–220. [Google Scholar] [CrossRef]
- Mak, S.Y.; Li, Z.; Frere, A.; Chan, T.C.; Shum, H.C. Musical interfaces: Visualization and reconstruction of music with a microfluidic two-phase flow. Sci. Rep. 2014, 4, 6675. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Mak, S.Y.; Sauret, A.; Shum, H.C. Syringe-pump-induced fluctuation in all-aqueous microfluidic system implications for flow rate accuracy. Lab Chip 2014, 14, 744–749. [Google Scholar] [CrossRef] [Green Version]
- D’Apolito, R.; Perazzo, A.; D’Antuono, M.; Preziosi, V.; Tomaiuolo, G.; Miller, R.; Guido, S. Measuring interfacial tension of emulsions in situ by microfluidics. Langmuir 2018, 34, 4991–4997. [Google Scholar] [CrossRef]
- Cui, Y.; Li, Y.; Wang, K.; Deng, J.; Luo, G. Determination of Dynamic Interfacial Tension during the Generation of Tiny Droplets in the Liquid–Liquid Jetting Flow Regime. Langmuir 2020, 36, 13633–13641. [Google Scholar] [CrossRef]
- Chou, W.L.; Lee, P.Y.; Yang, C.L.; Huang, W.Y.; Lin, Y.S. Recent advances in applications of droplet microfluidics. Micromachines 2015, 6, 1249–1271. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, D.; Serra, M.; Filippi, D.; Zago, L.; Guglielmin, E.; Pierno, M.; Descroix, S.; Viovy, J.L.; Mistura, G. Controlling the distance of highly confined droplets in a capillary by interfacial tension for merging on-demand. Lab Chip 2019, 19, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Fang, C.; Ravan, A.S.; Fuller, G.G.; Shen, A.Q. Temperature controlled tensiometry using droplet microfluidics. Lab Chip 2017, 17, 717–726. [Google Scholar] [CrossRef] [PubMed]
- Shang, L.; Cheng, Y.; Zhao, Y. Emerging droplet microfluidics. Chem. Rev. 2017, 117, 7964–8040. [Google Scholar] [CrossRef]
- Sohrabi, S.; Moraveji, M.K. Droplet microfluidics: Fundamentals and its advanced applications. RSC Adv. 2020, 10, 27560–27574. [Google Scholar] [CrossRef]
- Bhalla, N.; Jain, A.; Lee, Y.; Shen, A.Q.; Lee, D. Dewetting metal nanofilms—Effect of substrate on refractive index sensitivity of nanoplasmonic gold. Nanomaterials 2019, 9, 1530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, T.; Kreutz, J.; Chiu, D.T. The potential impact of droplet microfluidics in biology. Anal. Chem. 2013, 85, 3476–3482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhalla, N.; Lee, D.; Sathish, S.; Shen, A.Q. Dual-mode refractive index and charge sensing to investigate complex surface chemistry on nanostructures. Nanoscale 2017, 9, 547–554. [Google Scholar] [CrossRef]
- Gu, H.; Duits, M.H.; Mugele, F. Interfacial tension measurements with microfluidic tapered channels. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 389, 38–42. [Google Scholar] [CrossRef]
- de Ruiter, R.; Wennink, P.; Banpurkar, A.G.; Duits, M.H.; Mugele, F. Use of electrowetting to measure dynamic interfacial tensions of a microdrop. Lab Chip 2012, 12, 2832–2836. [Google Scholar] [CrossRef]
- Hudson, S.D.; Cabral, J.T.; Goodrum, W.J.; Beers, K.L.; Amis, E.J. Microfluidic interfacial tensiometry. Appl. Phys. Lett. 2005, 87, 81905. [Google Scholar] [CrossRef] [Green Version]
- Hetsroni, G.; Haber, S.; Wacholder, E. The flow fields in and around a droplet moving axially within a tube. J. Fluid Mech. 1970, 41, 689–705. [Google Scholar] [CrossRef]
- Zhou, H.; Yao, Y.; Chen, Q.; Li, G.; Yao, S. A facile microfluidic strategy for measuring interfacial tension. Appl. Phys. Lett. 2013, 103, 234102. [Google Scholar] [CrossRef]
- Chen, Y.; Narayan, S.; Dutcher, C.S. Phase-Dependent Surfactant Transport on the Microscale: Interfacial Tension and Droplet Coalescence. Langmuir 2020, 36, 14904–14923. [Google Scholar] [CrossRef]
- Cabral, J.T.; Hudson, S.D. Microfluidic approach for rapid multicomponent interfacial tensiometry. Lab Chip 2006, 6, 427–436. [Google Scholar] [CrossRef]
- Steegmans, M.L.; Warmerdam, A.; Schroen, K.G.; Boom, R.M. Dynamic interfacial tension measurements with microfluidic Y-junctions. Langmuir 2009, 25, 9751–9758. [Google Scholar] [CrossRef] [PubMed]
- Brosseau, Q.; Vrignon, J.; Baret, J.C. Microfluidic dynamic interfacial tensiometry (μDIT). Soft Matter 2014, 10, 3066–3076. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Honaker, L.W.; Lagerwall, J.P.; Jampani, V. Microfluidic tensiometry technique for the characterization of the interfacial tension between immiscible liquids. Langmuir 2018, 34, 2403–2409. [Google Scholar] [CrossRef] [Green Version]
- Rallison, J. The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 1984, 16, 45–66. [Google Scholar] [CrossRef]
- Rothstein, J.P.; McKinley, G.H. The axisymmetric contraction–expansion: The role of extensional rheology on vortex growth dynamics and the enhanced pressure drop. J. Non-Newton. Fluid Mech. 2001, 98, 33–63. [Google Scholar] [CrossRef]
- Zografos, K.; Pimenta, F.; Alves, M.; Oliveira, M. Microfluidic converging/diverging channels optimised for homogeneous extensional deformation. Biomicrofluidics 2016, 10, 043508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubash, N.; Cheung, P.; Shen, A.Q. Elastic instabilities in a microfluidic cross-slot flow of wormlike micellar solutions. Soft Matter 2012, 8, 5847–5856. [Google Scholar] [CrossRef]
- Haward, S.J.; McKinley, G.H.; Shen, A.Q. Elastic instabilities in planar elongational flow of monodisperse polymer solutions. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haward, S.J.; Odell, J.A.; Li, Z.; Yuan, X.F. Extensional rheology of dilute polymer solutions in oscillatory cross-slot flow: The transient behaviour of birefringent strands. Rheol. Acta 2010, 49, 633–645. [Google Scholar] [CrossRef]
- Haward, S.J.; Oliveira, M.S.; Alves, M.A.; McKinley, G.H. Optimized cross-slot flow geometry for microfluidic extensional rheometry. Phys. Rev. Lett. 2012, 109, 128301. [Google Scholar] [CrossRef] [Green Version]
- Narayan, S.; Moravec, D.B.; Dallas, A.J.; Dutcher, C.S. Droplet shape relaxation in a four-channel microfluidic hydrodynamic trap. Phys. Rev. Fluids 2020, 5, 113603. [Google Scholar] [CrossRef]
- Ulloa, C.; Ahumada, A.; Cordero, M.L. Effect of confinement on the deformation of microfluidic drops. Phys. Rev. E 2014, 89, 033004. [Google Scholar] [CrossRef] [Green Version]
- Taylor, G. The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. 1934, 146, 501–523. [Google Scholar]
- Bentley, B.; Leal, L. An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 1986, 167, 241–283. [Google Scholar] [CrossRef] [Green Version]
- Mulligan, M.K.; Rothstein, J.P. The effect of confinement-induced shear on drop deformation and breakup in microfluidic extensional flows. Phys. Fluids 2011, 23, 022004. [Google Scholar] [CrossRef] [Green Version]
- Buckmaster, J.; Flaherty, J. The bursting of two-dimensional drops in slow viscous flow. J. Fluid Mech. 1973, 60, 625–639. [Google Scholar] [CrossRef]
- Unger, M.A.; Chou, H.P.; Thorsen, T.; Scherer, A.; Quake, S.R. Monolithic microfabricated valves and pumps by multilayer soft lithography. Science 2000, 288, 113. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Lee, D.; Stober, B.; Fuller, G.G.; Shen, A.Q. Integrated microfluidic platform for instantaneous flow and localized temperature control. RSC Adv. 2015, 5, 85620–85629. [Google Scholar] [CrossRef]
- Tanyeri, M.; Schroeder, C.M. Manipulation and Confinement of Single Particles Using Fluid Flow. Nano Lett. 2013, 13, 2357–2364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanyeri, M.; Ranka, M.; Sittipolkul, N.; Schroeder, C.M. A microfluidic-based hydrodynamic trap: Design and implementation. Lab Chip 2011, 11, 1786–1794. [Google Scholar] [CrossRef]
- Rumscheidt, F.D.; Mason, S. Particle motions in sheared suspensions XII. Deformation and burst of fluid drops in shear and hyperbolic flow. J. Colloid Sci. 1961, 16, 238–261. [Google Scholar] [CrossRef]
- Yuan, Q.; Williams, R.A.; Biggs, S. Surfactant selection for accurate size control of microcapsules using membrane emulsification. Colloids Surf. A Physicochem. Eng. Asp. 2009, 347, 97–103. [Google Scholar] [CrossRef]
- Sugiura, S.; Nakajima, M.; Iwamoto, S.; Seki, M. Interfacial tension driven monodispersed droplet formation from microfabricated channel array. Langmuir 2001, 17, 5562–5566. [Google Scholar] [CrossRef]
- Metcalf, A.R.; Boyer, H.C.; Dutcher, C.S. Interfacial Tensions of Aged Organic Aerosol Particle Mimics Using a Biphasic Microfluidic Platform. Environ. Sci. Technol. 2016, 50, 1251–1259. [Google Scholar] [CrossRef] [PubMed]

| Symbol | Definition |
|---|---|
| A | Area of the droplet |
| b | Smallest distance of the droplet surface from its center |
| Capillary number | |
| D | Droplet deformation |
| Channel confinement parameter | |
| Strain rate | |
| Continuous phase viscosity | |
| Dispersed phase viscosity | |
| Effective viscosity | |
| Relative viscosity | |
| Droplet interface | |
| h | Channel height |
| l | Largest distance of the droplet surface from its center |
| p | Pressure |
| Velocity potential | |
| Stream function | |
| Flow rate of the continuous phase | |
| Flow rate of the dispersed phase | |
| Initial droplet radius | |
| Interfacial tension | |
| t | Time |
| u | Droplet velocity |
| Depth-averaged velocity of fluid around the droplet | |
| w | Complex potential |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Shen, A.Q. Interfacial Tension Measurements in Microfluidic Quasi-Static Extensional Flows. Micromachines 2021, 12, 272. https://doi.org/10.3390/mi12030272
Lee D, Shen AQ. Interfacial Tension Measurements in Microfluidic Quasi-Static Extensional Flows. Micromachines. 2021; 12(3):272. https://doi.org/10.3390/mi12030272
Chicago/Turabian StyleLee, Doojin, and Amy Q. Shen. 2021. "Interfacial Tension Measurements in Microfluidic Quasi-Static Extensional Flows" Micromachines 12, no. 3: 272. https://doi.org/10.3390/mi12030272






