Cutting Force Prediction Models by FEA and RSM When Machining X56 Steel with Single Diamond Grit
Abstract
:1. Introduction
2. Finite Element Modeling
2.1. The Mechanisms of Diamond Grits Cutting
2.2. Modeling of the Single Diamond Grit
2.3. Modeling of the Cutting Force
3. Response Surface Regression Modeling
3.1. Principle of Tribometer and Experiments
3.2. Response Surface Methodology and Design of Experiment
−0.0306B2 − 0.1671C2 − 0.00260ABC − 0.0391A2B − 0.0041 A2C + 0.0039AB2
4. Confirmation Experiment
5. Conclusions
- Two means were used to obtain the equation of the cutting force. In the first approach, AdvantEdge was used to simulate the cutting process, and the virtual experiment data were applied to fit the empirical equation of the cutting force. In the second one, the regression equation of the cutting force and the corresponding response surface was obtained by Design of Experiments.
- Twelve confirmation experiments were conducted, and the results indicate that both derived models can predict the cutting force with fair accuracy. The prediction errors of the developed models and experimental results vary from −11.7% to 10.02%, which are acceptable in engineering. Additionally, the predicted values of the regression model using FEM were generally lower than the experimental results because graphitization was not included in FEM.
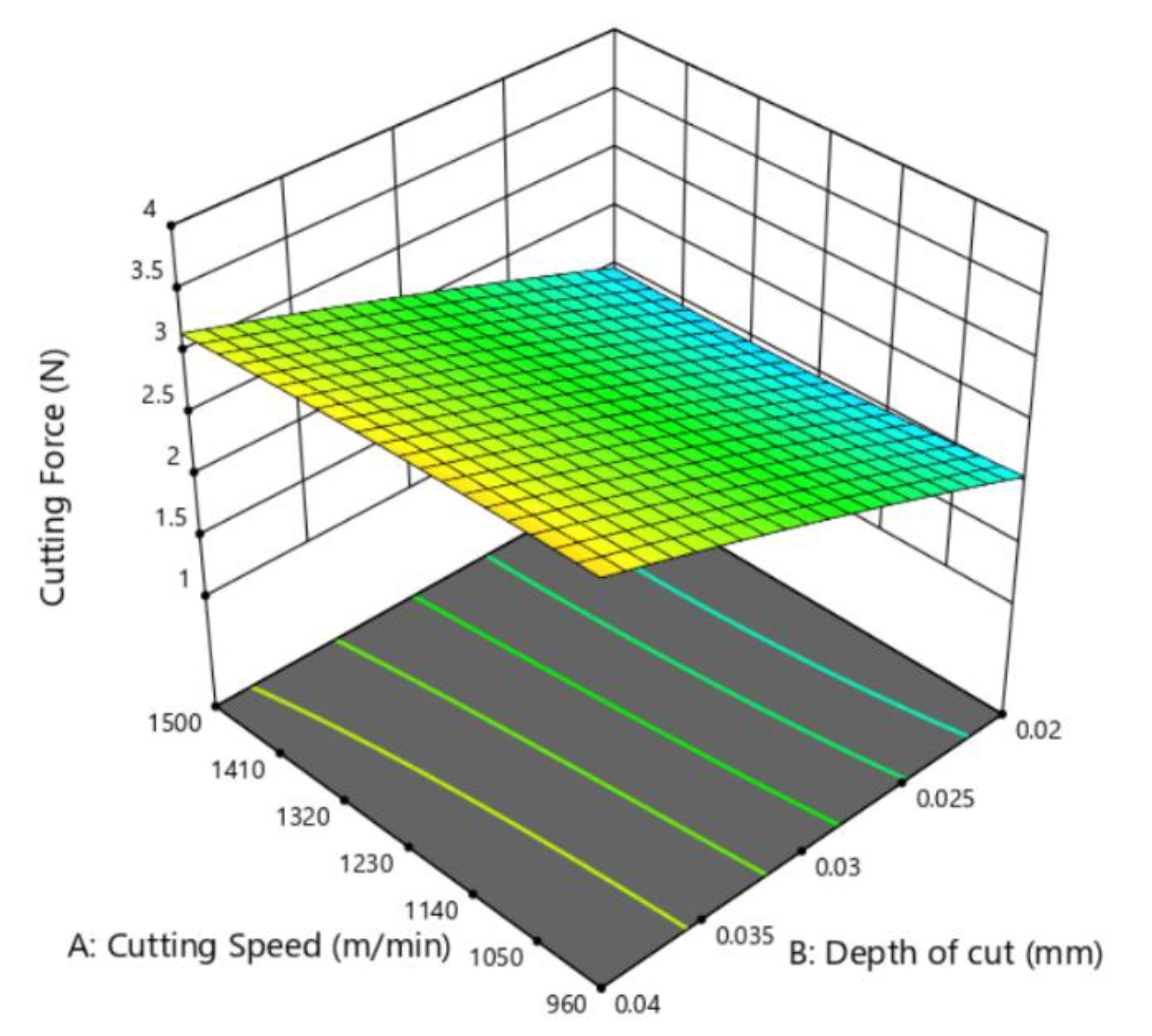
- The results of RSM reveal that with increasing depth of cut and coefficient of friction, cutting force shows an increasing trend. High cutting speed increases cutting efficiency while reducing the coefficient of friction. Hence, the cutting speed needs to be restricted to a specified range. The influence of the depth of the cut is the most significant among the three factors. However, high protrusion contributes to less grit–workpiece contact. Therefore, the protrusion heights of the diamond grits deserve first priority when manufacturing diamond beads that serve different purposes.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Num of Experiment | ν (m/min) | f (mm/r) | µ | F (N) |
|---|---|---|---|---|
| 1 | 960 | 0.01 | 0.1 | 0.9178 |
| 2 | 0.3 | 1.2018 | ||
| 3 | 0.5 | 1.4041 | ||
| 4 | 0.7 | 1.4081 | ||
| 5 | 0.02 | 0.1 | 1.5144 | |
| 6 | 0.3 | 1.9554 | ||
| 7 | 0.5 | 2.3423 | ||
| 8 | 0.7 | 2.3861 | ||
| 9 | 0.03 | 0.1 | 2.0514 | |
| 10 | 0.3 | 2.5581 | ||
| 11 | 0.5 | 3.0224 | ||
| 12 | 0.7 | 3.0845 | ||
| 13 | 0.04 | 0.1 | 2.5614 | |
| 14 | 0.3 | 3.1344 | ||
| 15 | 0.5 | 3.5284 | ||
| 16 | 0.7 | 3.6851 | ||
| 17 | 1140 | 0.01 | 0.1 | 0.8922 |
| 18 | 0.3 | 1.1736 | ||
| 19 | 0.5 | 1.3336 | ||
| 20 | 0.7 | 1.3224 | ||
| 21 | 0.02 | 0.1 | 1.5044 | |
| 22 | 0.3 | 1.9422 | ||
| 23 | 0.5 | 2.2216 | ||
| 24 | 0.7 | 2.2826 | ||
| 25 | 0.03 | 0.1 | 2.0472 | |
| 26 | 0.3 | 2.5521 | ||
| 27 | 0.5 | 2.9478 | ||
| 28 | 0.7 | 3.0292 | ||
| 29 | 0.04 | 0.1 | 2.5468 | |
| 30 | 0.3 | 3.0598 | ||
| 31 | 0.5 | 3.4636 | ||
| 32 | 0.7 | 3.5468 | ||
| 33 | 1320 | 0.01 | 0.1 | 0.8794 |
| 34 | 0.3 | 1.1662 | ||
| 35 | 0.5 | 1.3014 | ||
| 36 | 0.7 | 1.2626 | ||
| 37 | 0.02 | 0.1 | 1.4896 | |
| 38 | 0.3 | 1.9056 | ||
| 39 | 0.5 | 2.2318 | ||
| 40 | 0.7 | 2.2416 | ||
| 41 | 0.03 | 0.1 | 2.0496 | |
| 42 | 0.3 | 2.5364 | ||
| 43 | 0.5 | 2.9374 | ||
| 44 | 0.7 | 2.9072 | ||
| 45 | 0.04 | 0.1 | 2.5484 | |
| 46 | 0.3 | 3.0478 | ||
| 47 | 0.5 | 3.4502 | ||
| 48 | 0.7 | 3.5606 | ||
| 49 | 1500 | 0.01 | 0.1 | 0.8728 |
| 50 | 0.3 | 1.1494 | ||
| 51 | 0.5 | 1.2626 | ||
| 52 | 0.7 | 1.2232 | ||
| 53 | 0.02 | 0.1 | 1.4896 | |
| 54 | 0.3 | 1.8744 | ||
| 55 | 0.5 | 2.1764 | ||
| 56 | 0.7 | 2.2094 | ||
| 57 | 0.03 | 0.1 | 2.0292 | |
| 58 | 0.3 | 2.5174 | ||
| 59 | 0.5 | 2.8846 | ||
| 60 | 0.7 | 2.9058 | ||
| 61 | 0.04 | 0.1 | 2.5443 | |
| 62 | 0.3 | 3.0476 | ||
| 63 | 0.5 | 3.4006 | ||
| 64 | 0.7 | 3.5346 |
References
- Bai, Y.; Bai, Q. Risk Analysis for Subsea Pipelines. In Subsea Pipeline Integrity and Risk Management, 1st ed.; Gulf Professional Publishing: Oxford, UK, 2014; pp. 169–212. [Google Scholar]
- Maeda, H.; Takanabe, R.; Takeda, A.; Matsuda, S.; Kato, T. High-Speed Slicing of SiC Ingot by High-Speed Multi Wire Saw. Mater. Sci. Forum. 2014, 778, 771–775. [Google Scholar] [CrossRef]
- Cao, L.; Meng, Q.; Wang, L.; Tong, W. Research on Underwater Diamond Wire Saw. In Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1695–1700. [Google Scholar]
- Wang, Z.; Zhang, B.; Wang, L.Q.; Xu, D. Research on Experimentation of Diamond Wire Saw Cutting Compound Pipes Underwater. Mater. Sci. Forum. 2009, 626, 303–308. [Google Scholar] [CrossRef]
- Horita, Z.; Xiao, B.; Fu, Y.; Su, H.; Xu, J.; Xu, H. Machining Performance of Brazed Diamond Wire Saw with Optimum Grain Distribution. Key. Eng. Mat. 2006, 304, 43–47. [Google Scholar] [CrossRef]
- Ge, P.Q.; Gao, Y.F.; Li, S.J.; Hou, Z.J. Study on Electroplated Diamond Wire Saw Development and Wire Saw Wear Analysis. Key. Eng. Mat. 2009, 416, 311–315. [Google Scholar] [CrossRef]
- Huang, G.Q.; Xu, X.P. Analysis of the Breakage of Diamond Wire Saws in Sawing of Stone. Key. Eng. Mat. 2006, 4, 123–126. [Google Scholar] [CrossRef]
- Maity, K.P.; Das, N.S. A class of slipline field solutions for metal machining with slipping and sticking contact at the chip-tool interface. J. Mech. Sci. 2001, 43, 2435–2452. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Bouguecha, A.; Hadifi, T.; Mielke, J. Advanced friction modeling for bulk metal forming processes. Prod. Eng. 2011, 5, 621–627. [Google Scholar] [CrossRef]
- Schulze, V.; Michna, J.; Schneider, J.; Gumbsch, P. Modelling of cutting induced surface phase transformations considering friction effects. Proc. Eng. 2011, 19, 331–336. [Google Scholar] [CrossRef]
- Özel, T.; Zeren, E. A Methodology to Determine Work Material Flow Stress and Tool-Chip Interfacial Friction Properties by Using Analysis of Machining. J. Manufac. Sci. Eng. Trans. ASME 2006, 128, 119–129. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rahman, M.; Mia, M.; Gupta, M.K.; Sen, B.; Ahmed, A. Investigation of the specific cutting energy and its effect in shearing dominant precision micro cutting. J. Mater. Process. Tech. 2020, 283, 116688. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; He, N. Investigation on the burr formation mechanism in micro cutting. Precis. Eng. 2017, 47, 191–196. [Google Scholar] [CrossRef]
- Woon, K.S.; Rahman, M. Extrusion-like chip formation mechanism and its role in suppressing void nucleation. CIRP Annals 2010, 59, 129–132. [Google Scholar] [CrossRef]
- Rahman, M.; Rahman, M.; Anantharajan, S.K. Material perspective on the evolution of micro- and nano-scale cutting of metal alloys. J. Micromanuf. 2018, 1. [Google Scholar] [CrossRef]
- Rahman, M.A.; Woon, K.S.; Venkatesh, V.C.; Rahman, M. Modelling of the combined microstructural and cutting edge effects in ultraprecision machining. CIRP Ann. 2018, 67, 129–132. [Google Scholar] [CrossRef]
- Rahman, M.A.; Amrun, M.R.; Rahman, M.; Kumar, A.S. Variation of surface generation mechanisms in ultra-precision machining due to relative tool sharpness (RTS) and material properties. Int. J. Mach. Tool. Manu. 2017, 115, 15–28. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rahman, M.; Kumar, A.S. Modelling of flow stress by correlating the material grain size and chip thickness in ultra-precision machining. Int. J. Mach. Tool. Manu. 2017, 123, 57–75. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Liu, M.; Liu, M.; Wang, L. Research on the influence of cutting parameters on chips in the process of diamond bead cutting pipeline steel. Diam. Relat. Mater. 2021, 111, 108220. [Google Scholar] [CrossRef]
- Markopoulos, A.P. Application of FEM in Metal Cutting. In Finite Element Method in Machining Processes, 1st ed.; Markopoulos, A.P., Ed.; Springer: London, UK, 2013; pp. 59–69. [Google Scholar]
- Umbrello, D. Finite element simulation of conventional and high speed machining of Ti6Al4V alloy. J. Mater. Process. Tech. 2008, 196, 79–87. [Google Scholar] [CrossRef]
- Bil, H.; Kılıç, S.E.; Tekkaya, A.E. A comparison of orthogonal cutting data from experiments with three different finite element models. Int. J. Mach. Tool. Manu. 2004, 44, 933–944. [Google Scholar] [CrossRef]
- Yen, Y.-C.; Söhner, J.; Lilly, B.; Altan, T. Estimation of tool wear in orthogonal cutting using the finite element analysis. J. Mater. Process. Tech. 2004, 146, 82–91. [Google Scholar] [CrossRef]
- Pramanik, A.; Zhang, L.C.; Arsecularatne, J.A. An FEM investigation into the behavior of metal matrix composites: Tool–particle interaction during orthogonal cutting. Int. J. Mach. Tool. Manu. 2007, 47, 1497–1506. [Google Scholar] [CrossRef]
- Gonzalo, O.; Jauregi, H.; Uriarte, L.G.; López de Lacalle, L.N. Prediction of specific force coefficients from a FEM cutting model. Int. J. Adv. Manuf. Tech. 2008, 43, 348. [Google Scholar] [CrossRef]
- Jeyakumar, S.; Marimuthu, K.; Ramachandran, T. Prediction of cutting force, tool wear and surface roughness of Al6061/SiC composite for end milling operations using RSM. J. Mech. Sci. Technol. 2013, 27, 2813–2822. [Google Scholar] [CrossRef]
- Kathiravan, S.; Sathees, T. Application of RSM in the optimization of cutting conditions in metal matrix composites. Int. J. App. Eng. 2015, 10, 11018–11022. [Google Scholar]
- Kadirgama, K.; Abou-El-Hossein, K.; Mohammad, B.; Al-Ani, H.; Noor, M.M. Cutting force prediction model by FEA and RSM when machining Hastelloy C-22HS with 90° holder. J. Sci. Ind. Res. India 2008, 67, 421–427. [Google Scholar]
- Setia, S. Comparative analysis and optimization of FEM and RSM based regression model with experimental results for the dry turning of SiCp- Al7075 composite. Silicon 2020. [Google Scholar] [CrossRef]
- Sartkulvanich, P.; Altan, T.; Göcmen, A. Effects of flow stress abd friction models in finite element simulation of orthigonal cutting. Mach. Sci. Tech. 2005, 9, 1–26. [Google Scholar] [CrossRef]
- Wang, J.; Ye, R.; Tang, Y.; Bin, H. 3D dynamic finite element simulation analysis of single abrasive grain during surface grinding. Diam. Abras. Eng. 2009, 173, 41–45. [Google Scholar]
- Franchi, R.; del Prete, A.; Umbrello, D.; Mariano, E. Inverse analysis procedure to determine flow stress and friction data for metal cutting Finite Element Modeling. Key Eng. Mat. 2015, 651, 1345–1350. [Google Scholar] [CrossRef]
- Kwiatkowska, E.; Niesłony, P.; Grzesik, W. The numerical investigation of stress distribution on the rake face for grooved cutting tool inserts. Adv. Mater. Res. 2011, 223, 304–313. [Google Scholar] [CrossRef]
- Knight, W.A.; Boothroyd, G. Fundamentals of Metal Machining and Machine Tools, 3rd ed.; I K International Publishing House Pvt. Ltd.: New Delhi, India, 2019. [Google Scholar]
- Xu, X.P.; Zhang, G.Q.; Huang, H. Face Grinding of Granite with Brazed Diamond Grits. Key Eng. Mater. 2004, 259, 26–32. [Google Scholar] [CrossRef]
- Sterle, L.; Pušavec, F.; Kalin, M. Determination of Friction Coefficient in Cutting Processes: Comparison between Open and Closed Tribometers-Sciencedirect. Procedia CIRP 2019, 82, 101–106. [Google Scholar] [CrossRef]
- Cao, L. Research on Cutting Technology of Underwater Diamond Wire Saw. In Proceedings of the 2008 IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; pp. 2751–2756. [Google Scholar]




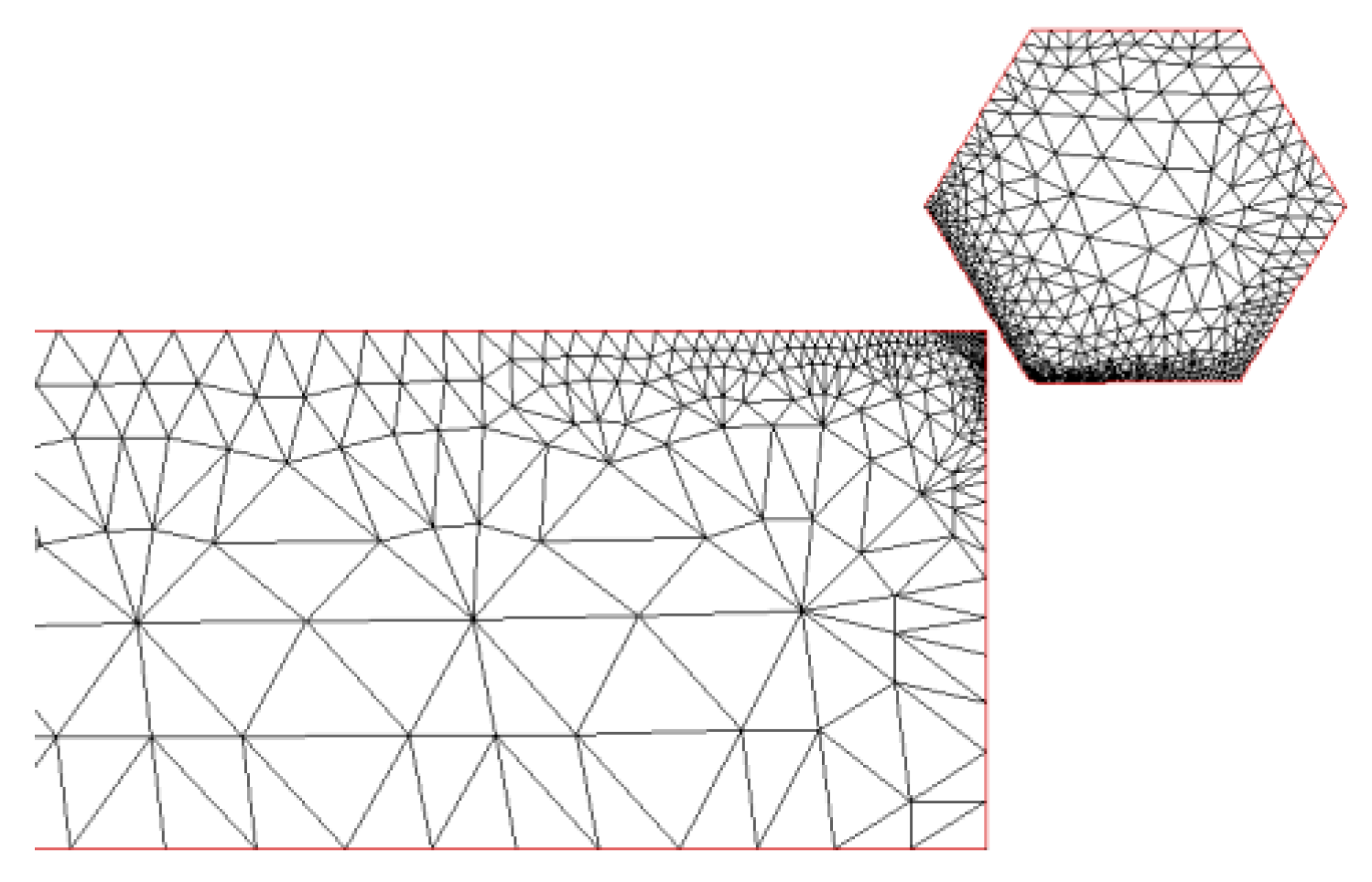
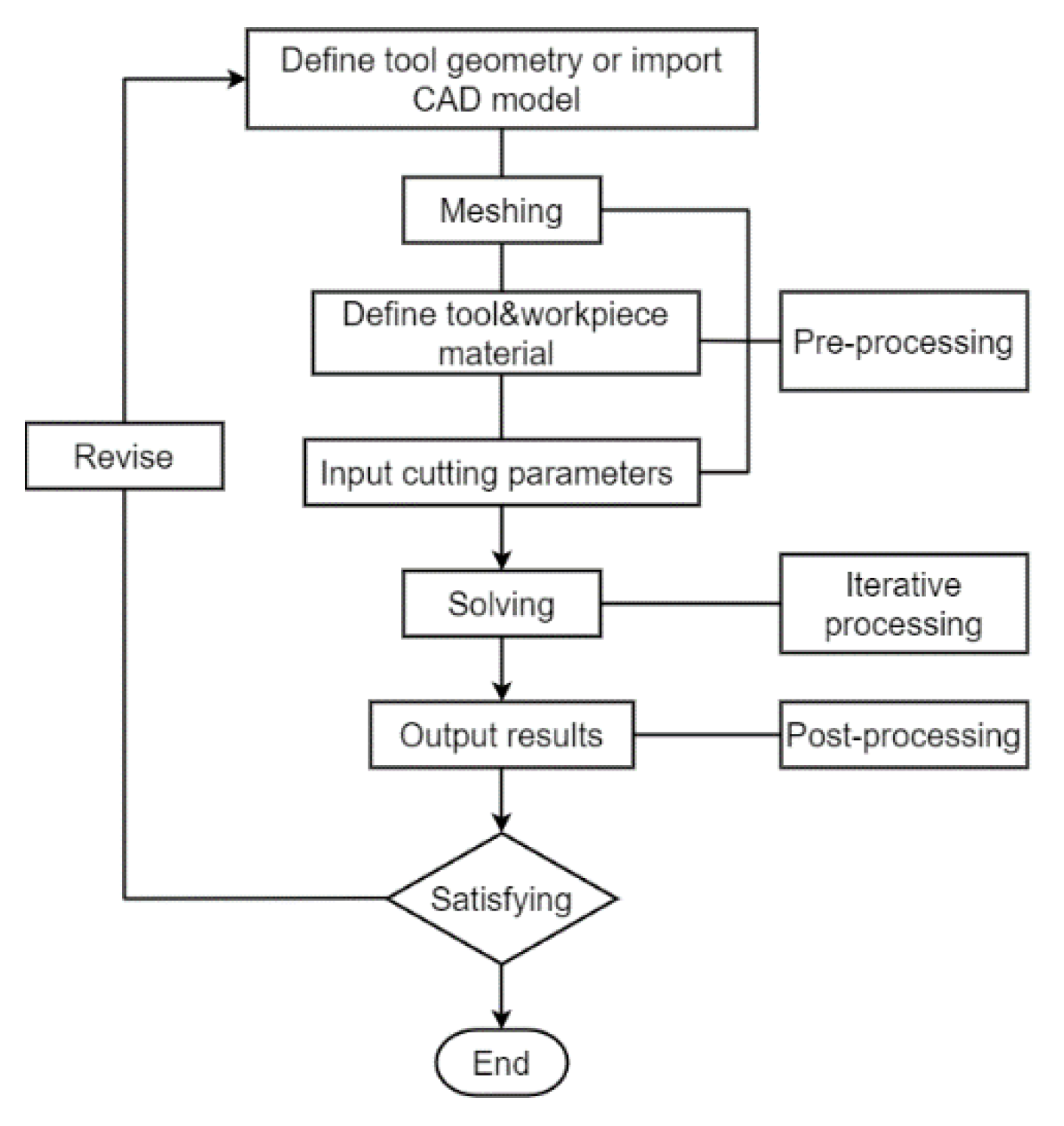
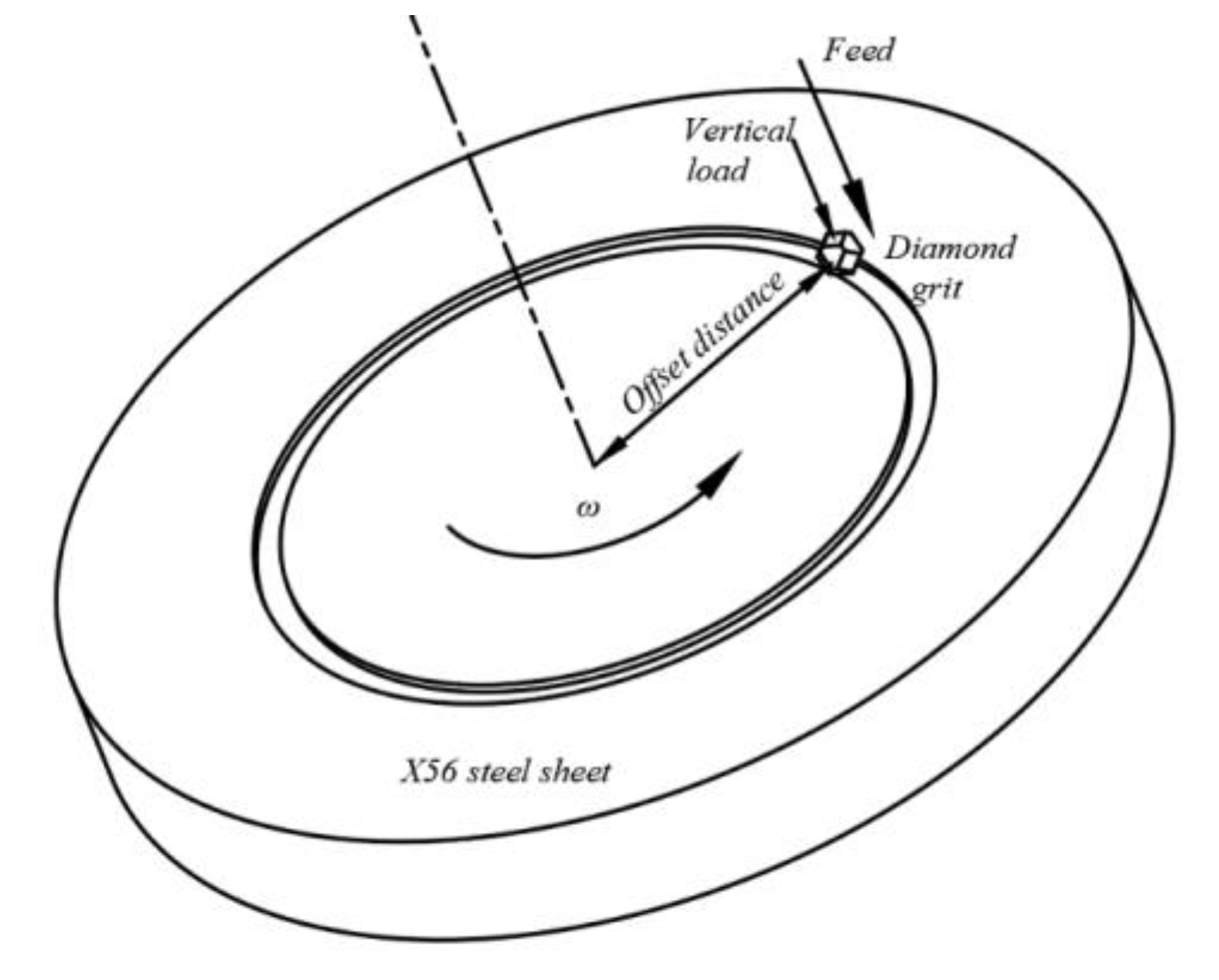


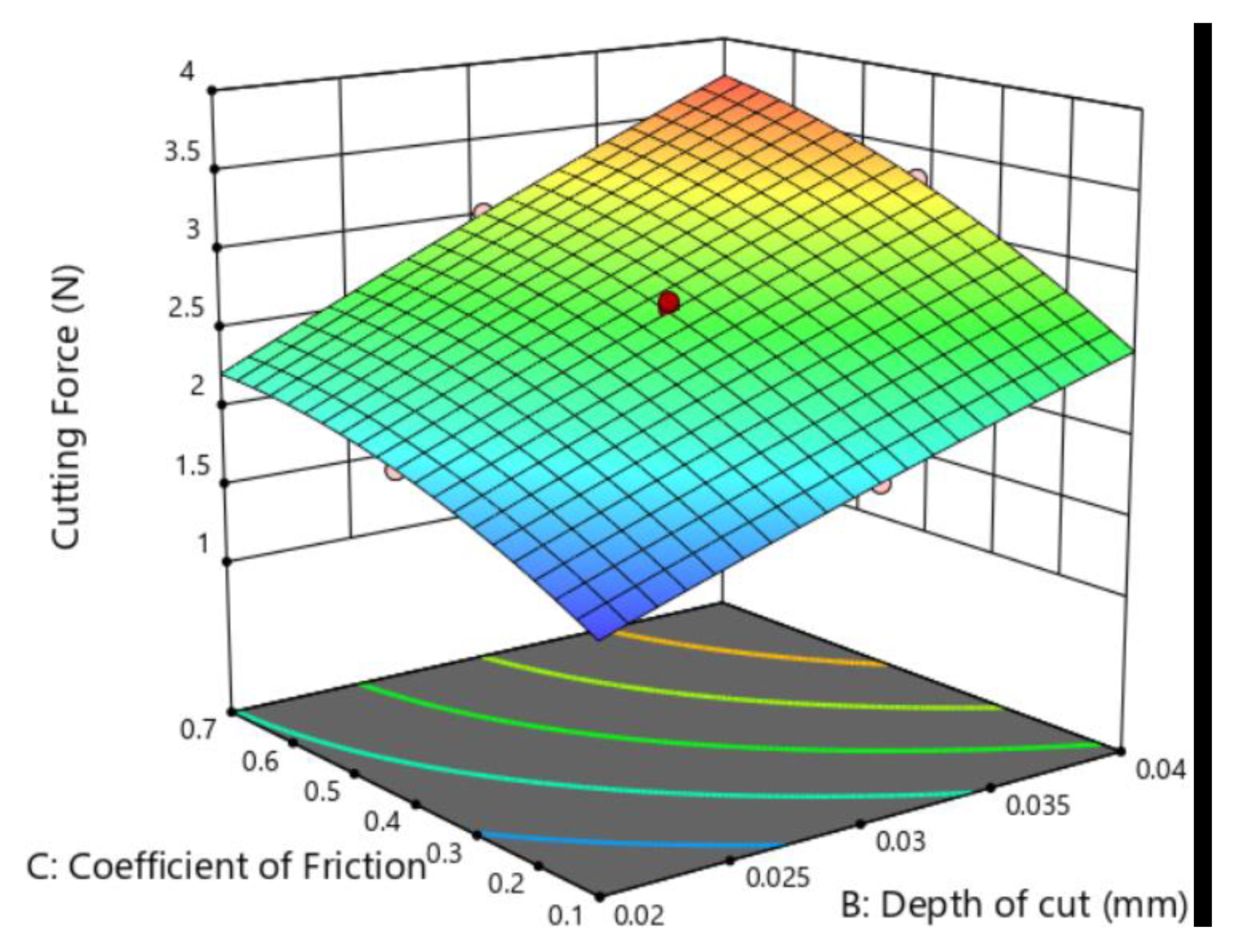
| Levels Parameters | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Cutting speed (m/min) | 960 | 1140 | 1320 | 1500 |
| Depth of cut (mm) | 0.01 | 0.02 | 0.03 | 0.04 |
| Coefficient of friction | 0.1 | 0.3 | 0.5 | 0.7 |
| Parameters | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Cutting Speed (m/min) | 960 | 1230 | 1500 |
| Depth of Cut (mm) | 0.02 | 0.03 | 0.04 |
| Coefficient of Friction | 0.1 | 0.4 | 0.7 |
| Run Order | Cutting Speed (m/min) | Depth of Cut (mm) | Coefficient of Friction | Cutting Force (N) |
|---|---|---|---|---|
| 1 | 1230 | 0.03 | 0.4 | 2.791 |
| 2 | 1230 | 0.03 | 0.1 | 2.134 |
| 3 | 1500 | 0.04 | 0.1 | 2.55 |
| 4 | 1230 | 0.02 | 0.4 | 2.114 |
| 5 | 960 | 0.02 | 0.1 | 1.66 |
| 6 | 960 | 0.04 | 0.7 | 3.892 |
| 7 | 1230 | 0.03 | 0.4 | 2.791 |
| 8 | 1500 | 0.02 | 0.1 | 1.593 |
| 9 | 960 | 0.04 | 0.1 | 2.659 |
| 10 | 960 | 0.02 | 0.7 | 2.411 |
| 11 | 1230 | 0.03 | 0.4 | 2.791 |
| 12 | 1500 | 0.02 | 0.7 | 2.312 |
| 13 | 1230 | 0.03 | 0.7 | 3.113 |
| 14 | 1230 | 0.03 | 0.4 | 2.79 |
| 15 | 1230 | 0.03 | 0.4 | 2.792 |
| 16 | 1230 | 0.03 | 0.4 | 2.789 |
| 17 | 960 | 0.03 | 0.4 | 2.857 |
| 18 | 1500 | 0.03 | 0.4 | 2.74 |
| 19 | 1500 | 0.04 | 0.7 | 3.73 |
| 20 | 1230 | 0.04 | 0.4 | 3.406 |
| Source | Sum of Squares | DOF | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 6.46 | 13 | 0.4965 | 5.566 | <0.0001 | Significant |
| A-Cutting Speed | 0.0068 | 1 | 0.0068 | 7672.82 | <0.0001 | - |
| B-Depth of cut | 0.8346 | 1 | 0.8346 | 9.356 | <0.0001 | |
| C-Coefficient of Friction | 0.4792 | 1 | 0.4792 | 5.372 | <0.0001 | |
| AB | 0.0014 | 1 | 0.0014 | 1544.90 | <0.0001 | |
| AC | 0.0009 | 1 | 0.0009 | 1012.42 | <0.0001 | |
| BC | 0.1112 | 1 | 0.1112 | 1.246 | <0.0001 | |
| A2 | 0.0002 | 1 | 0.0002 | 192.84 | <0.0001 | |
| B2 | 0.0026 | 1 | 0.0026 | 2884.90 | <0.0001 | |
| C2 | 0.0768 | 1 | 0.0768 | 86069.91 | <0.0001 | |
| ABC | 0.0001 | 1 | 0.0001 | 61.80 | 0.0002 | |
| A2B | 0.0024 | 1 | 0.0024 | 2745.63 | <0.0001 | |
| A2C | 0.0000 | 1 | 0.0000 | 30.52 | 0.0015 | |
| AB2 | 0.0000 | 1 | 0.0000 | 26.93 | 0.0020 | |
| AC2 | 0.0000 | 0 | - | - | - | |
| B2C | 0.0000 | 0 | ||||
| BC2 | 0.0000 | 0 | ||||
| A3 | 0.0000 | 0 | ||||
| B3 | 0.0000 | 0 | ||||
| C3 | 0.0000 | 0 | ||||
| Residual | 5.352 | 6 | 8.920 | |||
| Lack of Fit | 1.894 | 1 | 1.894 | 0.0178 | 0.8992 | Not significant |
| Pure Error | 5.333 | 5 | 1.067 | - | - | - |
| Cor Total | 6.46 | 19 | - |
| Numbers of Experiments | Cutting Speed (m/min) | Depth of Cut (mm) | Coefficient of Friction | Cutting Force (N) | RSM Results | Error% | FEM Results | Error% |
|---|---|---|---|---|---|---|---|---|
| 1 | 1300 | 0.02 | 0.5 | 1.796 | 1.996 | 10.02 | 2.096 | −11.7 |
| 2 | 1000 | 0.03 | 0.21 | 2.211 | 2.102 | 5.19 | 2.411 | −8.3 |
| 3 | 1100 | 0.04 | 0.51 | 3.11 | 2.83 | 9.89 | 3.51 | −11.4 |
| 4 | 1500 | 0.02 | 0.52 | 1.983 | 2.203 | −9.99 | 2.083 | −6.9 |
| 5 | 1150 | 0.03 | 0.48 | 2.611 | 2.761 | −5.43 | 2.811 | −7.11 |
| 6 | 1240 | 0.04 | 0.37 | 3.001 | 2.801 | 7.14 | 3.251 | −7.69 |
| 7 | 1340 | 0.02 | 0.61 | 1.825 | 1.985 | −8.06 | 1.675 | −8.96 |
| 8 | 980 | 0.03 | 0.4 | 2.602 | 2.5 | 4.08 | 2.752 | −6.81 |
| 9 | 1280 | 0.04 | 0.31 | 2.927 | 2.777 | 5.4 | 3.127 | −6.4 |
| 10 | 1160 | 0.02 | 0.49 | 1.961 | 1.83 | 7.16 | 2.111 | −7.11 |
| 11 | 1400 | 0.03 | 0.2 | 2.11 | 2.311 | −8.7 | 2.31 | −8.66 |
| 12 | 1340 | 0.04 | 0.35 | 2.891 | 3.191 | −9.4 | 3.105 | −9.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Sha, X.; Liu, M.; Wang, L.; Pang, Y. Cutting Force Prediction Models by FEA and RSM When Machining X56 Steel with Single Diamond Grit. Micromachines 2021, 12, 326. https://doi.org/10.3390/mi12030326
Zhang L, Sha X, Liu M, Wang L, Pang Y. Cutting Force Prediction Models by FEA and RSM When Machining X56 Steel with Single Diamond Grit. Micromachines. 2021; 12(3):326. https://doi.org/10.3390/mi12030326
Chicago/Turabian StyleZhang, Lan, Xianbin Sha, Ming Liu, Liquan Wang, and Yongyin Pang. 2021. "Cutting Force Prediction Models by FEA and RSM When Machining X56 Steel with Single Diamond Grit" Micromachines 12, no. 3: 326. https://doi.org/10.3390/mi12030326
APA StyleZhang, L., Sha, X., Liu, M., Wang, L., & Pang, Y. (2021). Cutting Force Prediction Models by FEA and RSM When Machining X56 Steel with Single Diamond Grit. Micromachines, 12(3), 326. https://doi.org/10.3390/mi12030326






