Optical-Trapping Laser Techniques for Characterizing Airborne Aerosol Particles and Its Application in Chemical Aerosol Study
Abstract
:1. Introduction
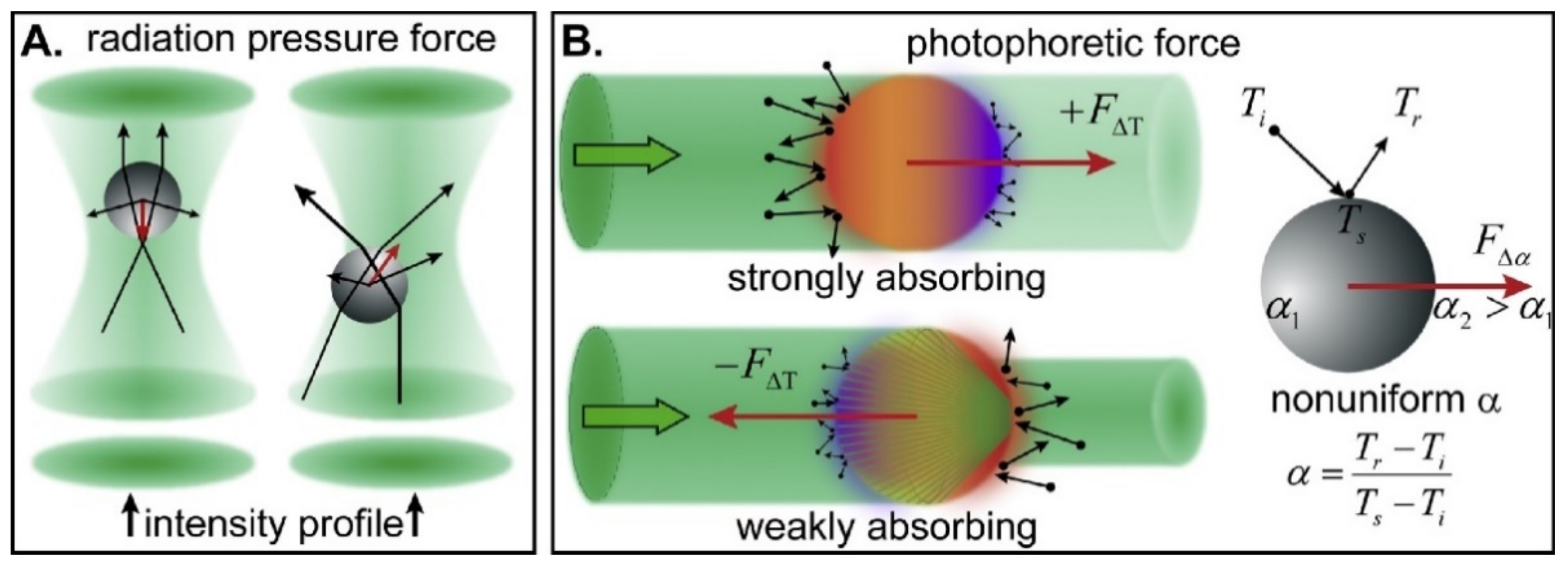
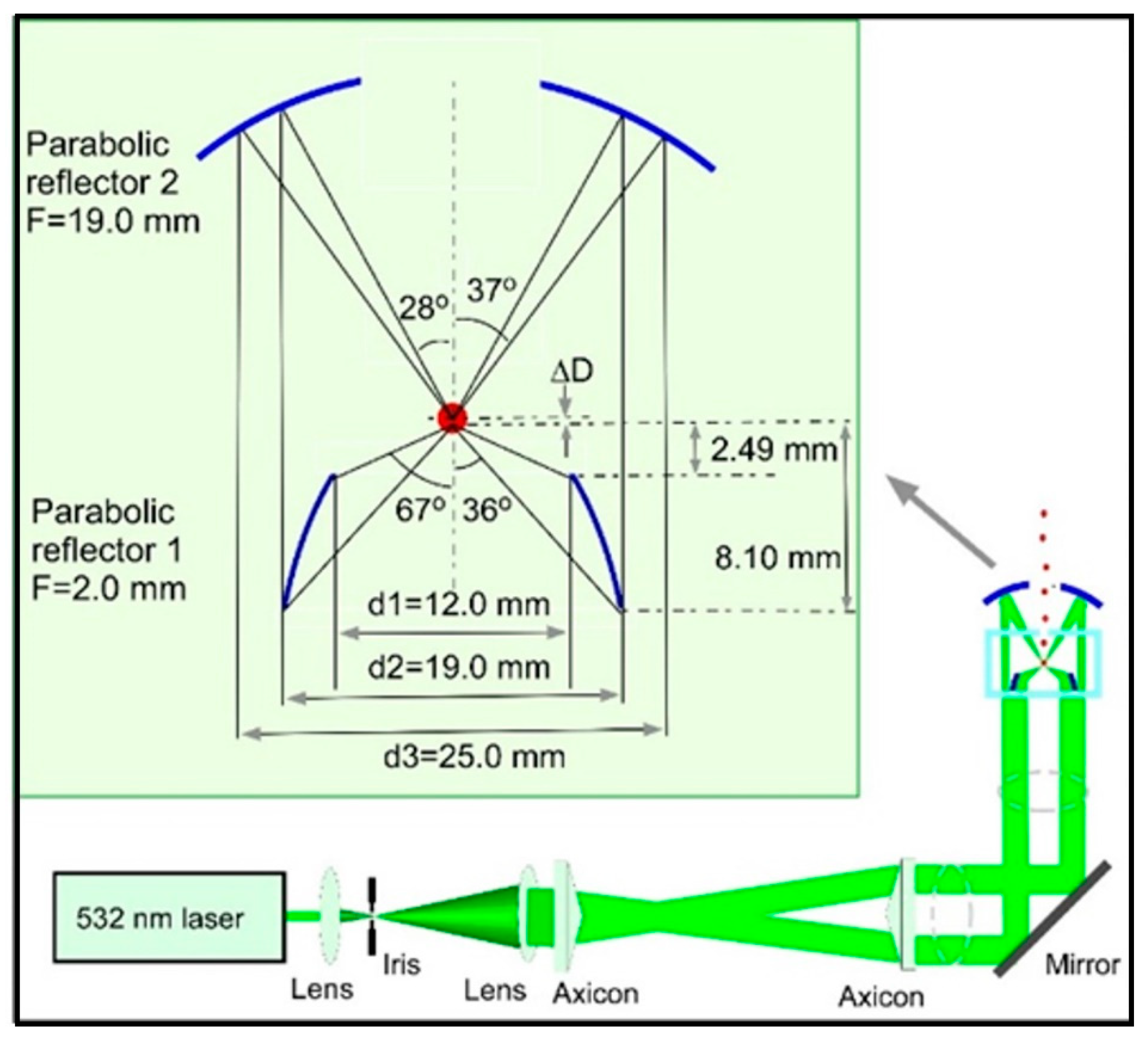
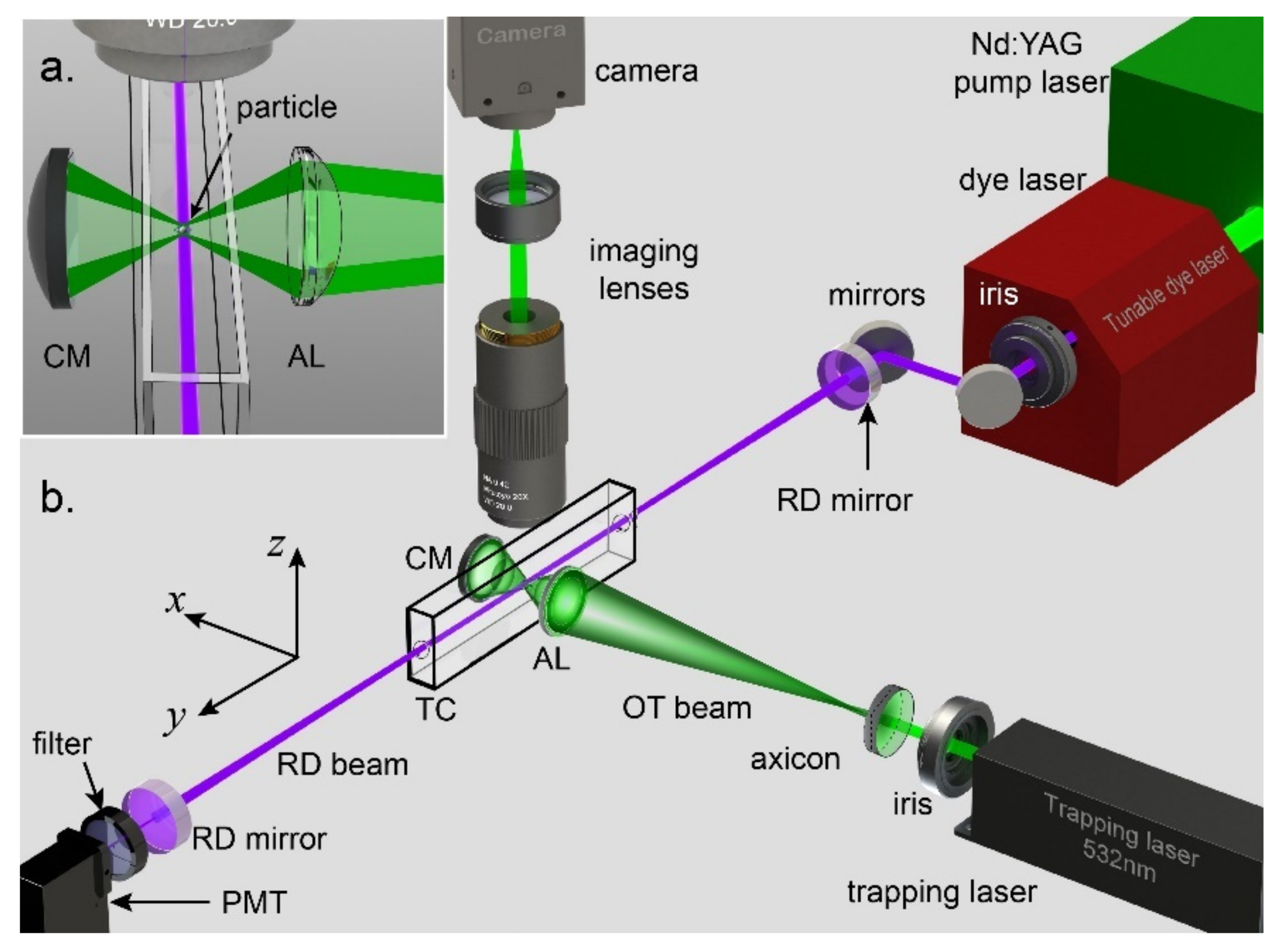
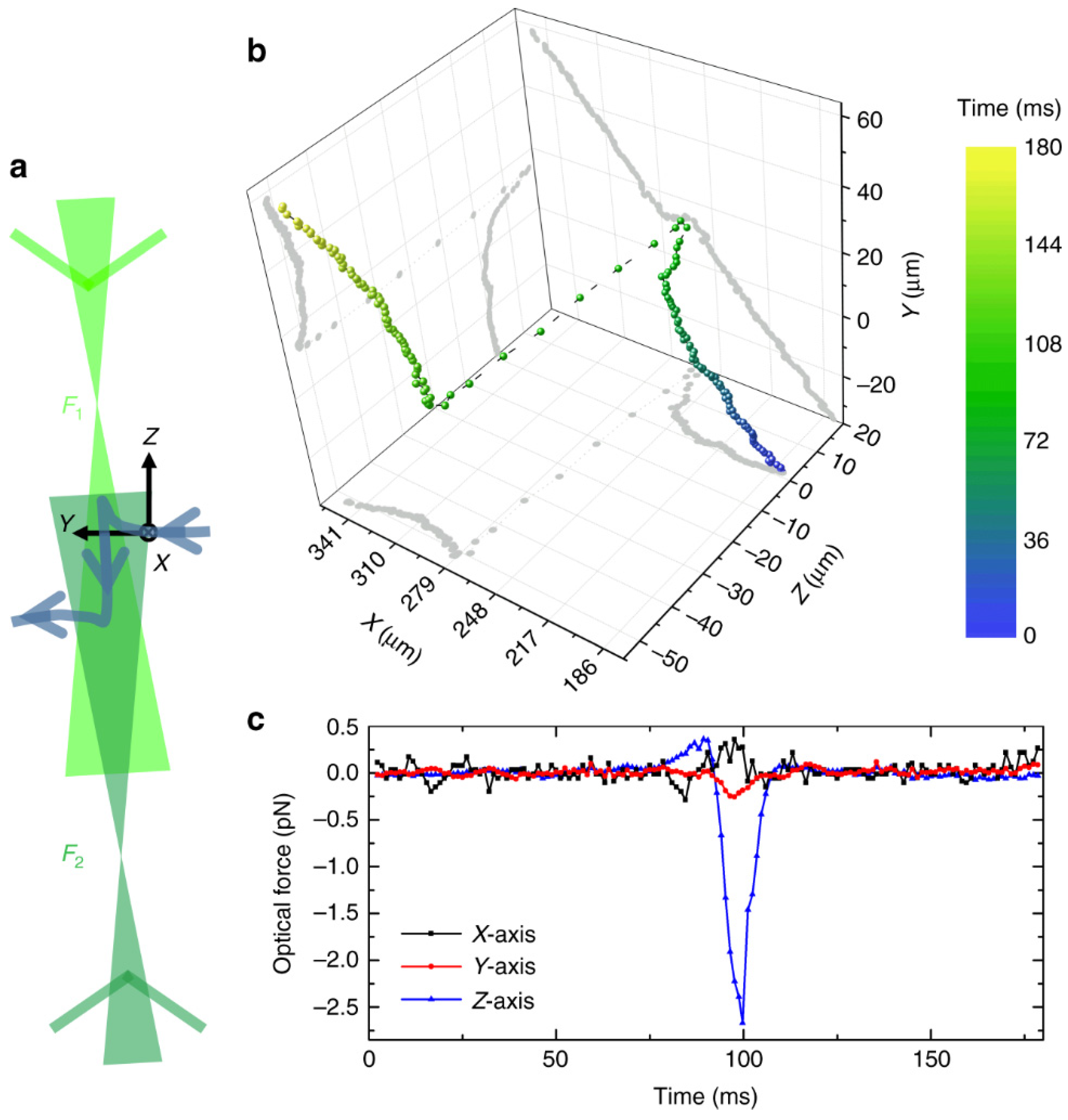
2. Single-Particle Optical Trapping
3. Single-Particle Laser-Based Characterization
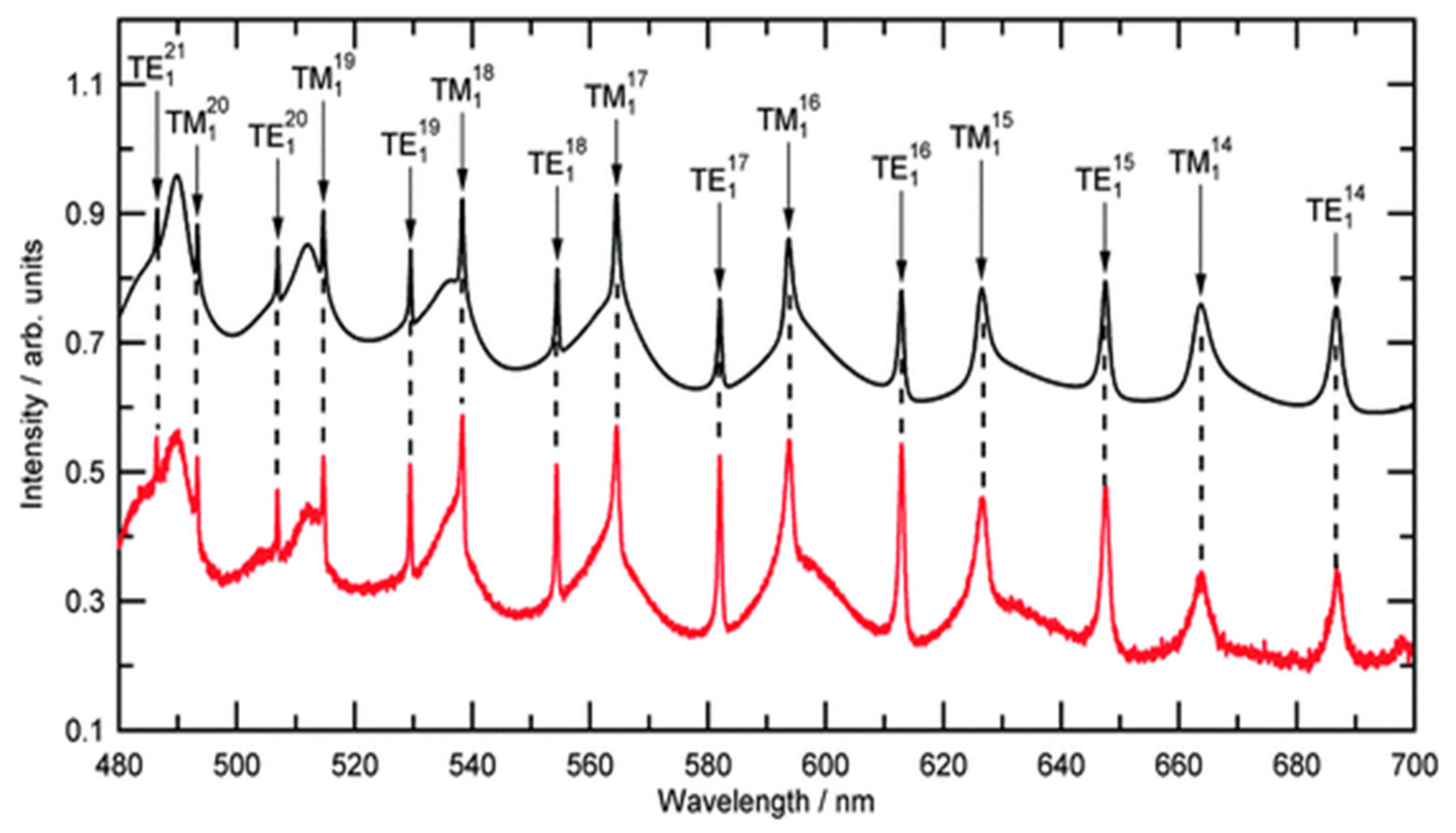
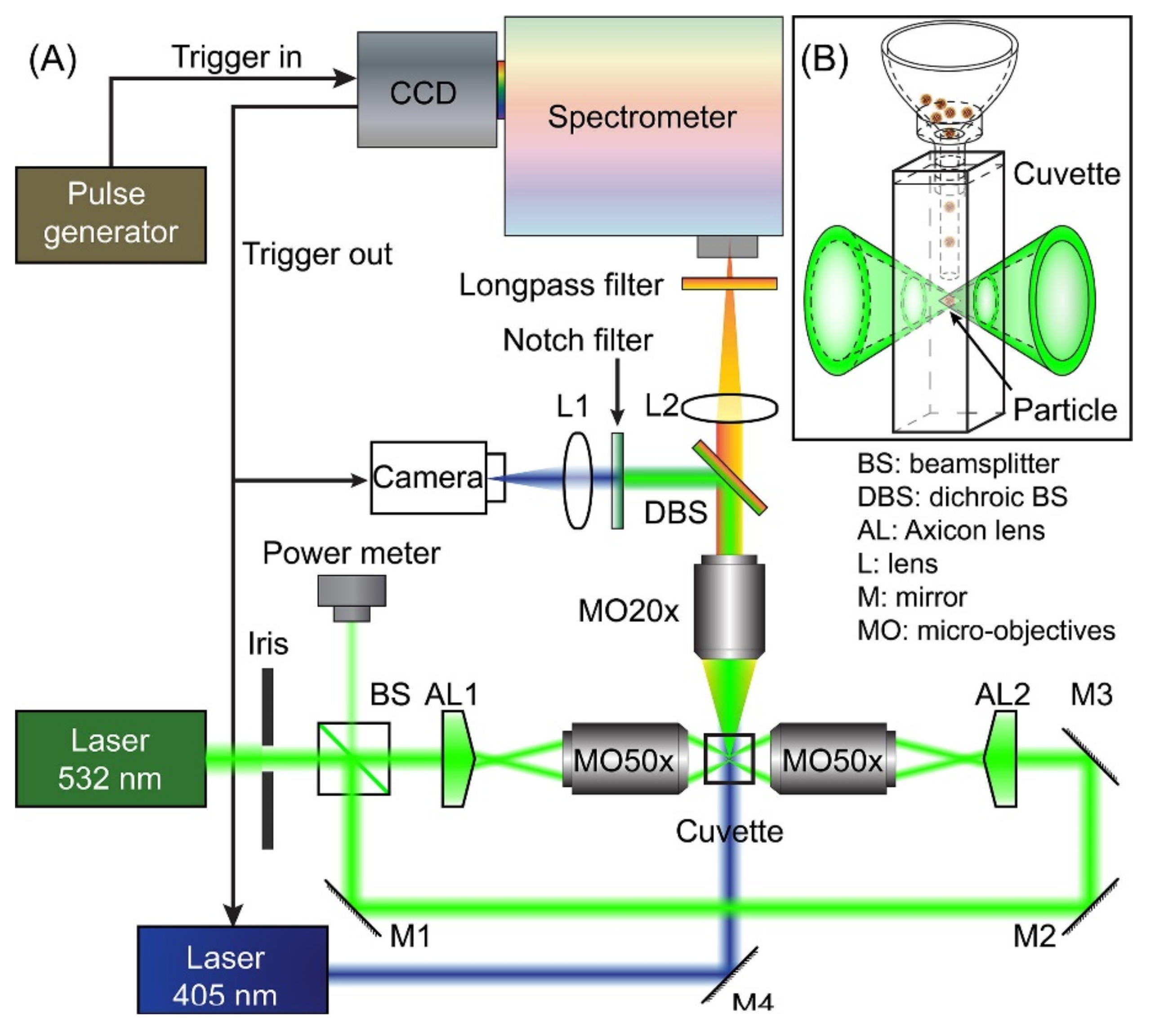
3.1. Elastic Light Scattering (ELS) Characterization
3.2. Light Absorption Spectroscopy
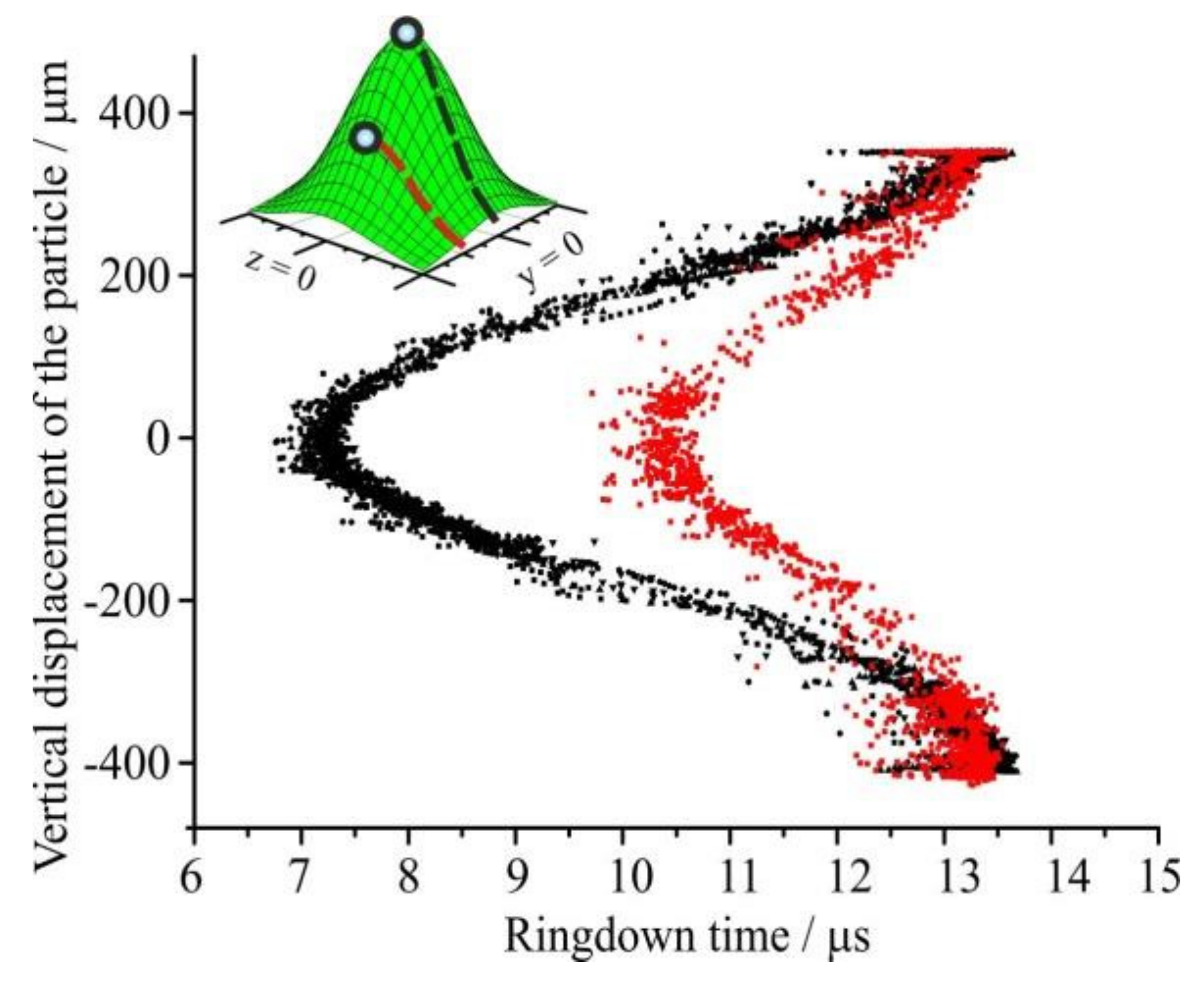
3.2.1. Cavity Ringdown Spectroscopy (CRDS)
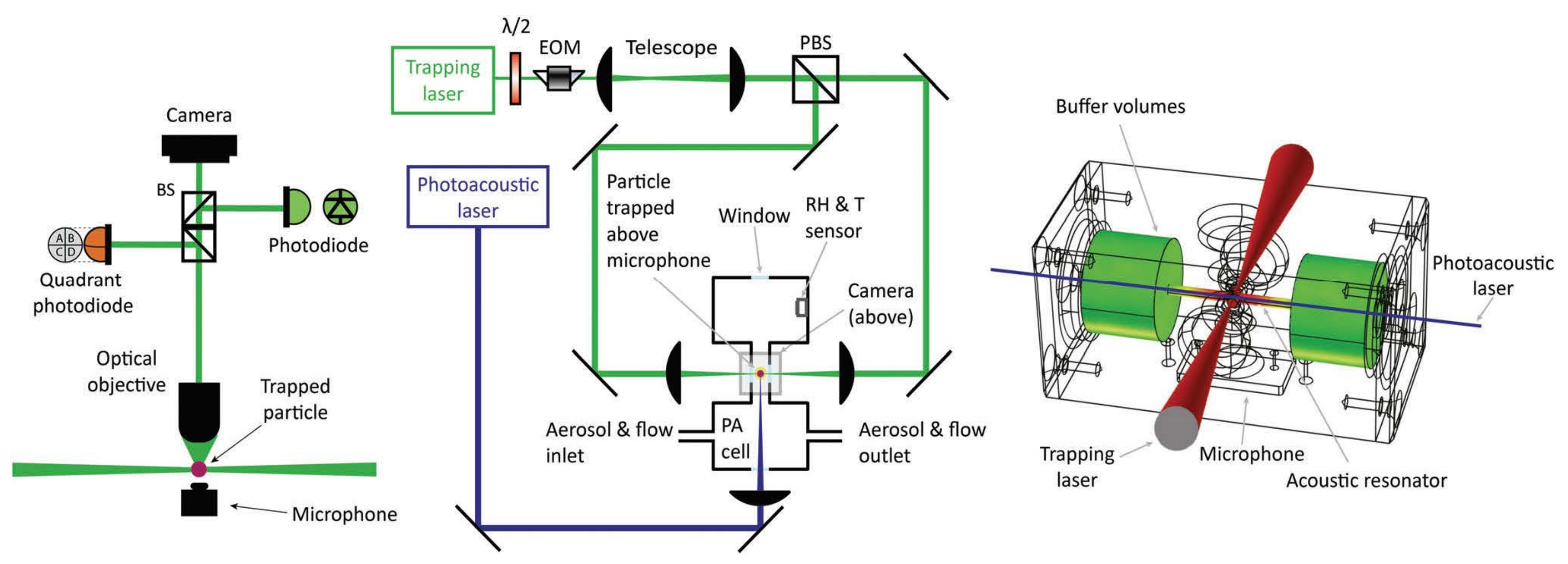
3.2.2. Photoacoustic Spectroscopy
3.3. Inelastic Light Scattering—Light Emission Spectroscopy
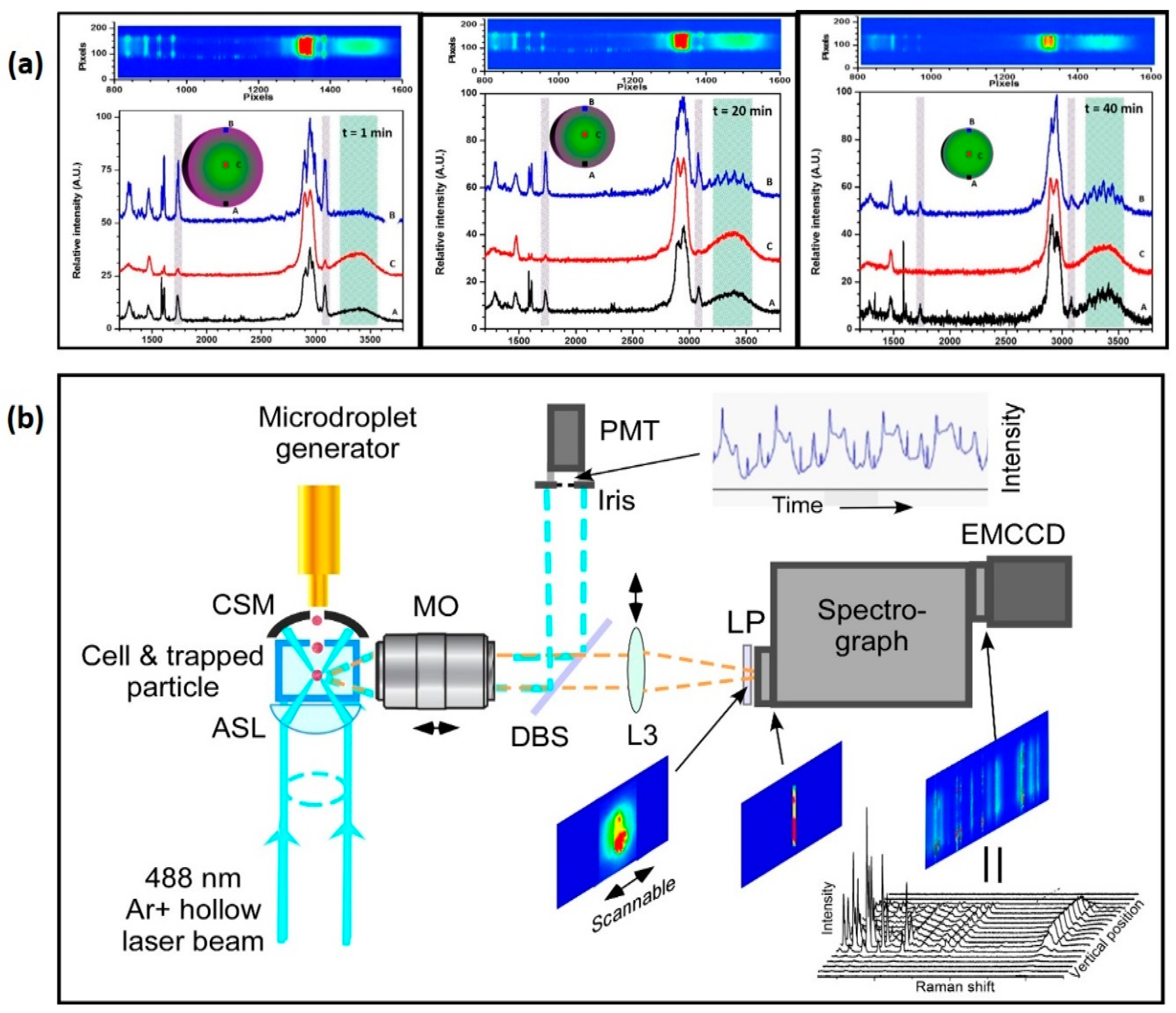
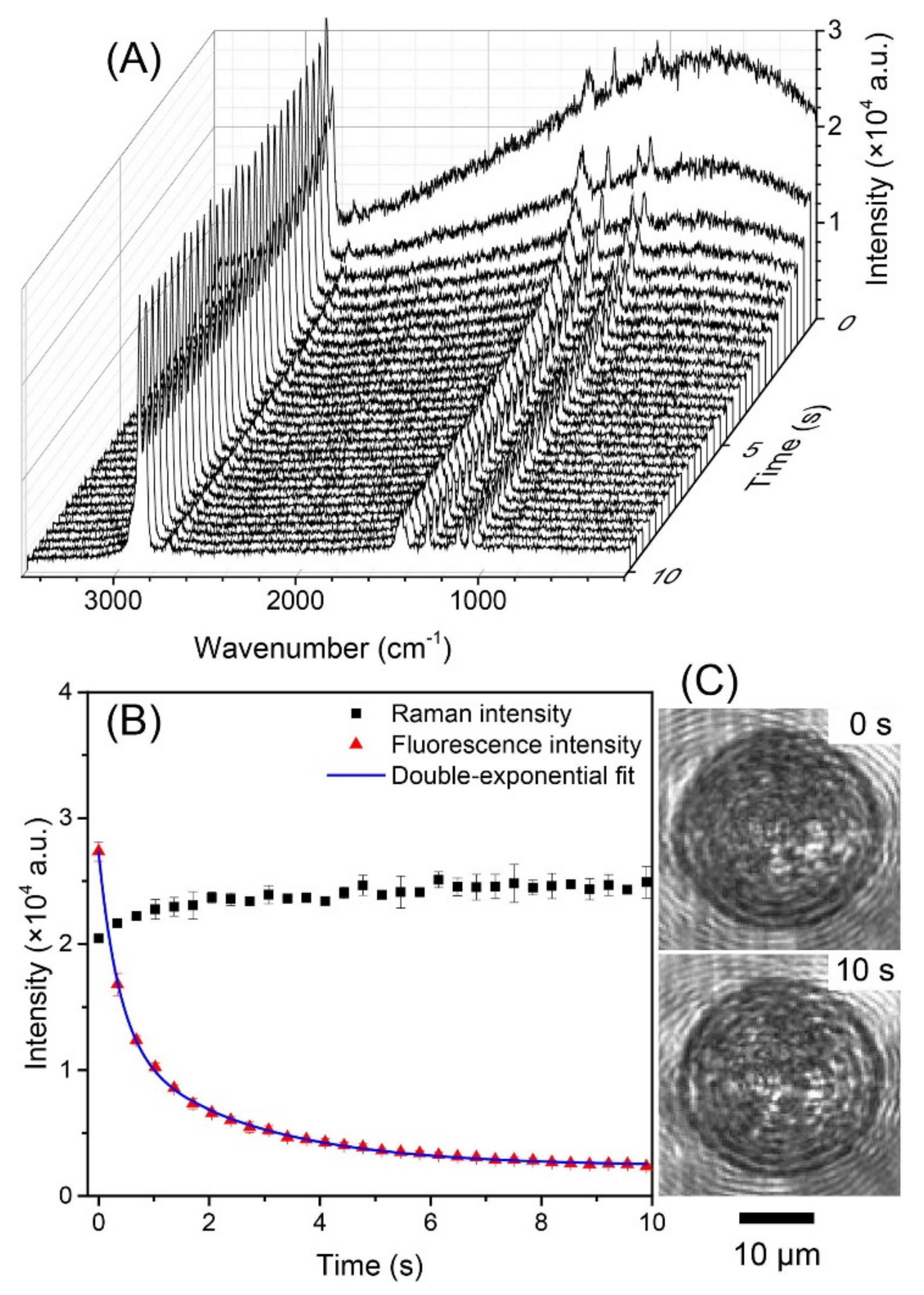
3.3.1. Raman Spectroscopy
3.3.2. Laser-Induced Fluorescence (LIF) Spectroscopy
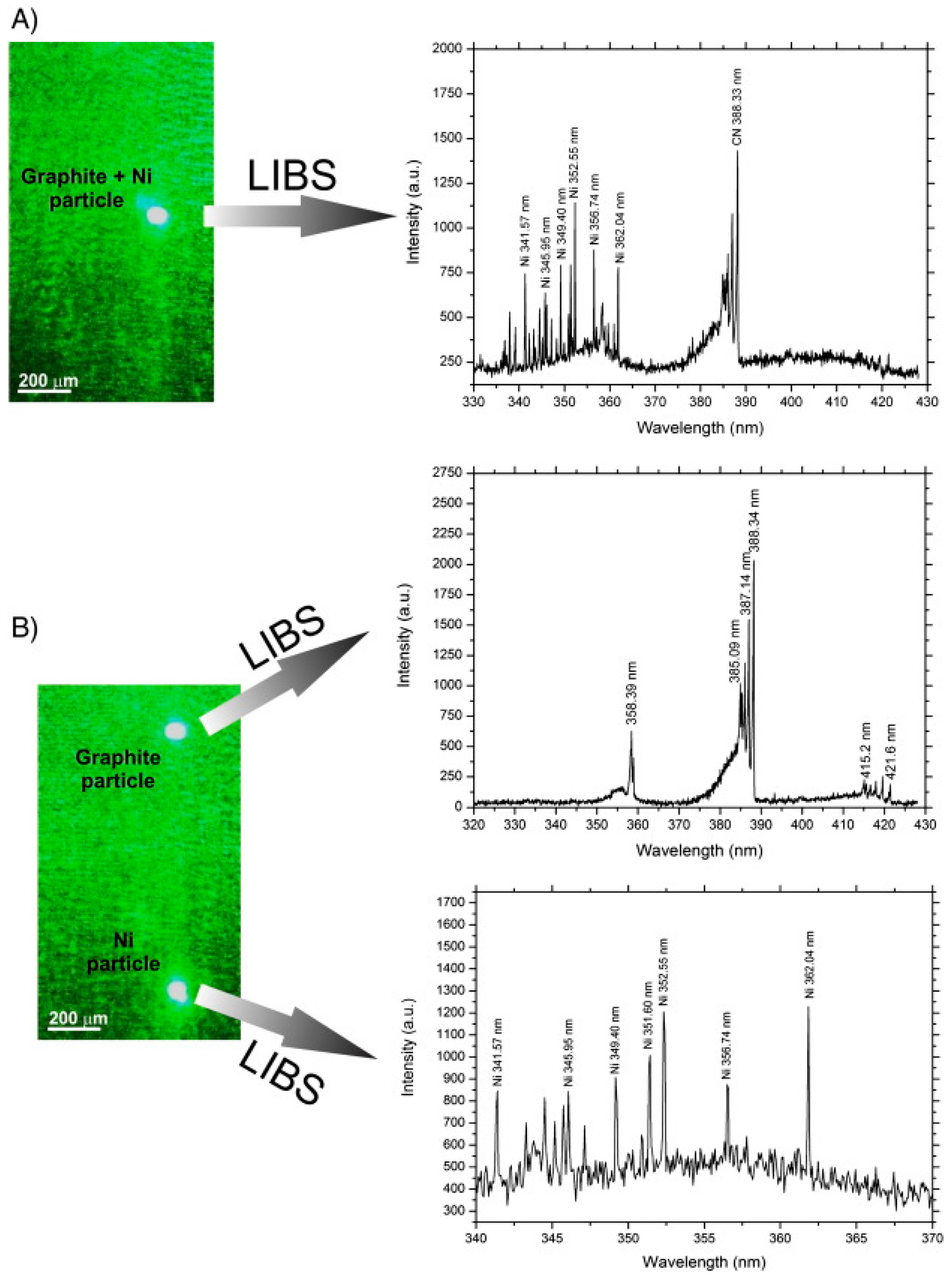
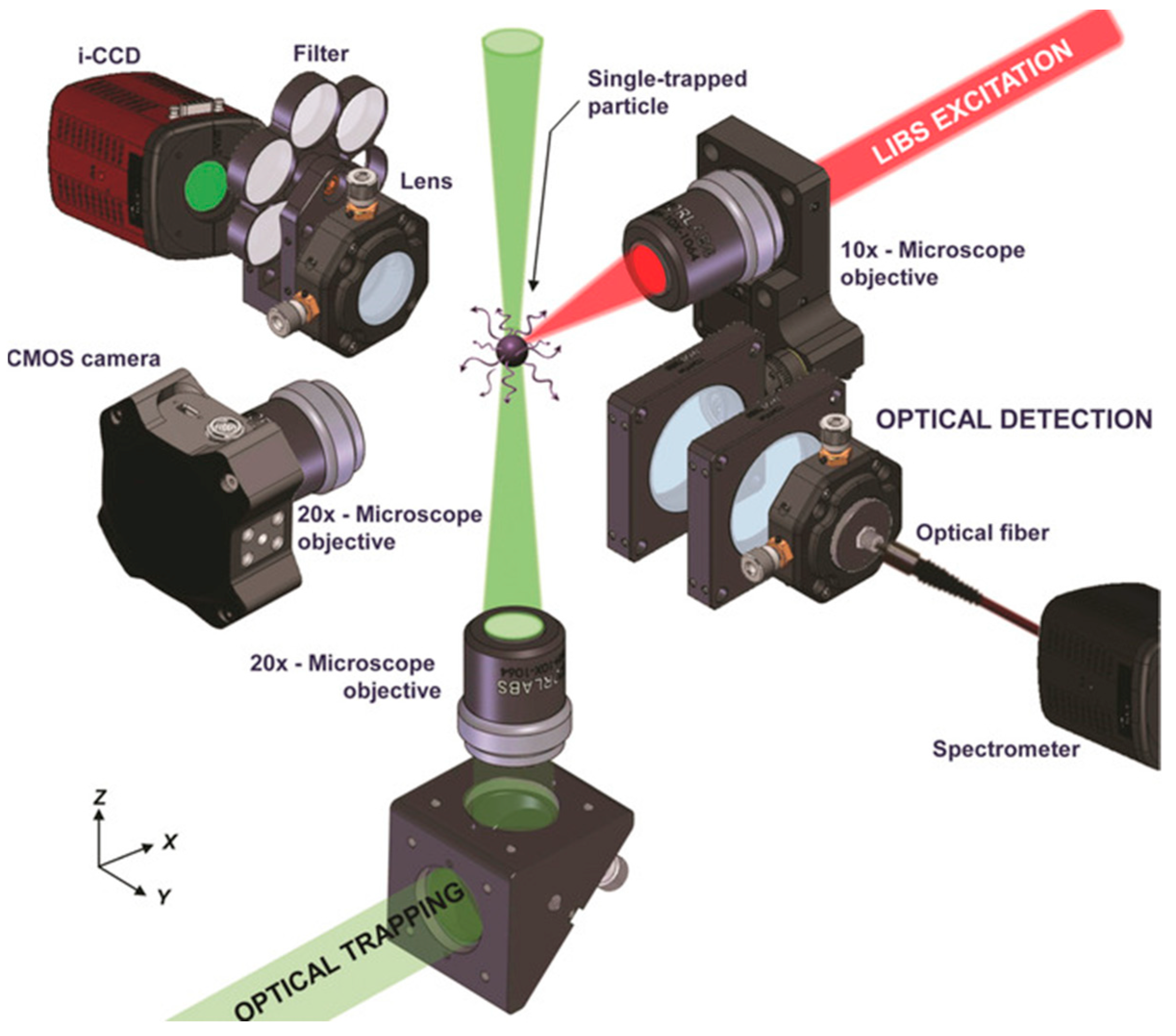
3.3.3. Laser-Induced Breakdown Spectroscopy
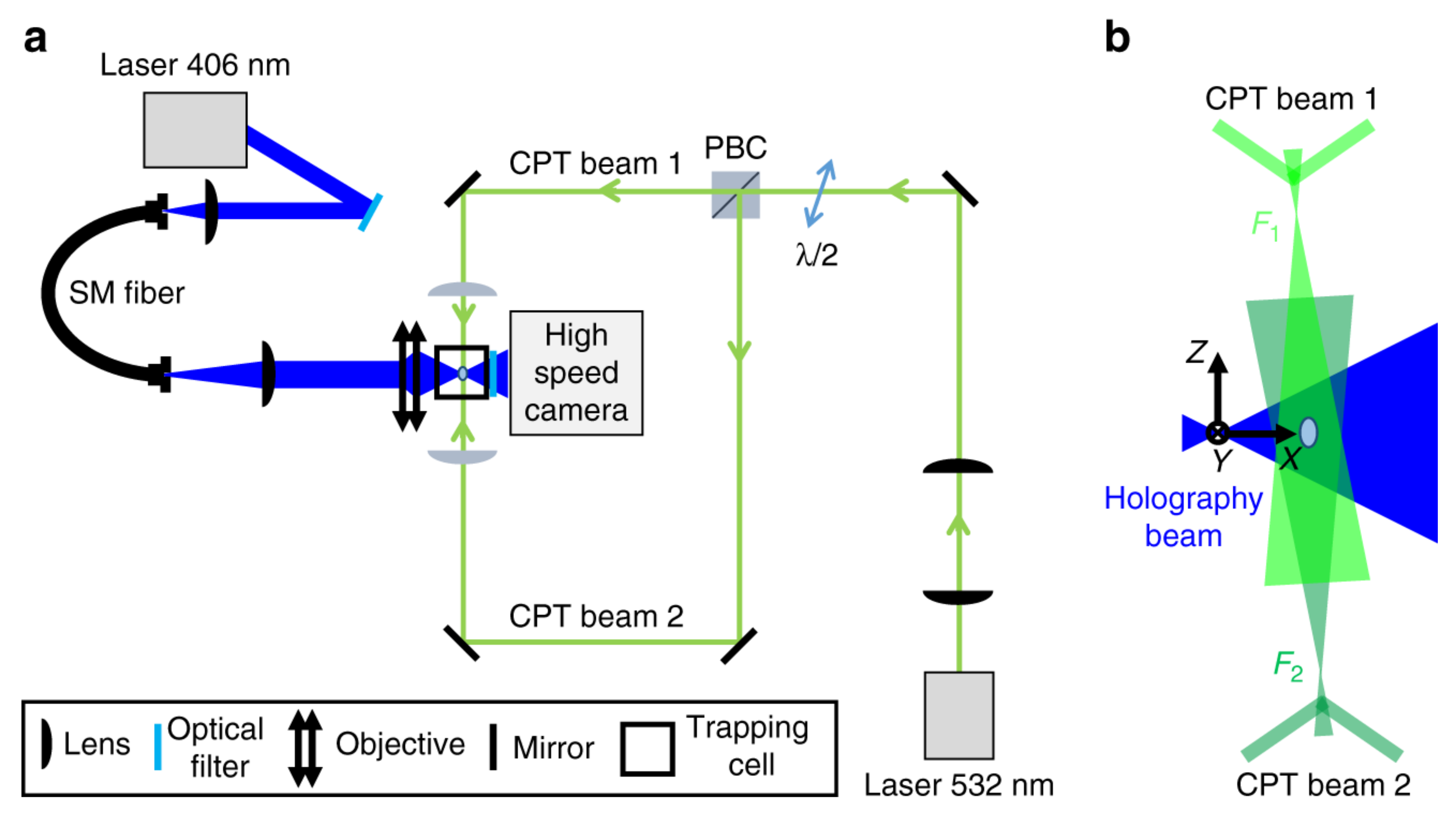
3.4. Digital Holography
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Andreae, M.O.; Crutzen, P.J. Atmospheric aerosols: Biogeochemical sources and role in atmospheric chemistry. Science 1997, 276, 1052–1058. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Jimenez, J.L.; Canagaratna, M.R.; Allan, J.D.; Coe, H.; Ulbrich, I.; Alfarra, M.R.; Takami, A.; Middlebrook, A.M.; Sun, Y.L.; et al. Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Ariya, P.A.; Amyot, M. New Directions: The role of bioaerosols in atmospheric chemistry and physics. Atmos. Environ. 2004, 38, 1231–1232. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Sherwood, S.; Wood, R.; Donner, L. Climate Effects of Aerosol-Cloud Interactions. Science 2014, 343, 379–380. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 1994: Radiative Forcing of Climate Change and an Evaluation of the IPCC IS92 Emission Scenarios; Cambridge University Press: Cambridge, UK, 1995; p. 339. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013; p. 1535. [Google Scholar]
- Baxter, P.J.; Horwell, C.J. Chapter 60—Impacts of Eruptions on Human Health. In The Encyclopedia of Volcanoes, 2nd ed.; Sigurdsson, H., Ed.; Academic Press: Amsterdam, The Netherlands, 2015; pp. 1035–1047. [Google Scholar] [CrossRef]
- Frohlich-Nowoisky, J.; Kampf, C.J.; Weber, B.; Huffman, J.A.; Pohlker, C.; Andreae, M.O.; Lang-Yona, N.; Burrows, S.M.; Gunthe, S.S.; Elbert, W.; et al. Bioaerosols in the Earth system: Climate, health, and ecosystem interactions. Atmos. Res. 2016, 182, 346–376. [Google Scholar] [CrossRef] [Green Version]
- Penner, J.E.; Dickinson, R.E.; O′Neill, C.A. Effects of Aerosol from Biomass Burning on the Global Radiation Budget. Science 1992, 256, 1432–1434. [Google Scholar] [CrossRef] [PubMed]
- Mahowald, N.; Albani, S.; Kok, J.F.; Engelstaeder, S.; Scanza, R.; Ward, D.S.; Flanner, M.G. The size distribution of desert dust aerosols and its impact on the Earth system. Aeolian Res. 2014, 15, 53–71. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-C.; Li, J.-L.F.; Lee, W.-L.; Diner, D.J.; Garay, M.J.; Jiang, J.H.; Wang, Y.-H.; Yu, J.-Y.; Kalashnikova, O.V. Evaluation of sea salt aerosols in climate systems: Global climate modeling and observation-based analyses. Environ. Res. Lett. 2020, 15, 034047. [Google Scholar] [CrossRef]
- Estillore, A.D.; Trueblood, J.V.; Grassian, V.H. Atmospheric chemistry of bioaerosols: Heterogeneous and multiphase reactions with atmospheric oxidants and other trace gases. Chem. Sci. 2016, 7, 6604–6616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marple, V.A.; Liu, B.Y.H. Aerosols in the Mining and Industrial Work Environments: Volume 1: Fundamentals and Status; Volume 2: Characterization; Volume 3: Instrumentation; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1983; Volume 72, p. 639. [Google Scholar]
- Afshar-Mohajer, N.; Foos, R.; Volckens, J.; Ramachandran, G. Variability of aerosol mass and number concentrations during taconite mining operations. J. Occup. Environ. Hyg. 2020, 17, 1–14. [Google Scholar] [CrossRef]
- Reid, J.S.; Koppmann, R.; Eck, T.F.; Eleuterio, D.P. A review of biomass burning emissions part II: Intensive physical properties of biomass burning particles. Atmos. Chem. Phys. 2005, 5, 799–825. [Google Scholar] [CrossRef] [Green Version]
- Rotatori, M.; Mosca, S.; Guerriero, E.; Febo, A.; Giusto, M.; Montagnoli, M.; Bianchini, M.; Ferrero, R. Emission of submicron aerosol particles in cement kilns: Total concentration and size distribution. J. Air Waste Manag. Assoc. 2015, 65, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Mccormick, M.P.; Thomason, L.W.; Trepte, C.R. Atmospheric Effects of the Mt-Pinatubo Eruption. Nature 1995, 373, 399–404. [Google Scholar] [CrossRef]
- Anderson, T.L.; Charlson, R.J.; Bellouin, N.; Boucher, O.; Chin, M.; Christopher, S.A.; Haywood, J.; Kaufman, Y.J.; Kinne, S.; Ogren, J.A.; et al. An “A-Train” strategy for quantifying direct climate forcing by anthropogenic aerosols. Bull. Am. Meteorol. Soc. 2005, 86, 1795–1810. [Google Scholar] [CrossRef]
- Reddy, M.S.; Boucher, O.; Balkanski, Y.; Schulz, M. Aerosol optical depths and direct radiative perturbations by species and source type. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Jaegle, L.; Quinn, P.K.; Bates, T.S.; Alexander, B.; Lin, J.T. Global distribution of sea salt aerosols: New constraints from in situ and remote sensing observations. Atmos. Chem. Phys. 2011, 11, 3137–3157. [Google Scholar] [CrossRef] [Green Version]
- Rauber, R.M.; Stevens, B.; Ochs, H.T.; Knight, C.; Albrecht, B.A.; Blyth, A.M.; Fairall, C.W.; Jensen, J.B.; Lasher-Trapp, S.G.; Mayol-Bracero, O.L.; et al. Rain in shallow cumulus over the ocean—The RICO campaign. Bull. Am. Meteorol. Soc. 2007, 88, 1912–1928. [Google Scholar] [CrossRef] [Green Version]
- Stratmann, F.; Mohler, O.; Shaw, R.; Wex, H. Laboratory Cloud Simulation: Capabilities and Future Directions. In Clouds in the Perturbed Climate System: Their Relationship to Energy Balance, Atmospheric Dynamics, and Precipitation; MIT Press: Cambridge, MA, USA, 2009; pp. 149–172. [Google Scholar]
- Korolev, A.; Field, P.R. The effect of dynamics on mixed-phase clouds: Theoretical considerations. J. Atmos. Sci. 2008, 65, 66–86. [Google Scholar] [CrossRef]
- Lance, S.; Shupe, M.D.; Feingold, G.; Brock, C.A.; Cozic, J.; Holloway, J.S.; Moore, R.H.; Nenes, A.; Schwarz, J.P.; Spackman, J.R.; et al. Cloud condensation nuclei as a modulator of ice processes in Arctic mixed-phase clouds. Atmos. Chem. Phys. 2011, 11, 8003–8015. [Google Scholar] [CrossRef] [Green Version]
- Ervens, B.; Feingold, G.; Sulia, K.; Harrington, J. The impact of microphysical parameters, ice nucleation mode, and habit growth on the ice/liquid partitioning in mixed-phase Arctic clouds. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Morrison, H.; de Boer, G.; Feingold, G.; Harrington, J.; Shupe, M.D.; Sulia, K. Resilience of persistent Arctic mixed-phase clouds. Nat. Geosci. 2012, 5, 11–17. [Google Scholar] [CrossRef]
- Singh, A.; Agrawal, M. Acid rain and its ecological consequences. J. Environ. Biol. 2008, 29, 15–24. [Google Scholar]
- Zhang, F.; Cheng, M.Z.; Sun, Z.G.; Wang, L.H.; Zhou, Q.; Huang, X.H. Combined acid rain and lanthanum pollution and its potential ecological risk for nitrogen assimilation in soybean seedling roots. Environ. Pollut. 2017, 231, 524–532. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Wallace, J.M.; Limpasuvan, V.; Thompson, D.W.J.; Holton, J.R. Can ozone depletion and global warming interact to produce rapid climate change? Proc. Natl. Acad. Sci. USA 2000, 97, 1412–1417. [Google Scholar] [CrossRef] [Green Version]
- Ganesan, K.; Raza, S.K.; Vijayaraghavan, R. Chemical warfare agents. J. Pharm. Bioallied Sci. 2010, 2, 166–178. [Google Scholar] [CrossRef]
- Patocka, J.; Fusek, J. Chemical agents and chemical terrorism. Cent. Eur. J. Public Health 2004, 12, S75–S77. [Google Scholar] [PubMed]
- Lazarev, A.I. Observations of the aerosol from space. J. Opt. Technol. 2002, 69, 802–807. [Google Scholar] [CrossRef]
- Lee, K.H.; Li, Z.; Kim, Y.J.; Kokhanovsky, A. Atmospheric Aerosol Monitoring from Satellite Observations: A History of Three Decades. In Atmospheric and Biological Environmental Monitoring; Kim, Y.J., Platt, U., Gu, M.B., Iwahashi, H., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 13–38. [Google Scholar] [CrossRef]
- Fisher, D.; Muller, J.P.; Yershov, V.N. Automated Stereo Retrieval of Smoke Plume Injection Heights and Retrieval of Smoke Plume Masks From AATSR and Their Assessment With CALIPSO and MISR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1249–1258. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Nakajima, T.; Tonna, G.; Rao, R.Z.; Boi, P.; Kaufman, Y.; Holben, B. Use of sky brightness measurements from ground for remote sensing of particulate polydispersions. Appl. Opt. 1996, 35, 2672–2686. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.R.; Hlavka, D.L.; Welton, E.J.; Flynn, C.J.; Turner, D.D.; Spinhirne, J.D.; Scott, V.S.; Hwang, I.H. Full-time, eye-safe cloud and aerosol lidar observation at atmospheric radiation measurement program sites: Instruments and data processing. J. Atmos. Ocean. Technol. 2002, 19, 431–442. [Google Scholar] [CrossRef]
- Willeke, K.; Baron, P.A. Aerosol Measurement: Principles, Techniques, and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Kalume, A.; Wang, C.; Santarpia, J.; Pan, Y.L. Liquid-liquid phase separation and evaporation of a laser-trapped organic-organic airborne droplet using temporal spatial-resolved Raman spectroscopy. Phys. Chem. Chem. Phys. 2018, 20, 19151–19159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuend, A.; Marcolli, C.; Peter, T.; Seinfeld, J.H. Computation of liquid-liquid equilibria and phase stabilities: Implications for RH-dependent gas/particle partitioning of organic-inorganic aerosols. Atmos. Chem. Phys. 2010, 10, 7795–7820. [Google Scholar] [CrossRef] [Green Version]
- Esat, K.; David, G.; Poulkas, T.; Shein, M.; Signorell, R. Phase transition dynamics of single optically trapped aqueous potassium carbonate particles. Phys. Chem. Chem. Phys. 2018, 20, 11598–11607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Brien, R.E.; Wang, B.B.; Kelly, S.T.; Lundt, N.; You, Y.; Bertram, A.K.; Leone, S.R.; Laskin, A.; Gilles, M.K. Liquid-Liquid Phase Separation in Aerosol Particles: Imaging at the Nanometer Scale. Environ. Sci. Technol. 2015, 49, 4995–5002. [Google Scholar] [CrossRef] [Green Version]
- You, Y.; Renbaum-Wolff, L.; Bertram, A.K. Liquid-liquid phase separation in particles containing organics mixed with ammonium sulfate, ammonium bisulfate, ammonium nitrate or sodium chloride. Atmos. Chem. Phys. 2013, 13, 11723–11734. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.L.; You, Y.; Kuwata, M.; Bertram, A.K.; Martin, S.T. Phase Transitions and Phase Miscibility of Mixed Particles of Ammonium Sulfate, Toluene-Derived Secondary Organic Material, and Water. J. Phys. Chem. A 2013, 117, 8895–8906. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156. [Google Scholar] [CrossRef] [Green Version]
- Ashkin, A.; Dziedzic, J.M. Optical Levitation by Radiation Pressure. Appl. Phys. Lett. 1971, 19, 283–285. [Google Scholar] [CrossRef]
- Roosen, G. Recent Advances in Optical Levitation. In Proceedings of the Abstracts of Papers of the American Chemical Society, Washington, WA, USA, 14 August 1980; Volume 180, pp. 124–130. [Google Scholar]
- Roosen, G.; Imbert, C. Optical Levitation–Theoretical and Experimental-Study. J. Opt. Soc. Am. 1977, 67, 1438. [Google Scholar]
- Redding, B.; Pan, Y.L. Optical trap for both transparent and absorbing particles in air using a single shaped laser beam. Opt. Lett. 2015, 40, 2798–2801. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.L.; Kalume, A.; Lenton, I.C.D.; Nieminen, T.A.; Stilgoe, A.B.; Rubinsztein-Dunlop, H.; Beresnev, L.A.; Wang, C.J.; Santarpia, J.L. Optical-trapping of particles in air using parabolic reflectors and a hollow laser beam. Opt. Express 2019, 27, 33061–33069. [Google Scholar] [CrossRef]
- Gong, Z.Y.; Pan, Y.L.; Wang, C.J. Optical configurations for photophoretic trap of single particles in air. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef] [PubMed]
- Gouesbet, G.; Lock, J.A.; Gréhan, G. Generalized Lorenz—Mie theories and description of electromagnetic arbitrary shaped beams: Localized approximations and localized beam models, a review. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1–27. [Google Scholar] [CrossRef]
- Lock, J.A.; Gouesbet, G. Generalized Lorenz-Mie theory and applications. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 800–807. [Google Scholar] [CrossRef]
- Lewittes, M.; Arnold, S.; Oster, G. Radiometric Levitation of Micron Sized Spheres. Appl. Phys. Lett. 1982, 40, 455–457. [Google Scholar] [CrossRef]
- Redding, B.; Hill, S.C.; Alexson, D.; Wang, C.J.; Pan, Y.L. Photophoretic trapping of airborne particles using ultraviolet illumination. Opt. Express 2015, 23, 3630–3639. [Google Scholar] [CrossRef]
- Gong, Z.Y.; Pan, Y.L.; Videen, G.; Wang, C.J. Optical trapping and manipulation of single particles in air: Principles, technical details, and applications. J. Quant. Spectrosc. Radiat. Transf. 2018, 214, 94–119. [Google Scholar] [CrossRef]
- Neuman, K.C.; Block, S.M. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molloy, J.E.; Padgett, M.J. Lights, action: Optical tweezers. Contemp. Phys. 2002, 43, 241–258. [Google Scholar] [CrossRef]
- Li, T.C.; Kheifets, S.; Medellin, D.; Raizen, M.G. Measurement of the Instantaneous Velocity of a Brownian Particle. Science 2010, 328, 1673–1675. [Google Scholar] [CrossRef] [Green Version]
- Thurn, R.; Kiefer, W. Raman-Microsampling Technique Applying Optical Levitation by Radiation Pressure. Appl. Spectrosc. 1984, 38, 78–83. [Google Scholar] [CrossRef]
- Pluchino, A.B. Radiometric Levitation of Spherical Carbon Aerosol-Particles Using a Nd-Yag Laser. Appl. Opt. 1983, 22, 1861–1866. [Google Scholar] [CrossRef]
- Zhang, Z.; Cannan, D.; Liu, J.J.; Zhang, P.; Christodoulides, D.N.; Chen, Z.G. Observation of trapping and transporting air-borne absorbing particles with a single optical beam. Opt. Express 2012, 20, 16212–16217. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.; Li, Y.Q. Measurement of Raman spectra of single airborne absorbing particles trapped by a single laser beam. Opt. Lett. 2013, 38, 416–418. [Google Scholar] [CrossRef]
- Manek, I.; Ovchinnikov, Y.B.; Grimm, R. Generation of a hollow laser beam for atom trapping using an axicon. Opt. Commun. 1998, 147, 67–70. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Stability of Optical Levitation by Radiation Pressure. Appl. Phys. Lett. 1974, 24, 586–588. [Google Scholar] [CrossRef]
- Roosen, G.; Imbert, C. TEM*01 Mode Laser-Beam—Powerful Tool for Optical Levitation of Various Types of Spheres. Opt. Commun. 1978, 26, 432–436. [Google Scholar] [CrossRef]
- Shvedov, V.G.; Hnatovsky, C.; Rode, A.V.; Krolikowski, W. Robust trapping and manipulation of airborne particles with a bottle beam. Opt. Express 2011, 19, 17350–17356. [Google Scholar] [CrossRef]
- Mazilu, M.; Stevenson, D.J.; Gunn-Moore, F.; Dholakia, K. Light beats the spread: ″non-diffracting″ beams. Laser Photonics Rev. 2010, 4, 529–547. [Google Scholar] [CrossRef]
- Carruthers, A.E.; Reid, J.P.; Orr-Ewing, A.J. Longitudinal optical trapping and sizing of aerosol droplets. Opt. Express 2010, 18, 14238–14244. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Z.; Prakash, J.; Huang, S.; Hernandez, D.; Salazar, M.; Christodoulides, D.N.; Chen, Z.G. Trapping and transporting aerosols with a single optical bottle beam generated by moire techniques. Opt. Lett. 2011, 36, 1491–1493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shvedov, V.G.; Rode, A.V.; Izdebskaya, Y.V.; Leykam, D.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Laser speckle field as a multiple particle trap. J. Opt. 2010, 12. [Google Scholar] [CrossRef] [Green Version]
- Shvedov, V.G.; Rode, A.V.; Izdebskaya, Y.V.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Selective trapping of multiple particles by volume speckle field. Opt. Express 2010, 18, 3137–3142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, F.R.; Zhang, Z.G.; Wei, Y.F.; Zhang, Q.C.; Cheng, T.; Wu, X.P. Photophoretic trapping of multiple particles in tapered-ring optical field. Opt. Express 2014, 22, 23716–23723. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.R.; Zhang, Z.G.; Fu, S.H.; Wei, Y.F.; Cheng, T.; Zhang, Q.C.; Wu, X.P. Manipulation of aerosols revolving in taper-ring optical traps. Opt. Lett. 2014, 39, 100–103. [Google Scholar] [CrossRef] [Green Version]
- Shvedov, V.G.; Desyatnikov, A.S.; Rode, A.V.; Krolikowski, W.; Kivshar, Y.S. Optical guiding of absorbing nanoclusters in air. Opt. Express 2009, 17, 5743–5757. [Google Scholar] [CrossRef]
- Pan, Y.L.; Hill, S.C.; Coleman, M. Photophoretic trapping of absorbing particles in air and measurement of their single-particle Raman spectra. Opt. Express 2012, 20, 5325–5334. [Google Scholar] [CrossRef]
- Carruthers, A.E.; Walker, J.S.; Casey, A.; Orr-Ewing, A.J.; Reid, J.P. Selection and characterization of aerosol particle size using a bessel beam optical trap for single particle analysis. Phys. Chem. Chem. Phys. 2012, 14, 6741–6748. [Google Scholar] [CrossRef]
- van de Hulst, H.C. Light Scattering by Small Particles; Dover Publications Inc.: New York, NY, USA, 1981. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Wyatt, P.J.; Schehrer, K.L.; Phillips, S.D.; Jackson, C.; Chang, Y.J.; Parker, R.G.; Phillips, D.T.; Bottiger, J.R. Aerosol-Particle Analyzer. Appl. Opt. 1988, 27, 217–221. [Google Scholar] [CrossRef]
- Gucker, F.T.; Egan, J.J. Measurement of Angular Variation of Light Scattered from Single Aerosol Droplets. J. Coll. Sci. 1961, 16, 68–84. [Google Scholar] [CrossRef]
- Kaye, P.H. Spatial light-scattering analysis as a means of characterizing and classifying non-spherical particles. Meas. Sci. Technol. 1998, 9, 141–149. [Google Scholar] [CrossRef]
- Fernandes, G.E.; Pan, Y.L.; Chang, R.K.; Aptowicz, K.; Pinnick, R.G. Simultaneous forward- and backward-hemisphere elastic-light-scattering patterns of respirable-size aerosols. Opt. Lett. 2006, 31, 3034–3036. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M. Feedback Stabilization of Optically Levitated Particles. Appl. Phys. Lett. 1977, 30, 202–204. [Google Scholar] [CrossRef]
- Schaschek, K.; Popp, J.; Kiefer, W. Observation of Morphology-Dependent Input and Output Resonances in Time-Dependent Raman-Spectra of Optically Levitated Microdroplets. J. Raman Spectrosc. 1993, 24, 69–75. [Google Scholar] [CrossRef]
- Gieseler, J.; Deutsch, B.; Quidant, R.; Novotny, L. Subkelvin Parametric Feedback Cooling of a Laser-Trapped Nanoparticle. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Li, T.C.; Kheifets, S.; Raizen, M.G. Millikelvin cooling of an optically trapped microsphere in vacuum. Nat. Phys. 2011, 7, 527–530. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Observation of Resonances in Radiation Pressure on Dielectric Spheres. Phys. Rev. Lett. 1977, 38, 1351–1354. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Observation of Optical Resonances of Dielectric Spheres by Light-Scattering. Appl. Opt. 1981, 20, 1803–1814. [Google Scholar] [CrossRef]
- Grehan, G.; Gouesbet, G. Optical Levitation of a Single-Particle to Study the Theory of the Quasi-Elastic Scattering of Light. Appl. Opt. 1980, 19, 2485–2487. [Google Scholar] [CrossRef]
- Kalume, A.; Beresnev, L.A.; Santarpia, J.; Pan, Y.L. Detection and characterization of chemical aerosol using laser-trapping single-particle Raman spectroscopy. Appl. Opt. 2017, 56, 6577–6582. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.H.; She, T.C.; Lee, W.K. Positions of low-order morphology-dependent resonances determined by elastic light scattering. J. Opt. Soc. Am. B 1995, 12, 1259–1266. [Google Scholar] [CrossRef]
- Chan, C.W.; Lee, W.K. Vertical motion and elastic light-scattering of a laser-levitated water droplet. J. Opt. Soc. Am. B 2001, 18, 1196–1202. [Google Scholar] [CrossRef]
- Jones, S.H.; King, M.D.; Ward, A.D. Determining the unique refractive index properties of solid polystyrene aerosol using broadband Mie scattering from optically trapped beads. Phys. Chem. Chem. Phys. 2013, 15, 20735–20741. [Google Scholar] [CrossRef] [Green Version]
- Paton, J. The Scattering of Light by Small Particles. Nature 1958, 182, 1470–1471. [Google Scholar] [CrossRef]
- Wriedt, T. A Review of Elastic Light Scattering Theories. Part. Part. Syst. Charact. 1998, 15, 67–74. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Videen, G.; Babenko, V.A.; Khlebtsov, N.G.; Wriedt, T. T-matrix theory of electromagnetic scattering by particles and its applications: A comprehensive reference database. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 357–406. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Videen, G.; Babenko, V.A.; Khlebtsov, N.G.; Wriedt, T. Comprehensive T-matrix reference database: A 2004–06 update. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 304–324. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Videen, G.; Khlebtsov, N.G.; Wriedt, T. Comprehensive T-matrix reference database: A 2012–2013 update. J. Quant. Spectrosc. Radiat. Transf. 2013, 123, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Videen, G.; Khlebtsov, N.G.; Wriedt, T.; Zakharova, N.T. Comprehensive T-matrix reference database: A 2006–07 update. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1447–1460. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Zakharova, N.T.; Khlebtsov, N.G.; Videen, G.; Wriedt, T. Comprehensive thematic T-matrix reference database: A 2014–2015 update. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 276–283. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Zakharova, N.T.; Khlebtsov, N.G.; Videen, G.; Wriedt, T. Comprehensive thematic T-matrix reference database: A 2015–2017 update. J. Quant. Spectrosc. Radiat. Transf. 2017, 202, 240–246. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Zakharova, N.T.; Khlebtsov, N.G.; Wriedt, T.; Videen, G. Comprehensive thematic T-matrix reference database: A 2013–2014 update. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 349–354. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Zakharova, N.T.; Videen, G.; Khlebtsov, N.G.; Wriedt, T. Comprehensive T-matrix reference database: A 2007–2009 update. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 650–658. [Google Scholar] [CrossRef] [Green Version]
- Conwell, P.R.; Rushforth, C.K.; Benner, R.E.; Hill, S.C. Efficient Automated Algorithm for the Sizing of Dielectric Microspheres Using the Resonance-Spectrum. J. Opt. Soc. Am. A 1984, 1, 1181–1187. [Google Scholar] [CrossRef]
- Hill, S.C.; Rushforth, C.K.; Benner, R.E.; Conwell, P.R. Sizing Dielectric Spheres and Cylinders by Aligning Measured and Computed Resonance Locations—Algorithm for Multiple Orders. Appl. Opt. 1985, 24, 2380–2390. [Google Scholar] [CrossRef]
- Eversole, J.D.; Lin, H.B.; Huston, A.L.; Campillo, A.J.; Leung, P.T.; Liu, S.Y.; Young, K. High-Precision Identification of Morphology-Dependent Resonances in Optical Processes in Microdroplets. J. Opt. Soc. Am. B 1993, 10, 1955–1968. [Google Scholar] [CrossRef]
- Miles, R.E.H.; Walker, J.S.; Burnham, D.R.; Reid, J.P. Retrieval of the complex refractive index of aerosol droplets from optical tweezers measurements. Phys. Chem. Chem. Phys. 2012, 14, 3037–3047. [Google Scholar] [CrossRef]
- Preston, T.C.; Reid, J.P. Accurate and efficient determination of the radius, refractive index, and dispersion of weakly absorbing spherical particle using whispering gallery modes. J. Opt. Soc. Am. B 2013, 30, 2113–2122. [Google Scholar] [CrossRef]
- Preston, T.C.; Reid, J.P. Determining the size and refractive index of microspheres using the mode assignments from Mie resonances. J. Opt. Soc. Am. A 2015, 32, 2210–2217. [Google Scholar] [CrossRef] [Green Version]
- Moridnejad, A.; Preston, T.C.; Krieger, U.K. Tracking Water Sorption in Glassy Aerosol Particles using Morphology-Dependent Resonances. J. Phys. Chem. A 2017, 121, 8176–8184. [Google Scholar] [CrossRef]
- Hightower, R.L.; Richardson, C.B. Resonant Mie Scattering from a Layered Sphere. Appl. Opt. 1988, 27, 4850–4855. [Google Scholar] [CrossRef] [PubMed]
- Lock, J.A. Interference Enhancement of the Internal Fields at Structural Scattering Resonances of a Coated Sphere. Appl. Opt. 1990, 29, 3180–3187. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, T.; Lange, S.; Schweiger, G. Structural Resonances in a Coated Sphere—Investigation of the Volume-Averaged Source Function and Resonance Positions. Appl. Opt. 1994, 33, 7789–7797. [Google Scholar] [CrossRef] [PubMed]
- Vennes, B.; Preston, T.C. Calculating and fitting morphology-dependent resonances of a spherical particle with a concentric spherical shell. J. Opt. Soc. Am. A 2019, 36, 2089–2103. [Google Scholar] [CrossRef] [PubMed]
- Song, M.J.; Marcolli, C.; Krieger, U.K.; Lienhard, D.M.; Peter, T. Morphologies of mixed organic/inorganic/aqueous aerosol droplets. Faraday Discuss. 2013, 165, 289–316. [Google Scholar] [CrossRef]
- Miscchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: New York, NY, USA, 2002; Volume 4. [Google Scholar]
- Sorensen, C.M.; Shi, D. Patterns in the ripple structure of Mie scattering. J. Opt. Soc. Am. A 2002, 19, 122–125. [Google Scholar] [CrossRef]
- Berg, M.J.; Sorensen, C.M.; Chakrabarti, A. Explanation of the patterns in Mie theory. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 782–794. [Google Scholar] [CrossRef]
- Videen, G.; Sun, W.B.; Fu, Q.; Secker, D.R.; Greenaway, R.S.; Kaye, P.H.; Hirst, E.; Bartley, D. Light scattering from deformed droplets and droplets with inclusions. II. Theoretical treatment. Appl. Opt. 2000, 39, 5031–5039. [Google Scholar] [CrossRef]
- Videen, G.; Sun, W.B.; Fu, Q. Light scattering from irregular tetrahedral aggregates. Opt. Commun. 1998, 156, 5–9. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Wang, C.; Beresnev, L.A.; Yuffa, A.J.; Videen, G.; Ligon, D.; Santarpia, J.L. Measurement of back-scattering patterns from single laser trapped aerosol particles in air. Appl. Opt. 2017, 56, B1–B4. [Google Scholar] [CrossRef] [PubMed]
- Fu, R.; Wang, C.J.; Munoz, O.; Videen, G.; Santarpia, J.L.; Pan, Y.L. Elastic back-scattering patterns via particle surface roughness and orientation from single trapped airborne aerosol particles. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 224–231. [Google Scholar] [CrossRef] [Green Version]
- Piedra, P.; Kalume, A.; Zubko, E.; Mackowski, D.; Pan, Y.L.; Videen, G. Particle-shape classification using light scattering: An exercise in deep learning. J. Quant. Spectrosc. Radiat. Transf. 2019, 231, 140–156. [Google Scholar] [CrossRef]
- Piedra, P.; Gobert, C.; Kalume, A.; Pan, Y.L.; Kocifaj, M.; Muinonen, K.; Penttila, A.; Zubko, E.; Videen, G. Where is the machine looking? Locating discriminative light-scattering features by class-activation mapping. J. Quant. Spectrosc. Radiat. Transf. 2020, 247. [Google Scholar] [CrossRef]
- Wheeler, M.D.; Newman, S.M.; Orr-Ewing, A.J.; Ashfold, M.N.R. Cavity ring-down spectroscopy. J. Chem. Soc. Faraday Trans. 1998, 94, 337–351. [Google Scholar] [CrossRef]
- O’Keefe, A.; Deacon, D.A.G. Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources. Rev. Sci. Instrum. 1988, 59, 2544–2551. [Google Scholar] [CrossRef] [Green Version]
- Baynard, T.; Lovejoy, E.R.; Pettersson, A.; Brown, S.S.; Lack, D.; Osthoff, H.; Massoli, P.; Ciciora, S.; Dube, W.P.; Ravishankara, A.R. Design and application of a pulsed cavity ring-down aerosol extinction spectrometer for field measurements. Aerosol Sci. Technol. 2007, 41, 447–462. [Google Scholar] [CrossRef]
- Dinar, E.; Riziq, A.A.; Spindler, C.; Erlick, C.; Kiss, G.; Rudich, Y. The complex refractive index of atmospheric and model humic-like substances (HULIS) retrieved by a cavity ring down aerosol spectrometer (CRD-AS). Faraday Discuss. 2008, 137, 279–295. [Google Scholar] [CrossRef] [PubMed]
- Lang-Yona, M.; Rudich, Y.; Segre, E.; Dinar, E.; Abo-Riziq, A. Complex Refractive Indices of Aerosols Retrieved by Continuous Wave-Cavity Ring Down Aerosol Spectrometer. Anal. Chem. 2009, 81, 1762–1769. [Google Scholar] [CrossRef]
- Kennedy, O.J.; Ouyang, B.; Langridge, J.M.; Daniels, M.J.S.; Bauguitte, S.; Freshwater, R.; McLeod, M.W.; Ironmonger, C.; Sendall, J.; Norris, O.; et al. An aircraft based three channel broadband cavity enhanced absorption spectrometer for simultaneous measurements of NO3, N2O5 and NO2. Atmos. Meas. Tech. 2011, 4, 1759–1776. [Google Scholar] [CrossRef] [Green Version]
- Attwood, A.R.; Greenslade, M.E. Deliquescence Behavior of Internally Mixed Clay and Salt Aerosols by Optical Extinction Measurements. J. Phys. Chem. A 2012, 116, 4518–4527. [Google Scholar] [CrossRef] [PubMed]
- Riziq, A.A.; Erlick, C.; Dinar, E.; Rudich, Y. Optical properties of absorbing and non-absorbing aerosols retrieved by cavity ring down (CRD) spectroscopy. Atmos. Chem. Phys. 2007, 7, 1523–1536. [Google Scholar] [CrossRef] [Green Version]
- Spindler, C.; Riziq, A.A.; Rudich, Y. Retrieval of aerosol complex refractive index by combining cavity ring down aerosol spectrometer measurements with full size distribution information. Aerosol Sci. Technol. 2007, 41, 1011–1017. [Google Scholar] [CrossRef] [Green Version]
- Cotterell, M.I.; Willoughby, R.E.; Bzdek, B.R.; Orr-Ewing, A.J.; Reid, J.P. A complete parameterisation of the relative humidity and wavelength dependence of the refractive index of hygroscopic inorganic aerosol particles. Atmos. Chem. Phys. 2017, 17, 9837–9851. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.S.; Carruthers, A.E.; Orr-Ewing, A.J.; Reid, J.P. Measurements of Light Extinction by Single Aerosol Particles. J. Phys. Chem. Lett. 2013, 4, 1748–1752. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.J.; Gong, Z.Y.; Pan, Y.L.; Videen, G. Optical trap-cavity ringdown spectroscopy as a single-aerosol-particle-scope. Appl Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
- Gong, Z.Y.; Pan, Y.L.; Wang, C.J. Characterization of single airborne particle extinction using the tunable optical trap-cavity ringdown spectroscopy (OT-CRDS) in the UV. Opt. Express 2017, 25, 6732–6745. [Google Scholar] [CrossRef]
- Cotterell, M.I.; Preston, T.C.; Orr-Ewing, A.J.; Reid, J.P. Assessing the accuracy of complex refractive index retrievals from single aerosol particle cavity ring-down spectroscopy. Aerosol Sci. Technol. 2016, 50, 1077–1095. [Google Scholar] [CrossRef] [Green Version]
- Alali, H.; Gong, Z.Y.; Videen, G.; Pan, Y.L.; Munoz, O.; Wang, C.J. Laser spectroscopic characterization of single extraterrestrial dust particles using optical trapping-cavity ringdown and Raman spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2020, 255. [Google Scholar] [CrossRef]
- Yoshinaga, A.; Hsieh, Y.M.; Sawada, T.; Gohshi, Y. Laser-Induced Photoacoustic Spectrometry with Single-Particle Sample. Anal. Sci. 1989, 5, 147–149. [Google Scholar] [CrossRef] [Green Version]
- Cremer, J.W.; Thaler, K.M.; Haisch, C.; Signorell, R. Photoacoustics of single laser-trapped nanodroplets for the direct observation of nanofocusing in aerosol photokinetics. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Diveky, M.E.; Roy, S.; Cremer, J.W.; David, G.; Signorell, R. Assessing relative humidity dependent photoacoustics to retrieve mass accommodation coefficients of single optically trapped aerosol particles. Phys. Chem. Chem. Phys. 2019, 21, 4721–4731. [Google Scholar] [CrossRef] [Green Version]
- Raspet, R.; Slaton, W.V.; Arnott, W.P.; Moosmuller, H. Evaporation-condensation effects on resonant photoacoustics of volatile aerosols. J. Atmos. Ocean. Technol. 2003, 20, 685–695. [Google Scholar] [CrossRef] [Green Version]
- Murphy, D.M. The Effect of Water Evaporation on Photoacoustic Signals in Transition and Molecular Flow. Aerosol Sci. Technol. 2009, 43, 356–363. [Google Scholar] [CrossRef] [Green Version]
- Baker, M.B. Energy-Absorption by Volatile Atmospheric Aerosol-Particles. Atmos. Environ. 1976, 10, 241–248. [Google Scholar] [CrossRef]
- Arnott, W.P.; Moosmuller, H.; Sheridan, P.J.; Ogren, J.A.; Raspet, R.; Slaton, W.V.; Hand, J.L.; Kreidenweis, S.M.; Collett, J.L. Photoacoustic and filter-based ambient aerosol light absorption measurements: Instrument comparisons and the role of relative humidity. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Cremer, J.W.; Covert, P.A.; Parmentier, E.A.; Signorell, R. Direct Measurement of Photoacoustic Signal Sensitivity to Aerosol Particle Size. J. Phys. Chem. Lett. 2017, 8, 3398–3403. [Google Scholar] [CrossRef] [Green Version]
- Lack, D.A.; Quinn, P.K.; Massoli, P.; Bates, T.S.; Coffman, D.; Covert, D.S.; Sierau, B.; Tucker, S.; Baynard, T.; Lovejoy, E.; et al. Relative humidity dependence of light absorption by mineral dust after long-range atmospheric transport from the Sahara. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Lewis, K.A.; Arnott, W.P.; Moosmüller, H.; Chakrabarty, R.K.; Carrico, C.M.; Kreidenweis, S.M.; Day, D.E.; Malm, W.C.; Laskin, A.; Jimenez, J.L.; et al. Reduction in biomass burning aerosol light absorption upon humidification: Roles of inorganically-induced hygroscopicity, particle collapse, and photoacoustic heat and mass transfer. Atmos. Chem. Phys. 2009, 9, 8949–8966. [Google Scholar] [CrossRef] [Green Version]
- Langridge, J.M.; Richardson, M.S.; Lack, D.A.; Brock, C.A.; Murphy, D.M. Limitations of the Photoacoustic Technique for Aerosol Absorption Measurement at High Relative Humidity. Aerosol Sci. Technol. 2013, 47, 1163–1173. [Google Scholar] [CrossRef] [Green Version]
- Diveky, M.E.; Roy, S.; David, G.; Cremer, J.W.; Signorell, R. Fundamental investigation of photoacoustic signal generation from single aerosol particles at varying relative humidity. Photoacoustics 2020, 18, 100170. [Google Scholar] [CrossRef]
- Harris, D.C.; Bertolucci, M.D. Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy; Dover Publications: New York, NY, USA, 1986. [Google Scholar]
- Cheung, C.K.; Jones, D.R.; Wang, C.H. Single-Particle Reorientation and Pair Correlations of Methyl-Iodide Solutions Studied by Depolarized Rayleigh and Raman-Scattering. J. Chem. Phys. 1976, 64, 3567–3572. [Google Scholar] [CrossRef]
- Knoll, P.; Marchl, M.; Kiefer, W. Raman-Spectroscopy of Microparticles in Laser-Light Traps. Indian J. Pure Appl. Phys. 1988, 26, 268–277. [Google Scholar]
- David, G.; Parmentier, E.A.; Taurino, I.; Signorell, R. Tracing the composition of single e-cigarette aerosol droplets in situ by laser-trapping and Raman scattering. Sci. Rep. 2020, 10, 1–8. [Google Scholar]
- Dennis-Smither, B.J.; Hanford, K.L.; Kwamena, N.-O.A.; Miles, R.E.H.; Reid, J.P. Phase, Morphology, and Hygroscopicity of Mixed Oleic Acid/Sodium Chloride/Water Aerosol Particles before and after Ozonolysis. J. Phys. Chem. A 2012, 116, 6159–6168. [Google Scholar] [CrossRef] [PubMed]
- Ishizaka, S.; Guo, F.; Tian, X.; Seng, S.; Tobon, Y.A.; Sobanska, S. In Situ Observation of Efflorescence and Deliquescence Phase Transitions of Single NaCl and NaNO3 Mixture Particles in Air Using a Laser Trapping Technique. Bull. Chem. Soc. Jpn. 2020, 93, 86–91. [Google Scholar] [CrossRef]
- King, M.D.; Thompson, K.C.; Ward, A.D.; Pfrang, C.; Hughes, B.R. Oxidation of biogenic and water-soluble compounds in aqueous and organic aerosol droplets by ozone: A kinetic and product analysis approach using laser Raman tweezers. Faraday Discuss. 2008, 137, 173–192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parmentier, E.A.; David, G.; Arroyo, P.C.; Bibawi, S.; Esat, K.; Signorell, R. Photochemistry of single optically trapped oleic acid droplets. J. Aerosol Sci. 2021, 151. [Google Scholar] [CrossRef]
- Athanasiadis, A.; Fitzgerald, C.; Davidson, N.M.; Giorio, C.; Botchway, S.W.; Ward, A.D.; Kalberer, M.; Pope, F.D.; Kuimova, M.K. Dynamic viscosity mapping of the oxidation of squalene aerosol particles. Phys. Chem. Chem. Phys. 2016, 18, 30385–30393. [Google Scholar] [CrossRef] [Green Version]
- Stewart, D.J.; Cai, C.; Nayler, J.; Preston, T.C.; Reid, J.P.; Krieger, U.K.; Marcolli, C.; Zhang, Y.H. Liquid-Liquid Phase Separation in Mixed Organic/Inorganic Single Aqueous Aerosol Droplets. J. Phys. Chem. A 2015, 119, 4177–4190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, M.; Marcolli, C.; Krieger, U.K.; Zuend, A.; Peter, T. Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles. Atmos. Chem. Phys. 2012, 12, 2691–2712. [Google Scholar] [CrossRef] [Green Version]
- Ciobanu, V.G.; Marcolli, C.; Krieger, U.K.; Weers, U.; Peter, T. Liquid-Liquid Phase Separation in Mixed Organic/Inorganic Aerosol Particles. J. Phys. Chem. A 2009, 113, 10966–10978. [Google Scholar] [CrossRef] [PubMed]
- Kwamena, N.O.A.; Buajarern, J.; Reid, J.P. Equilibrium Morphology of Mixed Organic/Inorganic/Aqueous Aerosol Droplets: Investigating the Effect of Relative Humidity and Surfactants. J. Phys. Chem. A 2010, 114, 5787–5795. [Google Scholar] [CrossRef]
- Lettieri, T.R.; Preston, R.E. Observation of sharp resonances in the spontaneous Raman spectrum of a single optically levitated microdroplet. Opt. Commun. 1985, 54, 349–352. [Google Scholar] [CrossRef]
- Schweiger, G. Observation of Morphology-Dependent Resonances Caused by the Input Field in the Raman-Spectrum of Microdroplets. J. Raman Spectrosc. 1990, 21, 165–168. [Google Scholar] [CrossRef]
- Schweiger, G. Observation of Input and Output Structural Resonances in the Raman-Spectrum of a Single Spheroidal Dielectric Microparticle. Opt. Lett. 1990, 15, 156–158. [Google Scholar] [CrossRef]
- Schaschek, K.; Popp, J.; Kiefer, W. Morphology Dependent Resonances in Raman-Spectra of Optically Levitated Microparticles—Determination of Radius and Evaporation Rate of Single Glycerol Water Droplets by Means of Internal-Mode Assignment. Ber. Bunsen. Phys. Chem. 1993, 97, 1007–1011. [Google Scholar] [CrossRef]
- Mitchem, L.; Reid, J.P. Optical manipulation and characterisation of aerosol particles using a single-beam gradient force optical trap. Chem. Soc. Rev. 2008, 37, 756–769. [Google Scholar] [CrossRef] [PubMed]
- Gorkowski, K.; Beydoun, H.; Aboff, M.; Walker, J.S.; Reid, J.P.; Sullivan, R.C. Advanced aerosol optical tweezers chamber design to facilitate phase-separation and equilibration timescale experiments on complex droplets. Aerosol Sci. Technol. 2016, 50, 1327–1341. [Google Scholar] [CrossRef]
- Sullivan, R.C.; Boyer-Chelmo, H.; Gorkowski, K.; Beydoun, H. Aerosol Optical Tweezers Elucidate the Chemistry, Acidity, Phase Separations, and Morphology of Atmospheric Microdroplets. Acc. Chem. Res. 2020, 53, 2498–2509. [Google Scholar] [CrossRef] [PubMed]
- Mitchem, L.; Buajarern, J.; Hopkins, R.J.; Ward, A.D.; Gilham, R.J.J.; Johnston, R.L.; Reid, J.P. Spectroscopy of growing and evaporating water droplets: Exploring the variation in equilibrium droplet size with relative humidity. J. Phys. Chem. A 2006, 110, 8116–8125. [Google Scholar] [CrossRef] [PubMed]
- Snow, J.B.; Qian, S.X.; Chang, R.K. Stimulated Raman-Scattering from Individual Water and Ethanol Droplets at Morphology-Dependent Resonances. Opt. Lett. 1985, 10, 37–39. [Google Scholar] [CrossRef] [PubMed]
- Mazumder, M.M.; Schaschek, K.; Chang, R.K.; Gillespie, J.B. Efficient Pumping of Minority Species Stimulated Raman-Scattering (Srs) by Majority Species Srs in a Microdroplet of a Binary Mixture. Chem. Phys. Lett. 1995, 239, 361–368. [Google Scholar] [CrossRef]
- Pasternack, L.; Fleming, J.W.; Owrutsky, J.C. Optically seeded stimulated Raman scattering of aqueous sulfate microdroplets. J. Opt. Soc. Am. B 1996, 13, 1510–1516. [Google Scholar] [CrossRef]
- Mitchem, L.; Buajarern, J.; Ward, A.D.; Reid, J.P. A strategy for characterizing the mixing state of immiscible aerosol components and the formation of multiphase aerosol particles through coagulation. J. Phys. Chem. B 2006, 110, 13700–13703. [Google Scholar] [CrossRef]
- Kuriakose, S.; Morrish, D.; Gan, X.; Chon, J.W.M.; Dholakia, K.; Gu, M. Near-field optical trapping with an ultrashort pulsed laser beam. Appl. Phys. Lett. 2008, 92. [Google Scholar] [CrossRef]
- Bhatt, J.; Kumar, A.; Singh, R.P.; Jaaffrey, S.N.A. Optical trapping of fluorescent beads. J. Exp. Nanosci. 2015, 10, 290–298. [Google Scholar] [CrossRef]
- Gong, Z.Y.; Pan, Y.L.; Videen, G.; Wang, C.J. The temporal evolution process from fluorescence bleaching to clean Raman spectra of single solid particles optically trapped in air. Chem. Phys. Lett. 2017, 689, 100–104. [Google Scholar] [CrossRef]
- Tzeng, H.M.; Wall, K.F.; Long, M.B.; Chang, R.K. Evaporation and condensation rates of liquid droplets deduced from structure resonances in the fluorescence spectra. Opt. Lett. 1984, 9, 273–275. [Google Scholar] [CrossRef]
- Pastel, R.; Struthers, A. Measuring evaporation rates of laser-trapped droplets by use of fluorescent morphology-dependent resonances. Appl. Opt. 2001, 40, 2510–2514. [Google Scholar] [CrossRef]
- Thompson, D.B.; Keating, D.A.; Guler, E.; Ichimura, K.; Williams, M.E.; Fuller, K.A. Separation-sensitive measurements of morphology dependent resonances in coupled fluorescent microspheres. Opt. Express 2010, 18, 19209–19218. [Google Scholar] [CrossRef] [PubMed]
- Gallou, G.; Sirven, J.B.; Dutouquet, C.; Le Bihan, O.; Frejafon, E. Aerosols Analysis by LIBS for Monitoring of Air Pollution by Industrial Sources. Aerosol Sci. Technol. 2011, 45, 918–926. [Google Scholar] [CrossRef]
- Boudhib, M.; Hermann, J.; Dutouquet, C. Compositional Analysis of Aerosols Using Calibration-Free Laser-Induced Breakdown Spectroscopy. Anal. Chem. 2016, 88, 4029–4035. [Google Scholar] [CrossRef] [PubMed]
- Hahn, D.W.; Lunden, M.M. Detection and analysis of aerosol particles by laser-induced breakdown spectroscopy. Aerosol Sci. Technol. 2000, 33, 30–48. [Google Scholar] [CrossRef] [Green Version]
- Hettinger, B.; Hohreiter, V.; Swingle, M.; Hahn, D.W. Laser-induced breakdown spectroscopy for ambient air particulate monitoring: Correlation of total and speciated aerosol particle counts. Appl. Spectrosc. 2006, 60, 237–245. [Google Scholar] [CrossRef]
- Dutouquet, C.; Gallou, G.; Le Bihan, O.; Sirven, J.B.; Dermigny, A.; Torralba, B.; Frejafon, E. Monitoring of heavy metal particle emission in the exhaust duct of a foundry using LIBS. Talanta 2014, 127, 75–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, G.; Kim, K.; Maeng, H.; Lee, H.; Park, K. Development of Aerosol-LIBS (Laser Induced Breakdown Spectroscopy) for Real-time Monitoring of Process-induced Particles. Aerosol Air Qual. Res. 2019, 19, 455–460. [Google Scholar] [CrossRef]
- Park, K.; Cho, G.; Kwak, J.H. Development of an Aerosol Focusing-Laser Induced Breakdown Spectroscopy (Aerosol Focusing-LIBS) for Determination of Fine and Ultrafine Metal Aerosols. Aerosol Sci. Technol. 2009, 43, 375–386. [Google Scholar] [CrossRef] [Green Version]
- Fortes, F.J.; Cabalín, L.M.; Laserna, J.J. Laser-induced breakdown spectroscopy of solid aerosols produced by optical catapulting. Spectrochim. Acta Part B At. Spectrosc. 2009, 64, 642–648. [Google Scholar] [CrossRef]
- Fortes, F.J.; Laserna, J.J. Characteristics of solid aerosols produced by optical catapulting studied by laser-induced breakdown spectroscopy. Appl. Surface Sci. 2010, 256, 5924–5928. [Google Scholar] [CrossRef]
- Fortes, F.J.; Fernandez-Bravo, A.; Laserna, J.J. Chemical characterization of single micro- and nano-particles by optical catapulting-optical trapping-laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2014, 100, 78–85. [Google Scholar] [CrossRef]
- Purohit, P.; Fortes, F.J.; Laserna, J.J. Spectral Identification in the Attogram Regime through Laser-Induced Emission of Single Optically Trapped Nanoparticles in Air. Angew. Chem. Int. Ed. 2017, 56, 14178–14182. [Google Scholar] [CrossRef]
- Purohit, P.; Fortes, F.J.; Laserna, J.J. Subfemtogram Simultaneous Elemental Detection in Multicomponent Nanomatrices Using Laser-Induced Plasma Emission Spectroscopy within Atmospheric Pressure Optical Traps. Anal. Chem. 2019, 91, 7444–7449. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.W.; Zhu, Y.; Li, S.F.; Zhu, L.G. Reutilization of nanosecond pulse laser energy and its performance in single particle triggered LIBS. RSC Adv. 2018, 8, 41915–41919. [Google Scholar] [CrossRef] [Green Version]
- Tahara, T.; Quan, X.Y.; Otani, R.; Takaki, Y.; Matoba, O. Digital holography and its multidimensional imaging applications: A review. Microscopy 2018, 67, 55–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berg, M.J.; Videen, G. Digital holographic imaging of aerosol particles in flight. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1776–1783. [Google Scholar] [CrossRef] [Green Version]
- David, G.; Esat, K.; Thanopulos, I.; Signorell, R. Digital holography of optically-trapped aerosol particles. Commun. Chem. 2018, 1, 46. [Google Scholar] [CrossRef]
- Horstmeyer, R.; Chung, J.; Ou, X.Z.; Zheng, G.A.; Yang, C.H. Diffraction tomography with Fourier ptychography. Optica 2016, 3, 827–835. [Google Scholar] [CrossRef]
- Zheng, G.A.; Shen, C.; Jiang, S.W.; Song, P.M.; Yang, C.H.E. Concept, implementations and applications of Fourier ptychography. Nat. Rev. Phys. 2021. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, J.; Park, Y. Simultaneous 3D visualization and position tracking of optically trapped particles using optical diffraction tomography. Optica 2015, 2, 343–346. [Google Scholar] [CrossRef]
- Higuchi, T.; Pham, Q.D.; Hasegawa, S.; Hayasaki, Y. Three-dimensional positioning of optically trapped nanoparticles. Appl. Opt. 2011, 50, H183–H188. [Google Scholar] [CrossRef] [PubMed]
- Hayasaki, Y.; Sato, A. Three-dimensional position measurement of a gold nanoparticle trapped in optical tweezers using in-line low-coherence digital holography. In Proceedings of the 11th Euro-American Workshop on Information Optics (Wio), Quebec, QC, Canada, 20–24 August 2012. [Google Scholar]
- Hayasaki, Y.; Sato, A. Holographic three-dimensional motion detection of an optically trapped sub-100 nm gold nanoparticle. Opt. Commun. 2014, 322, 22–26. [Google Scholar] [CrossRef]
- Sato, A.; Pham, Q.D.; Hasegawa, S.; Hayasaki, Y. Three-dimensional subpixel estimation in holographic position measurement of an optically trapped nanoparticle. Appl. Opt. 2013, 52, A216–A222. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalume, A.; Wang, C.; Pan, Y.-L. Optical-Trapping Laser Techniques for Characterizing Airborne Aerosol Particles and Its Application in Chemical Aerosol Study. Micromachines 2021, 12, 466. https://doi.org/10.3390/mi12040466
Kalume A, Wang C, Pan Y-L. Optical-Trapping Laser Techniques for Characterizing Airborne Aerosol Particles and Its Application in Chemical Aerosol Study. Micromachines. 2021; 12(4):466. https://doi.org/10.3390/mi12040466
Chicago/Turabian StyleKalume, Aimable, Chuji Wang, and Yong-Le Pan. 2021. "Optical-Trapping Laser Techniques for Characterizing Airborne Aerosol Particles and Its Application in Chemical Aerosol Study" Micromachines 12, no. 4: 466. https://doi.org/10.3390/mi12040466
APA StyleKalume, A., Wang, C., & Pan, Y. -L. (2021). Optical-Trapping Laser Techniques for Characterizing Airborne Aerosol Particles and Its Application in Chemical Aerosol Study. Micromachines, 12(4), 466. https://doi.org/10.3390/mi12040466






