An Investigation on Internal Material Loads and Modifications in Precision Turning of Steel 42CrMo4
Abstract
:1. Introduction
2. Materials and Methods
2.1. Workpiece Material
2.2. Cutting Tools
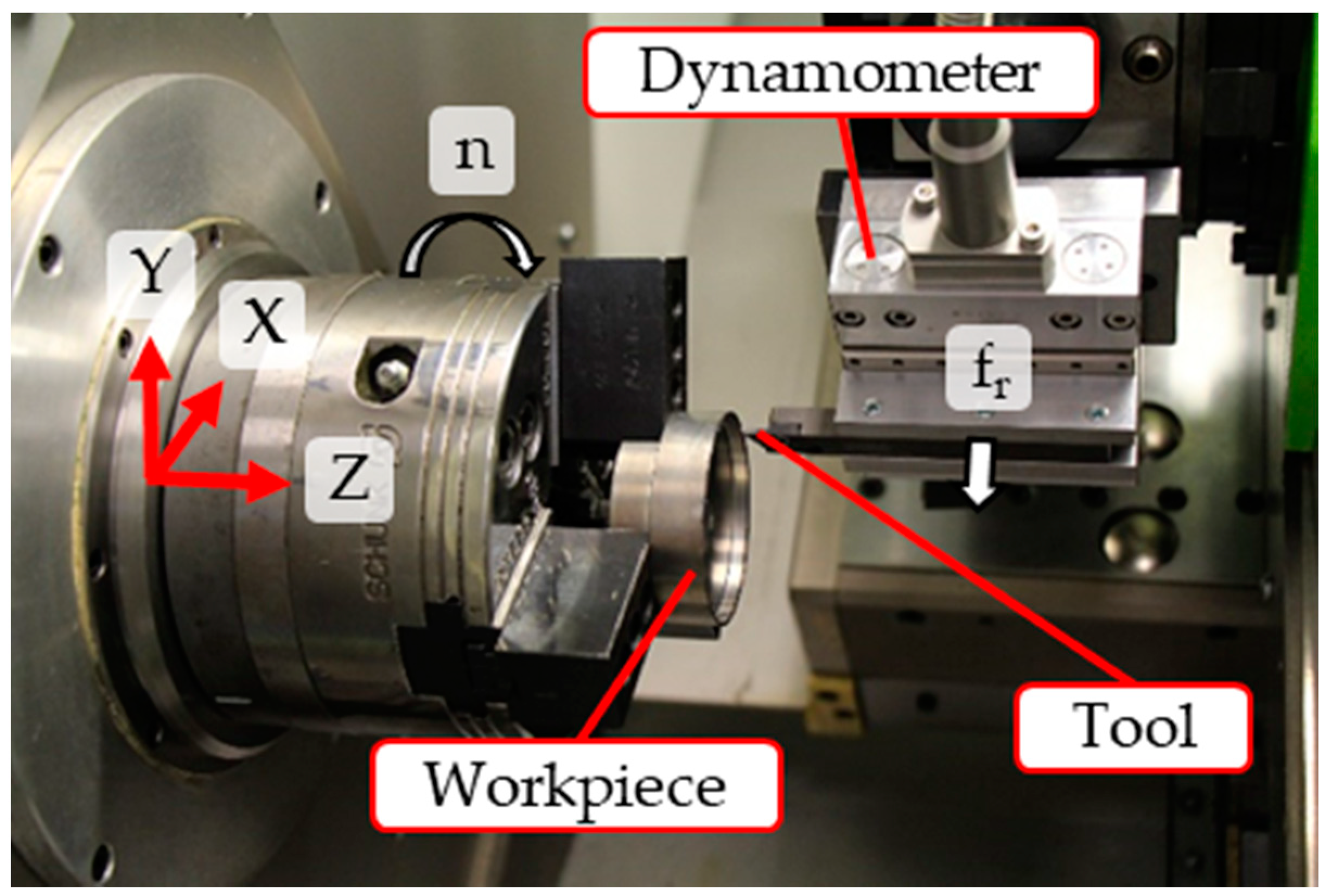
2.3. Experimental Procedure
2.4. Residual Stress Analysis
2.5. Modelling and Simulation
2.5.1. Material Model
2.5.2. Friction Model
2.5.3. Boundary Conditions and Mesh
2.5.4. Mass Scaling of Workpiece for Computational Efficiency
3. Results
3.1. Measurement Results
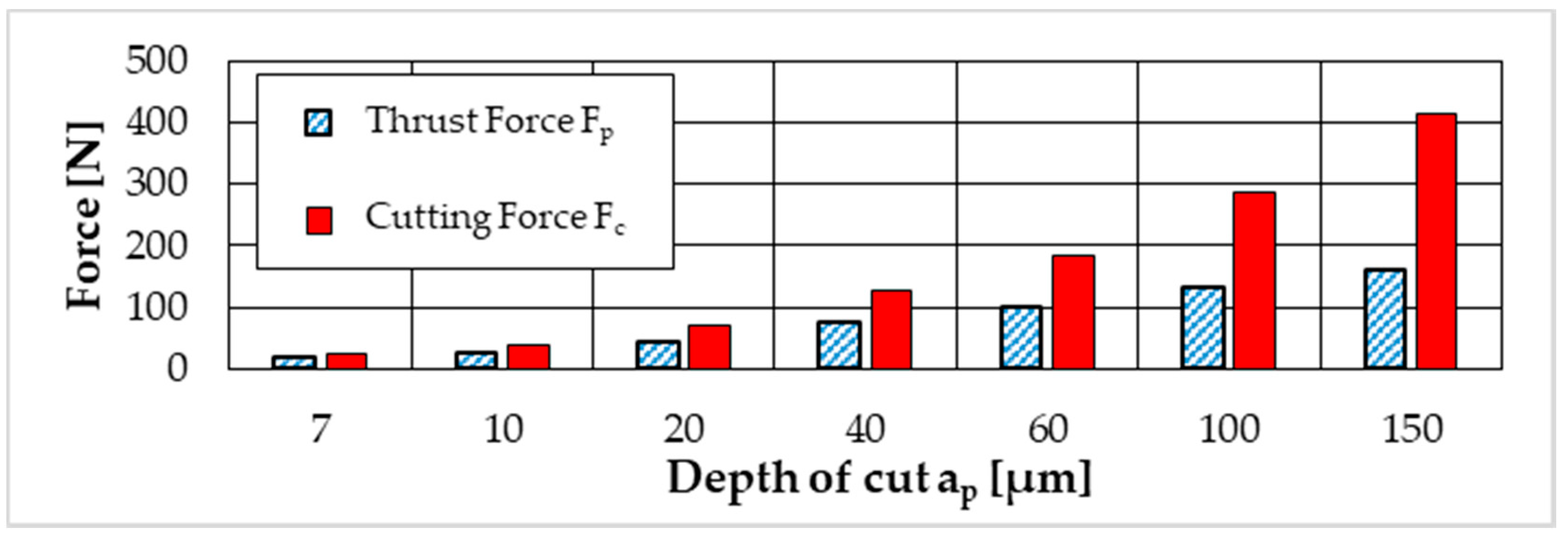
3.1.1. Process Forces
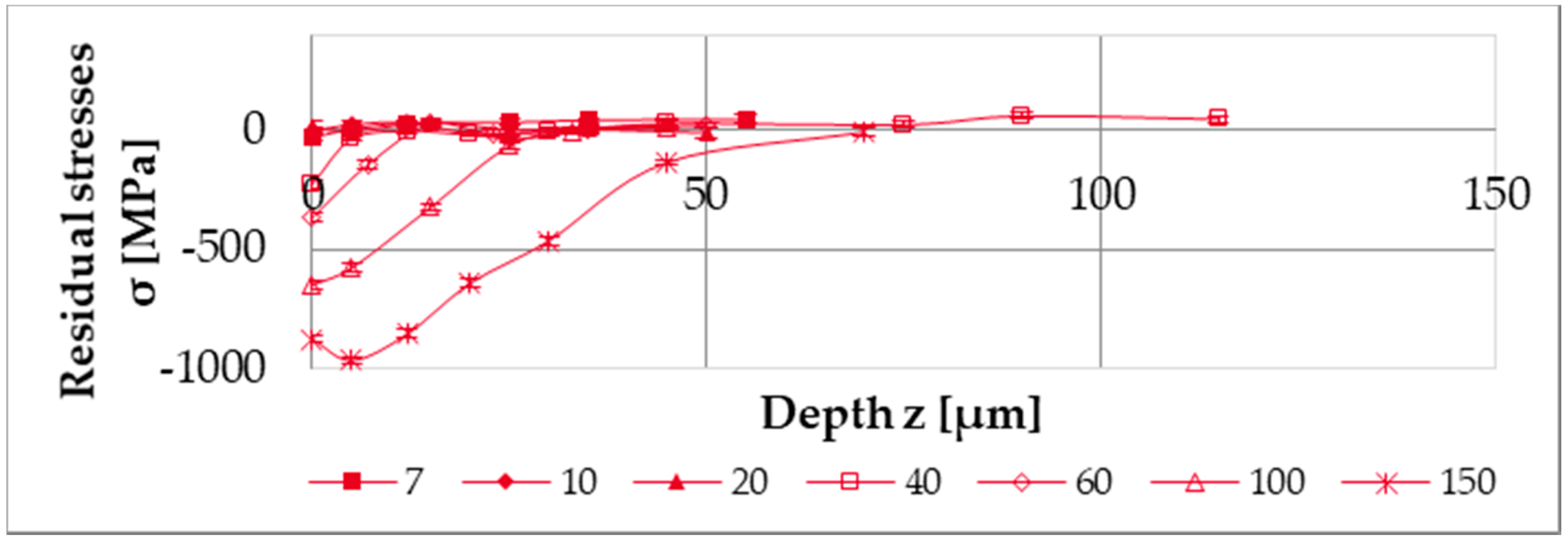
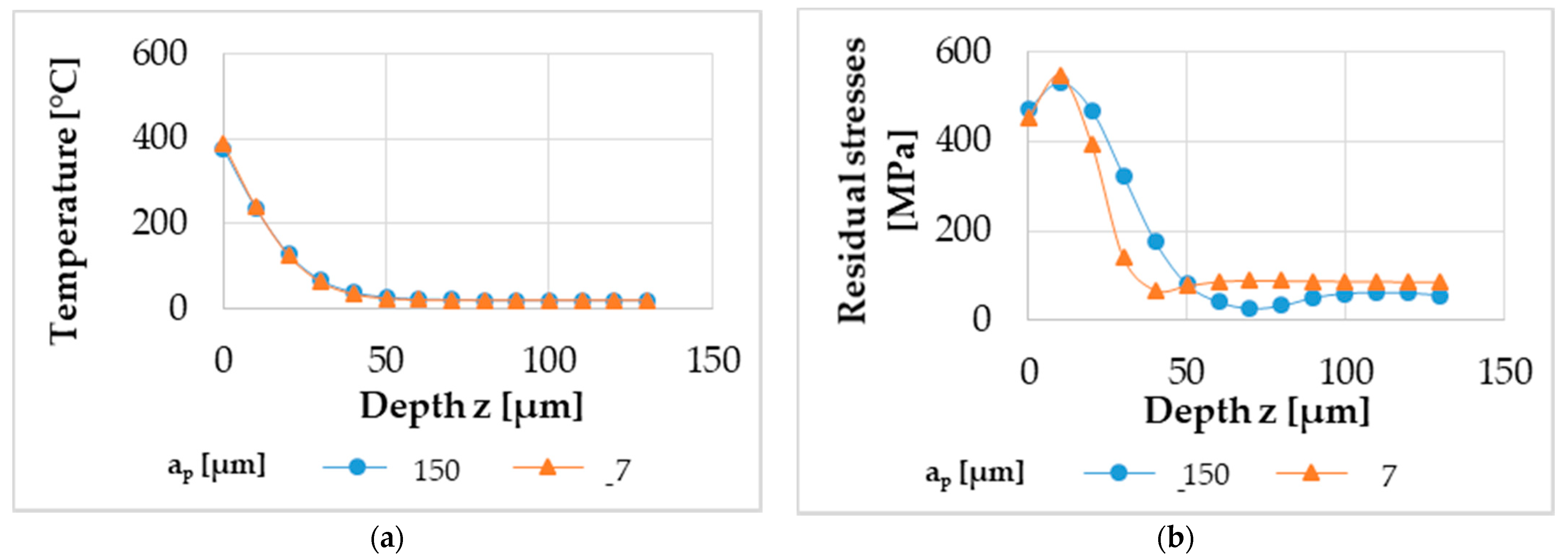
3.1.2. Residual Stresses
3.2. Simulation Results
3.2.1. Process Forces
3.2.2. Material Loads
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Field, M.; Kahles, J.F. Review of surface integrity of machined components. CIRP. Ann. Manuf. Technol. 1971, 20, 491–510. [Google Scholar]
- Brinksmeier, E.; Reese, S.; Klink, A.; Langenhorst, L.; Lübben, T.; Meinke, M.; Meyer, D.; Riemer, O.; Sölter, J. Underlying mechanisms for developing process signatures in manufacturing. Nanomanuf. Metrol. 2018, 1, 193–208. [Google Scholar] [CrossRef] [Green Version]
- Brinksmeier, E.; Gläbe, R.; Klocke, F.; Lucca, D.A. Process signatures an alternative approach to predicting functional workpiece properties. Procedia Eng. 2011, 19, 44–52. [Google Scholar] [CrossRef] [Green Version]
- Mansori, M.E.; Mezghani, S.; Sabri, L.; Zahouani, H. On concept of process signature in analysis of multistage surface formation. Surf. Eng. 2010, 26, 216–223. [Google Scholar] [CrossRef]
- Gräbner, D.; Zielinski, T.; Vovk, A.; Riemer, O.; Karpuschewski, B.; Lang, W. An investigation on high-resolution temperature measurement in precision fly-cutting. Sensors 2021, 21, 1530. [Google Scholar] [CrossRef] [PubMed]
- Ducobu, F.; Rivière-Lorphèvre, E.; Galindo-Fernandez, E.; Ayvar-Soberanis, S.; Arrazola, P.-J.; Ghadbeigi, H. Coupled eulerian-lagrangian (CEL) simulation for modelling of chip formation in AA2024-T3. Procedia CIRP 2019, 82, 142–147. [Google Scholar] [CrossRef]
- Ducobu, F.; Rivière-Lorphèvrea, E.; Filippi, E. Application of the coupled eulerian-lagrangian (CEL) method to the modeling of orthogonal cutting. Eur. J. Mech. 2016, 59, 58–66. [Google Scholar] [CrossRef]
- Abdelhafeez, A.; Soo, S.; Aspinwall, D.; Dowson, A.; Arnold, D. A coupled eulerian lagrangian finite element model of drilling titanium and aluminium alloys. Int. J. Aerosp. 2016, 9, 198–207. [Google Scholar] [CrossRef]
- Moussa, N.B.; Sidhom, H.; Braham, C. Numerical and experimental analysis of residual stress and plastic strain distributions in machined stainless steel. Int. J. Mech. Sci. 2012, 64, 82–93. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress: Measurement by Diffraction and Interpretation; Springer: New York, NY, USA, 2013. [Google Scholar]
- Seo, S.; Min, O.; Yang, H. Constitutive equation for Ti–6Al–4V at high temperatures measured using the SHPB technique. Int. J. Impact Eng. 2005, 31, 735–754. [Google Scholar] [CrossRef]
- Rech, J.; Arrazola, P.J.; Claudin, C.; Courbon, C.; Pusavec, F.; Kopac, J. Characterisation of friction and heat partition coefficients at the tool-work material interface in cutting. CIRP Ann. 2013, 62, 79–82. [Google Scholar] [CrossRef]
- Zorev, N. Inter-relationship between shear processes occurring along tool face and shear plane in metal cutting. In Proceedings of the Thirteenth International Machine Tool Design and Research Conference, Berlin, Germany, 18–22 September 1972. [Google Scholar]
- Özel, T.; Altan, T. Determination of workpiece flow stress and friction at the chip–tool contact for high-speed cutting. Int. J. Mach. Tools Manuf. 2000, 40, 133–152. [Google Scholar] [CrossRef]
- Ducobu, F.; Rivière-Lorphèvre, E.; Filippi, E. Mesh influence in orthogonal cutting modelling with the coupled eulerian-lagrangian (CEL) method. Eur. J. Mech. 2017, 65, 324–335. [Google Scholar] [CrossRef]
- Hammelmüller, F.; Zehetner, C. Increasing numerical efficiency in coupled Eulerian-Lagrangian metal forming simulations. In Proceedings of the XIII International Conference on Computational Plasticity, Fundamentals and Applications, Barcelona, Spain, 1–3 September 2015; pp. 727–733. [Google Scholar]
- Vovk, A.; Sölter, J.; Karpuschewski, B. Finite element simulations of the material loads and residual stresses in milling utilizing the CEL method. Procedia CIRP 2020, 87, 539–544. [Google Scholar] [CrossRef]
- Frerichs, F.; Sölter, J.; Lübben, T.; Brinksmeier, E.; Zoch, H.-W. A simulation based development of process signatures for manufacturing processes with thermal loads. Procedia CIRP 2016, 45, 327–330. [Google Scholar] [CrossRef] [Green Version]





| Material | C | Si | Mn | P | S | Cr | Mo |
|---|---|---|---|---|---|---|---|
| wt. % | 0.44 | 0.26 | 0.73 | 0.012 | 0.002 | 1.08 | 0.24 |
| Parameter | Value |
|---|---|
| Depth of cut ap (µm) | 7, 10, 20, 40, 60, 100, 150 |
| Cutting speed vc (m/min) | 100 |
| Feed fr (mm/rev) | 2.5 |
| Coolant | Dry |
| Parameter | Value |
|---|---|
| Radiation/Filter | Cr-Kα/V |
| Detector | Line detector |
| Primary beam | Ø 1 mm |
| Lattice plane | α{211} |
| Tube voltage/current | 33 kV/40 mA |
| Ψ angles | 11: from 45° to + 45° |
| Angular step | 0.1° |
| Angular range | 147° to 163° in 2θ |
| Coefficient | A (MPa) | B (MPa) | C | m | n | (°C) | (°C) | |
|---|---|---|---|---|---|---|---|---|
| Value | 900 | 650 | 0.034 | 0.328 | 0.45 | 0.001 | 1536 | 20 |
| Parameter | Material | Value |
|---|---|---|
| E (GPa) | AISI 4140 | 204 |
| ν | AISI 4140 | 0.3 |
| ρ (kg/m³) | AISI 4140 | 7850 |
| tungsten carbide | 15,000 | |
| k (W/mK) | AISI 4140 | 47 |
| tungsten carbide | 46 | |
| λ (1/K) | AISI 4140 | 12.3 × 10−6 |
| tungsten carbide | 4.7 × 10−6 | |
| Cp (J/kgK) | AISI 4140 | 475 |
| tungsten carbide | 203 | |
| Inelastic heat fraction | 0.9 |
| Parameter | Value |
|---|---|
| Columb friction coefficient | 0.6 |
| Friction energy converted to heat (%) | 100 |
| Fraction of converted heat distributed to tool surface | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zielinski, T.; Vovk, A.; Riemer, O.; Karpuschewski, B. An Investigation on Internal Material Loads and Modifications in Precision Turning of Steel 42CrMo4. Micromachines 2021, 12, 526. https://doi.org/10.3390/mi12050526
Zielinski T, Vovk A, Riemer O, Karpuschewski B. An Investigation on Internal Material Loads and Modifications in Precision Turning of Steel 42CrMo4. Micromachines. 2021; 12(5):526. https://doi.org/10.3390/mi12050526
Chicago/Turabian StyleZielinski, Tjarden, Andrey Vovk, Oltmann Riemer, and Bernhard Karpuschewski. 2021. "An Investigation on Internal Material Loads and Modifications in Precision Turning of Steel 42CrMo4" Micromachines 12, no. 5: 526. https://doi.org/10.3390/mi12050526
APA StyleZielinski, T., Vovk, A., Riemer, O., & Karpuschewski, B. (2021). An Investigation on Internal Material Loads and Modifications in Precision Turning of Steel 42CrMo4. Micromachines, 12(5), 526. https://doi.org/10.3390/mi12050526






