Coupling Analysis of Flexoelectric Effect on Functionally Graded Piezoelectric Cantilever Nanobeams
Abstract
:1. Introduction
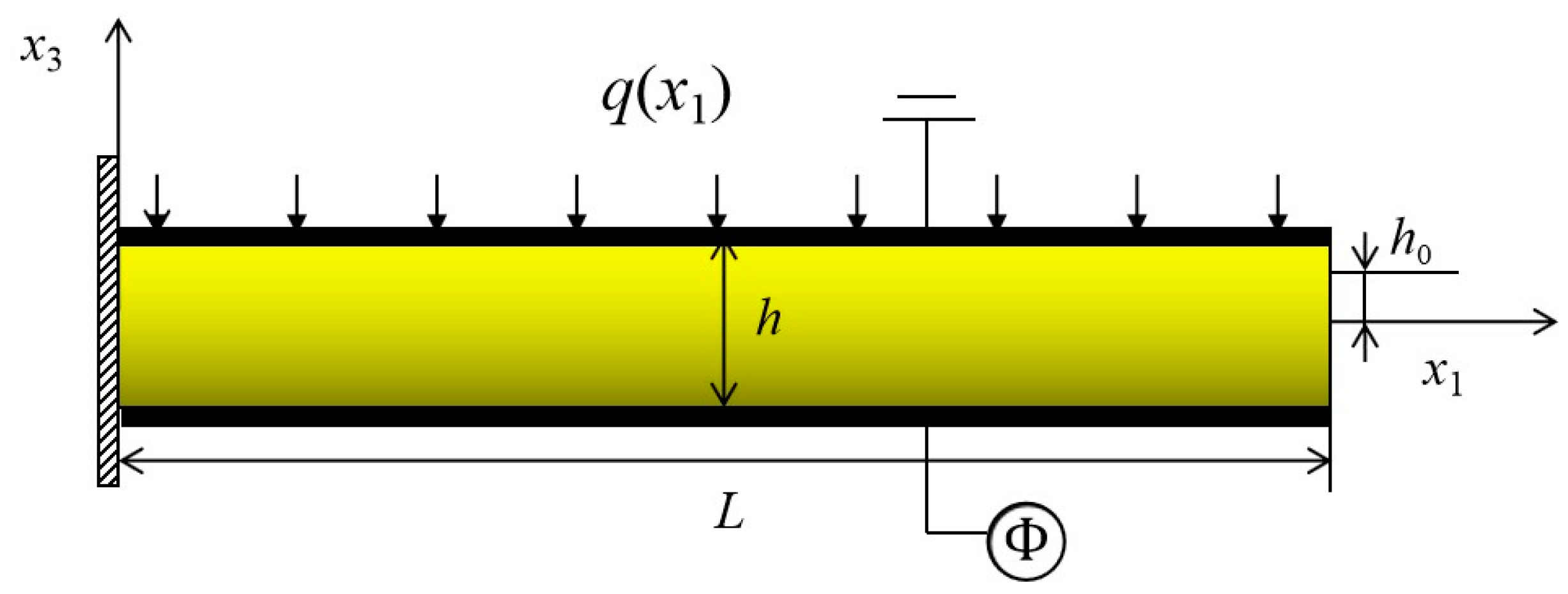
2. Formulation of Flexoelectric Materials
3. Beam Models of Functionally Graded Materials
4. Numerical Results and Discussion
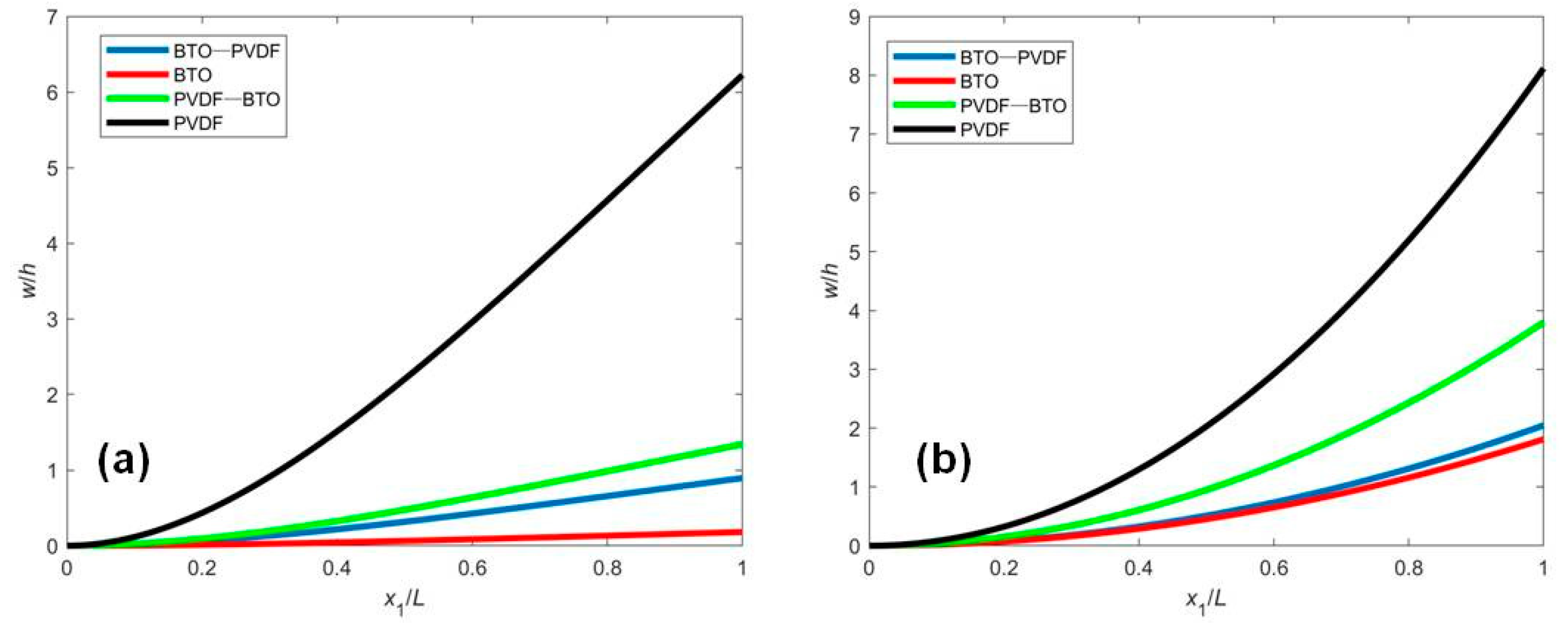
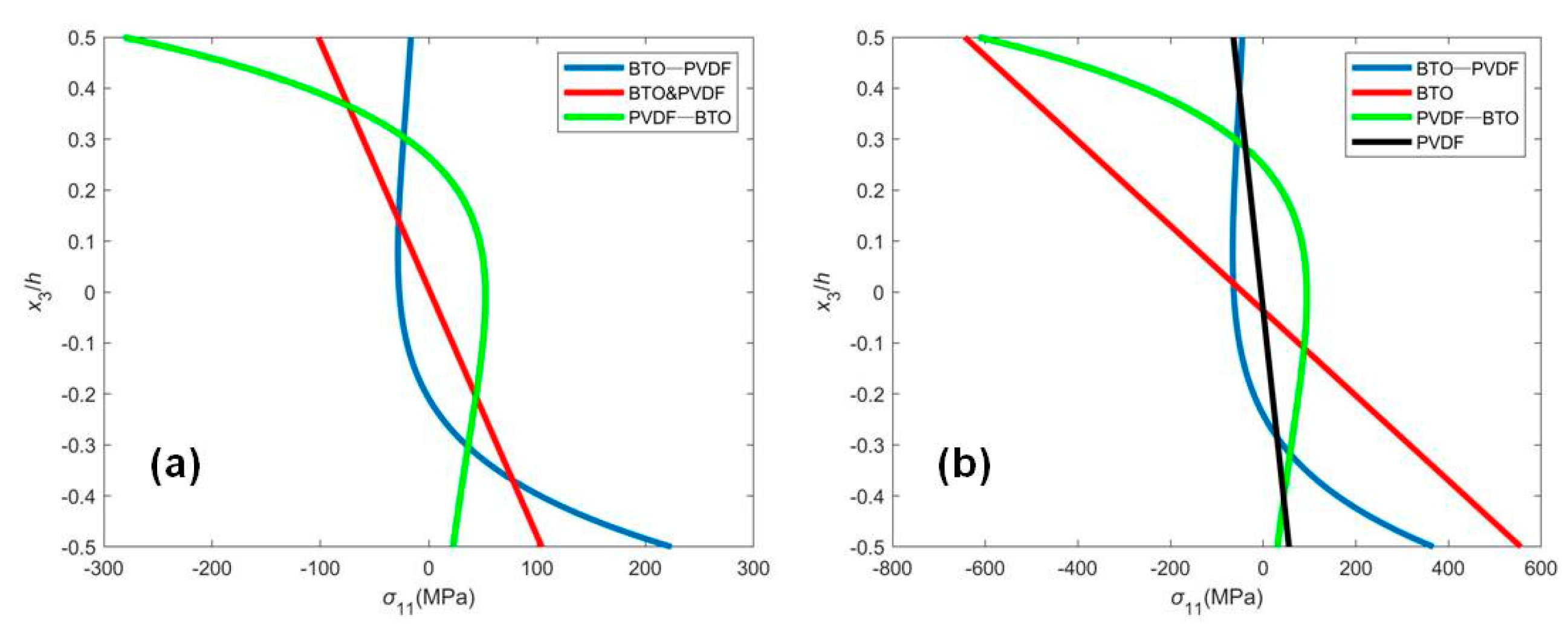
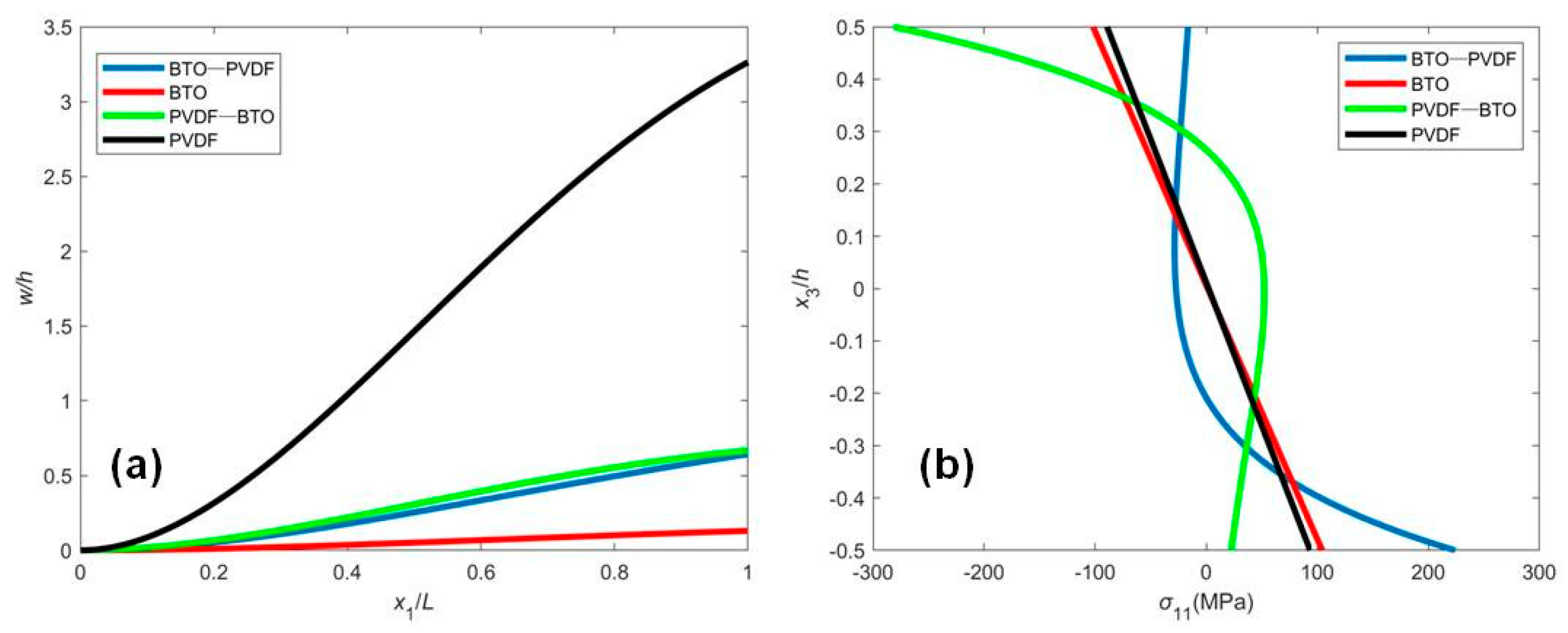
4.1. Closed Circuit with a Fixed External Electric Potential (CCF)
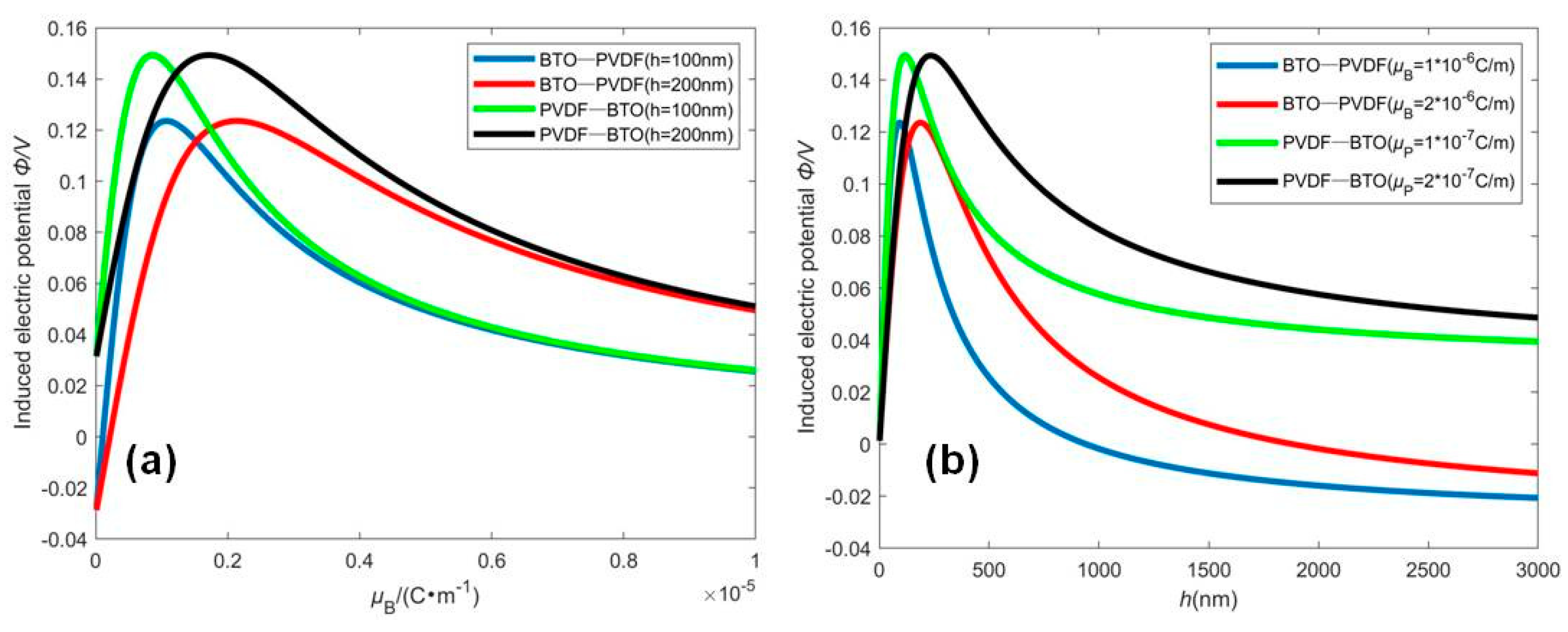
4.2. Open Circuit with Surface Electrodes and an Induced Electric Potential by Mechanical Deformation (OCI)
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, W.; Cross, L.E. Large flexoelectric polarization in ceramic lead magnesium niobite. Appl. Phys. Lett. 2001, 79, 4420–4422. [Google Scholar] [CrossRef]
- Madden, J.D.W.; Vandesteeg, N.A.; Anquetil, P.A.; Madden, P.G.A.; Takshi, A.; Pytel, R.Z.; Lafontaine, S.R.; Wieringa, P.A.; Hunter, I.W. Artificial muscle technology: Physical principles and naval prospects. IEEE J. Ocean. Eng. 2004, 29, 706–728. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Ann. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef] [Green Version]
- Labanca, M.; Azzola, F.; Vinci, R.; Rodella, L.F. Piezoelectric surgery: Twenty years of use. Br. J. Oral Maxillofac. Surg. 2008, 46, 265–269. [Google Scholar] [CrossRef]
- Cady, W.G.; Valasek, J. Piezoelectricity: An introduction to the theory and applications of electro-mechanical phenomena in crystals. Phys. Teach. 1965, 3, 130. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 65–99. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Hu, S.L.; Shen, S.P. Variational principles and governing equations in nano-dielectrics with the flexoelectric effect. Sci. China Phys. Mech. 2010, 53, 1497–1504. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 2013, 113, 194102. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Yang, C.P.; Su, Y.X.; Huang, R.; Lin, X.H. Electromechanical coupling in piezoelectric nanobeams due to flexoelectric effect. Smart Mater. Struct. 2017, 26, 095025. [Google Scholar] [CrossRef]
- Su, Y.X.; Zhou, Z.D.; Yang, F.P. Electromechanical analysis of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. AIP Adv. 2019, 9, 015207. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.X.; Zhou, Z.D. Electromechanical analysis of flexoelectric nanosensors based on nonlocal elasticity theory. Micromachines 2020, 11, 1077. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Lee, D. Exact solutions for nonlinear static responses of a shear deformable FGM beam under an in-plane thermal loading. Eur. J. Mech. A Solids 2012, 31, 13–20. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S.; Wang, Y.S. Axisymmetric postbuckling analysis of size-dependent functionally graded annular microplates using the physical neutral plane. Int. J. Eng. Sci. 2014, 81, 66–81. [Google Scholar] [CrossRef]
- Xin, L.; Dui, G.; Yang, S.; Zhang, J. An elasticity solution for functionally graded thick-walled tube subjected to internal pressure. Int. J. Mech. Sci. 2014, 89, 344–349. [Google Scholar] [CrossRef]
- Khoshgoftar, M.J.; Ghorbanpour Arani, A.; Arefi, M. Thermoelastic analysis of a thick-walled cylinder made of functionally graded piezoelectric material. Smart Mater. Struct. 2009, 18, 115007. [Google Scholar] [CrossRef]
- Chu, L.; Li, Y.; Dui, G. Nonlinear analysis of functionally graded flexoelectric nanoscale energy harvesters. Int. J. Mech. Sci. 2020, 167, 105282. [Google Scholar] [CrossRef]
- Yang, J.; Xiang, H.J. Thermo-electro-mechanical characteristics of functionally graded piezoelectric actuators. Smart Mater. Struct. 2007, 16, 784–797. [Google Scholar] [CrossRef]
- Abdollahi, A.; Arias, I. Constructive and destructive interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. J. Appl. Mech. Trans. ASME 2015, 82, 121003. [Google Scholar] [CrossRef] [Green Version]
- Mbarki, R.; Baccam, N.; Dayal, K.; Sharma, P. Piezoelectricity above the curie temperature? combining flexoelectricity and functional grading to enable high-temperature electromechanical coupling. Appl. Phys. Lett. 2014, 104, 122904. [Google Scholar] [CrossRef] [Green Version]
- Chu, L.; Dui, G.; Ju, C. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compo. Struct. 2017, 186, 39–49. [Google Scholar] [CrossRef]
- Xiang, S.; Kang, Y.L.; Li, X.F. Elasticity solution of functionally graded beams with consideration of the flexoelectric effect. J. Phys. D Appl. Phys. 2020, 53, 105301. [Google Scholar] [CrossRef]
- Chen, Q.; Zheng, S.; Li, Z.; Zeng, C. Size-dependent free vibration analysis of functionally graded porous piezoelectric sandwich nanobeam reinforced with graphene platelets with consideration of flexoelectric effect. Smart Mater. Struct. 2021, 30, 035008. [Google Scholar] [CrossRef]
- Abdollahi, A.; Vasquez-Sancho, F.; Catalan, G. Piezoelectric mimicry of flexoelectricity. Phys. Rev. Lett. 2018, 121, 205502. [Google Scholar] [CrossRef] [Green Version]
- Mao, S.; Purohit, P.K. Insights into flexoelectric solids from strain-gradient elasticity. J. Appl. Mech. 2014, 81, 081004. [Google Scholar] [CrossRef]
- He, Z.C.; Liu, G.R.; Zhong, Z.H.; Zhang, G.Y.; Cheng, A.G. Coupled analysis of 3D structural–acoustic problems using the edge-based smoothed finite element method/finite element method. Finite Elem. Anal. Des. 2010, 46, 1114–1121. [Google Scholar] [CrossRef]
- Sina, S.A.; Navazi, H.M.; Haddadpour, H. An analytical method for free vibration analysis of functionally graded beams. Mater. Des. 2009, 30, 741–747. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, Y.H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Hong, J.; Catalan, G.; Scott, J.F.; Artacho, E. The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 2010, 22, 112201. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Lv, J.; Liang, X.; Xu, M.; Shen, S. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 2016, 119, 094104. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, M.; Su, Y.; Zhou, Z. Coupling Analysis of Flexoelectric Effect on Functionally Graded Piezoelectric Cantilever Nanobeams. Micromachines 2021, 12, 595. https://doi.org/10.3390/mi12060595
Chen Y, Zhang M, Su Y, Zhou Z. Coupling Analysis of Flexoelectric Effect on Functionally Graded Piezoelectric Cantilever Nanobeams. Micromachines. 2021; 12(6):595. https://doi.org/10.3390/mi12060595
Chicago/Turabian StyleChen, Yuhang, Maomao Zhang, Yaxuan Su, and Zhidong Zhou. 2021. "Coupling Analysis of Flexoelectric Effect on Functionally Graded Piezoelectric Cantilever Nanobeams" Micromachines 12, no. 6: 595. https://doi.org/10.3390/mi12060595





