Femtosecond Laser-Pulse-Induced Surface Cleavage of Zinc Oxide Substrate
Abstract
:1. Introduction
2. Experimental Details
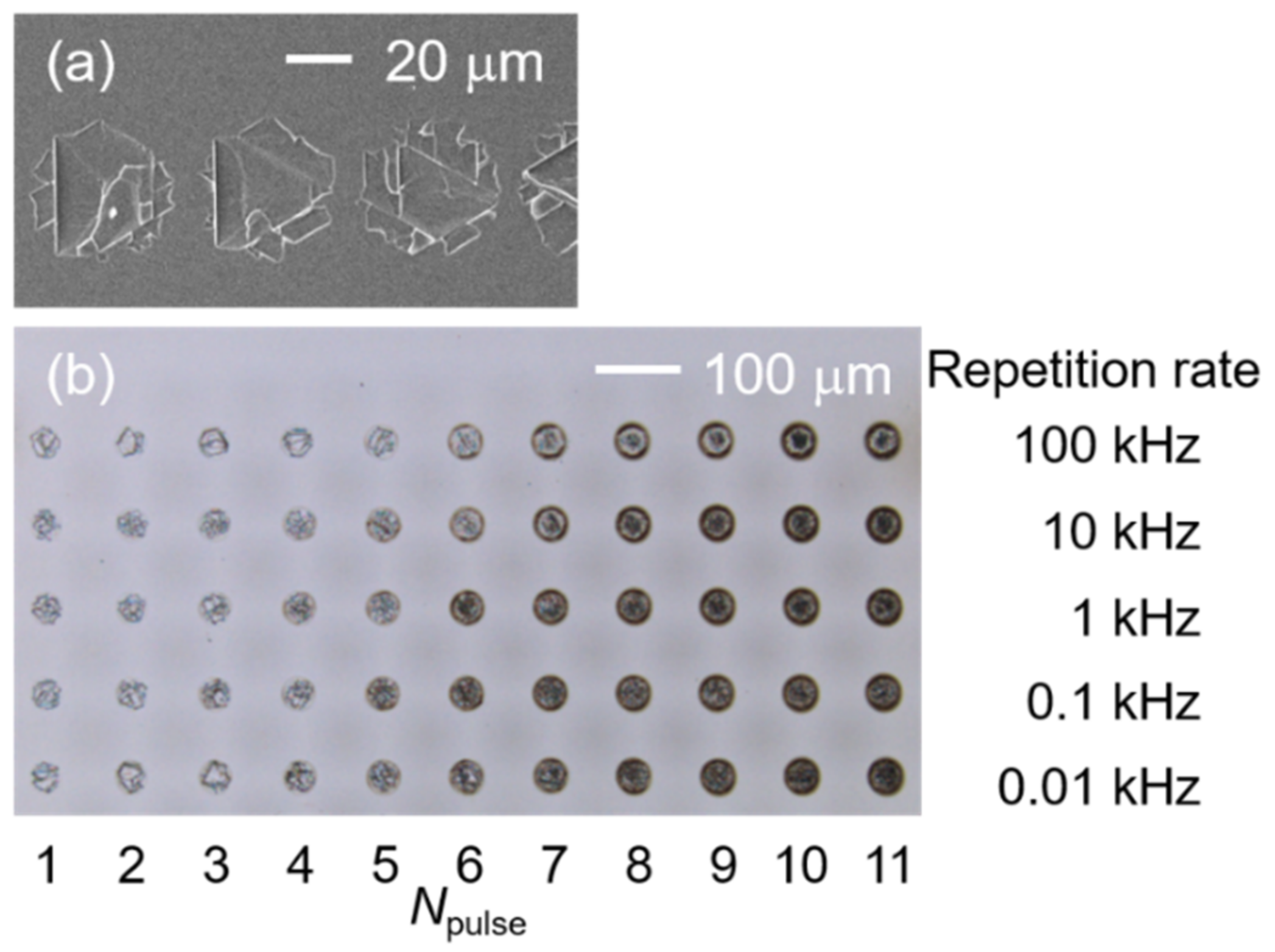
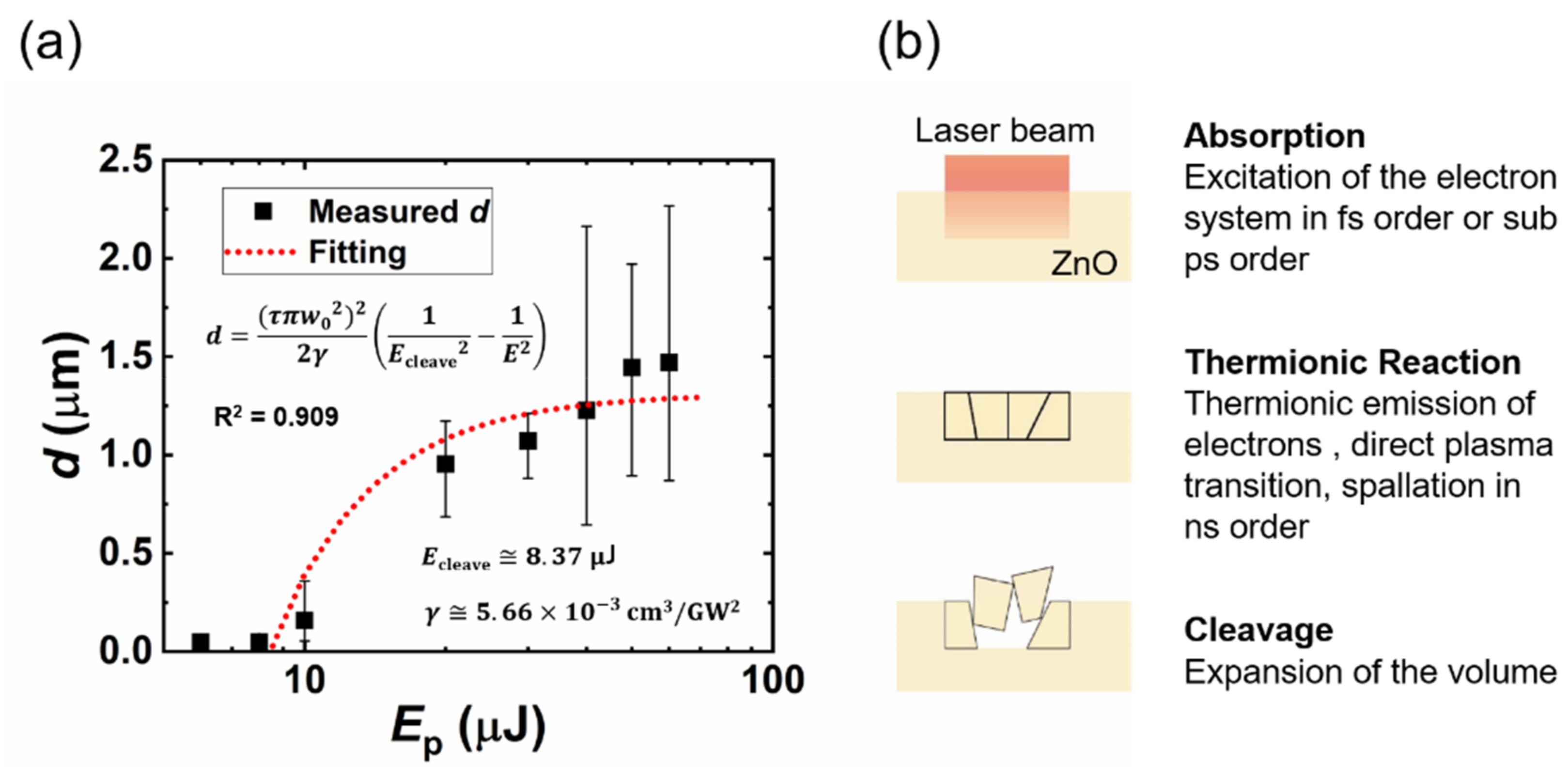
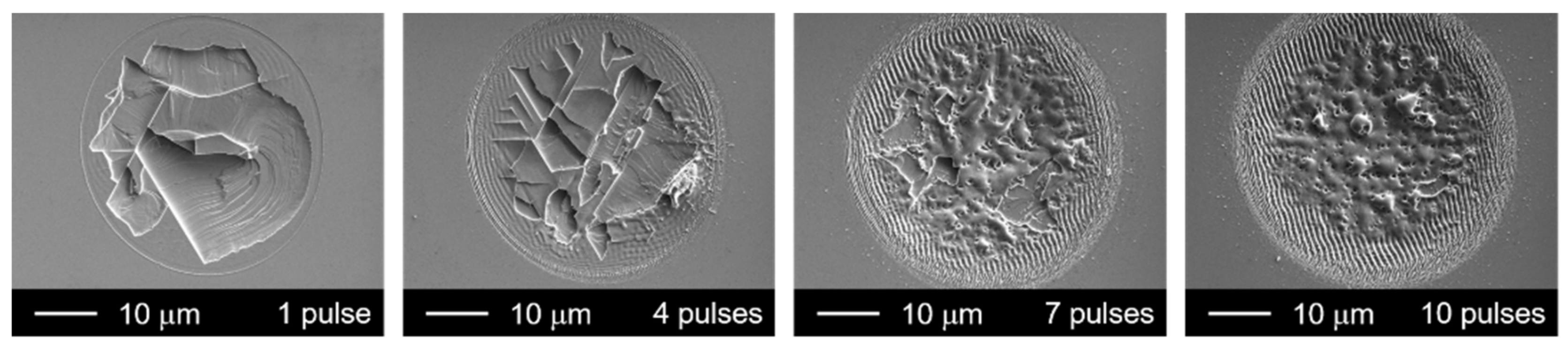
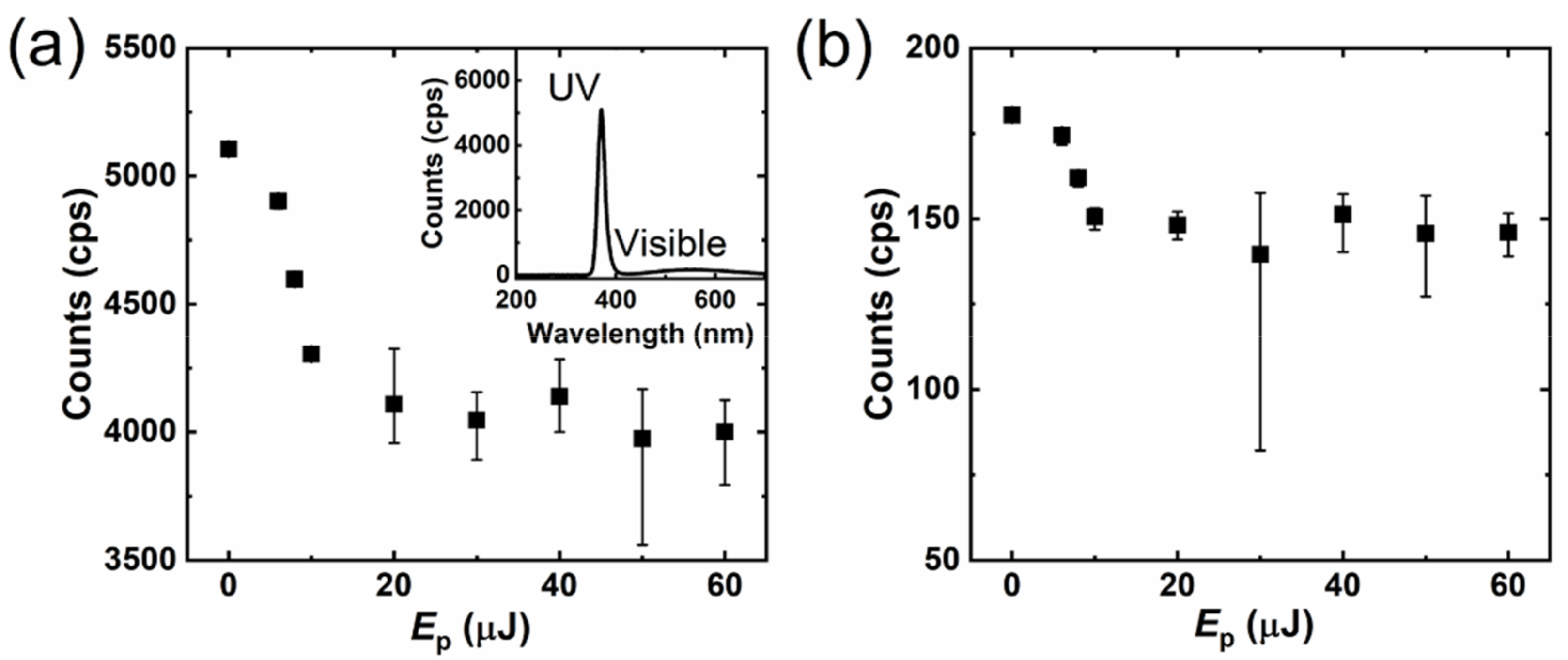
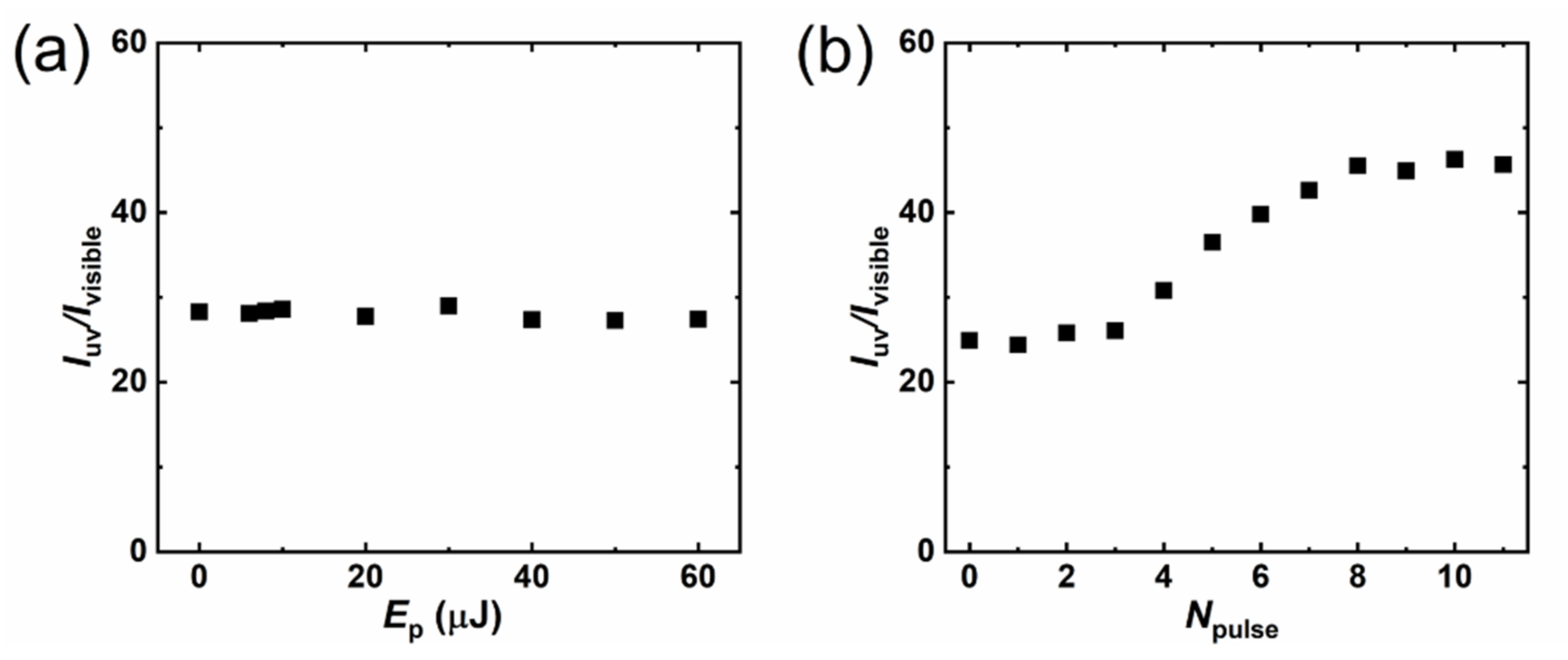
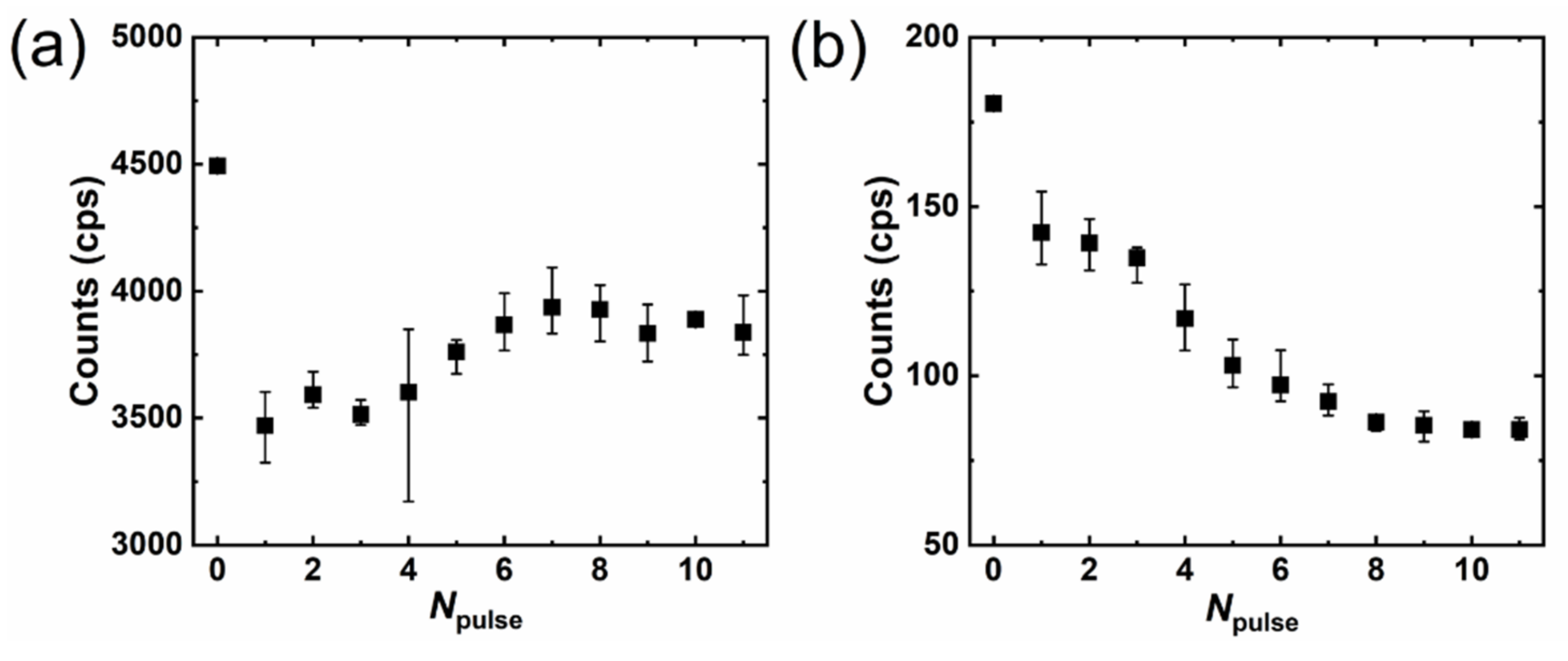
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doǧan, S.; Avrutin, V.; Cho, S.J.; Morko, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 11. [Google Scholar] [CrossRef] [Green Version]
- Series, S. Transparent Conductive Zinc Oxide; Ellmer, K., Klein, A., Rech, B., Eds.; Springer Series in Materials Science: Berlin/Heidelberg, Germany, 2008; Volume 104, ISBN 978-3-540-73611-0. [Google Scholar]
- Look, D.C.; Claflin, B.; Alivov, Y.I.; Park, S.J. The future of ZnO light emitters. Phys. Status Solidi C 2004, 1, 2203–2212. [Google Scholar] [CrossRef]
- Khokhra, R.; Bharti, B.; Lee, H.-N.; Kumar, R. Visible and UV photo-detection in ZnO nanostructured thin films via simple tuning of solution method. Sci. Rep. 2017, 7, 15032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adler, B.L.; DeLeo, V.A. Sunscreen Safety: A Review of Recent Studies on Humans and the Environment. Curr. Dermatol. Rep. 2020, 9, 1–9. [Google Scholar] [CrossRef]
- Vecht, A.; Gibbons, C.; Davies, D.; Jing, X.; Marsh, P.; Ireland, T.; Silver, J.; Newport, A.; Barber, D. Engineering phosphors for field emission displays. J. Vac. Sci. Technol. B 1999, 17, 750. [Google Scholar] [CrossRef]
- Seager, C.H.; Warren, W.L.; Tallant, D.R. Electron-beam-induced charging of phosphors for low voltage display applications. J. Appl. Phys. 1997, 81, 7994–8001. [Google Scholar] [CrossRef]
- Ono, S.; Murakami, H.; Quema, A.; Diwa, G.; Sarukura, N.; Nagasaka, R.; Ichikawa, Y.; Ogino, H.; Ohshima, E.; Yoshikawa, A.; et al. Generation of terahertz radiation using zinc oxide as photoconductive material excited by ultraviolet pulses. Appl. Phys. Lett. 2005, 87, 261112. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, J.; Kim, B.G.; Yee, D.S. Terahertz birefringence in zinc oxide. Jpn. J. Appl. Phys. 2011, 50, 2–4. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Mikhaylovskiy, R.V.; Grishunin, K.A.; Costa, J.D.; Rasing, T.; Kimel, A.V. Laser induced THz emission from femtosecond photocurrents in Co/ZnO/Pt and Co/Cu/Pt multilayers. J. Phys. D Appl. Phys. 2018, 51, 134001. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Ohta, M.; Takizawa, N.; Mikame, K.; Ono, S.; Bae, J. Femtosecond-laser-fabricated periodic tapered structures on a silicon substrate for terahertz antireflection. Appl. Opt. 2019, 58, 9595. [Google Scholar] [CrossRef]
- Yu, X.; Yasunaga, Y.; Goto, K.; Liu, D.; Ono, S. Profile control of femtosecond laser-fabricated moth-eye structures on Si substrate. Opt. Lasers Eng. 2021, 142, 106584. [Google Scholar] [CrossRef]
- Yu, X.; Cadatal-Raduban, M.; Kato, S.; Kase, M.; Ono, S. Femtosecond PLD-grown YF 3 nanoparticle thin films as improved filterless VUV photoconductive detectors. Nanotechnology 2021, 32, 015501. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Ono, S.; Bae, J. Application of laser generated moth-eye structure for a periodic terahertz-wave generator. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; Volume 2019, pp. 1–2. [Google Scholar]
- Yu, X.; Kato, S.; Ito, H.; Ono, S.; Kase, M.; Cadatal-Raduban, M. Filterless tunable photoconductive ultraviolet radiation detector using CeF 3 thin films grown by pulsed laser deposition. AIP Adv. 2020, 10, 045309. [Google Scholar] [CrossRef] [Green Version]
- Mans, T.; Dolkemeyer, J.; Schnitzler, C. High Power Femtosecond Lasers. Laser Tech. J. 2014, 11, 40–43. [Google Scholar] [CrossRef]
- Bernard, O.; Audouard, E.; Schöps, B.; Delaigue, M.; Dalla-Barba, G.; Mishchik, K.; Hönninger, C.; Mottay, E. Efficient micro processing with high power femtosecond lasers by beam engineering and modelling. Procedia CIRP 2018, 74, 310–314. [Google Scholar] [CrossRef]
- Huang, M.; Xu, Z. Spontaneous scaling down of femtosecond laser-induced apertures towards the 10-nanometer level: The excitation of quasistatic surface plasmons. Laser Photonics Rev. 2014, 8, 633–652. [Google Scholar] [CrossRef]
- Liu, J.; Jia, T.; Zhou, K.; Feng, D.; Zhang, S.; Zhang, H.; Jia, X.; Sun, Z.; Qiu, J. Direct writing of 150 nm gratings and squares on ZnO crystal in water by using 800 nm femtosecond laser. Opt. Express 2014, 22, 32361. [Google Scholar] [CrossRef]
- Tull, B.R.; Carey, J.E.; Mazur, E.; McDonald, J.P.; Yalisove, S.M. Silicon surface morphologies after femtosecond laser irradiation. MRS Bull. 2006, 31, 626–633. [Google Scholar] [CrossRef]
- Yu, X.; Sudo, M.; Itoigawa, F.; Ono, S. Patterning Oxidation via Femtosecond Laser Irradiation on Copper Substrate. In Proceedings of the Conference on Lasers and Electro-Optics/Pacific Rim 2018, Hong Kong, China, 29 July–3 August 2018; pp. 3–4. [Google Scholar]
- Pereira, A.; Cros, A.; Delaporte, P.; Georgiou, S.; Manousaki, A.; Marine, W.; Sentis, M. Surface nanostructuring of metals by laser irradiation: Effects of pulse duration, wavelength and gas atmosphere. Appl. Phys. A Mater. Sci. Process. 2004, 79, 1433–1437. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196. [Google Scholar] [CrossRef]
- Khosrofian, J.M.; Garetz, B.A. Measurement of a Gaussian laser beam diameter through the direct inversion of knife-edge data. Appl. Opt. 1983, 22, 3406. [Google Scholar] [CrossRef]
- Ben-Yakar, A.; Byer, R.L. Femtosecond laser ablation properties of borosilicate glass. J. Appl. Phys. 2004, 96, 5316–5323. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Qiu, J.; Jia, T.; Li, C.; Sun, H.; Xu, Z. Femtosecond laser ablation of crystals SiO2 and YAG. Opt. Commun. 2007, 274, 163–166. [Google Scholar] [CrossRef]
- Döring, S. Analysis of the Hole Shape Evolution in Ultrashort Pulse Laser Drilling; Cuvillier Verlag: Göttingen, Germany, 2014. [Google Scholar]
- Bäuerle, D. Laser Processing and Chemistry; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-17612-8. [Google Scholar]
- Vivas, M.G.; Shih, T.; Voss, T.; Mazur, E.; Mendonca, C.R. Nonlinear spectra of ZnO: Reverse saturable, two- and three-photon absorption. Opt. Express 2010, 18, 9628. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Qu, Y.; Li, H.; Mi, J.; Ji, W. Three-photon absorption in ZnO and ZnS crystals. Opt. Express 2005, 13, 9235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rumi, M.; Perry, J.W. Two-photon absorption: An overview of measurements and principles. Adv. Opt. Photonics 2010, 2, 451. [Google Scholar] [CrossRef]
- Gedvilas, M.; Mikšys, J.; Berzinš, J.; Stankevič, V.; Račiukaitis, G. Multi-photon absorption enhancement by dual-wavelength double-pulse laser irradiation for efficient dicing of sapphire wafers. Sci. Rep. 2017, 7, 5218. [Google Scholar] [CrossRef] [PubMed]
- Sohn, B.U.; Monmeyran, C.; Kimerling, L.C.; Agarwal, A.M.; Tan, D.T.H. Kerr nonlinearity and multi-photon absorption in germanium at mid-infrared wavelengths. Appl. Phys. Lett. 2017, 111, 2–6. [Google Scholar] [CrossRef]
- Boyd, R. Nonlinear Optics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Yates, B.; Cooper, R.F.; Kreitman, M.M. Low-temperature thermal expansion of zinc oxide. Vibrations in zinc oxide and sphalerite zinc sulfide. Phys. Rev. B 1971, 4, 1314–1323. [Google Scholar] [CrossRef]
- Ibach, H. Thermal Expansion of Silicon and Zinc Oxide (II). Phys. Status Solidi 1969, 33, 257–265. [Google Scholar] [CrossRef]
- CrysTec GmbH. Available online: http://www.crystec.de/datasheets-e.html (accessed on 21 March 2021).
- Emerson, D.; Collins, B.; Bergmann, M.; Edmond, J.; Tarsa, E.; Andrews, P.; Keller, B.; Hussell, C.; Salter, A. LED Package with Increased Feature Sizes. U.S. Patent Application US12/757,891, 21 October 2014. [Google Scholar]
- Emerson, D.T.; Lydon, J.; Rosado, R.; Britt, J.C. Light Emitter Devices and Methods with Reduced Dimensions and Improved Light Output. U.S. Patent Application US13/312,518, 13 June 2013. [Google Scholar]
- Wu, X.; Lee, J.; Varshney, V.; Wohlwend, J.L.; Roy, A.K.; Luo, T. Thermal Conductivity of Wurtzite Zinc-Oxide from First-Principles Lattice Dynamics-a Comparative Study with Gallium Nitride OPEN. Sci. Rep. 2016, 6, 22504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hull, R. Properties of Crystalline Silicon; Institute of Engineering & Technology: Stevenage, England, 1999. [Google Scholar]
- Ibach, H. Thermal Expansion of Silicon and Zinc Oxide (I). Phys. Status Solidi 1969, 31, 625–634. [Google Scholar] [CrossRef]
- Middelmann, T.; Walkov, A.; Bartl, G.; Schödel, R. Thermal expansion coefficient of single-crystal silicon from 7 K to 293 K. Phys. Rev. B 2015, 92, 174113. [Google Scholar] [CrossRef] [Green Version]
- Shanks, H.R.; Maycock, P.D.; Sidles, P.H.; Danielson, G.C. Thermal Conductivity of Silicon from 300 to 1400 °K. Phys. Rev. 1963, 130, 1743–1748. [Google Scholar] [CrossRef]
- Guo, L.; Yang, S.; Yang, C.; Yu, P.; Wang, J.; Ge, W.; Wong, G.K.L. Highly monodisperse polymer-capped ZnO nanoparticles: Preparation and optical properties. Appl. Phys. Lett. 2000, 76, 2901–2903. [Google Scholar] [CrossRef]
- Lin, B.; Fu, Z.; Jia, Y.; Liao, G. Defect Photoluminescence of Undoping ZnO Films and Its Dependence on Annealing Conditions. J. Electrochem. Soc. 2001, 148, G110. [Google Scholar] [CrossRef]
- Lin, B.; Fu, Z.; Jia, Y. Green luminescent center in undoped zinc oxide films deposited on silicon substrates. Appl. Phys. Lett. 2001, 79, 943–945. [Google Scholar] [CrossRef]
- Zhang, S.B.; Wei, S.H.; Zunger, A. Intrinsic n-type versus p-type doping asymmetry and the defect physics of ZnO. Phys. Rev. B 2001, 63, 075205. [Google Scholar] [CrossRef] [Green Version]
- Shan, F.K.; Liu, G.X.; Lee, W.J.; Lee, G.H.; Kim, I.S.; Shin, B.C. Aging effect and origin of deep-level emission in ZnO thin film deposited by pulsed laser deposition. Appl. Phys. Lett. 2005, 86, 221910. [Google Scholar] [CrossRef]
- Wang, Z.G.; Zu, X.T.; Zhu, S.; Wang, L.M. Green luminescence originates from surface defects in ZnO nanoparticles. Phys. E Low Dimens. Syst. Nanostruct. 2006, 35, 199–202. [Google Scholar] [CrossRef]
- Ou, Q.; Matsuda, T.; Mesko, M.; Ogino, A.; Nagatsu, M. Cathodoluminescence property of ZnO nanophosphors prepared by laser ablation. Jpn. J. Appl. Phys. 2008, 47, 389–393. [Google Scholar] [CrossRef]
- Zeng, H.; Duan, G.; Li, Y.; Yang, S.; Xu, X.; Cai, W. Blue luminescence of ZnO nanoparticles based on non-equilibrium processes: Defect origins and emission controls. Adv. Funct. Mater. 2010, 20, 561–572. [Google Scholar] [CrossRef]
- Camarda, P.; Messina, F.; Vaccaro, L.; Agnello, S.; Buscarino, G.; Schneider, R.; Popescu, R.; Gerthsen, D.; Lorenzi, R.; Gelardi, F.M.; et al. Luminescence mechanisms of defective ZnO nanoparticles. Phys. Chem. Chem. Phys. 2016, 18, 16237–16244. [Google Scholar] [CrossRef] [PubMed]
- Shalish, I.; Temkin, H.; Narayanamurti, V. Size-dependent surface luminescence in ZnO nanowires. Phys. Rev. B 2004, 69, 245401. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Itoigawa, F.; Ono, S. Femtosecond Laser-Pulse-Induced Surface Cleavage of Zinc Oxide Substrate. Micromachines 2021, 12, 596. https://doi.org/10.3390/mi12060596
Yu X, Itoigawa F, Ono S. Femtosecond Laser-Pulse-Induced Surface Cleavage of Zinc Oxide Substrate. Micromachines. 2021; 12(6):596. https://doi.org/10.3390/mi12060596
Chicago/Turabian StyleYu, Xi, Fumihiro Itoigawa, and Shingo Ono. 2021. "Femtosecond Laser-Pulse-Induced Surface Cleavage of Zinc Oxide Substrate" Micromachines 12, no. 6: 596. https://doi.org/10.3390/mi12060596





