Minimal Optimized Effective Potentials for Density Functional Theory Studies on Excited-State Proton Dissociation
Abstract
:1. Introduction
2. Methodology
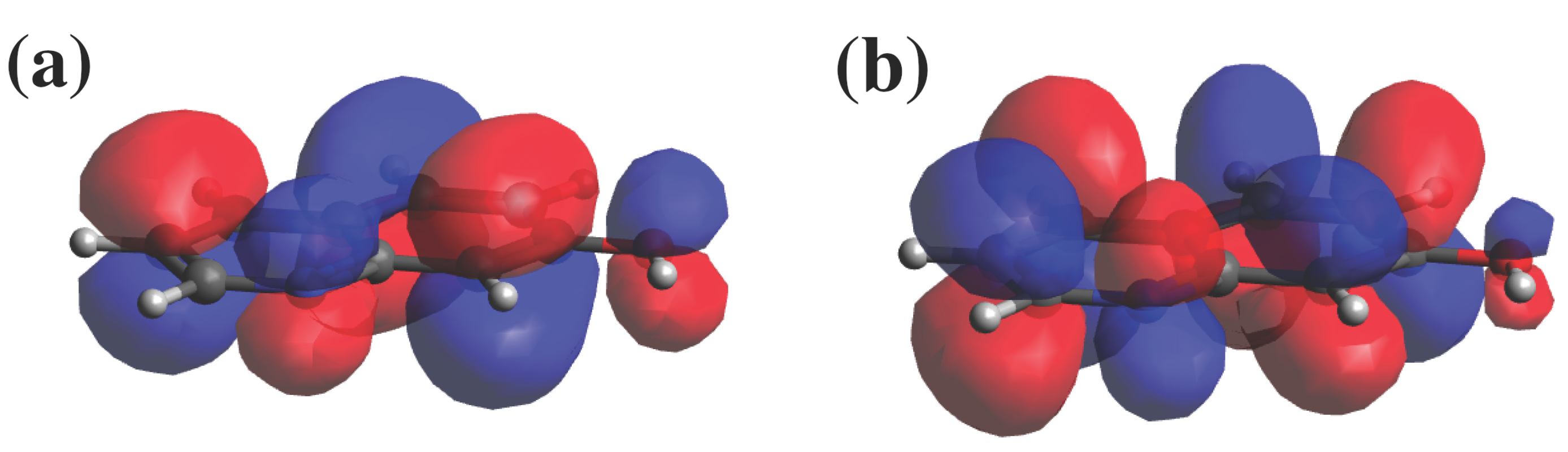
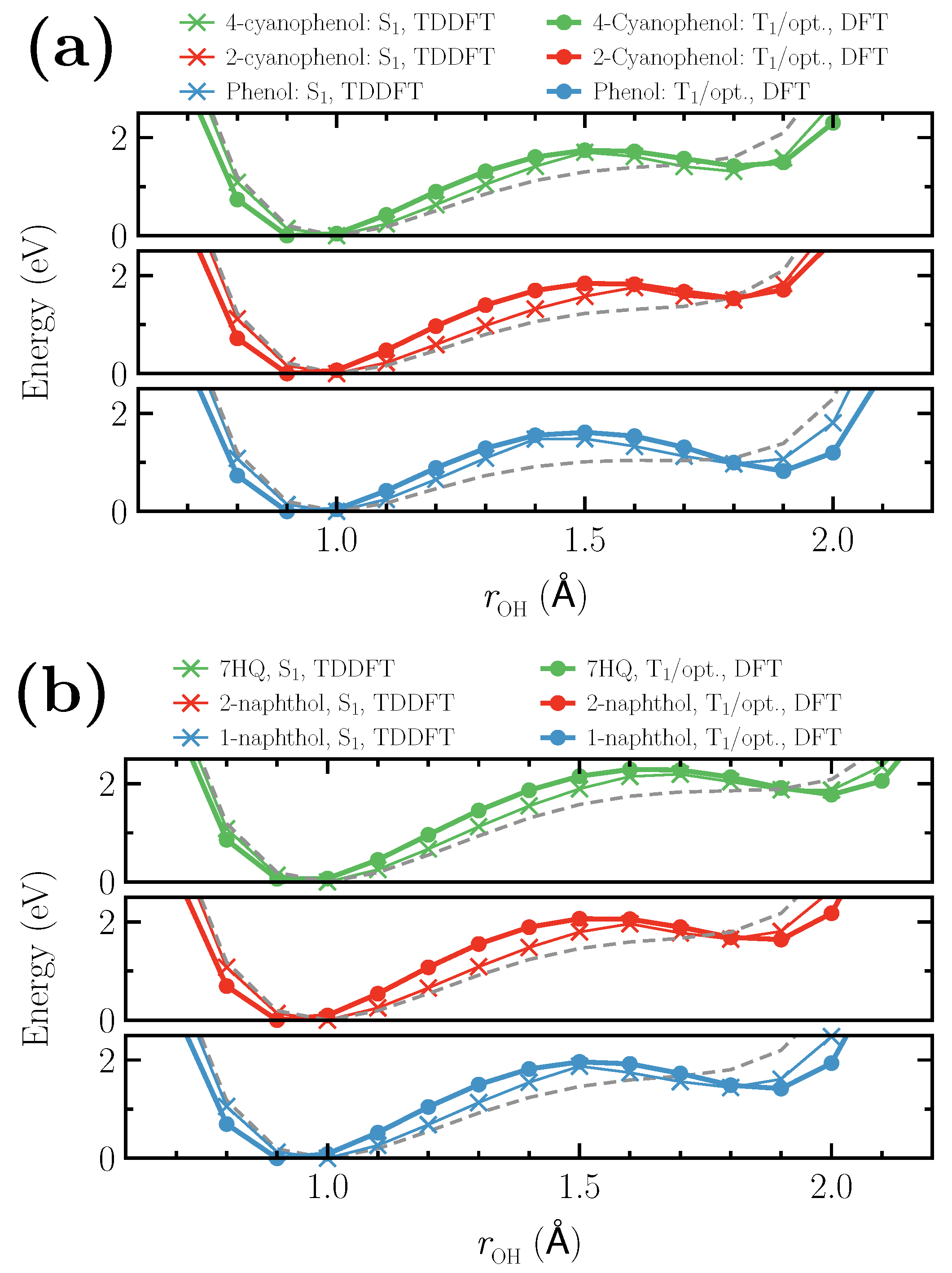
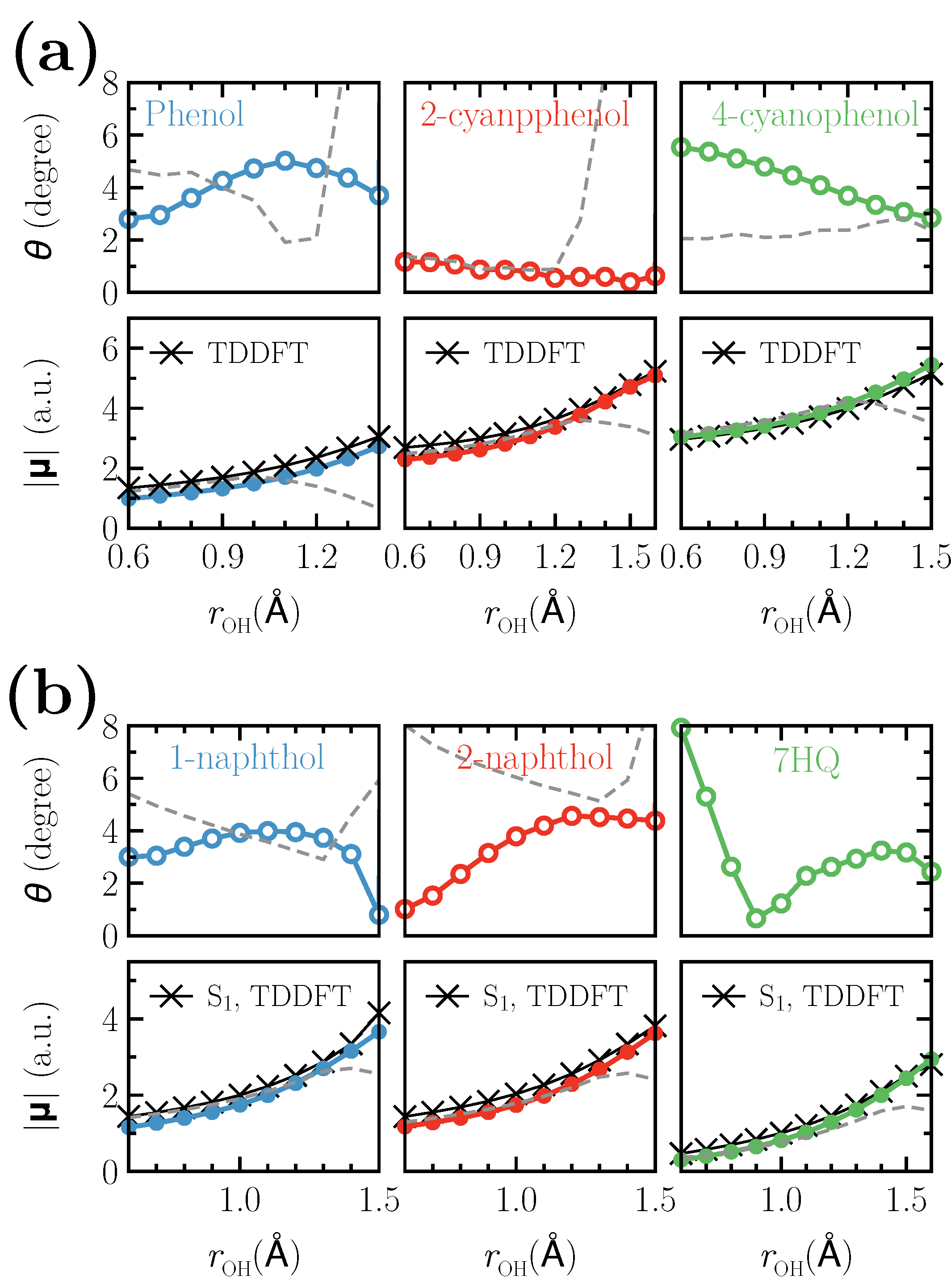
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horng, M.; Gardecki, J.; Papazyan, A.; Maroncelli, M. Subpicosecond measurements of polar solvation dynamics: Coumarin 153 revisited. J. Phys. Chem. 1995, 99, 17311–17337. [Google Scholar] [CrossRef]
- Haran, G.; Sun, W.D.; Wynne, K.; Hochstrasser, R.M. Femtosecond far-infrared pump-probe spectroscopy: A new tool for studying low-frequency vibrational dynamics in molecular condensed phases. Chem. Phys. Lett. 1997, 274, 365–371. [Google Scholar] [CrossRef]
- Dallmann, A.; Pfaffe, M.; Mügge, C.; Mahrwald, R.; Kovalenko, S.A.; Ernsting, N.P. Local THz time domain spectroscopy of duplex DNA via fluorescence of an embedded probe. J. Phys. Chem. B 2009, 113, 15619–15628. [Google Scholar] [CrossRef]
- Pérez Lustres, J.L.; Kovalenko, S.A.; Mosquera, M.; Senyushkina, T.; Flasche, W.; Ernsting, N.P. Ultrafast Solvation of N-Methyl-6-quinolone Probes Local IR Spectrum. Angew. Chem. Int. Ed. 2005, 44, 5635–5639. [Google Scholar] [CrossRef]
- Pérez-Lustres, J.; Rodriguez-Prieto, F.; Mosquera, M.; Senyushkina, T.; Ernsting, N.; Kovalenko, S. Ultrafast proton transfer to solvent: Molecularity and intermediates from solvation-and diffusion-controlled regimes. J. Am. Chem. Soc. 2007, 129, 5408–5418. [Google Scholar] [CrossRef] [PubMed]
- Syage, J.; Steadman, J. Picosecond measurements of phenol excited-state proton transfer in clusters. I. Solvent basicity and cluster size effects. J. Chem. Phys. 1991, 95, 2497–2510. [Google Scholar] [CrossRef]
- Arnaut, L.G.; Formosinho, S.J. Excited-state proton transfer reactions I. Fundamentals and intermolecular reactions. J. Photochem. Photobiol. A Chem. 1993, 75, 1–20. [Google Scholar] [CrossRef]
- Formosinho, S.J.; Arnaut, L.G. Excited-state proton transfer reactions II. Intramolecular reactions. J. Photochem. Photobiol. A Chem. 1993, 75, 21–48. [Google Scholar] [CrossRef]
- Allolio, C.; Sebastiani, D. Approaches to the solvation of the molecular probe N-methyl-6-quinolone in its excited state. Phys. Chem. Chem. Phys. 2011, 13, 16395–16403. [Google Scholar] [CrossRef]
- Bekçioğlu, G.; Hoffmann, F.; Sebastiani, D. Solvation-dependent latency of photoacid dissociation and transient IR signatures of protonation dynamics. J. Phys. Chem. A 2015, 119, 9244–9251. [Google Scholar] [CrossRef]
- Georgiev, A.; Antonov, L. 8-(Pyridin-2-yl) quinolin-7-ol as a Platform for Conjugated Proton Cranes: A DFT Structural Design. Micromachines 2020, 11, 901. [Google Scholar] [CrossRef] [PubMed]
- Bort, G.; Gallavardin, T.; Ogden, D.; Dalko, P.I. From one-photon to two-photon probes: “Caged” compounds, actuators, and photoswitches. Angew. Chem. Int. Ed. 2013, 52, 4526–4537. [Google Scholar] [CrossRef]
- Bucher, D.B.; Schlueter, A.; Carell, T.; Zinth, W. Watson–Crick Base Pairing Controls Excited-State Decay in Natural DNA. Angew. Chem. Int. Ed. 2014, 53, 11366–11369. [Google Scholar] [CrossRef]
- Conrad, K.S.; Manahan, C.C.; Crane, B.R. Photochemistry of flavoprotein light sensors. Nat. Chem. Biol. 2014, 10, 801–809. [Google Scholar] [CrossRef]
- Morrone, J.A.; Tuckerman, M.E. Ab initio molecular dynamics study of proton mobility in liquid methanol. J. Chem. Phys. 2002, 117, 4403–4413. [Google Scholar] [CrossRef]
- Kermis, H.R.; Kostov, Y.; Harms, P.; Rao, G. Dual excitation ratiometric fluorescent pH sensor for noninvasive bioprocess monitoring: Development and application. Biotechnol. Prog. 2002, 18, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S.; Voth, G.A. Ab initio molecular-dynamics simulation of aqueous proton solvation and transport revisited. J. Chem. Phys. 2005, 123, 044505. [Google Scholar] [CrossRef]
- Geissler, P.L.; Dellago, C.; Chandler, D.; Hutter, J.; Parrinello, M. Ab initio analysis of proton transfer dynamics in (H2O)3H+. Chem. Phys. Lett. 2000, 321, 225–230. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab initio molecular dynamics: Theory and implementation. Mod. Methods Algorithms Quantum Chem. 2000, 1, 141. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Runge, E.; Gross, E.K. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Stanton, J.F.; Bartlett, R.J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029–7039. [Google Scholar] [CrossRef]
- Levchenko, S.V.; Krylov, A.I. Equation-of-motion spin-flip coupled-cluster model with single and double substitutions: Theory and application to cyclobutadiene. J. Chem. Phys. 2004, 120, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Watts, J.D. An introduction to equation-of-motion and linear-response coupled-cluster methods for electronically excited states of molecules. In Radiation Induced Molecular Phenomena in Nucleic Acids; Springer: Berlin/Heidelberg, Germany, 2008; pp. 65–92. [Google Scholar]
- Martínez, T.J. Insights for light-driven molecular devices from ab initio multiple spawning excited-state dynamics of organic and biological chromophores. Acc. Chem. Res. 2006, 39, 119–126. [Google Scholar] [CrossRef]
- Coe, J.D.; Martínez, T.J. Ab initio molecular dynamics of excited-state intramolecular proton transfer around a three-state conical intersection in malonaldehyde. J. Phys. Chem. A 2006, 110, 618–630. [Google Scholar] [CrossRef] [PubMed]
- Coe, J.D.; Levine, B.G.; Martínez, T.J. Ab initio molecular dynamics of excited-state intramolecular proton transfer using multireference perturbation theory. J. Phys. Chem. A 2007, 111, 11302–11310. [Google Scholar] [CrossRef]
- Tao, H.; Levine, B.G.; Martínez, T.J. Ab initio multiple spawning dynamics using multi-state second-order perturbation theory. J. Phys. Chem. A 2009, 113, 13656–13662. [Google Scholar] [CrossRef]
- Chakravorty, D.K.; Soudackov, A.V.; Hammes-Schiffer, S. Hybrid quantum/classical molecular dynamics simulations of the proton transfer reactions catalyzed by ketosteroid isomerase: Analysis of hydrogen bonding, conformational motions, and electrostatics. Biochemistry 2009, 48, 10608–10619. [Google Scholar] [CrossRef] [Green Version]
- Olsen, S.; Lamothe, K.; Martinez, T.J. Protonic gating of excited-state twisting and charge localization in GFP chromophores: A mechanistic hypothesis for reversible photoswitching. J. Am. Chem. Soc. 2010, 132, 1192–1193. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S. Current theoretical challenges in proton-coupled electron transfer: Electron–proton nonadiabaticity, proton relays, and ultrafast dynamics. J. Phys. Chem. Lett. 2011, 2, 1410–1416. [Google Scholar] [CrossRef]
- Mashaghi, A.; Partovi-Azar, P.; Jadidi, T.; Anvari, M.; Jand, S.P.; Nafari, N.; Tabar, M.R.R.; Maass, P.; Bakker, H.J.; Bonn, M. Enhanced autoionization of water at phospholipid interfaces. J. Phys. Chem. C 2013, 117, 510–514. [Google Scholar] [CrossRef] [Green Version]
- Partovi-Azar, P.; Sebastiani, D. Optimized effective potentials to increase the accuracy of approximate proton transfer energy calculations in the excited state. J. Chem. Phys. 2020, 152, 064101. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Lin, Y.S.; Li, G.D.; Mao, S.P.; Chai, J.D. Long-range corrected hybrid density functionals with improved dispersion corrections. J. Chem. Theory Comput. 2013, 9, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703. [Google Scholar] [CrossRef] [Green Version]
- Krack, M. Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals. Theor. Chem. Acc. 2005, 114, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471. [Google Scholar] [CrossRef] [Green Version]
- Hutter, J.; Curioni, A. Car—Parrinello molecular dynamics on massively parallel computers. ChemPhysChem 2005, 6, 1788–1793. [Google Scholar] [CrossRef] [Green Version]
- Gonze, X.; Amadon, B.; Anglade, P.M.; Beuken, J.M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Barzilai, J.; Borwein, J.M. Two-point step size gradient methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.L. Natural transition orbitals. J. Chem. Phys. 2003, 118, 4775–4777. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Phenol-Based Photoacids | |||
|---|---|---|---|
| (a.u.) | |||
| Phenol | 2.112996 | 0.465280 | 0.460871 |
| 2-Cyanophenol | 1.797464 | 0.094554 | 0.395386 |
| 4-Cyanophenol | 2.002620 | 0.176501 | 0.479233 |
| Naphthol-Based Photoacids | |||
| (a.u.) | |||
| 1-Naphthol | 2.019293 | 0.333423 | 0.4976893 |
| 2-Naphthol | 1.979366 | 0.269279 | 0.3800635 |
| 7HQ | 2.085884 | 0.132695 | 0.3663171 |
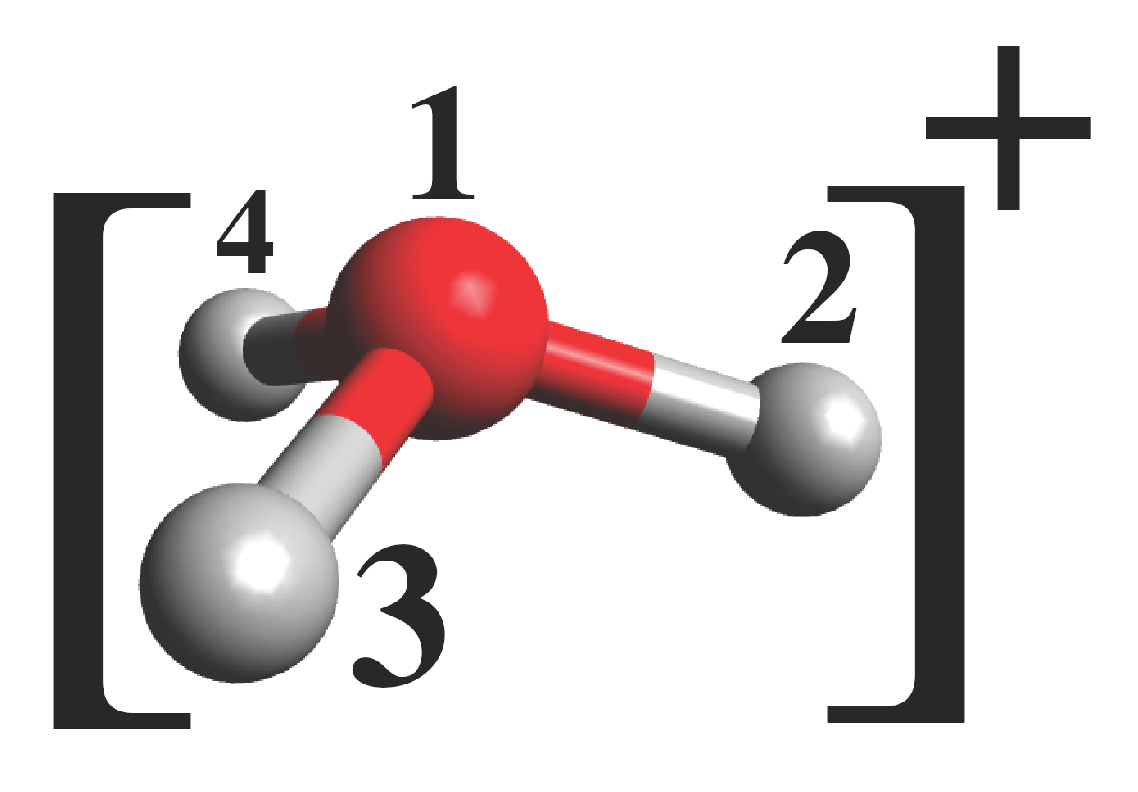
| From | d (Å) | d (Å) | d (Å) | ∠213 () | ∠214 () | ∠314 () |
|---|---|---|---|---|---|---|
| Phenol | 0.99 | 0.97 | 0.99 | 106 | 106 | 106 |
| 2-cyanophenol | 0.99 | 0.97 | 0.99 | 110 | 109 | 110 |
| 4-cyanophenol | 0.99 | 0.97 | 0.99 | 108 | 108 | 108 |
| 1-naphthol | 0.99 | 0.97 | 0.99 | 108 | 107 | 108 |
| 2-naphthol | 0.99 | 0.97 | 0.99 | 109 | 108 | 109 |
| 7HQ | 0.99 | 0.97 | 0.99 | 109 | 109 | 109 |
| No OEP | 0.99 | 0.99 | 0.99 | 111 | 111 | 111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Partovi-Azar, P.; Sebastiani, D. Minimal Optimized Effective Potentials for Density Functional Theory Studies on Excited-State Proton Dissociation. Micromachines 2021, 12, 679. https://doi.org/10.3390/mi12060679
Partovi-Azar P, Sebastiani D. Minimal Optimized Effective Potentials for Density Functional Theory Studies on Excited-State Proton Dissociation. Micromachines. 2021; 12(6):679. https://doi.org/10.3390/mi12060679
Chicago/Turabian StylePartovi-Azar, Pouya, and Daniel Sebastiani. 2021. "Minimal Optimized Effective Potentials for Density Functional Theory Studies on Excited-State Proton Dissociation" Micromachines 12, no. 6: 679. https://doi.org/10.3390/mi12060679
APA StylePartovi-Azar, P., & Sebastiani, D. (2021). Minimal Optimized Effective Potentials for Density Functional Theory Studies on Excited-State Proton Dissociation. Micromachines, 12(6), 679. https://doi.org/10.3390/mi12060679







