Performance Research and Structure Optimization of Labyrinth Screw Pump
Abstract
:1. Introduction
2. Geometry of Labyrinth Screw Pump
3. Steady-State Calculation of Fluid Domain of Labyrinth Screw Pump
3.1. Governing Equations
- (1)
- Mass conservation equation:
- (2)
- Momentum conservation equation:
- (3)
- Energy conservation equation
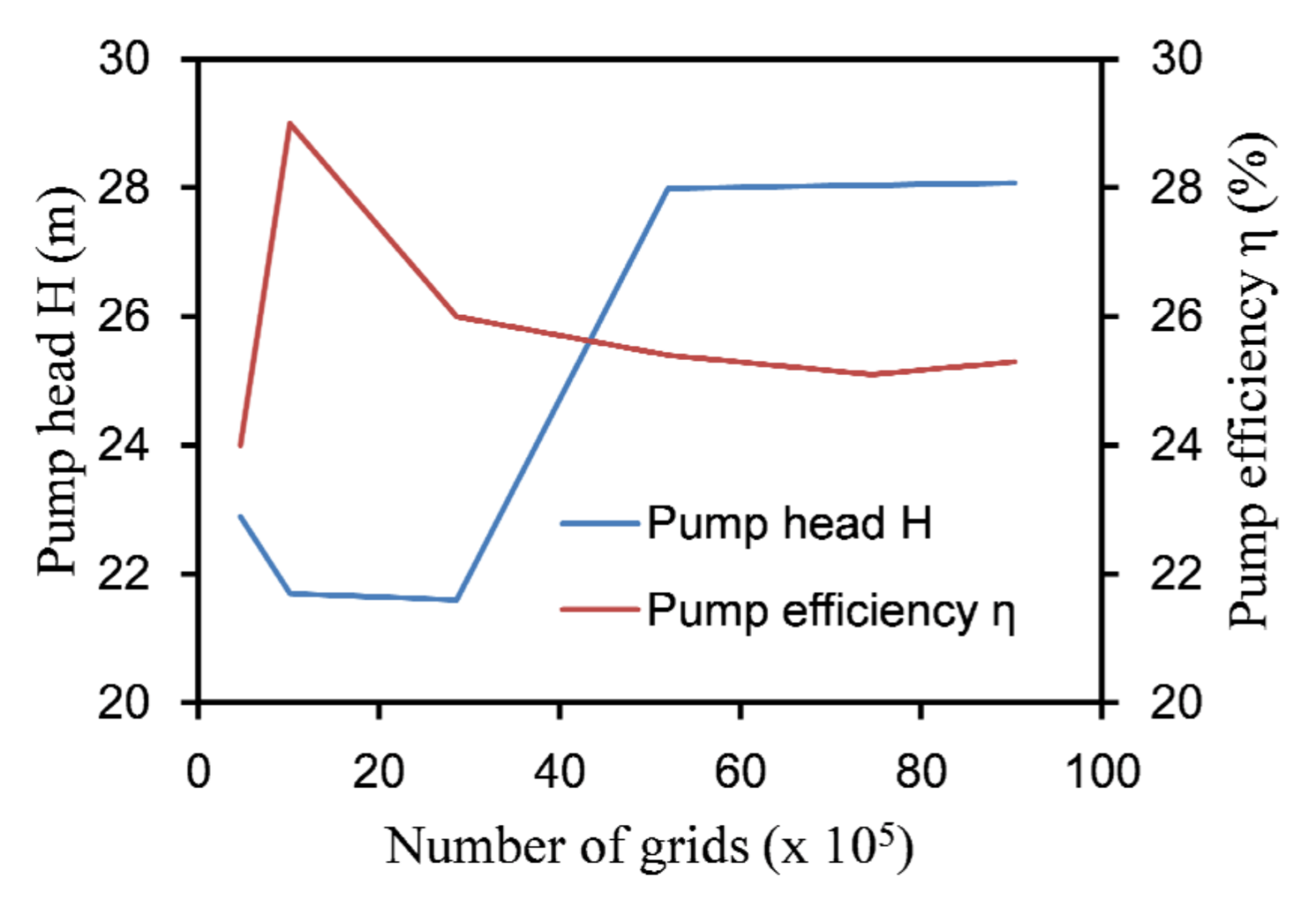
3.2. Mesh Division and Mesh Verification
3.3. Model Settings and Boundary Conditions
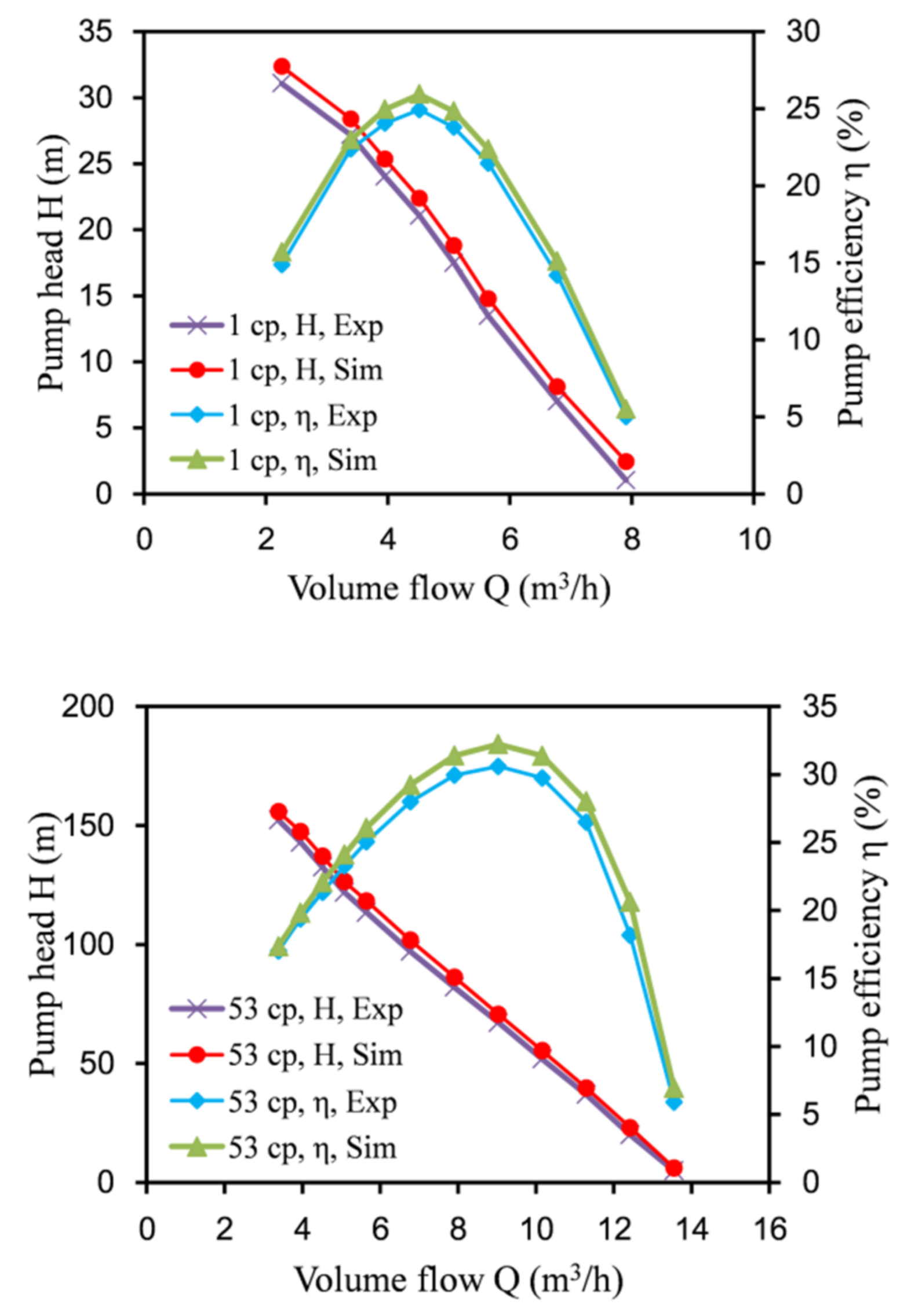
3.4. Test Validation
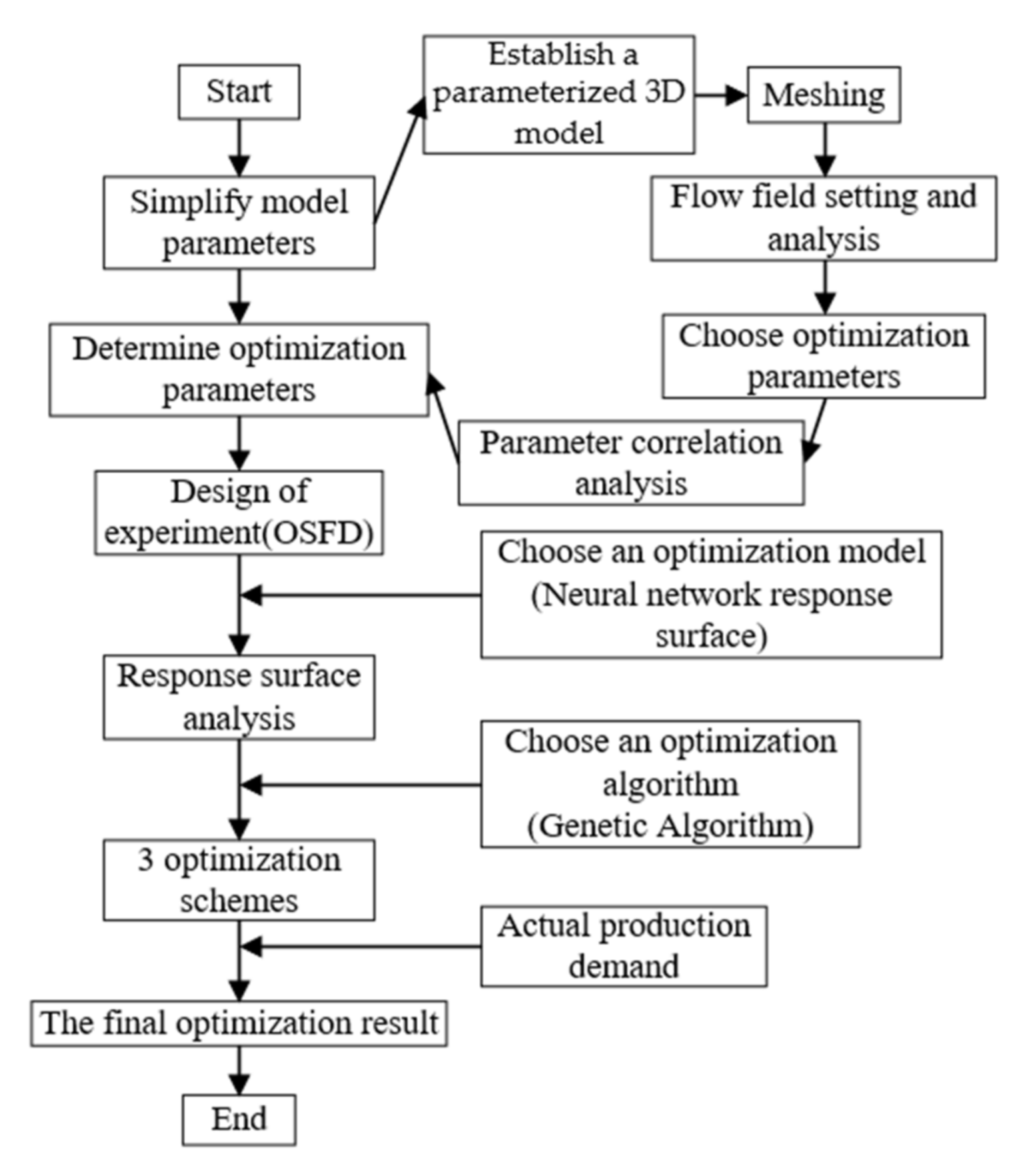
4. Structure Optimization
4.1. Parameter Correlation Analysis and Optimized Space-Filling Design
4.2. Neural Network Response Surface
4.3. Genetic Algorithm Optimization
5. Results and Discussion
5.1. Analysis of Flow and Pressure Fields
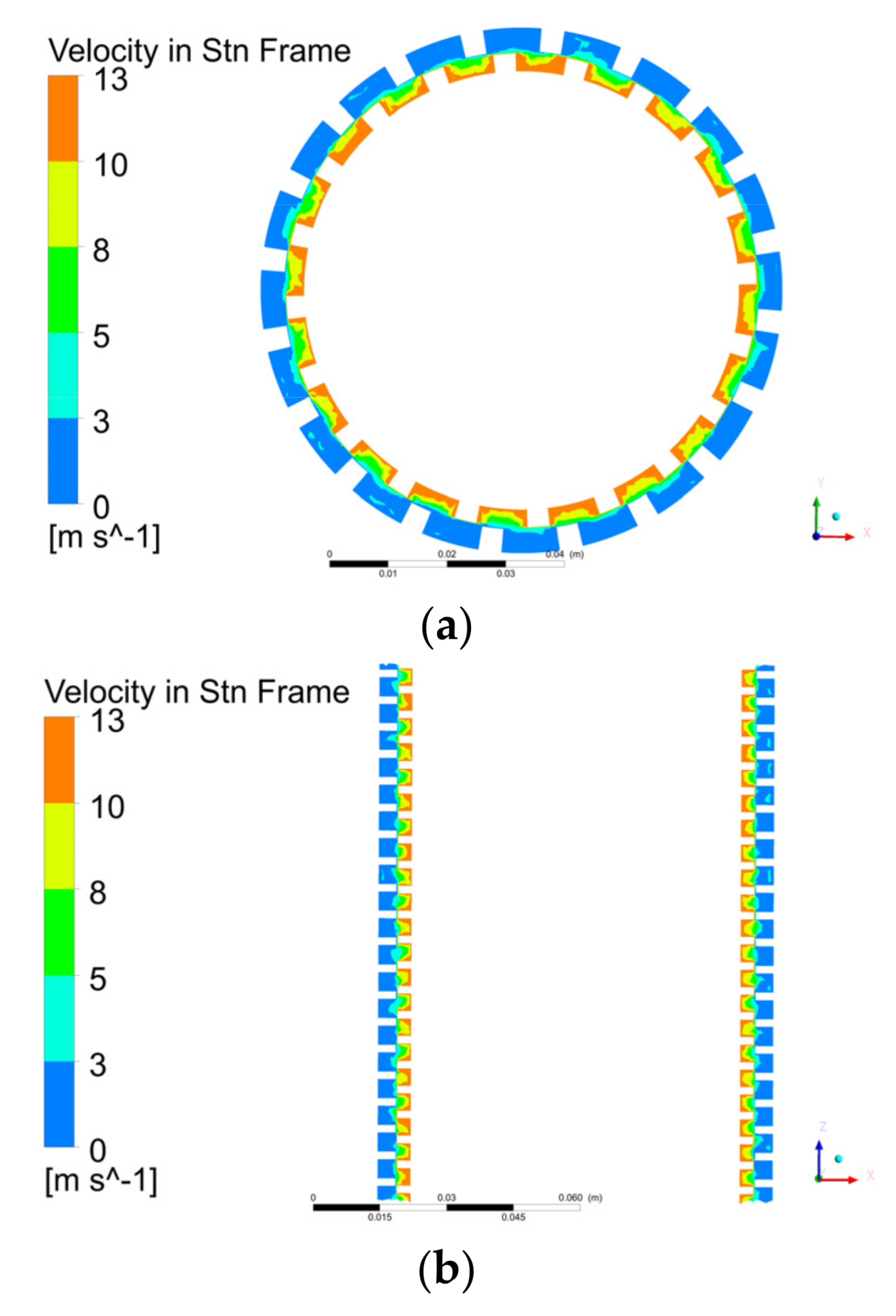
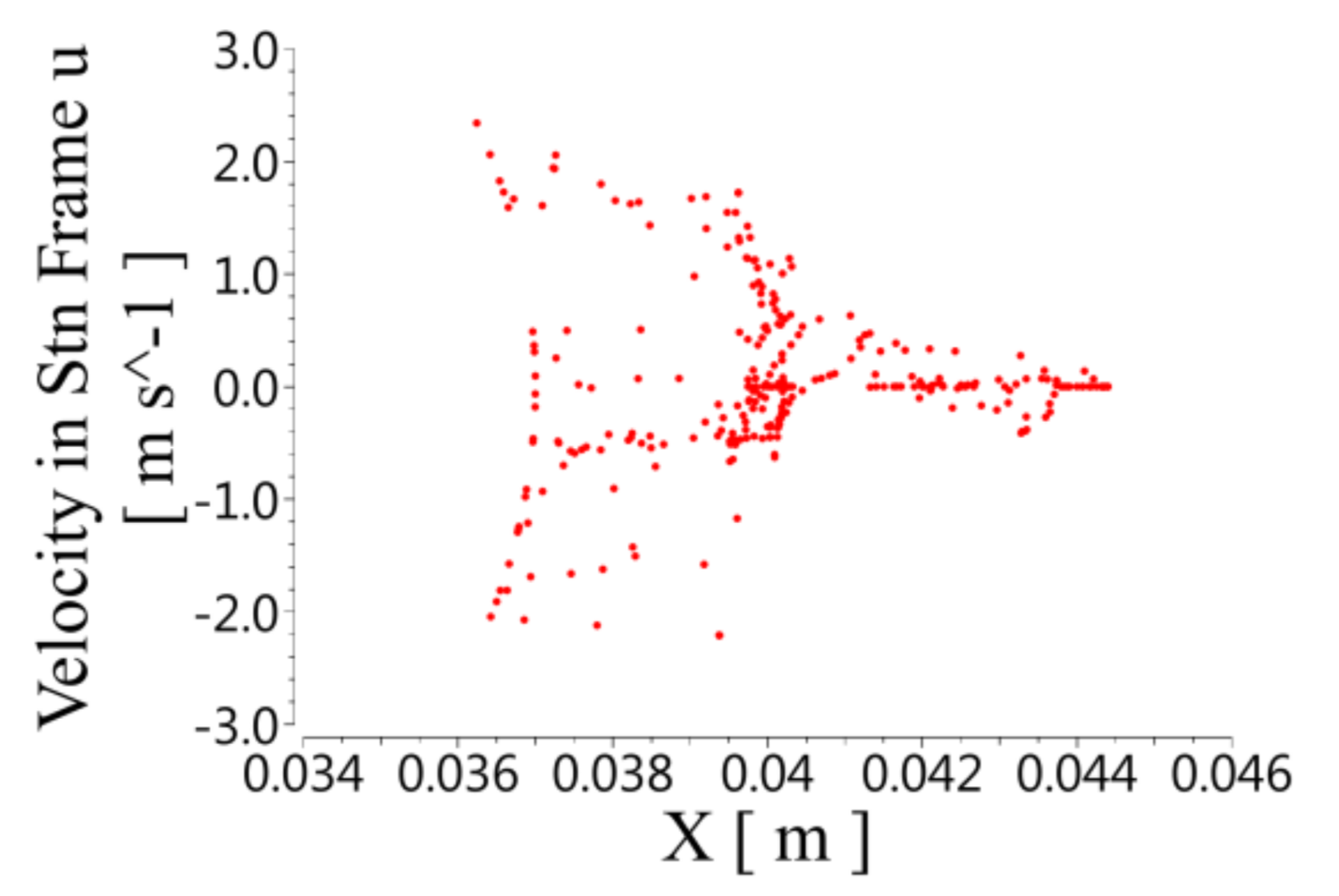
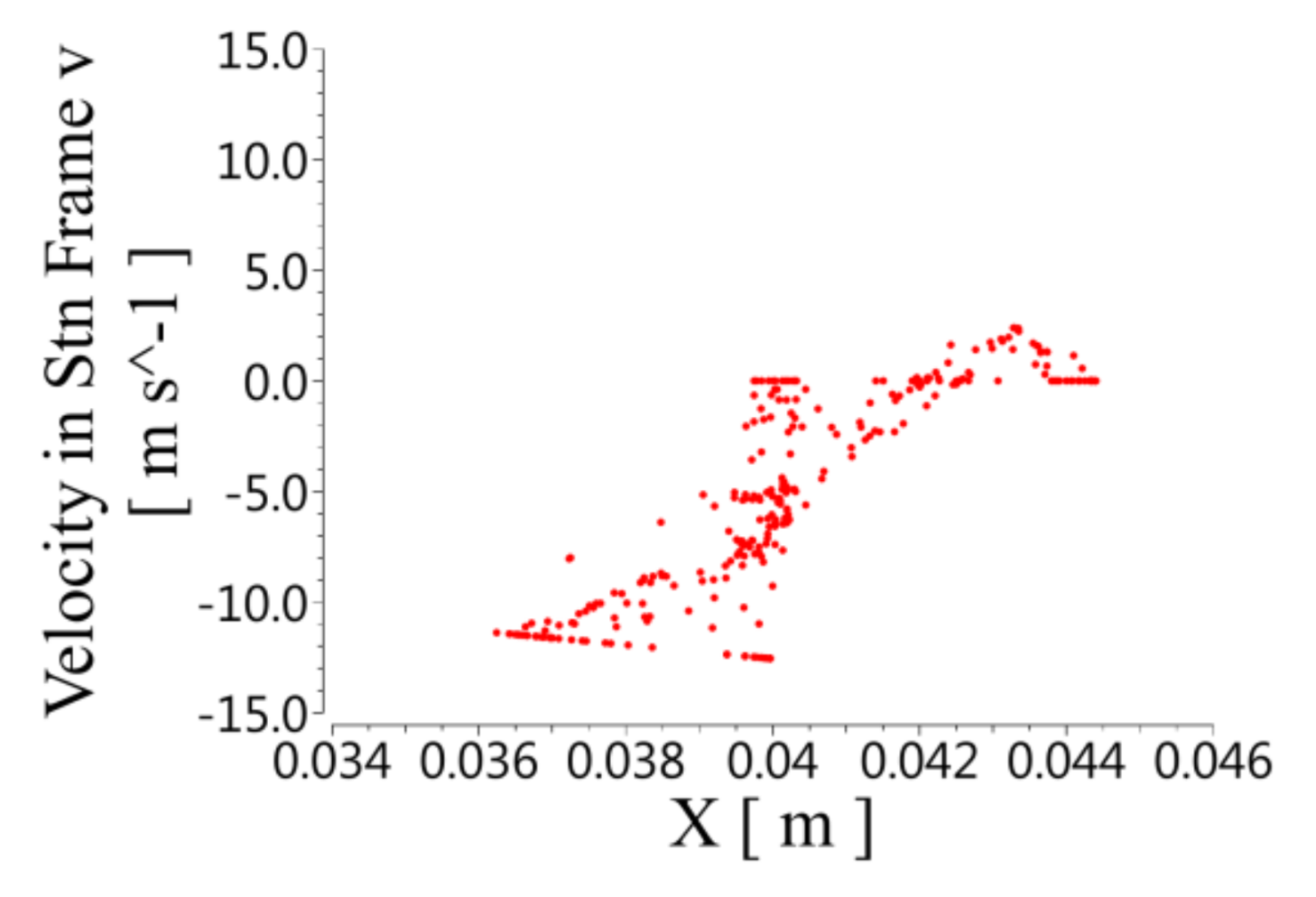
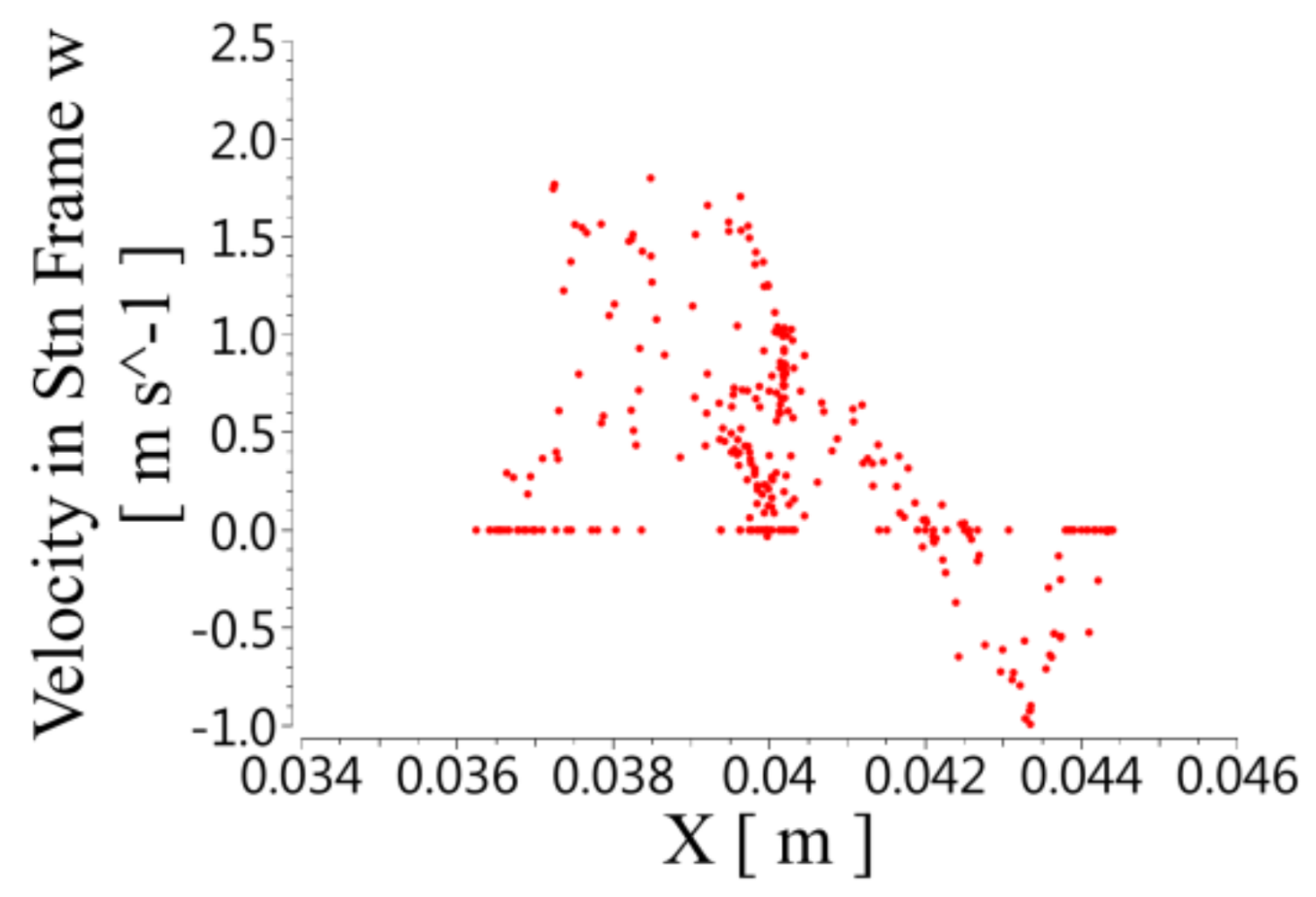
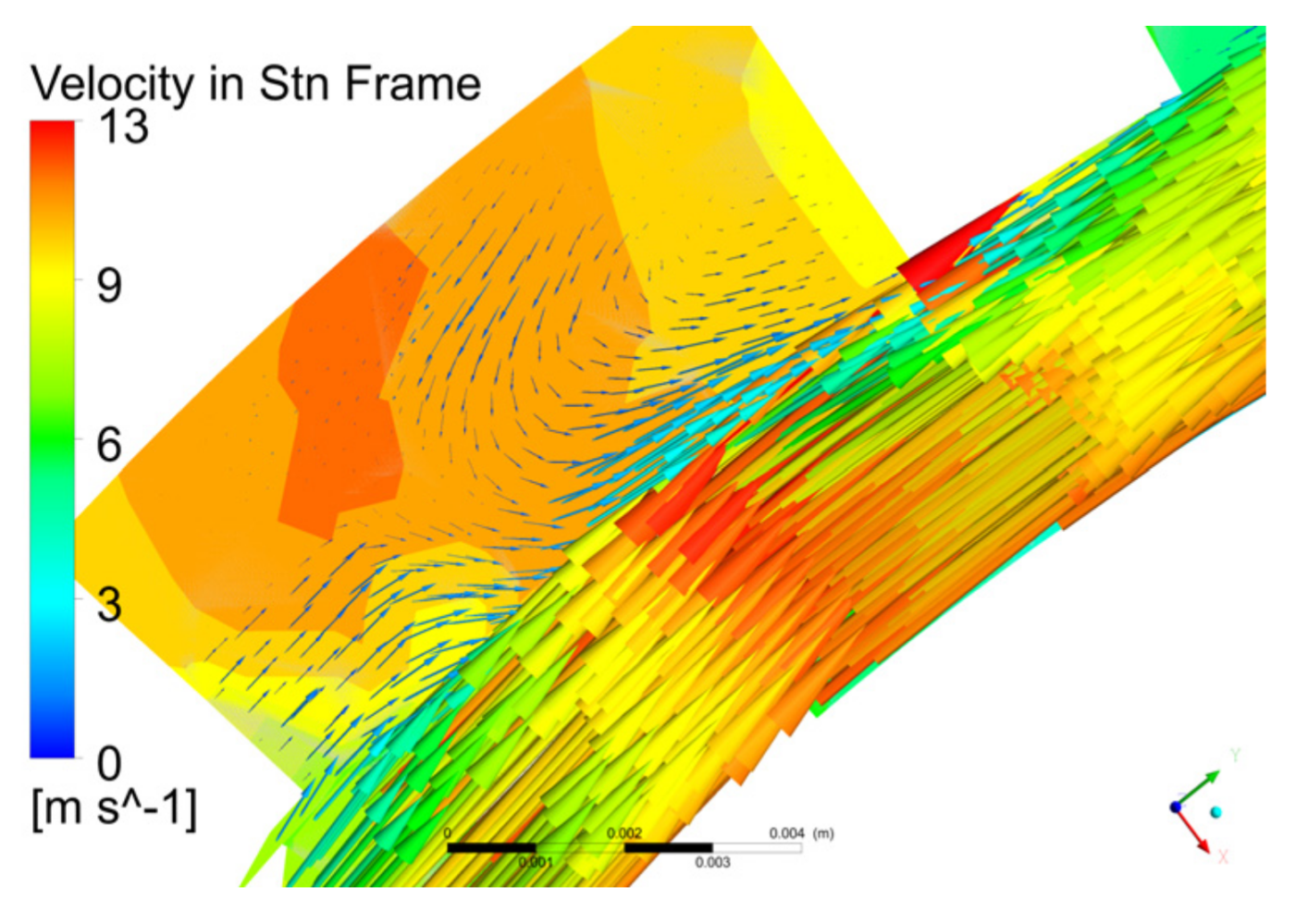
5.1.1. Velocity Distribution
- (1)
- Radial velocity distribution in spiral unit
- (2)
- Circumferential velocity distribution in spiral unit
- (3)
- Axial velocity distribution in spiral unit
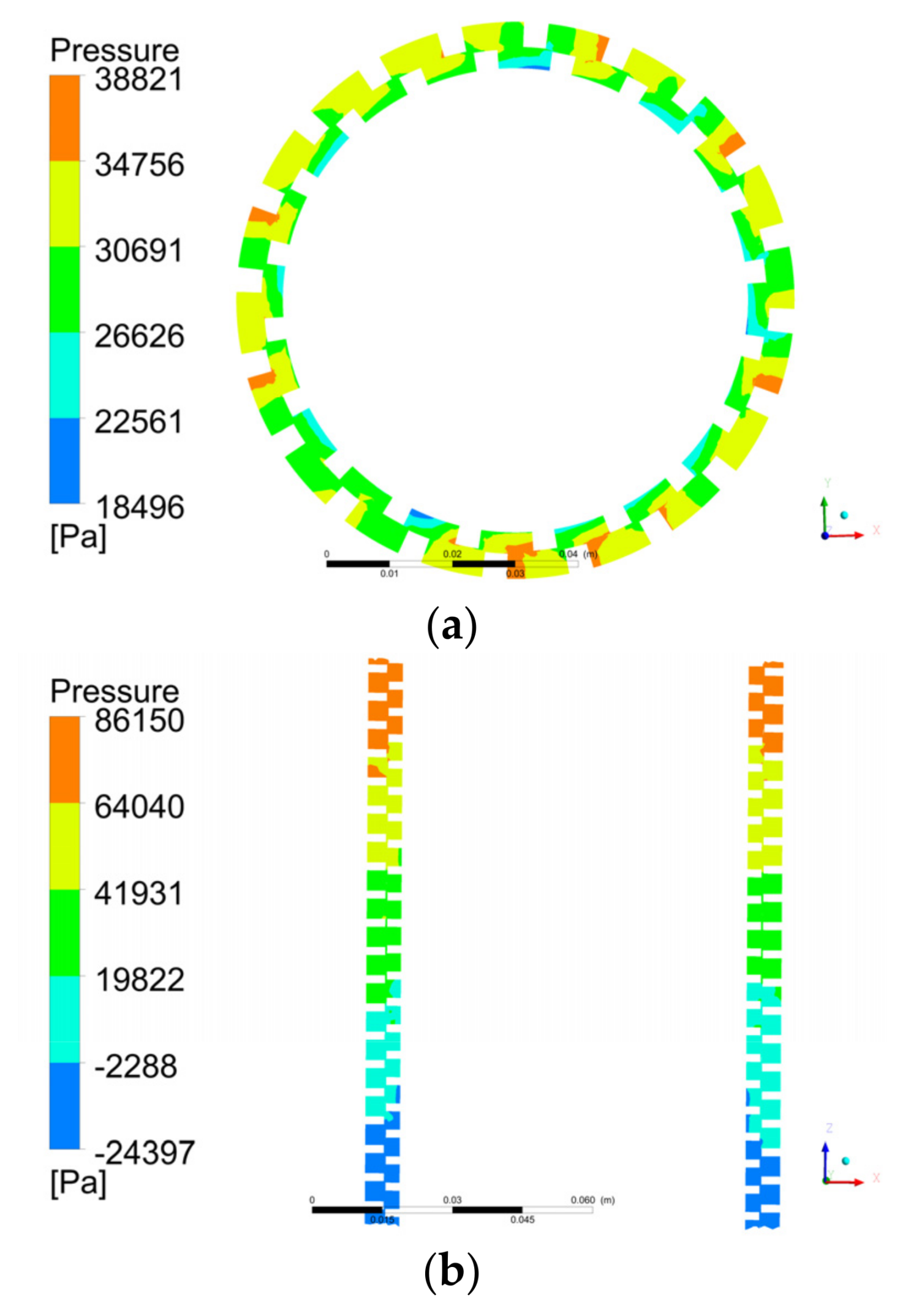
5.1.2. Pressure Distribution in Pump
5.1.3. Pumping Mechanism
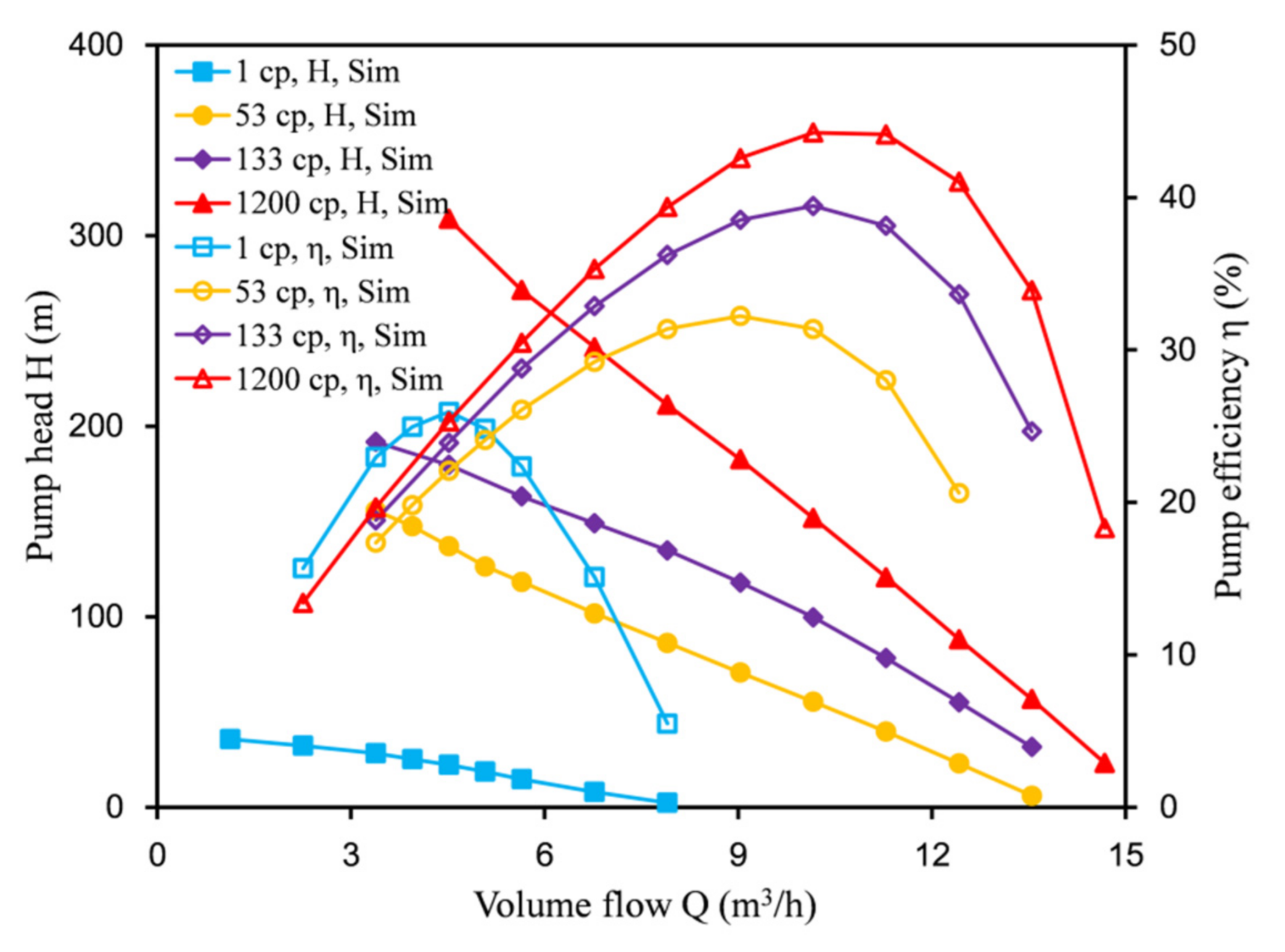
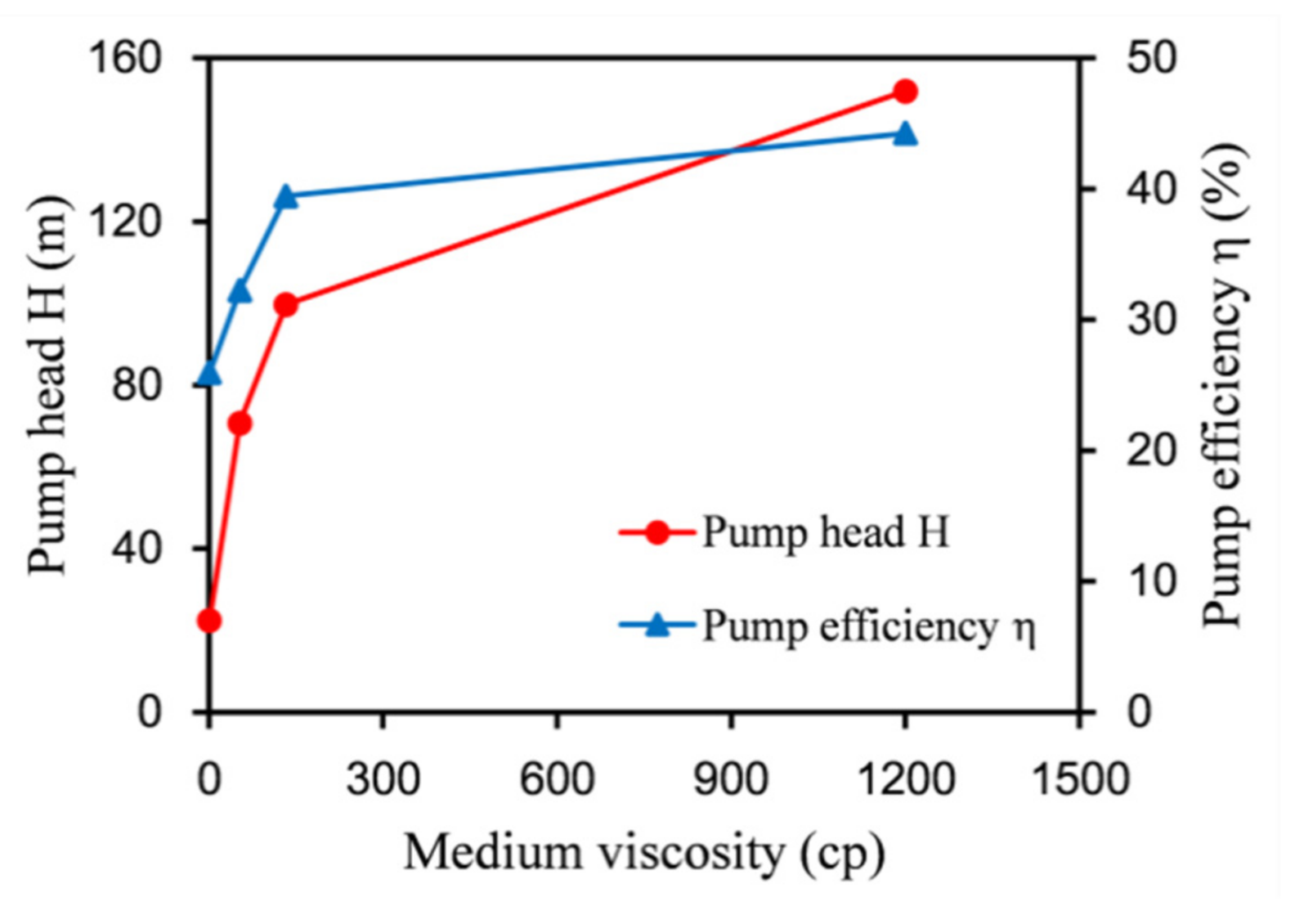
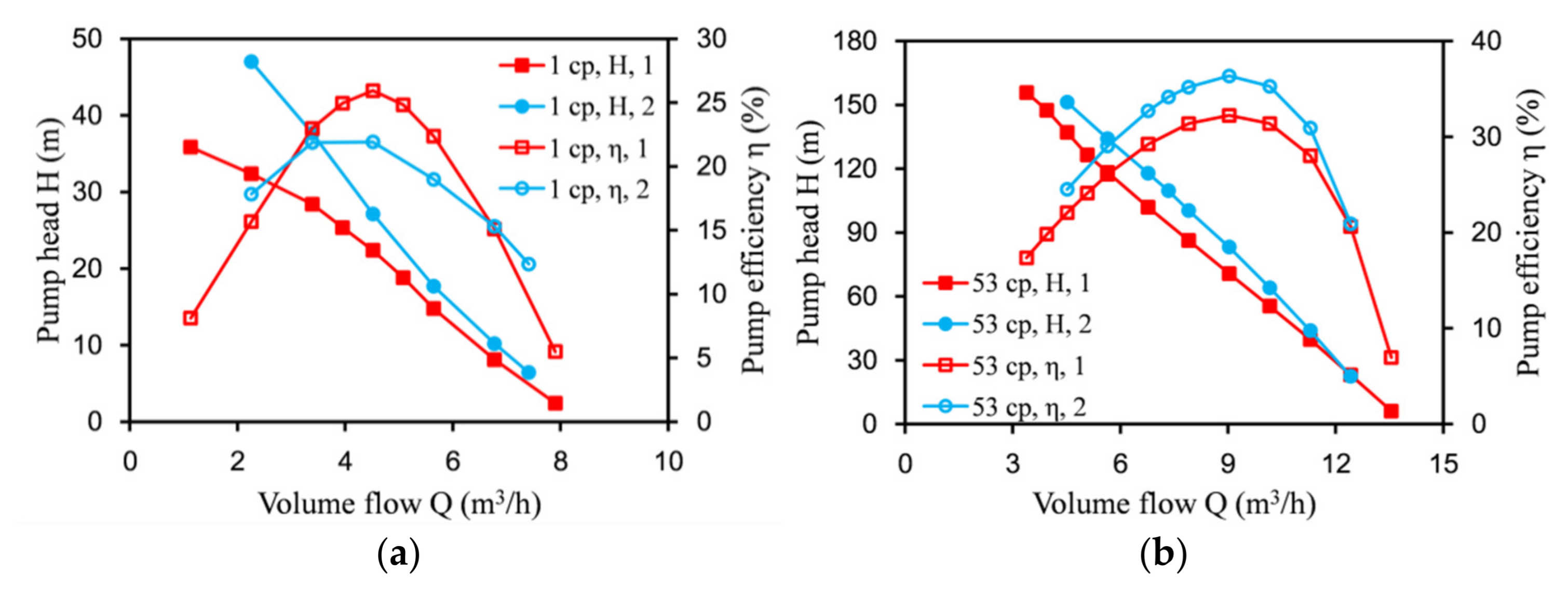
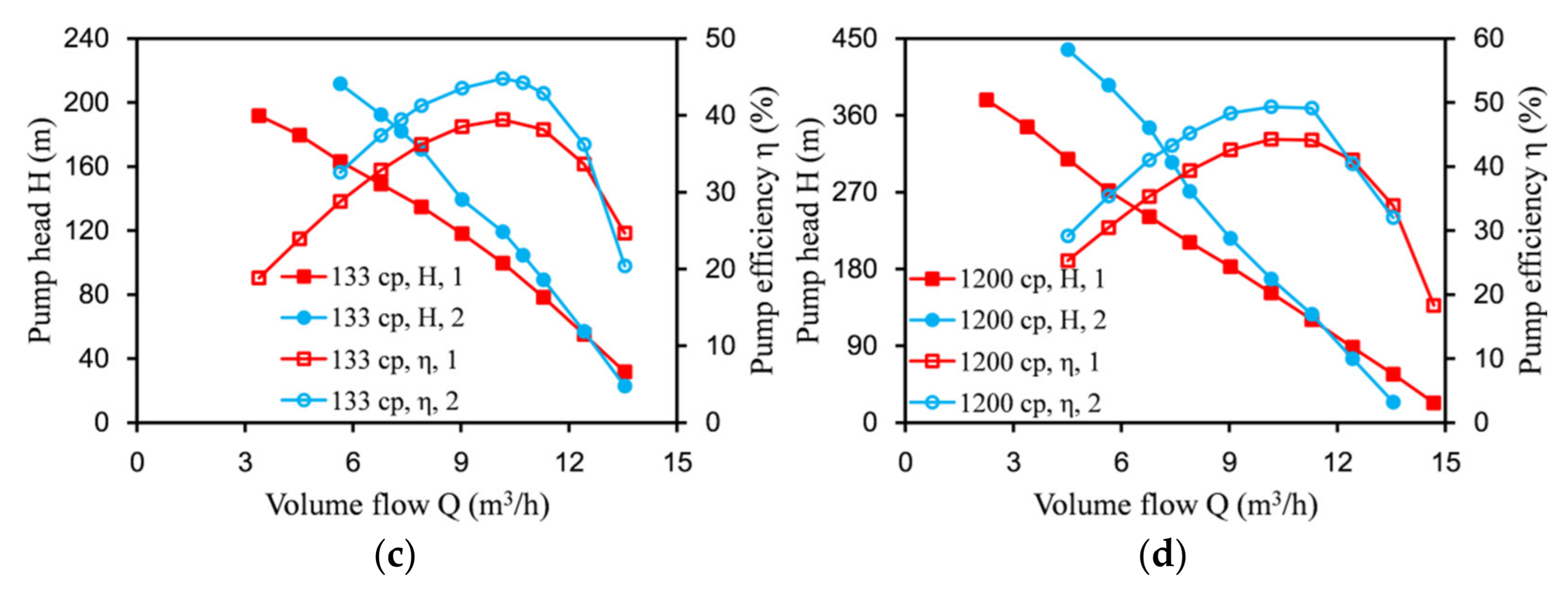
5.2. Influence of Oil Viscosity on Performance of Labyrinth Screw Pump
5.3. Structure Optimization
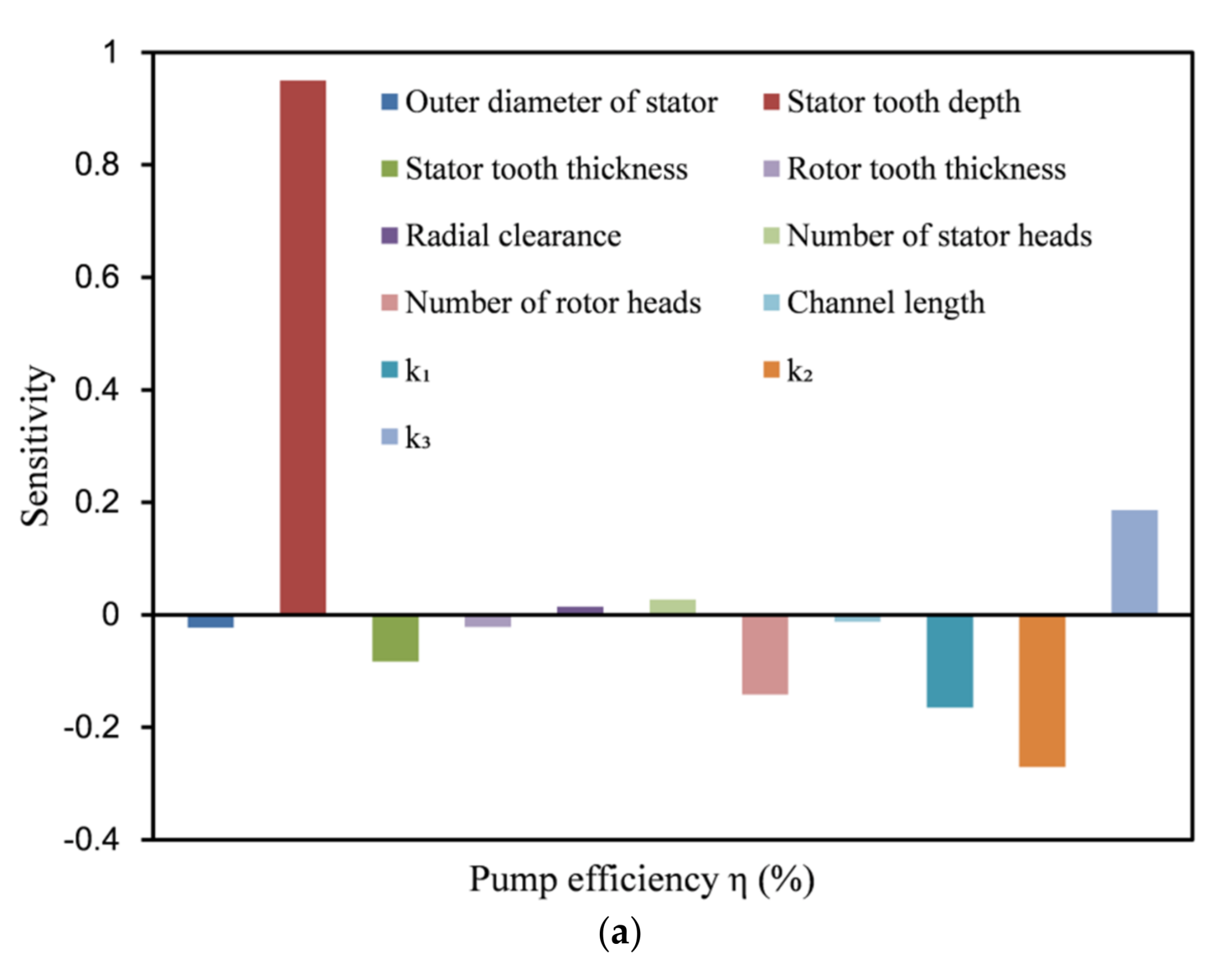
5.3.1. Parameter Correlation Analysis and Sample Space
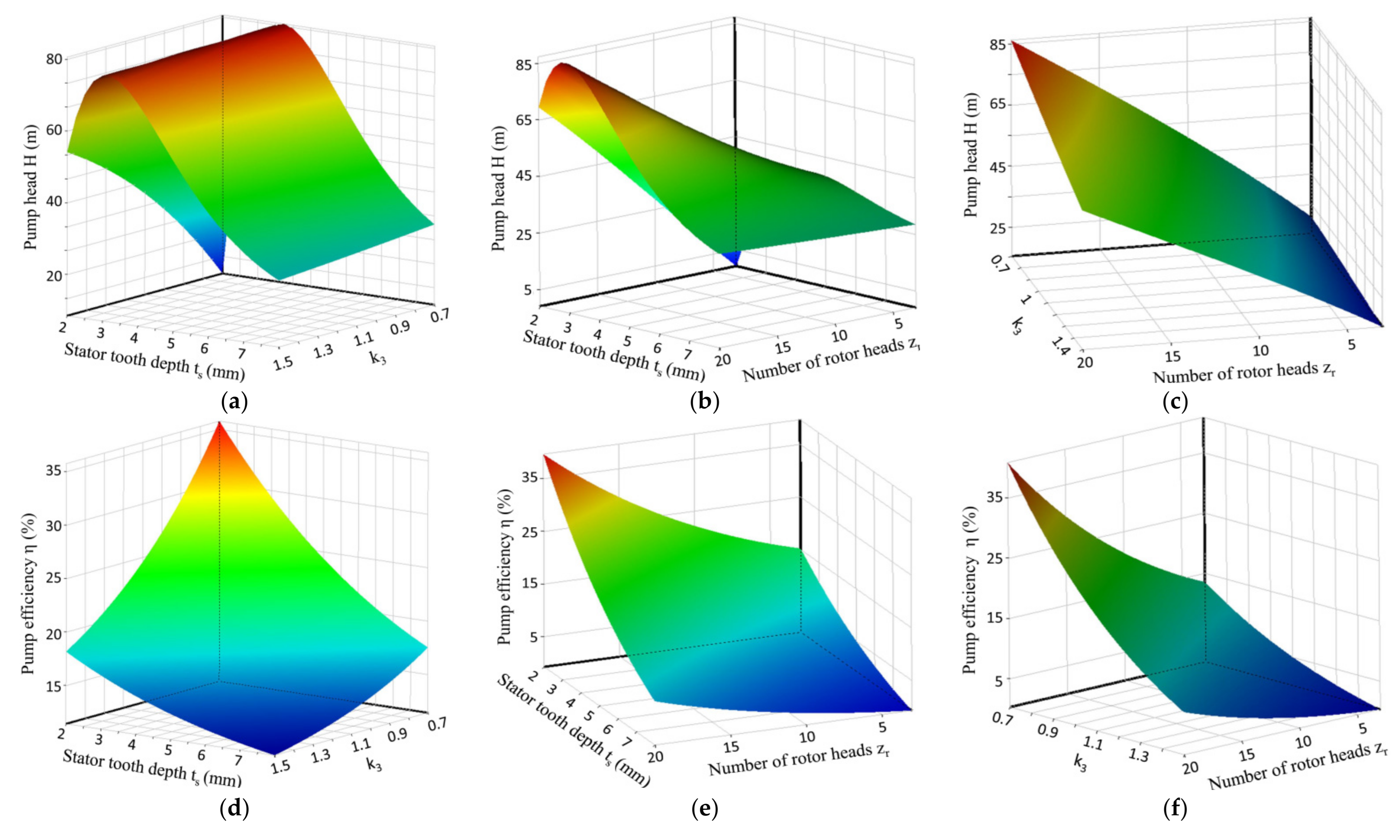
5.3.2. Response Surface Analysis
5.3.3. Analysis of Optimization Results
6. Conclusions and Future Work
6.1. Conclusions
- (1)
- The performances of rectangular labyrinth pumps when conveying viscous oil are better than those when conveying water. As the viscosity of the conveying medium increases, the lift and efficiency of the pump will increase. This is because the increase in the viscosity of the medium reduces the leakage of the pump during the conveying process and reduces the energy loss.
- (2)
- Based on the mathematical model of the pump performance parameters obtained by the response surface method, the calculation results are similar to the test results. Therefore, the optimization design method of the labyrinth screw pump based on the response surface method is reliable.
- (3)
- After optimization, when the viscosity of the medium varied, the efficiency and head under each flow condition were significantly improved, except that the efficiency of pure water was reduced by 7.77%, and the head and efficiency for the other viscosities were increased by more than 10%.
- (4)
- The surface response method can truly reflect the highly non-linear relationship and interactive influence between the design variables of the main structure of the labyrinth screw pump and the optimization goal. Furthermore, it provides an intuitive, efficient, and reliable optimization method for the control of the booster performance and efficiency of the labyrinth screw pump method.
- (5)
- When the speed was 3000 rpm and the viscosity of the conveying medium was 133 cp, the efficiency of the optimized labyrinth screw pump reached 44.79%. This performance is higher than those of electric submersible pumps under the same working conditions. This shows that the labyrinth screw pump has the ability to handle high-viscosity liquids and exhibit better performances than electric submersible pumps when transporting viscous media.
6.2. Future Work
- (1)
- When the viscosity of the conveying medium increases, the performance change of the labyrinth pump is opposite to that of the centrifugal pump. At present, the performance changes of pumps can only be obtained based on test data or simulation results, and there is no definitive theory on the pumping mechanism of labyrinth pumps.
- (2)
- Since the radial gap between the stator and rotor of the labyrinth pump is small, the machining accuracy and materials of the stator and rotor will have certain requirements. Thus, we can study the processing costs and process issues.
- (3)
- In actual production, the temperature of the liquid will change when the viscous medium is transported. However, in the simulation in this article, to simplify the calculation, we did not consider the temperature changes. Therefore, the influence of temperature on the performance of the labyrinth pump can be studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| dws | Outer diameter of stator (mm) |
| ts | Stator tooth depth (mm) |
| tr | Rotor tooth depth (mm) |
| as | Stator tooth thickness (mm) |
| ar | Rotor tooth thickness (mm) |
| zr | Number of rotor thread |
| zr | Number of stator thread |
| ss | Stator thread lead (mm) |
| sr | Rotor thread lead (mm) |
| c | Radial clearance (mm) |
| L | Spiral length (mm) |
| k1 | The ratio of the stator inner diameter to the stator lead |
| k2 | The ratio of the rotor outer diameter to the rotor lead |
| k3 | The ratio of the rotor tooth depth to the stator tooth depth |
| H | Pump head (m) |
| η | Pump efficiency (%) |
| dns | Inner diameter of stator (mm) |
| dnr | Inner diameter of rotor (mm) |
References
- Tian, G.W.; Zhang, Y.C.; Li, J.Z. CFD simulation of the internal flow of the labyrinth screw pump. J. Beijing Univ. Chem. Technol. 2007, 17, 218–220. [Google Scholar]
- Xing, Y. Theoretical Design, CFD Numerical Calculation and Experimental Study on Triangular Labyrinth Screw Pump; Jiangsu University: Zhenjiang, China, 2006. [Google Scholar]
- Golubiev, A.I. The Development of a Three-stage Screw-Type Labyrinth Seal. In Proceedings of the 4th International Conference on Fluid Sealing, Philadelphia, PA, USA, 5–9 May 1969; pp. 348–350. [Google Scholar]
- Bilgen, B.; Akgungor, A.C. The turbulent double screw pump-theory. In Proceedings of the 6th International Conference on Fluid Sealing, Munich, Germany, 27 February–2 March 1973; pp. 45–60. [Google Scholar]
- Karow, K. Concentric Double Srew Seals with Laminar Flow. In Proceedings of the 6th International Conference on Fluid Sealing, Munich, Germany, 27 February–2 March 1971; pp. 375–382. [Google Scholar]
- Zhu, Y.Z.; Luo, J.; Korean, A. Numerical Analysis of Labyrinth Screw Pump and Seal. Acta Aeronaut. Sin. 1991, 36, 323–331. [Google Scholar]
- Ludwing, I.P.; Storm, T.N.; Allen, G.P. Experiment Study of End Effect and Pressure Patterns in Helical Groove Fluid Seal; NASA TND-3096; NASA: Washington, DC, USA, 1965. [Google Scholar]
- Rhode, D.L.; Guidry, M.J. Importance of labyrinth seal through flow deflection for enlarging clearance without increasing leakage. Tribol. Trans. 1993, 36, 477–483. [Google Scholar] [CrossRef]
- Golubiev, A.I. Determination of optimal parameters of labyrinth-screw seals and pumps. In Proceedings of the 16th International Conference on Fluid Sealing, Brugge, Belgium, 18–20 September 2000; pp. 473–481. [Google Scholar]
- Golubiev, A.I. Studies on seal for rotating shafts of high-pressure pumps. Wear 1965, 34, 210–288. [Google Scholar] [CrossRef]
- Li, J.J.; Zhang, Y.C. Numerical simulation of series combined labyrinth screw pump based on Fluent. J. Drain. Irrig. Mach. Eng. 2014, 32, 296–301. [Google Scholar]
- Zhang, S.; Zhang, Y.C.; Yan, H.; Yang, W.M. Numerical simulation and experimental study of gas-liquid two-phase flow of series-connected combined labyrinth screw pump. Ind. Saf. Environ. Prot. 2016, 42, 14–17. [Google Scholar]
- Ma, Q.Y.; Zhang, Q.Z.; Zhang, L.F.; Silan, F. Numerical simulation and experimental research on the internal flow field of rectangular labyrinth pump. Fluid Mach. 2017, 45, 1–4. [Google Scholar]
- Ma, R.M.; Wang, K.S. CFD Numerical Simulation and Experimental Study of Effects of Screw-Sleeve Fitting Clearance upon Triangular Thread Labyrinth Screw Pump (LSP) Performance. J. Appl. Fluid Mech. 2010, 3, 23–35. [Google Scholar]
- Wang, C.; Zhang, Y.C.; Li, J.Z. CFD simulation of maze screw pump coal water slurry transportation and preliminary discussion of internal wear. Guangdong Chem. Ind. 2011, 38, 57–59. [Google Scholar]
- Zhang, Y.C.; Yang, C.L.; Li, J.Z. Numerical simulation and experiment of gas-liquid two-phase flow field of labyrinth screw pump. J. Drain. Irrig. Mach. Eng. 2010, 28, 492–496. [Google Scholar]
- Zhang, D.S.; Mei, J.; Zhao, R.J.; Huang, J.; Jin, Y.X. Response surface method-based optimization of impeller of fluoroplastic two-phase flow centrifugal pump. J. Drain. Irrig. Mach. Eng. 2020, 38, 898–903. [Google Scholar]
- Gao, Y.; Zhang, W.B.; Jiang, Q.F.; Deng, W.Q.; Han, T. Optimization of Impeller for Rotary Pump of Hydrodynamic Turbine Based on Response Surface Method. Hydropower 2017, 43, 67–72. [Google Scholar]
- Shi, Y. Research on the Internal Flow Pattern and Stage by Stage Design of a Multi-Stage Rotodynamic Gas-Liquid Pump; China University of Petroleum (Beijing): Beijing, China, 2019. [Google Scholar]
- Li, T.T. Theoretical Design, CFD Numerical Calculation and Experimental Study on Rectangle Labyrinth Screw Pump; Jiangsu University: Zhenjiang, China, 2007. [Google Scholar]
- Jia, F. Large Eddy Simulation and Experimental Study on Trapezium Labyrinth Screw Pump; Jiangsu University: Zhenjiang, China, 2013. [Google Scholar] [CrossRef]
- Gabelli, A.; Poll, G. Formation of lubricant film in rotary sealing contacts: Part I-lubricant film modeling. Trans. ASME 1992, 114, 280–286. [Google Scholar] [CrossRef]
- Wang, B.Q.; Peng, X.D.; Meng, X.K. A thermoelasto-hydrodynamic lubrication model for hydraulic rod O-ring seals under mixed lubrication conditions. Tribol. Int. 2019, 129, 442–458. [Google Scholar] [CrossRef]
- Peng, G.J.; Huang, X.; You, B.J. Optimization Design of Pipeline Pump Based on Response Surface Method. Hydropower Energy Sci. 2021, 39, 138–141. [Google Scholar]
- Wang, K.F. Construction method of sparse representation response surface based on mixed basis. Comput. Knowl. Technol. 2019, 15, 277–278. [Google Scholar]
- Liu, J.; Zhang, H.; Huang, H.; Chang, P. Optimization Design for Crankshaft of Mud Pump Based on Response Surface Model. J. Syst. Simul. 2019, 31, 879–885. [Google Scholar]
- Chen, H.L.; Liu, J.F.; Ren, K.T.; Li, T.; Fu, J.; Zou, Q.; Yin, Y.X. Optimization of upstream pumping mechanical seal based on response surface method. J. Drain. Irrig. Mach. Eng. 2016, 34, 232–237. [Google Scholar]
- Tao, J.X.; Chen, W.Q.; Li, X.Y. Optimization Design Based on Response Surface Methodology for Vortex Pump with Bowed Blade. Hydraul. Pneum. 2018, 43, 12–18. [Google Scholar]

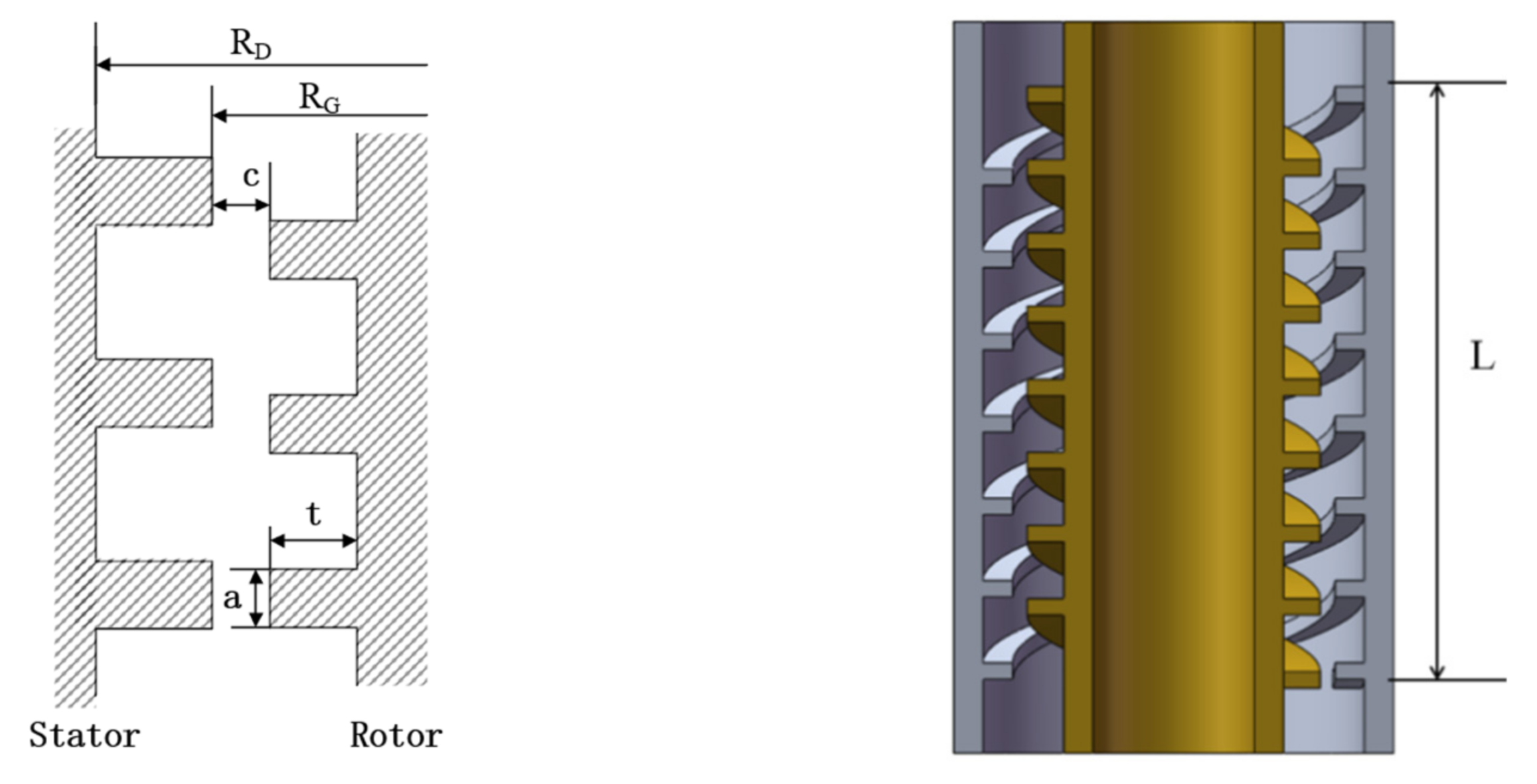


| Structural Parameters of Pump | Symbol | Rotor | Stator |
|---|---|---|---|
| Tooth depth (mm) | t | 3 | 4 |
| Number of threads | z | 20 | 20 |
| Addendum circle radius (mm) | RD | 40 | 44.4 |
| Root radius (mm) | RG | 37 | 40.4 |
| Tooth thickness (mm) | a | 1.7 | 1.7 |
| Lead of thread (mm) | s | 112 | 120 |
| Channel length of components (mm) | L | 160 | |
| Radial clearance (mm) | c | 0.4 | |
| Design Parameters | Parameter Description | Initial Value (mm) | Optimization Range (mm) |
|---|---|---|---|
| dws | Outer diameter of stator | 88.8 | 88–91 |
| ts | Stator tooth depth | 4 | 2–8 |
| as | Stator tooth thickness | 1.7 | 0.5–2.0 |
| c | Radial clearance | 0.4 | 0.5–1.5 |
| ar | Rotor tooth thickness | 1.7 | 0.5–2.5 |
| k1 | k1 = dns/ss | 0.673 | 0.5–1.5 |
| k2 | k2 = dnr/sr | 0.714 | 0.7–1.5 |
| k3 | k3 = tr/ts | 0.75 | 0.5–1.5 |
| zr | Number of rotor thread | 20 | 3–20 |
| zs | Number of stator thread | 20 | 3–20 |
| L | Spiral length | 160 | 150–220 |
| Design Point | ts (mm) | as (mm) | c (mm) | k1 | zr | zs | k2 | k3 | ar (mm) | η (%) | H (m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.33 | 1.41 | 0.20 | 0.90 | 12 | 8 | 0.71 | 0.85 | 2.37 | 29.33 | 27.41 |
| 2 | 3.41 | 0.66 | 0.25 | 1.39 | 19 | 9 | 0.89 | 1.00 | 1.46 | 36.65 | 84.29 |
| 3 | 2.58 | 0.90 | 0.40 | 0.71 | 11 | 16 | 0.82 | 0.75 | 2.06 | 32.01 | 41.26 |
| 4 | 2.02 | 1.50 | 0.43 | 1.09 | 16 | 17 | 1.20 | 1.25 | 1.92 | 30.24 | 20.09 |
| 5 | 3.97 | 0.73 | 0.26 | 0.83 | 12 | 12 | 1.07 | 0.72 | 0.59 | 36.14 | 57.25 |
| 6 | 4.17 | 1.26 | 0.30 | 0.77 | 15 | 16 | 1.69 | 0.89 | 0.82 | 29.36 | 19.06 |
| 7 | 3.01 | 1.42 | 0.24 | 0.95 | 16 | 16 | 1.04 | 1.08 | 0.75 | 36.36 | 83.18 |
| 8 | 3.05 | 1.81 | 0.41 | 1.16 | 15 | 12 | 0.92 | 1.34 | 0.94 | 32.36 | 45.78 |
| 9 | 5.95 | 1.97 | 0.20 | 1.11 | 9 | 8 | 0.76 | 0.73 | 2.23 | 36.00 | 27.52 |
| … | … | … | … | … | … | … | … | … | |||
| 283 | 2.70 | 1.00 | 0.26 | 1.43 | 16 | 13 | 1.76 | 0.91 | 1.55 | 33.47 | 55.62 |
| Optimizing Parameters | Parameter Symbol and Unit | Original Model | Optimization Results | ||
|---|---|---|---|---|---|
| Plan 1 | Plan 2 | Plan 3 | |||
| Stator tooth depth | ts (mm) | 4 | 3.41 | 3.01 | 3.97 |
| Stator tooth thickness | as (mm) | 1.7 | 0.66 | 1.42 | 0.73 |
| Radial clearance | c (mm) | 0.4 | 0.25 | 0.24 | 0.26 |
| Rotor tooth thickness | ar (mm) | 1.7 | 1.46 | 0.75 | 0.59 |
| k1 | - | 0.67 | 1.39 | 0.95 | 0.83 |
| k2 | - | 0.71 | 0.89 | 1.04 | 1.07 |
| k3 | - | 0.75 | 1.00 | 1.08 | 0.72 |
| Number of rotor heads | zr | 20 | 19 | 16 | 12 |
| Number of stator heads | zs | 20 | 9 | 16 | 12 |
| Pump efficiency | η (%) | 32.23 | 35.71 | 36.36 | 36.14 |
| Pump head | H (m) | 70.72 | 84.29 | 83.18 | 57.25 |
| Optimizing Parameters | Parameter Symbol and Unit | Original Model | Optimized Model |
|---|---|---|---|
| Stator tooth depth | ts (mm) | 4 | 3.01 |
| Stator tooth thickness | as (mm) | 1.7 | 1.42 |
| Radial clearance | c (mm) | 0.4 | 0.24 |
| Rotor tooth depth | tr (mm) | 3 | 3.25 |
| Rotor tooth thickness | ar (mm) | 1.7 | 0.75 |
| Stator thread lead | ss (mm) | 120 | 88.26 |
| Rotor thread lead | sr (mm) | 112 | 80.32 |
| Number of stator heads | zr | 20 | 16 |
| Number of rotor heads | zs | 20 | 16 |
| Medium Viscosity | Project | Original Model | Optimized Model | Rate of Change (%) |
|---|---|---|---|---|
| 1 cp | η (%) | 25.94 | 23.92 | −7.77 |
| H (m) | 22.39 | 27.14 | 21.18 | |
| 53 cp | η (%) | 32.23 | 36.36 | 12.80 |
| H (m) | 70.73 | 83.18 | 17.61 | |
| 133 cp | η (%) | 39.45 | 44.79 | 13.55 |
| H (m) | 99.74 | 119.21 | 19.53 | |
| 1200 cp | η (%) | 44.26 | 49.35 | 11.50 |
| H (m) | 151.87 | 168.36 | 10.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, X.; Zhu, H.; Hu, B. Performance Research and Structure Optimization of Labyrinth Screw Pump. Micromachines 2021, 12, 790. https://doi.org/10.3390/mi12070790
Rong X, Zhu H, Hu B. Performance Research and Structure Optimization of Labyrinth Screw Pump. Micromachines. 2021; 12(7):790. https://doi.org/10.3390/mi12070790
Chicago/Turabian StyleRong, Xin, Hongwu Zhu, and Biao Hu. 2021. "Performance Research and Structure Optimization of Labyrinth Screw Pump" Micromachines 12, no. 7: 790. https://doi.org/10.3390/mi12070790
APA StyleRong, X., Zhu, H., & Hu, B. (2021). Performance Research and Structure Optimization of Labyrinth Screw Pump. Micromachines, 12(7), 790. https://doi.org/10.3390/mi12070790






