Power Dissipation of an Inductively Coupled Plasma Torch under E Mode Dominated Regime
Abstract
:1. Introduction
2. Main Issues in ICP
2.1. The Plasma Modes of ICP Torches: E Mode and H Mode
2.2. Energy Coupling during E-H Mode Transition
2.3. The Unusual Long E Mode Range of the Plasma Torch
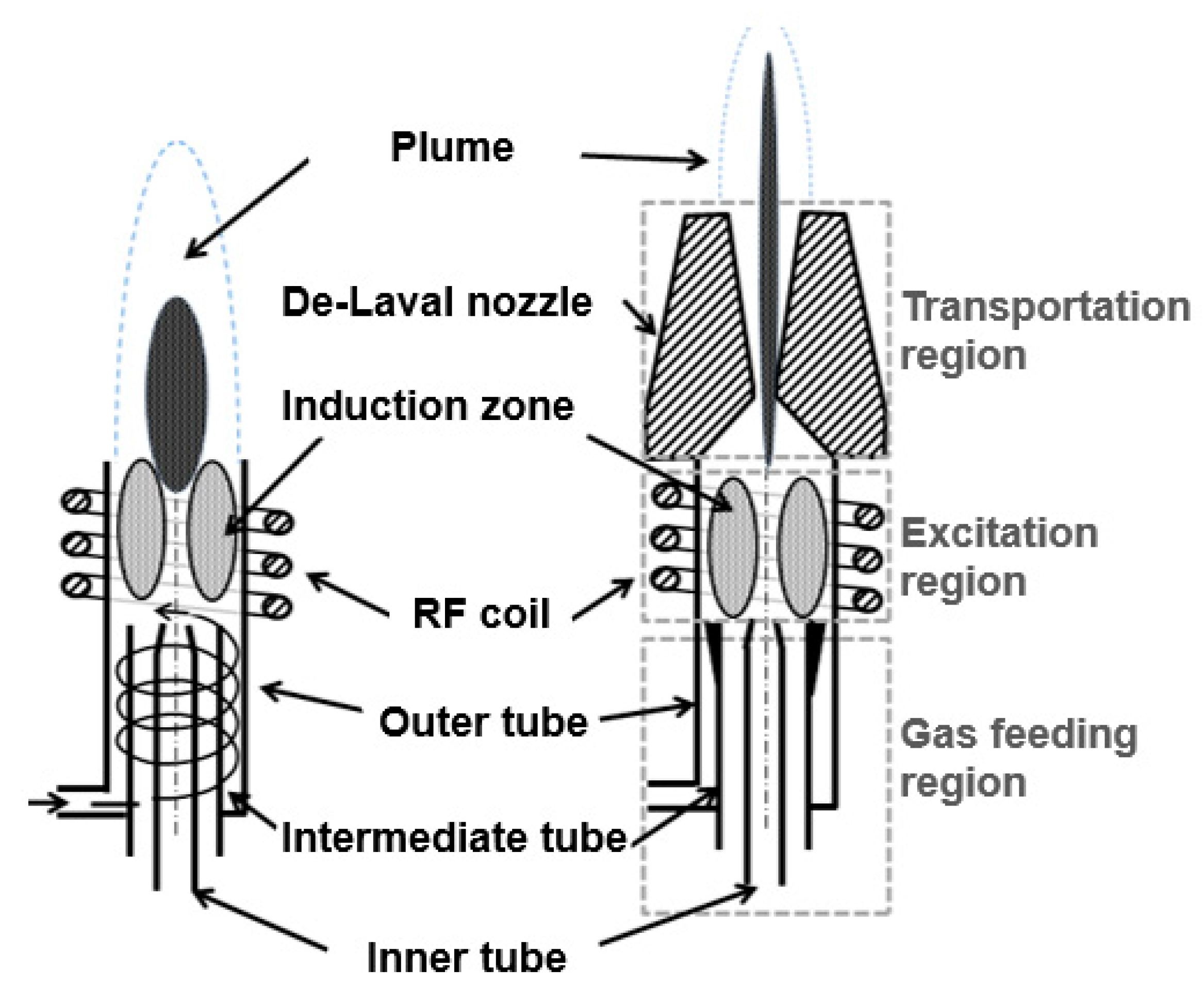
3. Experimental Approaches
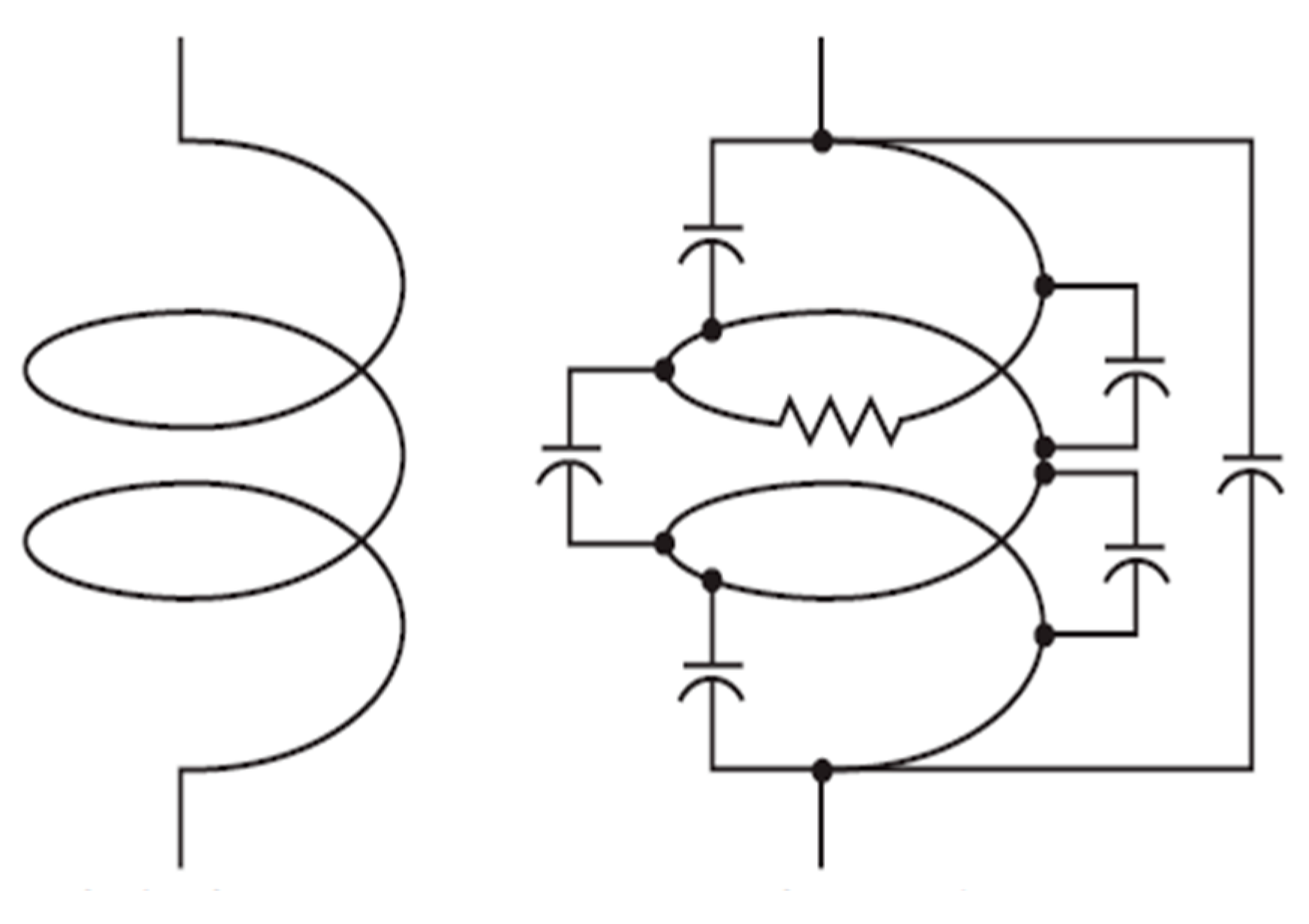
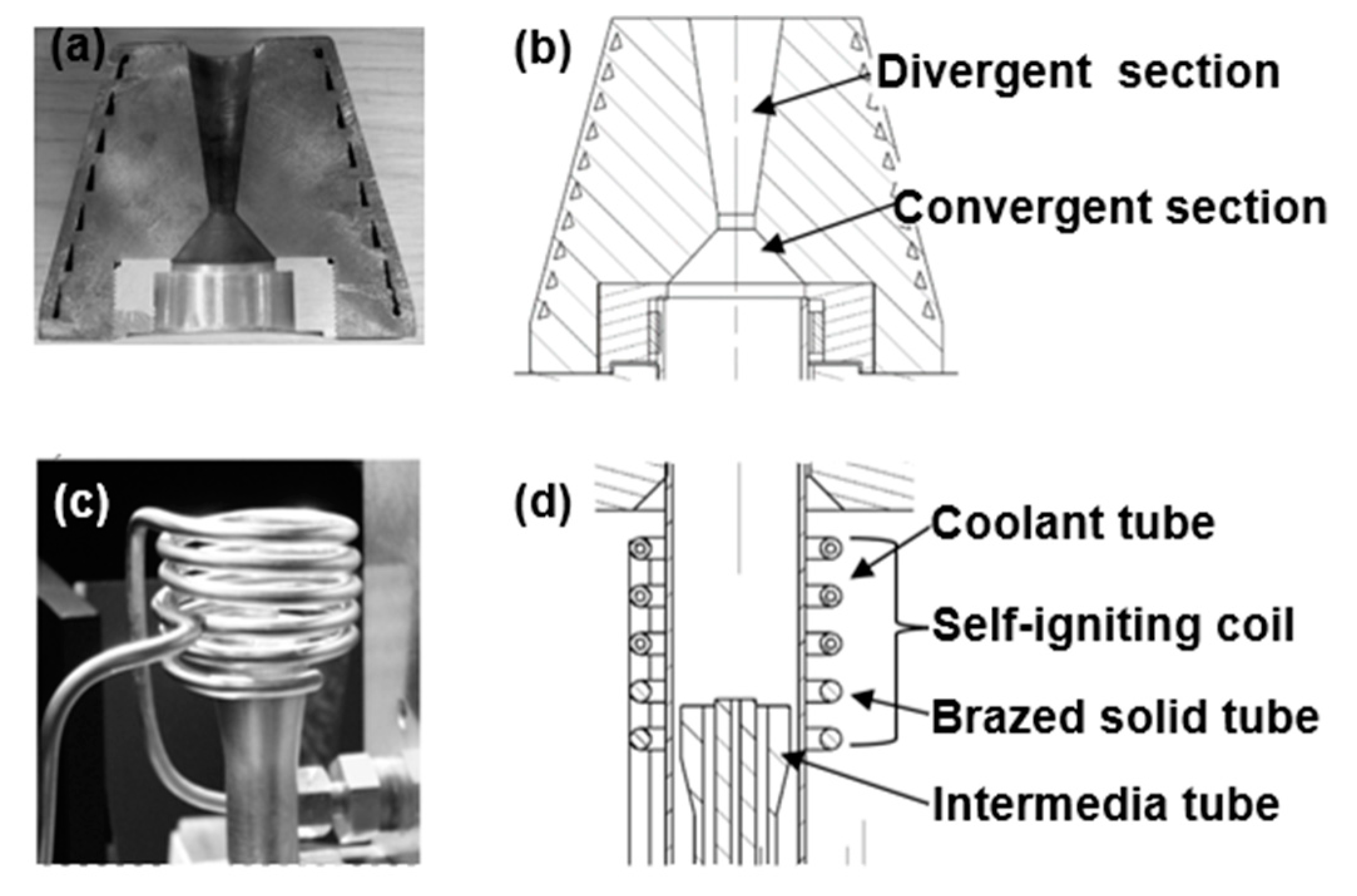
3.1. Plasma Delivery System
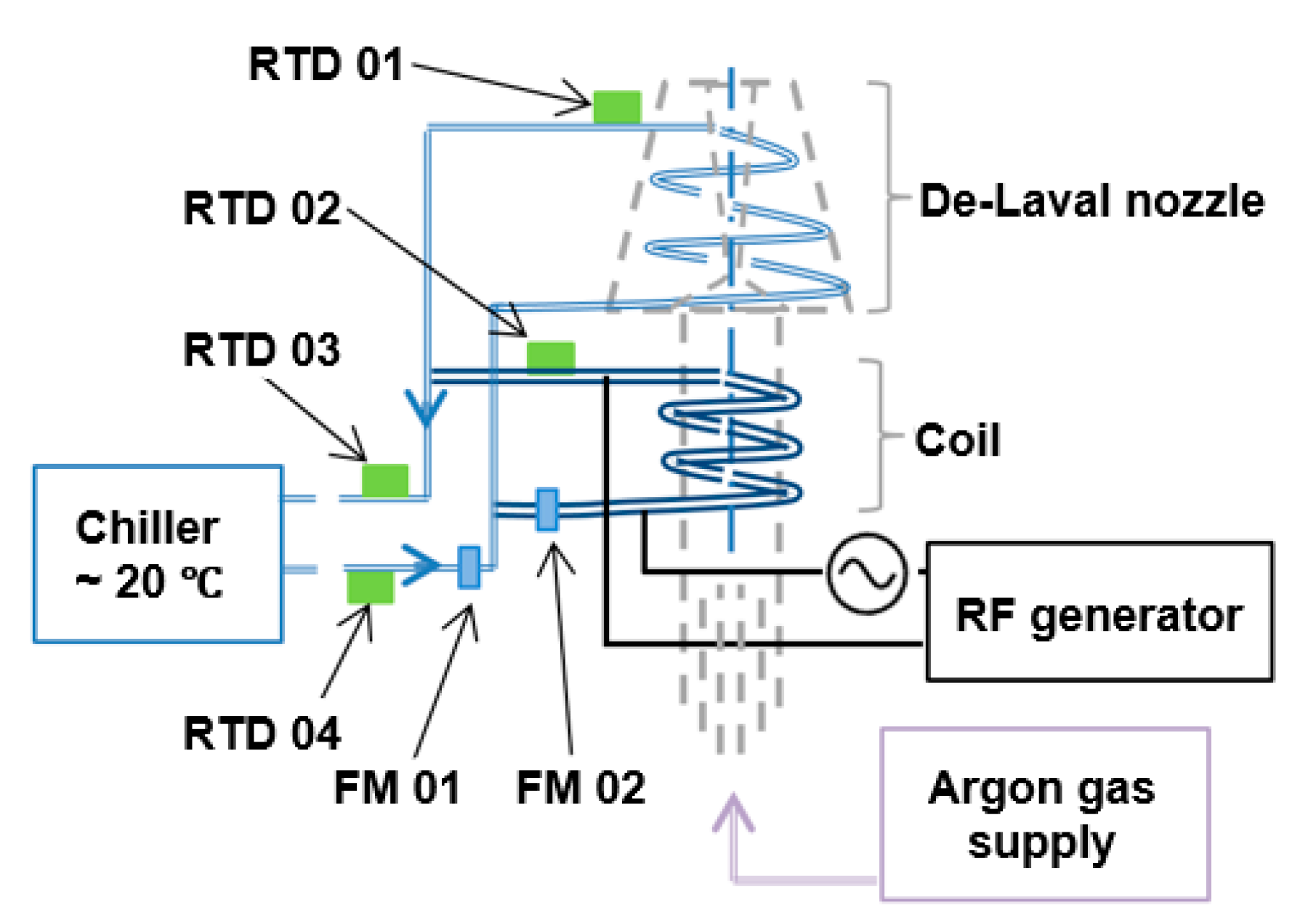
3.2. Coolant Flow Rate Measurement
3.3. Coolant Supply
3.4. Temperature Measurement
3.5. Gas Supply
3.6. RF Signal Generator
4. Analysis of the Power Dissipated in E Mode
4.1. Balance of Power Dissipation from the Plasma Delivery System
4.2. Power Dissipated by Coolants
4.3. Uncertainty Analysis
5. Discussion
5.1. Experimental Approach Analysis
5.2. Power Dissipation Analysis
5.3. Power Dissipation and Torch Efficiency of the ICP Torch
6. Conclusions
- (1)
- The result showed for the very first time the temperature increases in the coil of an ICP torch. A total of 48.7% of the RF power was absorbed by the coolant in this ICP torch. This study highlighted the near linear correlation between the RF power and the dissipated power through the coolant channels of the two key components.
- (2)
- The unique mechanical design of the developed torch experienced an E-H mode transition at circa 800 W RF power. Both the high RF power for E-H transition and the complex torch construction highlight the need for a robust RF generator and transmission line, in order to control the reflected power under E-H transition.
- (3)
- The creation of the power dissipation assessment method can be implemented to monitor and assess the torch performance during the digitally supported plasma processing in the future.
Author Contributions
Funding
Conflicts of Interest
References
- Dai, Z.; Xie, X.; Chen, H.; Zhou, L. Non-linear Compensated Dwell Time for Efficient Fused Silica Surface Figuring Using Inductively Coupled Plasma. Plasma Chem. Plasma Process. 2018, 38, 443–459. [Google Scholar] [CrossRef]
- Bennett, A.; Yu, N.; Castelli, M.; Chen, G.; Balleri, A.; Urayama, T.; Fang, F. Characterisation of a microwave induced plasma torch for glass surface modification. Front. Mech. Eng. 2021, 16, 122–132. [Google Scholar] [CrossRef]
- Kazemi, F.; Arnold, T.; Lorenz, P.; Ehrhardt, M.; Zimmer, K. Combined reactive plasma jet-laser etching method for technical optical glass containing metal oxides. Appl. Surf. Sci. 2021, 551, 149339. [Google Scholar] [CrossRef]
- Bennett, A.; Yu, N.; Castelli, M.; Chen, G.; Fang, F. Etching characteristics of crystal quartz by surface wave microwave induced plasma. In Proceedings of the AOPC 2020: Optics Ultra Precision Manufacturing and Testing, Beijing, China, 30 November–2 December 2020. [Google Scholar]
- Sun, R.; Yang, X.; Watanabe, K.; Miyazaki, S.; Fukano, T.; Kitada, M.; Arima, K.; Kawai, K.; Yamamura, K. Etching Characteristics of Quartz Crystal Wafers Using Argon-Based Atmospheric Pressure CF4 Plasma Stabilized by Ethanol Addition. Nanomanuf. Metrol. 2019, 2, 168–176. [Google Scholar] [CrossRef]
- Yu, N.; Jourdain, R.; Gourma, M.; Shore, P. Analysis of De-Laval nozzle designs employed for plasma figuring of surfaces. Int. J. Adv. Manuf. Technol. 2016, 87, 735–745. [Google Scholar] [CrossRef] [Green Version]
- Jourdain, R.; Castelli, M.; Yu, N.; Gourma, M.; Shore, P. Estimation of the power absorbed by the surface of optical components processed by an inductively coupled plasma torch. Appl. Therm. Eng. 2016, 108, 1372–1382. [Google Scholar] [CrossRef] [Green Version]
- Reed, T.B. Induction-coupled plasma torch. J. Appl. Phys. 1961, 32, 821–824. [Google Scholar] [CrossRef]
- Boulos, M.; Fauchais, P.; Pfender, E. Handbook of Thermal Plasmas; Springer International Publishing: New York, NY, USA, 2019. [Google Scholar]
- Chen, X. Heat transfer and flow in a radio frequency plasma torch-a new modelling approach. Int. J. Heat Mass Transfer 1990, 33, 815–826. [Google Scholar]
- Lee, H.-C. Review of inductively coupled plasmas: Nano-applications and bistable hysteresis physics. Appl. Phys. Rev. 2018, 5, 011108. [Google Scholar] [CrossRef]
- Barua, S.; Rahman, M.; Miyaguchi, M.; Mashio, S.; Maki, T.; Hasegawa, H. On-site analysis of gold, palladium, or platinum in acidic aqueous matrix using liquid electrode plasma-optical emission spectrometry combined with ion-selective preconcentration. Sens. Actuators B Chem. 2018, 272, 91–99. [Google Scholar] [CrossRef]
- Fiebrandt, M.; Oberberg, M.; Awakowicz, P. Comparison of Langmuir probe and multipole resonance probe measurements in argon, hydrogen, nitrogen, and oxygen mixtures in a double ICP discharge. J. Appl. Phys. 2017, 122, 013302. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.-K.; Cao, J.-X.; Liu, Y.; Yu, P.-C. The influence of gas pressure on E↔ H mode transition in argon inductively coupled plasmas. AIP Adv. 2018, 8, 035121. [Google Scholar] [CrossRef] [Green Version]
- Razzak, M.A.; Kondo, K.; Uesugi, Y.; Ohno, N.; Takamura, S. Transition from electrostatic-to-electromagnetic mode in a radio-frequency Ar inductively coupled plasma in atmospheric pressure. J. Appl. Phys. 2004, 95, 427–433. [Google Scholar] [CrossRef] [Green Version]
- Razzak, M.A.; Takamura, S. Coupling characteristic of induction coil in atmospheric pressure inductively coupled plasma. In Proceedings of the 2005 IEEE International Conference on Plasma Science, Monterey, CA, USA, 20–23 June 2005. [Google Scholar]
- Chabert, P.; Braithwaite, N. Physics of Radio-Frequency Plasmas; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Jorabchi, K.; Montaser, A. New coil geometries for the study of secondary discharge in atmospheric-pressure helium inductively coupled plasma mass spectrometry. Spectrochim. Acta Part B At. Spectrosc. 2004, 59, 1471. [Google Scholar] [CrossRef]
- Zhou, H.; Bennett, A.; Castelli, M.; Jourdain, R.; Guo, J.H.; Yu, N. Design of a motorised plasma delivery system for ultra-precision large optical fabrication. Int. J. Extrem. Manuf. 2020, 2, 045301. [Google Scholar] [CrossRef]
- Freeman, P.R.; Dietrich, C.F. Uncertainty, Calibration and Probability. The Statistics of Scientific and Industrial Measurment. J. R. Stat. Soc. Ser. A 1974, 137, 441. [Google Scholar] [CrossRef]
- Merkhouf, A.; Boulos, M.I. Distributed energy analysis for an integrated radio frequency induction plasma system. J. Phys. D Appl. Phys. 2000, 33, 1581. [Google Scholar] [CrossRef]
- Yu, N.; Yang, Y.; Jourdain, R.; Gourma, M.; Bennett, A.; Fang, F. Design and optimization of plasma jet nozzles based on computational fluid dynamics. Int. J. Adv. Manuf. Technol. 2020, 108, 2559–2568. [Google Scholar] [CrossRef]
- Yu, N. Thermal Analysis of Energy Beam Using De-laval Nozzle in Plasma Figuring Process. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2016. [Google Scholar]
- Fang, Z.; Zhang, Y.; Li, R.; Liang, Y.; Deng, H. An efficient approach for atomic-scale polishing of single-crystal silicon via plasma-based atom-selective etching. Int. J. Mach. Tools Manuf. 2020, 159, 103649. [Google Scholar] [CrossRef]
- Shibata, Y.; Sakairi, Y.; Shimada, K.; Mizutani, M.; Kuriyagawa, T. Effects of Topography and Modified Layer by Plasma-Shot Treatment on High-Speed Steel. Nanomanuf. Metrol. 2020, 3, 133–141. [Google Scholar] [CrossRef]
- Klecka, J.; Cizek, J.; Matejicek, J.; Lukac, F.; Zlatnik, R.; Chraska, T. Tailoring the structure of RF-ICP tungsten coatings. Surf. Coat. Technol. 2020, 406, 126745. [Google Scholar] [CrossRef]
- Rashid, M.M.; Archenti, A. Manufacturing and Characterization of a Carbon-Based Amorphous (a-CN X) Coating Material. Nanomanuf. Metrol. 2018, 1, 156–170. [Google Scholar] [CrossRef] [Green Version]

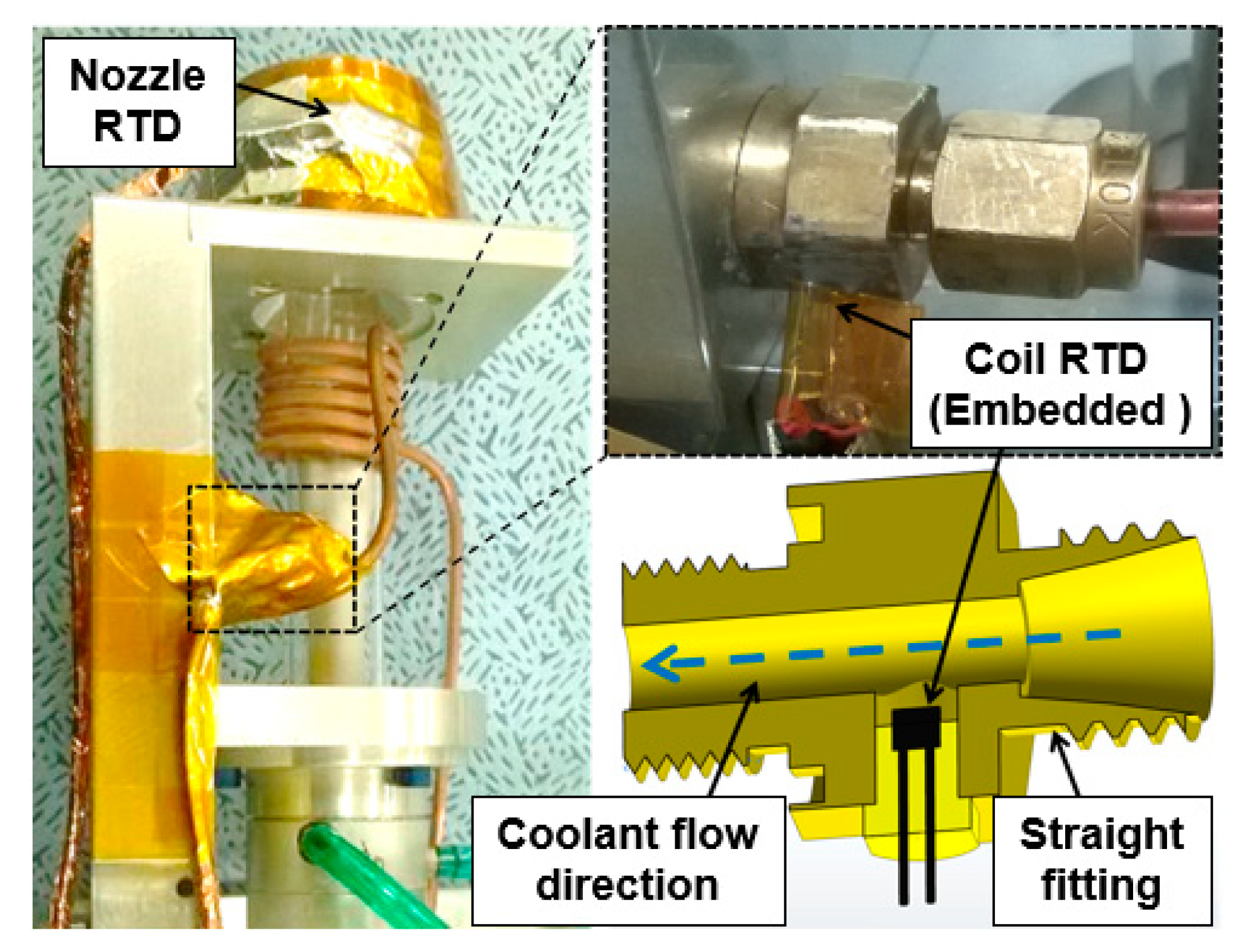
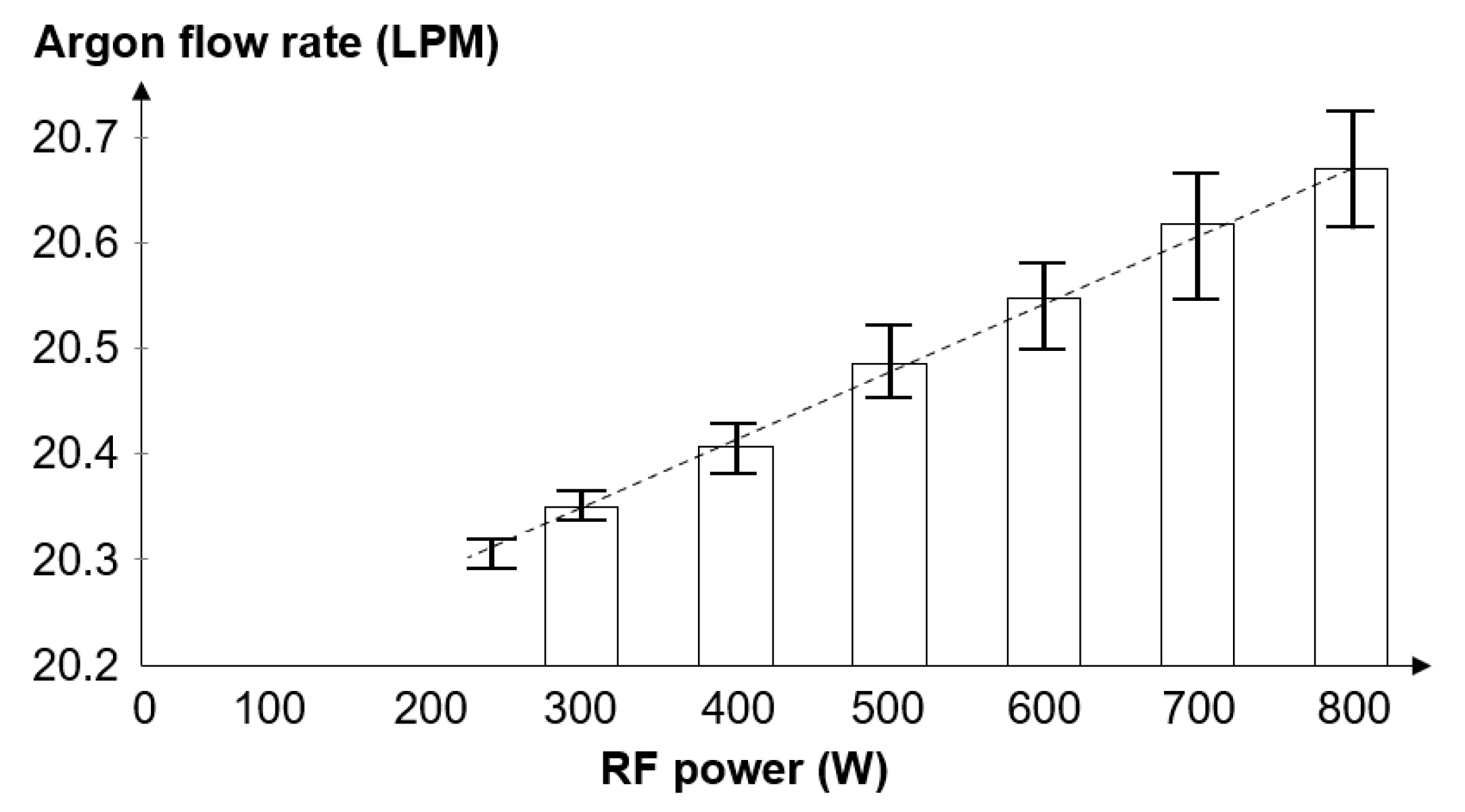
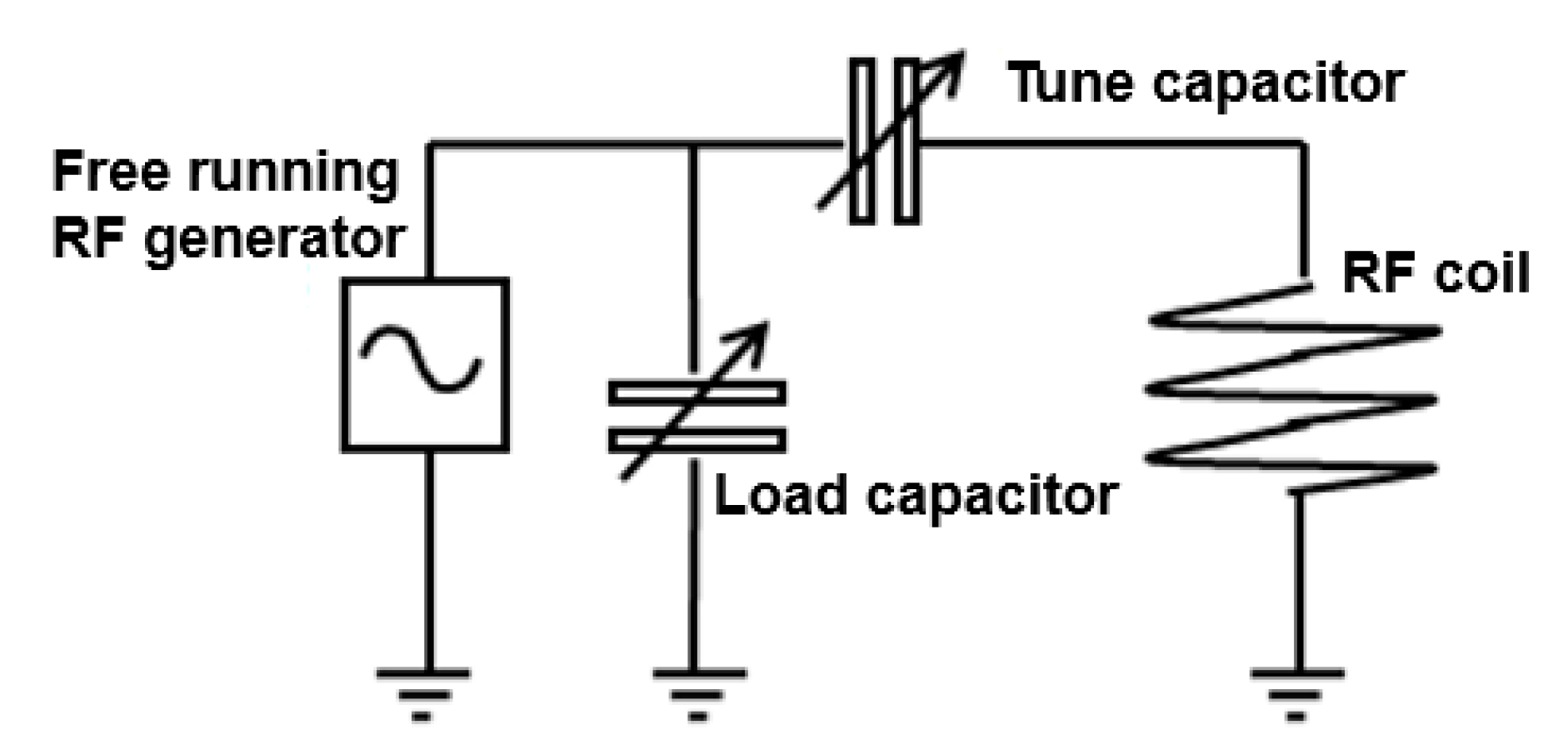


| Parameters | Values |
|---|---|
| Processing gas | Argon (research grade) |
| Gas flow rate | 22 LPM |
| Radio frequency | ~ 40.250 MHz |
| RF power | 300, 400, 500, 600, 700, 800 W |
| Source of Uncertainty | Value (±) | Probability Distribution | Divisor | Uncertainty Value |
|---|---|---|---|---|
| Temperature Measurement | 10−3 °C | 10−3 °C | ||
| SURR | 63.3 | Normal | 1 | 63.3 |
| Resolution | 10−3 | Normal | 2 | 5 × 10−4 |
| Combined | Normal | 63.3 | ||
| Expanded | Normal (k = 2) | 126.6 | ||
| Mass Flow Rate Measurement | g/min | g/min | ||
| SURR | 11.55 | Normal | 1 | 11.55 |
| Operator reading | 0.527 | Normal | 2 | 0.263 |
| Instrument | 20.56 | Normal | 2 | 10.28 |
| Combined | Normal | 15.46 | ||
| Expanded | Normal (k = 2) | 30.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, N.; Jourdain, R.; Gourma, M.; Xu, F.; Bennett, A.; Fang, F. Power Dissipation of an Inductively Coupled Plasma Torch under E Mode Dominated Regime. Micromachines 2021, 12, 834. https://doi.org/10.3390/mi12070834
Yu N, Jourdain R, Gourma M, Xu F, Bennett A, Fang F. Power Dissipation of an Inductively Coupled Plasma Torch under E Mode Dominated Regime. Micromachines. 2021; 12(7):834. https://doi.org/10.3390/mi12070834
Chicago/Turabian StyleYu, Nan, Renaud Jourdain, Mustapha Gourma, Fangda Xu, Adam Bennett, and Fengzhou Fang. 2021. "Power Dissipation of an Inductively Coupled Plasma Torch under E Mode Dominated Regime" Micromachines 12, no. 7: 834. https://doi.org/10.3390/mi12070834
APA StyleYu, N., Jourdain, R., Gourma, M., Xu, F., Bennett, A., & Fang, F. (2021). Power Dissipation of an Inductively Coupled Plasma Torch under E Mode Dominated Regime. Micromachines, 12(7), 834. https://doi.org/10.3390/mi12070834







