Micro Satellite Orbital Boost by Electrodynamic Tethers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mechanics
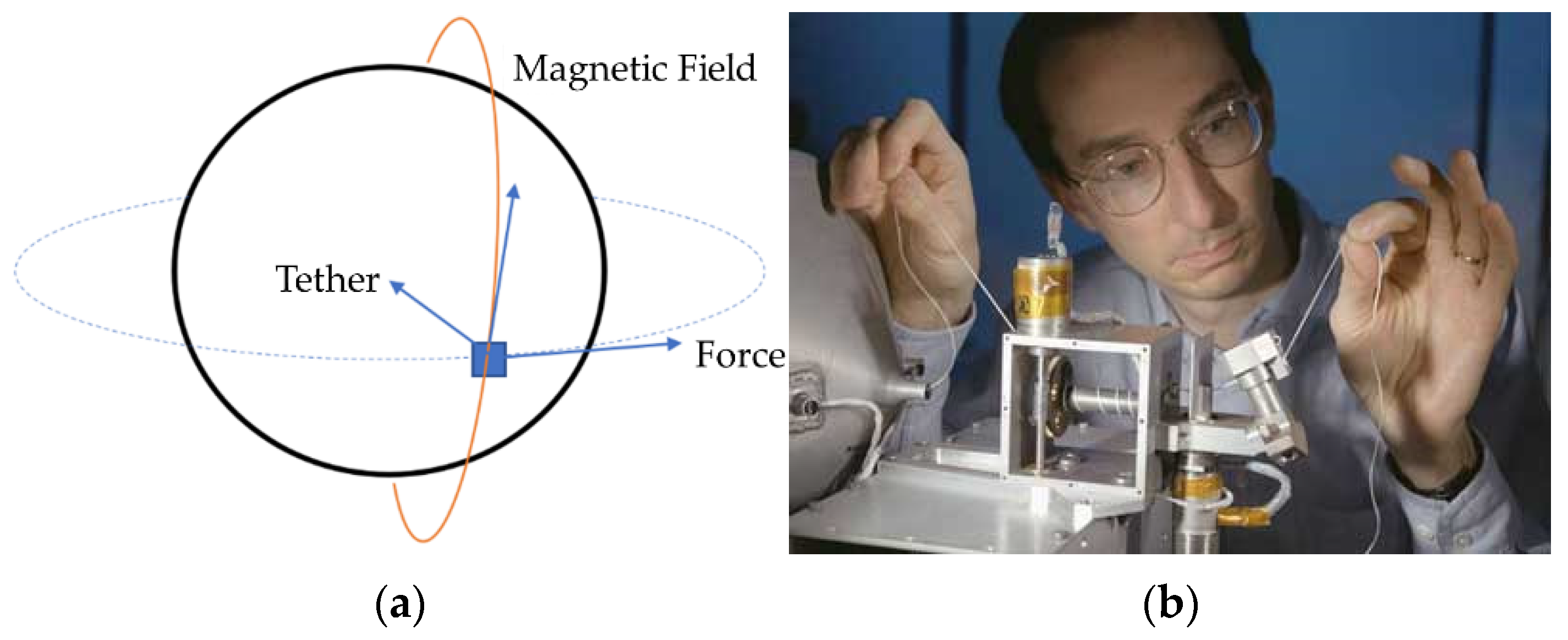
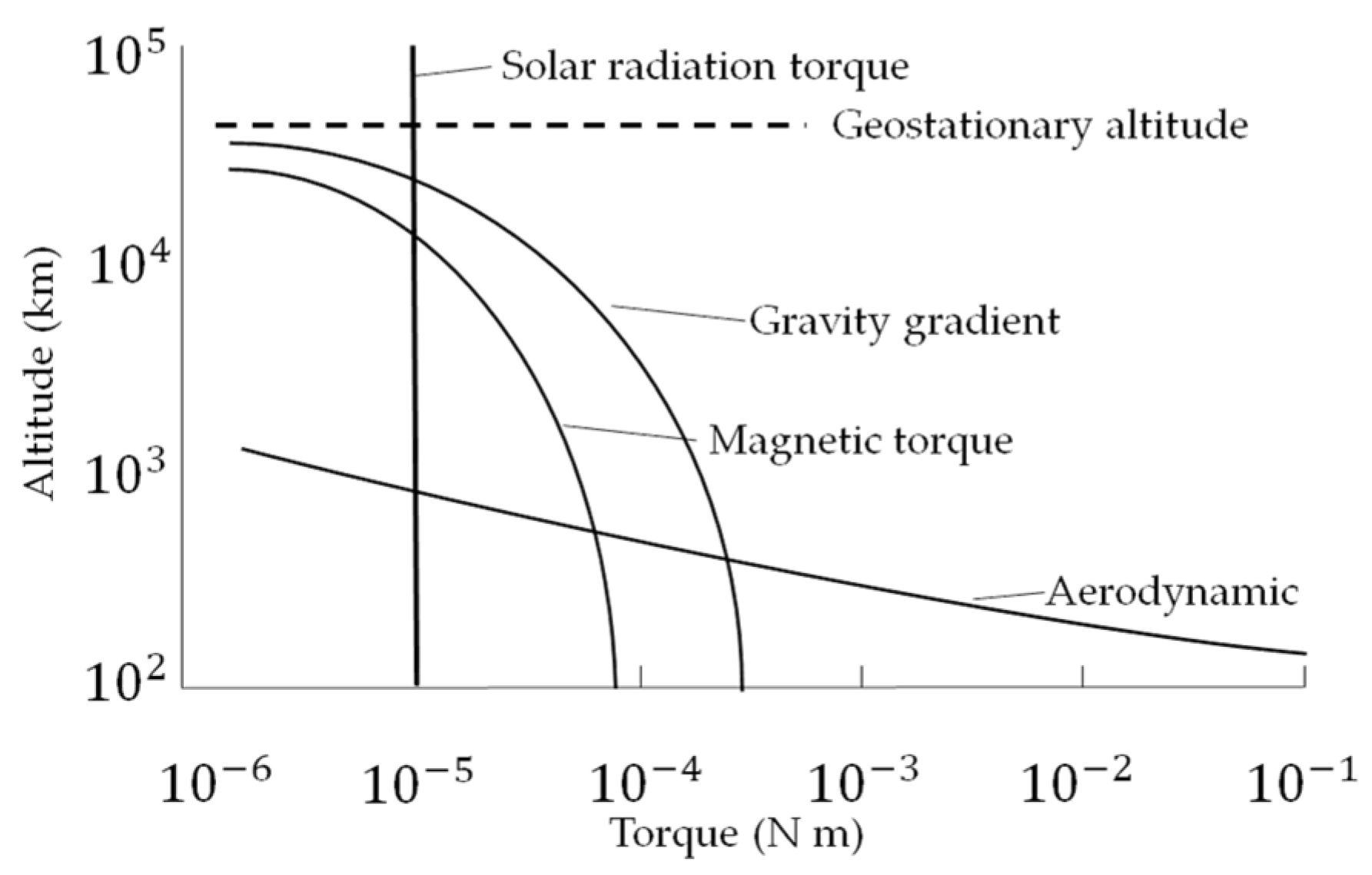
2.2. External Forces and Torques, and
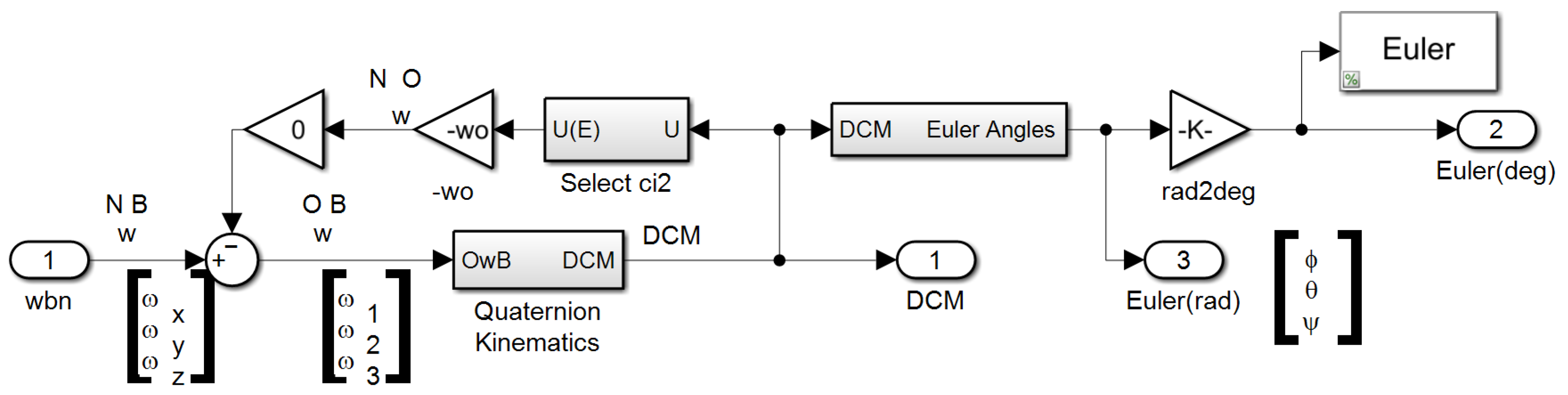
2.3. Spacecraft Simulation
2.4. Validating Simulations
2.5. Simulation Accuracy
3. Results
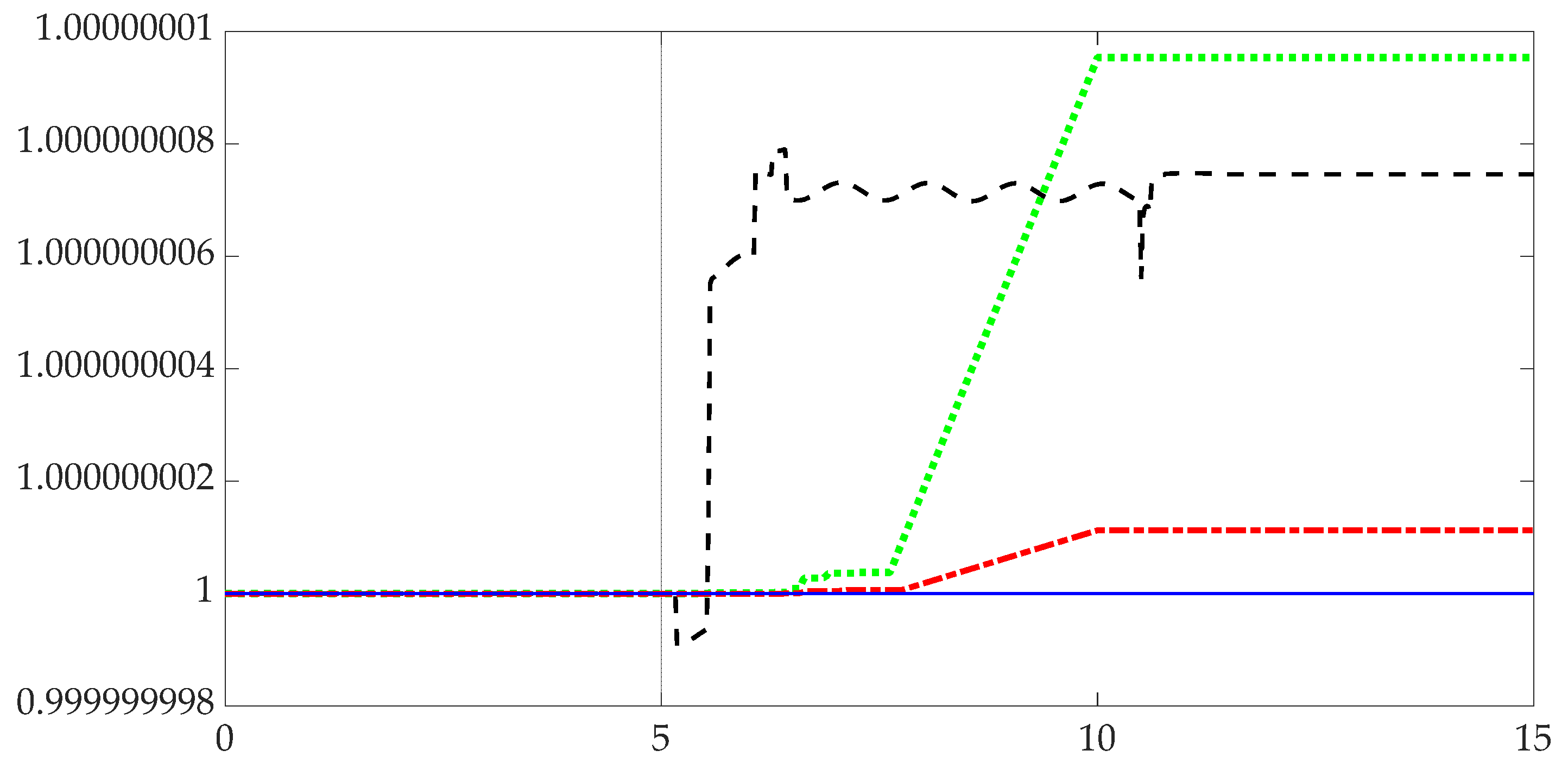
3.1. Verification of Simulation Accuracy
3.2. Performance of Electrodynamic Tether Reboost
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Consolidated Variables and Acronyms
| Variable/Acronym | Definition |
|---|---|
| mass moment of inertia | |
| angular acceleration | |
| angular velocity | |
| applied torque | |
| regression matrix | |
| regression vector | |
| Angular acceleration about x-direction | |
| Angular acceleration about y-direction | |
| Angular acceleration about z-direction | |
| Angular velocity about x-direction | |
| Angular velocity about y-direction | |
| Angular velocity about z-direction | |
| mass moment of inertia with respect to the x-axis | |
| mass moment of inertia with respect to the y-axis | |
| mass moment of inertia with respect to the z-axis | |
| mass product of inertia—sum of the products formed by multiplying each element of mass by the product of the x and y coordinates | |
| mass product of inertia—sum of the products formed by multiplying each element of mass by the product of the y and z coordinates | |
| mass product of inertia—sum of the products formed by multiplying each element of mass by the product of the x and z coordinates | |
| applied torque about x-direction | |
| applied torque about y-direction | |
| applied torque about z-direction | |
| applied force | |
| mass | |
| acceleration | |
| displacement rate relative to rotating frame | |
| displacement relative to rotating frame | |
| apparent acceleration | |
| atmospheric density | |
| µ | gravitational parameter |
| R | orbit altitude |
| tether length | |
| differential tether length | |
| Lorentz torques | |
| number of coils in magneto-torquer | |
| A | magneto-torquer vector area |
| I | magneto-torquer current |
| B | Earth’s magnetic field |
| Lorentz forces |
Appendix B
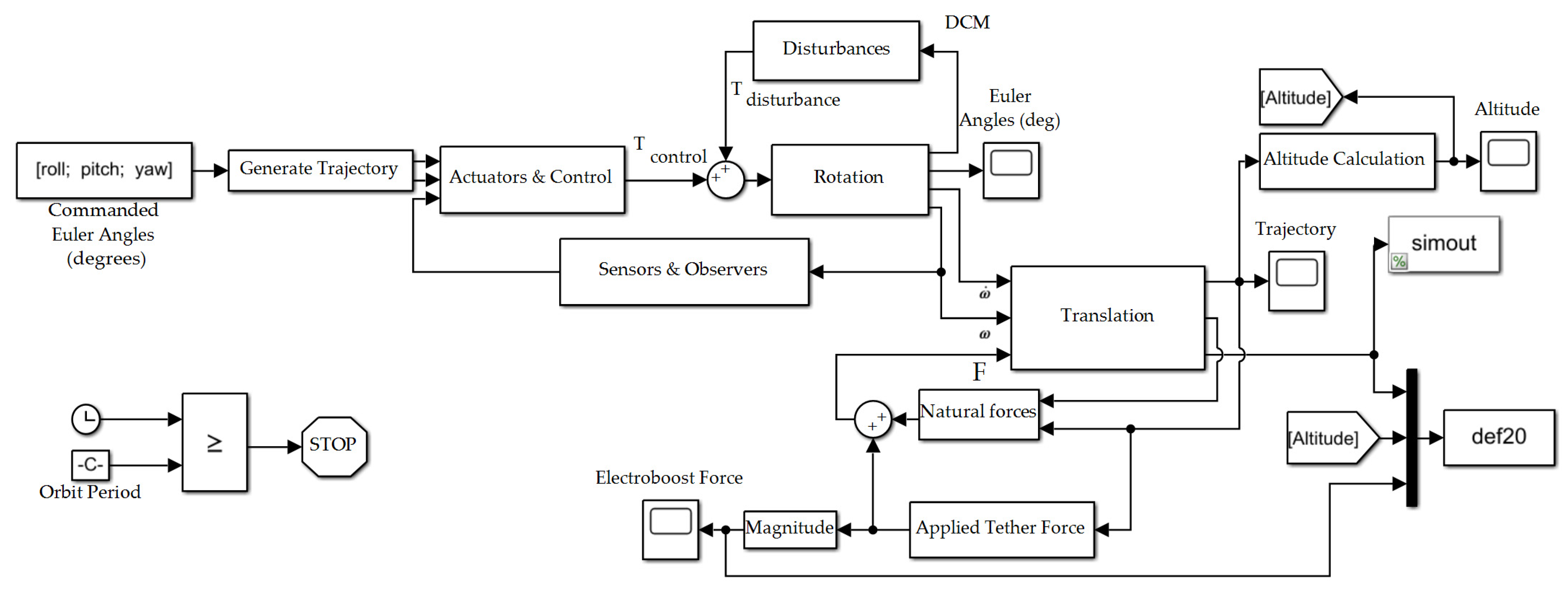


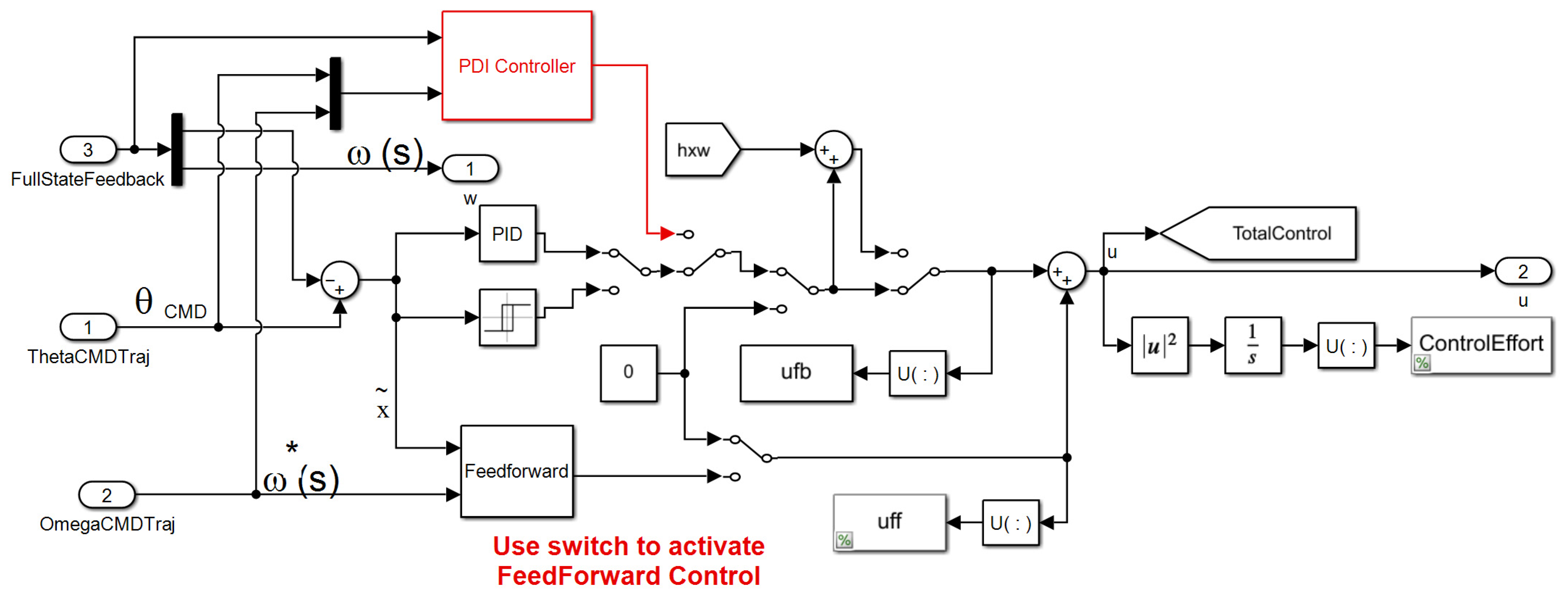
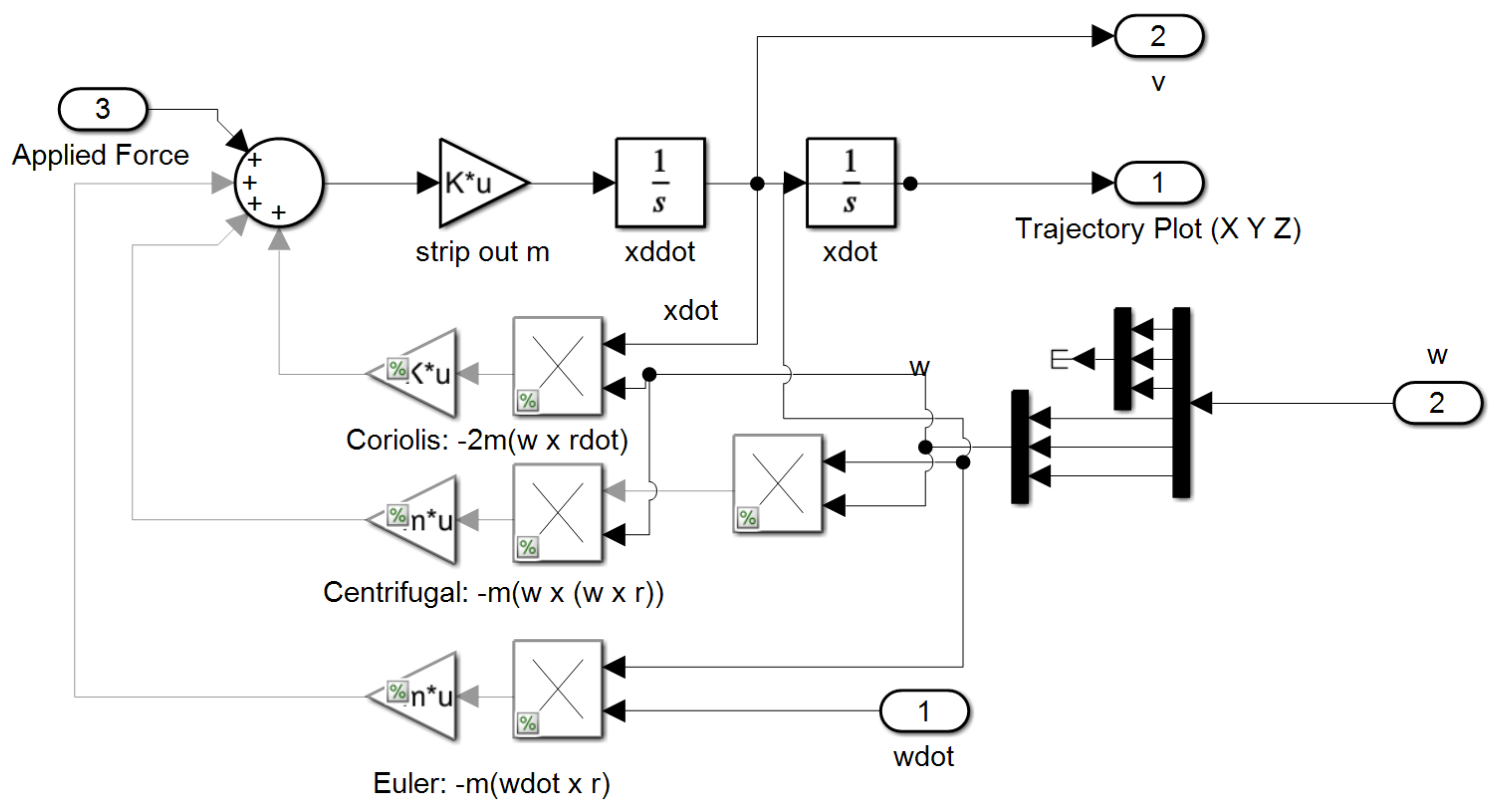
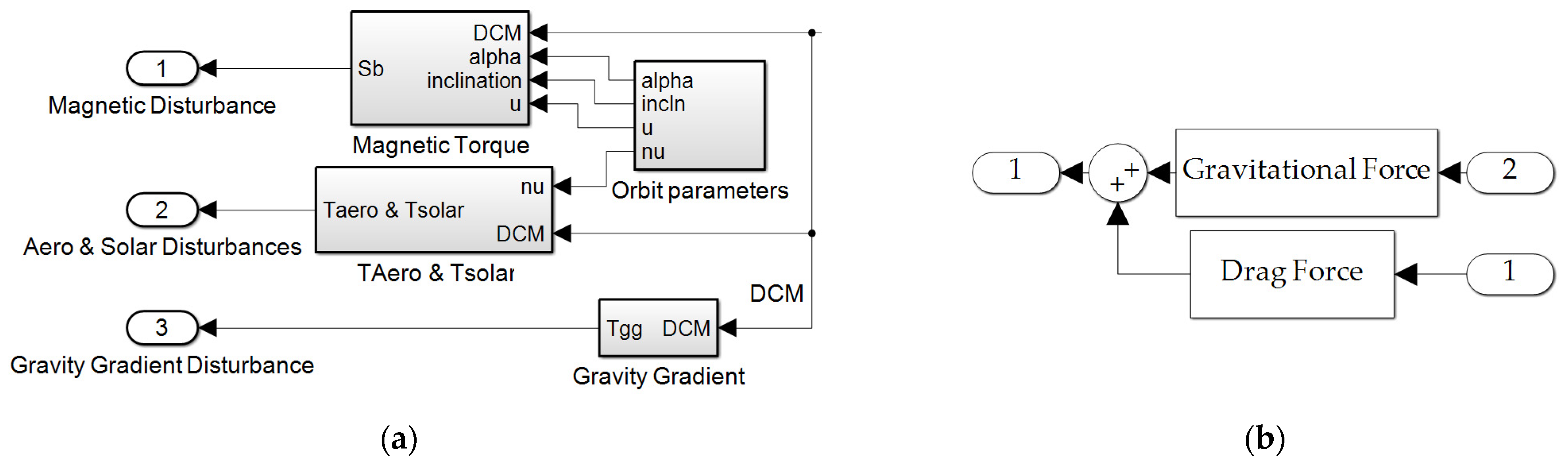


| Algorithm A1. InitFcn callbacks for SIMULINK model depicted in Figure 3, Figure 4, Figure 5 and Figure 6 |
| % Simulation run parameters Rate = 34.3; DeltaT = 1/Rate; %Constants0 Re = 6371.2e3; mu = 398601.2e9; %earth radius and universal gravitation constant %Spacecraft orbit R = Re + h; %orbit radius from center of earth we = 0.000072921158553; %earth’s angular velocity rad/solar sec(Vallado) wo = sqrt(mu/(R)^3); %orbit angular velocity epsilon = 11.5*pi/180; %angle between magnetic and geographic pole axes alphao = 0; uo = 0; nuo = 0; %Start S/C beneath subsolar point betasun = 60; gamma = 1.5; a = 1; b = 1; c = 1; %Assumed spacecraft rectangular size Area = [b*c a*c a*b]; %projected area~m^2 in body x, y, z directions kpre = −9.9639/24/3600/180*pi*0; %nodal precession constant assumed zero here wn = kpre*(Re/(Re + h))^3.5*cos(incln); %nodal precession (zero eccentricity) V = wo*(Re + h); rho = asin(Re/(h + Re)); %earth angular radius psun = 4.5E-6; %solar pressure constant~N/m^2 NOT USED dL = [0.1 0 0]; %predicted distance between cp and cg kilometerse = 2.3390e-005; %drag properties Cd = 2.2; %drag coeff corresponding to shape Kaero = −0.5*Cd*V^2; Psolar = 2*psun; %constants for aero and solar torque calculation density; %Spacecraft Magnetic Properties (assumed) mresid = [0 0 0.001]; %Spacecraft residual magnetic moment M = mresid; %Magnetic unit dipole vector K = 7.943e15; % ACTUAL Spacecraft Inertia conditions Ix = 16.67; Iy = 16.67; Iz = 16.67; Ixy = 0; Iyz = 0; Ixz = 0; Imo = [Ix −Ixy −Ixz; −Ixy Iy −Iyz; −Ixz −Iyz Iz]; %Moment of inertia matrix Iinv = inv(Imo); %Moment of inertia inverse goes in dynamics block %Spacecraft initial Euler state angles and rates phio = 0; thetao = 0; psio = 0; %Initial Euler Angles phidoto = 0; thetadoto = 0; psidoto = 0; %Initial Euler Rates %Calculation of initial quaternion (qo) and angular momentum (Ho) s1 = sin(phio/2); s2 = sin(thetao/2); s3 = sin(psio/2); c1 = cos(phio/2); c2 = cos(thetao/2); c3 = cos(psio/2); q1o = s1*c2*c3-c1*s2*s3; q2o = c1*s2*c3 + s1*c2*s3; %Wie pg. 321 q3o = c1*c2*s3-s1*s2*c3; q4o = c1*c2*c3 + s1*s2*s3; S1 = sin(phio); S2 = sin(thetao); S3 = sin(psio); C1 = cos(phio); C2 = cos(thetao); C3 = cos(psio); wxo = phidoto − psidoto*S2 − wo*S3*C2; wyo = thetadoto*C1 + psidoto*C2*S1 − wo*(C3*C1 + S3*S2*S1); wzo = psidoto*C2*C1 − thetadoto*S1 − wo*(S3*S2*C1-C3*S1); qo = [q1o q2o q3o q4o]; Ho = Imo*[wxo wyo wzo]’; norm(Ho)*1000; %Calculate eclipse time for comparison with EPS calculations Te = 100.87*2*V/2/pi; %CMG Properties (in degrees) %beta = 90*pi/180; %Skew angle in degrees converted to radians beta = [90; 90; −90; 0]; beta = beta.*pi./180; %beta = [54.73; 54.73; −54.73; 0]; beta = beta.*pi./180; Gimbal0 = [−30*pi/180; 90*pi/180; −30*pi/180; 0]; % Initial Gimbal angles for 0 H spin up w_wheel = 2800*(2*pi/60); %Wheel speed in RPM converted to rad/s Iwheel = 0.0614*1.3558179483314; % Wheel inertia in slug-ft^2 converted (exact) to kilogram m^2 h_wheel = Iwheel*w_wheel; % CMG Wheel Angular Momentum %FEEDFORWARD (ASSUMED) Spacecraft Inertia conditions Ix = 16.67; Iy = 16.67; Iz = 16.67; Ixy = 0; Iyz = 0; Ixz = 0; Imo = [Ix −Ixy −Ixz; −Ixy Iy −Iyz; −Ixz −Iyz Iz]; %Moment of inertia matrix THETAo = [Ix Ixy Ixz Iy Iyz Iz 0 0 0]; % [Fossen]’s adaptive feedforward parameters ETA = 1; LAMBDA = 0; uffGain = 1; %FEEDBACK CONTROLLERS Follow %PDI Controller Gains % TUNED Well for Presence of LOWPASS (Kp = 0.5; Kd = Kp*750; Ki = 0.1) %Kp = 0.5; Kd = Kp*750; Ki = 0.1; %PDI Controller Gains % TUNED WELL FOR NO-NOISE (Kp = 1; Kd = 2000*Kp; Ki = 5) Kp = 1; Kd = Kp*6000; Ki = 5; %PDI Controller Gains % TUNED WELL FOR NOISE (Kp = 1; Kd = Kp*3000; Ki = 1) %Kp = 1; %Kd = Kp*3000; %Ki = 1; %PID Controller Gains tuned well for uff and ufb decoupling Kpx = 20; Kdx = 1000; Kix = 0.1; %Bandpass filter pole per Bong Wie 2nd Edition pg 137–138 wp = 10*pi/SlewTime; % Product of pole frequency and zero frequency establishes max phase lag wz = 2*wp; dampZ = 1; % >0 but small for good tracking. dampP = dampZ; % Sensor Noise Parameters NoiseVariance = 1e-9; BADNoiseVariance = NoiseVariance*1e3; % Observer Gains MaxI = 100; lambda1 = 12.5; lambda2 = 50; lambda3 = 200; Kdo = MaxI*(lambda1 + lambda2 + lambda3)/10; Kpo = MaxI*(lambda1*(lambda2 + lambda3) + lambda2*lambda3)/10; Kio = MaxI*lambda1*lambda2*lambda3/9; m = 100*eye(3); minv = pinv(m); x0 = [R; 0; 0]; xdot0 = cross([0; 0; wo], x0) %gravity = −mu/(R^2); orbitperiod = 2*pi*sqrt((R^3)/mu); |
| Algorithm A2. StopFcn callbacks for SIMULINK model depicted in Figure 3, Figure 4, Figure 5 and Figure 6 |
| %% Means and Standard Deviations for solvers quaternion format long load(‘qneuler.mat’); load(‘qnheun.mat’); load(‘qnrk.mat’); load(‘qnode5.mat’); load(‘qnrk50.mat’); load(‘qnrk100.mat’); load(‘qnrk500.mat’); qnorm = [qneuler(2,:); qnheun(2,:); qnrk(2,:); qnode5(2,:)]; QNORMSTD = zeros(1,4); for i = 1:4 QNORMSTD(i) = std(qnorm(i,:)); QNORMSTDSTRING = num2str(QNORMSTD); QnormLEGEND = [‘||q||=’, QNORMSTDSTRING]; end QNORMSTD; figure; plot(qnrk50(1,:),qnrk50(2,:),‘k--’,‘linewidth’,1.5); hold on; qnorm = std(qnrk50(2,:));QNORMSTDSTRING = num2str(qnorm); Q50 = [‘ ||q_{50}||=’, QNORMSTDSTRING]; plot(qnrk100(1,:),qnrk100(2,:),‘g:’,‘linewidth’,1.5); hold on; qnorm = std(qnrk100(2,:));QNORMSTDSTRING = num2str(qnorm); Q100 = [‘||q_{250}||=’, QNORMSTDSTRING]; plot(qnrk500(1,:),qnrk500(2,:),‘r-.’,‘linewidth’,1.5); hold on; qnorm = std(qnrk500(2,:));QNORMSTDSTRING = num2str(qnorm); Q500 = [‘||q_{500}||=’, QNORMSTDSTRING]; plot(qnrk(1,:),qnrk(2,:),‘b’,‘linewidth’,1.5); hold on; qnorm = std(qnrk(2,:));QNORMSTDSTRING = num2str(qnorm); Q1000 = [‘||q_{1000}||=’, QNORMSTDSTRING]; legend([Q50],[Q100],[Q500],[Q1000],‘FontName’,‘Palatino Linotype’,‘FontSize’,10,‘location’,‘best’); xlabel(‘Time (s)’,‘FontName’,‘Palatino Linotype’,‘FontSize’,10) set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); grid on; set(gcf,‘units’,‘inches’,‘Position’,[1 1 7 2.5]) %% 3D Trajectory and altitude change over orbits load(‘long300.mat’) subplot(2,1,1); plot3(long300(2,:),long300(3,:),long300(4,:),‘Linewidth’,1.5); zlim([-175 175]); hold on; grid on subplot(2,1,2); plot(long300(1,:),long300(6,:)-300e3,‘Linewidth’,1.5); ylim([−80 350]); grid on; xlabel({‘Time (s)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10), ylabel({‘\Delta h (m)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); set(gcf,‘units’,‘inches’,‘Position’,[1 1 7 3]) %% Altitude change over single orbit—with and without tether load(‘rise200.mat’); load(‘rise250.mat’); load(‘rise300.mat’); load(‘rise350.mat’); load(‘rise500.mat’); load(‘fall200.mat’); load(‘fall250.mat’); load(‘fall300.mat’); load(‘fall350.mat’); load(‘fall500.mat’); figure; subplot(1,2,1); plot(fall200(1,:),fall200(6,:)-200e3,‘-.’,fall250(1,:),fall250(6,:)-250e3,‘--’,fall300(1,:),fall300(6,:)-300e3,fall350(1,:),fall350(6,:)-350e3,‘:’,fall500(1,:),fall500(6,:)-500e3,‘--’,‘LineWidth’,1.5); grid on; ylim([−1000 1000]); xlabel({‘Time (s)’; ‘(a)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10), ylabel({‘\Delta h (m)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10); legend(‘200 kilometers’,‘250 kilometers’,‘300 kilometers’,‘350 kilometers’,‘500 kilometers’,‘location’,‘best’); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); subplot(1,2,2); plot(rise200(1,:),rise200(6,:)-200e3,‘-.’,rise250(1,:),rise250(6,:)-250e3,‘--’,rise300(1,:),rise300(6,:)-300e3,rise350(1,:),rise350(6,:)-350e3,‘:’,rise500(1,:),rise500(6,:)-500e3,‘--’,‘LineWidth’,1.5); grid on; ylim([−1000 1000]); xlabel({‘Time (s)’; ‘(a)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10), ylabel({‘\Delta h (m)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10); %legend(‘200 kilometers’,‘250 kilometers’,‘300 kilometers’,‘350 kilometers’,‘500 kilometers’,‘location’,‘best’); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); set(gcf,‘units’,‘inches’,‘Position’,[1 1 7 3]) %% Numerical Values for Spacecraft Altitude %DATA REQUIRED: all files from prev format long; at200 = [rise200(1,end), fall200(6,end), rise200(6,end), rise200(6,end)- fall200(6,end)] at250 = [rise250(1,end), fall250(6,end), rise250(6,end), rise250(6,end)- fall250(6,end)] at300 = [rise300(1,end), fall300(6,end), rise300(6,end), rise300(6,end)- fall300(6,end)] at350 = [rise350(1,end), fall350(6,end), rise350(6,end), rise350(6,end)- fall350(6,end)] at500 = [rise500(1,end), fall500(6,end), rise500(6,end), rise500(6,end)- fall500(6,end)] %% Lorentz force extracted from tether—altitude and inclination load(‘inc0.mat’); load(‘inc10.mat’); load(‘inc30.mat’); load(‘inc60.mat’); load(‘inc90.mat’); figure subplot(1,2,1); plot(rise200(1,:),rise200(7,:),‘-.’,rise250(1,:),rise250(7,:),‘--’,rise300(1,:),rise300(7,:),rise350(1,:),rise350(7,:),‘:’,rise500(1,:),rise500(7,:),‘--’,‘LineWidth’,1.5); grid on; ylim([0 0.02]); xlabel({‘Time (s)’; ‘(b)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10), ylabel({‘\Delta h (m)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10); legend(‘200 kilometers’,‘250 kilometers’,‘300 kilometers’,‘350 kilometers’,‘500 kilometers’,‘location’,‘best’); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); subplot(1,2,2); plot(inc0(1,:),inc0(7,:),‘-.’,inc10(1,:),inc10(2,:),‘--’,inc30(1,:),inc30(2,:),inc60(1,:),inc60(2,:),‘:’,inc90(1,:),inc90(2,:),‘--’,‘LineWidth’,1.5); grid on; ylim([0 0.02]); xlabel({‘Time (s)’; ‘(b)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10), ylabel({‘Force (N)’},‘FontName’,‘Palatino Linotype’,‘FontSize’,10); legend(‘0’,‘10’,‘30’,‘60’,‘90’,‘location’,‘best’,‘NumColumns’,2); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); set(gcf,‘units’,‘inches’,‘Position’,[1 1 7 3]) %% Lorentz force means and standard deviations varying inclinations m0 = mean(inc0(7,:)) m10 = mean(inc10(2,:)) m30 = mean(inc30(2,:)) m60 = mean(inc60(2,:)) m90 = mean(inc90(2,:)) sd0 = std(inc0(7,:)) sd10 = std(inc10(2,:)) sd30 = std(inc30(2,:)) sd60 = std(inc60(2,:)) sd90 = std(inc90(2,:)) %% Deflection 3D plot load(‘def0.mat’); load(‘def10.mat’); load(‘def20.mat’); figure; plot3(def0(2,:),def0(3,:),def0(4,:),‘Linewidth’,1.5); hold on; plot3(def10(2,:),def10(3,:),def10(4,:),‘Linewidth’,1.5); hold on; plot3(def20(2,:),def20(3,:),def20(4,:),‘Linewidth’,1.5); hold on; legend(‘0’,‘10’,‘20’,‘location’,‘best’); view(−45,15); set(gca,‘FontName’,‘Palatino Linotype’,‘FontSize’,10); set(gcf,‘units’,‘inches’,‘Position’,[1 1 7 2]); grid on %xlim([0 400]); ylim([−200 20]); zlim([−1 2]); view(−45,15); |
References
- Garcia, M. Space Debris and Human Spacecraft. NASA Space Station Articles. 2021. Available online: https://www.nasa.gov/mission_pages/station/news/orbital_debris.html (accessed on 31 May 2021).
- Ecuador Pegasus Satellite Fears over Space Debris Crash. BBC News Website, 24 May 2013. Available online: https://www.bbc.com/news/world-latin-america-22635671 (accessed on 31 May 2021).
- Foust, J. ESA Spacecraft Dodges Potential Collision with Starlink Satellite. Space News. 2 September 2019. Available online: https://spacenews.com/esa-spacecraft-dodges-potential-collision-with-starlink-satellite/ (accessed on 31 May 2021).
- Bedrossian, N.; Bhatt, S.; Kang, W.; Ross, I.M. Zero propellant maneuver guidance. IEEE Control. Syst. Mag. 2009, 29, 53–73. [Google Scholar]
- Wie, B. Singularity analysis and visualization for single-gimbal Control Moment Gyros System. J. Guid. Control Dyn. 2004, 30, 272–282. [Google Scholar] [CrossRef]
- Qian, Z.; Guojin, T. Technical note: Space station zero propellant maneuver path planning considering SGCMG saturation and singularity. J. Astronaut. Sci. 2014, 61, 305–318. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B. Singularity Penetration with Unit Delay (SPUD). Mathematics 2018, 6, 23. [Google Scholar] [CrossRef] [Green Version]
- Hassa, C.L. Drag Coefficient Estimation Using Satellite Attitude and Orbit Data. Master’s Thesis, Department of Aerospace Engineering, Pennsylvania State University, State College, PA, USA, 2013. [Google Scholar]
- Hughes, P. Spacecraft Attitude Dynamics; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Johnson, L.; Herrmann, M. International Space Station Electrodynamic Tether Reboost Study; Marshall Space Flight Center: Huntsville, AL, USA, 1998.
- Vas, I.E.; Kelly, T.J.; Scarl, E.A. Space Station Reboost with Electrodynamic Tethers; The Boeing Company: Hunstville, AL, USA, 2000. [Google Scholar]
- Weis, L.; Peck, M. Chip-scale satellite control with multiple electrodynamic tethers. J. Guid. Con. Dyn. 2016, 39, 1643–1646. [Google Scholar] [CrossRef]
- Reinhardt, B.; Peck, M. New electromagnetic actuator for on-orbit inspection. J. Space Roc. 2016, 53, 241–248. [Google Scholar] [CrossRef]
- Zeledon, R.; Peck, M. Attitude dynamics and control of electrolysis propulsion cubesats. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef] [Green Version]
- Levchenko, I.; Xu, S.; Teel, G.; Mariotti, D.; Walker, M.L.R.; Keidar, M. Recent Progress and perspectives of space electric propulsion systems based on smart nanomaterials. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, I.; Xu, S.; Mazouffre, S.; Lev, D.; Pedrini, D.; Goebel, D.; Garrigues, L.; Taccogna, F.; Bazaka, K. Perspectives, frontiers, and new horizons for plasma-based space electric propulsion. Phys. Plasmas 2020, 27, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Lev, D.R.; Emsellem, G.D.; Hallock, A.K. The rise of the electric age for satellite propulsion. New Space 2017, 5, 4–14. [Google Scholar] [CrossRef]
- Nizhnik, O. The space mission design example using LEO bolos. Aerospace 2014, 1, 31–51. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft fine tracking pointing using adaptive control. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007; International Astronautical Federation: Paris, France, 2007. [Google Scholar]
- Sands, T.; Kim, J.; Agrawal, B. Improved Hamiltonian adaptive control of spacecraft. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft adaptive control evaluation. In Proceedings of the Infotech@ Aerospace, Garden Grove, CA, USA, 19–21 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; pp. 2012–2476. [Google Scholar]
- Olivieri, L.; Sansone, F.; Duzzi, M.; Francesconi, A. TED project: Conjugating technology development and educational activities. Aerospace 2019, 6, 73. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric propulsion methods for small satellites: A review. Aerospace 2021, 8, 22. [Google Scholar] [CrossRef]
- Reichhardt, T. NASA aims high with orbital transport system. Nature 2003, 423, 470. [Google Scholar] [CrossRef] [PubMed]
- NASA Prepares to Launch Space Tether Experiment. NASA-MSFC Release, 5 February 2002. Available online: https://spaceflightnow.com/news/n0202/05proseds/ (accessed on 3 June 2021).
- Chasles, M. Note sur les propriétés générales du système de deux corps semblables entr’eux. Bull. Sci. Math. Astron. Phys. Chem. 1830, 14, 321–326. (In French) [Google Scholar]
- Newton, I. Principia, Jussu Societatis Regiæ ac Typis Joseph Streater; Cambridge University Library: London, UK, 1687. [Google Scholar]
- Euler, L. Formulae generales pro translatione quacunque corporum rigidorum (General formulas for the translation of arbitrary rigid bodies. Novi Comment. Acad. Sci. Petropolitanae 1776, 20, 189–207. Available online: https://math.dartmouth.edu/~euler/docs/originals/E478.pdf (accessed on 31 May 2021).
- Smeresky, B.; Rizzo, A.; Sands, T. Optimal learning and self-awareness versus PDI. Algorithms 2020, 13, 23. [Google Scholar] [CrossRef] [Green Version]
- Sands, T. Development of deterministic artificial intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Picone, J.; Hedin, A.; Drob, D.; Aikin, A. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geol. Res. Space Physics 2012, 107, 1468. [Google Scholar] [CrossRef]
- Kuznetsova, M. MSIS-E-90 Atmosphere Model. Community Coordinated Modeling Center. Available online: https://ccmc.gsfc.nasa.gov/modelweb/models/msis_vitmo.php (accessed on 31 May 2021).
- Standish, E. Report of the IAU WGAS Sub-Group on Numerical Standards, Highlights of Astronomy; Appenzeller, I., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Standish, E. JPL Planetary and Lunar Ephemerides, DE405/LE405. JPL IOM 312.F-98-048. 1998. Available online: https://ssd.jpl.nasa.gov/?planet_eph_export (accessed on 31 May 2021).
- Park, R. Astrodynamic Constants. Solar System Dynamics JPL Website. Available online: https://ssd.jpl.nasa.gov/?constants (accessed on 31 May 2021).
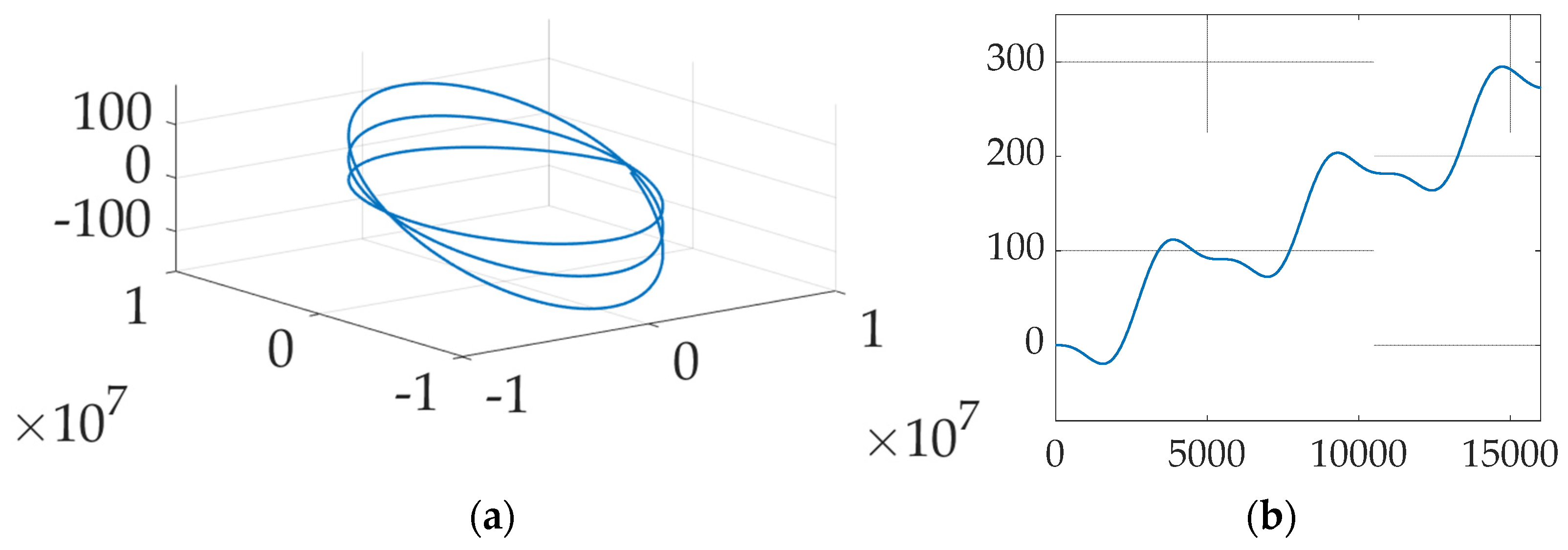
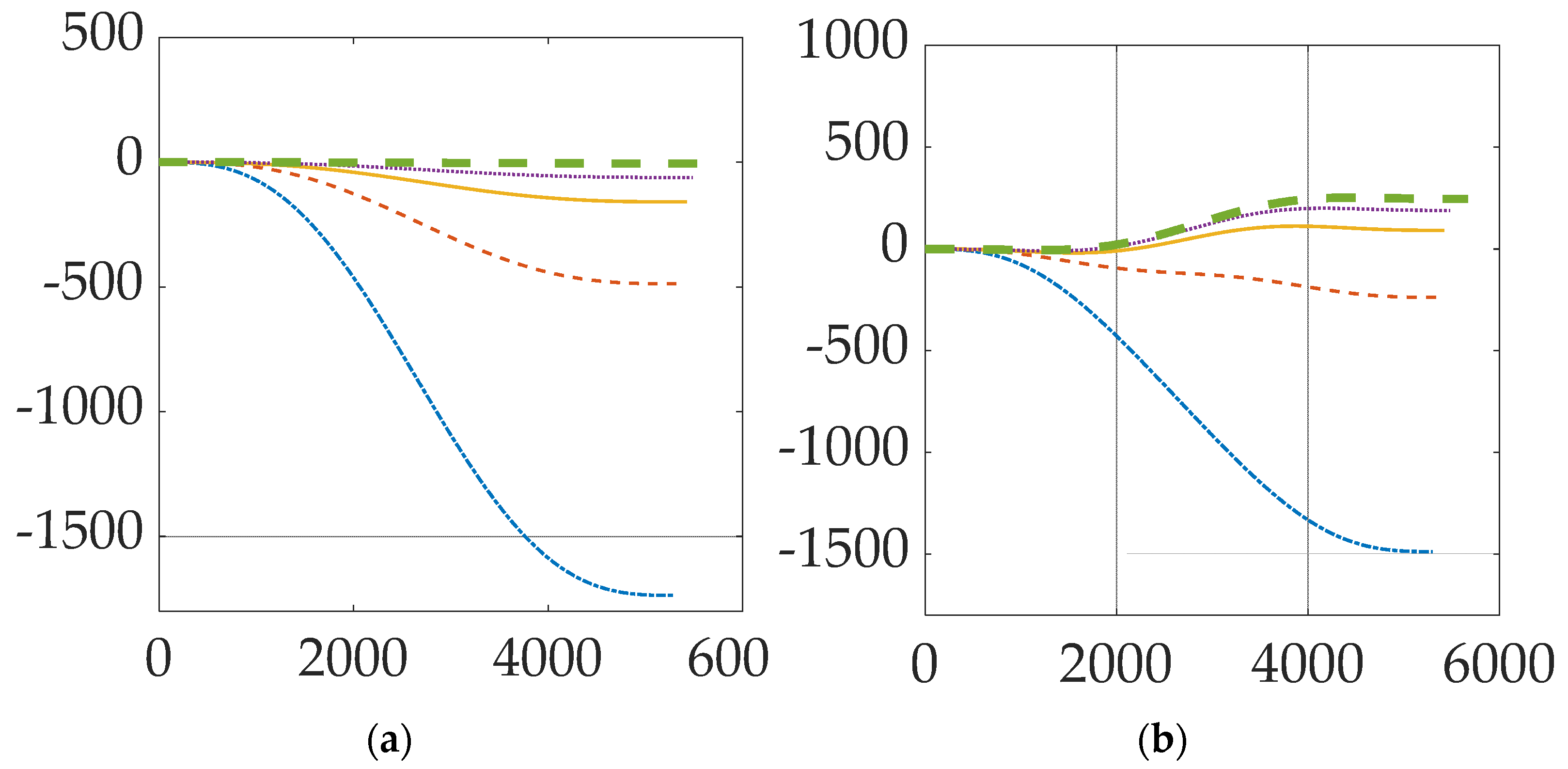

| Variable | Definition | Variable | Definition | Variable | Definition | Variable | Definition |
|---|---|---|---|---|---|---|---|
| mass moment of inertia | applied torque | Angular acceleration about x-direction | Angular velocity about x-direction | ||||
| angular acceleration | regression matrix | Angular acceleration about y-direction | Angular velocity about y-direction | ||||
| angular velocity | regression vector | Angular acceleration about z-direction | Angular velocity about z-direction |
| Variable | Definition | Variable | Definition |
|---|---|---|---|
| mass moment of inertia with respect to the x-axis | mass product of inertia–sum of the products formed by multiplying each element of mass by the product of the x and y coordinates | ||
| mass moment of inertia with respect to the z-axis | mass product of inertia–sum of the products formed by multiplying each element of mass by the product of the y and z coordinates | ||
| mass moment of inertia with respect to the y-axis | mass product of inertia–sum of the products formed by multiplying each element of mass by the product of the x and z coordinates |
| Variable | Definition | Variable | Definition | Variable | Definition |
|---|---|---|---|---|---|
| applied torque about x-direction | applied force | displacement rate relative to rotating frame | |||
| applied torque about y-direction | mass | displacement relative to rotating frame | |||
| applied torque about z-direction | acceleration | apparent acceleration |
| Variable | Definition | Variable | Definition |
|---|---|---|---|
| Atmospheric density | Lorentz torque | ||
| µ | Standard gravitational parameter | Number of coils | |
| R | Earth radius | A | Area |
| MI | Magnetic moment | I | Current |
| Tether length | B | Magnetic Field Vector | |
| Tether length differential | Lorentz Force |
| Solver | Step Size | Mean | Standard Deviation |
|---|---|---|---|
| Euler (ode1) | 0.001 | ||
| Heun (ode2) | 0.001 | ||
| Dormand–Prince (ode5) | 0.001 | ||
| Runge–Kutta (ode4) | 0.020 | ||
| Runge–Kutta (ode4) | 0.010 | ||
| Runge–Kutta (ode4) | 0.002 | ||
| Runge–Kutta (ode4) | 0.001 |
| Initial Altitude (km) | Orbit Period (s) | Final Altitude without Tether (km) | Final Altitude with Tether (km) | Altitude Gain from Tether (m) |
|---|---|---|---|---|
| 200 | 5301.245 | 198.264 | 198.513 | 249.680 |
| 250 | 5361.245 | 249.513 | 249.763 | 249.796 |
| 300 | 5422.715 | 299.841 | 300.091 | 249.828 |
| 350 | 5483.790 | 349.939 | 350.189 | 249.838 |
| 500 | 5668.390 | 499.995 | 500.245 | 249.848 |
| Inclination (°) | Mean Force (N) | Standard Deviation |
|---|---|---|
| 0 | 0.01324 | 9.462776735569736 × 10−5 |
| 10 | 0.013374031380808 | 1.633511026861032 × 10−6 |
| 11.5 | 0.013376428353265 | 1.077122200582248 × 10−7 |
| 20 | 0.013374031380808 | 5.225155534655572 × 10−5 |
| 30 | 0.013034404952252 | 2.449844931947672 × 10−4 |
| 60 | 0.011209316951912 | 0.001576691931541 |
| 90 | 0.008873540981345 | 0.003581649585287 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, P.; Sands, T. Micro Satellite Orbital Boost by Electrodynamic Tethers. Micromachines 2021, 12, 916. https://doi.org/10.3390/mi12080916
Yao P, Sands T. Micro Satellite Orbital Boost by Electrodynamic Tethers. Micromachines. 2021; 12(8):916. https://doi.org/10.3390/mi12080916
Chicago/Turabian StyleYao, Peter, and Timothy Sands. 2021. "Micro Satellite Orbital Boost by Electrodynamic Tethers" Micromachines 12, no. 8: 916. https://doi.org/10.3390/mi12080916
APA StyleYao, P., & Sands, T. (2021). Micro Satellite Orbital Boost by Electrodynamic Tethers. Micromachines, 12(8), 916. https://doi.org/10.3390/mi12080916







