A Curve-Shaped Beam Bistable Piezoelectric Energy Harvester with Variable Potential Well: Modeling and Numerical Simulation
Abstract
:1. Introduction
2. Finite-Element Simulation
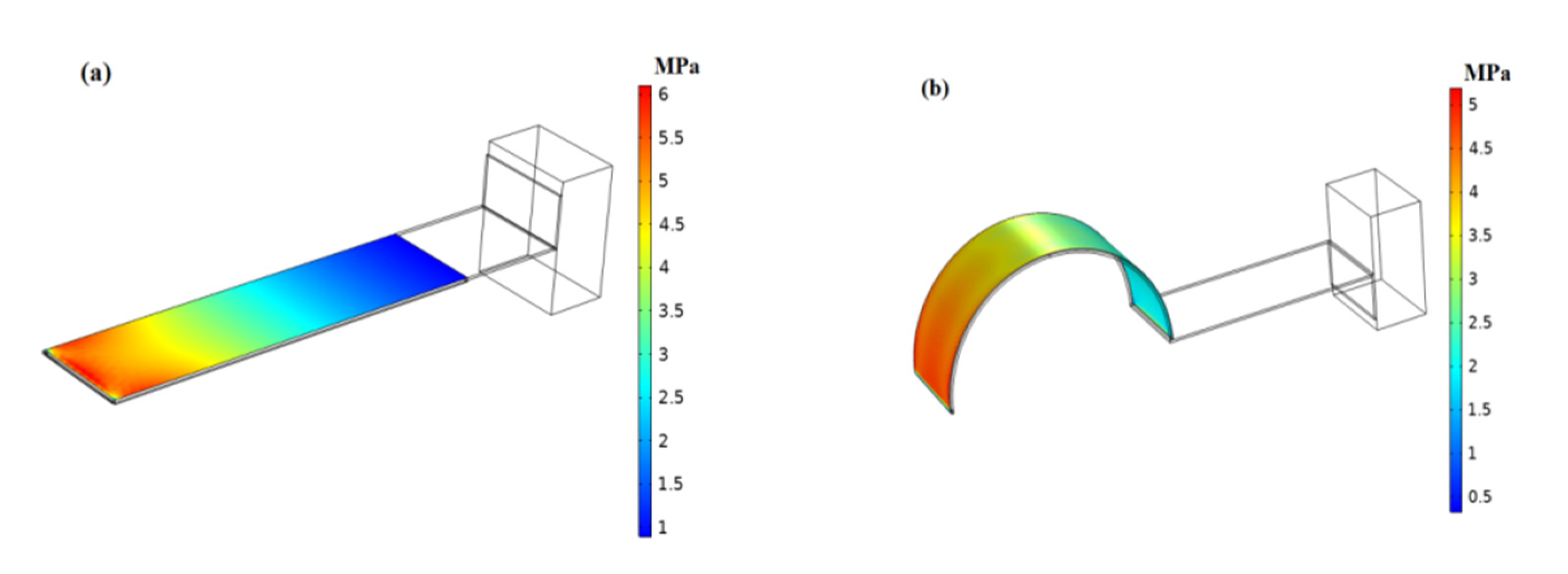
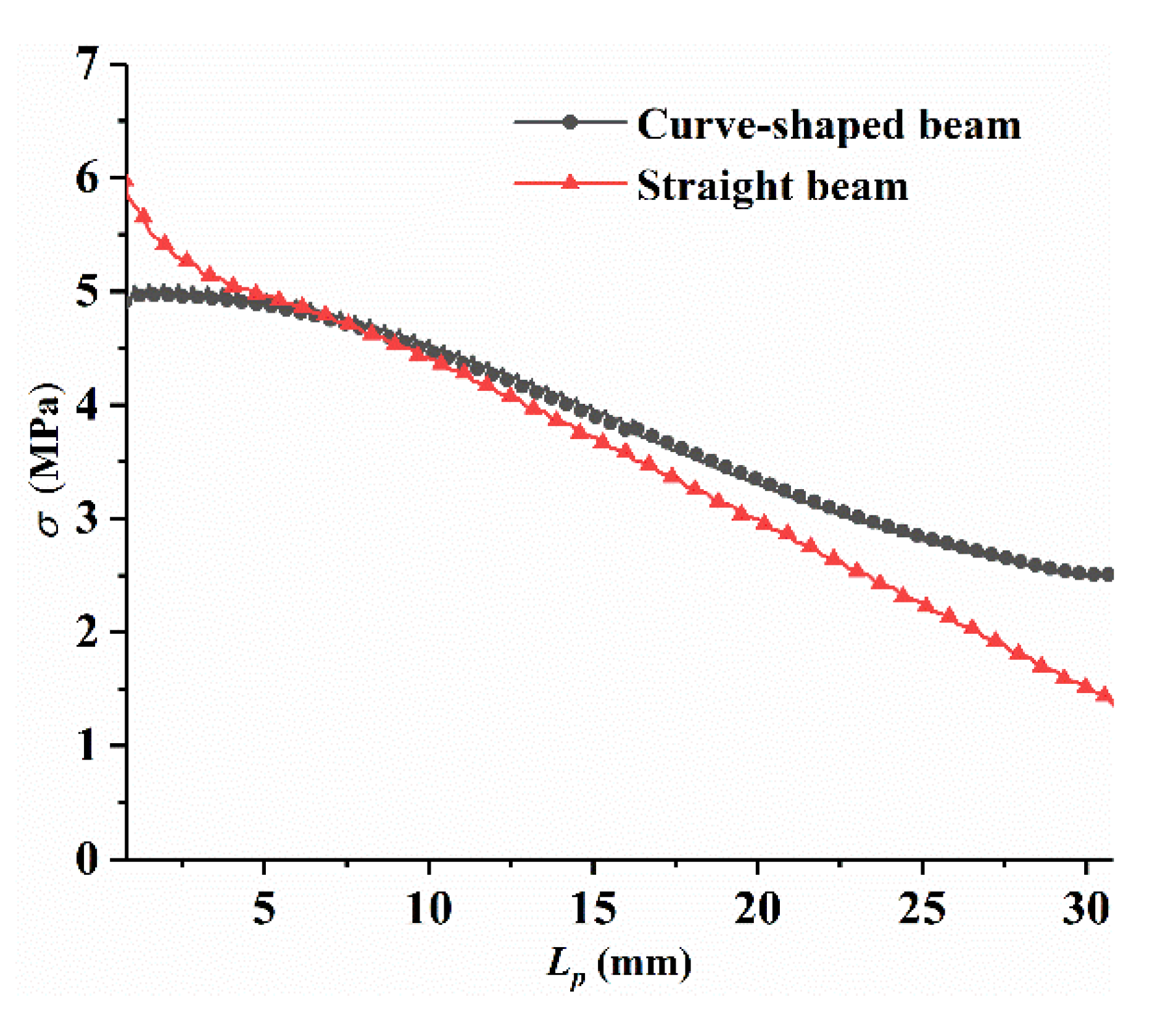
2.1. Stress Analysis
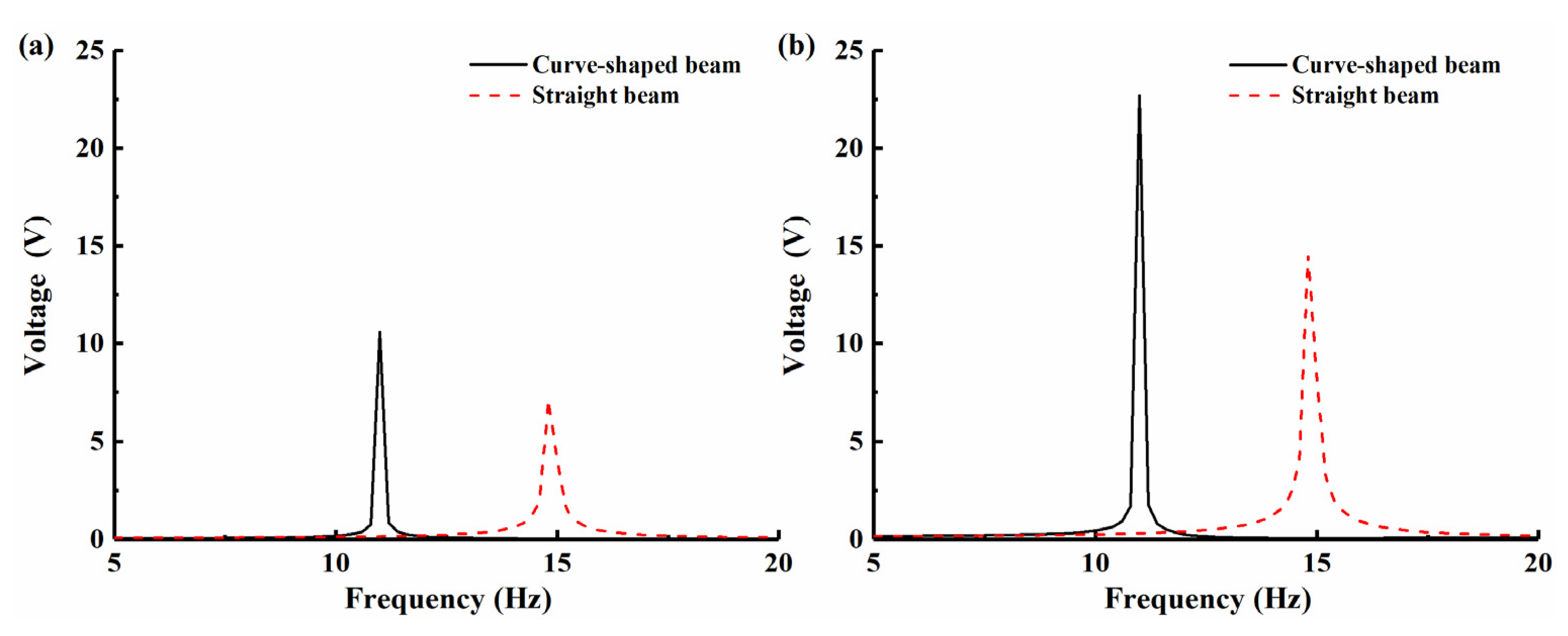
2.2. Generation Performance Comparisons
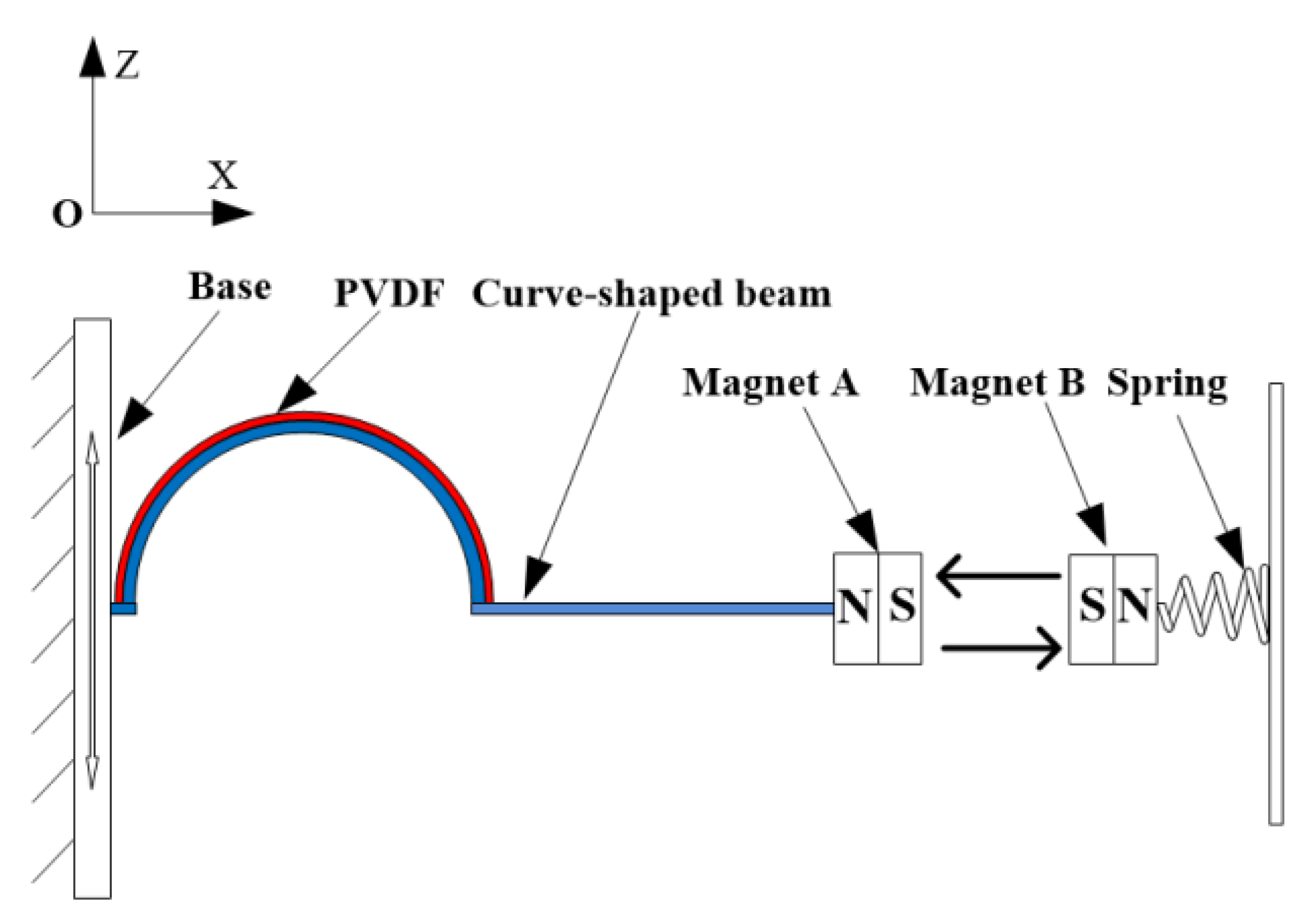
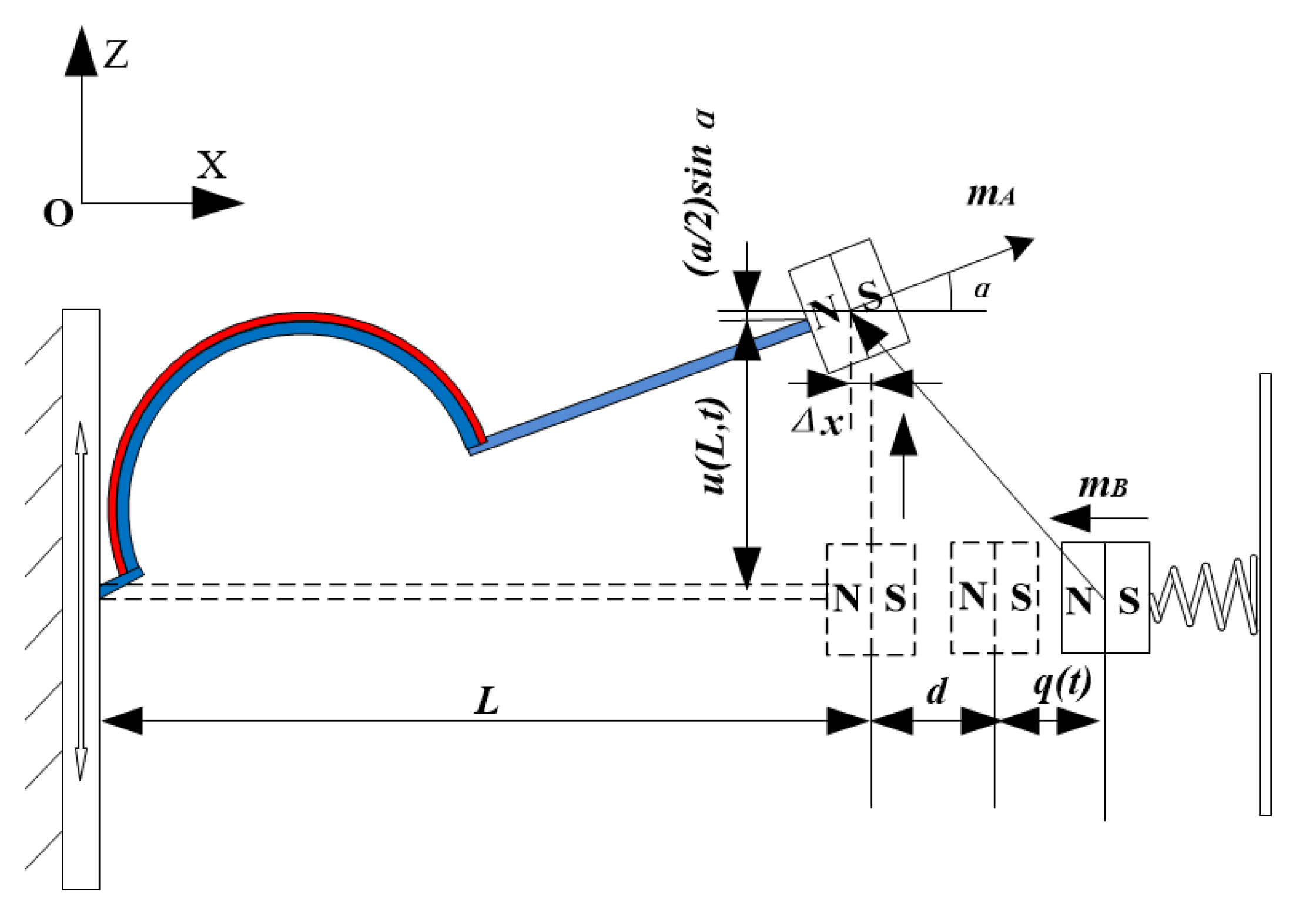
3. BPEH-V Configuration
3.1. Theoretical Modeling
3.1.1. Modeling of Nonlinear Restoring Force
3.1.2. Modeling of Magnetic Force
3.1.3. Dynamical Model
4. Numerical Simulation
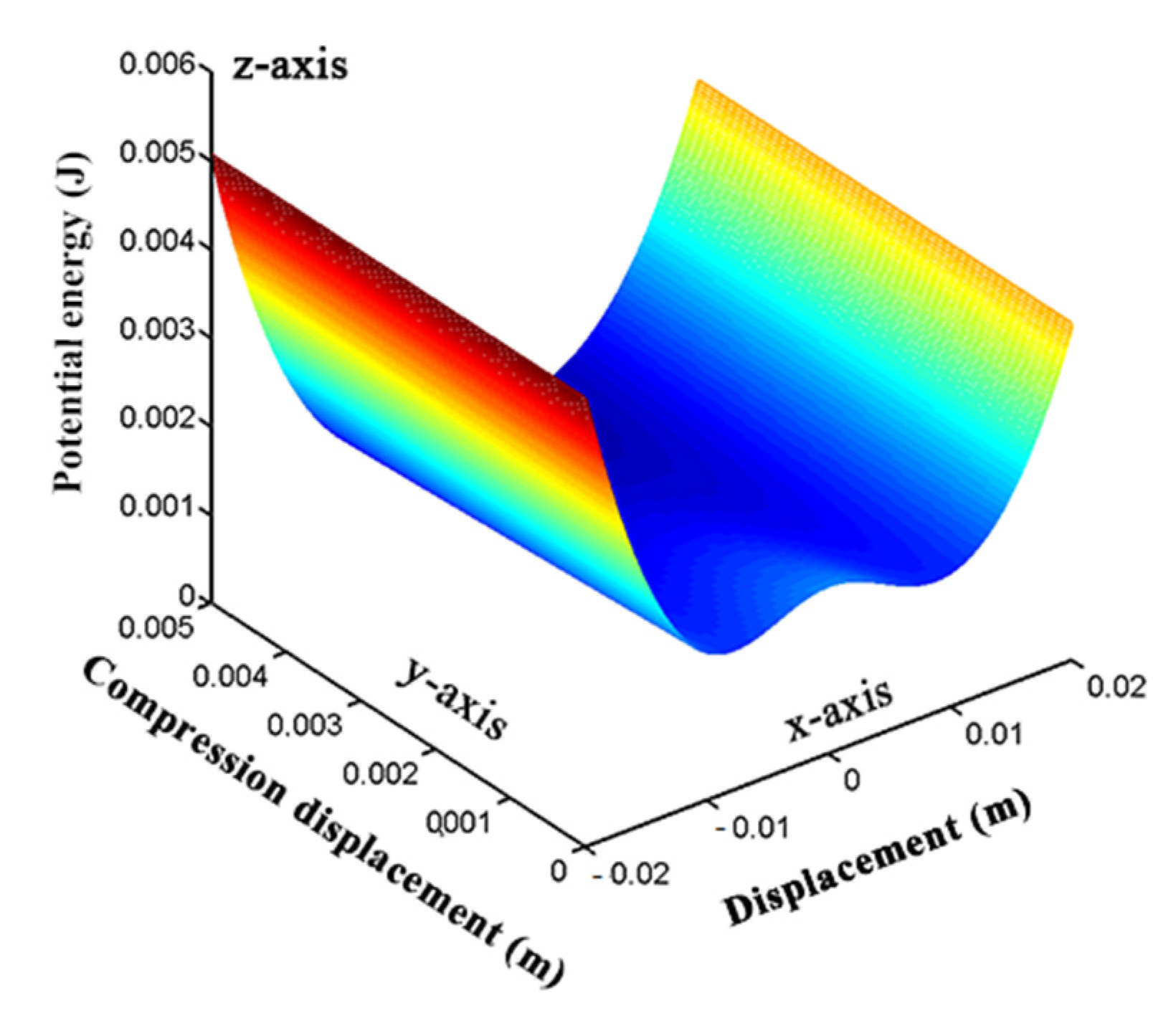
4.1. Study on the Potential Energy of BPEH-V
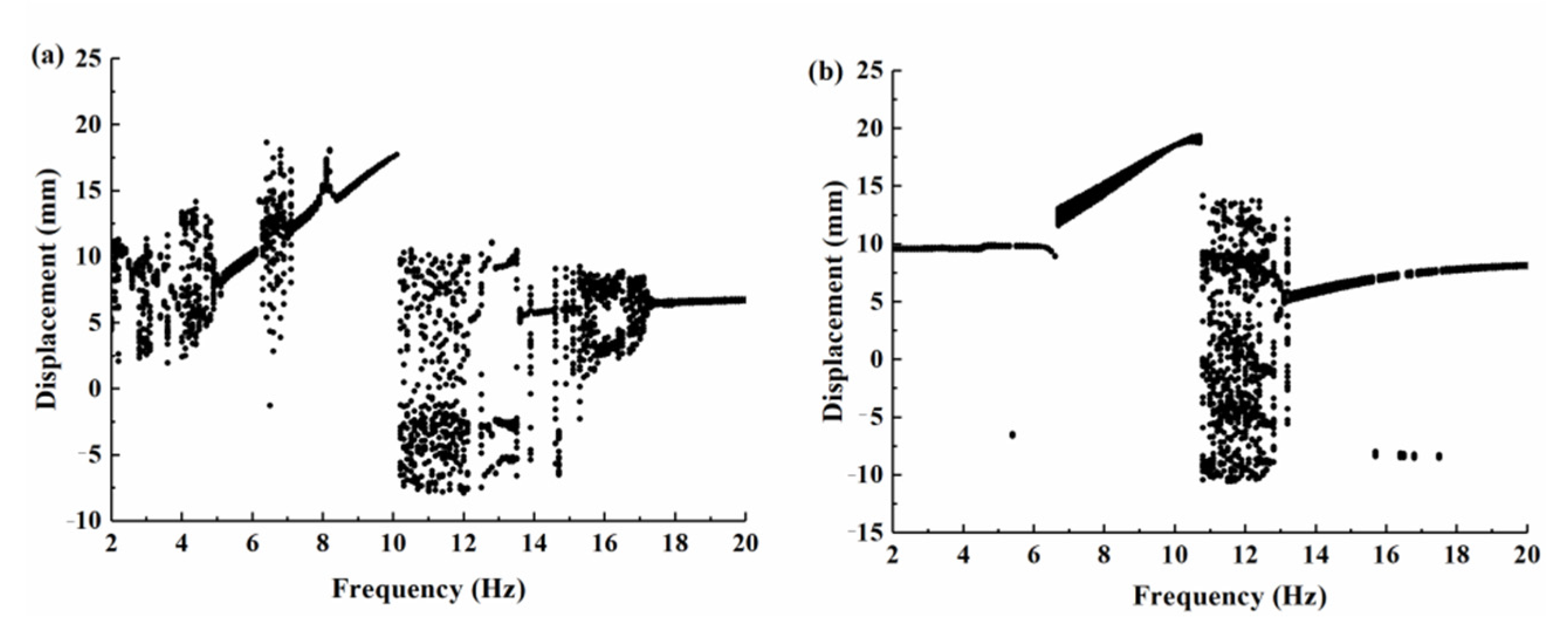
4.2. The Dynamics Analysis of BPEH-V
4.3. The Influence of the Spring Stiffness K on Harvesting Performance
5. Conclusions
- The curve-shaped configuration beams had a larger and more uniform strain distribution than the straight beam due to the special arched structure. Under the same excitation conditions, compared with the traditional straight beam, the curve-shaped configuration beam had a higher output voltage. Therefore, the curve-shaped beam was introduced into the nonlinear piezoelectric energy harvester, which can help to improve the harvesting efficiency of the energy harvesting device.
- A spring was connected with an external magnet to form an elastically supported bistable system. The potential energy of the system was affected by the magnetic distance and spring stiffness. The elastic connection of the external magnet could adjust the height of the system’s barrier to realize an adaptive potential barrier. Compared with the rigidly connected bistable system, the elastically connected system can makes large-amplitude oscillations easier, which is beneficial to improve the performance of the energy harvester, especially suitable for energy harvesting in a low frequency environment.
- The spring stiffness has an important effect on the performance of the proposed system. A spring with a small spring stiffness is beneficial for the system to achieve a large-amplitude oscillation over a wider frequency band. However, in practical applications, the spring stiffness affects the position of the equilibrium points of the system, the minimum spring stiffness must be able to maintain the bistable characteristics of the system, which is a problem that must be considered in the design. Otherwise, the elastically connected bistable system will lose its bistable characteristics and degenerate into a nonlinear monostable system, thus resulting in poor energy harvesting performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Geng, L.; Zhou, S.; Zhang, Z.; Lai, Z.; Yurchenko, D. Design, modeling and experiments of broadband tristable galloping piezoelectric energy harvester. Acta Mech. Sin. 2020, 36, 592–605. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A Critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar] [CrossRef] [Green Version]
- Karadag, C.V.; Ertarla, S.; Topaloglu, N.; Okyar, F. Optimization of beam profiles for improved piezoelectric energy harvesting efficiency. Struct. Multidiscip. Optim. 2021, 63, 631–643. [Google Scholar] [CrossRef]
- Tao, K.Z.; Chen, Z.S.; Yi, H.P.; Zhang, R.R.; Shen, Q.; Wu, J.; Tang, L.H.; Fan, K.Q.; Fu, J.Q.; Miao, J.M.; et al. Hierarchical honeycomb-structured electret/triboelectric nanogenerator for biomechanical and morphing wing energy harvesting. Nano-Micro Lett. 2021, 13, 1–16. [Google Scholar] [CrossRef]
- Zou, H.-X.; Zhao, L.-C.; Gao, Q.-H.; Zuo, L.; Liu, M.; Tan, T.; Wei, K.-X.; Zhang, W.-M. Mechanical modulations for enhancing energy harvesting: Principles, methods and applications. Appl. Energy 2019, 255, 113871. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yang, W.; Zuo, M.; Tan, H.; Fan, H.; Mao, Q.; Wan, X. An Arc-shaped piezoelectric bistable vibration energy harvester: Modeling and experiments. Sensors 2018, 18, 4472. [Google Scholar] [CrossRef] [Green Version]
- Rubes, O.; Brablc, M.; Hadas, Z. Nonlinear vibration energy harvester: Design and oscillating stability analyses. Mech. Syst. Signal Process. 2019, 125, 170–184. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Assumed-modes formulation of piezoelectric energy harvesters: Euler-Bernoulli, Rayleigh and Timoshenko models with axial deformations. In Proceedings of the ASME 2010 10th Biennial Conference on Engineering Systems Design and Analysis, Istanbul, Turkey, 12–14 July 2010; pp. 405–414. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Li, K.; Yang, Z.; Zhou, S. Performance enhancement for a magnetic-coupled bi-stable flutter-based energy harvester. Smart Mater. Struct. 2020, 29, 085045. [Google Scholar] [CrossRef]
- Singh, K.A.; Kumar, R.; Weber, R.J. A broadband bistable piezoelectric energy harvester with nonlinear high-power extraction power electronics. IEEE Trans. 2015, 30, 6763–6774. [Google Scholar]
- Zhou, Z.; Qin, W.; Du, W.; Zhu, P.; Liu, Q. Improving energy harvesting from random excitation by nonlinear flexible bi-stable energy harvester with a variable potential energy function. Mech. Syst. Signal Process. 2019, 115, 162–172. [Google Scholar] [CrossRef]
- Cao, J.; Wang, W.; Zhou, S.; Inman, D.J.; Lin, J. Nonlinear time-varying potential bistable energy harvesting from human motion. Appl. Phys. Lett. 2015, 107, 143904. [Google Scholar] [CrossRef]
- Nguyen, M.S.; Yoon, Y.-J.; Kwon, O.; Kim, P. Lowering the potential barrier of a bistable energy harvester with mechanically rectified motion of an auxiliary magnet oscillator. Appl. Phys. Lett. 2017, 111, 253905. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. Internal resonance and low frequency vibration energy harvesting. Smart Mater. Struct. 2017, 26, 095008. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. Low frequency energy harvesting with a variable potential function under random vibration. Smart Mater. Struct. 2018, 27, 114004. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. A parametric resonator with low threshold excitation for vibration energy harvesting. J. Sound Vib. 2019, 446, 129–143. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Shan, G.; Wang, D.F.; Song, J.; Fu, Y.; Yang, X. A spring-assisted adaptive bistable energy harvester for high output in low-excitation. Microsyst. Technol. 2018, 24, 3579–3588. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, H.; Wu, Z.; Huang, Z.; Mao, H.; Cao, Y. Broadband spring-connected bi-stable piezoelectric vibration energy harvester with variable potential barrier. Results Phys. 2020, 18, 103173. [Google Scholar] [CrossRef]
- Kim, J.; Dorin, P.; Wang, K.W. Vibration energy harvesting enhancement exploiting magnetically coupled bistable and linear harvesters. Smart Mater. Struct. 2020, 29, 065006. [Google Scholar] [CrossRef]
- Qian, F.; Zhou, S.; Zuo, L. Approximate solutions and their stability of a broadband piezoelectric energy harvester with a tunable potential function. Commun. Nonlinear Sci. Numer. Simul. 2020, 80, 104984. [Google Scholar] [CrossRef]
- Ooi, B.L.; Gilbert, J.M.; Aziz, A.R.A. Analytical and finite-element study of optimal strain distribution in various beam shapes for energy harvesting applications. Acta Mech. Sin. 2016, 32, 670–683. [Google Scholar] [CrossRef]
- Xie, X.; Wang, Z.; Liu, D.; Du, G.; Zhang, J. An experimental study on a novel cylinder harvester made of L-shaped piezoelectric coupled beams with a high efficiency. Energy 2020, 212, 118752. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Liu, Y.; Yang, Z. Thickness-variable composite beams for vibration energy harvesting. Compos. Struct. 2020, 244, 112232. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.Q.; Zuo, L.; Zu, J. Introducing arc-shaped piezoelectric elements into energy harvesters. Energy Convers. Manag. 2017, 148, 260–266. [Google Scholar] [CrossRef]
- Yung, K.W.; Landecker, P.B.; Villani, D.D. An analytic solution for the force between two magnetic dipoles. Magn. Electr. Sep. 1998, 9, 39–52. [Google Scholar] [CrossRef]
- Hartog, D.J. Mechanical Vibrations; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Erturk, A.; Inman, D.J. Piezolectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]





| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Substrate layer (beryllium bronze) | |||
| Density | ρs | 8300 | kg/m3 |
| Elastic modulus | Es | 128 | GPa |
| Arc-shaped radius | Rs | 10 × 10−3 | m |
| Horizontal length | Ls | 40 × 10−3 | m |
| Height | hs | 2 × 10−4 | m |
| Width | bs | 8 × 10−3 | m |
| Piezoelectric layer (PVDF) | |||
| Density | ρp | 1780 | kg/m3 |
| Elastic modulus | Ep | 3 | GPa |
| Length | Lp | 31.4 × 10−3 | m |
| Height | hp | 1.1 × 10−4 | m |
| Width | bp | 8 × 10−3 | m |
| Piezoelectric stress constant | 11.5 | C/m2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, X.; Chen, L.; Guo, Y.; Zhu, F. A Curve-Shaped Beam Bistable Piezoelectric Energy Harvester with Variable Potential Well: Modeling and Numerical Simulation. Micromachines 2021, 12, 995. https://doi.org/10.3390/mi12080995
Chen X, Zhang X, Chen L, Guo Y, Zhu F. A Curve-Shaped Beam Bistable Piezoelectric Energy Harvester with Variable Potential Well: Modeling and Numerical Simulation. Micromachines. 2021; 12(8):995. https://doi.org/10.3390/mi12080995
Chicago/Turabian StyleChen, Xiaoyu, Xuhui Zhang, Luyang Chen, Yan Guo, and Fulin Zhu. 2021. "A Curve-Shaped Beam Bistable Piezoelectric Energy Harvester with Variable Potential Well: Modeling and Numerical Simulation" Micromachines 12, no. 8: 995. https://doi.org/10.3390/mi12080995
APA StyleChen, X., Zhang, X., Chen, L., Guo, Y., & Zhu, F. (2021). A Curve-Shaped Beam Bistable Piezoelectric Energy Harvester with Variable Potential Well: Modeling and Numerical Simulation. Micromachines, 12(8), 995. https://doi.org/10.3390/mi12080995







