A Multi-Fidelity Model for Simulations and Sensitivity Analysis of Piezoelectric Inkjet Printheads
Abstract
:1. Introduction
2. Three-Dimensional Model of Inkjet Head Channel
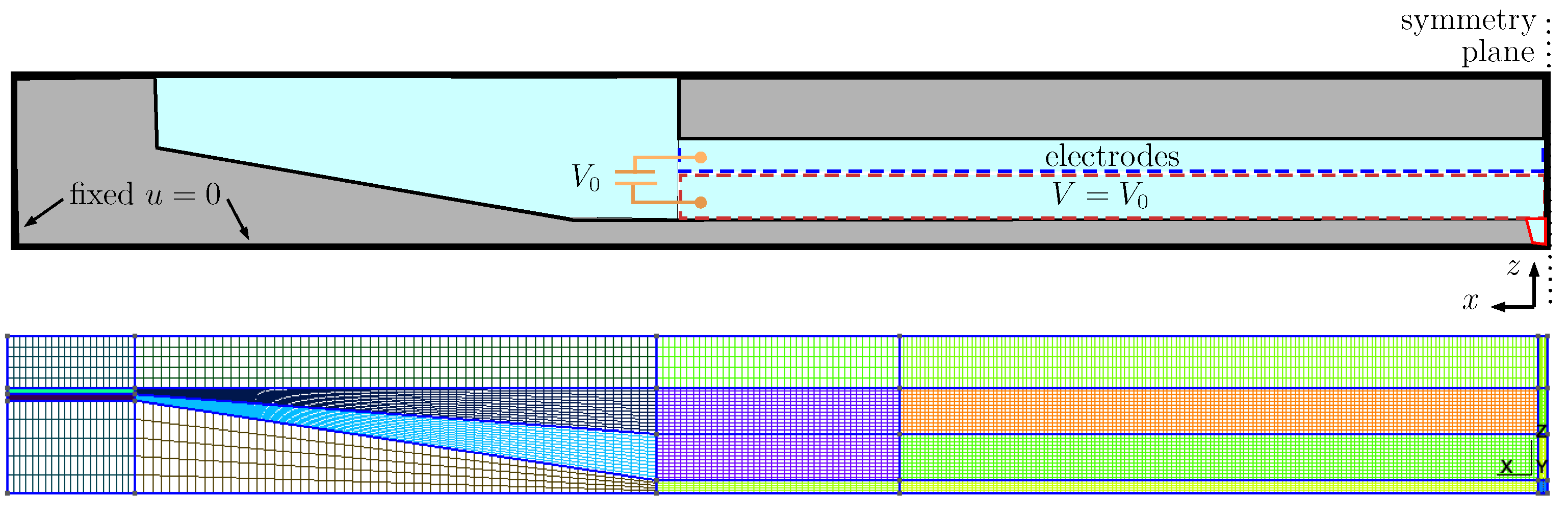
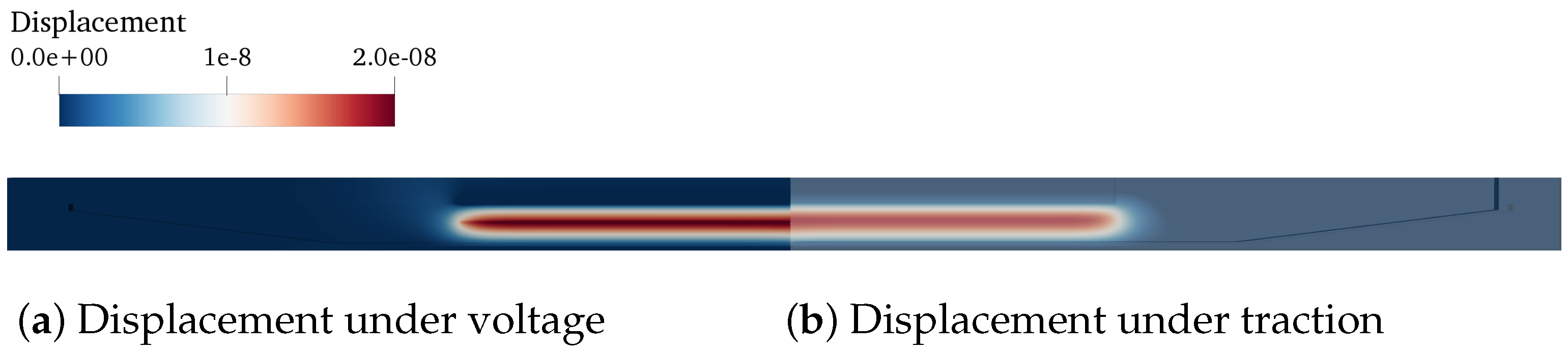
2.1. Electromechanical Coupled Model of Channel Walls
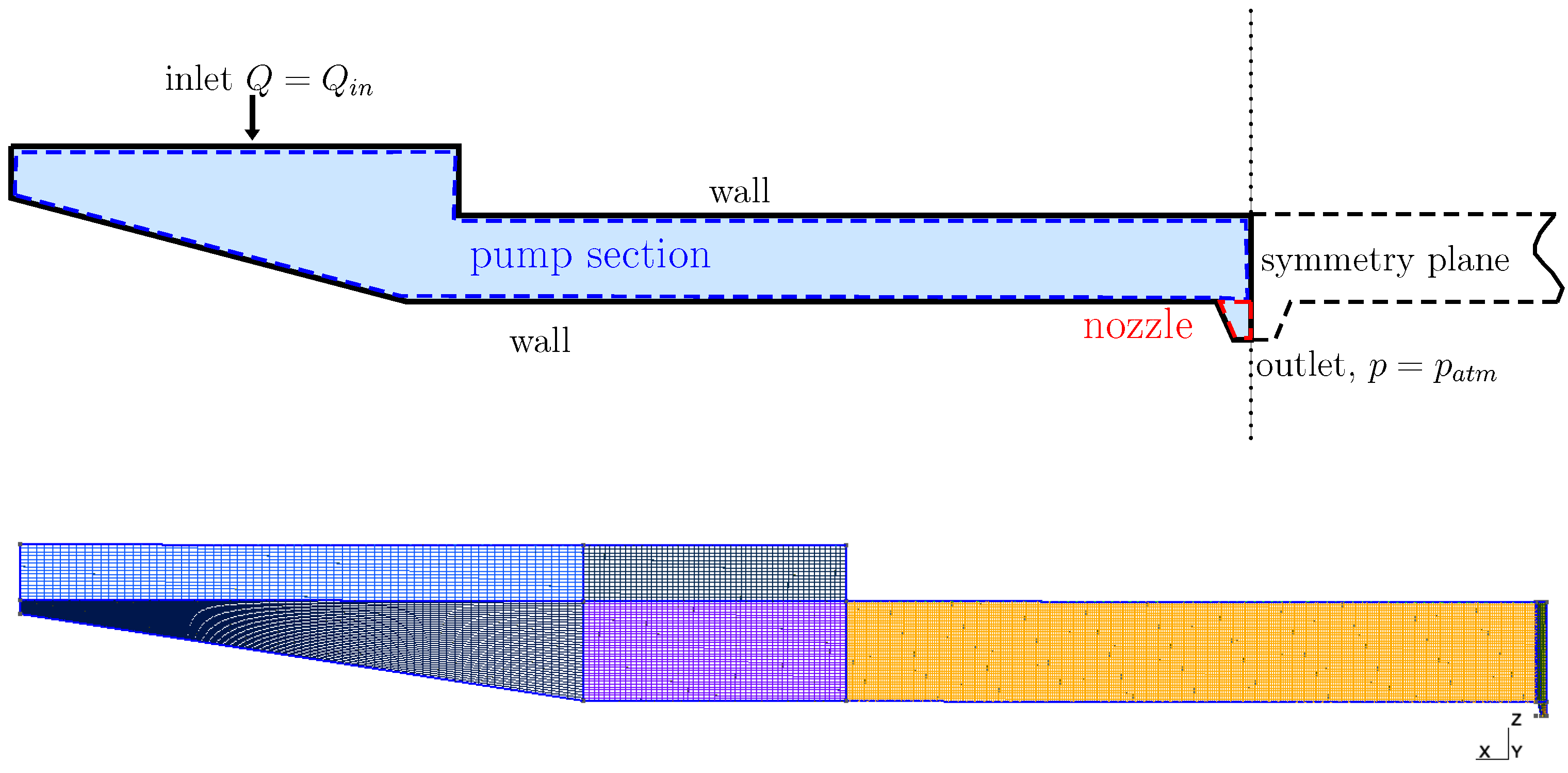
2.2. Ink Flow Model
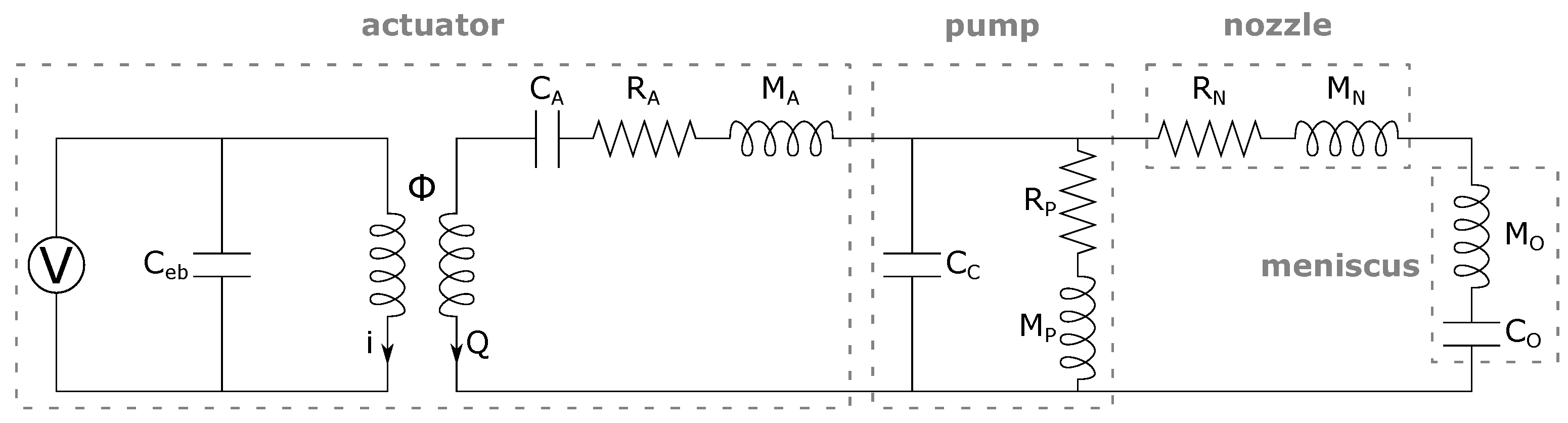
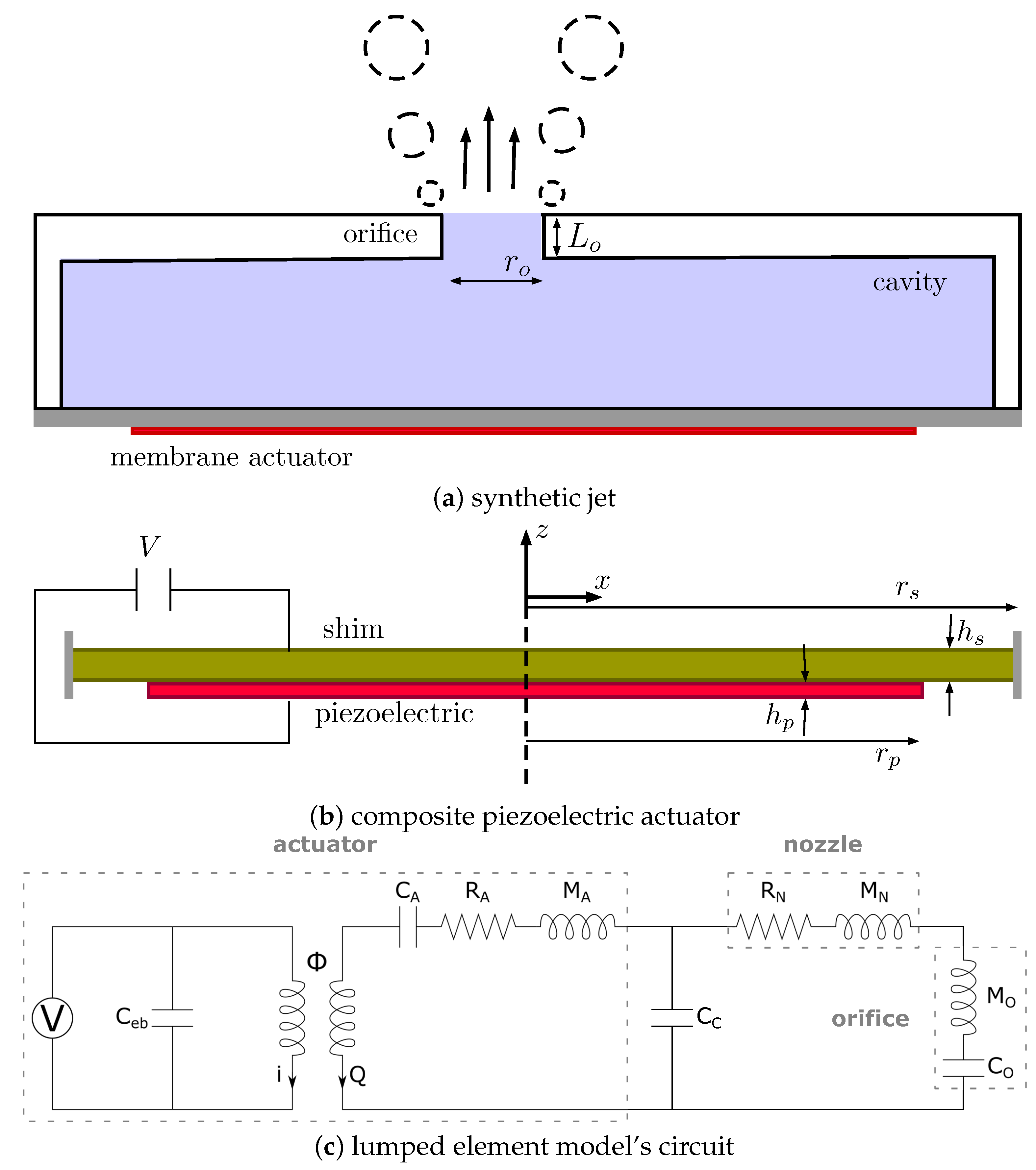
3. Equivalent Circuit Model of Inkjet Head Channel
3.1. Equivalent Circuit Model
3.2. 3D Simulation-Based LEM Parameters
4. Numerical Validation of the Models
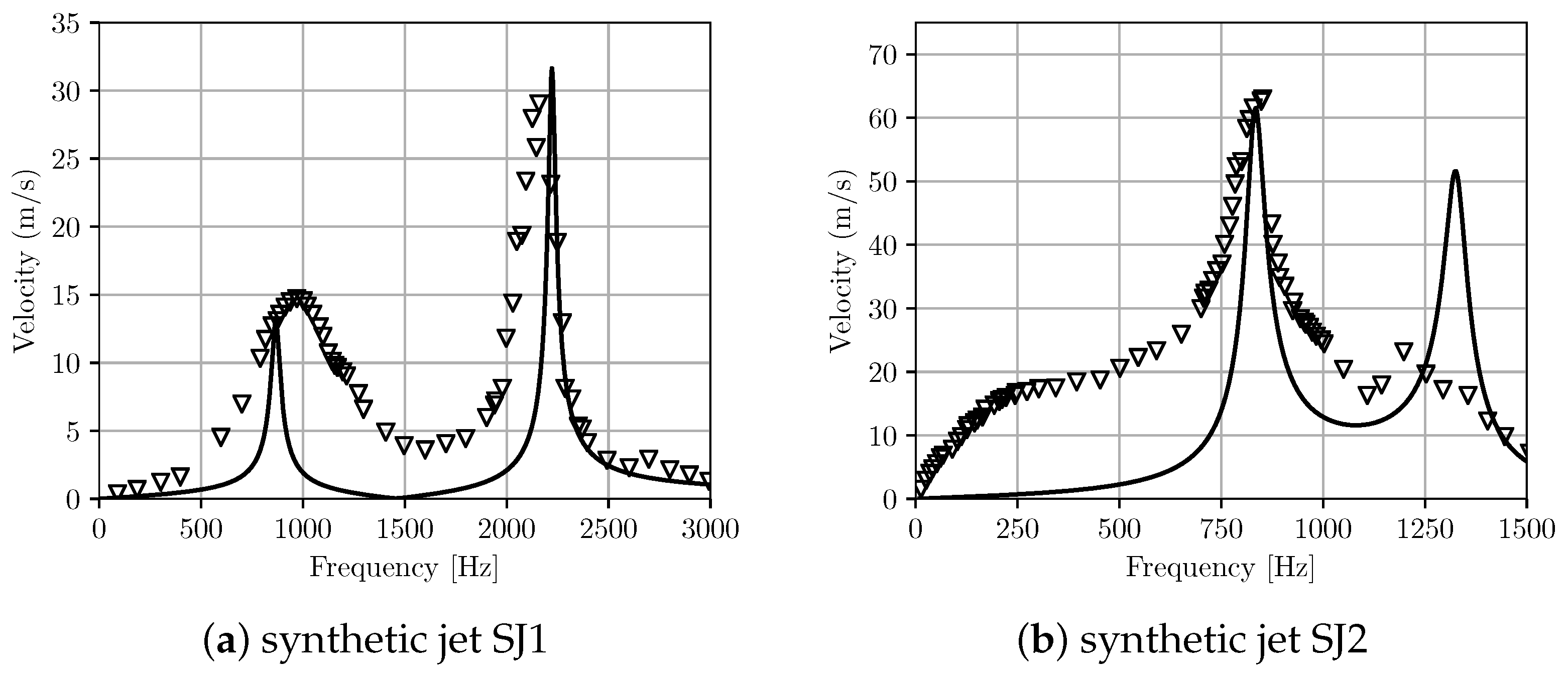
4.1. LEM Modelling of Piezoelectric-Driven Synthetic Jets
4.2. Prediction of LEM for Print Heads
5. Analysis of Inkjet Head Performance Using LEM
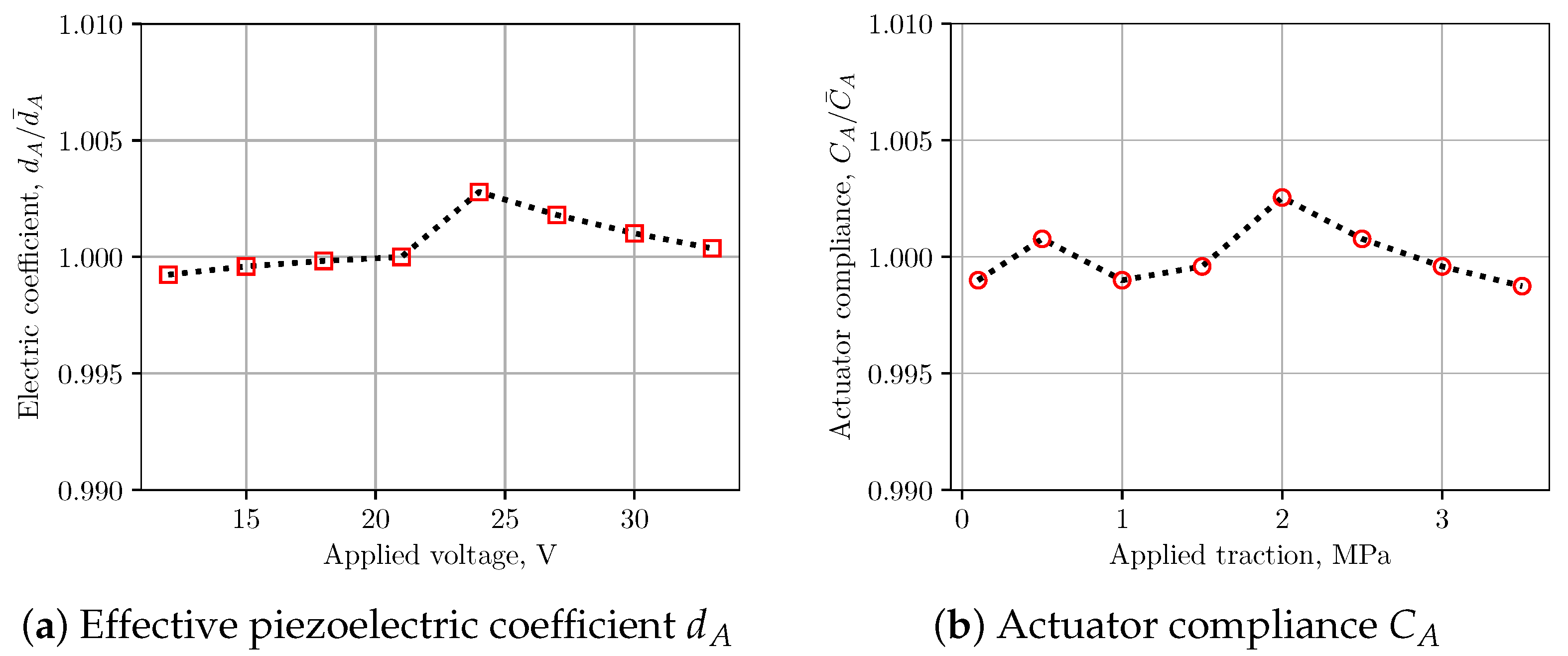
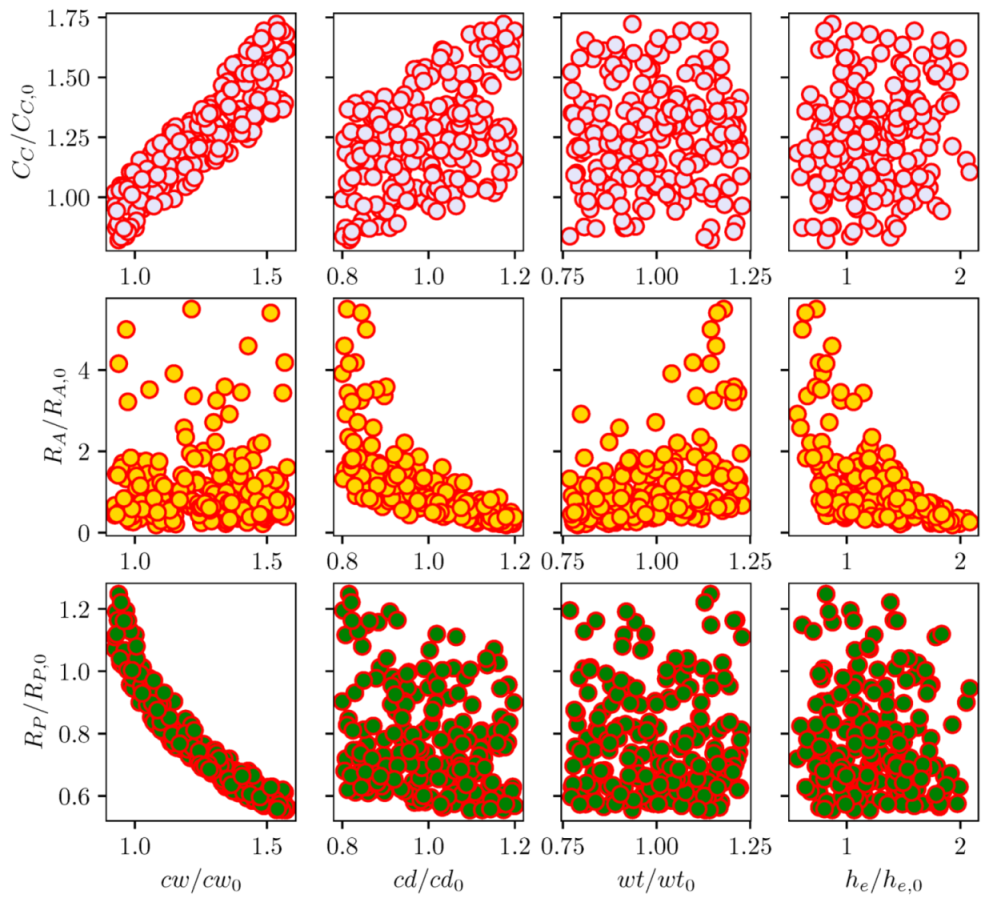
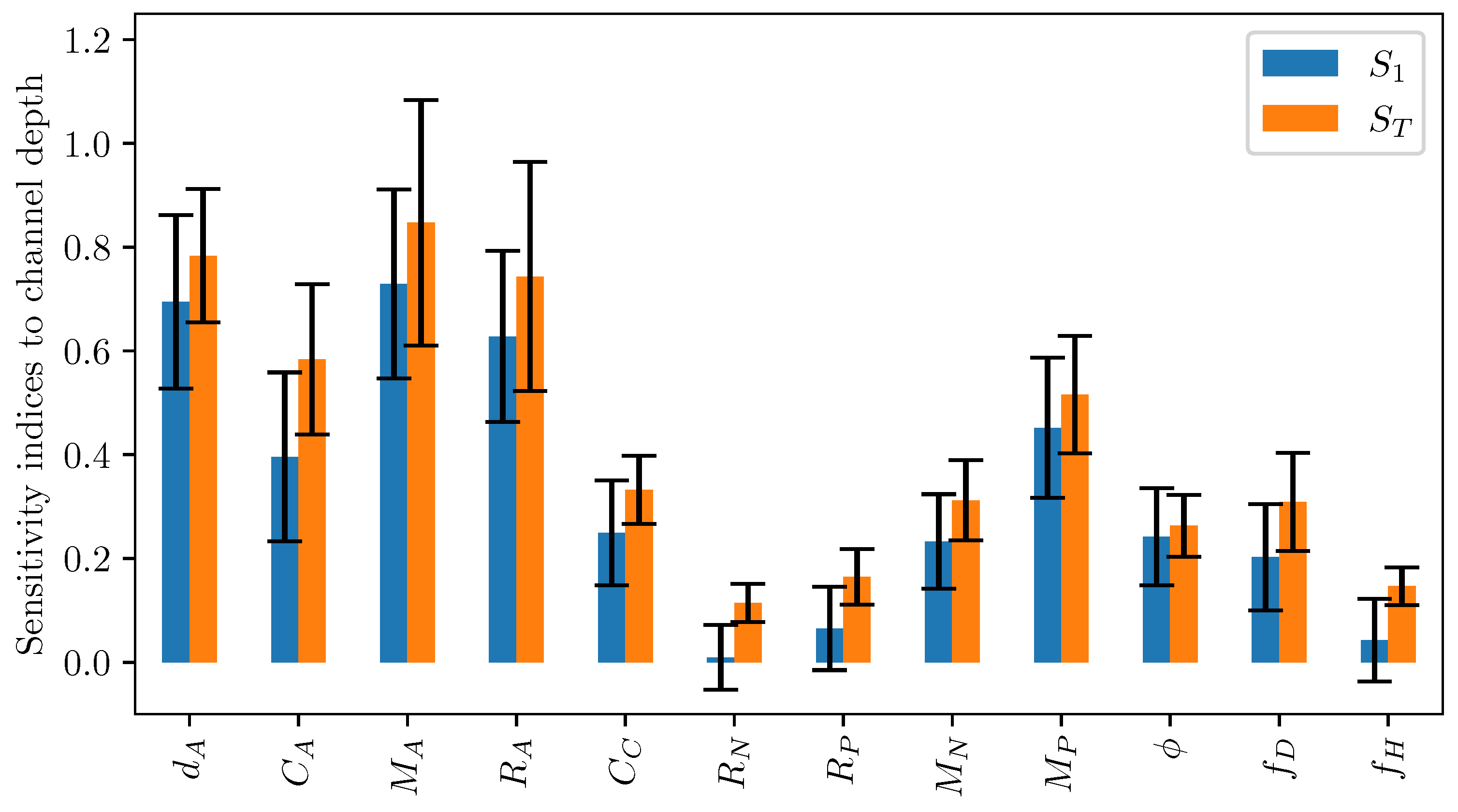
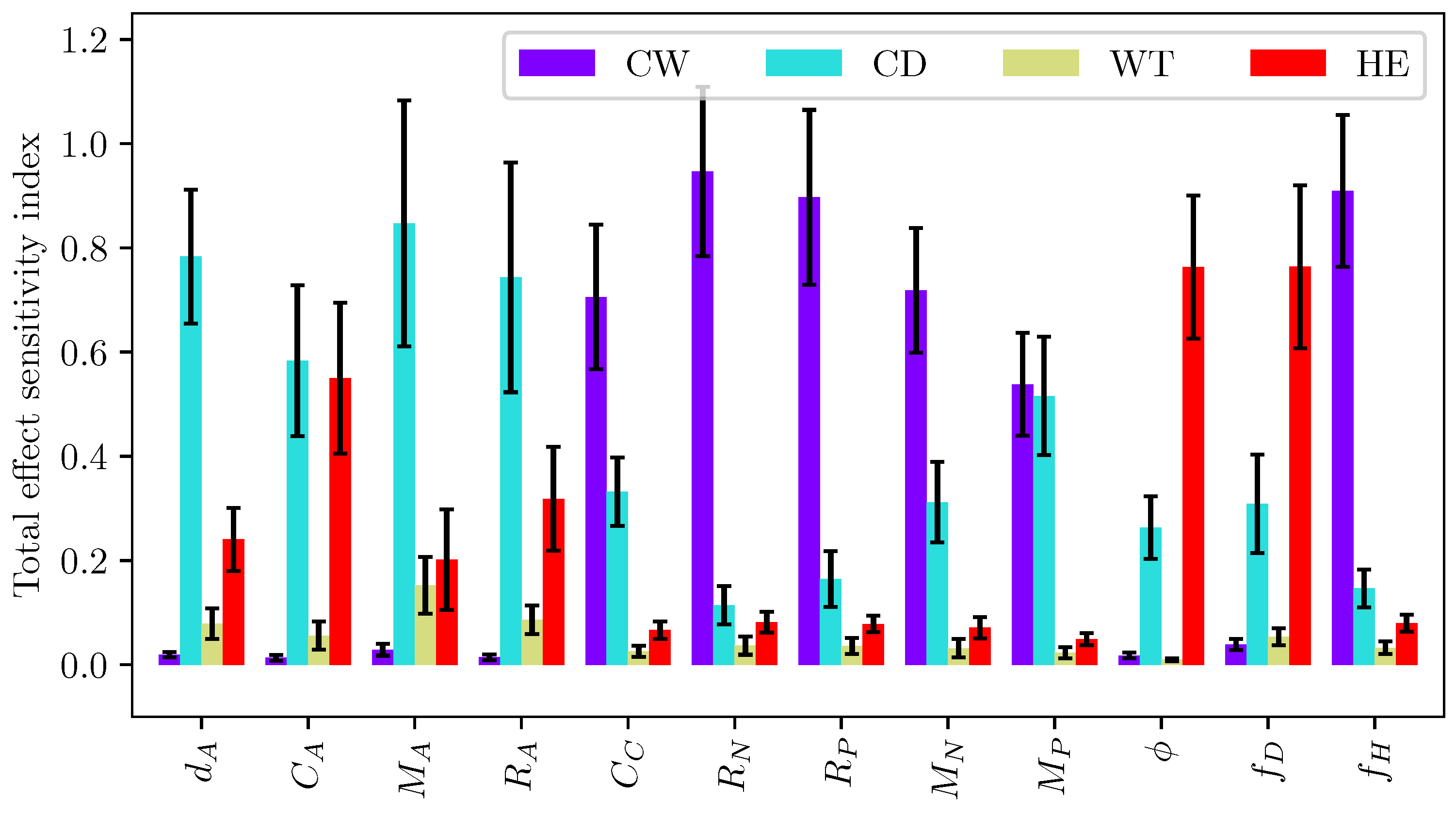
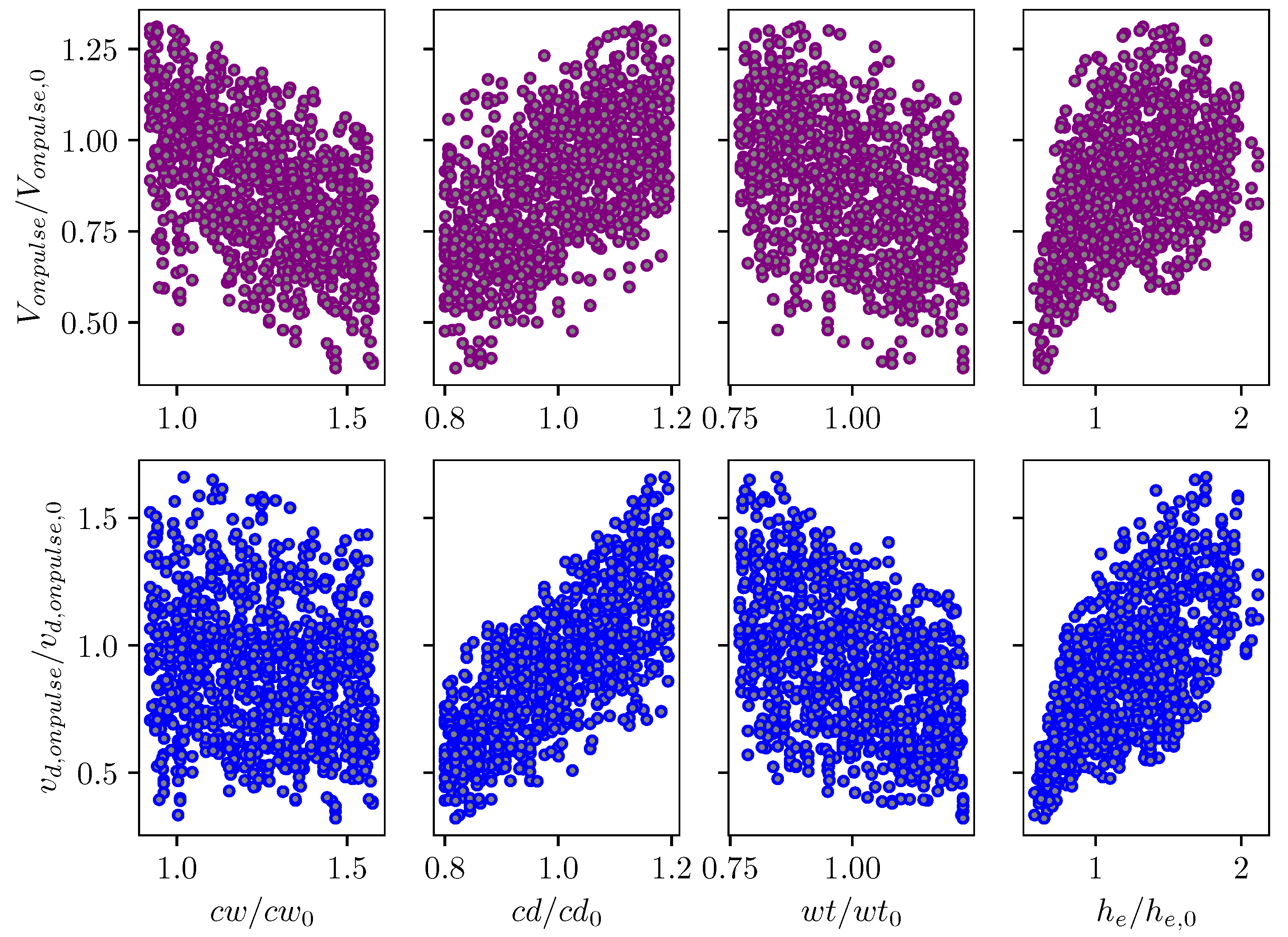
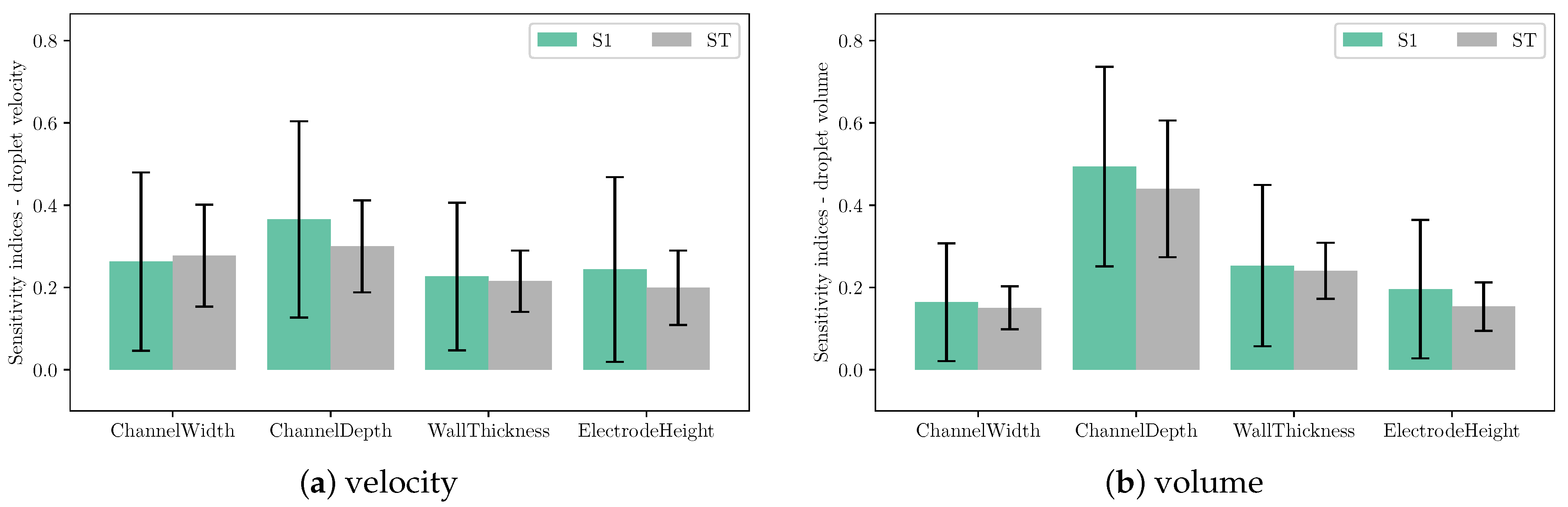
5.1. Sensitivity Analysis of LEM Parameters
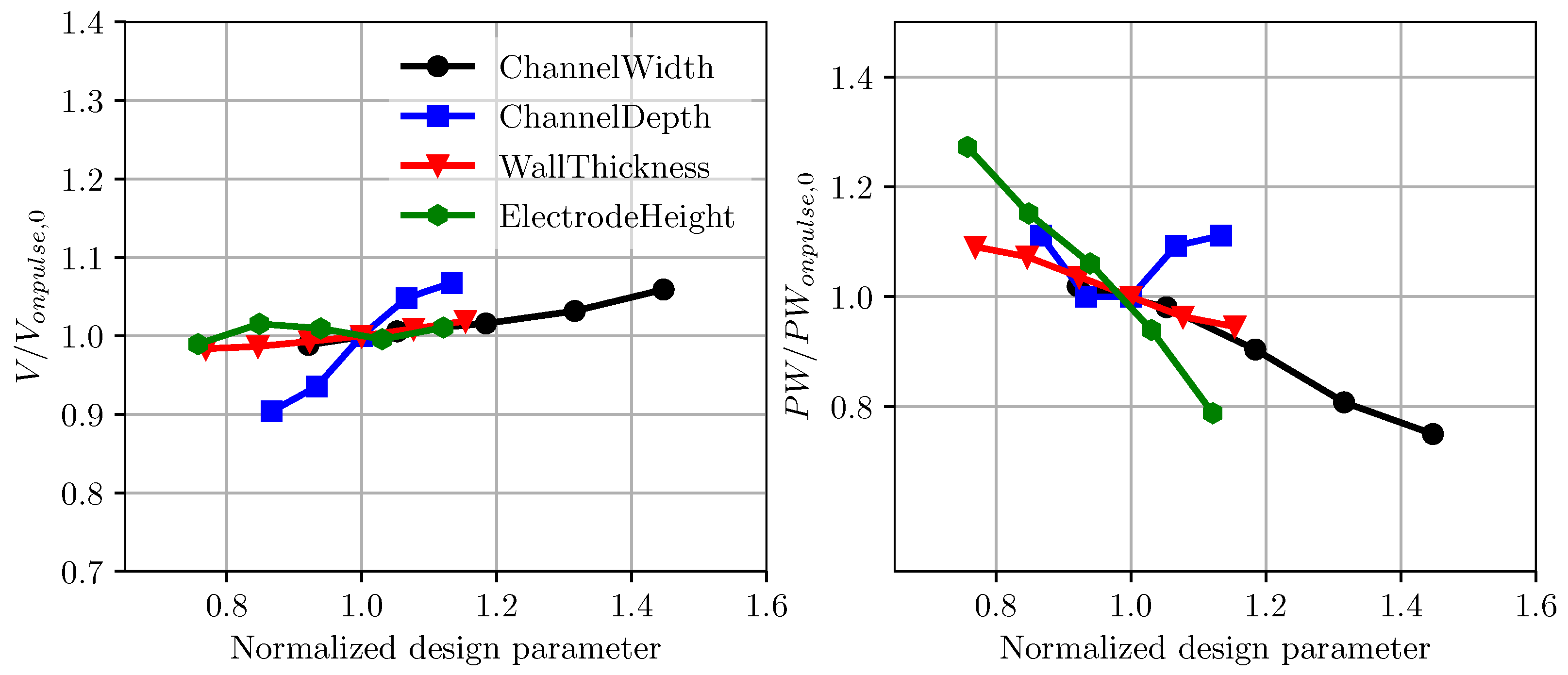
5.2. Analysis of Inkjet Head Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koto, H. Low Voltage Ink-Jet Printhead. U.S. Patent 4,502,058, 26 February 1985. [Google Scholar]
- Kim, B.H.; Kim, S.I.; Lee, J.C.; Shin, S.J.; Kim, S.J. Dynamic characteristics of a piezoelectric driven inkjet printhead fabricated using MEMS technology. Sens. Actuators A Phys. 2012, 173, 244–253. [Google Scholar] [CrossRef]
- Martin, G.D.; Hoath, S.D.; Hutchings, I.M. Inkjet printing - the physics of manipulating liquid jets and drops. J. Phys. Conf. Ser. 2008, 105, 012001. [Google Scholar] [CrossRef] [Green Version]
- Silverbrook, K. Printhead with multiple nozzles sharing single nozzle data. U.S. Patent 7,712,859 B2, 5 November 2010. [Google Scholar]
- Seitz, H.; Heinzl, J. Modelling of a microfluidic device with piezoelectric actuators. J. Micromech. Microeng. 2004, 14, 1140–1147. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Kumar, P.; Leong, J. Finite Element Modelling and Simulations of Piezoelectric Actuators Responses with Uncertainty Quantification. Computation 2018, 6, 60. [Google Scholar] [CrossRef] [Green Version]
- Wijshoff, H.M.A. Free surface flow and acousto-elastic interaction in piezo inkjet. In Proceedings of the 2004 NSTI Nanotechnology Conference and Trade Show, Boston, MA, USA, 7–11 March 2004; Volume 2, pp. 215–218. [Google Scholar]
- Pan, F.; Kubby, J.; Chen, J. Numerical simulation of fluid-structure interaction in a MEMS diaphragm drop ejector. J. Micromech. Microeng. 2001, 12, 70–76. [Google Scholar] [CrossRef]
- He, M.; Sun, L.; Hu, K.; Zhu, Y.; Ma, L.; Chen, H. Drop-on-Demand Inkjet Printhead Performance Enhancement by Dynamic Lumped Element Modeling for Printable Electronics Fabrication. Math. Probl. Eng. 2014, 2014, 270679. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.H.; Lee, H.S.; Kim, S.W.; Kang, P.; Park, Y.S. Hydrodynamic responses of a piezoelectric driven MEMS inkjet print-head. Sens. Actuators A Phys. 2014, 210, 131–140. [Google Scholar] [CrossRef]
- Yoshida, Y.; Izumi, K.; Tokito, S. A push-mode piezo inkjet equivalent circuit model enhanced by diaphragm displacement measurements. AIP Adv. 2019, 9, 025319. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, Y.; Huang, J. Equivalent Circuit Modeling for a Valveless Piezoelectric Pump. Sensors 2018, 18, 2881. [Google Scholar] [CrossRef] [Green Version]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2012, 12, 515–545. [Google Scholar] [CrossRef]
- Nakata, A.; Tanaka, S.; Sugano, K.; Tsuchiya, T.; Tabata, O. Electrical equivalent circuit model of microfluidic system containing piezoelectric valveless micropump and viscoelastic PDMS microchannnel. In Proceedings of the Twelfth International Conference on Miniaturized Systems for Chemistry and Life Sciences—MicroTAS 2008, San Diego, CA, USA, 12–16 October 2008; Royal Society of Chemistry: London, UK, 2008; pp. 730–732. [Google Scholar]
- Li, S.S.; Cheng, C.M. Analogy among microfluidics, micromechanics, and microelectronics. Lab Chip 2013, 13, 3782. [Google Scholar] [CrossRef]
- RC1536 Recirculation Series of Printheads. Available online: https://www.seiko-instruments.de/products/inkjet-print-heads/rc1536-recirculation-inkjet-printhead.html?cHash=9212ca5dbe07a63352da8a21370db323 (accessed on 25 August 2021).
- OpenFOAM Home Page. Available online: https://www.openfoam.org/ (accessed on 25 August 2021).
- Jasak, H.; Jemcov, A.; Tuković, Ž. OpenFOAM: A C++ Library for Complex Physics Simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007; pp. 1–20. [Google Scholar]
- Prasad, S.A.; Gallas, Q.; Horowitz, S.B.; Homeijer, B.D.; Sankar, B.V.; Cattafesta, L.N.; Sheplak, M. Analytical Electroacoustic Model of a Piezoelectric Composite Circular Plate. AIAA J. 2006, 44, 2311–2318. [Google Scholar] [CrossRef]
- Gallas, Q.; Holman, R.; Nishida, T.; Carroll, B.; Sheplak, M.; Cattafesta, L. Lumped Element Modeling of Piezoelectric-Driven Synthetic Jet Actuators. AIAA J. 2003, 41, 240–247. [Google Scholar] [CrossRef] [Green Version]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 78001. [Google Scholar] [CrossRef] [Green Version]
- Mane, P.; Mossi, K.; Rostami, A.; Bryant, R.; Castro, N. Piezoelectric actuators as synthetic jets: Cavity dimension effects. J. Intell. Mater. Syst. Struct. 2007, 18, 1175–1190. [Google Scholar] [CrossRef]
- Rimasauskiene, R.; Matejka, M.; Ostachowicz, W.; Kurowski, M.; Malinowski, P.; Wandowski, T.; Rimasauskas, M. Experimental research of the synthetic jet generator designs based on actuation of diaphragm with piezoelectric actuator. Mech. Syst. Signal Process. 2015, 50–51, 607–614. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Leong, J.Y.C.; Watanabe, S.; Morooka, S. Numerical Simulations of Piezoelectric Inkjet Printer using Fully Coupled Fluid Structure Interaction Approach. Computation 2021. Submitted. [Google Scholar]
- Mimura, T.; Sakai, S. Micro-Piezoelectric Head Technology of Color Inkjet Printer. IST’s Inter. Conf. Digital Prod. Print. Ind. Appl. 2001, 2001, 230–234. [Google Scholar]
- Adams, B.M.; Ebeida, M.S.; Eldred, M.S.; Jakeman, J.D.; Swiler, L.P.; Eddy, J.P.; Dakota, A. Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis Version 6.7 Theory Manual; Sandia Technical Report SAND2014-4633; Sandia National Lab.: Albuquerque, NM, USA, 2014. [Google Scholar]
- Sobol’, I.M.; Kucherenko, S. Derivative based global sensitivity measures and their link with global sensitivity indices. Math. Comput. Simul. 2009, 79, 3009–3017. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]


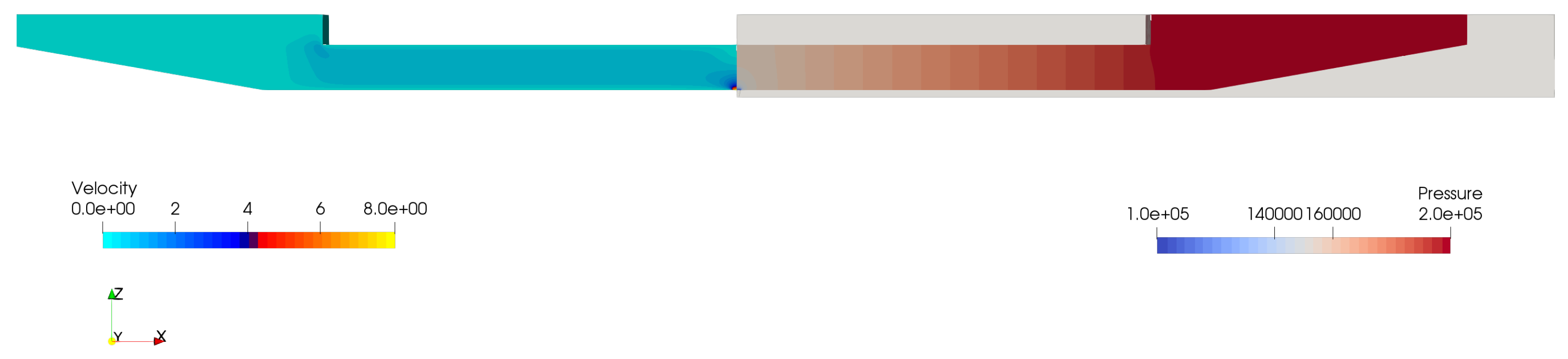


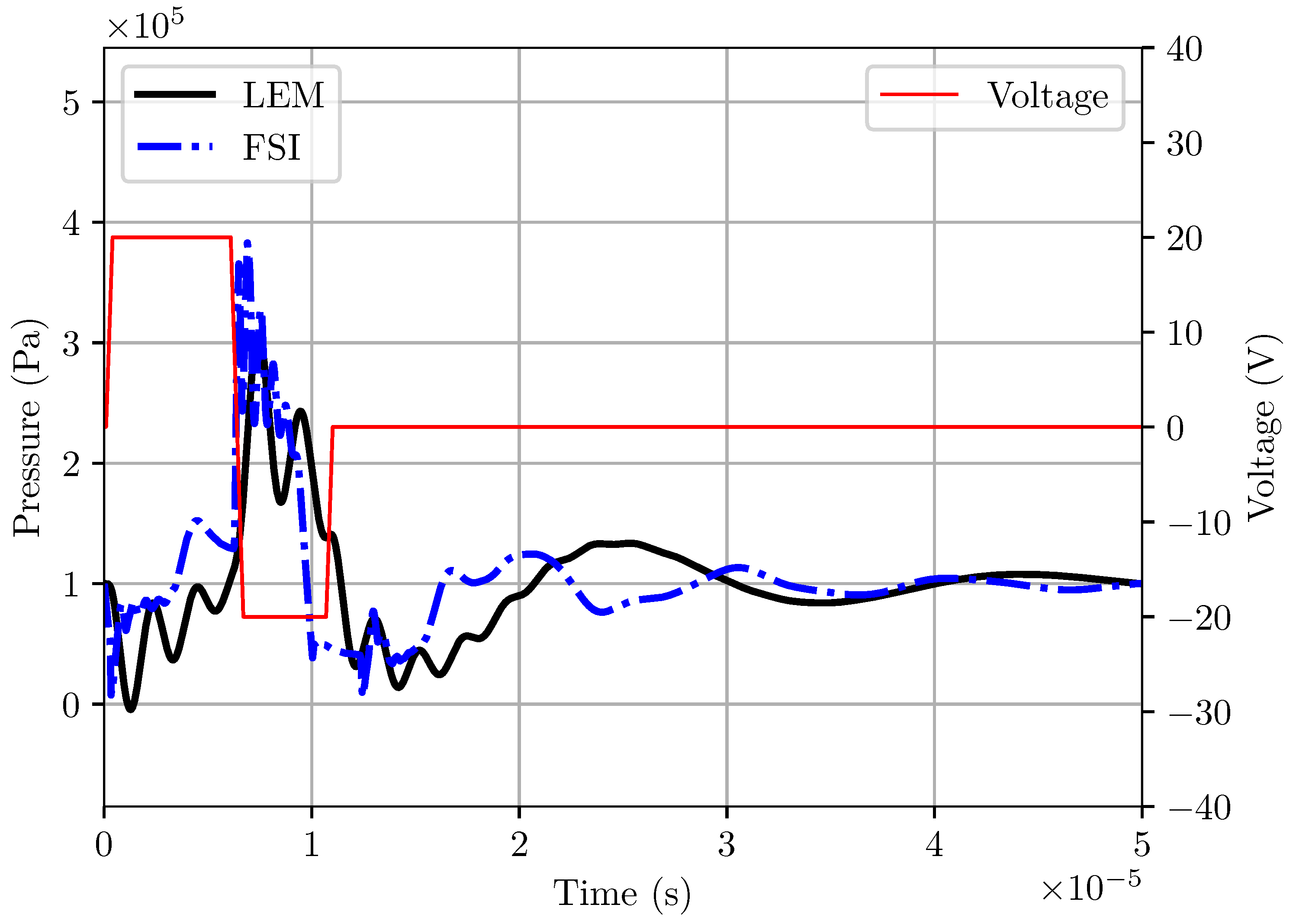

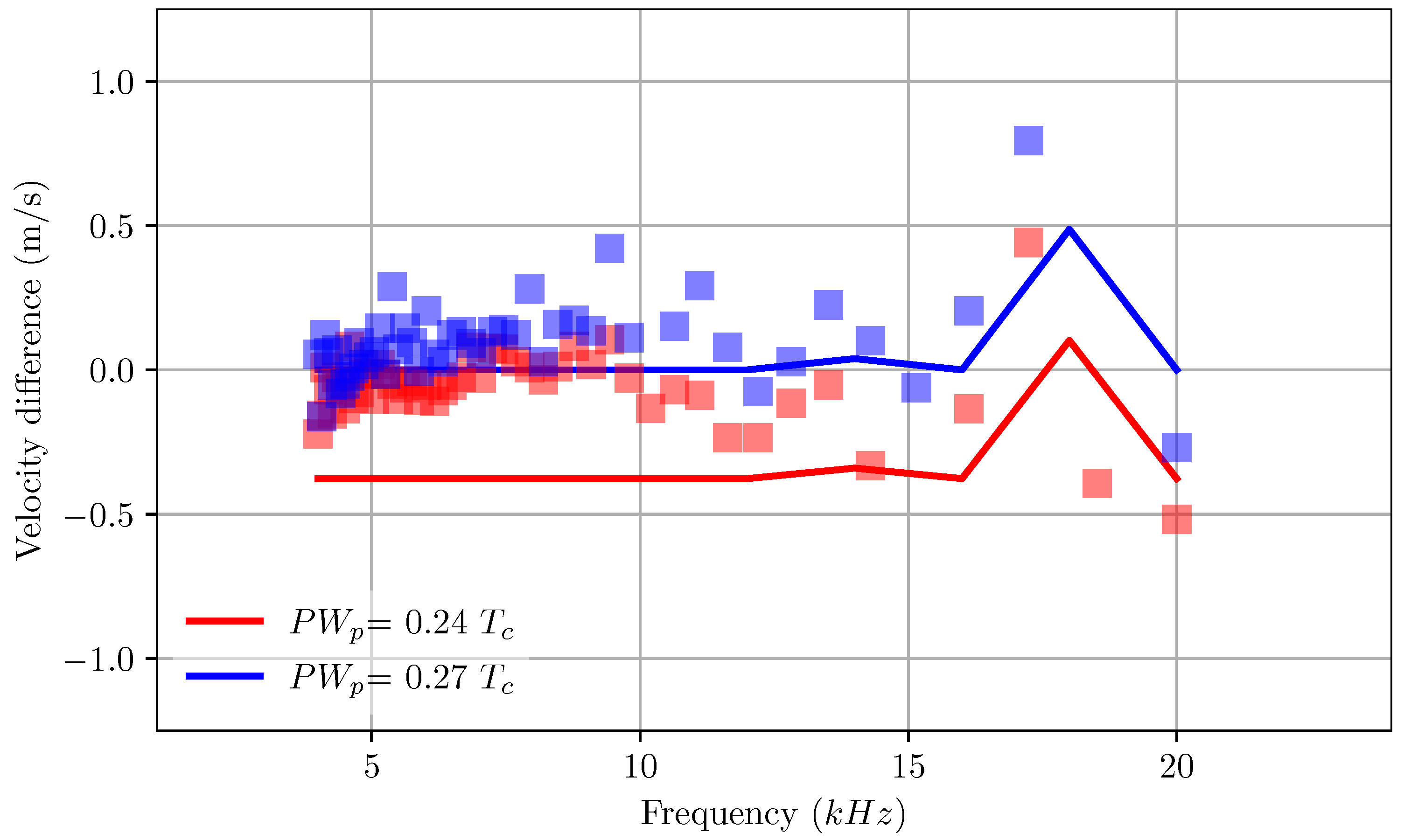
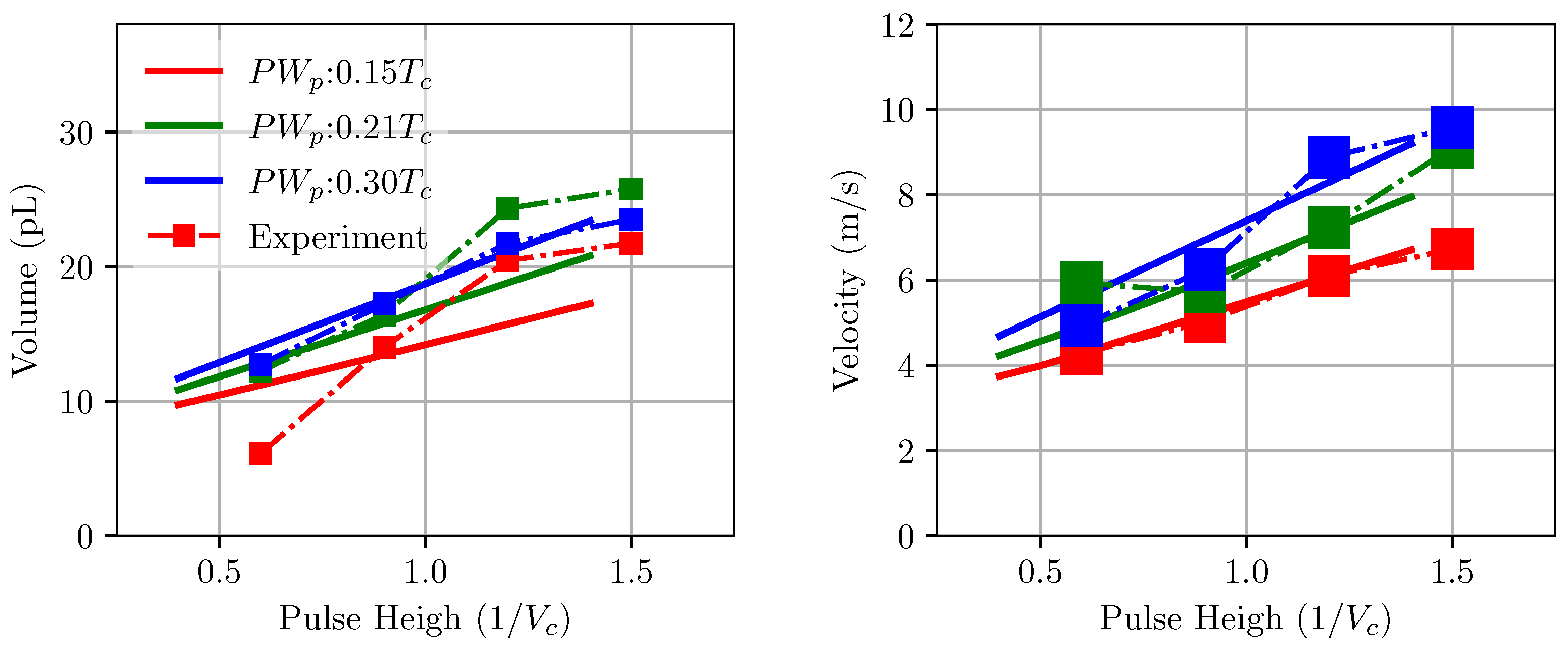
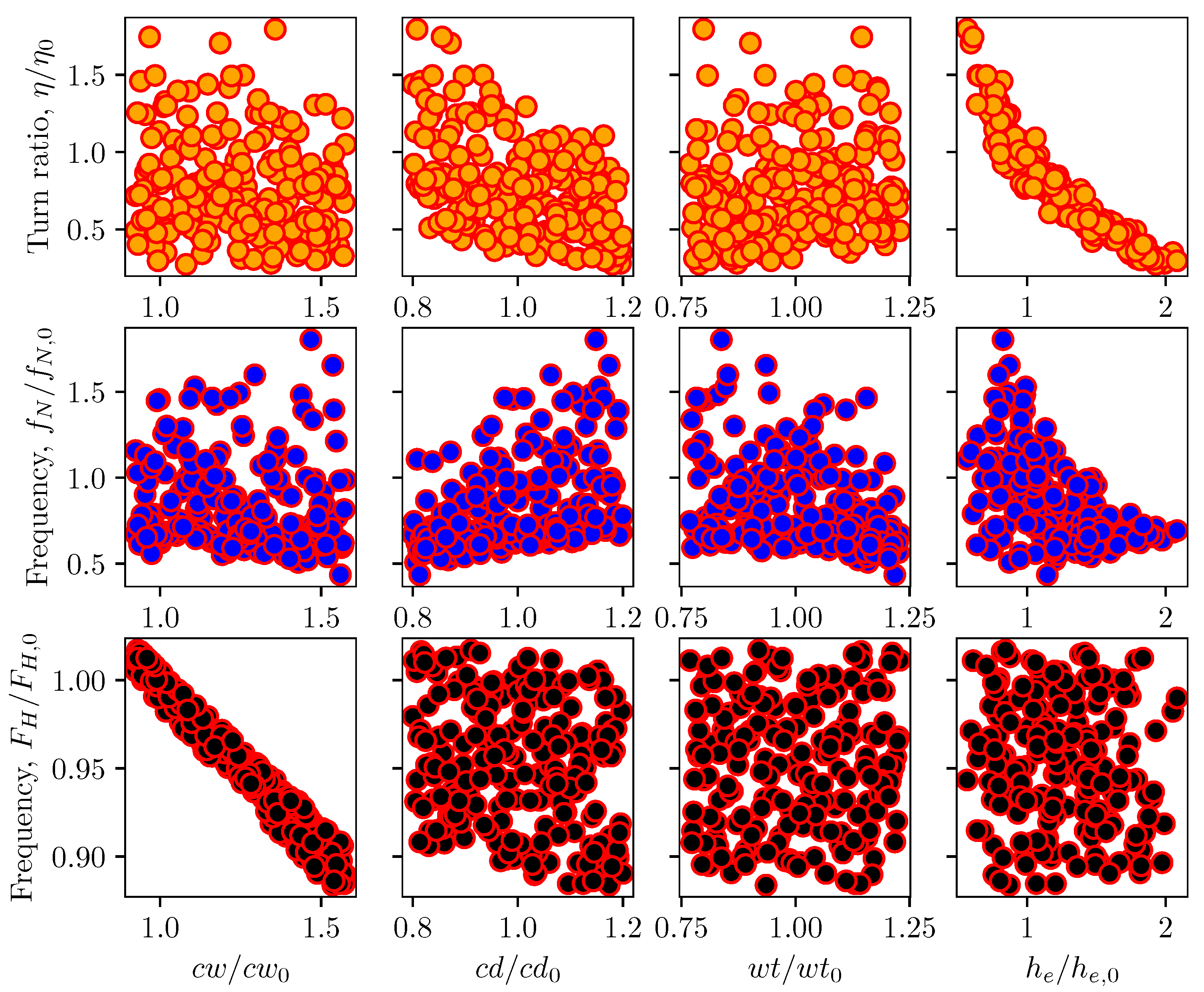

| Mesh | Grid Convergence Index (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Cells | ||||||||
| G0 | 1.25 | 2.50 | 5.0 | 42,420 | - | - | - | - |
| G1 | 1.875 | 3.75 | 7.5 | 82,264 | 7.56 | 0.50 | 1.86 | 0.77 |
| G2 | 2.50 | 5.00 | 10.0 | 136,992 | 2.87 | 0.21 | 0.67 | 0.15 |
| G3 | 3.75 | 7.50 | 15.0 | 306,308 | 0.82 | 0.11 | 0.16 | 0.06 |
| Mesh | Grid Convergence Index (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Cells | ||||||||
| G0 | 2.0 | 8.0 | 2.0 | 35,416 | - | - | - | - |
| G1 | 3.0 | 12.0 | 3.0 | 96,312 | 6.50 | 1.02 | 1.39 | 1.07 |
| G2 | 4.0 | 16.0 | 4.0 | 196,576 | 2.24 | 0.42 | 0.57 | 0.57 |
| G3 | 6.0 | 24.0 | 6.0 | 596,928 | 0.52 | 0.12 | 0.16 | 0.23 |
| Configuration | SJ0 | SJ1 | SJ2 |
|---|---|---|---|
| Shim radius, [mm] | 11.5 | 11.5 | 18.5 |
| Shim thickness, [mm] | 0.201 | 0.150 | 0.100 |
| Piezo-plate radius, [mm] | 10.0 | 10.0 | 12.5 |
| Piezo plate thickness, [mm] | 0.232 | 0.08 | 0.11 |
| Cavity volume, [mm] | - | 2.50 | 5.50 |
| Orifice radius, [mm] | - | 0.825 | 0.420 |
| Orifice length, [mm] | - | 1.65 | 0.84 |
| (sm/kg) | (m/V) | (kg/m) | (Pa/V) | - | (Hz) | ||
|---|---|---|---|---|---|---|---|
| SJ0 | Analytical [20] | 1.491 | 2.077 | 13,538.0 | 139.3 | 0.117 | 3542.4 |
| 3D based, present | 0.998 | 1.977 | 12,956.1 | 198.0 | 0.254 | 4425.1 | |
| SJ1 | Analytical [20] | 7.391 | 5.528 | 7670.0 | 74.79 | - | 2114.0 |
| 3D based, present | 5.188 | 5.285 | 7003.6 | 101.87 | 0.297 | 2640.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-T.; Leong, J.Y.C.; Watanabe, S.; Morooka, T.; Shimizu, T. A Multi-Fidelity Model for Simulations and Sensitivity Analysis of Piezoelectric Inkjet Printheads. Micromachines 2021, 12, 1038. https://doi.org/10.3390/mi12091038
Nguyen V-T, Leong JYC, Watanabe S, Morooka T, Shimizu T. A Multi-Fidelity Model for Simulations and Sensitivity Analysis of Piezoelectric Inkjet Printheads. Micromachines. 2021; 12(9):1038. https://doi.org/10.3390/mi12091038
Chicago/Turabian StyleNguyen, Vinh-Tan, Jason Yu Chuan Leong, Satoshi Watanabe, Toshimitsu Morooka, and Takayuki Shimizu. 2021. "A Multi-Fidelity Model for Simulations and Sensitivity Analysis of Piezoelectric Inkjet Printheads" Micromachines 12, no. 9: 1038. https://doi.org/10.3390/mi12091038
APA StyleNguyen, V.-T., Leong, J. Y. C., Watanabe, S., Morooka, T., & Shimizu, T. (2021). A Multi-Fidelity Model for Simulations and Sensitivity Analysis of Piezoelectric Inkjet Printheads. Micromachines, 12(9), 1038. https://doi.org/10.3390/mi12091038





