A Review of the Methods of Modeling Multi-Phase Flows within Different Microchannels Shapes and Their Applications
Abstract
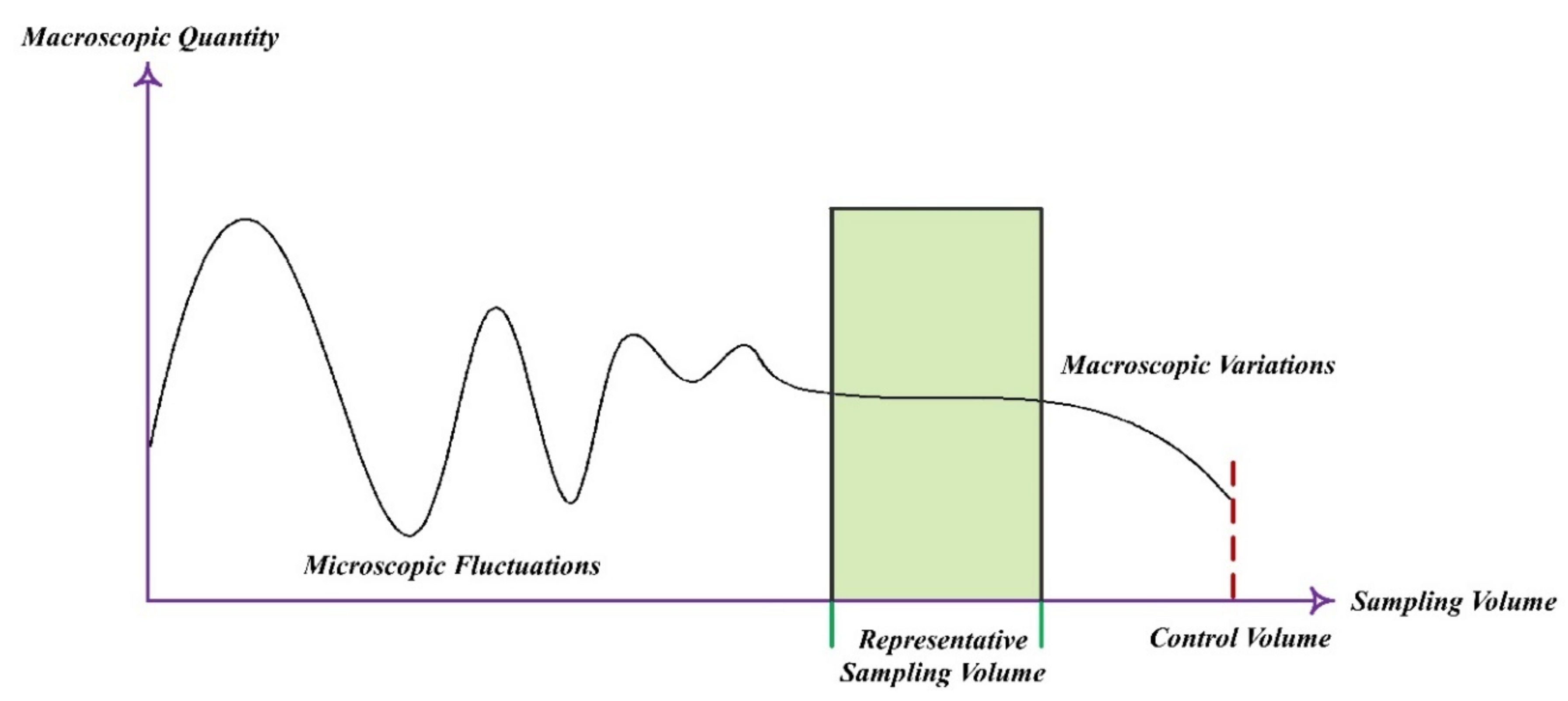
:1. Introduction to Microstructures
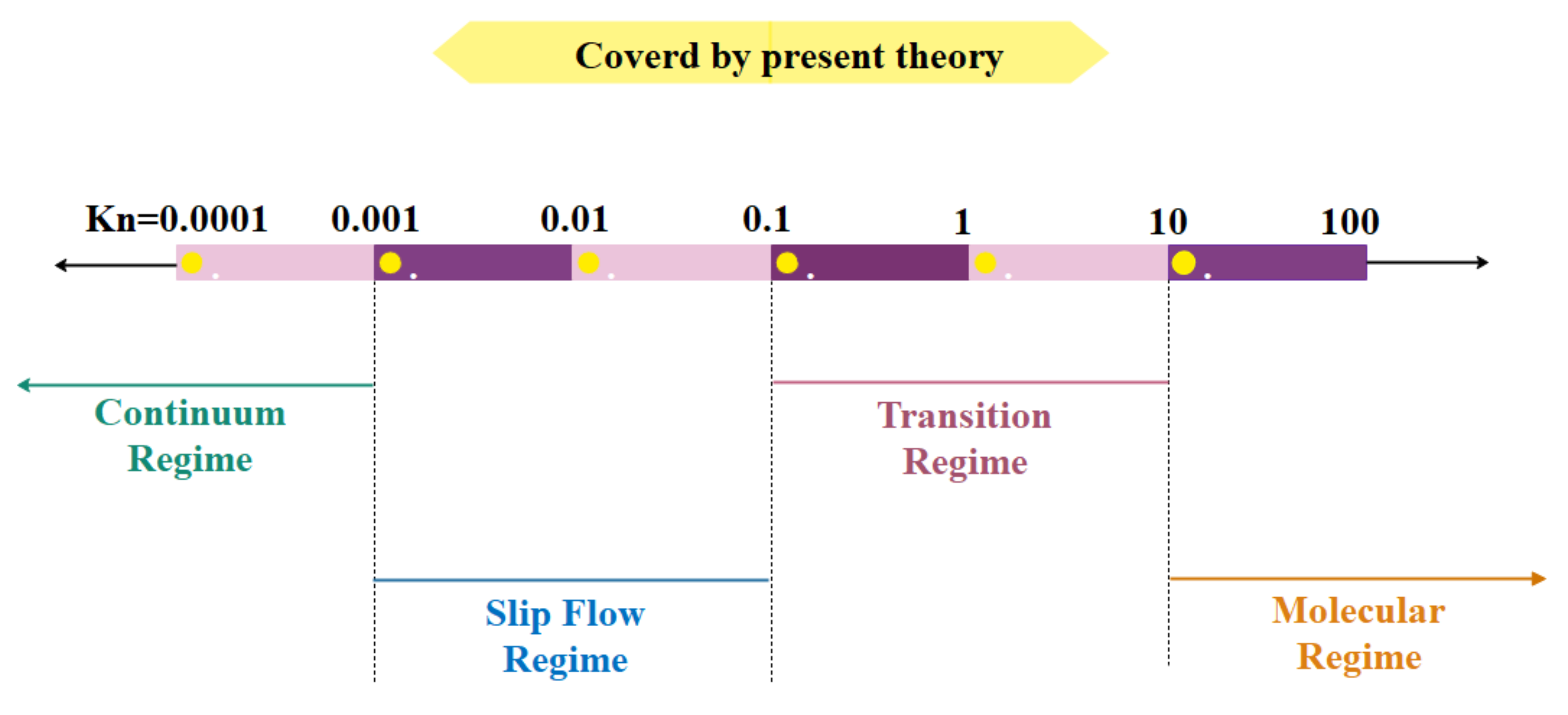
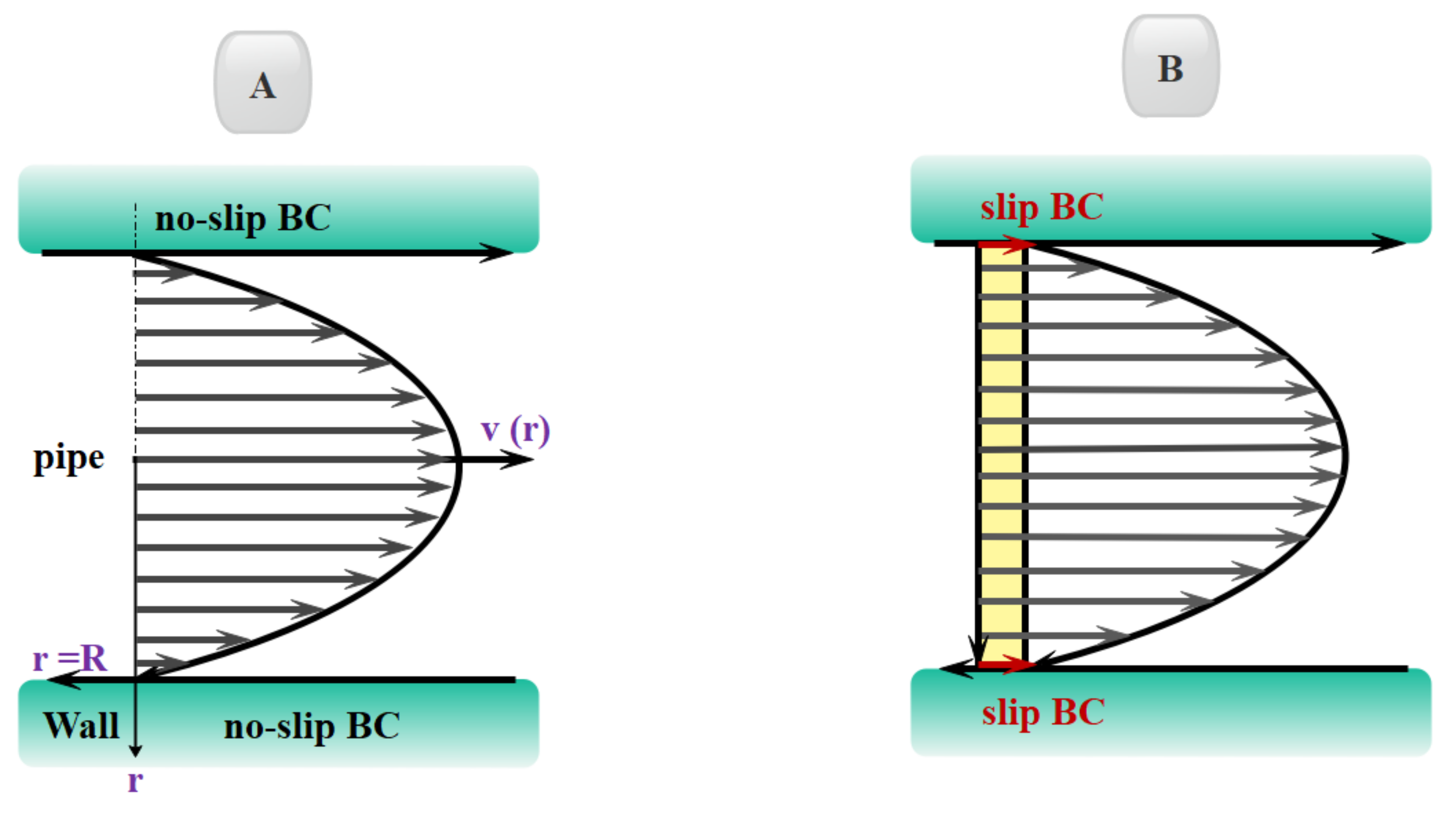
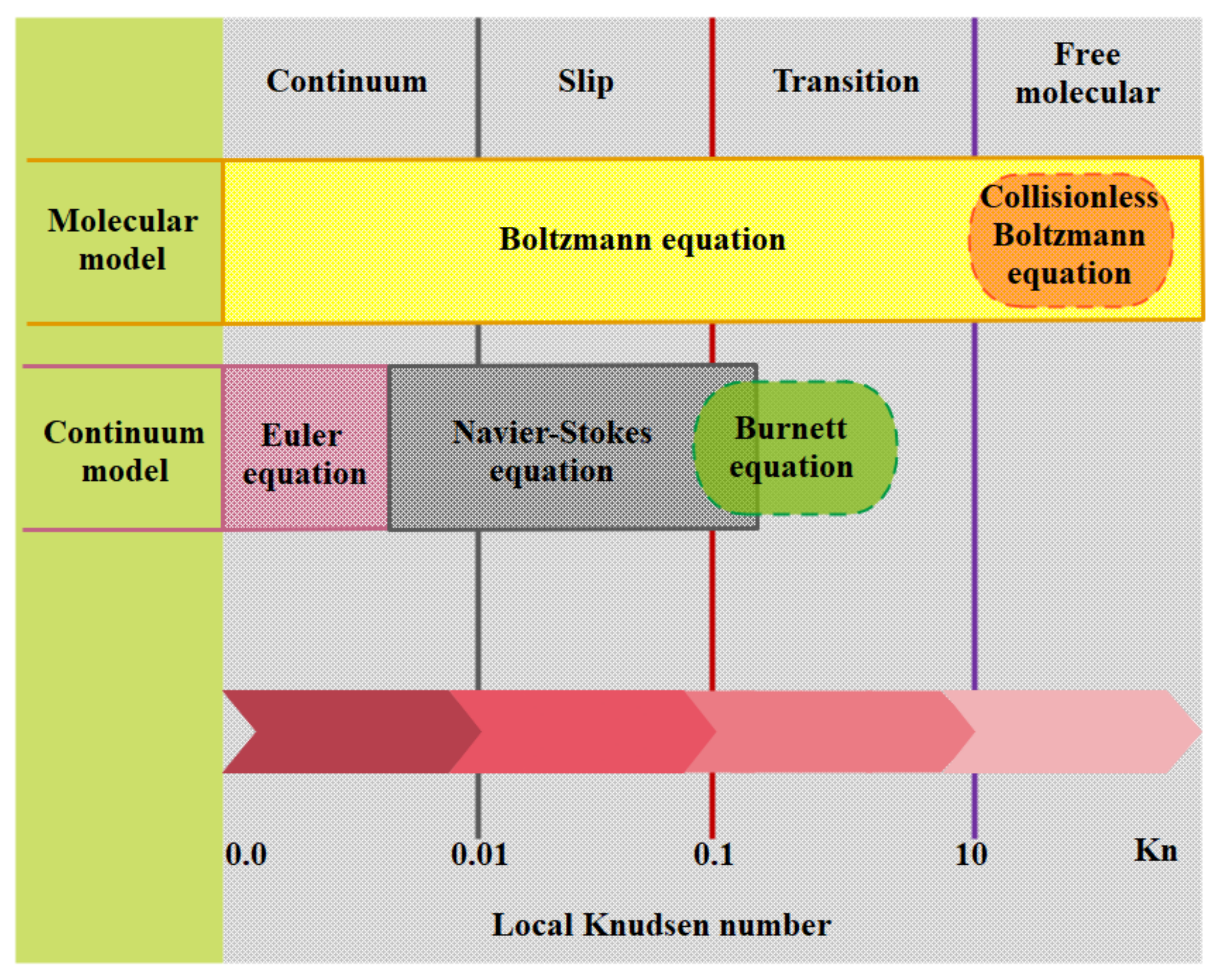
1.1. Different Flow Regimes
1.2. Intra-Microchannel Flow Modeling Methods
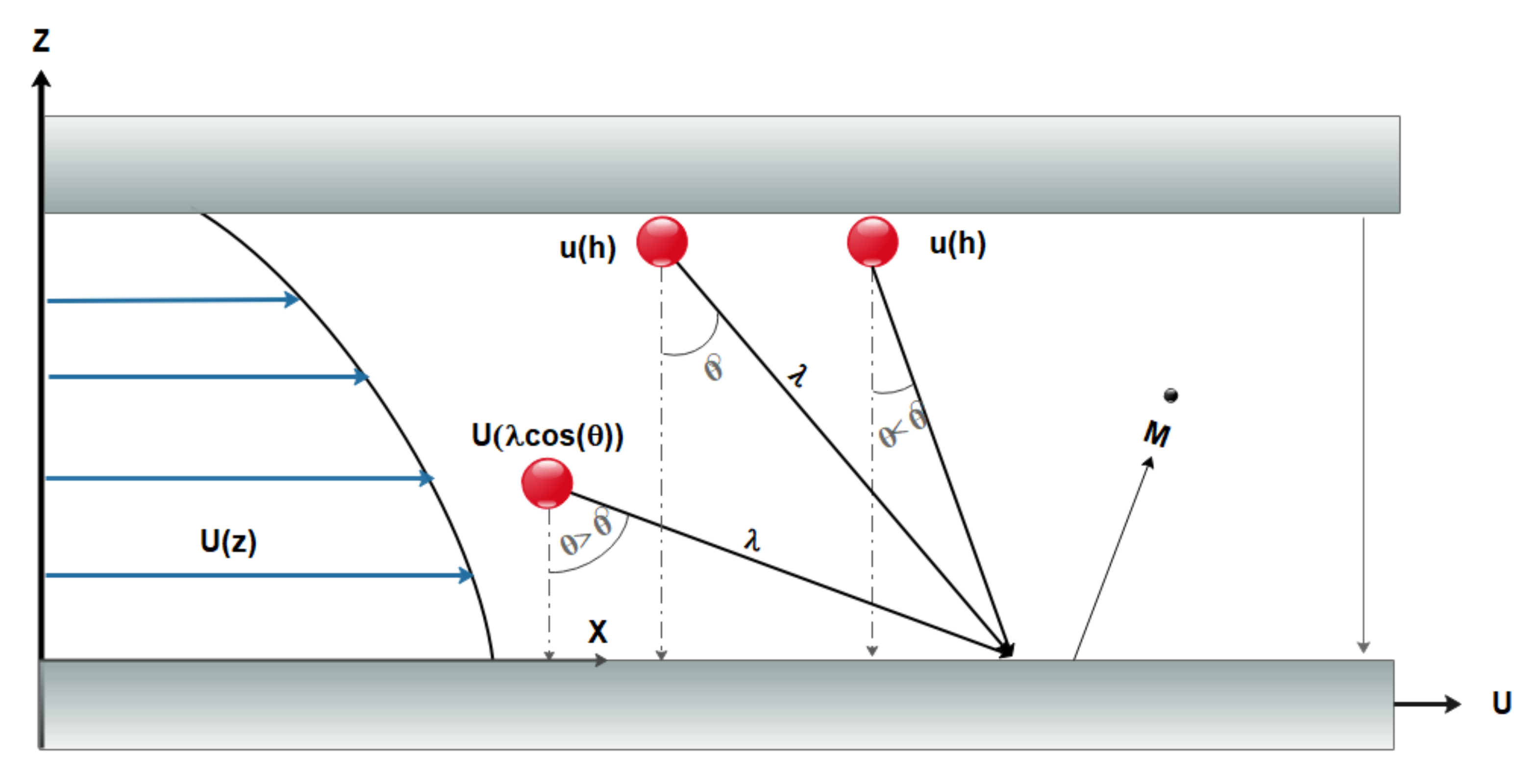
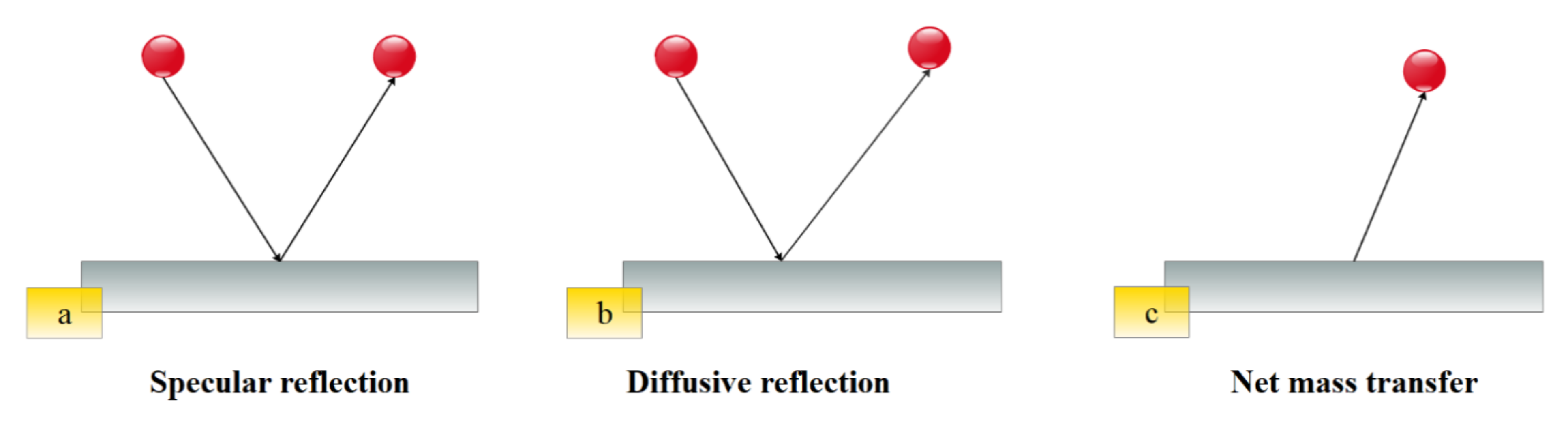
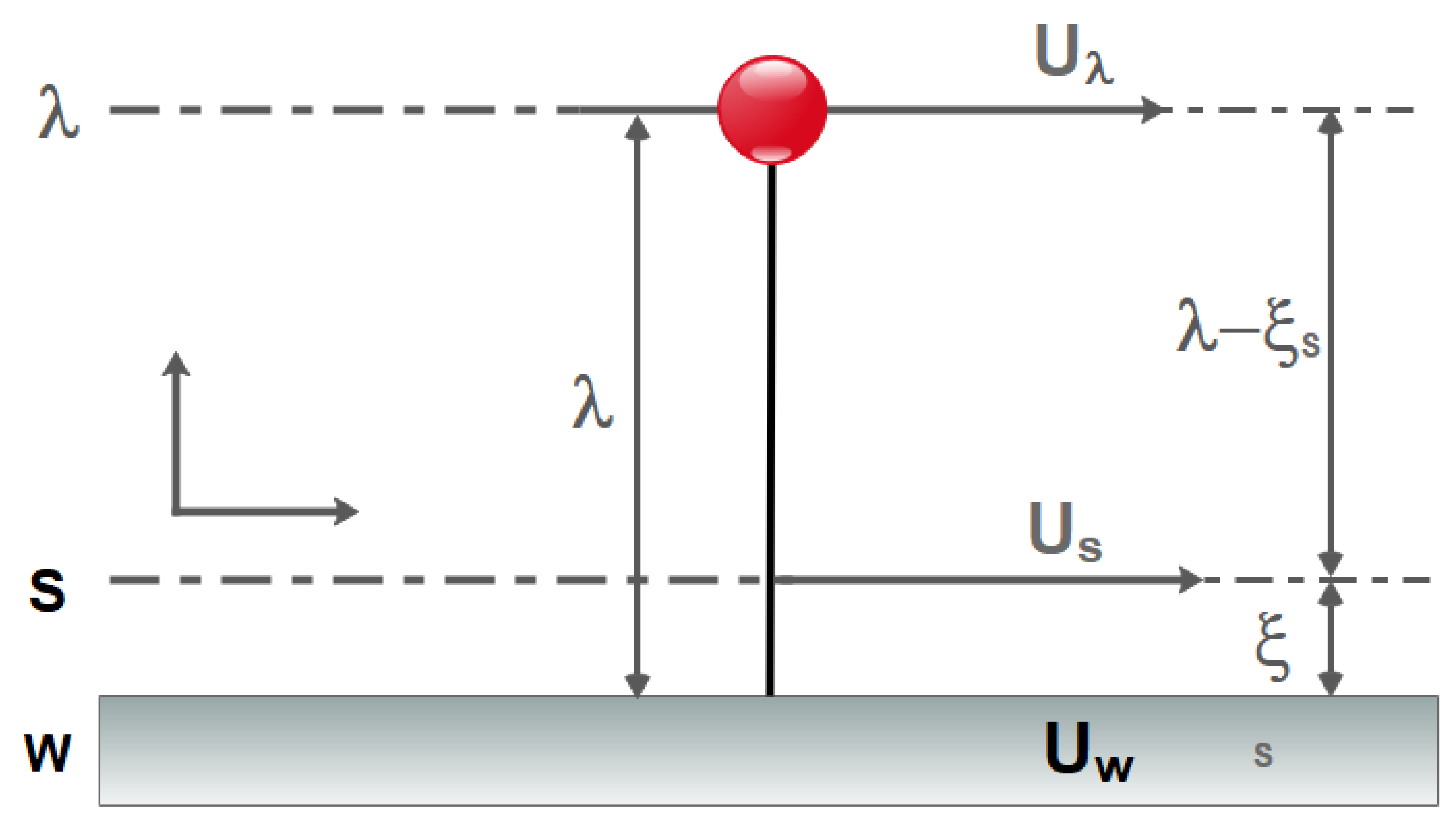
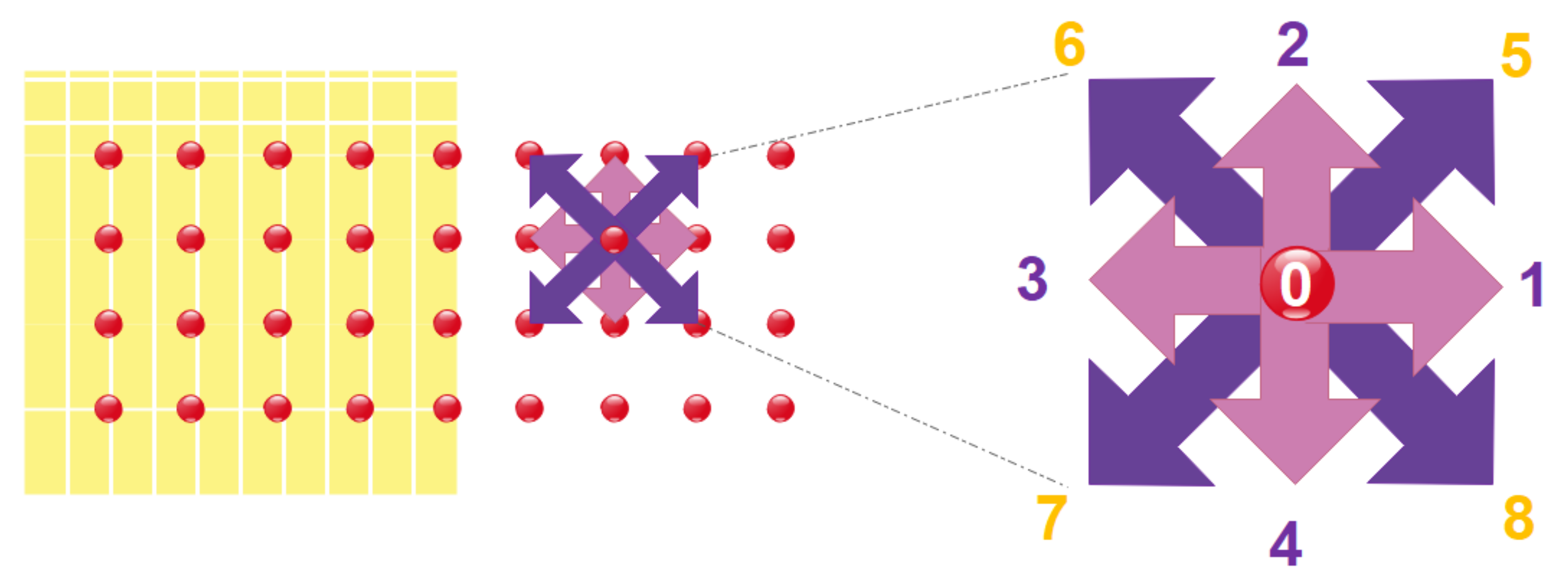
1.3. Study of Slip Velocity Models and Lattice Boltzmann Method
1.4. Compressible Flow within Microchannels
2. Multi-Phase Flows within Microchannels
2.1. Flow Boiling and Bubble Growth in Microchannels
2.2. Bubble Formation in Microchannels
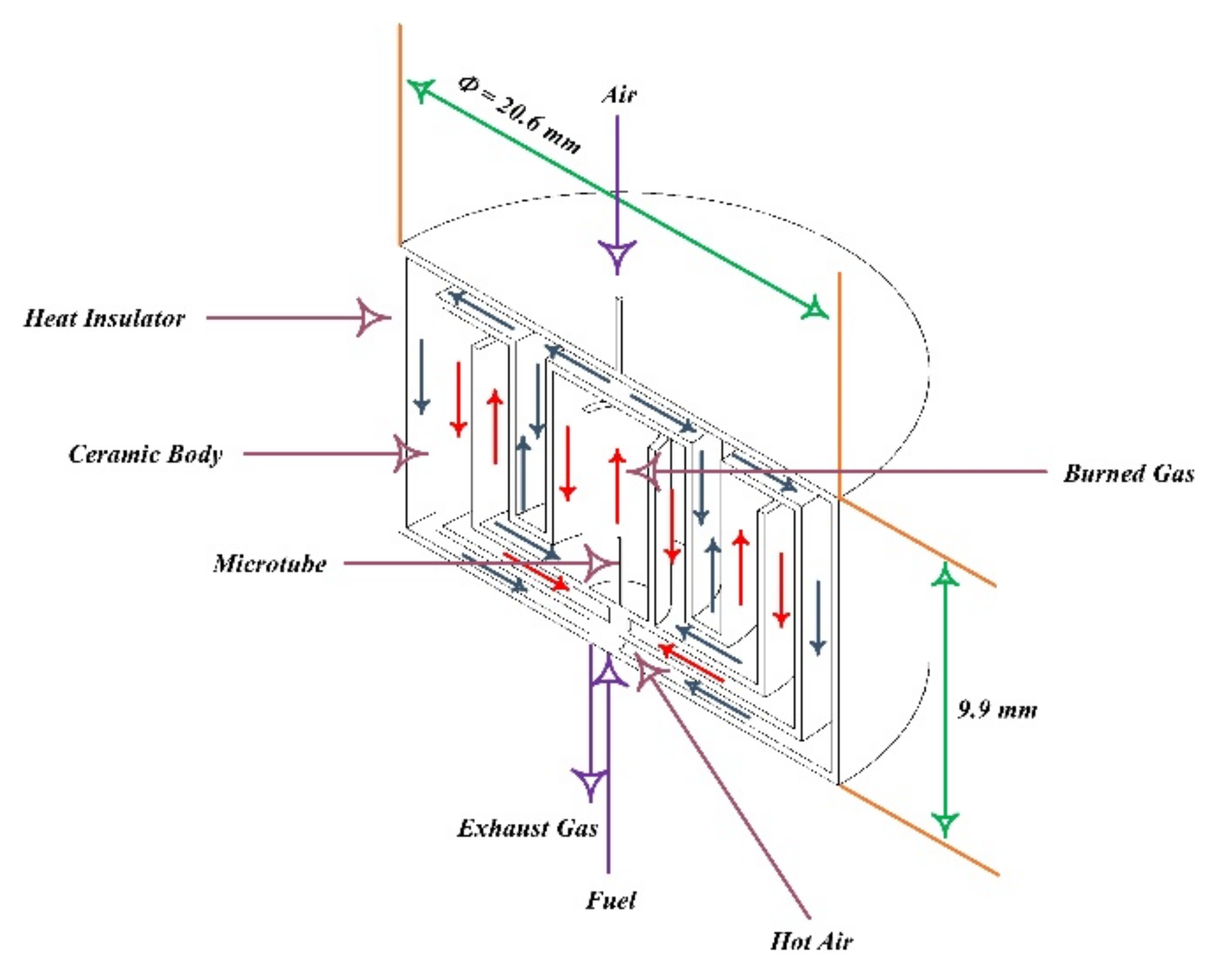
2.3. Combustion in Microchannels
3. Applications of Microscale
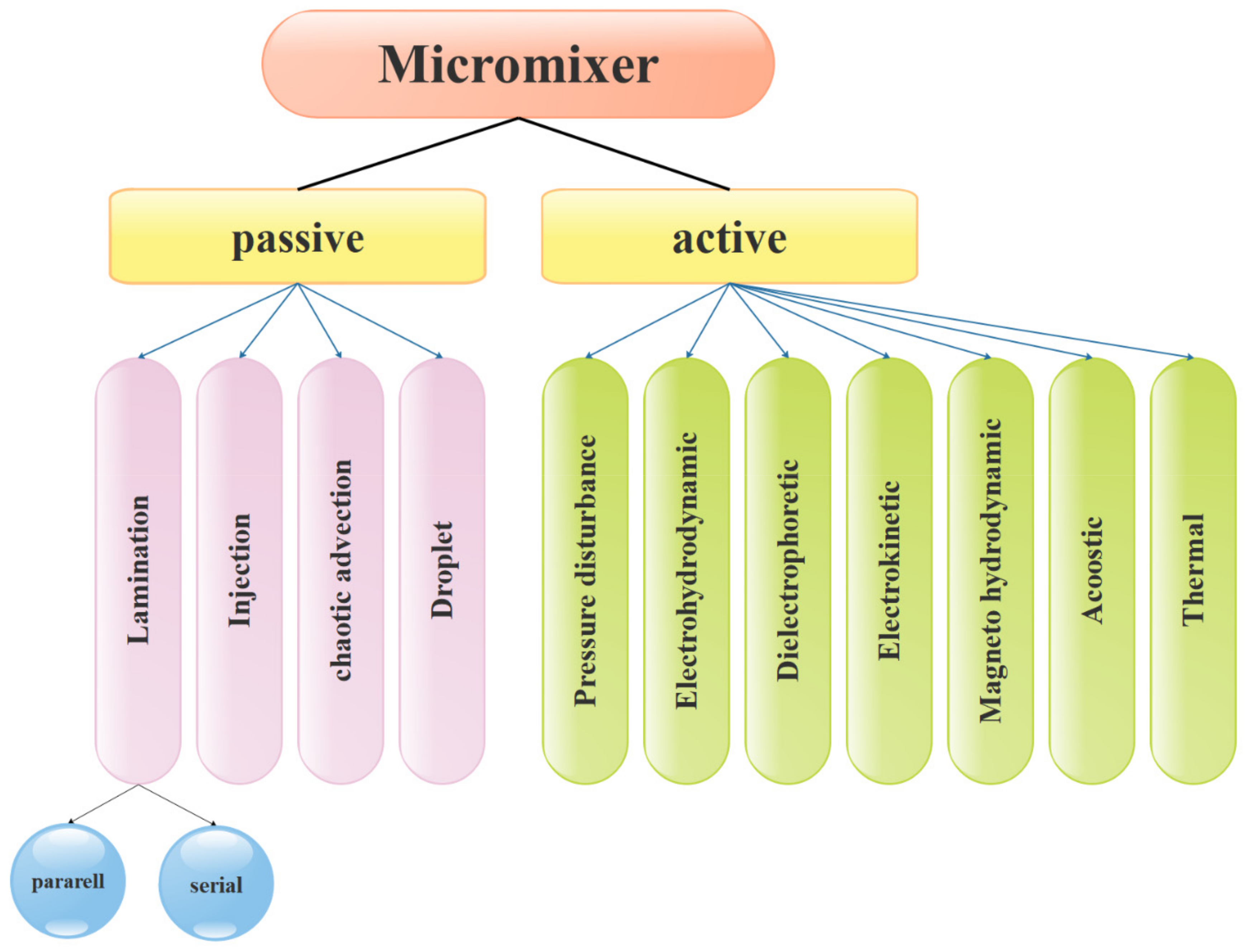
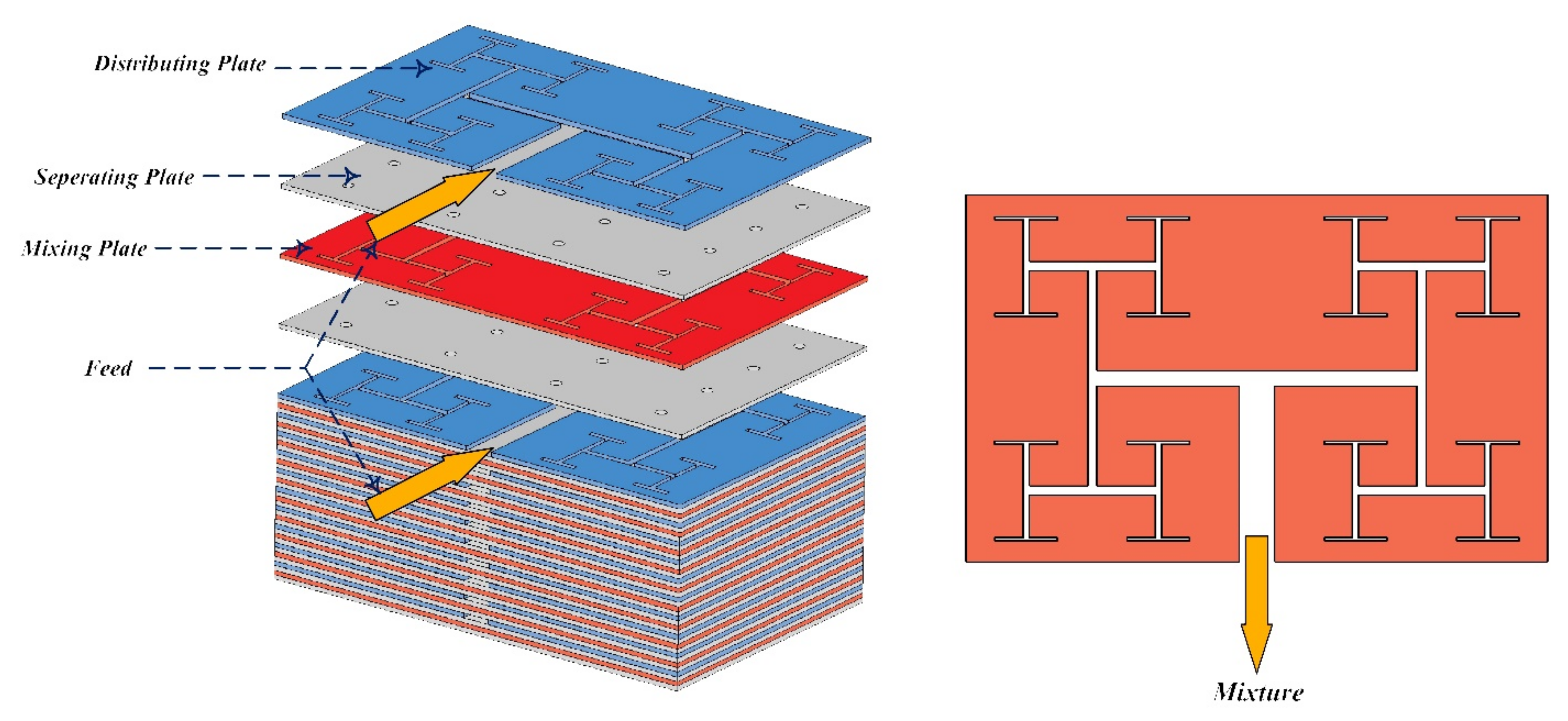
3.1. Micromixers
3.2. Microturbines
3.3. Micropumps
4. Challenges, Suggestions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chau, L.; Doran, M.; Cooper-White, J. A novel multishear microdevice for studying cell mechanics. Lab Chip 2009, 9, 1897–1902. [Google Scholar] [CrossRef]
- Nisisako, T.; Torii, T.; Higuchi, T. Droplet formation in a microchannel network. Lab Chip 2002, 2, 24–26. [Google Scholar] [CrossRef]
- Jendrejack, R.M.; Dimalanta, E.T.; Schwartz, D.C.; Graham, M.; De Pablo, J.J. DNA Dynamics in a Microchannel. Phys. Rev. Lett. 2003, 91, 038102. [Google Scholar] [CrossRef]
- Phillips, R.J. Microchannel heat sinks. Linc. Lab. J. 1988, 1, 31–48. [Google Scholar]
- Hu, P.; Cao, L.; Su, J.; Li, Q.; Li, Y. Distribution characteristics of salt-out particles in steam turbine stage. Energy 2020, 192, 116626. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.-X.; Wang, Z.-G.; Li, J.-Q.; Ji, H.-H. Influence of Mach Number of Main Flow on Film Cooling Characteristics under Supersonic Condition. Symmetry 2021, 13, 127. [Google Scholar] [CrossRef]
- Afrand, M. Using a magnetic field to reduce natural convection in a vertical cylindrical annulus. Int. J. Therm. Sci. 2017, 118, 12–23. [Google Scholar] [CrossRef]
- Afrand, M.; Farahat, S.; Nezhad, A.H.; Sheikhzadeh, G.A.; Sarhaddi, F. 3-D numerical investigation of natural convection in a tilted cylindrical annulus containing molten potassium and controlling it using various magnetic fields. Int. J. Appl. Electromagn. Mech. 2014, 46, 809–821. [Google Scholar] [CrossRef]
- Afrand, M.; Farahat, S.; Nezhad, A.H.; Sheikhzadeh, G.A.; Sarhaddi, F.; Wongwises, S. Multi-objective optimization of natural convection in a cylindrical annulus mold under magnetic field using particle swarm algorithm. Int. Commun. Heat Mass Transf. 2015, 60, 13–20. [Google Scholar] [CrossRef]
- Cheraghian, G.; Wu, Q.; Mostofi, M.; Li, M.-C.; Afrand, M.; Sangwai, J.S. Effect of a novel clay/silica nanocomposite on water-based drilling fluids: Improvements in rheological and filtration properties. Colloids Surf. A Physicochem. Eng. Asp. 2018, 555, 339–350. [Google Scholar] [CrossRef]
- Cheraghian, G.; Khalili Nezhad, S.S.; Bazgir, S. Improvement of thermal stability of polyacryl amide solution used as a nano-fluid in enhanced oil recovery process by nanoclay. Int. J. Nanosci. Nanotechnol. 2015, 11, 201–208. [Google Scholar]
- Bahiraei, M.; Jamshidmofid, M.; Goodarzi, M. Efficacy of a hybrid nanofluid in a new microchannel heat sink equipped with both secondary channels and ribs. J. Mol. Liq. 2019, 273, 88–98. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Esfandeh, S.; Afrand, M. Proposing new hybrid nano-engine oil for lubrication of internal combustion engines: Preventing cold start engine damages and saving energy. Energy 2019, 170, 228–238. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esfandeh, S.; Afrand, M.; Rejvani, M.; Rostamian, S.H. Experimental evaluation, new correlation proposing and ANN modeling of thermal properties of EG based hybrid nanofluid containing ZnO-DWCNT nanoparticles for internal combustion engines applications. Appl. Therm. Eng. 2018, 133, 452–463. [Google Scholar] [CrossRef]
- Esfe, M.H.; Esfandeh, S.; Amiri, M.K.; Afrand, M. A novel applicable experimental study on the thermal behavior of SWCNTs(60%)-MgO(40%)/EG hybrid nanofluid by focusing on the thermal conductivity. Powder Technol. 2019, 342, 998–1007. [Google Scholar] [CrossRef]
- Esfe, M.H.; Raki, H.R.; Emami, M.R.S.; Afrand, M. Viscosity and rheological properties of antifreeze based nanofluid containing hybrid nano-powders of MWCNTs and TiO2 under different temperature conditions. Powder Technol. 2019, 342, 808–816. [Google Scholar] [CrossRef]
- Cheraghian, G. Improved Heavy Oil Recovery by Nanofluid Surfactant Flooding—An Experimental Study. In Proceedings of the 78th EAGE Conference and Exhibition, Online, 30 May–2 June 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Nguyen, Q.; Bahrami, D.; Kalbasi, R.; Karimipour, A. Functionalized Multi-Walled carbon Nano Tubes nanoparticles dispersed in water through an Magneto Hydro Dynamic nonsmooth duct equipped with sinusoidal-wavy wall: Diminishing vortex intensity via nonlinear Navier–Stokes equations. Math. Methods Appl. Sci. 2020, 1–18, Early view. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, Y.; Band, S.S.; Bahrami, D.; Kalbasi, R.; Karimipour, A.; Jahangiri, M.; Chau, K.-W.; Mosavi, A. Role of gradients and vortexes on suitable location of discrete heat sources on a sinusoidal-wall microchannel. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1176–1190. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Xu, H.; Mahian, O.; Maheri, A. Fundamental and engineering thermal aspects of energy and environment. J. Therm. Anal. Calorim. 2020, 139, 2395–2398. [Google Scholar] [CrossRef]
- Eshgarf, H.; Kalbasi, R.; Maleki, A.; Shadloo, M.S.; Karimipour, A. A review on the properties, preparation, models and stability of hybrid nanofluids to optimize energy consumption. J. Therm. Anal. Calorim. 2021, 144, 1959–1983. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S. Numerical Investigation of Natural Convection and Irreversibilities between Two Inclined Concentric Cylinders in Presence of Uniform Magnetic Field and Radiation. Heat Transf. Eng. 2021, 1–21. [Google Scholar] [CrossRef]
- Kalbasi, R.; Afrand, M.; Alsarraf, J.; Tran, M.-D. Studies on optimum fins number in PCM-based heat sinks. Energy 2019, 171, 1088–1099. [Google Scholar] [CrossRef]
- Karimi, A.; Afrand, M. Numerical study on thermal performance of an air-cooled heat exchanger: Effects of hybrid nanofluid, pipe arrangement and cross section. Energy Convers. Manag. 2018, 164, 615–628. [Google Scholar] [CrossRef]
- Toghraie, D.; Karami, A.; Afrand, M.; Karimipour, A. Effects of geometric parameters on the performance of solar chimney power plants. Energy 2018, 162, 1052–1061. [Google Scholar] [CrossRef]
- Cheraghian, G.; Tardasti, S. Improved oil recovery by the efficiency of nano-particle in imbibition mechanism. In 2nd EAGE international conference KazGeo European Association of Geoscientists & Engineers. Almaty, Kazakhstan, 29–31 October 2012; 315. [Google Scholar] [CrossRef]
- Nariman, A.; Kalbasi, R.; Rostami, S. Sensitivity of AHU power consumption to PCM implementation in the wall-considering the solar radiation. J. Therm. Anal. Calorim. 2021, 143, 2789–2800. [Google Scholar] [CrossRef]
- Li, Z.; Du, C.; Ahmadi, D.; Kalbasi, R.; Rostami, S. Numerical modeling of a hybrid PCM-based wall for energy usage reduction in the warmest and coldest months. J. Therm. Anal. Calorim. 2021, 144, 1985–1998. [Google Scholar] [CrossRef]
- Nguyen, Q.; Naghieh, A.; Kalbasi, R.; Akbari, M.; Karimipour, A.; Tlili, I. Efficacy of incorporating PCMs into the commercial wall on the energy-saving annual thermal analysis. J. Therm. Anal. Calorim. 2021, 143, 2179–2187. [Google Scholar] [CrossRef]
- Li, Z.; Al-Rashed, A.A.; Rostamzadeh, M.; Kalbasi, R.; Shahsavar, A.; Afrand, M. Heat transfer reduction in buildings by embedding phase change material in multi-layer walls: Effects of repositioning, thermophysical properties and thickness of PCM. Energy Convers. Manag. 2019, 195, 43–56. [Google Scholar] [CrossRef]
- Ghazvini, M.; Pourkiaei, S.; Pourfayaz, F. Thermo-Economic Assessment and Optimization of Actual Heat Engine Performance by Implemention of NSGA II. Renew. Energy Res. Appl. 2020, 1, 235–245. [Google Scholar]
- Kaushal, R.; Kumar, R. Heat Transfer Enhancement Using Augmented Tubes for Desalination Using Fuzzy-TOPSIS Approach. Renew. Energy Res. Appl. 2020, 1, 19–26. [Google Scholar]
- Sultan, S.M.; Tso, E.E.C. A Case Study on Effect of Inclination Angle on Performance of Photovoltaic Solar Thermal Collector in Forced Fluid Mode. Renew. Energy Res. Appl. 2020, 1, 187–196. [Google Scholar]
- Zhang, W.; Maleki, A.; Pourfayaz, F.; Shadloo, M.S. An artificial intelligence approach to optimization of an off-grid hybrid wind/hydrogen system. Int. J. Hydrogen Energy 2021, 46, 12725–12738. [Google Scholar] [CrossRef]
- Cademartori, S.; Cravero, C.; Marini, M.; Marsano, D. CFD Simulation of the Slot Jet Impingement Heat Transfer Process and Application to a Temperature Control System for Galvanizing Line of Metal Band. Appl. Sci. 2021, 11, 1149. [Google Scholar] [CrossRef]
- Parsa, S.M.; Rahbar, A.; Koleini, M.; Aberoumand, S.; Afrand, M.; Amidpour, M. A renewable energy-driven thermoelectric-utilized solar still with external condenser loaded by silver/nanofluid for simultaneously water disinfection and desalination. Desalination 2020, 480, 114354. [Google Scholar] [CrossRef]
- Parsa, S.M.; Rahbar, A.; Koleini, M.; Javadi, Y.D.; Afrand, M.; Rostami, S.; Amidpour, M. First approach on nanofluid-based solar still in high altitude for water desalination and solar water disinfection (SODIS). Desalination 2020, 491, 114592. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Akhgar, A.; Musivand, S.; Afrand, M. Effects of graphene oxide-silicon oxide hybrid nanomaterials on rheological behavior of water at various time durations and temperatures: Synthesis, preparation and stability. Powder Technol. 2018, 335, 375–387. [Google Scholar] [CrossRef]
- Shahsavani, E.; Afrand, M.; Kalbasi, R. Using experimental data to estimate the heat transfer and pressure drop of non-Newtonian nanofluid flow through a circular tube: Applicable for use in heat exchangers. Appl. Therm. Eng. 2018, 129, 1573–1581. [Google Scholar] [CrossRef]
- Ye, R.; Liu, P.; Shi, K.; Yan, B. State Damping Control: A Novel Simple Method of Rotor UAV With High Performance. IEEE Access 2020, 8, 214346–214357. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Alamian, R.; Yan, W.-M.; Li, L.K.B.; Leveneur, S.; Shadloo, M.S.; Jamalabadi, A.; Yan, L.; Shadloo, S. Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers. Symmetry 2019, 11, 1353. [Google Scholar] [CrossRef] [Green Version]
- Shahrestani, M.I.; Maleki, A.; Shadloo, M.S.; Tlili, I. Numerical Investigation of Forced Convective Heat Transfer and Performance Evaluation Criterion of Al2O3/Water Nanofluid Flow inside an Axisymmetric Microchannel. Symmetry 2020, 12, 120. [Google Scholar] [CrossRef] [Green Version]
- Kalbasi, R. Introducing a novel heat sink comprising PCM and air—Adapted to electronic device thermal management. Int. J. Heat Mass Transf. 2021, 169, 120914. [Google Scholar] [CrossRef]
- Salimpour, M.R.; Kalbasi, R.; Lorenzini, G. Constructal multi-scale structure of PCM-based heat sinks. Contin. Mech. Thermodyn. 2017, 29, 477–491. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Li, L.K.; Doranehgard, M.H. Special Issue on Multiphase and Turbulent Flows in Energy Engineering Applications. J. Energy Resour. Technol. 2020, 142, 110301. [Google Scholar] [CrossRef]
- Akbari, O.A.; Safaei, M.R.; Goodarzi, M.; Akbar, N.S.; Zarringhalam, M.; Shabani, G.A.S.; Dahari, M. A modified two-phase mixture model of nanofluid flow and heat transfer in a 3-D curved microtube. Adv. Powder Technol. 2016, 27, 2175–2185. [Google Scholar] [CrossRef]
- O’Neill, L.E.; Mudawar, I. Review of two-phase flow instabilities in macro- and micro-channel systems. Int. J. Heat Mass Transf. 2020, 157, 119738. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Y.; Ma, H.; Liu, Y.; Zhao, Q.; Chen, G. Two-phase flow and mass transfer in microchannels: A review from local mechanism to global models. Chem. Eng. Sci. 2021, 229, 116017. [Google Scholar] [CrossRef]
- Etminan, A.; Muzychka, Y.S.; Pope, K. Liquid film thickness of two-phase slug flows in capillary microchannels: A review paper. Can. J. Chem. Eng. 2021. Early view. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Sharifpur, M.; Meyer, J.P.; Xu, H.; Ali, H.M.; Karimi, N.; Cheraghian, G. Nanofluids: Physical phenomena, applications in thermal systems and the environment effects—A critical review. J. Clean. Prod. 2021, 320, 128573. [Google Scholar] [CrossRef]
- Huang, H.; Sun, T.; Zhang, G.; Li, D.; Wei, H. Evaluation of a developed SST k-ω turbulence model for the prediction of turbulent slot jet impingement heat transfer. Int. J. Heat Mass Transf. 2019, 139, 700–712. [Google Scholar] [CrossRef]
- Almasi, F.; Shadloo, M.; Hadjadj, A.; Ozbulut, M.; Tofighi, N.; Yildiz, M. Numerical simulations of multi-phase electro-hydrodynamics flows using a simple incompressible smoothed particle hydrodynamics method. Comput. Math. Appl. 2021, 81, 772–785. [Google Scholar] [CrossRef]
- Panda, K.; Hirokawa, T.; Huang, L. Design study of microchannel heat exchanger headers using experimentally validated multiphase flow CFD simulation. Appl. Therm. Eng. 2020, 178, 115585. [Google Scholar] [CrossRef]
- Chatterjee, S.; Ghanta, K.C.; Hens, A. Study of multiphase flow inside straight and spiral microchannel and effect of two phase flow on Dean’s vortices. Chem. Eng. Res. Des. 2021, 165, 398–408. [Google Scholar] [CrossRef]
- Bakhshan, M.; Wörner, M.; Dadvand, A. Simulation of droplet impingement on a rigid square obstacle in a microchannel using multiphase lattice Boltzmann method. Comput. Part. Mech. 2021, 8, 973–991. [Google Scholar] [CrossRef]
- Chen, S.; Lan, J.; Zhang, Y.; Guo, J.; Cao, Z.; Sha, Y. 3D multiphase flow simulation of Marangoni convection on reactive absorption of CO2 by monoethanolamine in microchannel. Chin. J. Chem. Eng. 2021, in press. [Google Scholar] [CrossRef]
- Lima, R.; Vega, E.J.; Moita, A.S.; Miranda, J.M.; Pinho, D.; Moreira, A.L.N. Fast, flexible and low-cost multiphase blood analogue for biomedical and energy applications. Exp. Fluids 2020, 61, 231. [Google Scholar] [CrossRef]
- Sattari, A.; Hanafizadeh, P.; Hoorfar, M. Multiphase flow in microfluidics: From droplets and bubbles to the encapsulated structures. Adv. Colloid Interface Sci. 2020, 282, 102208. [Google Scholar] [CrossRef]
- Dinh, T.; Cubaud, T. Influence of interfacial tension on viscous multiphase flows in coaxial microchannels. In APS Division of Fluid Dynamics Meeting Abstracts; American Physical Society: College Park, MD, USA, 2020; p. J07-009. [Google Scholar]
- Laziz, A.M.; KuShaari, K.; Azeem, B.; Yusup, S.; Chin, J.; Denecke, J. Rapid production of biodiesel in a microchannel reactor at room temperature by enhancement of mixing behaviour in methanol phase using volume of fluid model. Chem. Eng. Sci. 2020, 219, 115532. [Google Scholar] [CrossRef]
- Guimarães, G.M.; Pinto, K.L.; Lobosco, R.J. Comparative Analysis of Multiphase Flow in a T Type Micro Junction. In Proceedings of the 6th Brazilian Technology Symposium (BTSym’20), Angwin, CA, USA, 26–28 October 2020; Springer International Publishing: Chaam, The Netherlands, 2021; pp. 723–731. [Google Scholar]
- Shadloo, M.S.; Rahmat, A.; Li, L.K.; Mahian, O.; Alagumalai, A. High-performance computing and machine learning applied in thermal systems analysis Preface. J. Therm. Anal. Calorim. 2021, 145, 1733–1737. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, K.; Zou, Z.; Zhong, L.; Akkurt, N.; Feng, J.; Xiong, Y.; Han, J.; Wang, J.; Du, Y. A new type of two-supply, one-return, triple pipe-structured heat loss model based on a low temperature district heating system. Energy 2021, 218, 119569. [Google Scholar] [CrossRef]
- Kandlikar, S.; Garimella, S.; Li, D.; Colin, S.; King, M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Akbar, M.K.; Plummer, D.A.; Ghiaasiaan, S.M. Gas-Liquid Two-Phase Flow Regimes in Microchannels. In Heat Transfer, Volume 7; ASME Digital Collection: New York, NY, USA, 2002; pp. 527–534. [Google Scholar]
- Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. Influence of Flow Regime on Mass Transfer in Different Types of Microchannels. Ind. Eng. Chem. Res. 2011, 50, 6906–6914. [Google Scholar] [CrossRef]
- Shao, N.; Gavriilidis, A.; Angeli, P. Flow regimes for adiabatic gas–liquid flow in microchannels. Chem. Eng. Sci. 2009, 64, 2749–2761. [Google Scholar] [CrossRef]
- Harirchian, T.; Garimella, S.V. A comprehensive flow regime map for microchannel flow boiling with quantitative transition criteria. Int. J. Heat Mass Transf. 2010, 53, 2694–2702. [Google Scholar] [CrossRef] [Green Version]
- Hassan, I.; Vaillancourt, M.; Pehlivan, K. Two-Phase Flow Regime Transitions in Microchannels: A Comparative Experimental Study. Microscale Thermophys. Eng. 2005, 9, 165–182. [Google Scholar] [CrossRef]
- Akbarinia, A.; Abdolzadeh, M.; Laur, R. Critical investigation of heat transfer enhancement using nanofluids in microchannels with slip and non-slip flow regimes. Appl. Therm. Eng. 2011, 31, 556–565. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, X.; Chénier, E.; Lauriat, G. Thermal boundary conditions for convective heat transfer of dilute gases in slip flow regime. Int. J. Therm. Sci. 2018, 135, 298–301. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, X.; Chénier, E.; Tchekiken, C.; Lauriat, G. Revisited analysis of gas convection and heat transfer in micro channels: Influence of viscous stress power at wall on Nusselt number. Int. J. Therm. Sci. 2018, 134, 565–584. [Google Scholar] [CrossRef] [Green Version]
- Hooman, K.; Li, J.; Dahari, M. Slip flow forced convection through microducts of arbitrary cross-section: Heat and momentum analogy. Int. Commun. Heat Mass Transf. 2016, 71, 176–179. [Google Scholar] [CrossRef]
- Tamayol, A.; Hooman, K. Slip-Flow in Microchannels of Non-Circular Cross Sections. J. Fluids Eng. 2011, 133, 091202. [Google Scholar] [CrossRef]
- Miyazaki, M.; Maeda, H. Microchannel enzyme reactors and their applications for processing. Trends Biotechnol. 2006, 24, 463–470. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Vafai, K. Comparative analysis of jet impingement and microchannel cooling for high heat flux applications. Int. J. Heat Mass Transf. 1999, 42, 1555–1568. [Google Scholar] [CrossRef]
- Nicolas, A.; Barrat, J.-L. A mesoscopic model for the rheology of soft amorphous solids, with application to microchannel flows. Faraday Discuss. 2013, 167, 567–600. [Google Scholar] [CrossRef] [Green Version]
- Zaidani, M.; Hasan, A.; Al-Musharfy, M.; Sassi, M. Numerical investigation of surface wettability on gas—Liquid flow hydrodynamics in microchannel: Application to trickle bed reactors. J. Pet. Sci. Eng. 2019, 184, 106576. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Molana, M.; Rahnama, A.; Ghadami, F. On the nanofluids applications in microchannels: A comprehensive review. Powder Technol. 2018, 332, 287–322. [Google Scholar] [CrossRef]
- Silva, G.; Semiao, V.; Reis, N. Rotating microchannel flow velocity measurements using the stationary micro-PIV technique with application to lab-on-a-CD devices. Flow Meas. Instrum. 2019, 67, 153–165. [Google Scholar] [CrossRef]
- Sarafraz, M.; Arjomandi, M. Demonstration of plausible application of gallium nano-suspension in microchannel solar thermal receiver: Experimental assessment of thermo-hydraulic performance of microchannel. Int. Commun. Heat Mass Transf. 2018, 94, 39–46. [Google Scholar] [CrossRef]
- Amiri-Jaghargh, A.; Niazmand, H.; Renksizbulut, M. Effects of thermal creep on cooling of microflows in short microchannels with constant wall temperature. Int. J. Mod. Phys. C 2012, 23, 1250072. [Google Scholar] [CrossRef]
- Dongari, N.; Zhang, Y.; Reese, J.M. Modeling of Knudsen Layer Effects in Micro/Nanoscale Gas Flows. J. Fluids Eng. 2011, 133, 071101. [Google Scholar] [CrossRef] [Green Version]
- Bushehri, M.R.S.; Ramin, H.; Salimpour, M.R. A new coupling method for slip-flow and conjugate heat transfer in a parallel plate micro heat sink. Int. J. Therm. Sci. 2015, 89, 174–184. [Google Scholar] [CrossRef]
- Kakac, S.; Vasiliev, L.; Bayazitoglu, Y.; Yener, Y. Microscale Heat Transfer-Fundamentals and Applications. In Proceedings of the NATO Advanced Study Institute on Microscale Heat Transfer-Fundamentals and Applications in Biological and Microelectromechanical Systems, Cesme, Izmir, Turkey, 18–30 July 2004. [Google Scholar]
- Sreehari, D.; Sharma, A.K. On thermal performance of serpentine silicon microchannels. Int. J. Therm. Sci. 2019, 146, 106067. [Google Scholar] [CrossRef]
- Zhou, F.; Ling, W.; Zhou, W.; Qiu, Q.; Chu, X. Heat transfer characteristics of Cu-based microchannel heat exchanger fabricated by multi-blade milling process. Int. J. Therm. Sci. 2019, 138, 559–575. [Google Scholar] [CrossRef]
- Pan, M.; Wang, H.; Zhong, Y.; Hu, M.; Zhou, X.; Dong, G.; Huang, P. Experimental investigation of the heat transfer performance of microchannel heat exchangers with fan-shaped cavities. Int. J. Heat Mass Transf. 2019, 134, 1199–1208. [Google Scholar] [CrossRef]
- Redo, M.A.; Jeong, J.; Giannetti, N.; Enoki, K.; Yamaguchi, S.; Saito, K.; Kim, H. Characterization of two-phase flow distribution in microchannel heat exchanger header for air-conditioning system. Exp. Therm. Fluid Sci. 2019, 106, 183–193. [Google Scholar] [CrossRef]
- Sun, X.; Dai, Y.; Ge, T.; Zhao, Y.; Wang, R. Heat and mass transfer comparisons of desiccant coated microchannel and fin-and-tube heat exchangers. Appl. Therm. Eng. 2019, 150, 1159–1167. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, W.; Qiu, Q.; Yu, W.; Chu, X. Investigation of fluid flow and heat transfer characteristics of parallel flow double-layer microchannel heat exchanger. Appl. Therm. Eng. 2018, 137, 616–631. [Google Scholar] [CrossRef]
- Hooman, K. Entropy generation for microscale forced convection: Effects of different thermal boundary conditions, velocity slip, temperature jump, viscous dissipation, and duct geometry. Int. Commun. Heat Mass Transf. 2007, 34, 945–957. [Google Scholar] [CrossRef] [Green Version]
- Hooman, K.; Ejlali, A. Effects of viscous heating, fluid property variation, velocity slip, and temperature jump on convection through parallel plate and circular microchannels. Int. Commun. Heat Mass Transf. 2010, 37, 34–38. [Google Scholar] [CrossRef]
- Hooman, K.; Hooman, F.; Famouri, M. Scaling effects for flow in micro-channels: Variable property, viscous heating, velocity slip, and temperature jump. Int. Commun. Heat Mass Transf. 2009, 36, 192–196. [Google Scholar] [CrossRef]
- Dehkordi, K.S.; Fazilati, M.; Hajatzadeh, A. Surface Scraped Heat Exchanger for cooling Newtonian fluids and enhancing its heat transfer characteristics, a review and a numerical approach. Appl. Therm. Eng. 2015, 87, 56–65. [Google Scholar] [CrossRef]
- Anderson, J.D.; Wendt, J. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Karimipour, A.; Bahrami, D.; Kalbasi, R.; Marjani, A. Diminishing vortex intensity and improving heat transfer by applying magnetic field on an injectable slip microchannel containing FMWNT/water nanofluid. J. Therm. Anal. Calorim. 2020, 144, 2235–2246. [Google Scholar] [CrossRef]
- Maxwell, J.C., VII. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 1879, 170, 231–256. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.-M.; Meng, G.; Wei, X. A review on slip models for gas microflows. Microfluid. Nanofluid. 2012, 13, 845–882. [Google Scholar] [CrossRef]
- Wu, L. A slip model for rarefied gas flows above a moving surface with mass transfer. J. Appl. Phys. 2014, 116, 054503. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Alishahi, M.M.; Emdad, H. New velocity-slip and temperature-jump boundary conditions for Navier–Stokes computation of gas mixture flows in microgeometries. Mech. Res. Commun. 2011, 38, 417–424. [Google Scholar] [CrossRef]
- Mehendale, S.S.; Jacobi, A.; Shah, R.K. Fluid Flow and Heat Transfer at Micro- and Meso-Scales With Application to Heat Exchanger Design. Appl. Mech. Rev. 2000, 53, 175–193. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Grande, W.J. Evolution of Microchannel Flow Passages—Thermohydraulic Performance and Fabrication Technology. Heat Transf. Eng. 2003, 24, 3–17. [Google Scholar] [CrossRef]
- Kalteh, M.; Abbassi, A.; Saffar-Avval, M.; Harting, J. Eulerian–Eulerian two-phase numerical simulation of nanofluid laminar forced convection in a microchannel. Int. J. Heat Fluid Flow 2011, 32, 107–116. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Chen, H.-T.; Wang, Y.-N.; Lin, C.-H.; Fu, L.-M. Capabilities and limitations of 2-dimensional and 3-dimensional numerical methods in modeling the fluid flow in sudden expansion microchannels. Microfluid. Nanofluid. 2006, 3, 13–18. [Google Scholar] [CrossRef]
- Hoang, D.A.; van Steijn, V.; Portela, L.M.; Kreutzer, M.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Shen, C.; Tian, D.B.; Xie, C.; Fan, J. Examination of the LBM in simulation of microchannel flow in transitional regime. Microscale Thermophys. Eng. 2004, 8, 423–432. [Google Scholar] [CrossRef] [Green Version]
- Cai, C.; Boyd, I.D.; Fan, J.; Candler, G.V. Direct Simulation Methods for Low-Speed Microchannel Flows. J. Thermophys. Heat Transf. 2000, 14, 368–378. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, Z. Lattice Poisson–Boltzmann simulations of electro-osmotic flows in microchannels. J. Colloid Interface Sci. 2006, 296, 729–736. [Google Scholar] [CrossRef]
- Kalteh, M.; Abbassi, A.; Saffar-Avval, M.; Frijns, A.J.; Darhuber, A.; Harting, J. Experimental and numerical investigation of nanofluid forced convection inside a wide microchannel heat sink. Appl. Therm. Eng. 2012, 36, 260–268. [Google Scholar] [CrossRef]
- Nance, R.P.; Hash, D.B.; Hassan, H.A. Role of Boundary Conditions in Monte Carlo Simulation of Microelectromechanical Systems. J. Thermophys. Heat Transf. 1998, 12, 447–449. [Google Scholar] [CrossRef]
- Cheng, Y. Numerical simulation of stacked microchannel heat sink with mixing-enhanced passive structure. Int. Commun. Heat Mass Transf. 2007, 34, 295–303. [Google Scholar] [CrossRef]
- Sarrazin, F.; Loubiere, K.; Prat, L.; Gourdon, C.; Bonometti, T.; Magnaudet, J. Experimental and numerical study of droplets hydrodynamics in microchannels. AIChE J. 2006, 52, 4061–4070. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Raisi, A.; Ghasemi, B. Numerical simulation of the magnetic field and Joule heating effects on force convection flow through parallel-plate microchannel in the presence of viscous dissipation effect. Numer. Heat Transf. Part. A Appl. 2019, 76, 499–516. [Google Scholar] [CrossRef]
- Raj, R.; Mathur, N.; Buwa, V.V. Numerical Simulations of Liquid−Liquid Flows in Microchannels. Ind. Eng. Chem. Res. 2010, 49, 10606–10614. [Google Scholar] [CrossRef]
- Mehdizadeh, A.; Sherif, S.; Lear, W. Numerical simulation of thermofluid characteristics of two-phase slug flow in microchannels. Int. J. Heat Mass Transf. 2011, 54, 3457–3465. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A. Numerical simulation of heat transfer and turbulent flow of water nanofluids copper oxide in rectangular microchannel with semi-attached rib. Adv. Mech. Eng. 2016, 8, 1687814016641016. [Google Scholar] [CrossRef] [Green Version]
- Szczukiewicz, S.; Magnini, M.; Thome, J. Proposed models, ongoing experiments, and latest numerical simulations of microchannel two-phase flow boiling. Int. J. Multiph. Flow 2014, 59, 84–101. [Google Scholar] [CrossRef]
- Zhuan, R.; Wang, W. Flow pattern of boiling in micro-channel by numerical simulation. Int. J. Heat Mass Transf. 2011, 55, 1741–1753. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.F.; Haynes, B. On the CFD modelling of Taylor flow in microchannels. Chem. Eng. Sci. 2009, 64, 2941–2950. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Lai, F.-H. Numerical study of flow and heat transfer characteristics of alumina-water nanofluids in a microchannel using the lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2011, 38, 607–614. [Google Scholar] [CrossRef]
- Zhu, L.; Tretheway, D.; Petzold, L.; Meinhart, C. Simulation of fluid slip at 3D hydrophobic microchannel walls by the lattice Boltzmann method. J. Comput. Phys. 2005, 202, 181–195. [Google Scholar] [CrossRef]
- Wang, M.; Li, Z. Gas mixing in microchannels using the direct simulation Monte Carlo method. Int. J. Heat Mass Transf. 2006, 49, 1696–1702. [Google Scholar] [CrossRef]
- Wu, L.; Tsutahara, M.; Kim, L.S.; Ha, M. Three-dimensional lattice Boltzmann simulations of droplet formation in a cross-junction microchannel. Int. J. Multiph. Flow 2008, 34, 852–864. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, R.; Emerson, D.R. Lattice Boltzmann simulation of rarefied gas flows in microchannels. Phys. Rev. E 2005, 71, 047702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afrand, M.; Farahat, S.; Nezhad, A.H.; Sheikhzadeh, G.A.; Sarhaddi, F. Numerical simulation of electrically conducting fluid flow and free convective heat transfer in an annulus on applying a magnetic field. Heat Transf. Res. 2014, 45, 749–766. [Google Scholar] [CrossRef]
- Myong, R.S.; Reese, J.; Barber, R.W.; Emerson, D.R. Velocity slip in microscale cylindrical Couette flow: The Langmuir model. Phys. Fluids 2005, 17, 087105. [Google Scholar] [CrossRef]
- Dongari, N.; Agrawal, A. Analytical solution of gaseous slip flow in long microchannels. Int. J. Heat Mass Transf. 2007, 50, 3411–3421. [Google Scholar] [CrossRef]
- Shen, S.; Chen, G.; Crone, R.M.; Anaya-Dufresne, M. A kinetic-theory based first order slip boundary condition for gas flow. Phys. Fluids 2007, 19, 086101. [Google Scholar] [CrossRef]
- Kundt, A.; Warburg, E., IX. On friction and heat-conduction in rarefied gases. In The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science; Taylor & Francis: London, UK, 1875; Volume 50, pp. 53–62. [Google Scholar]
- Wu, L. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, Z.; Zheng, Y.; Ye, H. Corrected second-order slip boundary condition for fluid flows in nanochannels. Phys. Rev. E 2010, 81, 066303. [Google Scholar] [CrossRef]
- Gibelli, L. Velocity slip coefficients based on the hard-sphere Boltzmann equation. Phys. Fluids 2012, 24, 022001. [Google Scholar] [CrossRef]
- Szalmás, L. Viscous velocity, diffusion and thermal slip coefficients for ternary gas mixtures. Eur. J. Mech.-B Fluids 2015, 53, 264–271. [Google Scholar] [CrossRef]
- Colin, S. Gas Microflows in the Slip Flow Regime: A Review on Heat Transfer. In Proceedings of the ASME 8th International Conference on Nanochannels, Microchannels, and Minichannels: Parts A and B, Montreal, QC, Canada, 1–5 August 2010; pp. 383–396. [Google Scholar]
- Colin, S. Gas Microflows in the Slip Flow Regime: A Critical Review on Convective Heat Transfer. J. Heat Transf. 2011, 134, 020908. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Succi, S. Analytical calculation of slip flow in lattice Boltzmann models with kinetic boundary conditions. Phys. Fluids 2005, 17, 093602. [Google Scholar] [CrossRef]
- Qi, H.; Liang, A.; Jiang, H.; Chong, X.; Wang, Y. Effect of Pipe Surface Wettability on Flow Slip Property. Ind. Eng. Chem. Res. 2018, 57, 12543–12550. [Google Scholar] [CrossRef]
- Nikkhah, Z.; Karimipour, A.; Safaei, M.R.; Forghani-Tehrani, P.; Goodarzi, M.; Dahari, M.; Wongwises, S. Forced convective heat transfer of water/functionalized multi-walled carbon nanotube nanofluids in a microchannel with oscillating heat flux and slip boundary condition. Int. Commun. Heat Mass Transf. 2015, 68, 69–77. [Google Scholar] [CrossRef]
- Nguyen, Q.; Bahrami, D.; Kalbasi, R.; Bach, Q. Nanofluid flow through microchannel with a triangular corrugated wall: Heat transfer enhancement against entropy generation intensification. Math. Methods Appl. Sci. 2020. Early view. [Google Scholar] [CrossRef]
- Niu, J.; Fu, C.; Tan, W. Slip-Flow and Heat Transfer of a Non-Newtonian Nanofluid in a Microtube. PLoS ONE 2012, 7, e37274. [Google Scholar] [CrossRef] [Green Version]
- Bahrami, D.; Abbasian-Naghneh, S.; Karimipour, A.; Karimipour, A. Efficacy of injectable rib height on the heat transfer and entropy generation in the microchannel by affecting slip flow. Math. Methods Appl. Sci. 2020. Early view. [Google Scholar] [CrossRef]
- Cercignani, C.; Daneri, A. Flow of a Rarefied Gas between Two Parallel Plates. J. Appl. Phys. 1963, 34, 3509–3513. [Google Scholar] [CrossRef]
- Xue, H.; Fan, Q. A high Order Modification on the Analytic Solution of 2-D Microchannel Gaseous Flows; ASME Fluids Engineering Division: New York, NY, USA, 2000; Volume 253, pp. 711–716. [Google Scholar]
- Pan, L.S.; Liu, G.R.; Lam, K.Y. Determination of slip coefficient for rarefied gas flows using direct simulation Monte Carlo. J. Micromech. Microeng. 1999, 9, 89–96. [Google Scholar] [CrossRef]
- Karniadakis, G.; Beskok, A.; Gad-El-Hak, M. Micro Flows: Fundamentals and Simulation. Appl. Mech. Rev. 2002, 55, B76. [Google Scholar] [CrossRef]
- Zohar, Y.; Lee, S.Y.K.; Lee, W.Y.; Jiang, L.; Tong, P. Subsonic gas flow in a straight and uniform microchannel. J. Fluid Mech. 2002, 472, 125–151. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Yang, I.-H. Friction Numbers and Viscous Dissipation Heating for Laminar Flows of Water in Microtubes. J. Heat Transf. 2008, 130, 082405. [Google Scholar] [CrossRef]
- Celata, G.; Cumo, M.; McPhail, S.J.; Zummo, G. Characterization of fluid dynamic behaviour and channel wall effects in microtube. Int. J. Heat Fluid Flow 2006, 27, 135–143. [Google Scholar] [CrossRef]
- Karimipour, A.; Afrand, M.; Akbari, M.; Safaei, M. Simulation of fluid flow and heat transfer in the inclined enclosure. Int. J. Mech. Aerosp. Eng. 2012, 6, 86–91. [Google Scholar]
- Goodarzi, M.; Safaei, M.R.; Karimipour, A.; Hooman, K.; Dahari, M.; Kazi, S.N.; Sadeghinezhad, E. Comparison of the Finite Volume and Lattice Boltzmann Methods for Solving Natural Convection Heat Transfer Problems inside Cavities and Enclosures. Abstr. Appl. Anal. 2014, 2014, 762184. [Google Scholar] [CrossRef]
- Bird, G.A.; Brady, J. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press Oxford: Oxford, UK, 1994. [Google Scholar]
- D’Orazio, A.; Karimipour, A.; Nezhad, A.H.; Shirani, E. Mixed convection in inclined lid driven cavity by Lattice Boltzmann Method and heat flux boundary condition. J. Phys. Conf. Ser. 2014, 547, 012031. [Google Scholar] [CrossRef] [Green Version]
- Karimipour, A.; Nezhad, A.H.; D’Orazio, A.; Shirani, E. The effects of inclination angle and Prandtl number on the mixed convection in the inclined lid driven cavity using lattice Boltzmann method. J. Theor. Appl. Mech. 2013, 51, 447–462. [Google Scholar]
- Karimipour, A.; Nezhad, A.H.; D’Orazio, A.; Shirani, E. Investigation of the gravity effects on the mixed convection heat transfer in a microchannel using lattice Boltzmann method. Int. J. Therm. Sci. 2012, 54, 142–152. [Google Scholar] [CrossRef]
- Khazaeli, R.; Mortazavi, S.; Ashrafizaadeh, M. Application of a ghost fluid approach for a thermal lattice Boltzmann method. J. Comput. Phys. 2013, 250, 126–140. [Google Scholar] [CrossRef]
- Khazaeli, R.; Mortazavi, S.; Ashrafizaadeh, M. Isfahan University of Technology A Ghost Fluid Approach for Thermal Lattice Boltzmann Method in Dealing with Heat Flux Boundary Condition in Thermal Problems with Complex Geometries. J. Appl. Fluid Mech. 2015, 8, 439–452. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Abbassi, A. Heat transfer and fluid flow in microchannels and nanochannels at high Knudsen number using thermal lattice-Boltzmann method. Phys. Rev. E 2010, 82, 026307. [Google Scholar] [CrossRef]
- Wang, C.H.; Yang, R. A numerical study for slip flow heat transfer. Appl. Math. Comput. 2006, 173, 1246–1264. [Google Scholar] [CrossRef]
- Tian, Z.-W.; Zou, C.; Liu, H.-J.; Guo, Z.-L.; Liu, Z.-H.; Zheng, C.-G. Lattice Boltzmann scheme for simulating thermal micro-flow. Phys. A Stat. Mech. Appl. 2007, 385, 59–68. [Google Scholar] [CrossRef]
- Riaud, A.; Wang, K.; Luo, G. A combined Lattice-Boltzmann method for the simulation of two-phase flows in microchannel. Chem. Eng. Sci. 2013, 99, 238–249. [Google Scholar] [CrossRef]
- Alizadeh, A.; Zhang, L.; Wang, M. Mixing enhancement of low-Reynolds electro-osmotic flows in microchannels with temperature-patterned walls. J. Colloid Interface Sci. 2014, 431, 50–63. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Chen, C.-L. Analysis of electroosmotic flow with periodic electric and pressure fields via the lattice Poisson–Boltzmann method. Appl. Math. Model. 2013, 37, 2816–2829. [Google Scholar] [CrossRef]
- Nie, X.; Doolen, G.D.; Chen, S. Lattice-Boltzmann Simulations of Fluid Flows in MEMS. J. Stat. Phys. 2002, 107, 279–289. [Google Scholar] [CrossRef]
- Tang, G.H.; Tao, W.Q.; He, Y.L. Lattice Boltzmann method for gaseous microflows using kinetic theory boundary conditions. Phys. Fluids 2005, 17, 058101. [Google Scholar] [CrossRef]
- Shirani, E.; Jafari, S. Application of LBM in simulation of flow in simple micro-geometries and micro porous media. Afr. Rev. Phys. 2007, 1, 3. [Google Scholar]
- Perumal, D.A.; Krishna, V.; Sarvesh, G.; Dass, A.K. Numerical Simulation of Gaseous Microflows by Lattice Boltzmann Method. Int. J. Prod. Ind. Eng. 2011, 2, 11. [Google Scholar]
- Cheraghian, G. A new thermal method concept for IOR from oil reservoir using optimized in-situ combustion. In 78th EA-GE Conference and Exhibition; European Association of Geoscientists & Engineers: Houten, the Netherlands, 2016; Volume 1, pp. 1–3. [Google Scholar]
- Prasianakis, N.; Ansumali, S. Microflow Simulations via the Lattice Boltzmann Method. Commun. Comput. Phys. 2011, 9, 1128–1136. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Chen, L.; Kang, Q.; Rahman, S.S. The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: A review. Int. J. Heat Mass Transf. 2016, 95, 94–108. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.; Lin, C.-L. Rarefaction and compressibility effects of the lattice-Boltzmann-equation method in a gas microchannel. Phys. Rev. E 2005, 71, 046706. [Google Scholar] [CrossRef]
- Wang, D.; Summers, J.L.; Gaskell, P.H. Modelling of electrokinetically driven mixing flow in microchannels with patterned blocks. Comput. Math. Appl. 2008, 55, 1601–1610. [Google Scholar] [CrossRef] [Green Version]
- Zhao-Li, G.; Chu-Guang, Z.; Bao-Chang, S. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 2002, 11, 366–374. [Google Scholar] [CrossRef]
- Chen, S.; Martínez, D.; Mei, R. On boundary conditions in lattice Boltzmann methods. Phys. Fluids 1996, 8, 2527–2536. [Google Scholar] [CrossRef]
- Reis, T.; Dellar, P.J. Moment-Based Formulation of Navier–Maxwell Slip Boundary Conditions for Lattice Boltzmann Simulations of Rarefied Flows in Microchannels; University of Oxford: Oxford, UK, 2012. [Google Scholar]
- Jeong, N. Lattice Boltzmann approach for the simulation of rarefied gas flow in the slip flow regime. J. Mech. Sci. Technol. 2013, 27, 1753–1761. [Google Scholar] [CrossRef]
- D’Orazio, A.; Nikkhah, Z.; Karimipour, A. Simulation of copper–water nanofluid in a microchannel in slip flow regime using the lattice Boltzmann method with heat flux boundary condition. J. Phys. Conf. Ser. 2015, 655, 012029. [Google Scholar] [CrossRef]
- Liu, X.; Guo, Z. A lattice Boltzmann study of gas flows in a long micro-channel. Comput. Math. Appl. 2013, 65, 186–193. [Google Scholar] [CrossRef]
- Agrawal, A.; Djenidi, L. Simulation of gas flow in microchannels with a single 90 bend. Comput. Fluids 2009, 38, 1629–1637. [Google Scholar] [CrossRef]
- Li, Z.-X.; Du, D.; Guo, Z.-Y. Characteristics of frictional resistance for gas flow in microtubes. In Proceedings of the Symposium on Energy Engineering in the 21st Century, Copenhagen, Denmark, 21–24 June 1999; pp. 658–664. [Google Scholar]
- Colin, S. Rarefaction and compressibility effects on steady and transient gas flows in microchannels. Microfluid. Nanofluid. 2004, 1, 268–279. [Google Scholar] [CrossRef]
- Languri, E.M.; Hooman, K. Slip flow forced convection in a microchannel with semi-circular cross-section. Int. Commun. Heat Mass Transf. 2011, 38, 139–143. [Google Scholar] [CrossRef]
- White, C.; Borg, M.K.; Scanlon, T.J.; Reese, J. A DSMC investigation of gas flows in micro-channels with bends. Comput. Fluids 2013, 71, 261–271. [Google Scholar] [CrossRef] [Green Version]
- Rohlf, K. Compressible slip flow through constricted cylinders with density-dependent viscosity. Dynam. Cont. Dis. Ser. B 2018, 25, 233–257. [Google Scholar]
- Pai, S.-I. Magnetogasdynamics and Plasma Dynamics; Springer: Berlin/Heidelberg, Germany, 1962. [Google Scholar]
- Varela, S.; Rivas, A.; Vernet, A.; Pallarès, J. Experimental Study of the Deposition of Magnetic Particles on the Walls of Microchannels. Micromachines 2021, 12, 712. [Google Scholar] [CrossRef]
- Shen, S.; Wang, X.; Niu, Y. Multi-Vortex Regulation for Efficient Fluid and Particle Manipulation in Ultra-Low Aspect Ratio Curved Microchannels. Micromachines 2021, 12, 758. [Google Scholar] [CrossRef]
- Guan, H.; Huang, S.; Ding, J.; Tian, F.; Xu, Q.; Zhao, J. Chemical environment and magnetic moment effects on point defect formations in CoCrNi-based concentrated solid-solution alloys. Acta Mater. 2020, 187, 122–134. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Safaei, M.R.; Goodarzi, M.; Dahari, M. Particle size and type effects on heat transfer enhancement of Ferro-nanofluids in a pulsating heat pipe. Powder Technol. 2016, 301, 1218–1226. [Google Scholar] [CrossRef]
- Weng, H.C.; Chen, D.C. Magnetogasdynamic flow and heat transfer in a microchannel with isothermally heated walls. Int. J. Heat Mass Transf. 2013, 57, 16–21. [Google Scholar] [CrossRef]
- Weng, C.-I.; Li, W.-L.; Hwang, C.-C. Gaseous flow in microtubes at arbitrary Knudsen numbers. Nanotechnology 1999, 10, 373–379. [Google Scholar] [CrossRef]
- Zhou, S.; Shu, B.; Yu, Z.; Huang, Y.; Zhang, Y. Experimental Study and Mechanism Analysis of the Flow Boiling and Heat Transfer Characteristics in Microchannels with Different Surface Wettability. Micromachines 2021, 12, 881. [Google Scholar] [CrossRef]
- Thaweskulchai, T.; Schulte, A. A Low-Cost 3-in-1 3D Printer as a Tool for the Fabrication of Flow-Through Channels of Microfluidic Systems. Micromachines 2021, 12, 947. [Google Scholar] [CrossRef]
- Elsafy, K.M.; Saghir, M.Z. Forced Convection in Wavy Microchannels Porous Media Using TiO2 and Al2O3–Cu Nanoparticles in Water Base Fluids: Numerical Results. Micromachines 2021, 12, 654. [Google Scholar] [CrossRef]
- Cravero, C.; Leutcha, P.; Marsano, D. CFD Modelling of Regenerative Pre-heating Systems for Recycled Glass Raw Material. Tec. Ital. J. Eng. Sci. 2019, 63, 189–197. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kandlikar, S.G. Numerical simulation of growth of a vapor bubble during flow boiling of water in a microchannel. Microfluid. Nanofluid. 2005, 1, 137–145. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kandlikar, S.; Edel, Z. Numerical study of bubble growth and wall heat transfer during flow boiling in a microchannel. Int. J. Heat Mass Transf. 2011, 54, 3702–3718. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Nucleation characteristics and stability considerations during flow boiling in microchannels. Exp. Therm. Fluid Sci. 2006, 30, 441–447. [Google Scholar] [CrossRef]
- Lee, P.C.; Tseng, F.-G.; Pan, C. Bubble dynamics in microchannels. Part I: Single microchannel. Int. J. Heat Mass Transf. 2004, 47, 5575–5589. [Google Scholar] [CrossRef]
- Cornwell, K.; Kew, P.A. Boiling in Small Parallel Channels. In Energy Efficiency in Process Technology; Springer Science and Business: Berlin/Heidelberg, Germany, 1993; pp. 624–638. [Google Scholar]
- Yu, Z.; Hemminger, O.; Fan, L.-S. Experiment and lattice Boltzmann simulation of two-phase gas–liquid flows in microchannels. Chem. Eng. Sci. 2007, 62, 7172–7183. [Google Scholar] [CrossRef]
- Gheitaghy, A.M.; Saffari, H.; Mohebbi, M. Investigation pool boiling heat transfer in U-shaped mesochannel with electrodeposited porous coating. Exp. Therm. Fluid Sci. 2016, 76, 87–97. [Google Scholar] [CrossRef]
- Young, N.O.; Goldstein, J.S.; Block, M.J. The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 1959, 6, 350. [Google Scholar] [CrossRef]
- Richter, M.; Woias, P.; Wei, D. Microchannels for applications in liquid dosing and flow-rate measurement. Sens. Actuators A Phys. 1997, 62, 480–483. [Google Scholar] [CrossRef]
- Cal, K. How does the type of vehicle influence the in vitro skin absorption and elimination kinetics of terpenes? Arch. Dermatol. Res. 2005, 297, 311–315. [Google Scholar] [CrossRef]
- Burns, M.A.; Johnson, B.N.; Brahmasandra, S.N.; Handique, K.; Webster, J.R.; Krishnan, M.; Sammarco, T.S.; Man, P.M.; Jones, D.; Heldsinger, D.; et al. An Integrated Nanoliter DNA Analysis Device. Science 1998, 282, 484–487. [Google Scholar] [CrossRef] [Green Version]
- Losey, M.; Jackman, R.; Firebaugh, S.; Schmidt, M.; Jensen, K. Design and fabrication of microfluidic devices for multiphase mixing and reaction. J. Microelectromech. Syst. 2002, 11, 709–717. [Google Scholar] [CrossRef]
- Abrishamkar, A.; Rane, A.; Elvira, K.; Wootton, R.; Sainio, T.; deMello, A. A COMSOL Multiphysics® Model of Droplet Formation at a Flow Focusing Device. In Proceedings of the COMSOL Conference, Rotterdam, The Netherlands, 23–25 October 2013. [Google Scholar]
- Chandorkar, A.; Palit, S. Simulation of droplet dynamics and mixing in microfluidic devices using a VOF-based method. Sens. Transducers J. 2009, 7, 136–149. [Google Scholar]
- Azarmanesh, M.; Farhadi, M. The effect of weak-inertia on droplet formation phenomena in T-junction microchannel. Meccanica 2016, 51, 819–834. [Google Scholar] [CrossRef]
- Gong, S.; Cheng, P.; Quan, X. Lattice Boltzmann simulation of droplet formation in microchannels under an electric field. Int. J. Heat Mass Transf. 2010, 53, 5863–5870. [Google Scholar] [CrossRef]
- Qiu, D.; Silva, L.; Tonkovich, A.L.; Arora, R. Micro-droplet formation in non-Newtonian fluid in a microchannel. Microfluid. Nanofluid. 2010, 8, 531–548. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.; Jin, Y.; Cheng, Y. LBM simulation of droplet formation in micro-channels. Chem. Eng. J. 2011, 173, 828–836. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lee, W.; Son, G. Numerical study of droplet breakup and merging in a microfluidic channel. J. Mech. Sci. Technol. 2013, 27, 1693–1699. [Google Scholar] [CrossRef]
- Conchouso, D.; Rawashdeh, E.; Castro, D.; Arevalo, A.; Foulds, I. Optimized Channel Geometry of a Flow-Focusing Droplet Generator for Parallelization. In Proceedings of the 2013 COMSOL Conference, Rotterdam, The Netherlands, 23–25 October 2013. [Google Scholar]
- Afkhami, S.; Leshansky, A.; Renardy, Y. Numerical investigation of elongated drops in a microfluidic T-junction. Phys. Fluids 2011, 23, 022002. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Pello, A.C. Micropower generation using combustion: Issues and approaches. Proc. Combust. Inst. 2002, 29, 883–899. [Google Scholar] [CrossRef] [Green Version]
- Vican, J.; Gajdeczko, B.; Dryer, F.; Milius, D.; Aksay, I.; Yetter, R. Development of a microreactor as a thermal source for microelectromechanical systems power generation. Proc. Combust. Inst. 2002, 29, 909–916. [Google Scholar] [CrossRef]
- Milius, D.; Vartuli, J.; Aksay, I.A.; Gajdeczko, B.; Vican, J.; Dryer, F.; Yetter, R.A. Development of a microreactor as a thermal source for MEMS power generation. In Proceedings of the Chemical and Physical Processes in Combustion, Fall Technical Meeting, The Eastern States Section, Charlottesville, VA, USA, 21–24 October 2007. [Google Scholar]
- Duan, X.; Xu, Z.; Sun, X.; Deng, B.; Liu, J. Effects of injection timing and EGR on combustion and emissions characteristics of the diesel engine fuelled with acetone–butanol–ethanol/diesel blend fuels. Energy 2021, 231, 121069. [Google Scholar] [CrossRef]
- Norton, D.; Vlachos, D. Combustion characteristics and flame stability at the microscale: A CFD study of premixed methane/air mixtures. Chem. Eng. Sci. 2003, 58, 4871–4882. [Google Scholar] [CrossRef]
- Norton, D.; Vlachos, D. A CFD study of propane/air microflame stability. Combust. Flame 2004, 138, 97–107. [Google Scholar] [CrossRef]
- Lee, K.; Kwon, O. A numerical study on structure of premixed methane–air microflames for micropower generation. Chem. Eng. Sci. 2007, 62, 3710–3719. [Google Scholar] [CrossRef]
- Zarvandi, J.; Tabejamaat, S.; Baigmohammadi, M. Numerical study of the effects of heat transfer methods on CH4/(CH4+H2)-AIR pre-mixed flames in a micro-stepped tube. Energy 2012, 44, 396–409. [Google Scholar] [CrossRef]
- Fan, A.; Wan, J.; Maruta, K.; Yao, H.; Liu, W. Interactions between heat transfer, flow field and flame stabilization in a micro-combustor with a bluff body. Int. J. Heat Mass Transf. 2013, 66, 72–79. [Google Scholar] [CrossRef]
- Pizza, G.; Frouzakis, C.E.; Mantzaras, J.; Tomboulides, A.G.; Boulouchos, K. Dynamics of premixed hydrogen/air flames in microchannels. Combust. Flame 2008, 152, 433–450. [Google Scholar] [CrossRef]
- Cheraghian, G.; Masoud, A. "Nanotechnology for drilling operations.". In Emerging Nanotechnologies for Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2021; pp. 135–148. [Google Scholar] [CrossRef]
- Pizza, G.; Frouzakis, C.E.; Mantzaras, J.; Tomboulides, A.G.; Boulouchos, K. Three-dimensional simulations of premixed hydrogen/air flames in microtubes. J. Fluid Mech. 2010, 658, 463–491. [Google Scholar] [CrossRef] [Green Version]
- Tang, A.; Xu, Y.; Pan, J.; Yang, W.; Jiang, D.; Lu, Q. Combustion characteristics and performance evaluation of premixed methane/air with hydrogen addition in a micro-planar combustor. Chem. Eng. Sci. 2015, 131, 235–242. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A.; Maruta, K.; Yao, H.; Liu, W. Experimental and numerical investigation on combustion characteristics of premixed hydrogen/air flame in a micro-combustor with a bluff body. Int. J. Hydrogen Energy 2012, 37, 19190–19197. [Google Scholar] [CrossRef]
- Bagheri, G.; Hosseini, S.E.; Wahid, M.A. Effects of bluff body shape on the flame stability in premixed micro-combustion of hydrogen–air mixture. Appl. Therm. Eng. 2014, 67, 266–272. [Google Scholar] [CrossRef]
- Kuo, C.; Ronney, P. Numerical modeling of non-adiabatic heat-recirculating combustors. Proc. Combust. Inst. 2007, 31, 3277–3284. [Google Scholar] [CrossRef]
- Nguyen, N. Micromixers: Fundamentals, Design and Fabrication; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Zeraatkar, M.; de Tullio, M.; Percoco, G. Fused Filament Fabrication (FFF) for Manufacturing of Microfluidic Micromixers: An Experimental Study on the Effect of Process Variables in Printed Microfluidic Micromixers. Micromachines 2021, 12, 858. [Google Scholar] [CrossRef] [PubMed]
- Varmazyar, M.; Habibi, M.; Amini, M.; Pordanjani, A.H.; Afrand, M.; Vahedi, S.M. Numerical simulation of magnetic nanoparticle-based drug delivery in presence of atherosclerotic plaques and under the effects of magnetic field. Powder Technol. 2020, 366, 164–174. [Google Scholar] [CrossRef]
- EPaul, L.; Atiemo-Obeng, V.A.; Kresta, S.M. Handbook of Industrial Mixing: Science and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Nguyen, N.-T.; Wu, Z. Micromixers—A review. J. Micromech. Microeng. 2004, 15, R1. [Google Scholar] [CrossRef]
- Kanaris, A.G.; Stogiannis, I.A.; Mouza, A.A.; Kandlikar, S.G. Comparing the Mixing Performance of Common Types of Chaotic Micromixers: A Numerical Study. Heat Transf. Eng. 2015, 36, 1122–1131. [Google Scholar] [CrossRef]
- Afzal, A.; Kim, K.-Y. Passive split and recombination micromixer with convergent–divergent walls. Chem. Eng. J. 2012, 203, 182–192. [Google Scholar] [CrossRef]
- Wang, L.; Wu, W.; Li, X. Numerical and experimental investigation of mixing characteristics in the constructal tree-shaped microchannel. Int. J. Heat Mass Transf. 2013, 67, 1014–1023. [Google Scholar] [CrossRef]
- Solehati, N.; Bae, J.; Sasmito, A.P. Numerical investigation of mixing performance in microchannel T-junction with wavy structure. Comput. Fluids 2014, 96, 10–19. [Google Scholar] [CrossRef]
- Chen, J.M.; Horng, T.-L.; Tan, W.Y. Analysis and measurements of mixing in pressure-driven microchannel flow. Microfluid. Nanofluid. 2006, 2, 455–469. [Google Scholar] [CrossRef]
- Song, H.; Wang, Y.; Pant, K. Cross-stream diffusion under pressure-driven flow in microchannels with arbitrary aspect ratios: A phase diagram study using a three-dimensional analytical model. Microfluid. Nanofluid. 2012, 12, 265–277. [Google Scholar] [CrossRef] [Green Version]
- Miranda, J.; Oliveira, H.; Teixeira, J.; Vicente, A.; Correia, J.; Minas, G. Numerical study of micromixing combining alternate flow and obstacles. Int. Commun. Heat Mass Transf. 2010, 37, 581–586. [Google Scholar] [CrossRef] [Green Version]
- Afzal, A.; Kim, K.-Y. Flow and mixing analysis of non-Newtonian fluids in straight and serpentine microchannels. Chem. Eng. Sci. 2014, 116, 263–274. [Google Scholar] [CrossRef]
- Alam, A.; Afzal, A.; Kim, K.-Y. Mixing performance of a planar micromixer with circular obstructions in a curved microchannel. Chem. Eng. Res. Des. 2014, 92, 423–434. [Google Scholar] [CrossRef]
- Bahrami, D.; Nadooshan, A.A.; Bayareh, M. Numerical study on the effect of planar normal and Halbach magnet arrays on micromixing. Int. J. Chem. React. Eng. 2020, 18, 20200080. [Google Scholar] [CrossRef]
- Sadegh-Cheri, M.; Latifi, H.; Moghaddam, M.S.; Shahraki, H. Simulation and experimental investigation of planar micromixers with short-mixing-length. Chem. Eng. J. 2013, 234, 247–255. [Google Scholar] [CrossRef]
- Daghighi, Y.; Li, D. Numerical study of a novel induced-charge electrokinetic micro-mixer. Anal. Chim. Acta 2013, 763, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Sun, C.-P.; Fields, M.; Li, Y.; Haake, D.; Churchill, B.M.; Ho, C.-M. An unsteady microfluidic T-form mixer perturbed by hydrodynamic pressure. J. Micromech. Microeng. 2008, 18, 045015. [Google Scholar] [CrossRef] [PubMed]
- Minakov, A.; Rudyak, V.; Dekterev, A.; Gavrilov, A. Investigation of slip boundary conditions in the T-shaped microchannel. Int. J. Heat Fluid Flow 2013, 43, 161–169. [Google Scholar] [CrossRef]
- Hashim, U.; Diyana, P.N.A.; Adam, T. Numerical simulation of Microfluidic devices. In Proceedings of the 10th IEEE International Conference on Semiconductor Electronics (ICSE), Kuala Lumpur, Malaysia, 19–21 September 2012; pp. 26–29. [Google Scholar]
- Wang, C.; Hu, Y. Mixing of liquids using obstacles in y-type microchannels. Tamkang J. Sci. Eng. 2010, 13, 385–394. [Google Scholar]
- Ameri, M.; Behbahaninia, A.; Tanha, A.A. Thermodynamic analysis of a tri-generation system based on micro-gas turbine with a steam ejector refrigeration system. Energy 2010, 35, 2203–2209. [Google Scholar] [CrossRef]
- Ehyaei, M.; Bahadori, M. Selection of micro turbines to meet electrical and thermal energy needs of residential buildings in Iran. Energy Build. 2007, 39, 1227–1234. [Google Scholar] [CrossRef]
- Ehyaei, M.; Mozafari, A. Energy, economic and environmental (3E) analysis of a micro gas turbine employed for on-site combined heat and power production. Energy Build. 2010, 42, 259–264. [Google Scholar] [CrossRef]
- Ameli, S.; Agnew, B.; Potts, I. Integrated distributed energy evaluation software (IDEAS): Simulation of a micro-turbine based CHP system. Appl. Therm. Eng. 2007, 27, 2161–2165. [Google Scholar] [CrossRef]
- Chatterjee, D.; Amiroudine, S. Lattice Boltzmann simulation of thermofluidic transport phenomena in a DC magnetohydrodynamic (MHD) micropump. Biomed. Microdevices 2010, 13, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Khozeymeh-Nezhad, H.; Niazmand, H. LBM simulation of fluid flow in a viscous micropump with non-circular rotors and RSM approach for multiple response optimization. Int. J. Heat Fluid Flow 2018, 71, 392–405. [Google Scholar] [CrossRef]
- Ho, J.-E. Characteristic study of MHD pump with channel in rectangular ducts. J. Mar. Sci. Technol. 2007, 15, 6. [Google Scholar] [CrossRef]
- Kiyasatfar, M.; Pourmahmoud, N.; Golzan, M.; Mirzaee, I. Investigation of thermal behavior and fluid motion in direct current magnetohydrodynamic pumps. Therm. Sci. 2014, 18, 551–562. [Google Scholar] [CrossRef]
- Ito, K.; Takahashi, T.; Fujino, T.; Ishikawa, M. Influences of Channel Size and Operating Conditions on Fluid Behavior in a MHD Micro Pump for Micro Total Analysis System. J. Int. Counc. Electr. Eng. 2014, 4, 220–226. [Google Scholar] [CrossRef] [Green Version]





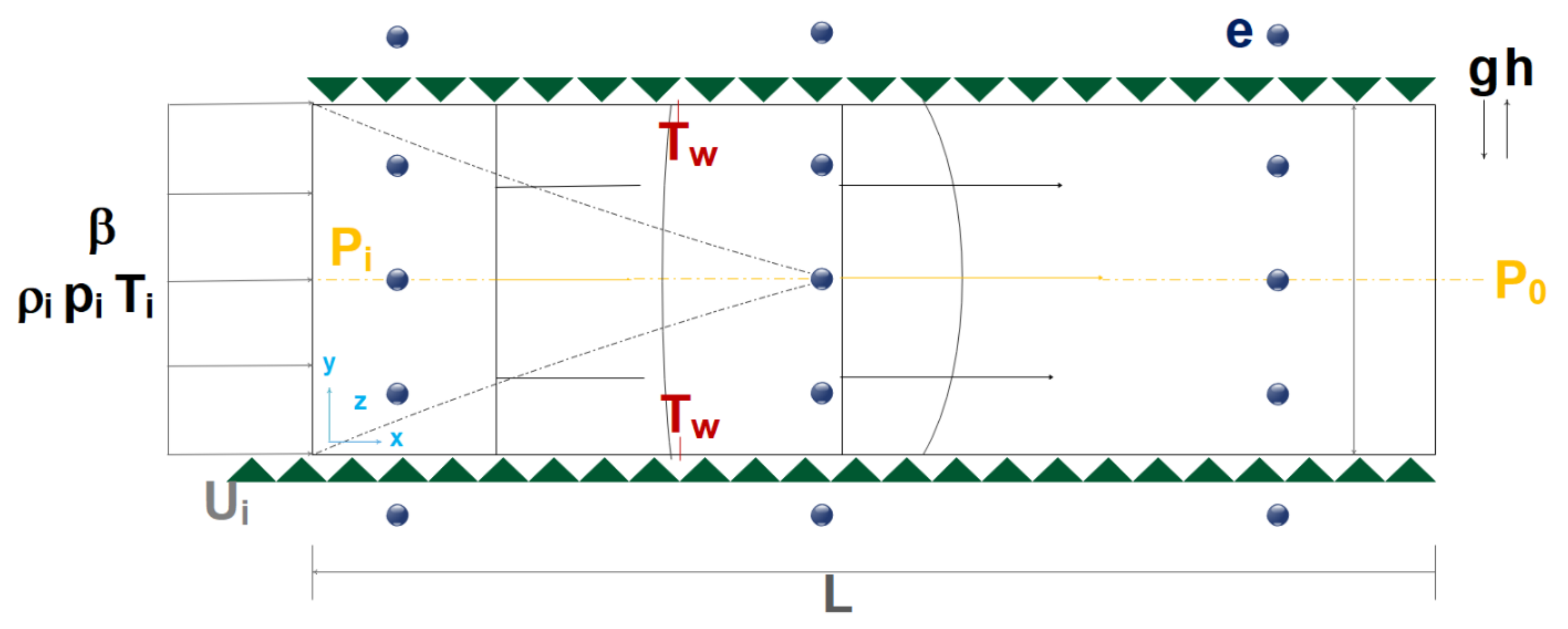



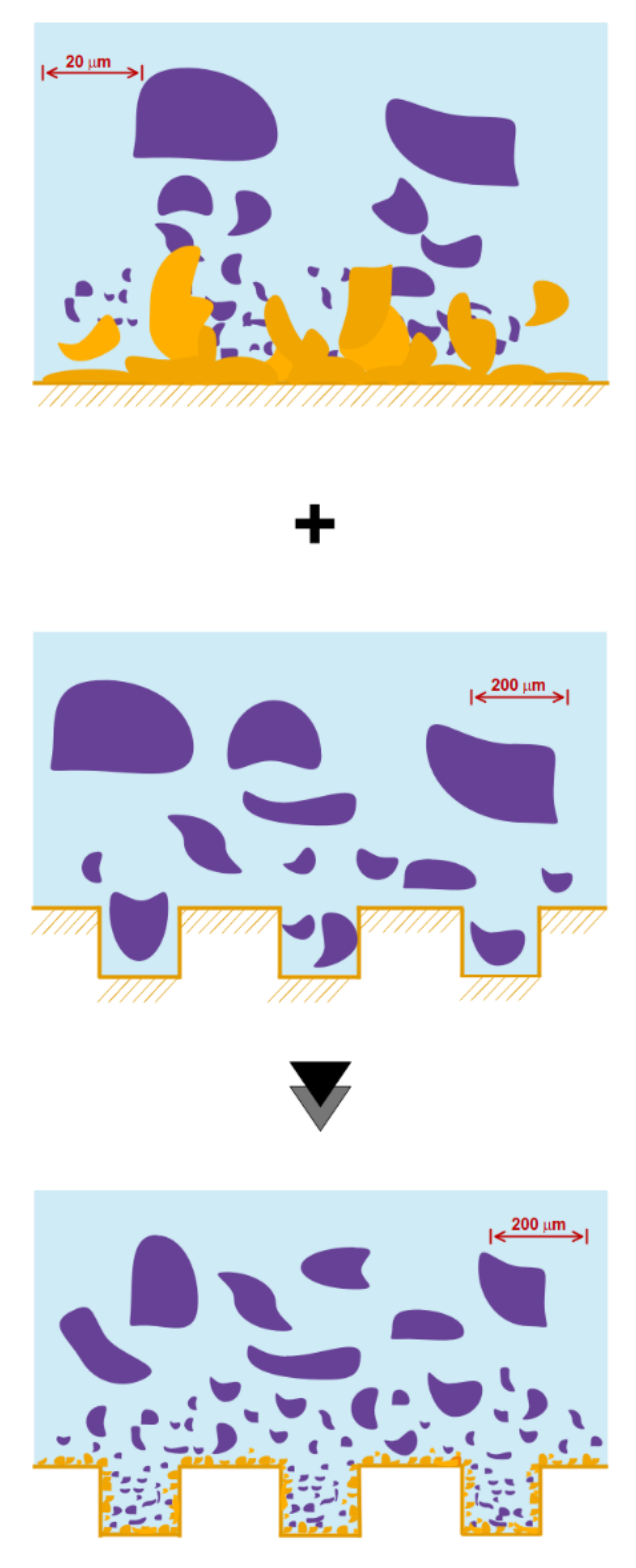
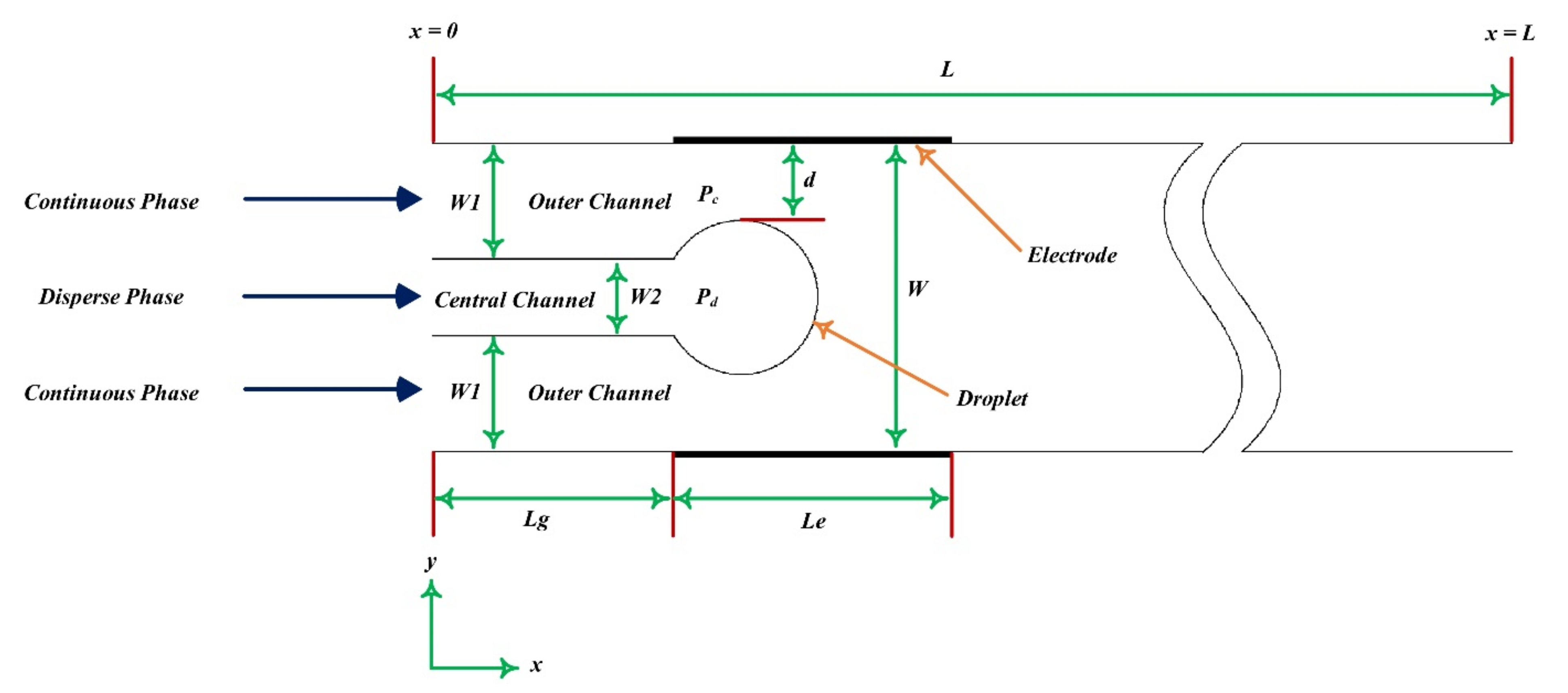

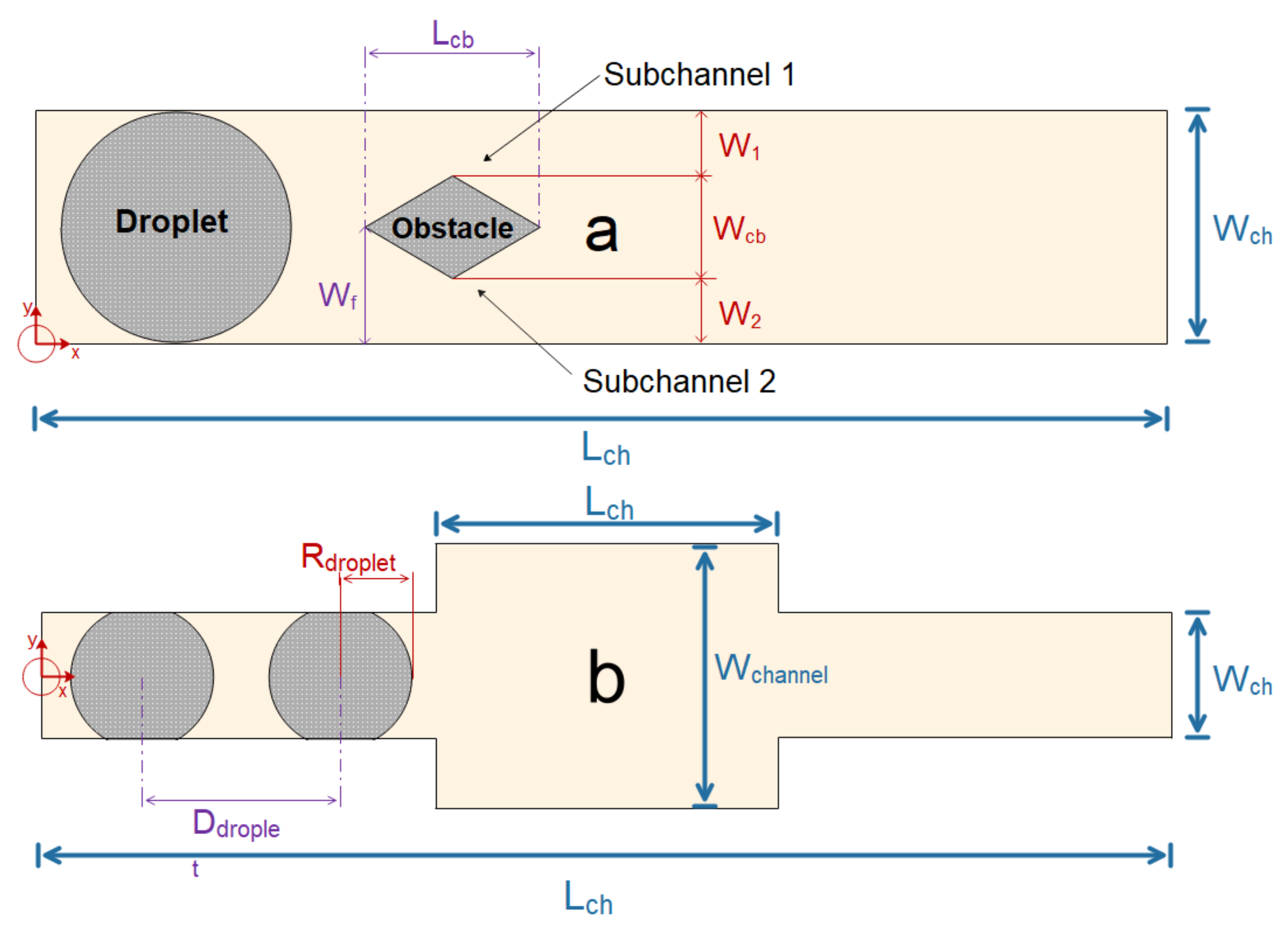



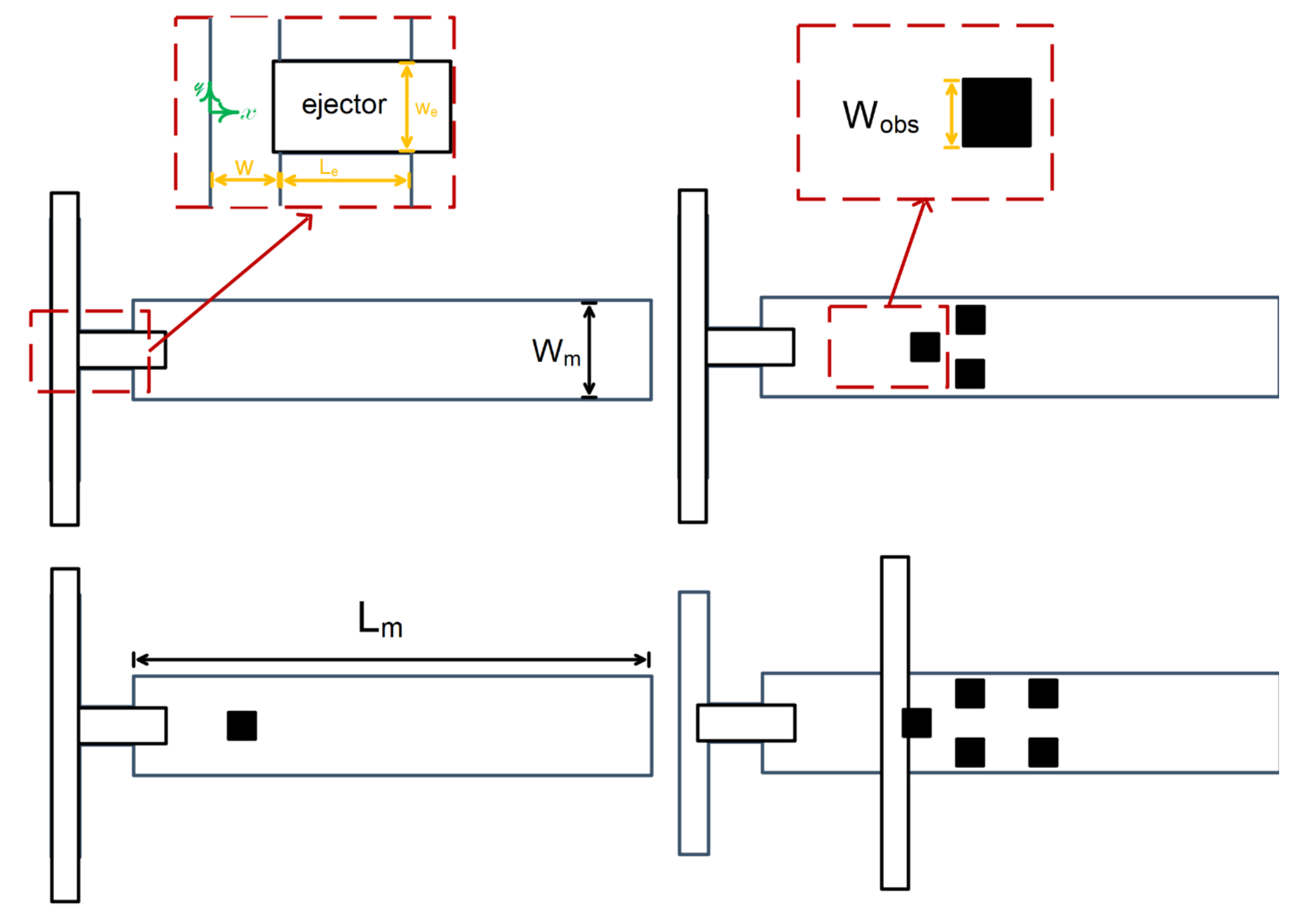
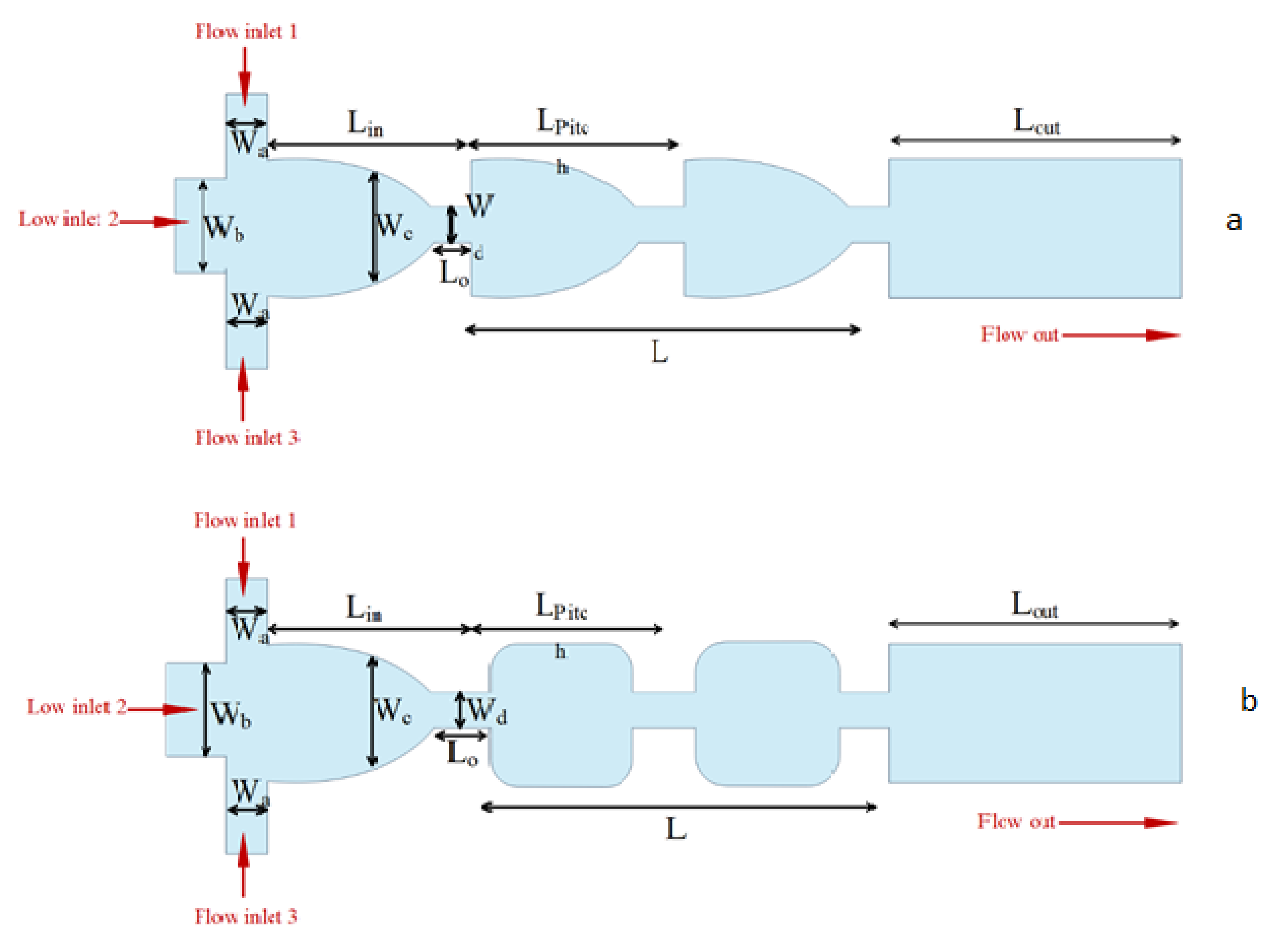

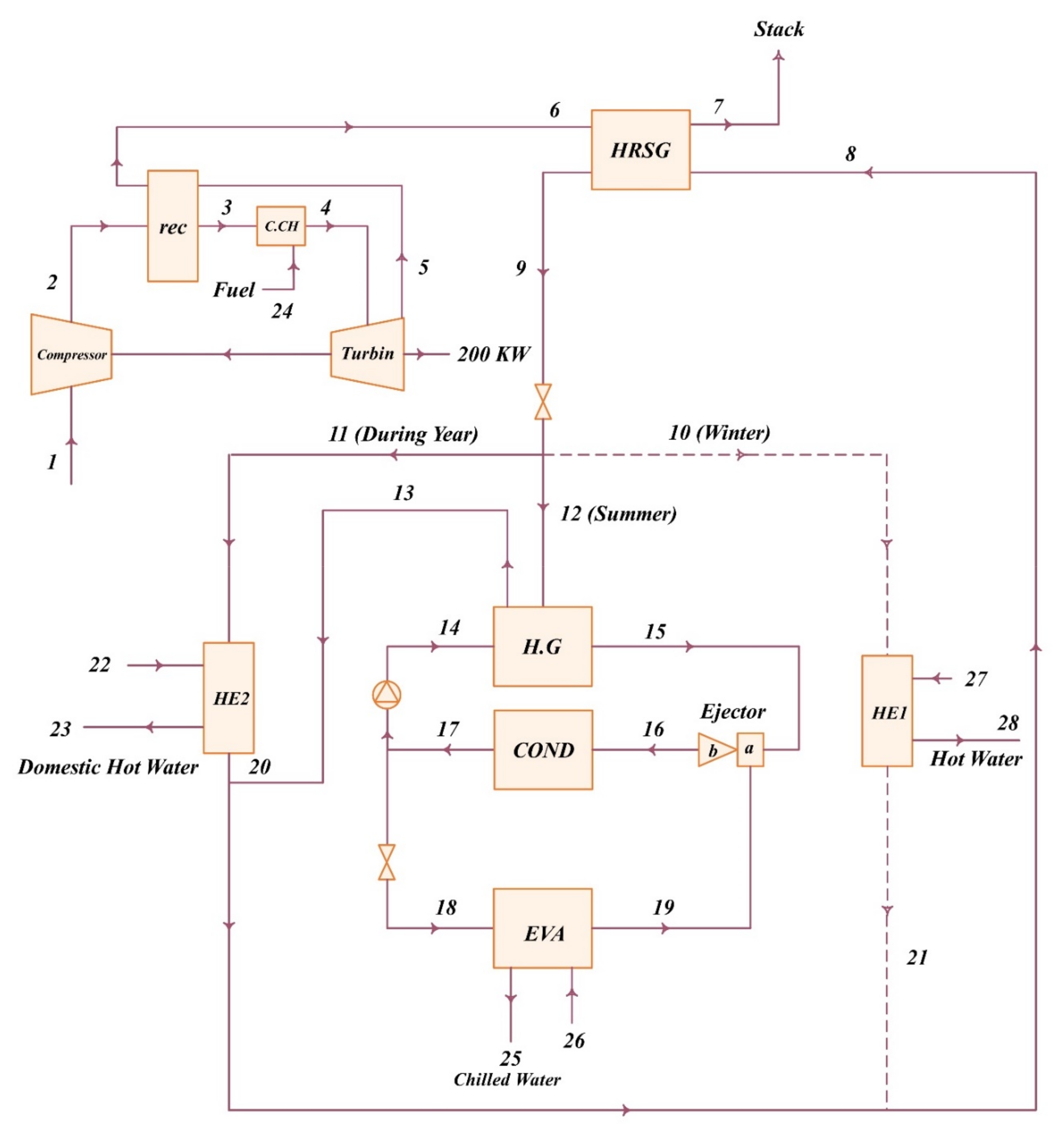
| Research Method | Methods and Type of Paper | Device | Ref |
|---|---|---|---|
| Numerical CFD simulation | Multi-phase flow (VOF) | Microchannel heat exchangers | Panda et al. [53] |
| Numerical 3D CFD simulations | Multi-phase flow (VOF) | Straight and spiral microchannel | Chatterjee et al. [54] |
| Numerical Lattice Boltzmann method | Multi-phase lattice Boltzmann method | Impingement on a rigid square obstacle in a microchannel | Bakhshan et al. [55] |
| Numerical 3D CFD simulations | Multi-phase flow (VOF) | Falling film microchannel | Chen et al. [56] |
| Experimental | Multi-phase blood flow | Microchannel | Lima et al. [57] |
| Numerical methods Experimental Application | Review | Microfluidic systems | Sattari et al. [58] |
| Experimental | Multi-phase flow Liquid/liquid microfluidic flows | Coaxial micro-device | Dinh and Cubaud [59] |
| Numerical 3D CFD simulations | Multi-phase transesterification reaction Multi-phase flow (VOF) | Microchannel reactor | Laziz et al. [60] |
| Mixing and mass transfer Two-phase micro-flow Bubble/droplet formation | Review | Two-phase flow and mass transfer in microchannels | Yao et al. [48] |
| Numerical simulations Droplet’s formation behavior | OpenFOAM InterFOAM solver using the VOF | Micro-T-junction channel | Guimarães et al. [61] |
| Conventional Channels | |
|---|---|
| Mini channels | |
| Microchannel | |
| Transition channels | |
| Molecular nanochannels |
| Channel Dimensions | ||||
|---|---|---|---|---|
| Continuum Flow | Slip Flow | Transition Flow | Free Molecular Flow | Gas |
| >67 | 0.67–67 | 0.0067–0.67 | >0.0067 | Air |
| >194 | 1.94–194 | 0.0194–1.94 | >0.0194 | Helium |
| >123 | 1.23–123 | 0.0123–1.23 | >0.0123 | Hydrogen |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abidi, A.; Ahmadi, A.; Enayati, M.; Sajadi, S.M.; Yarmand, H.; Ahmed, A.; Cheraghian, G. A Review of the Methods of Modeling Multi-Phase Flows within Different Microchannels Shapes and Their Applications. Micromachines 2021, 12, 1113. https://doi.org/10.3390/mi12091113
Abidi A, Ahmadi A, Enayati M, Sajadi SM, Yarmand H, Ahmed A, Cheraghian G. A Review of the Methods of Modeling Multi-Phase Flows within Different Microchannels Shapes and Their Applications. Micromachines. 2021; 12(9):1113. https://doi.org/10.3390/mi12091113
Chicago/Turabian StyleAbidi, Awatef, Amir Ahmadi, Mojtaba Enayati, S. Mohammad Sajadi, Hooman Yarmand, Arslan Ahmed, and Goshtasp Cheraghian. 2021. "A Review of the Methods of Modeling Multi-Phase Flows within Different Microchannels Shapes and Their Applications" Micromachines 12, no. 9: 1113. https://doi.org/10.3390/mi12091113
APA StyleAbidi, A., Ahmadi, A., Enayati, M., Sajadi, S. M., Yarmand, H., Ahmed, A., & Cheraghian, G. (2021). A Review of the Methods of Modeling Multi-Phase Flows within Different Microchannels Shapes and Their Applications. Micromachines, 12(9), 1113. https://doi.org/10.3390/mi12091113








