Real-Time Built-In Self-Test of MEMS Gyroscope Based on Quadrature Error Signal
Abstract
:1. Introduction
2. Principle of the Online BIST of the MEMS Gyroscope
2.1. The Quadrature Error Signal of the Gyroscope
2.2. The BIST Based on Quadrature Error
- The parameter φs is determined by the circuit. Any change in the phase value will have an effect on the gyroscope’s bias, scale factor, and quadrature error;
- The parameter Ks is determined by the circuit and the structure. Any change of this parameter will affect the gyroscope’s bias, scale factor, and quadrature error at the same time;
- If the gyroscope fails after a strong impact or vibration, at this time, the parameters my, Ax, ωd, bxy, and kxy will all change. The bias, scale factor, and quadrature signal amplitude will deviate from the initial value;
- If the mass of the gyroscope changes slightly after strong impact or vibration, the gyroscope can still work. At this time, the parameter my has changed. This will cause the structure’s modal stiffness kx and ky, coupling stiffness kxy, driving frequency ωd, and driving amplitude Ax to change. The gyroscope’s bias, scale factor, and quadrature signal amplitude will all change accordingly;
- If the damping of the gyroscope changes slightly after the impact or vibration, the damping coupling coefficient bxy will change slightly. The bias and quadrature signal amplitude will change accordingly;
- If the stiffness of the gyroscope changes slightly after a strong impact or vibration, that is, kx and ky change, the coupling stiffness kxy, drive frequency ωd, and drive amplitude Ax will change. The gyroscope’s bias, scale factor, and quadrature signal amplitude will all change accordingly.
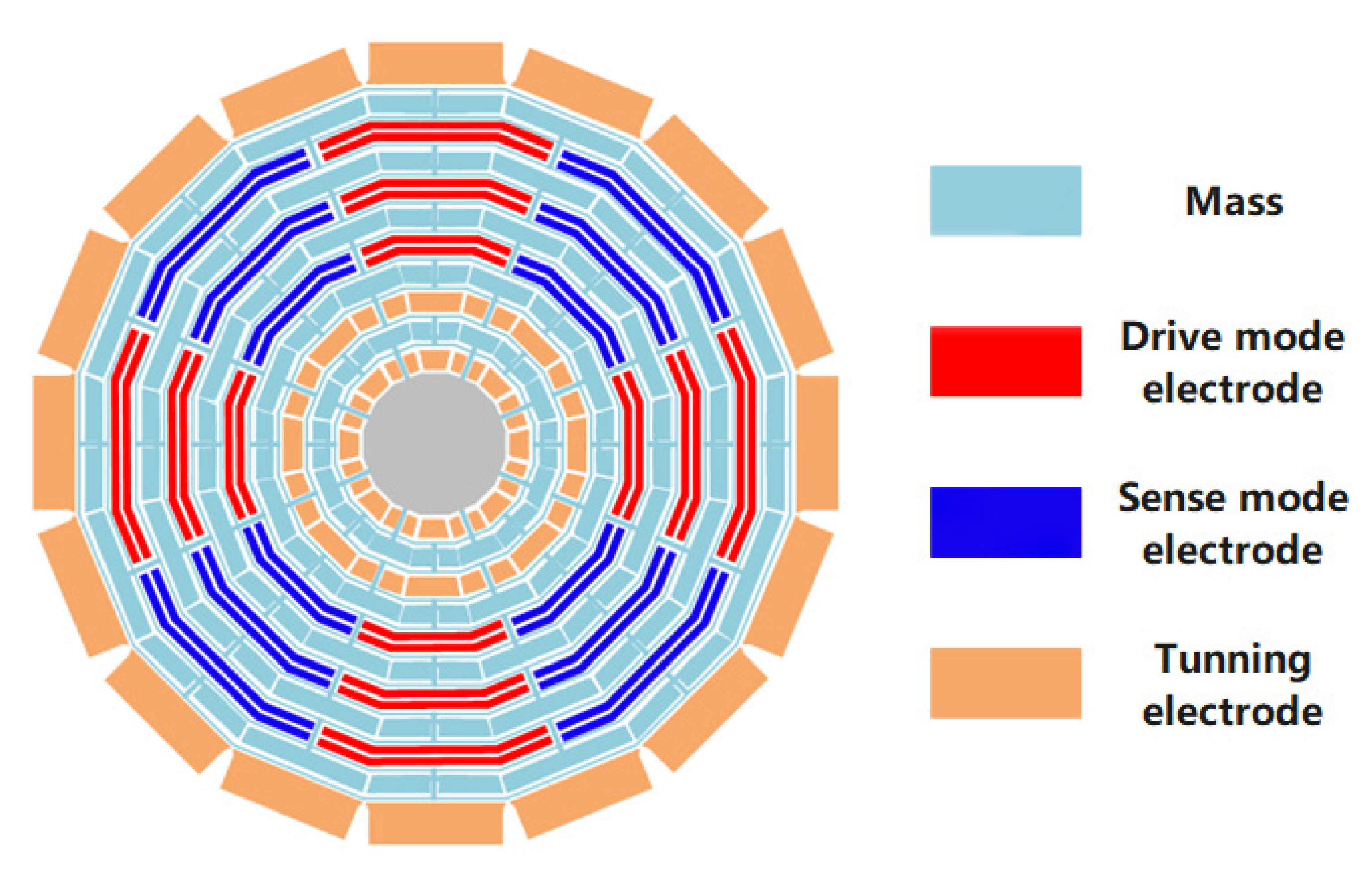
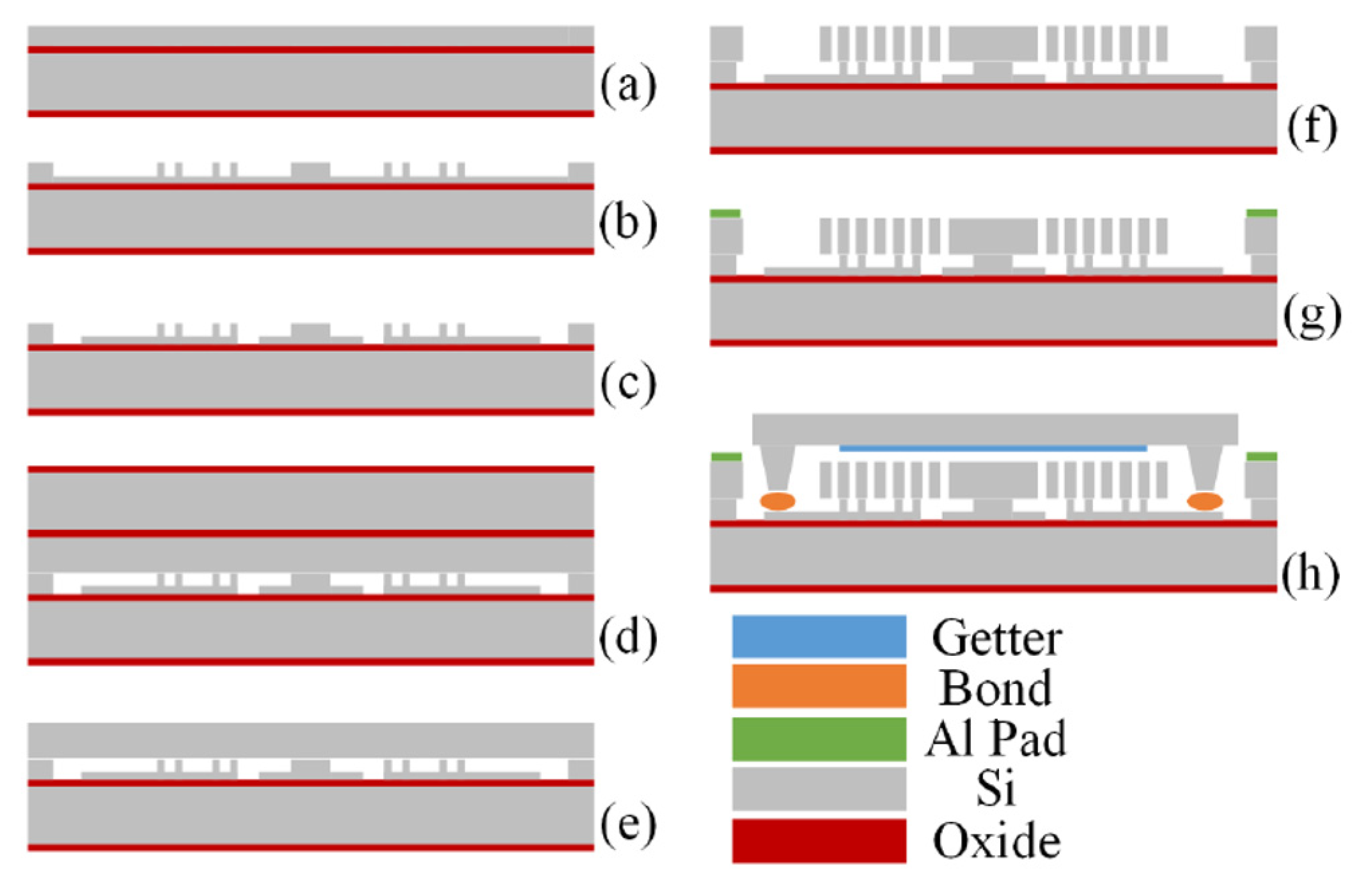
3. MEMS Gyroscope Design and Fabrication
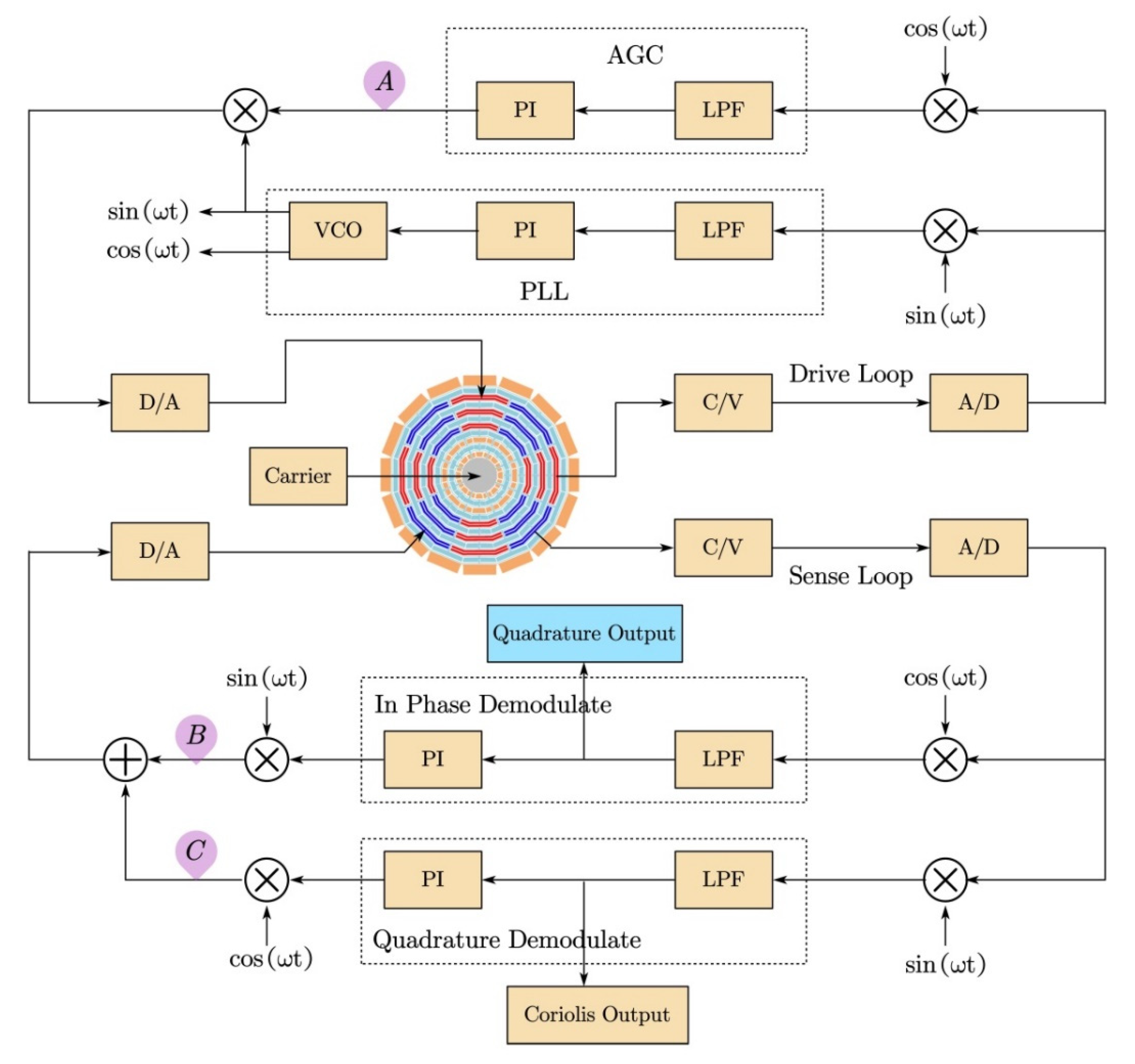
4. BIST Design Based on Force-to-Balance Control Loop Architecture
- (a)
- The MEMS block: Both the Coriolis signal and quadrature signal were affected by the MEMS structure. If the MEMS structure malfunctioned, both the Coriolis signal and quadrature signal would change significantly. It was not likely that the Coriolis signal would change significantly, but the quadrature signal changed slightly;
- (b)
- All of the drive loop blocks: any drive loop blocks’ malfunction would change both the Coriolis signal and quadrature signal significantly;
- (c)
- The C/V, A/D, and D/A blocks of the sense loop: these circuit modules had no selectivity for the Coriolis signal and the quadrature signal, and the influence on the Coriolis signal and the quadrature signal was exactly the same;
- (d)
- The Coriolis signal and quadrature signal control blocks, which contained the demodulators, lowpass filters, PI controllers, and modulators: Since the Coriolis signal and the quadrature signal were separated by quadrature demodulation under low-phase-error conditions, PI controllers for each signal were performed separately. Therefore, if the Coriolis signal control part failed, it would cause serious changes in the Coriolis signal but very weak changes in the quadrature signal. The self-test method that we proposed would be invalid. However, this is a very rare situation, as most MEMS sensor failures are due to the MEMS structure, not the circuit. We could design the circuit self-test function module to realize the detection of this part of the circuit, or redundantly design this function module to reduce the possibility of failure.
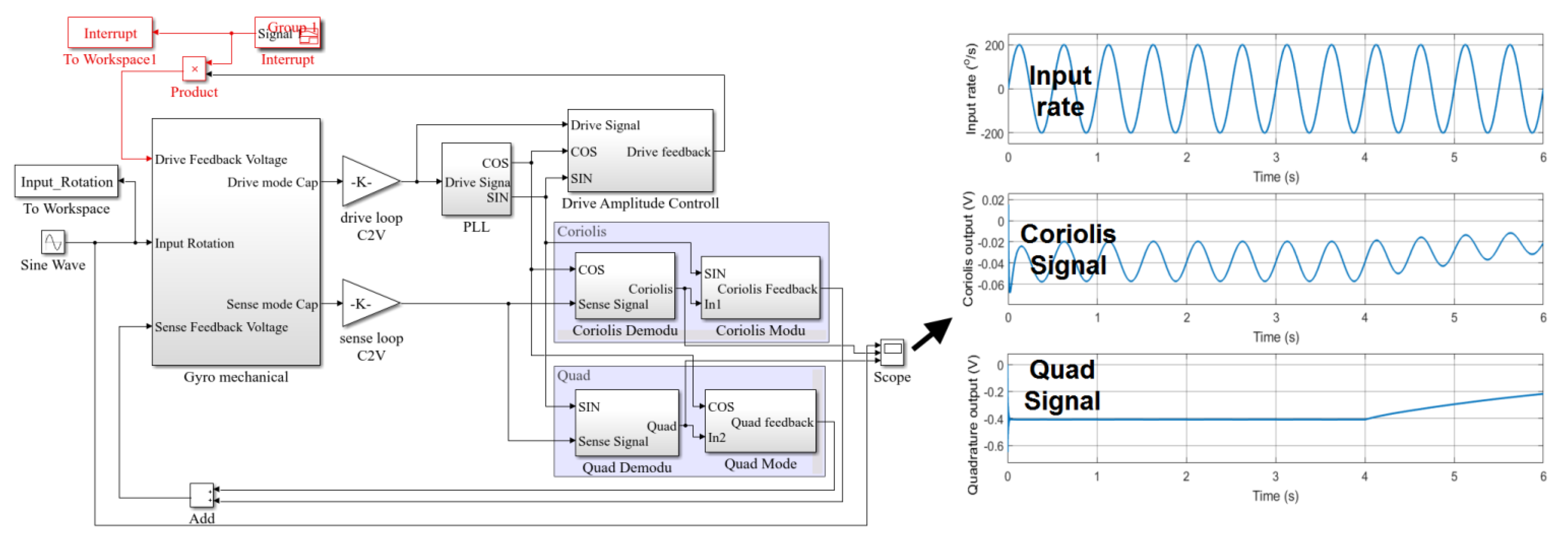
5. BIST Simulation of the MEMS Gyroscope
6. The BIST Experiment
6.1. The Electric Malfunction Imitated Test
- Scenario A: The value of point A was set to zero. Once the AGC output of the drive loop was zero, the gyroscope structure did no resonate. The drive loop of the gyroscope malfunctioned. The output value of the Coriolis signal and the quadrature signal were almost zero, which shifted from the correct ones;
- Scenario B: The value of point B was set to zero. In this scenario, the quadrature control loop changed from a closed loop to an open loop. Due to the small phase error, the quadrature feedback signal would not be coupled to the Coriolis signal through the demodulation signal process. Ideally, the Coriolis signal would not change. However, in the real situation, because the quadrature feedback signal was zero, the structure’s quadrature error was not effectively suppressed. The original closed loop of the Coriolis signal became unstable. The true Coriolis signal was subsumed in the error signal. The gyroscope output had no linear relationship with the input angular velocity;
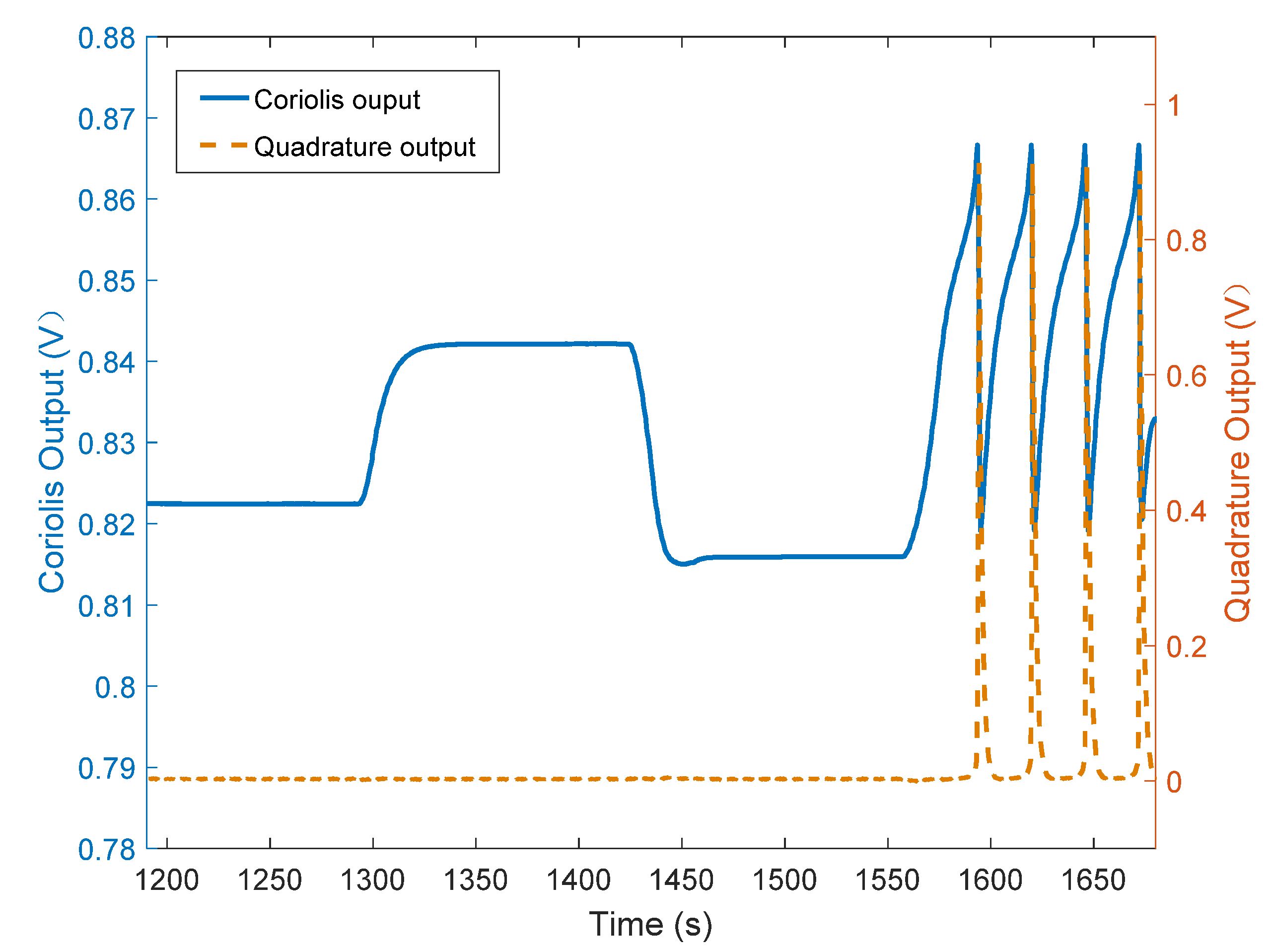
- Scenario C: The value of point C was set to zero. In this scenario, the Coriolis control loop changed from a closed loop to an open loop. Due to the small phase error, the Coriolis feedback signal would not be coupled to the quadrature signal through the demodulation signal process. The gyroscope output had a linear relationship with the input angular velocity, but the gyroscope bias and the output of the quadrature signal shifted from the normal ones. During this experiment, it was found that the Coriolis output signal became unstable when input angular velocity reached −100°/s, as shown in Figure 10.
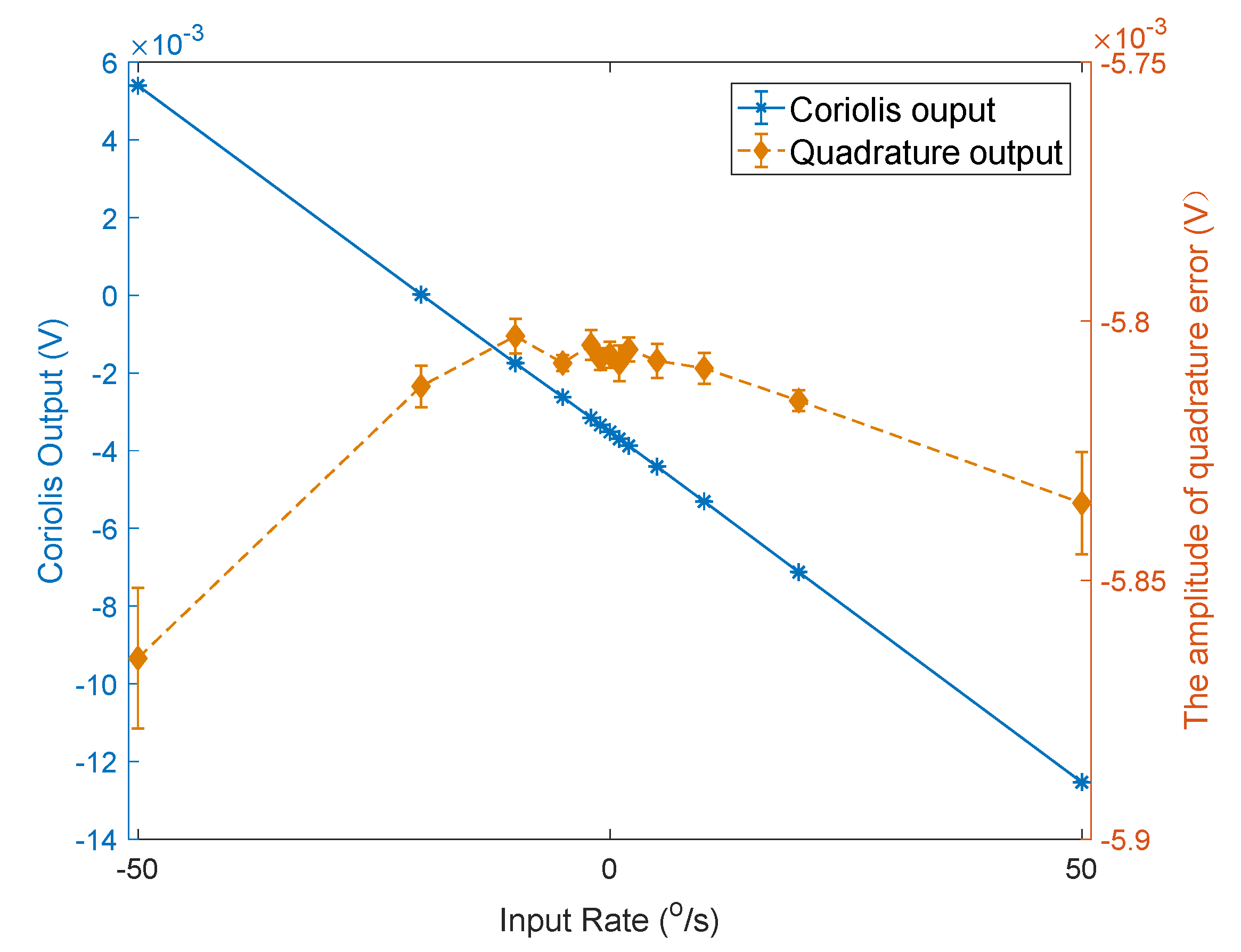
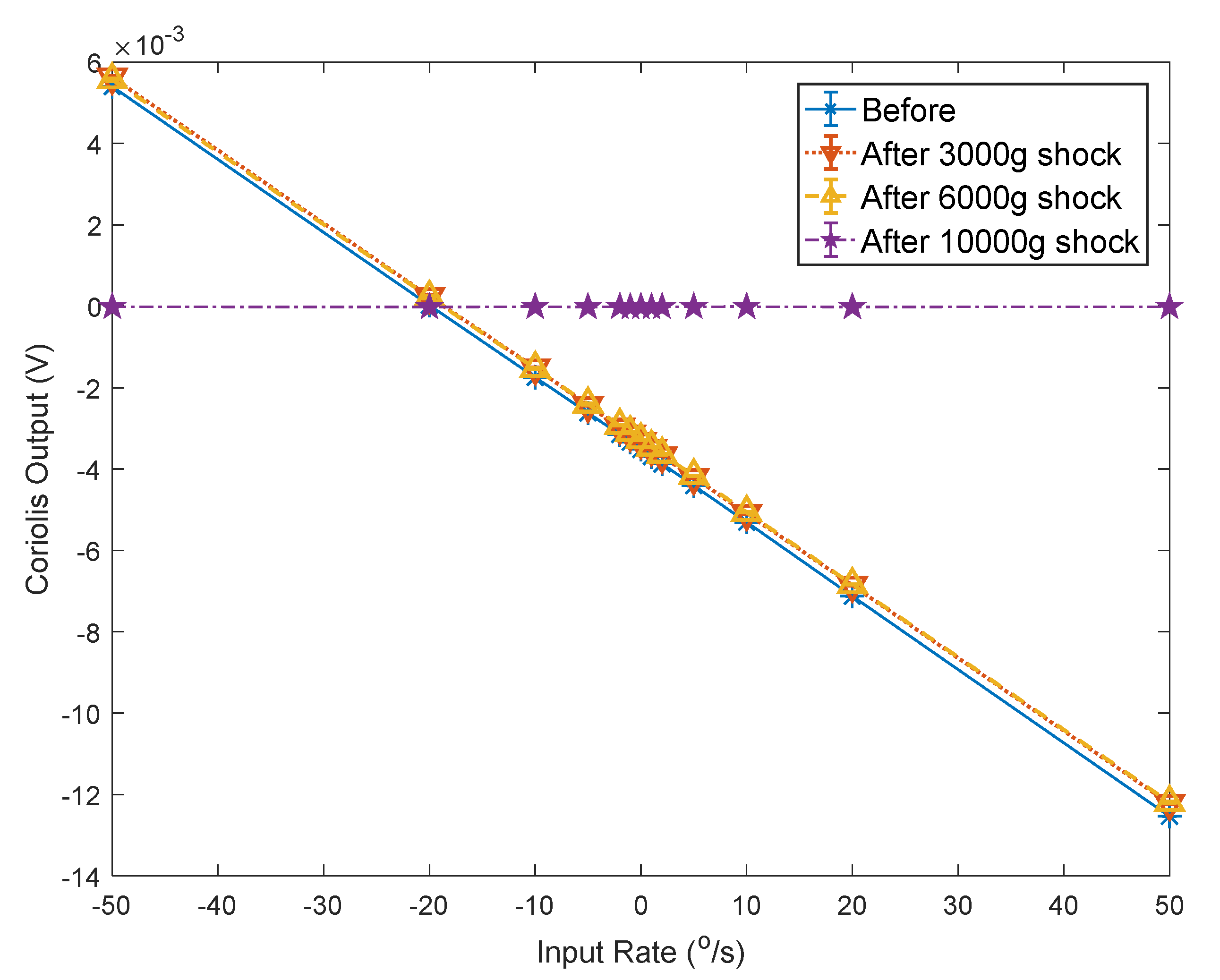
6.2. The Mechanical Shock Test
7. Discussion
8. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Norr, R.M.; Shkel, A.M. Dynamically amplified dual-mass gyroscopes with in-situ shock survival mechanism. In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems, Hiroshima, Japan, 23–26 March 2020. [Google Scholar]
- Cameron, C.P.; Imamura, T.; Devmalya, C.; Vukasin, G.; Alter, A.; Kenny, T. Design comparison and survivability of epitaxially encapsulated MEMS disc resonating gyroscopes at high shock (>27,000 g). In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems, Hiroshima, Japan, 23–26 March 2020. [Google Scholar]
- Zhou, J.; Jiang, T.; Jiao, J.; Wu, M. Design and fabrication of a micromachined gyroscope with high shock resistance. Microsyst. Technol. 2014, 20, 137–144. [Google Scholar] [CrossRef]
- Schofiled, A.R.; Trusov, A.A.; Shkel, A.M. Multi-degree of freedom tuning fork gyroscope demonstrating shock rejection. In Proceedings of the 2007 IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007. [Google Scholar]
- Yoon, S.; Park, U.; Rhim, J.; Yang, S.S. Tactical grade MEMS vibrating ring gyroscope with high shock reliability. Microelectron. Eng. 2015, 142, 22–29. [Google Scholar] [CrossRef]
- Florida, A.V.; Gupta, P.K.; Macy, D.F.; Morris, H.D. Rotation Rate Sensor with Built in Test Circuit. U.S. Patent 5,426,970, 27 June 1995. [Google Scholar]
- Anac, O.; Seeger, J. Gyroscope Self Test by Applying Rotation on Coriolis Sense Mass. U.S. Patent 2013/0233048A1, 12 September 2013. [Google Scholar]
- ADIS16080 Datasheet. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/ADIS16080 (accessed on 22 June 2021).
- Balachandran, G.K.; Petkov, V.P.; Mayer, T.; Balslink, T. A 3-axis gyroscope for electronic stability control with continuous self-test. IEEE J. Solid-State Circuits 2016, 51, 177–186. [Google Scholar]
- Mirzaei, M.; Hosseini, I.; Ghaffari, V. MEMS gyroscope fault detection and elimination for an underwater robot using the combination of smooth switching and dynamic redundancy method. Microelectron. Reliab. 2020, 109, 113677. [Google Scholar] [CrossRef]
- Hantos, G.; Flynn, D.; Desmulliez, M.P.Y. Built-In Self-Test (BIST) methods for MEMS: A review. Micromachines 2021, 12, 40. [Google Scholar] [CrossRef]
- Mir, S.; Rufer, L.; Dhayni, A. Built-in-self-test techniques for MEMS. Microelectron. J. 2006, 37, 1591–1597. [Google Scholar] [CrossRef]
- Deb, N.; Blanton, R.D. Built-in self test of CMOS-MEMS accelerometers. In Proceedings of the ITC International Test Conference, Baltimore, MD, USA, 10 December 2002. [Google Scholar]
- Deb, N.; Blanton, R.D. Built-in self-test of MEMS accelerometers. J. Microelectromech. Syst. 2006, 15, 52–68. [Google Scholar] [CrossRef]
- Chen, D.; Liu, X.; Yin, L.; Wang, Y.; Shi, Z.; Zhang, G. A ΣΔ closed-loop interface for a MEMS accelerometer with digital built-in self-test function. Micromachines 2018, 9, 444. [Google Scholar] [CrossRef] [Green Version]
- de Bruyker, D.; Cozma, A.; Puers, R. A combined piezoresistive/capacitive pressure sensor with self-test function based on thermal actuation. Proc. Solid State Sens. Actuators 1997, 2, 1461–1464. [Google Scholar]
- Lapadatu, A.C.; De Bruyker, D.; Jakobsen, H.; Puers, R. A new concept for a self-testable pressure sensor based on the bimetal effect. Sens. Actuators A Phys. 2000, 82, 69–73. [Google Scholar] [CrossRef]
- Xu, P.; Wei, Z.; Guo, Z.; Jia, L.; Han, G.; Si, C.; Ning, J.; Yang, F. A real-time circuit phase delay correction system for MEMS vibratory gyroscopes. Micromachines 2021, 12, 506. [Google Scholar] [CrossRef]
- Walther, A.; le Blanc, C.; Delorme, N.; Deimerly, Y.; Anciant, R.; Willemin, J. Bias contributions in a MEMS tuning fork gyroscope. J. Microelectromech. Syst. 2013, 22, 303–308. [Google Scholar] [CrossRef]
- Jia, J.; Ding, X.; Gao, Y.; Li, H. Automatic frequency tuning technology for dual-mass MEMS gyroscope based on a quadrature modulation signal. Micromachines 2018, 9, 511. [Google Scholar] [CrossRef] [Green Version]
- Saukoski, M.; Aaltonen, L.; Halonen, K.A.I. Zero-rate output and quadrature compensation in vibratory MEMS gyroscopes. IEEE Sens. J. 2007, 7, 1639–1652. [Google Scholar] [CrossRef]
- Wu, K.; Lu, K.; Li, Q.; Zhang, Y.; Zhuo, M.; Yu, S.; Wu, X.; Xiao, D. Analysis of parametric and subharmonic excitation in push-pull driven disk resonator gyroscopes. Micromachines 2021, 12, 61. [Google Scholar] [CrossRef] [PubMed]
- Askari, S.; Asadian, M.H.; Shkel, A.M. Performance of quad mass gyroscope in the angular rate mode. Micromachines 2021, 12, 266. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wen, H.; Wisher, S.; Norouzpour-Shirazi, A.; Lei, J.; Chen, H.; Ayazi, F. An FPGA-based interface system for high-frequency bulk-acoustic-wave microgyroscopes with in-run automatic mode-matching. IEEE Trans. Instrum. Meas. 2020, 69, 1783–1793. [Google Scholar] [CrossRef]
- Xia, D.; Yu, C.; Kong, L. The development of micromachined gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, B.; Guo, S.; Cheng, M.; Yu, L.; Zhou, M.; Hu, W.; Chen, Z.; Xu, D. A novel high-symmetry cobweb-like disk resonantor gyroscope. IEEE Sens. J. 2019, 19, 10289–10297. [Google Scholar] [CrossRef]
- Bu, F.; Guo, S.; Cheng, M.; Zheng, F.; Xu, D.; Zhao, H. Effect of circuit phase delay on bias stability of MEMS gyroscope under force rebalance detection and self-compensation method. J. Micromech. Microeng. 2019, 29, 095002. [Google Scholar] [CrossRef]
- Bu, F.; Wang, X.; Fan, B.; Guo, S.; Xu, D.; Xu, X.; Zhao, H. Noise model considering electrical feed-through under force rebalance closed-loop detection of MEMS gyroscope. J. Micromech. Microeng. 2019, 30, 055007. [Google Scholar] [CrossRef]
- Pagani, L.G.; Guerinoni, L.; Falorni, L.; Fedeli, P.; Carulli, P.; Langfelder, G. Direct phase measurement and compensation to enhance MEMS gyrsocopes ZRO stability. J. Microelectromech. Syst. 2021, 1–9. [Google Scholar] [CrossRef]







| Normal Condition | Scenario A | Scenario B | Scenario C | |
|---|---|---|---|---|
| Scale factor (V/°/s) | −1.73 × 10−4 | - | - | −2.11 × 10−4 |
| Bias (V) | −5.12 × 10−4 | −4.05 × 10−7 | −1.19 | 3.33 × 10−2 |
| Bias stability (V) | 1.29 × 10−5 | 1.33 × 10−5 | 1.13 | 2.51 × 10−4 |
| The average of the quadrature signal (V) | 2.92 × 10−3 | 4.58 × 10−7 | 8.84 × 10−3 | 2.54 × 10−3 |
| The standard deviation of the quadrature signal (V) | 2.24 × 10−6 | 1.13 × 10−6 | 1.81 × 10−2 | 5.19 × 10−5 |
| Scale Factor (V/°/s) | Bias (°/s) | The Amplitude of Quadrature Error (V) | |
|---|---|---|---|
| before | −1.79 × 10−4 | 19.70 | −5.81 × 10−3 |
| after 3000 g | −1.78 × 10−4 | 18.59 | −5.58 × 10−3 |
| after 6000 g | −1.77 × 10−4 | 18.56 | −5.59 × 10−3 |
| after 10,000 g | — | −1093.17 | −1.02 × 10−5 |
| Scale Factor Variation | Bias Variation | Quadrature Error Amplitude Variation | |
|---|---|---|---|
| after 3000 g | −0.49% | −5.62% | −3.94% |
| after 6000 g | −1.02% | −5.76% | −3.74% |
| after 10,000 g | −100% | −5648.09% | −99.82% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, R.; Wang, J.; Qiao, W.; Wang, F.; Zhou, M.; Shang, X.; Yu, L.; Zhou, L.; Guo, S. Real-Time Built-In Self-Test of MEMS Gyroscope Based on Quadrature Error Signal. Micromachines 2021, 12, 1115. https://doi.org/10.3390/mi12091115
Feng R, Wang J, Qiao W, Wang F, Zhou M, Shang X, Yu L, Zhou L, Guo S. Real-Time Built-In Self-Test of MEMS Gyroscope Based on Quadrature Error Signal. Micromachines. 2021; 12(9):1115. https://doi.org/10.3390/mi12091115
Chicago/Turabian StyleFeng, Rui, Jiong Wang, Wei Qiao, Fu Wang, Ming Zhou, Xinglian Shang, Lei Yu, Liuhui Zhou, and Shuwen Guo. 2021. "Real-Time Built-In Self-Test of MEMS Gyroscope Based on Quadrature Error Signal" Micromachines 12, no. 9: 1115. https://doi.org/10.3390/mi12091115
APA StyleFeng, R., Wang, J., Qiao, W., Wang, F., Zhou, M., Shang, X., Yu, L., Zhou, L., & Guo, S. (2021). Real-Time Built-In Self-Test of MEMS Gyroscope Based on Quadrature Error Signal. Micromachines, 12(9), 1115. https://doi.org/10.3390/mi12091115





