Intelligent Design Optimization System for Additively Manufactured Flow Channels Based on Fluid–Structure Interaction
Abstract
:1. Introduction
2. Literature Review
2.1. Intelligence in FSI Simulation
2.2. FSI-Based Design Optimization
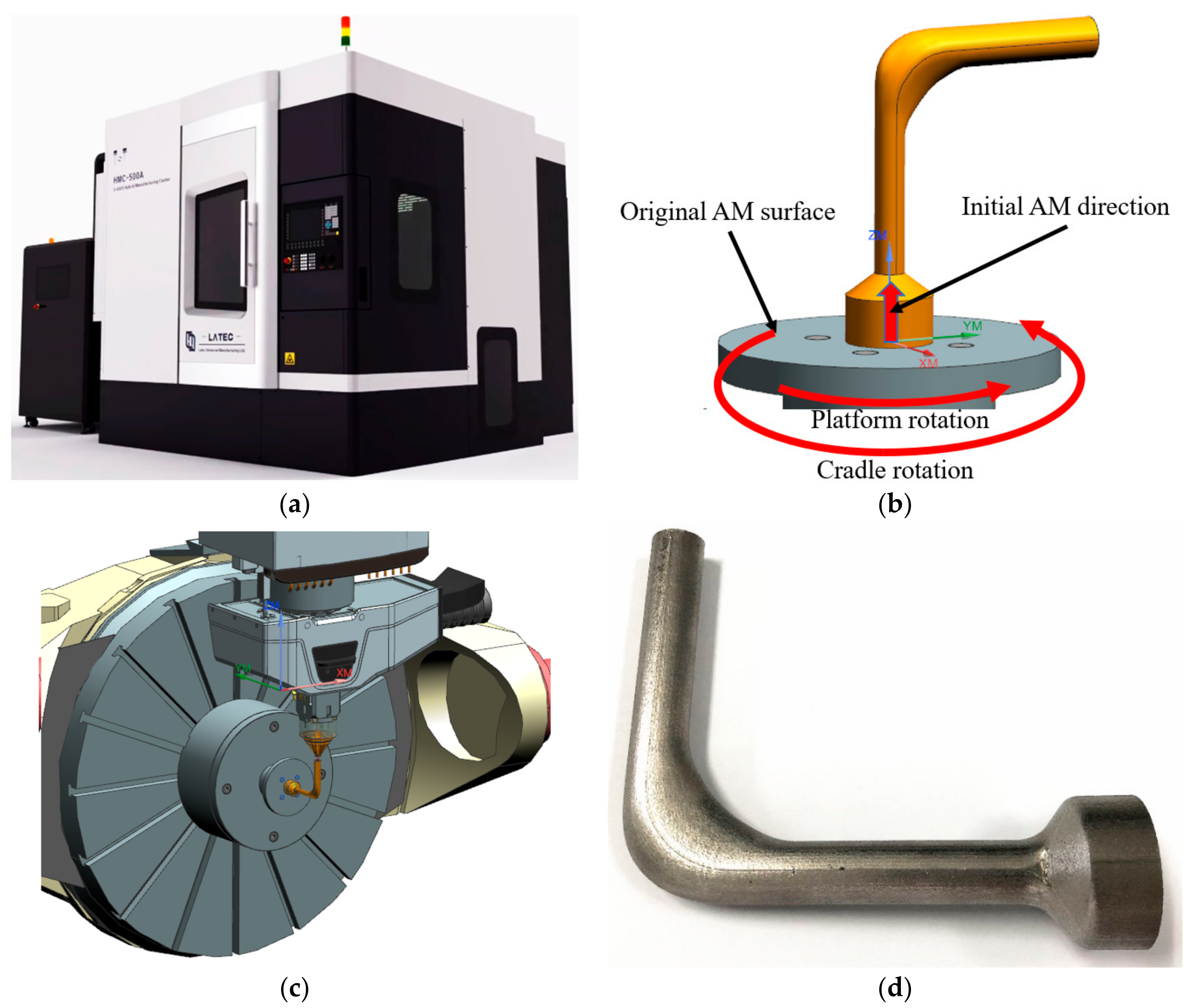
2.3. AM in the Fabrication of Optimized Flow Channels
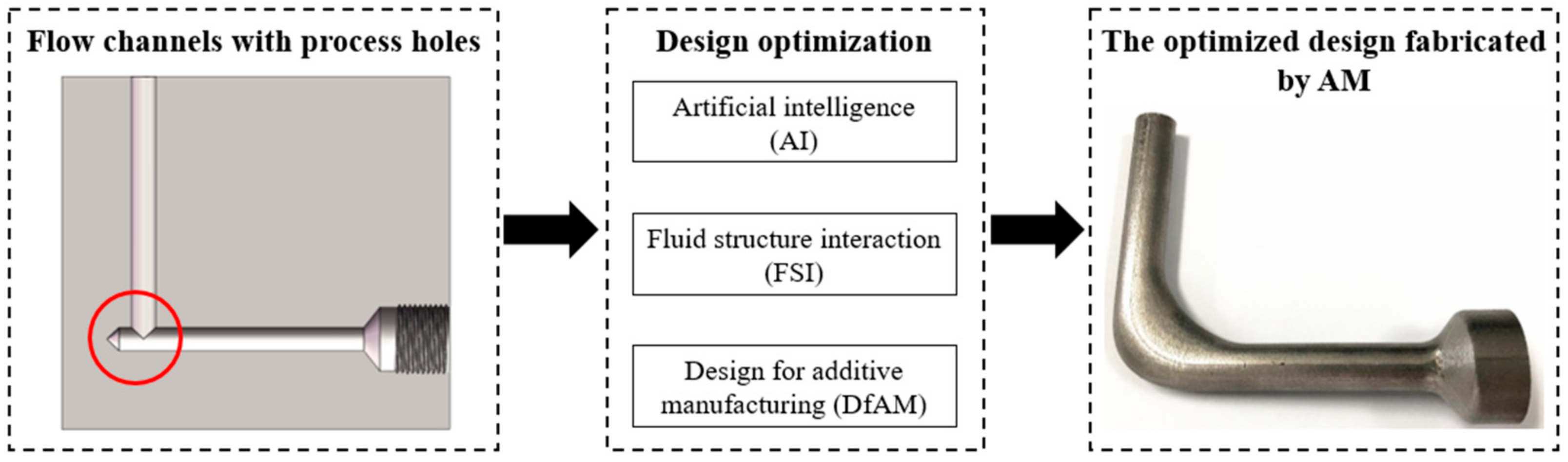
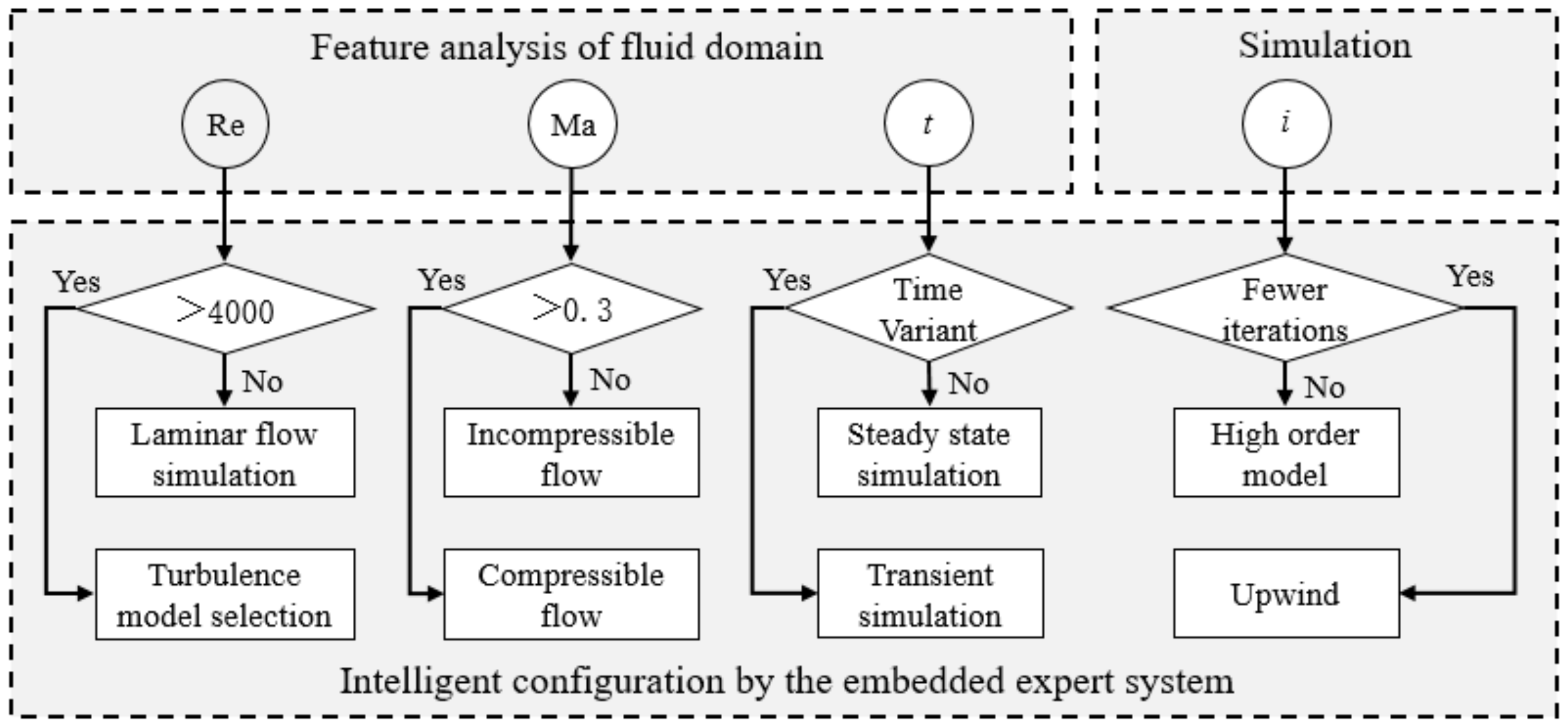
3. Intelligent FSI Simulation System
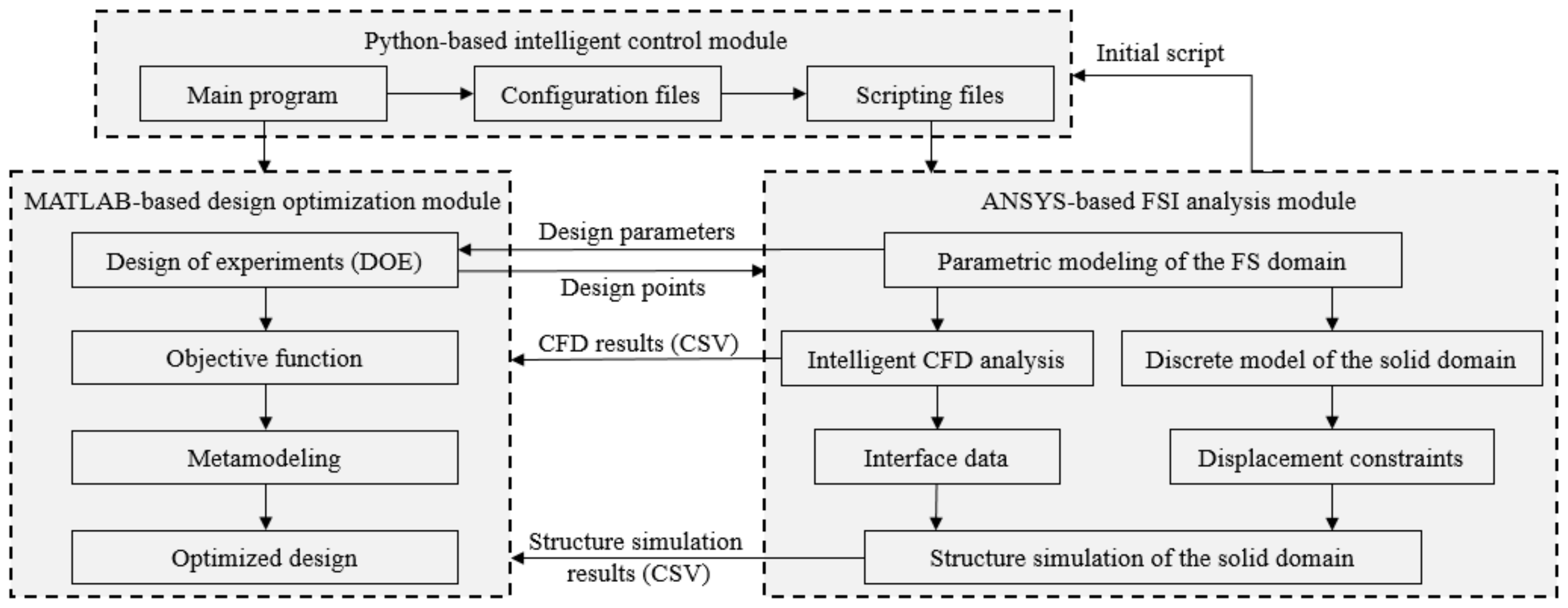
4. Intelligent Design Optimization System
4.1. System Architecture
4.2. Principle of the Intelligent System
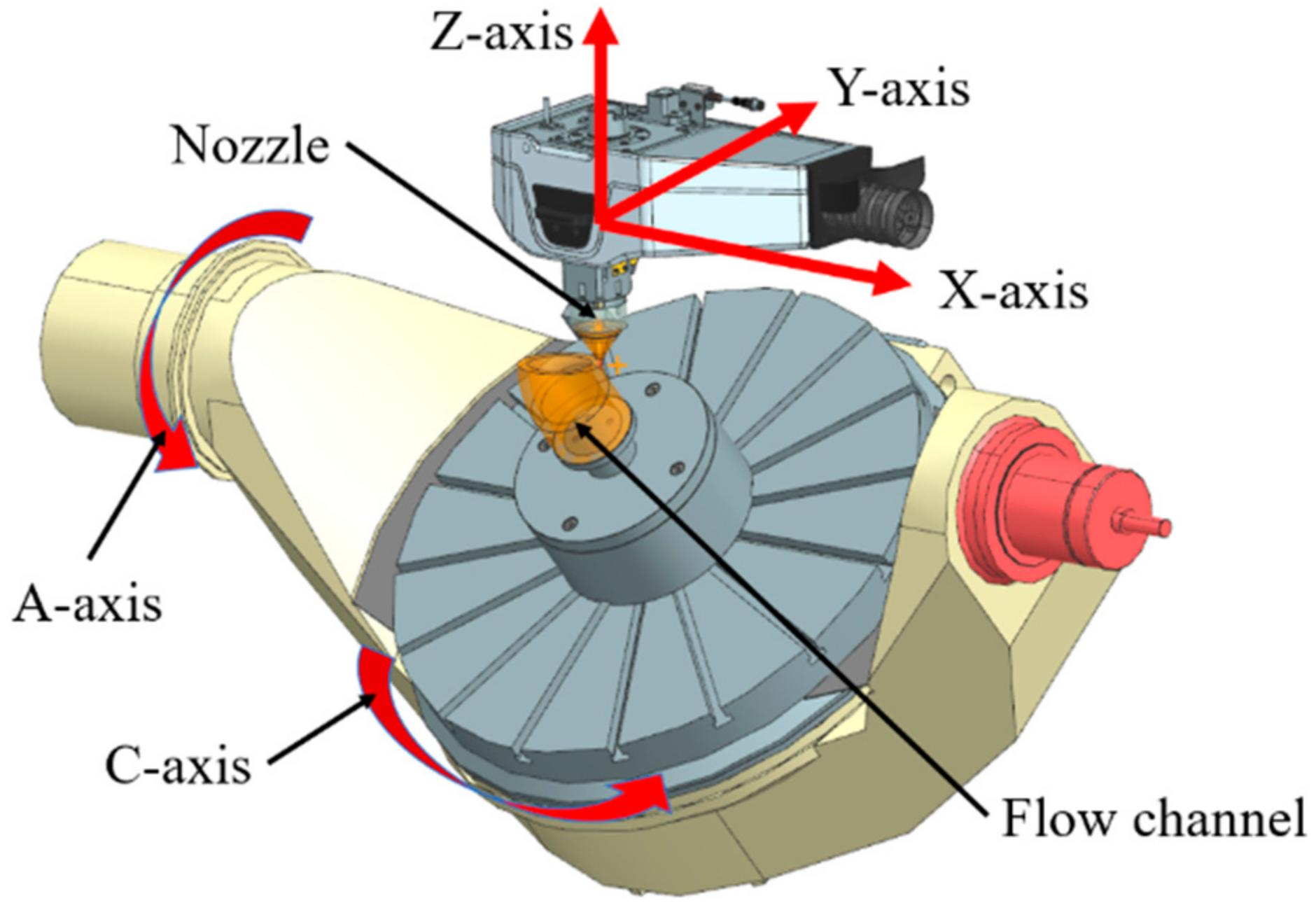
4.2.1. The Parametric Modeling for AM
- The process hole should be replaced by a section of integrated bent channel, which will not only improve the energy efficiency, but also take advantage of AM in producing complex surfaces;
- The bent section should be designed with variable wall thickness to achieve the goal of weight reduction and satisfy the strength requirement simultaneously;
- Five-axis DED can obtain flow channels without supporting structures. The premise is that the maximum flow channel bent angle should not exceed 90 degrees to avoid collisions of DED machine tools;
- Additional geometric constraints should be added to the bent section of the flow channel to smooth the transition between the bent section and the straight section, which guarantees stable machining paths and platform rotation in five-axis DED process;
- As flow channels belong to thin-walled parts, the wall thickness of its 3D model should be greater than the minimum thickness that can be formed by DED.
4.2.2. FSI Analysis Module
- The model parameters are input into the main program, and the Reynolds number and Mach number corresponding to different models are calculated based on the aforementioned Equations (7) and (8), respectively;
- The initial scripting file generated by ANSYS Workbench is used as the source template, and then the source template is updated as new scripting files, which have the same quantity extracted from design models. The configurations of simulation in each new scripting file are also updated by the script statement modification function in the expert system based on the values calculated in the previous step;
- The new scripting files can run in the specified project one after another calling ANSYS Workbench, which ensures that each design model can be processed automatically;
- After the FSI simulation is completed, the results corresponding to each design model can be obtained by reading the CSV output file generated by ANSYS.
4.2.3. Design Optimization Module
5. Case Study
5.1. Problem Description
5.2. Design Optimization of the Fluid Domain
5.2.1. Design and Analysis
5.2.2. Optimization Based on RSM
5.3. Optimization of the Solid Domain
5.3.1. Design and Analysis
5.3.2. Optimization Based on RSM
5.4. Manufacturing of the Optimized Flow Channel
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Design Point | x1 (mm) | x2 (mm) | x3 (mm) | x4 (mm) | x5 (mm) | x6 (mm) | Volume (mm3) | Maximum Stress (MPa) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3.6 | 4.2 | 4.2 | 6 | 4 | 2.4 | 17,897.476 | 83.875 |
| 2 | 3.6 | 4.2 | 4.2 | 6 | 4 | 3.6 | 20,968.032 | 77.451 |
| 3 | 3.6 | 4.2 | 4.2 | 6 | 6 | 2.4 | 18,048.811 | 80.785 |
| 4 | 3.6 | 4.2 | 4.2 | 6 | 6 | 3.6 | 21,152.207 | 78.199 |
| 5 | 3.6 | 4.2 | 4.2 | 4 | 6 | 2.4 | 17,875.377 | 82.833 |
| 6 | 3.6 | 4.2 | 4.2 | 4 | 6 | 3.6 | 20,966.183 | 77.099 |
| 7 | 3.6 | 4.2 | 4.2 | 4 | 4 | 2.4 | 17,710.653 | 86.241 |
| 8 | 3.6 | 4.2 | 4.2 | 4 | 4 | 3.6 | 20,786.965 | 79.586 |
| 9 | 3.6 | 4.2 | 2.8 | 6 | 4 | 2.4 | 17,771.738 | 83.405 |
| 10 | 3.6 | 4.2 | 2.8 | 6 | 4 | 3.6 | 20,848.548 | 77.13 |
| 11 | 3.6 | 4.2 | 2.8 | 6 | 6 | 2.4 | 17,902.091 | 80.711 |
| 12 | 3.6 | 4.2 | 2.8 | 6 | 6 | 3.6 | 21,002.514 | 76.702 |
| 13 | 3.6 | 4.2 | 2.8 | 4 | 6 | 2.4 | 17,742.931 | 82.403 |
| 14 | 3.6 | 4.2 | 2.8 | 4 | 6 | 3.6 | 20,804.92 | 76.954 |
| 15 | 3.6 | 4.2 | 2.8 | 4 | 4 | 2.4 | 17,587.042 | 85.323 |
| 16 | 3.6 | 4.2 | 2.8 | 4 | 4 | 3.6 | 20,635.994 | 78.576 |
| 17 | 3.6 | 2.8 | 4.2 | 6 | 4 | 2.4 | 17,766.073 | 83.68 |
| 18 | 3.6 | 2.8 | 4.2 | 6 | 4 | 3.6 | 20,830.547 | 77.7 |
| 19 | 3.6 | 2.8 | 4.2 | 6 | 6 | 2.4 | 17,907.069 | 80.76 |
| 20 | 3.6 | 2.8 | 4.2 | 6 | 6 | 3.6 | 21,007.847 | 77.399 |
| 21 | 3.6 | 2.8 | 4.2 | 4 | 6 | 2.4 | 17,737.808 | 82.23 |
| 22 | 3.6 | 2.8 | 4.2 | 4 | 6 | 3.6 | 20,819.957 | 77.307 |
| 23 | 3.6 | 2.8 | 4.2 | 4 | 4 | 2.4 | 17,577.73 | 85.738 |
| 24 | 3.6 | 2.8 | 4.2 | 4 | 4 | 3.6 | 20,636.711 | 78.545 |
| 25 | 3.6 | 2.8 | 2.8 | 6 | 4 | 2.4 | 17,629.393 | 83.133 |
| 26 | 3.6 | 2.8 | 2.8 | 6 | 4 | 3.6 | 20,677.002 | 76.828 |
| 27 | 3.6 | 2.8 | 2.8 | 6 | 6 | 2.4 | 17,789.481 | 80.755 |
| 28 | 3.6 | 2.8 | 2.8 | 6 | 6 | 3.6 | 20,852.685 | 77.18 |
| 29 | 3.6 | 2.8 | 2.8 | 4 | 6 | 2.4 | 17,609.845 | 82.125 |
| 30 | 3.6 | 2.8 | 2.8 | 4 | 6 | 3.6 | 20,682.307 | 77.352 |
| 31 | 3.6 | 2.8 | 2.8 | 4 | 4 | 2.4 | 17,460.586 | 84.905 |
| 32 | 3.6 | 2.8 | 2.8 | 4 | 4 | 3.6 | 20,499.801 | 78.604 |
| 33 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 34 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 35 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 36 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 37 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 38 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 39 | 2.4 | 4.2 | 4.2 | 6 | 4 | 2.4 | 15,119.431 | 93.836 |
| 40 | 2.4 | 4.2 | 4.2 | 6 | 4 | 3.6 | 18,189.79 | 85.819 |
| 41 | 2.4 | 4.2 | 4.2 | 6 | 6 | 2.4 | 15,273.54 | 90.887 |
| 42 | 2.4 | 4.2 | 4.2 | 6 | 6 | 3.6 | 18,349.325 | 83.995 |
| 43 | 2.4 | 4.2 | 4.2 | 4 | 6 | 2.4 | 15,160.95 | 93.869 |
| 44 | 2.4 | 4.2 | 4.2 | 4 | 6 | 3.6 | 18,194.569 | 87.043 |
| 45 | 2.4 | 4.2 | 4.2 | 4 | 4 | 2.4 | 14,972.612 | 97.894 |
| 46 | 2.4 | 4.2 | 4.2 | 4 | 4 | 3.6 | 18,036.759 | 89.345 |
| 47 | 2.4 | 4.2 | 2.8 | 6 | 4 | 2.4 | 15,002.218 | 93.788 |
| 48 | 2.4 | 4.2 | 2.8 | 6 | 4 | 3.6 | 18,048.514 | 85.408 |
| 49 | 2.4 | 4.2 | 2.8 | 6 | 6 | 2.4 | 15,145.882 | 90.865 |
| 50 | 2.4 | 4.2 | 2.8 | 6 | 6 | 3.6 | 18,206.417 | 84.055 |
| 51 | 2.4 | 4.2 | 2.8 | 4 | 6 | 2.4 | 14,998.914 | 93.891 |
| 52 | 2.4 | 4.2 | 2.8 | 4 | 6 | 3.6 | 18,060.763 | 86.783 |
| 53 | 2.4 | 4.2 | 2.8 | 4 | 4 | 2.4 | 14,857.127 | 97.363 |
| 54 | 2.4 | 4.2 | 2.8 | 4 | 4 | 3.6 | 17,929.129 | 88.834 |
| 55 | 2.4 | 2.8 | 4.2 | 6 | 4 | 2.4 | 15,005.44 | 93.953 |
| 56 | 2.4 | 2.8 | 4.2 | 6 | 4 | 3.6 | 18,067.713 | 85.678 |
| 57 | 2.4 | 2.8 | 4.2 | 6 | 6 | 2.4 | 15,150.937 | 90.986 |
| 58 | 2.4 | 2.8 | 4.2 | 6 | 6 | 3.6 | 18,230.22 | 84.009 |
| 59 | 2.4 | 2.8 | 4.2 | 4 | 6 | 2.4 | 15,011.626 | 93.745 |
| 60 | 2.4 | 2.8 | 4.2 | 4 | 6 | 3.6 | 18,064.973 | 86.61 |
| 61 | 2.4 | 2.8 | 4.2 | 4 | 4 | 2.4 | 14,863.887 | 97.405 |
| 62 | 2.4 | 2.8 | 4.2 | 4 | 4 | 3.6 | 17,910.394 | 88.809 |
| 63 | 2.4 | 2.8 | 2.8 | 6 | 4 | 2.4 | 14,878.343 | 93.982 |
| 64 | 2.4 | 2.8 | 2.8 | 6 | 4 | 3.6 | 17,918.057 | 85.383 |
| 65 | 2.4 | 2.8 | 2.8 | 6 | 6 | 2.4 | 15,037.007 | 91.242 |
| 66 | 2.4 | 2.8 | 2.8 | 6 | 6 | 3.6 | 18,098.979 | 83.893 |
| 67 | 2.4 | 2.8 | 2.8 | 4 | 6 | 2.4 | 14,890.674 | 93.835 |
| 68 | 2.4 | 2.8 | 2.8 | 4 | 6 | 3.6 | 17,944.428 | 86.406 |
| 69 | 2.4 | 2.8 | 2.8 | 4 | 4 | 2.4 | 14,746.24 | 97.228 |
| 70 | 2.4 | 2.8 | 2.8 | 4 | 4 | 3.6 | 17,778.339 | 88.442 |
| 71 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 72 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 73 | 1.3 | 3.5 | 3.5 | 5 | 5 | 3 | 14,385.117 | 105.84 |
| 74 | 4.7 | 3.5 | 3.5 | 5 | 5 | 3 | 22,185.297 | 76.622 |
| 75 | 3 | 1.52 | 3.5 | 5 | 5 | 3 | 17,614.667 | 89.408 |
| 76 | 3 | 5.48 | 3.5 | 5 | 5 | 3 | 17,980.02 | 83.986 |
| 77 | 3 | 3.5 | 1.52 | 5 | 5 | 3 | 17,614.18 | 89.593 |
| 78 | 3 | 3.5 | 5.48 | 5 | 5 | 3 | 17,990.502 | 84.071 |
| 79 | 3 | 3.5 | 3.5 | 2.17 | 5 | 3 | 17,562.815 | 91.662 |
| 80 | 3 | 3.5 | 3.5 | 7.83 | 5 | 3 | 17,998.965 | 81.625 |
| 81 | 3 | 3.5 | 3.5 | 5 | 2.17 | 3 | 17,559.502 | 91.296 |
| 82 | 3 | 3.5 | 3.5 | 5 | 7.83 | 3 | 18,010.566 | 81.606 |
| 83 | 3 | 3.5 | 3.5 | 5 | 5 | 1.3 | 13,899.297 | 96.837 |
| 84 | 3 | 3.5 | 3.5 | 5 | 5 | 4.7 | 22,567.122 | 77.509 |
| 85 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 86 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 87 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 88 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 89 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
| 90 | 3 | 3.5 | 3.5 | 5 | 5 | 3 | 17,798.702 | 84.732 |
References
- Xie, G.; Dong, Y.; Zhou, J.; Sheng, Z. Topology Optimization Design of Hydraulic Valve Blocks for Additive Manufacturing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1899–1912. [Google Scholar] [CrossRef]
- Habla, F.; Fernandes, C.; Maier, M.; Densky, L.; Ferrás, L.L.; Rajkumar, A.; Carneiro, O.S.; Hinrichsen, O.; Nóbrega, J.M. Development and Validation of a Model for the Temperature Distribution in the Extrusion Calibration Stage. Appl. Therm. Eng. 2016, 100, 538–552. [Google Scholar] [CrossRef]
- Tao, M.; Guo, K.; Huang, Z.; Liu, H.; Liu, C. A Hybrid Optimization Method to Design Shapes of Three-Dimensional Flow Channels. Chem. Eng. Res. Des. 2016, 114, 190–201. [Google Scholar] [CrossRef]
- Li, L.; Liu, J.; Ma, Y.; Ahmad, R.; Qureshi, A. Multi-View Feature Modeling for Design-for-Additive Manufacturing. Adv. Eng. Inform. 2019, 39, 144–156. [Google Scholar] [CrossRef]
- Fernandes, C.; Vukčević, V.; Uroić, T.; Simoes, R.; Carneiro, O.S.; Jasak, H.; Nóbrega, J.M. A Coupled Finite Volume Flow Solver for the Solution of Incompressible Viscoelastic Flows. J. Non-Newton. Fluid Mech. 2019, 265, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Baraheni, M.; Azarhoushang, B.; Daneshi, A.; Kadivar, M.; Amini, S. Development of an Expert System for Optimal Design of the Grinding Process. Int. J. Adv. Manuf. Technol. 2021, 116, 2823–2833. [Google Scholar] [CrossRef]
- Li, L.; Zheng, Y.; Yang, M.; Leng, J.; Cheng, Z.; Xie, Y.; Jiang, P.; Ma, Y. A Survey of Feature Modeling Methods: Historical Evolution and New Development. Robot. Comput. Integr. Manuf. 2020, 61, 101851. [Google Scholar] [CrossRef]
- Grandmont, C.; Vergnet, F. Existence for a Quasi-Static Interaction Problem between a Viscous Fluid and an Active Structure. J. Math. Fluid Mech. 2021, 23, 45. [Google Scholar] [CrossRef]
- Jiao, J.; Huang, S.; Guedes Soares, C. Viscous Fluid–Flexible Structure Interaction Analysis on Ship Springing and Whipping Responses in Regular Waves. J. Fluids Struct. 2021, 106, 103354. [Google Scholar] [CrossRef]
- Simão, M.; Mora, J.; Ramos, H.M. Fluid–Structure Interaction with Different Coupled Models to Analyse an Accident Occurring in a Water Supply System. J. Water Supply Res. Technol. Aqua 2015, 64, 302–315. [Google Scholar] [CrossRef]
- McVicar, J.; Lavroff, J.; Davis, M.R.; Thomas, G. Fluid–Structure Interaction Simulation of Slam-Induced Bending in Large High-Speed Wave-Piercing Catamarans. J. Fluids Struct. 2018, 82, 35–58. [Google Scholar] [CrossRef]
- Wijesooriya, K.; Mohotti, D.; Amin, A.; Chauhan, K. Comparison between an Uncoupled One-Way and Two-Way Fluid Structure Interaction Simulation on a Super-Tall Slender Structure. Eng. Struct. 2021, 229, 111636. [Google Scholar] [CrossRef]
- Boustani, J.; Barad, M.F.; Kiris, C.C.; Brehm, C. An Immersed Boundary Fluid–Structure Interaction Method for Thin, Highly Compliant Shell Structures. J. Comput. Phys. 2021, 438, 110369. [Google Scholar] [CrossRef]
- Li, L.; Lange, C.F.; Ma, Y. Association of Design and Computational Fluid Dynamics Simulation Intent in Flow Control Product Optimization. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 2309–2322. [Google Scholar] [CrossRef]
- Boosari, H. Predicting the Dynamic Parameters of Multiphase Flow in CFD (Dam-Break Simulation) Using Artificial Intelligence (Cascading Deployment). Fluids 2019, 4, 44. [Google Scholar] [CrossRef] [Green Version]
- Babanezhad, M.; Rezakazemi, M.; Hajilary, N.; Shirazian, S. Liquid-phase Chemical Reactors: Development of 3D Hybrid Model Based on CFD-adaptive Network-based Fuzzy Inference System. Can. J. Chem. Eng. 2019, 97, 1676–1684. [Google Scholar] [CrossRef]
- Shamshirband, S.; Malvandi, A.; Karimipour, A.; Goodarzi, M.; Afrand, M.; Petković, D.; Dahari, M.; Mahmoodian, N. Performance Investigation of Micro- and Nano-Sized Particle Erosion in a 90° Elbow Using an ANFIS Model. Powder Technol. 2015, 284, 336–343. [Google Scholar] [CrossRef]
- Lee, S.; Kevrekidis, I.G.; Karniadakis, G.E. A General CFD Framework for Fault-Resilient Simulations Based on Multi-Resolution Information Fusion. J. Comput. Phys. 2017, 347, 290–304. [Google Scholar] [CrossRef]
- Ren, J.; Cao, S.-J. Development of Self-Adaptive Low-Dimension Ventilation Models Using OpenFOAM: Towards the Application of AI Based on CFD Data. Build. Environ. 2020, 171, 106671. [Google Scholar] [CrossRef]
- Kang, H.-S.; Kim, Y.-J. Optimal Design of Impeller for Centrifugal Compressor under the Influence of One-Way Fluid-Structure Interaction. J. Mech. Sci. Technol. 2016, 30, 3953–3959. [Google Scholar] [CrossRef]
- Wen, J.; Li, K.; Wang, C.; Zhang, X.; Wang, S. Optimization Investigation on Configuration Parameters of Sine Wavy Fin in Plate-Fin Heat Exchanger Based on Fluid Structure Interaction Analysis. Int. J. Heat Mass Transf. 2019, 131, 385–402. [Google Scholar] [CrossRef]
- Huang, J.; Xu, S.; Ma, Y.; Liu, J. A Topology Optimization Method for Hyperelastic Porous Structures Subject to Large Deformation. Int. J. Mech. Mater. Des. 2021, 1–20. [Google Scholar] [CrossRef]
- Jenkins, N.; Maute, K. Level Set Topology Optimization of Stationary Fluid-Structure Interaction Problems. Struct. Multidisc. Optim. 2015, 52, 179–195. [Google Scholar] [CrossRef]
- Yoon, G.H. Stress-Based Topology Optimization Method for Steady-State Fluid–Structure Interaction Problems. Comput. Methods Appl. Mech. Eng. 2014, 278, 499–523. [Google Scholar] [CrossRef]
- Jang, H.-L.; Cho, H.; Choi, K.K.; Cho, S. Reliability-Based Design Optimization of Fluid–Solid Interaction Problems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1724–1742. [Google Scholar] [CrossRef]
- Aghajari, N.; Schäfer, M. Efficient Shape Optimization for Fluid–Structure Interaction Problems. J. Fluids Struct. 2015, 57, 298–313. [Google Scholar] [CrossRef]
- Heners, J.P.; Radtke, L.; Hinze, M.; Düster, A. Adjoint Shape Optimization for Fluid–Structure Interaction of Ducted Flows. Comput. Mech. 2018, 61, 259–276. [Google Scholar] [CrossRef]
- Wick, T.; Wollner, W. Optimization with Nonstationary, Nonlinear Monolithic Fluid-structure Interaction. Int. J. Numer. Methods Eng. 2021, 122, 5430–5449. [Google Scholar] [CrossRef] [Green Version]
- Alessi, G.; Verstraete, T.; Koloszar, L.; Blocken, B.; van Beeck, J.P.A.J. Adjoint Shape Optimization Coupled with LES-Adapted RANS of a U-Bend Duct for Pressure Loss Reduction. Comput. Fluids 2021, 228, 105057. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive Manufacturing of Metallic Components—Process, Structure and Properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Yan, J.; Li, L.; Li, S. Full Sensitivity-Driven Gap/Overlap Free Design of Carbon Fiber-Reinforced Composites for 3D Printing. Appl. Math. Model. 2022, 103, 308–326. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G.; Ding, R.; Zhang, K.; Pan, M.; Liu, S. 3D Printing for Energy-Saving: Evidence from Hydraulic Manifolds Design. Energies 2019, 12, 2462. [Google Scholar] [CrossRef] [Green Version]
- Alshare, A.A.; Calzone, F.; Muzzupappa, M. Hydraulic Manifold Design via Additive Manufacturing Optimized with CFD and Fluid-Structure Interaction Simulations. RPJ 2019, 25, 1516–1524. [Google Scholar] [CrossRef]
- Kumke, M.; Watschke, H.; Vietor, T. A New Methodological Framework for Design for Additive Manufacturing. Virtual Phys. Prototyp. 2016, 11, 3–19. [Google Scholar] [CrossRef]
- Diegel, O.; Schutte, J.; Ferreira, A.; Chan, Y.L. Design for Additive Manufacturing Process for a Lightweight Hydraulic Manifold. Addit. Manuf. 2020, 36, 101446. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Ma, Y. Residual Stress Constrained Self-Support Topology Optimization for Metal Additive Manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 389, 114380. [Google Scholar] [CrossRef]
- Biedermann, M.; Beutler, P.; Meboldt, M. Automated Design of Additive Manufactured Flow Components with Consideration of Overhang Constraint. Addit. Manuf. 2021, 46, 102119. [Google Scholar] [CrossRef]
- Ponche, R.; Kerbrat, O.; Mognol, P.; Hascoet, J.-Y. A Novel Methodology of Design for Additive Manufacturing Applied to Additive Laser Manufacturing Process. Robot. Comput. Integr. Manuf. 2014, 30, 389–398. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Lange, C.F.; Xu, Z.; Jiang, P.; Ma, Y. Feature-Based Intelligent System for Steam Simulation Using Computational Fluid Dynamics. Adv. Eng. Inform. 2018, 38, 357–369. [Google Scholar] [CrossRef]
- Li, L.; Cheng, Z.; Lange, C.F. CFD-Based Optimization of Fluid Flow Product Aided by Artificial Intelligence and Design Space Validation. Math. Probl. Eng. 2018, 2018, 8465020. [Google Scholar] [CrossRef]
- Yu, P.X.; Tian, Z.F. An Upwind Compact Difference Scheme for Solving the Streamfunction–Velocity Formulation of the Unsteady Incompressible Navier–Stokes Equation. Comput. Math. Appl. 2018, 75, 3224–3243. [Google Scholar] [CrossRef]
- Upreti, K.; Subbarayan, G. Signed Algebraic Level Sets on NURBS Surfaces and Implicit Boolean Compositions for Isogeometric CAD–CAE Integration. Comput. Aided Des. 2017, 82, 112–126. [Google Scholar] [CrossRef]
- Sun, Q.; Bao, F.; Duan, Q. A Surface Modeling Method by Using C2 Piecewise Rational Spline Interpolation. J. Math. Imaging Vis. 2015, 53, 12–20. [Google Scholar] [CrossRef]
- Du, X.; Leifsson, L. Optimum Aerodynamic Shape Design under Uncertainty by Utility Theory and Metamodeling. Aerosp. Sci. Technol. 2019, 95, 105464. [Google Scholar] [CrossRef]
- You, Y.-M. Optimal Design of PMSM Based on Automated Finite Element Analysis and Metamodeling. Energies 2019, 12, 4673. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Xu, S.; Ma, Y.; Chen, X.; Wang, X. An Adaptive Bayesian Sequential Sampling Approach for Global Metamodeling. J. Mech. Des. 2016, 138, 011404. [Google Scholar] [CrossRef]
- Asadollahi-Yazdi, E.; Gardan, J.; Lafon, P. Multi-Objective Optimization Approach in Design for Additive Manufacturing for Fused Deposition Modeling. RPJ 2019, 25, 875–887. [Google Scholar] [CrossRef]
- Wang, X.; Zou, B.; Li, L.; Xing, H.; Huang, C.; Wang, Y.; Shi, Z.; Liu, J.; Yao, P.; Xue, K. Manufacturing of a Ceramic Groove Part Based on Additive and Subtractive Technologies. Ceram. Int. 2021, 47, 740–747. [Google Scholar] [CrossRef]
- Zardin, B.; Cillo, G.; Rinaldini, C.; Mattarelli, E.; Borghi, M. Pressure Losses in Hydraulic Manifolds. Energies 2017, 10, 310. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Rännar, L.-E.; Liu, L.; Koptyug, A.; Wikman, S.; Olsen, J.; Cui, D.; Shen, Z. Additive Manufacturing of 316L Stainless Steel by Electron Beam Melting for Nuclear Fusion Applications. J. Nucl. Mater. 2017, 486, 234–245. [Google Scholar] [CrossRef]



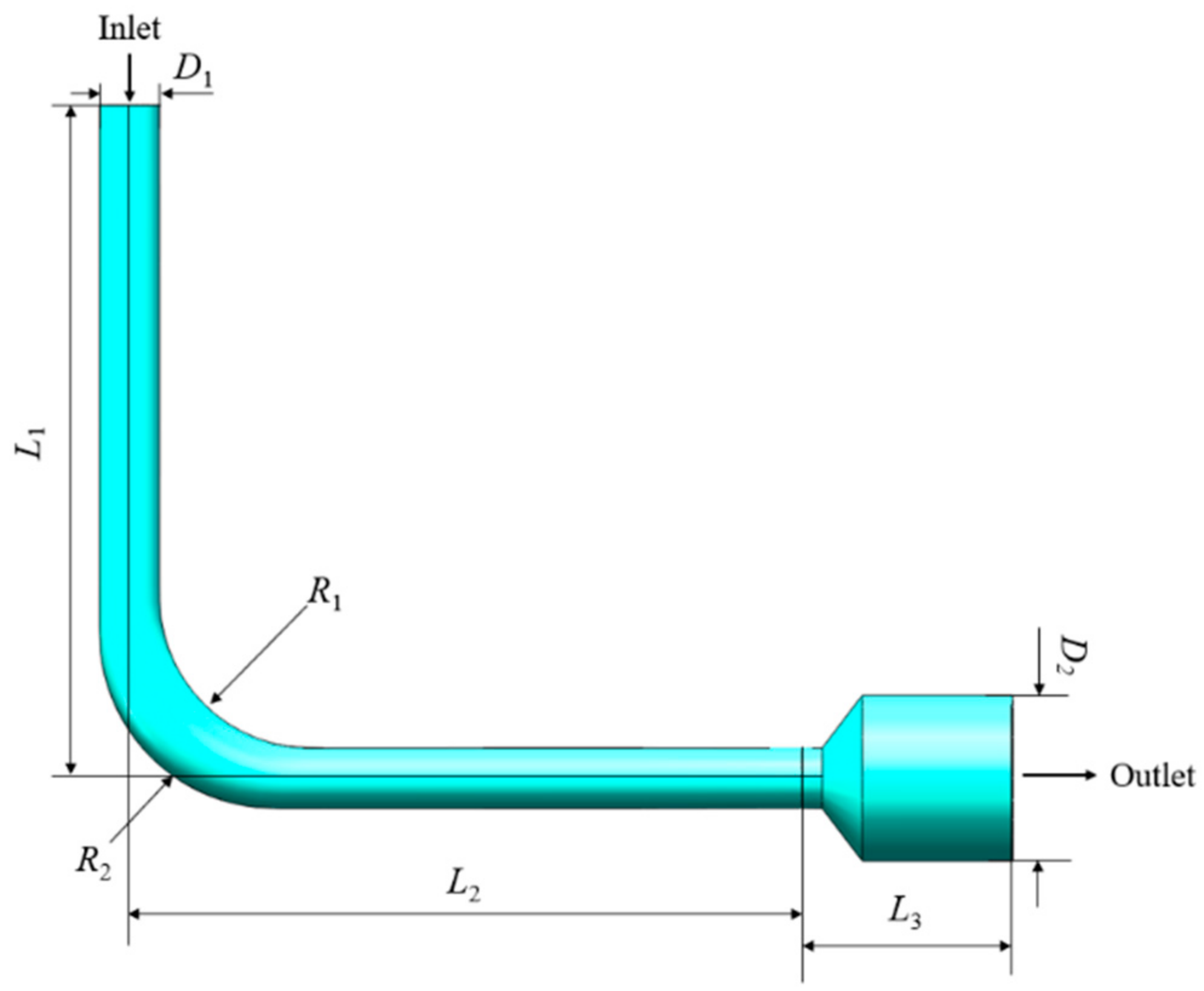
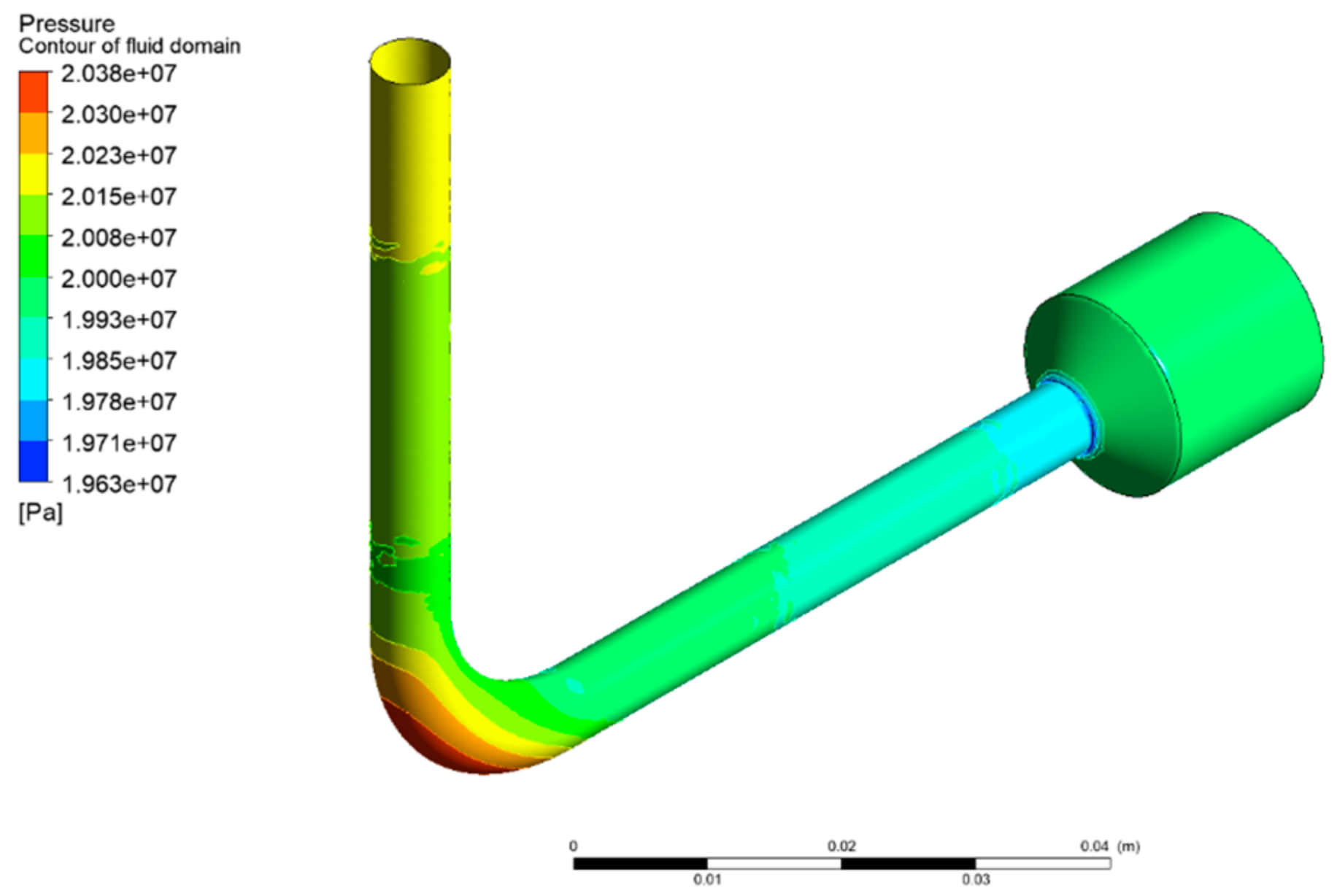
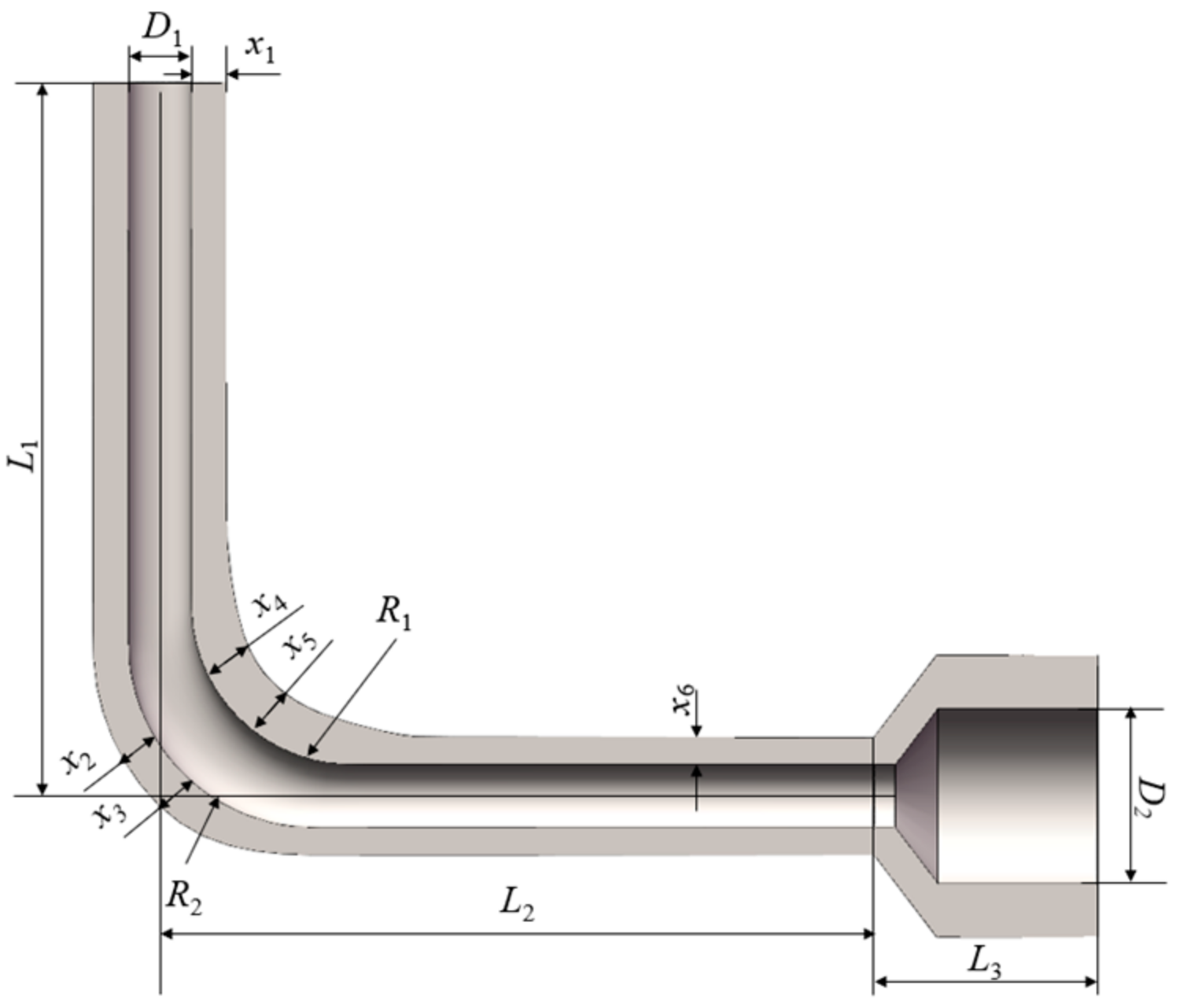
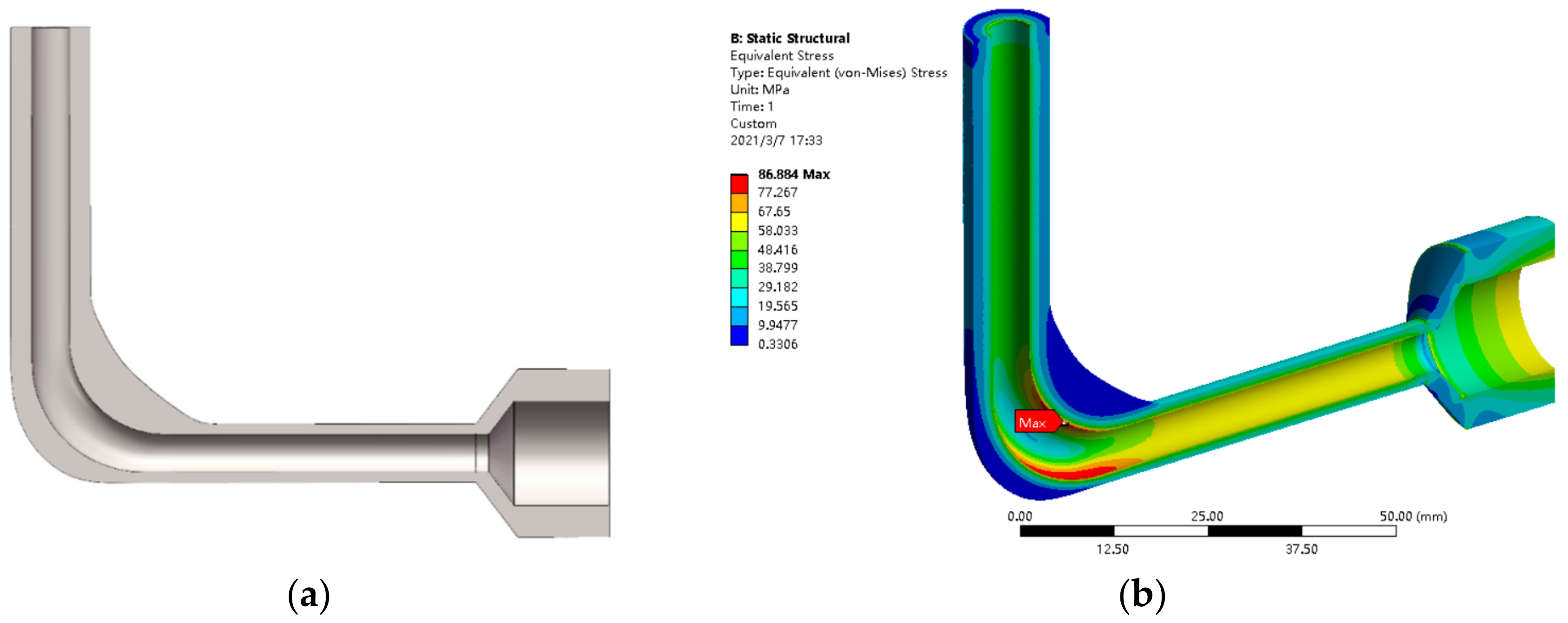

| Parameter | Value (mm) |
|---|---|
| D1 | 6 |
| D2 | 16.5 |
| L1 | 67 |
| L2 | 67 |
| L3 | 21 |
| Parameter | Value | Unit |
|---|---|---|
| T | 323.15 | K |
| p | 20 | MPa |
| ρ | 870.15 | kg/m3 |
| C | 4812 | Cal/(g·K) |
| μ | 0.02501 | kg/(m s) |
| Level | R1 (mm) | R2 (mm) |
|---|---|---|
| 1.828 | 14.398 | 20.398 |
| 1 | 11.5 | 17.5 |
| 0 | 8 | 14 |
| −1 | 4.5 | 10.5 |
| −1.828 | 1.602 | 7.602 |
| Design Point | R1 (mm) | R2 (mm) | Δp (Pa) |
|---|---|---|---|
| 1 | 4.5 | 10.5 | 251,030 |
| 2 | 4.5 | 17.5 | 366,420 |
| 3 | 11.5 | 10.5 | 234,500 |
| 4 | 11.5 | 17.5 | 214,860 |
| 5 | 1.6 | 14 | 369,470 |
| 6 | 14.4 | 14 | 203,640 |
| 7 | 8 | 7.6 | 262,250 |
| 8 | 8 | 20.4 | 347,080 |
| 9 | 8 | 14 | 230,700 |
| 10 | 8 | 14 | 230,700 |
| Level | x1 (mm) | x2 (mm) | x3 (mm) | x4 (mm) | x5 (mm) | x6 (mm) |
|---|---|---|---|---|---|---|
| 2.828 | 4.7 | 5.48 | 5.48 | 7.83 | 7.83 | 4.7 |
| 1 | 3.6 | 4.2 | 4.2 | 6 | 6 | 3.6 |
| 0 | 3 | 3.5 | 3.5 | 5 | 5 | 3 |
| −1 | 2.4 | 2.8 | 2.8 | 4 | 4 | 2.4 |
| −2.828 | 1.3 | 1.52 | 1.52 | 2.17 | 2.17 | 1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, H.; Zou, B.; Ma, Y.; Lange, C.F.; Liu, J.; Li, L. Intelligent Design Optimization System for Additively Manufactured Flow Channels Based on Fluid–Structure Interaction. Micromachines 2022, 13, 100. https://doi.org/10.3390/mi13010100
Ji H, Zou B, Ma Y, Lange CF, Liu J, Li L. Intelligent Design Optimization System for Additively Manufactured Flow Channels Based on Fluid–Structure Interaction. Micromachines. 2022; 13(1):100. https://doi.org/10.3390/mi13010100
Chicago/Turabian StyleJi, Haonan, Bin Zou, Yongsheng Ma, Carlos F. Lange, Jikai Liu, and Lei Li. 2022. "Intelligent Design Optimization System for Additively Manufactured Flow Channels Based on Fluid–Structure Interaction" Micromachines 13, no. 1: 100. https://doi.org/10.3390/mi13010100






