Performance Analysis of Electromyogram Signal Compression Sampling in a Wireless Body Area Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. WBSN
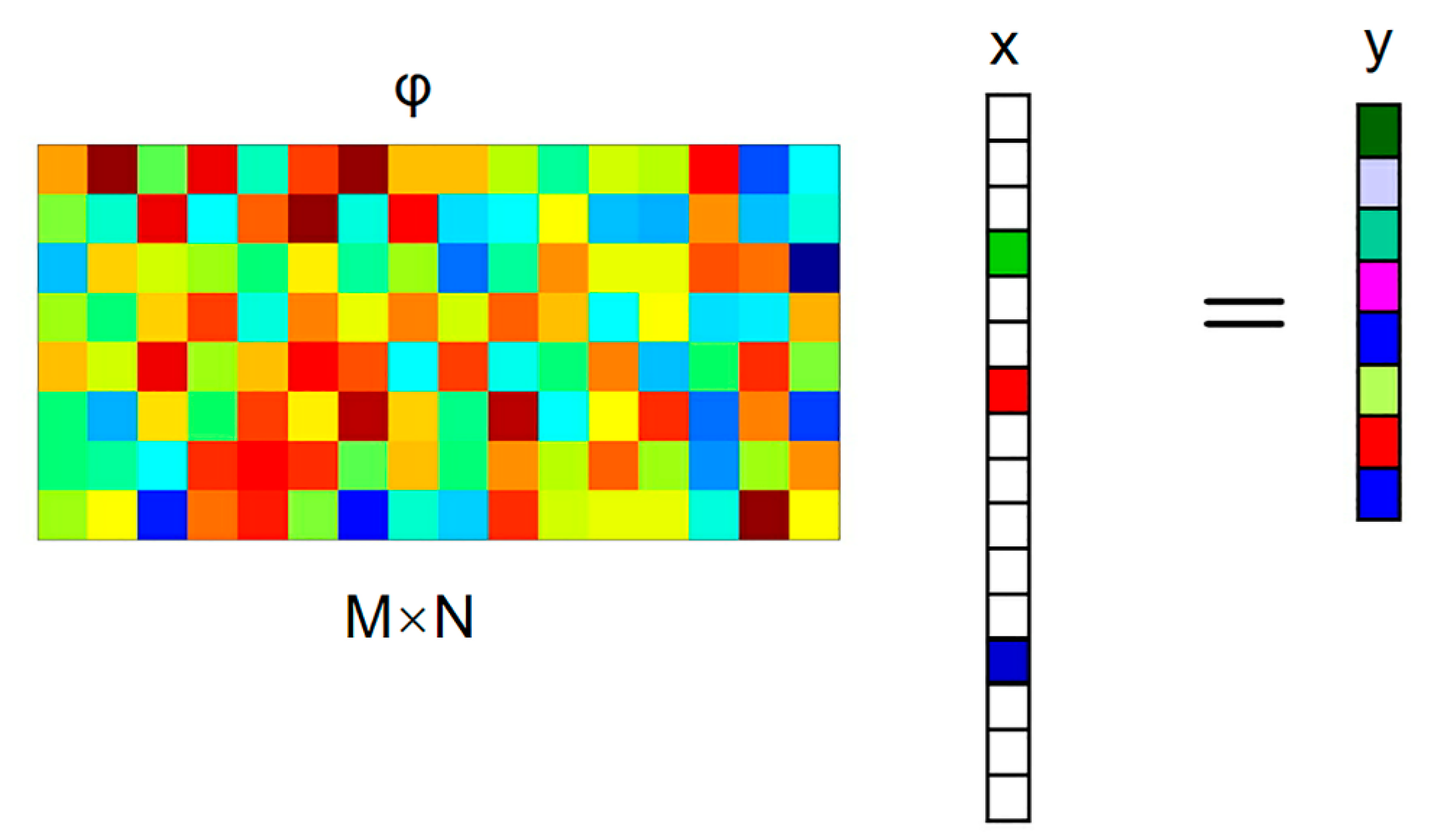
2.2. Compressed Sensing
| Algorithm 1 Orthogonal matching pursuit (OMP) |
| Input: matrix , measurements y, sparsity K |
| Output: sparse reconstruction |
| 1: and |
| 2: for…, K do |
3:  Find best fitting column Find best fitting column |
| 4: |
5:  LS optimization LS optimization |
6:  Residual update Residual update |
| 7: end for |
2.3. Description of the EMG Datasets
2.4. Performance Indicator
2.5. Compression Ratio
2.6. Percentage Root Mean Square Distortion
2.7. Sparse Basis
2.8. Reconstruction Algorithms
2.9. Hardware Platform
3. Results
3.1. Compressed Sensing with Different Kinds of Wavelet Bases
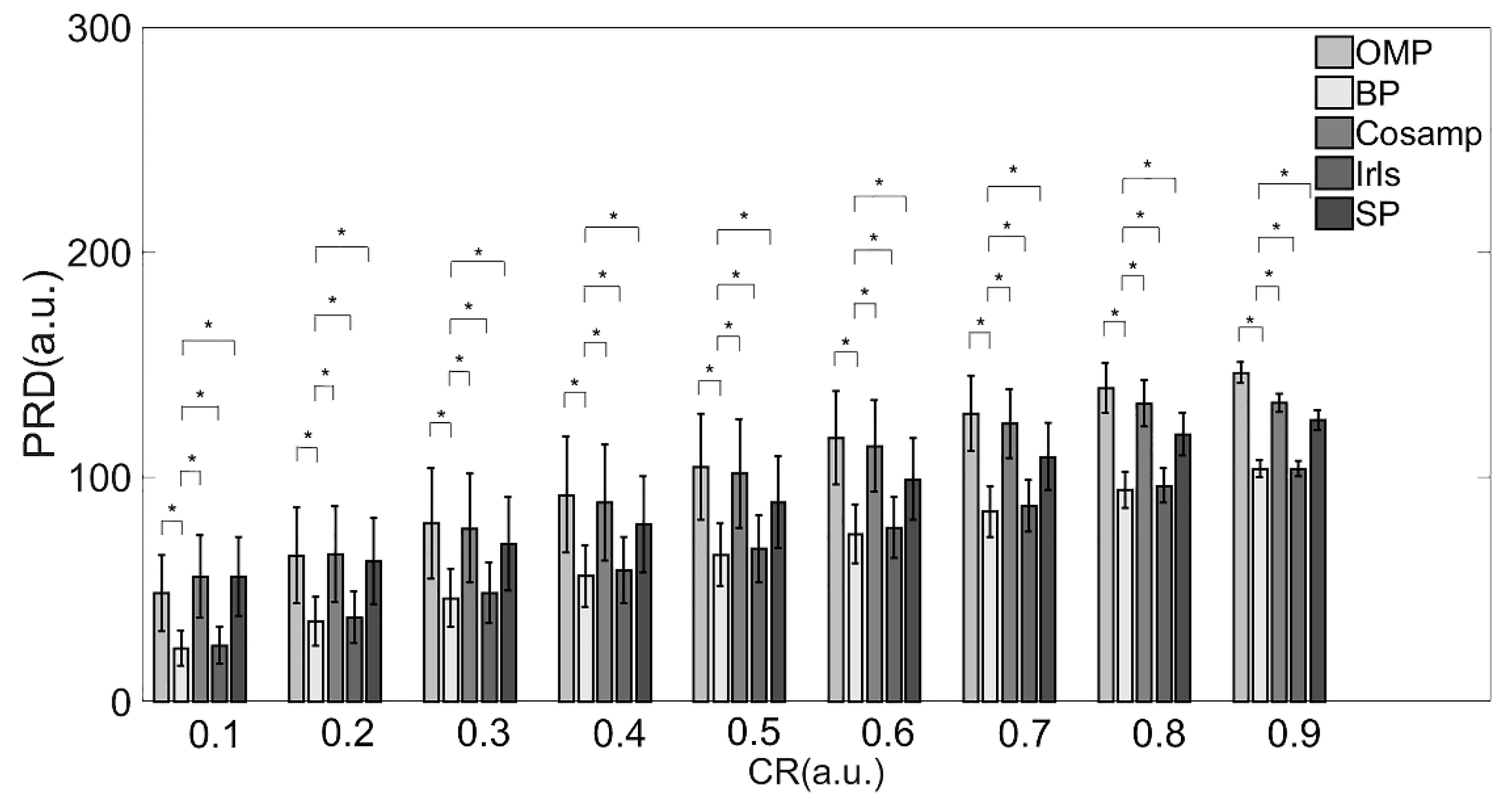
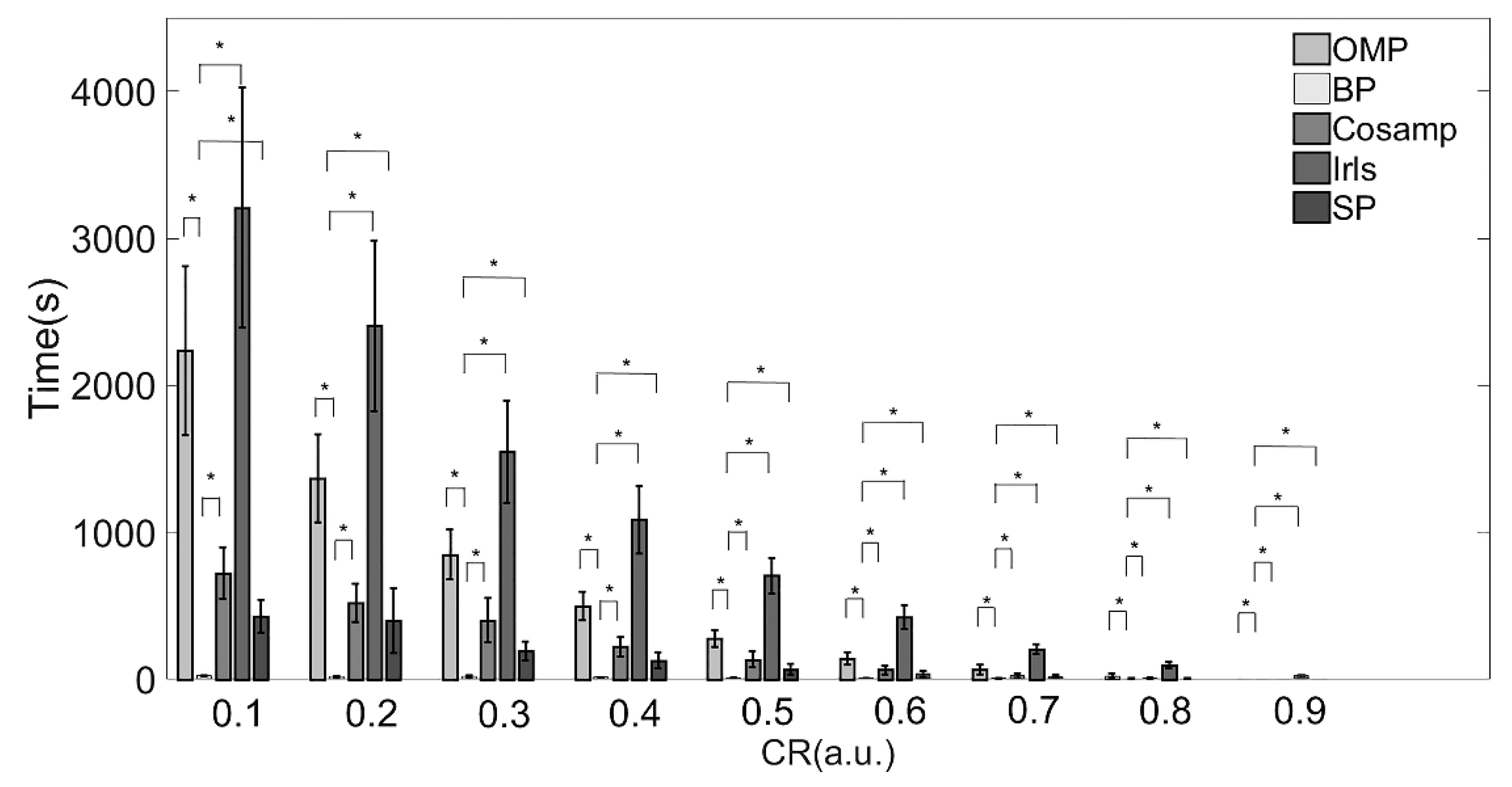
3.2. Compressed Sensing with Different Kinds of Construction Algorithms
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paoletti, M.; Belli, A.; Palma, L.; Vallasciani, M.; Pierleoni, P.J.E. A Wireless Body Sensor Network for Clinical Assessment of the Flexion-Relaxation Phenomenon. Electronics 2020, 9, 1044. [Google Scholar] [CrossRef]
- Kobylarz, J.; Bird, J.J.; Faria, D.R.; Ribeiro, E.P.; Intelligence, A.E.J.J.o.A.; Computing, H. Thumbs up, thumbs down: Non-verbal human-robot interaction through real-time EMG classification via inductive and supervised transductive transfer learning. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 6021–6031. [Google Scholar] [CrossRef] [Green Version]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef] [Green Version]
- Akyildiz, I.F.; Vuran, M.C.; Akan, O.B.; Su, W. Wireless sensor networks: A survey revisited. Comput. Netw. J. Elsevier Sci. 2004, 45, 1–39. [Google Scholar]
- Jovanov, E.; Milenkovic, A.; Otto, C.; de Groen, P.C. A wireless body area network of intelligent motion sensors for computer assisted physical rehabilitation. J. Neuroeng. Rehabil. 2005, 2, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, W.; Zhang, M.; Sawchuk, A.A.; Sarrafzadeh, M. Robust human activity and sensor location corecognition via sparse signal representation. IEEE Trans. Biomed. Eng. 2012, 59, 3169–3176. [Google Scholar] [PubMed]
- Yildirim, O.; San Tan, R.; Acharya, U.R.J.C.S.R. An Efficient Compression of ECG Signals Using Deep Convolutional Autoencoders. Cogn. Syst. Res. 2022, 52, 198–211. [Google Scholar] [CrossRef]
- Shoaib, M.; Jha, N.K.; Verma, N. A Compressed-Domain Processor for Seizure Detection to Simultaneously Reduce Computation and Communication Energy. In Proceedings of the IEEE 2012 Custom Integrated Circuits Conference, San Jose, CA, USA, 9–12 September 2012; pp. 1–4. [Google Scholar]
- Zhang, Z.; Jung, T.-P.; Makeig, S.; Rao, B.D. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware. IEEE Trans. Biomed. Eng. 2012, 60, 221–224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imtiaz, S.A.; Casson, A.J.; Rodriguez-Villegas, E. Compression in wearable sensor nodes: Impacts of node topology. IEEE Trans. Biomed. Eng. 2013, 61, 1080–1090. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; de Vos, M.; van Huffel, S. Compressed sensing of multichannel EEG signals: The simultaneous cosparsity and low-rank optimization. IEEE Trans. Biomed. Eng. 2015, 62, 2055–2061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aviyente, S. Compressed Sensing Framework for EEG Compression. In Proceedings of the IEEE 14th Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; pp. 181–184. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Abdulghani, A.M.; Casson, A.J.; Rodriguez-Villegas, E. Compressive sensing scalp EEG signals: Implementations and practical performance. Med. Biol. Eng. Comput. 2012, 50, 1137–1145. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Sun, B.; Tong, W.; Zhi, Y. On-Chip Neural Data Compression based on Compressed Sensing with Sparse Sensing Matrices. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 242–254. [Google Scholar] [CrossRef] [PubMed]
- Quwaider, M.; Rao, J.; Biswas, S.K. Body-posture-based dynamic link power control in wearable sensor networks. Commun. Mag. IEEE 2010, 48, 134–142. [Google Scholar] [CrossRef]
- Mamaghanian, H.; Khaled, N.; Atienza, D.; Vandergheynst, P. Compressed Sensing for Real-Time Energy-Efficient ECG Compression on Wireless Body Sensor Nodes. IEEE Trans. Biomed. Eng. 2011, 58, 2456–2466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Jung, T.P.; Makeig, S.; Rao, B.D. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning. IEEE Trans. Biomed. Eng. 2012, 60, 300–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dixon, A.M.; Allstot, E.G.; Gangopadhyay, D.; Allstot, D.J. Compressed sensing system considerations for ECG and EMG wireless biosensors. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 156–166. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef] [Green Version]
- Ashton, K. That ‘internet of things’ thing. RFID J. 2009, 22, 97–114. [Google Scholar]
- Da Xu, L.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar]
- Hur, K.; Sohn, W.-S.; Kim, J.-K.; Lee, Y. A Real-Time Localization Platform Design in WUSB over WBAN Protocol for Wearable Computer Systems. In Proceedings of the International Conference on Future Generation Information Technology, Jeju Island, Korea, 8–10 December 2011; pp. 173–180. [Google Scholar]
- Azhari, M.E.; Toumanari, A.; Latif, R. Performance analysis of IEEE 802.15.6 and IEEE 802.15.4 for wireless body sensor networks. In Proceedings of the International Conference on Multimedia Computing & Systems, Marrakech, Morocco, 14–16 April 2014. [Google Scholar]
- Huque, M.; Munasinghe, K.S.; Jamalipour, A. A Probabilistic Energy-Aware Routing Protocol for Wireless Body Area Networks. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014. [Google Scholar]
- Chen, G.; Naganawa, J.-I.; Takada, J.-I.; Kim, M. Development of a tri-polarized dynamic channel sounder for wireless body area network. In Proceedings of the 2015 9th International Symposium on Medical Information and Communication Technology (ISMICT), Kamakura, Japan, 14 May 2015; pp. 30–34. [Google Scholar]
- Jain, P.C. Wireless body area network for medical healthcare. IETE Tech. Rev. 2011, 28, 362–371. [Google Scholar] [CrossRef]
- Gelogo, Y.E.; Hwang, H.J.; Kim, H.-K. Internet of things (IoT) framework for u-healthcare system. Int. J. Smart Home 2015, 9, 323–330. [Google Scholar] [CrossRef] [Green Version]
- Gelogo, Y.E.; Kim, H.-K. Unified ubiquitous healthcare system architecture with collaborative model. Int. J. Multimed. Ubiquitous Eng. 2013, 8, 239–244. [Google Scholar]
- Alkhayyat, A.; Thabit, A.A.; Al-Mayali, F.A.; Abbasi, Q.H. WBSN in IoT health-based application: Toward delay and energy consumption minimization. J. Sens. 2019, 2019, 2508452. [Google Scholar] [CrossRef]
- Kumari, R.S.S.; Rajalakshmi, E. Very large-scale integration architecture for wavelet-based ECG signal adaptive coder. IET Signal Process. 2019, 13, 56–64. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef] [Green Version]
- Erlich, Y.; Chang, K.; Gordon, A.; Ronen, R.; Navon, O.; Rooks, M.; Hannon, G.J. DNA Sudoku—Harnessing high-throughput sequencing for multiplexed specimen analysis. Genome Res. 2009, 19, 1243–1253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal 1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Gui, G.; Wan, Q.; Peng, W.; Adachi, F. Sparse multipath channel estimation using compressive sampling matching pursuit algorithm. arXiv 2010, arXiv:1005.2270. [Google Scholar]
- Ramani, S.; Fessler, J.A. An Accelerated Iterative Reweighted least squares algorithm for compressed sensing MRI. In Proceedings of the 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Rotterdam, The Netherlands, 14–17 April 2010; pp. 257–260. [Google Scholar]
- Liu, J.; Huang, K.; Yao, X. Common-innovation subspace pursuit for distributed compressed sensing in wireless sensor networks. IEEE Sens. J. 2018, 19, 1091–1103. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.-L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Bai, L.; Maechler, P.; Muehlberghuber, M.; Kaeslin, H. High-speed compressed sensing reconstruction on FPGA using OMP and AMP. In Proceedings of the 2012 19th IEEE International Conference on Electronics, Circuits, and Systems (ICECS 2012), Seville, Spain, 9–12 December 2012; pp. 53–56. [Google Scholar]
- Nguyen, R.; Brown, M.S. Fast and Effective L0 Gradient Minimization by Region Fusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 208–216. [Google Scholar]
- Bandeira, A.S.; Fickus, M.; Mixon, D.G.; Wong, P. The Road to Deterministic Matrices with the Restricted Isometry Property. J. Fourier Anal. Appl. 2012, 19, 1123–1149. [Google Scholar] [CrossRef]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.C.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.; Stanley, H. Components of a new research resource for complex physiologic signals. PhysioBank PhysioToolkit Physionet. 2000, 101, 215–220. [Google Scholar]
- Casson, A.J.; Rodriguez-Villegas, E. Signal agnostic compressive sensing for body area networks: Comparison of signal reconstructions. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 4497–4500. [Google Scholar]

| Wavelet | CR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | |
| haar | 30.67 ± 9.64 | 44.71 ± 15.35 | 56.62 ± 19.77 | 67.72 ± 21.97 | 78.64 ± 21.76 | 89.84 ± 21.33 | 100.41 ± 20.97 | 111.34 ± 20.98 | 120.4 ± 21.71 |
| db2 | 23.74 ± 7.82 | 35.66 ± 10.63 | 45.99 ± 12.71 | 55.71 ± 13.83 | 65.23 ± 13.93 | 74.68 ± 13.09 | 84.34 ± 11.21 | 94.2 ± 7.93 | 103.48 ± 3.77 |
| db3 | 34 ± 13.6 | 45.17 ± 15.65 | 55.86 ± 18.73 | 66.26 ± 20.84 | 77.4 ± 20.99 | 88.59 ± 19.82 | 99.2 ± 18.65 | 109.18 ± 17.97 | 115.23 ± 14.19 |
| db4 | 24.15 ± 7.61 | 36.33 ± 10.45 | 46.9 ± 12.67 | 56.74 ± 13.94 | 66.32 ± 13.87 | 75.88 ± 12.83 | 85.49 ± 10.6 | 95.25 ± 7.36 | 103.65 ± 3.57 |
| db5 | 34.51 ± 13.95 | 44.91 ± 14.47 | 54.38 ± 16.07 | 63.69 ± 16.75 | 73.42 ± 16.39 | 83.56 ± 14.94 | 93.56 ± 13.43 | 104.01 ± 11.12 | 112.27 ± 9.95 |
| db6 | 26.25 ± 5.08 | 39.05 ± 6.1 | 50.01 ± 6.96 | 60.13 ± 7.2 | 69.63 ± 7.34 | 78.71 ± 6.83 | 87.81 ± 5.66 | 96.87 ± 3.88 | 104.78 ± 1.8 |
| db7 | 26.4 ± 4.98 | 39.31 ± 5.96 | 50.19 ± 6.92 | 60.12 ± 7.26 | 69.65 ± 7 | 78.77 ± 6.6 | 87.91 ± 5.4 | 96.76 ± 3.74 | 104.87 ± 1.59 |
| db8 | 26.5 ± 5.15 | 39.23 ± 6.17 | 50.09 ± 6.9 | 60.22 ± 7.02 | 69.8 ± 6.9 | 78.99 ± 6.15 | 88.17 ± 5.45 | 96.97 ± 3.83 | 105.06 ± 1.38 |
| db9 | 26.55 ± 4.99 | 39.41 ± 6 | 50.43 ± 6.77 | 60.41 ± 7.09 | 69.92 ± 6.84 | 79.2 ± 6.34 | 88.16 ± 5.32 | 96.98 ± 3.71 | 104.93 ± 1.49 |
| db10 | 26.65 ± 5.08 | 39.52 ± 6.05 | 50.42 ± 6.92 | 60.55 ± 6.97 | 69.82 ± 6.88 | 79.18 ± 6.27 | 88.12 ± 5.57 | 97.13 ± 3.66 | 104.99 ± 1.51 |
| sym2 | 25.7 ± 5.1 | 38.51 ± 6.02 | 49.29 ± 7.08 | 59.37 ± 7.65 | 68.93 ± 7.56 | 78.25 ± 7.06 | 87.46 ± 6.07 | 96.44 ± 4.25 | 104.82 ± 1.61 |
| sym3 | 25.81 ± 5.31 | 38.49 ± 6.26 | 49.4 ± 7.19 | 59.53 ± 7.45 | 68.94 ± 7.54 | 78.17 ± 6.89 | 87.44 ± 6.05 | 96.35 ± 4.19 | 104.64 ± 1.82 |
| sym4 | 25.87 ± 5.2 | 38.58 ± 6.31 | 49.38 ± 7.16 | 59.44 ± 7.48 | 68.92 ± 7.71 | 78.27 ± 6.9 | 87.46 ± 6.16 | 96.39 ± 4.49 | 104.54 ± 1.81 |
| sym5 | 25.93 ± 5.16 | 38.61 ± 6.2 | 49.49 ± 7.1 | 59.41 ± 7.46 | 69.03 ± 7.55 | 78.2 ± 6.99 | 87.41 ± 5.92 | 96.44 ± 4.17 | 104.63 ± 1.86 |
| sym6 | 25.93 ± 5.16 | 38.67 ± 6.21 | 49.56 ± 7.17 | 59.54 ± 7.44 | 69.04 ± 7.74 | 78.33 ± 6.83 | 87.57 ± 6.03 | 96.36 ± 4.53 | 104.61 ± 1.8 |
| sym7 | 26.03 ± 5.32 | 38.79 ± 6.21 | 49.55 ± 7.03 | 59.68 ± 7.36 | 69 ± 7.58 | 78.42 ± 6.84 | 87.42 ± 6.05 | 96.53 ± 4.24 | 104.68 ± 1.71 |
| sym8 | 25.99 ± 5.13 | 38.73 ± 6.14 | 49.64 ± 7.15 | 59.62 ± 7.38 | 69.07 ± 7.7 | 78.35 ± 6.79 | 87.63 ± 5.98 | 96.4 ± 4.47 | 104.67 ± 1.7 |
| coif1 | 25.65 ± 5.12 | 38.39 ± 6.07 | 49.19 ± 7.01 | 59.22 ± 7.68 | 68.78 ± 7.61 | 78.06 ± 7.03 | 87.33 ± 5.92 | 96.49 ± 4.24 | 104.5 ± 1.77 |
| coif2 | 25.83 ± 5.21 | 38.51 ± 6.23 | 49.25 ± 7.13 | 59.41 ± 7.49 | 68.9 ± 7.62 | 78.06 ± 7 | 87.35 ± 6.08 | 96.22 ± 4.35 | 104.54 ± 1.8 |
| coif3 | 25.95 ± 5.14 | 38.82 ± 6.17 | 49.55 ± 7.07 | 59.63 ± 7.39 | 69.15 ± 7.3 | 78.34 ± 6.98 | 87.54 ± 5.61 | 96.71 ± 4.09 | 104.47 ± 1.94 |
| coif4 | 26.01 ± 5.12 | 38.77 ± 6.18 | 49.54 ± 7.12 | 59.64 ± 7.42 | 69.16 ± 7.47 | 78.29 ± 6.77 | 87.53 ± 5.86 | 96.39 ± 4.32 | 104.69 ± 1.57 |
| coif5 | 26.05 ± 5.1 | 38.89 ± 6.12 | 49.73 ± 6.89 | 59.84 ± 7.32 | 69.25 ± 7.17 | 78.59 ± 6.57 | 87.69 ± 5.56 | 96.57 ± 4.06 | 104.7 ± 1.64 |
| bior1.1 | 25.38 ± 5.22 | 38.16 ± 6.3 | 48.93 ± 7.15 | 59.22 ± 7.62 | 68.59 ± 7.79 | 77.89 ± 7.23 | 87.16 ± 6.47 | 96.3 ± 4.47 | 104.3 ± 2.35 |
| bior1.3 | 26.13 ± 5.24 | 39.08 ± 6.3 | 50.02 ± 7.15 | 60.3 ± 7.49 | 69.84 ± 7.63 | 79.06 ± 7.09 | 88.03 ± 6.27 | 97.12 ± 4.09 | 104.76 ± 2.07 |
| bior1.5 | 26.74 ± 5.32 | 39.89 ± 6.35 | 50.99 ± 7.15 | 61.28 ± 7.4 | 70.8 ± 7.56 | 79.95 ± 6.96 | 88.81 ± 6.19 | 97.68 ± 3.98 | 105.06 ± 1.99 |
| bior2.2 | 27.19 ± 5.32 | 40.77 ± 6.25 | 52.45 ± 7.26 | 63.25 ± 7.7 | 73.29 ± 7.6 | 83.16 ± 6.78 | 92.33 ± 5.58 | 101.39 ± 3.46 | 108.44 ± 1.31 |
| bior2.4 | 27.01 ± 5.31 | 40.46 ± 6.25 | 51.98 ± 7.13 | 62.56 ± 7.57 | 72.54 ± 7.48 | 82.12 ± 6.77 | 91.22 ± 5.52 | 100.33 ± 3.73 | 107.45 ± 1.33 |
| bior2.6 | 27.12 ± 5.33 | 40.6 ± 6.26 | 52.09 ± 7.05 | 62.61 ± 7.49 | 72.56 ± 7.4 | 82.17 ± 6.75 | 91.22 ± 5.54 | 100.28 ± 3.79 | 107.41 ± 1.44 |
| bior2.8 | 27.28 ± 5.33 | 40.83 ± 6.25 | 52.32 ± 7.02 | 62.83 ± 7.45 | 72.76 ± 7.32 | 82.4 ± 6.71 | 91.43 ± 5.51 | 100.39 ± 3.81 | 107.48 ± 1.45 |
| bior3.1 | 31.7 ± 5.32 | 47.76 ± 6.35 | 61.99 ± 7.2 | 75.45 ± 7.31 | 88.62 ± 6.63 | 101.05 ± 5.78 | 114.82 ± 5.26 | 128.26 ± 3.62 | 135.14 ± 1.27 |
| bior3.3 | 30.81 ± 5.07 | 45.97 ± 6.38 | 59.09 ± 7.18 | 71.06 ± 7.51 | 82.48 ± 6.86 | 93.13 ± 6.18 | 103.41 ± 4.95 | 113.08 ± 2.79 | 118.76 ± 0.9 |
| bior3.5 | 30.59 ± 5.12 | 45.37 ± 6.41 | 58.1 ± 7.21 | 69.95 ± 7.44 | 80.92 ± 6.9 | 91.26 ± 6.02 | 100.76 ± 4.87 | 110.2 ± 2.87 | 115.69 ± 0.84 |
| bior3.7 | 30.52 ± 5.2 | 45.12 ± 6.41 | 57.72 ± 7.17 | 69.49 ± 7.41 | 80.36 ± 6.94 | 90.51 ± 6.07 | 99.96 ± 4.93 | 109.31 ± 2.89 | 115.01 ± 0.85 |
| bior3.9 | 28.26 ± 5.08 | 41.86 ± 6.01 | 53.02 ± 7.04 | 63.32 ± 7.44 | 72.8 ± 7.2 | 81.82 ± 6.59 | 90.73 ± 5.4 | 99.52 ± 3.82 | 106.96 ± 2.08 |
| bior4.4 | 27.66 ± 5.05 | 40.99 ± 5.95 | 52.06 ± 6.98 | 62.27 ± 7.29 | 71.89 ± 7.03 | 81.06 ± 6.43 | 90.17 ± 5.35 | 99.19 ± 3.77 | 106.92 ± 1.97 |
| bior5.5 | 27.71 ± 5.07 | 41.03 ± 5.97 | 52.08 ± 6.95 | 62.32 ± 7.19 | 71.96 ± 6.89 | 81.11 ± 6.29 | 90.26 ± 5.25 | 99.28 ± 3.64 | 107.03 ± 1.92 |
| bior6.8 | 27.83 ± 5.08 | 41.19 ± 6.01 | 52.25 ± 6.94 | 62.53 ± 7.13 | 72.17 ± 6.8 | 81.29 ± 6.2 | 90.45 ± 5.16 | 99.43 ± 3.53 | 107.15 ± 1.87 |
| rbio1.1 | 51.95 ± 6.79 | 67.99 ± 5.93 | 78.33 ± 5.85 | 85.43 ± 5.45 | 91.67 ± 4.53 | 97 ± 4.04 | 102.15 ± 3.49 | 107.48 ± 3.11 | 110.34 ± 2.02 |
| rbio1.3 | 35.01 ± 5.42 | 52.02 ± 5.99 | 64.7 ± 6.58 | 74.85 ± 6.3 | 83.53 ± 5.58 | 91.01 ± 4.74 | 98.25 ± 3.97 | 105.47 ± 3.28 | 110.4 ± 2.1 |
| rbio1.5 | 32.77 ± 5.26 | 48.84 ± 6 | 61.35 ± 6.63 | 71.9 ± 6.64 | 81.07 ± 5.98 | 89.16 ± 4.99 | 96.97 ± 4.23 | 104.85 ± 3.29 | 110.48 ± 2.09 |
| rbio2.2 | 32.44 ± 5.2 | 48.1 ± 6.06 | 60.4 ± 6.69 | 70.97 ± 6.71 | 80.14 ± 6.1 | 88.41 ± 5.18 | 96.51 ± 4.25 | 104.61 ± 3.34 | 110.57 ± 2.08 |
| rbio2.4 | 32.4 ± 5.19 | 47.84 ± 6.13 | 60.06 ± 6.72 | 70.61 ± 6.73 | 79.78 ± 6.13 | 88.18 ± 5.24 | 96.38 ± 4.21 | 104.55 ± 3.35 | 110.63 ± 2.11 |
| rbio2.6 | 26.28 ± 5.16 | 39.22 ± 6.13 | 50.06 ± 7.12 | 60.13 ± 7.62 | 69.82 ± 7.49 | 79.08 ± 6.87 | 88.16 ± 5.78 | 97.04 ± 4.05 | 104.8 ± 1.8 |
| rbio2.8 | 26.57 ± 5.3 | 39.77 ± 6.33 | 50.96 ± 7.18 | 61.36 ± 7.69 | 71.29 ± 7.64 | 80.76 ± 7.05 | 89.85 ± 5.76 | 98.73 ± 4 | 106.28 ± 1.68 |
| rbio3.1 | 26.19 ± 5.13 | 39.06 ± 6.13 | 49.83 ± 6.98 | 59.83 ± 7.46 | 69.44 ± 7.28 | 78.71 ± 6.7 | 87.85 ± 5.63 | 96.82 ± 3.94 | 104.92 ± 1.8 |
| rbio3.3 | 28.26 ± 5.08 | 41.86 ± 6.01 | 53.02 ± 7.04 | 63.32 ± 7.44 | 72.8 ± 7.2 | 81.82 ± 6.59 | 90.73 ± 5.4 | 99.52 ± 3.82 | 106.96 ± 2.08 |
| rbio3.5 | 27.66 ± 5.05 | 40.99 ± 5.95 | 52.06 ± 6.98 | 62.27 ± 7.29 | 71.89 ± 7.03 | 81.06 ± 6.43 | 90.17 ± 5.35 | 99.19 ± 3.77 | 106.92 ± 1.97 |
| rbio3.7 | 27.71 ± 5.07 | 41.03 ± 5.97 | 52.08 ± 6.95 | 62.32 ± 7.19 | 71.96 ± 6.89 | 81.11 ± 6.29 | 90.26 ± 5.25 | 99.28 ± 3.64 | 107.03 ± 1.92 |
| rbio3.9 | 27.83 ± 5.08 | 41.19 ± 6.01 | 52.25 ± 6.94 | 62.53 ± 7.13 | 72.17 ± 6.8 | 81.29 ± 6.2 | 90.45 ± 5.16 | 99.43 ± 3.53 | 107.15 ± 1.87 |
| rbio4.4 | 51.95 ± 6.79 | 67.99 ± 5.93 | 78.33 ± 5.85 | 85.43 ± 5.45 | 91.67 ± 4.53 | 97 ± 4.04 | 102.15 ± 3.49 | 107.48 ± 3.11 | 110.34 ± 2.02 |
| rbio5.5 | 35.01 ± 5.42 | 52.02 ± 5.99 | 64.7 ± 6.58 | 74.85 ± 6.3 | 83.53 ± 5.58 | 91.01 ± 4.74 | 98.25 ± 3.97 | 105.47 ± 3.28 | 110.4 ± 2.1 |
| rbio6.8 | 32.77 ± 5.26 | 48.84 ± 6 | 61.35 ± 6.63 | 71.9 ± 6.64 | 81.07 ± 5.98 | 89.16 ± 4.99 | 96.97 ± 4.23 | 104.85 ± 3.29 | 110.48 ± 2.09 |
| Method | CR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| OMP | 48.24 ± 16.85 | 65.04 ± 21.35 | 79.3 ± 24.66 | 92.13 ± 25.64 | 104.56 ± 23.64 | 117.41 ± 20.89 | 128.26 ± 16.89 | 139.69 ± 11.11 | 146.37 ± 4.82 |
| BP | 23.87 ± 7.98 | 35.71 ± 10.75 | 46.1 ± 12.81 | 55.87 ± 13.86 | 65.31 ± 13.97 | 74.71 ± 13.07 | 84.48 ± 11.31 | 94.23 ± 7.95 | 103.51 ± 3.86 |
| CoSaMP | 55.61 ± 18.29 | 65.58 ± 21.42 | 77.07 ± 24.22 | 88.58 ± 25.93 | 101.44 ± 24.29 | 113.75 ± 20.46 | 123.59 ± 15.49 | 132.66 ± 10.19 | 132.89 ± 4.04 |
| Irls | 24.99 ± 8.44 | 37.53 ± 11.39 | 48.37 ± 13.65 | 58.42 ± 14.87 | 68.03 ± 14.85 | 77.49 ± 13.62 | 87 ± 11.47 | 96.1 ± 7.79 | 103.63 ± 3.59 |
| SP | 55.51 ± 17.55 | 62.37 ± 19.22 | 70.17 ± 20.76 | 78.89 ± 21.43 | 88.76 ± 20.44 | 98.88 ± 18.09 | 108.94 ± 14.9 | 119.03 ± 9.39 | 125.35 ± 4.43 |
| Method | CR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| OMP | 2236.66 ± 574.21 | 1368.17 ± 300.14 | 849.29 ± 169.05 | 496.98 ± 96.43 | 275.77 ± 57.91 | 141.54 ± 41.09 | 65.38 ± 32.34 | 23.88 ± 17.25 | 21.01 ± 0.82 |
| BP | 24.35 ± 3.71 | 20.49 ± 3.18 | 19.55 ± 6.75 | 13.43 ± 1.62 | 10.68 ± 1.75 | 9 ± 2.73 | 6.8 ± 2 | 5.43 ± 1.51 | 3.89 ± 0.82 |
| CoSaMP | 722.35 ± 173.09 | 519.86 ± 130.66 | 401.89 ± 152.8 | 221.14 ± 64.39 | 134.06 ± 54.4 | 63.89 ± 29.86 | 26.77 ± 15.09 | 9.69 ± 5.96 | 1.9 ± 1.4 |
| Irls | 3207.79 ± 817.23 | 2405.05 ± 578.46 | 1548.56 ± 346.9 | 1086.58 ± 230.09 | 705.22 ± 120.33 | 423.7 ± 83.59 | 206.53 ± 34.87 | 94.26 ± 20.81 | 26.17 ± 9.02 |
| SP | 431.65 ± 112.13 | 397.19 ± 221.28 | 194.22 ± 61.99 | 128.29 ± 55.02 | 68.97 ± 35.96 | 36.75 ± 20.47 | 18.9 ± 12.11 | 4.48 ± 1.7 | 1.33 ± 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Chen, J.; Ma, C.; Liu, X.; Xu, L. Performance Analysis of Electromyogram Signal Compression Sampling in a Wireless Body Area Network. Micromachines 2022, 13, 1748. https://doi.org/10.3390/mi13101748
Zhang L, Chen J, Ma C, Liu X, Xu L. Performance Analysis of Electromyogram Signal Compression Sampling in a Wireless Body Area Network. Micromachines. 2022; 13(10):1748. https://doi.org/10.3390/mi13101748
Chicago/Turabian StyleZhang, Liangyu, Junxin Chen, Chenfei Ma, Xiufang Liu, and Lisheng Xu. 2022. "Performance Analysis of Electromyogram Signal Compression Sampling in a Wireless Body Area Network" Micromachines 13, no. 10: 1748. https://doi.org/10.3390/mi13101748
APA StyleZhang, L., Chen, J., Ma, C., Liu, X., & Xu, L. (2022). Performance Analysis of Electromyogram Signal Compression Sampling in a Wireless Body Area Network. Micromachines, 13(10), 1748. https://doi.org/10.3390/mi13101748








