An Adaptive Fusion Attitude and Heading Measurement Method of MEMS/GNSS Based on Covariance Matching
Abstract
:1. Introduction
2. MEMS/GNSS Combined Attitude
2.1. Error State Equation
2.2. Measurement Equation
2.3. Filter Reset
3. Parameter Adaptive Logic Adjustment
4. Adaptive Kalman Filtering Method Combining Innovation and Fading
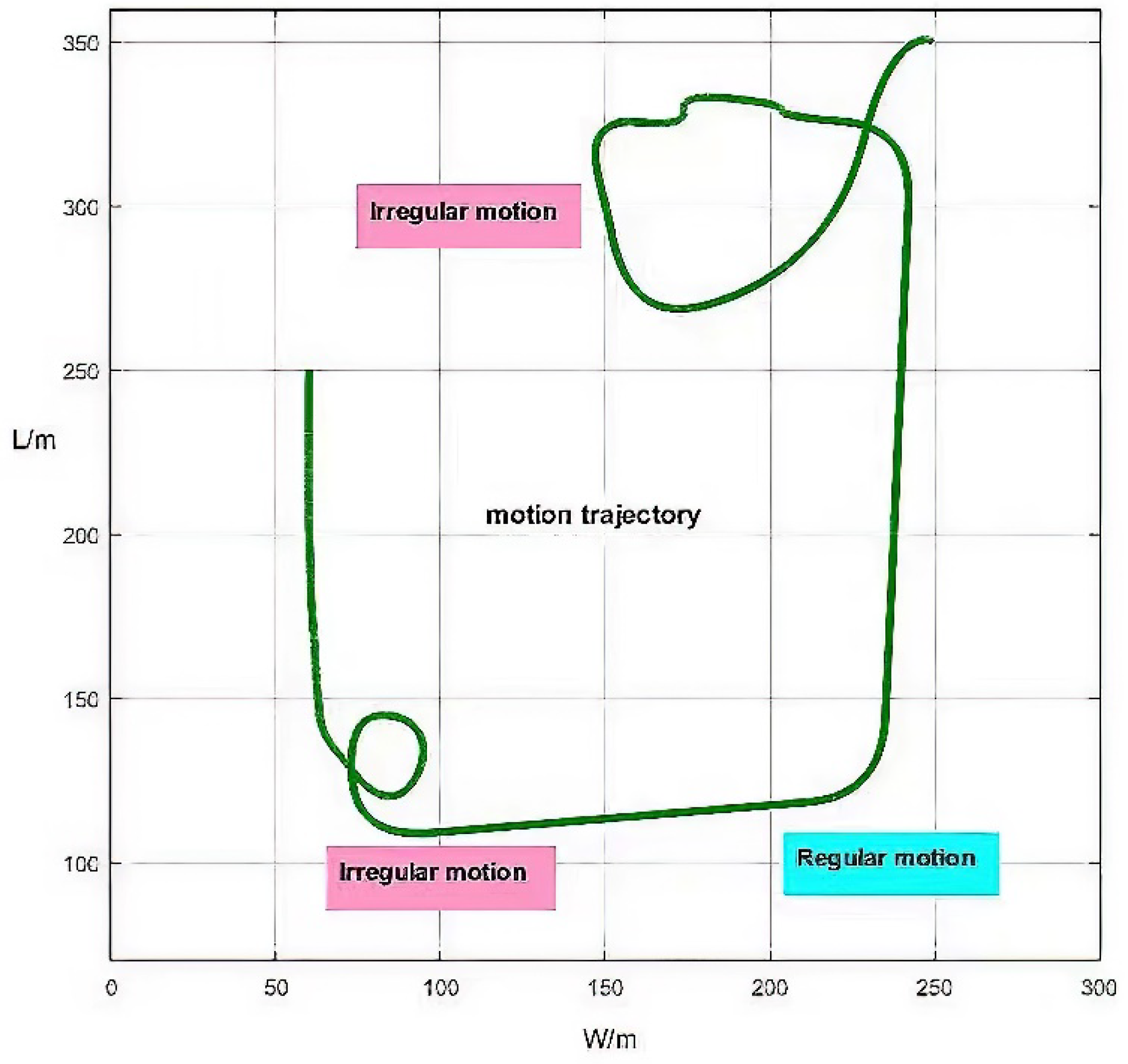
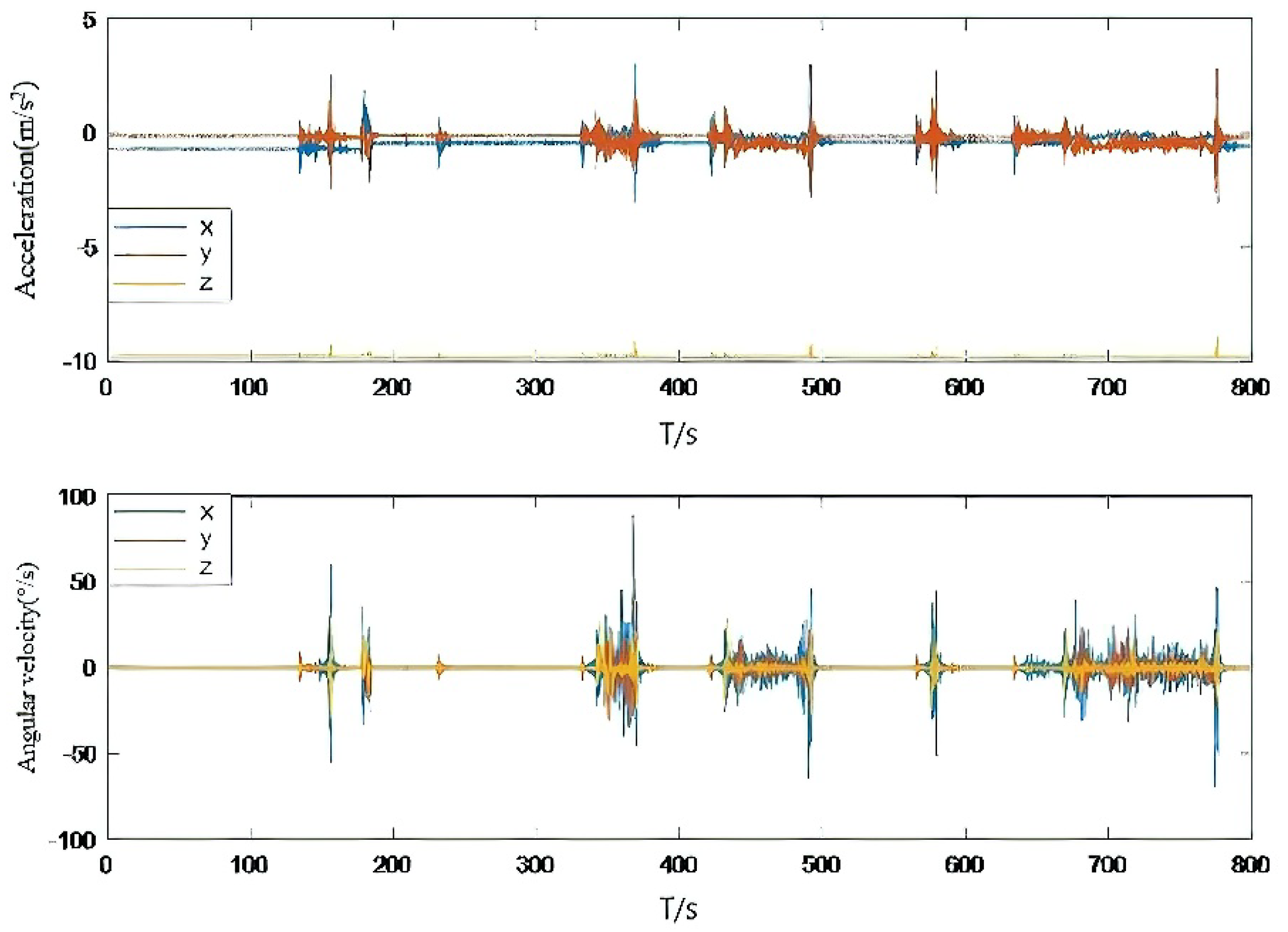
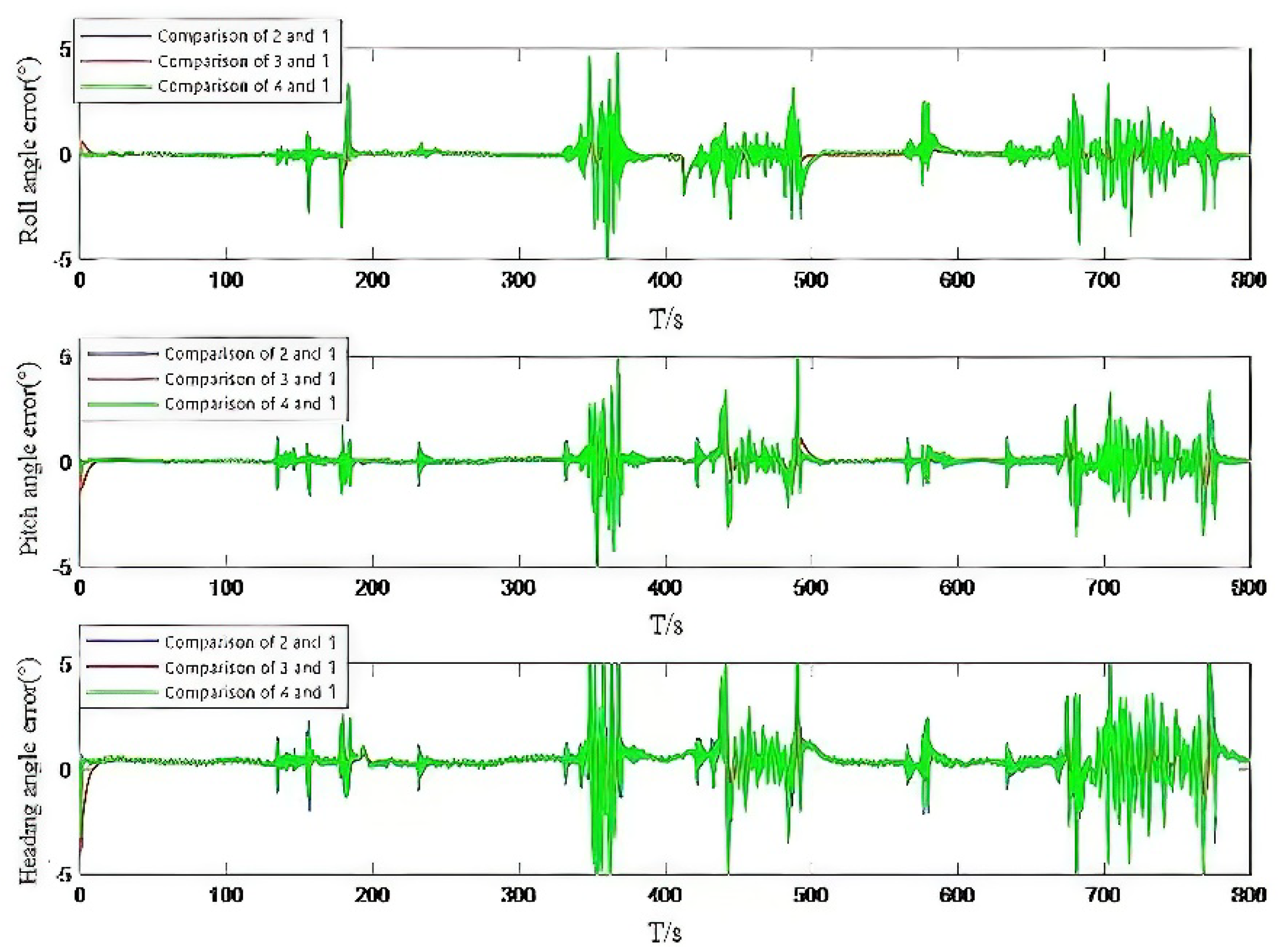
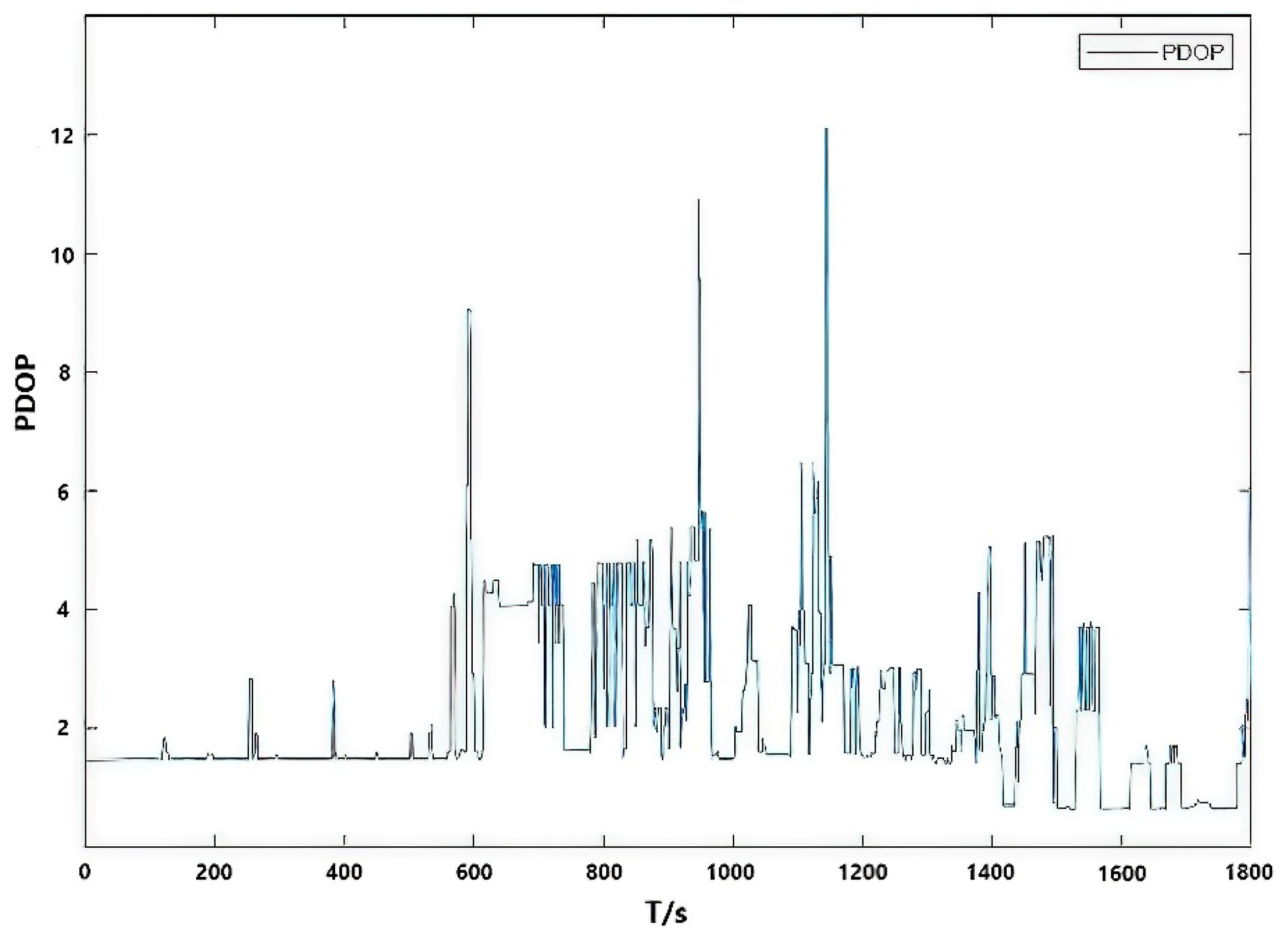
5. Experimental Results and Analysis
5.1. Verification Experiment of Algorithm Feasibility
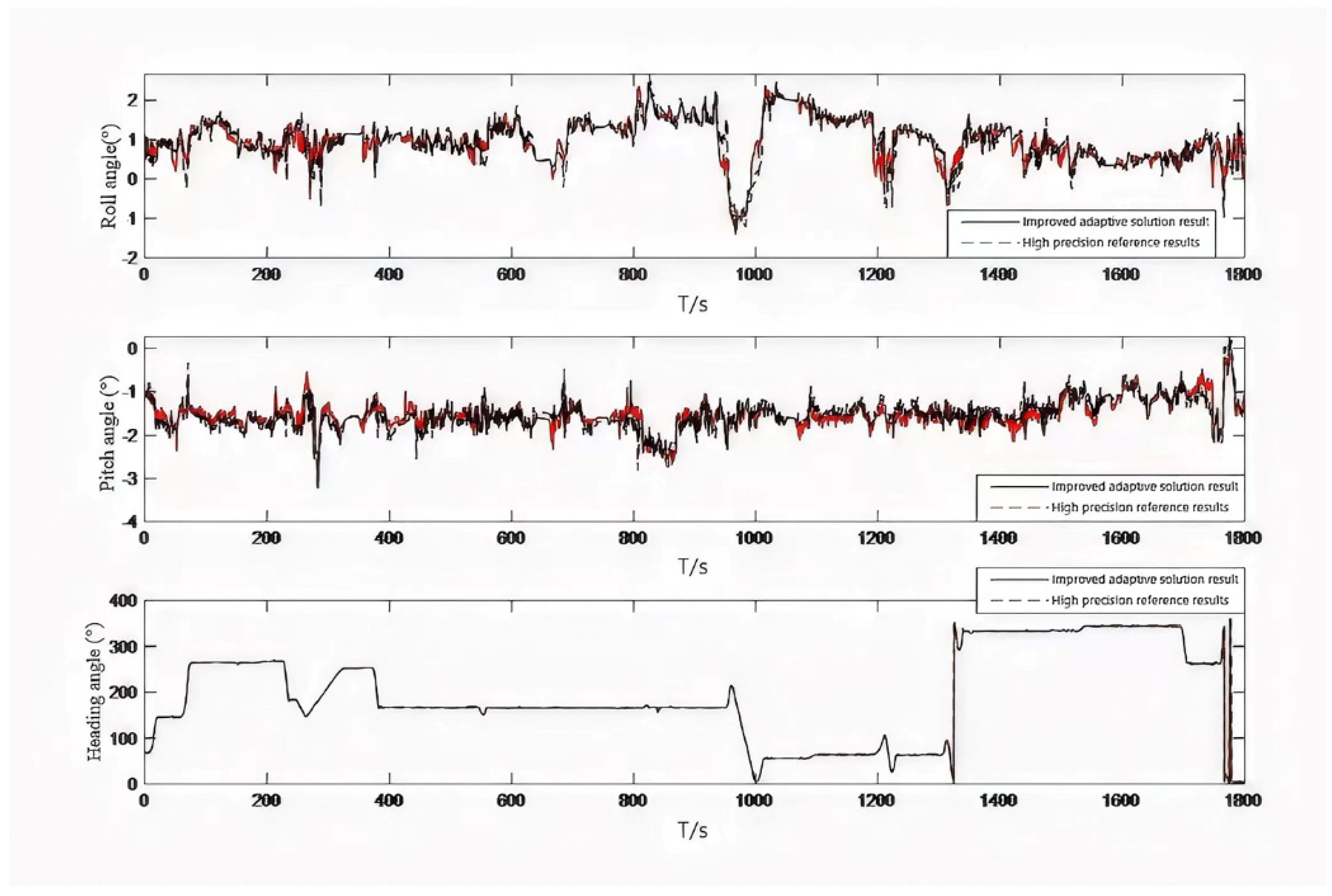
5.2. City Car-Borne Experiment in Urban Environment Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Li, W.; Huang, Y. Multisensor measurement data fusion based on Kalman filter. J. Wuhan Univ. 2011, 44, 521–525+529. [Google Scholar]
- Zhang, W. Research on Multisensor Data Fusion Algorithm Based on Neural Network. World Sci. Res. J. 2022, 8, 1–5. [Google Scholar]
- Xu, E.; Lu, W.; Liu, Y. Research on data fusion algorithm and application based on Kalman filter. Comput. Technol. Dev. 2020, 30, 143–147. [Google Scholar]
- Yan, G.; Deng, Y. Review of practical Kalman filtering technology in traditional integrated navigation. Navig. Position. Timing 2020, 7, 50–64. [Google Scholar]
- He, R.; Chen, S.; Wu, H. Efficient extended cubature Kalman filtering for nonlinear target tracking. Int. J. Syst. Sci. 2021, 52, 392–406. [Google Scholar] [CrossRef]
- Duan, S.; Sun, W.; Wu, Z. Application of robust adaptive EKF in INS/GNSS compact combination. J. Univ. Electron. Sci. Technol. 2019, 48, 216–220. [Google Scholar]
- Hu, G.; Wang, W.; Zhong, Y.; Gao, B.; Gu, C. A new direct filtering approach to INS/GNSS integration. Aerosp. Sci. Technol. 2018, 77, 755–764. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature Kalman Filter with Both Adaptability and Robustness for Tightly-Coupled GNSS/INS Integration. IEEE Sens. J. 2021, 21, 14997–15011. [Google Scholar] [CrossRef]
- Hu, G.; Gao, B.; Zhong, Y.; Gu, C. Unscented Kalman Filter with Process Noise Covariance Estimation for Vehicular INS/GPS Integration System. Inf. Fusion 2020, 64, 194–204. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Li, W.; Zhao, Y.; Zhong, Y. Maximum Likelihood-Based Measurement Noise Covariance Estimation Using Sequential Quadratic Programming for Cubature Kalman Filter Applied in INS/BDS Integration. Math. Probl. Eng. 2021. [Google Scholar] [CrossRef]
- Gao, B.; Gao, S.; Hu, G.; Zhong, Y.; Gu, C. Maximum likelihood principle and moving horizon estimation based adaptive unscented Kalman filter. Aerosp. Sci. Technol. 2018, 73, 184–196. [Google Scholar]
- Gao, Z.; Gu, C.; Yang, J.; Gao, S.; Zhong, Y. Random Weighting-Based Nonlinear Gaussian Filtering. IEEE Access 2020, 8, 19590–19605. [Google Scholar] [CrossRef]
- Gao, Z.; Mu, D.; Gao, S.; Zhong, Y.; Gu, C. Adaptive unscented Kalman filter based on maximum posterior and random weighting. Aerosp. Sci. Technol. 2017, 71, 12–24. [Google Scholar] [CrossRef]
- Gao, S.; Hu, G.; Zhong, Y. Windowing and random weighting-based adaptive unscented Kalman filter. Int. J. Adapt. Control. Signal Process. 2015, 29, 201–223. [Google Scholar] [CrossRef]
- Gao, S.; Gao, Y.; Zhong, Y.; Wei, W. Random Weighting Estimation Method for Dynamic Navigation Positioning. Chin. J. Aeronaut. 2011, 24, 318–323. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Mu, D.; Gao, S.; Zhong, Y.; Gu, C. Robust adaptive filter allowing systematic model errors for transfer alignment. Aerosp. Sci. Technol. 2016, 59, 32–40. [Google Scholar] [CrossRef]
- Wei, W.; Gao, S.; Zhong, Y.; Gu, C.; Hu, G. Adaptive Square-Root Unscented Particle Filtering Algorithm for Dynamic Navigation. Sensors 2018, 18, 2337. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Gao, S.; Zhong, Y.; Hu, G.; Subic, A. Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration. Acta Astronaut. 2016, 120, 171–181. [Google Scholar] [CrossRef]
- Zhang, F.; Yin, L.; Kang, J. Enhancing Stability and Robustness of State-of-Charge Estimation for Lithium-Ion Batteries by Using Improved Adaptive Kalman Filter Algorithms. Energies 2021, 14, 6284. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, W.; Guo, X. Research on integrated navigation technology of multi rotor UAV Based on AFKF. Comput. Meas. Control. 2019, 27, 200–204. [Google Scholar]
- Sun, W.; Wu, J.; Ding, W.; Duan, S. A Robust Indirect Kalman Filter Based on the Gradient Descent Algorithm for Attitude Estimation During Dynamic Conditions. IEEE Access 2020, 8, 96487–96494. [Google Scholar] [CrossRef]
- Tripathi, R.P.; Singh, A.K.; Gangwar, K. Innovation-based fractional order adaptive Kalman filter. J. Electr. Eng. 2020, 71, 60–64. [Google Scholar] [CrossRef]
- Woo, R.; Yang, E.-J.; Seo, D.-W. A Fuzzy-Innovation-Based Adaptive Kalman Filter for Enhanced Vehicle Positioning in Dense Urban Environments. Sensors 2019, 19, 1142. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liu, Z.; Zhao, L. Improved robust Kalman filter for state model errors in GNSS-PPP/MEMS-IMU double state integrated navigation. Adv. Space Res. 2021, 67, 3156–3168. [Google Scholar] [CrossRef]
- Tang, Y.; Jiang, J.; Liu, J.; Yan, P.; Tao, Y.; Liu, J. A GRU and AKF-Based Hybrid Algorithm for Improving INS/GNSS Navigation Accuracy during GNSS Outage. Remote Sens. 2022, 14, 752. [Google Scholar] [CrossRef]
- Ma, C.; Pan, S.; Gao, W.; Ye, F.; Liu, L.; Wang, H. Improving GNSS/INS Tightly Coupled Positioning by Using BDS-3 Four-Frequency Observations in Urban Environments. Remote Sens. 2022, 14, 615. [Google Scholar] [CrossRef]
- Hu, G.; Gao, S.; Zhong, Y. A derivative UKF for tightly coupled INS/GPS integrated navigation. ISA Trans. 2015, 56, 135–144. [Google Scholar] [CrossRef]
- Hu, G.; Gao, B.; Zhong, Y.; Ni, L.; Gu, C. Robust Unscented Kalman Filtering With Measurement Error Detection for Tightly Coupled INS/GNSS Integration in Hypersonic Vehicle Navigation. IEEE Access 2019, 7, 151409–151421. [Google Scholar] [CrossRef]
- Khider, M.; Jost, T.; Robertson, P.; Abdo-Sánchez, E. Global navigation satellite system pseudorange based multisensor positioning incorporating a multipath error model. IET Radar Sonar Navig. 2013, 7, 881–894. [Google Scholar] [CrossRef]
- Xia, Q.; Rao, M.; Ying, Y.; Shen, X. Adaptive Fading Kalman Filter with an Application. Automatica 1994, 30, 1333–1338. [Google Scholar] [CrossRef]




| Gyroscope | Accelerometer | |
|---|---|---|
| Full range | ±1000°/s | ±18 g |
| Bias stability | 10 °/h | 40 μg |
| Noise density | 0.01°/s/√Hz | 80 μg/√Hz |
| Nonlinearity | 0.01 % | 0.03 % |
| Full range | ±1000°/s | ±18 g |
| a. Attitude angle calculation error of IAE method | |||
| Roll Angle | Pitch Angle | Heading Angle | |
| Mean square error | 0.3180° | −0.5892° | −1.3980° |
| Maximum error | 3.7212° | 2.7815° | 8.5192° |
| Minimum error | −4.2544° | −2.7833° | −7.4890° |
| Average error | −0.2036° | 0.3023° | 0.8874° |
| b. Attitude angle calculation error of AFKF method | |||
| Roll angle | Pitch angle | Heading angle | |
| Mean square error | 0. 4710° | 0.2750° | 1.3212° |
| Maximum error | 2.9892° | 2.8896° | 8.0192° |
| Minimum error | −3.9210° | −3.1158° | −7.8504° |
| Average error | 0.1138° | 0.1484° | 0.8249° |
| c. Attitude angle calculation error of fusion IAE and AFKF adaptive method | |||
| Roll angle | Pitch angle | Heading angle | |
| Mean square error | 0.1180° | 0.2471° | 1.2633° |
| Maximum error | 1.9952° | 2.3727° | 4.8672° |
| Minimum error | −3.7170° | −2.7108° | −7.4280° |
| Average error | −0.0037° | 0.1136° | 0.8029° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Sun, P.; Wu, J. An Adaptive Fusion Attitude and Heading Measurement Method of MEMS/GNSS Based on Covariance Matching. Micromachines 2022, 13, 1787. https://doi.org/10.3390/mi13101787
Sun W, Sun P, Wu J. An Adaptive Fusion Attitude and Heading Measurement Method of MEMS/GNSS Based on Covariance Matching. Micromachines. 2022; 13(10):1787. https://doi.org/10.3390/mi13101787
Chicago/Turabian StyleSun, Wei, Peilun Sun, and Jiaji Wu. 2022. "An Adaptive Fusion Attitude and Heading Measurement Method of MEMS/GNSS Based on Covariance Matching" Micromachines 13, no. 10: 1787. https://doi.org/10.3390/mi13101787
APA StyleSun, W., Sun, P., & Wu, J. (2022). An Adaptive Fusion Attitude and Heading Measurement Method of MEMS/GNSS Based on Covariance Matching. Micromachines, 13(10), 1787. https://doi.org/10.3390/mi13101787





