New Solutions of Fractional Jeffrey Fluid with Ternary Nanoparticles Approach
Abstract
1. Introduction
- Research questions
- How to do fractional modeling in heat transfer?
- How is the rate of heat transfer of ternary nanoparticles greater than hybrid and mono nanoparticles, respectively?
- What is the advantage of choosing different base fluids for three types of nanoparticles?
2. Mathematical Formulation
3. Ternary Nanoparticles
3.1. Solution of Temperature with Ternary Nanoparticles
3.2. Solution of Velocity with Ternary Nanoparticles
4. Solution of Temperature and Velocity with Hybrid Nanoparticles
5. Solution of Temperature and Velocity with Mono Nanoparticles
6. Nusselt Numbers
6.1. Nusselt Number for Ternary Nanoparticles
6.2. Nusselt Number for Hybrid Nanoparticles
6.3. Nusselt Number for Mono Nanoparticles
7. Skin Friction
7.1. Skin Friction for Ternary Nanoparticles
7.2. Skin Friction for Hybrid Nanoparticles
7.3. Skin Friction for Mono Nanoparticles
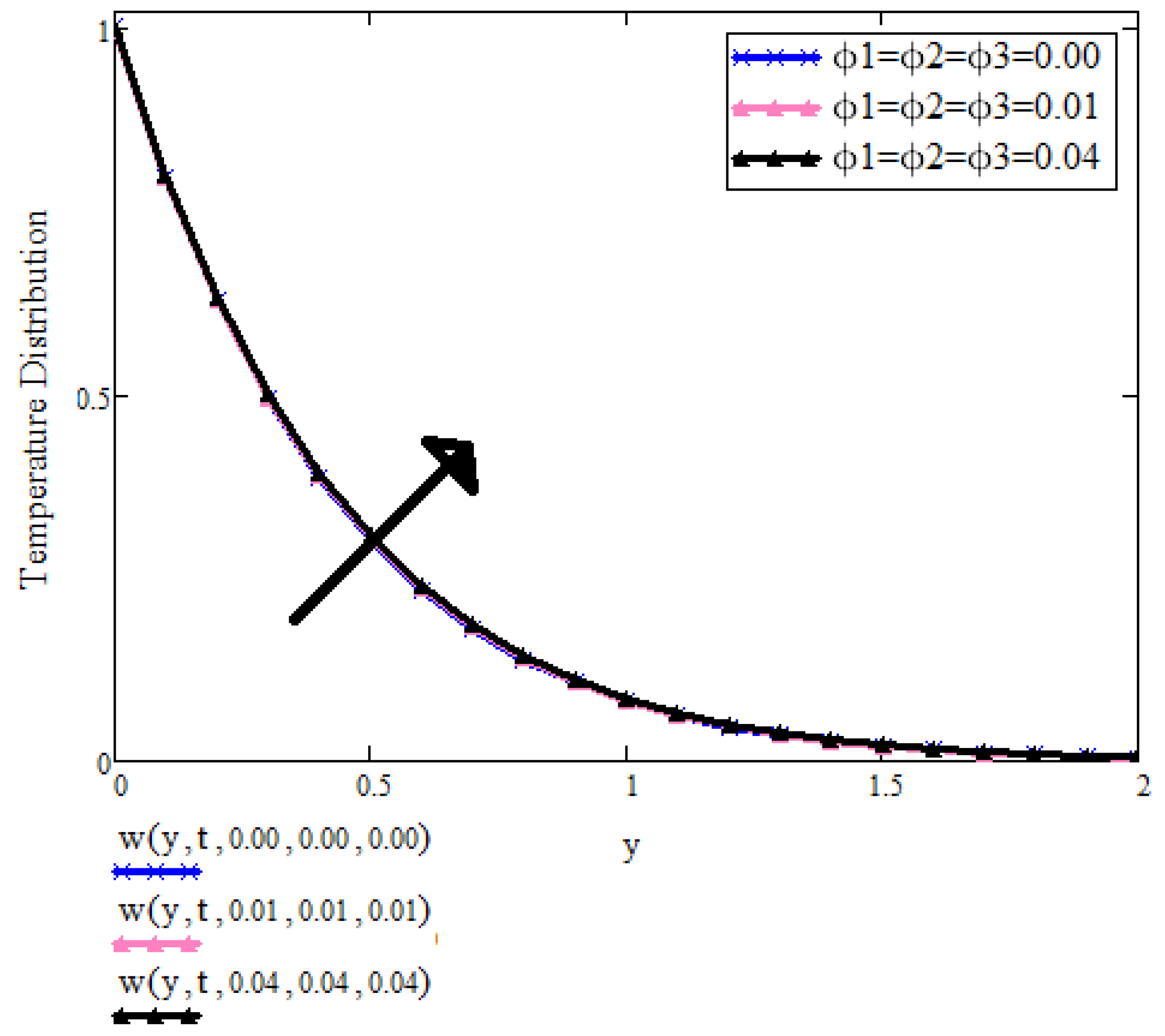
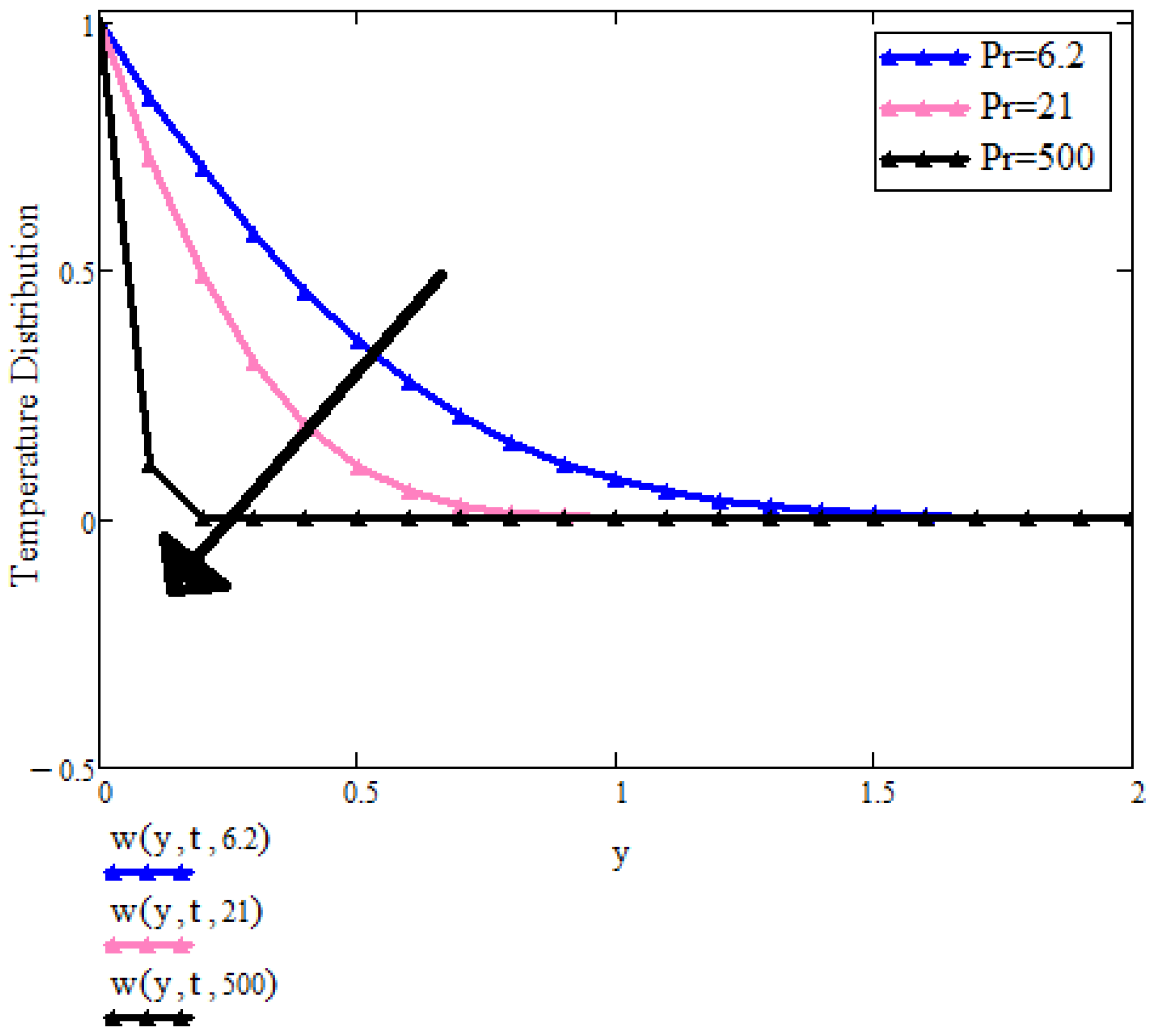
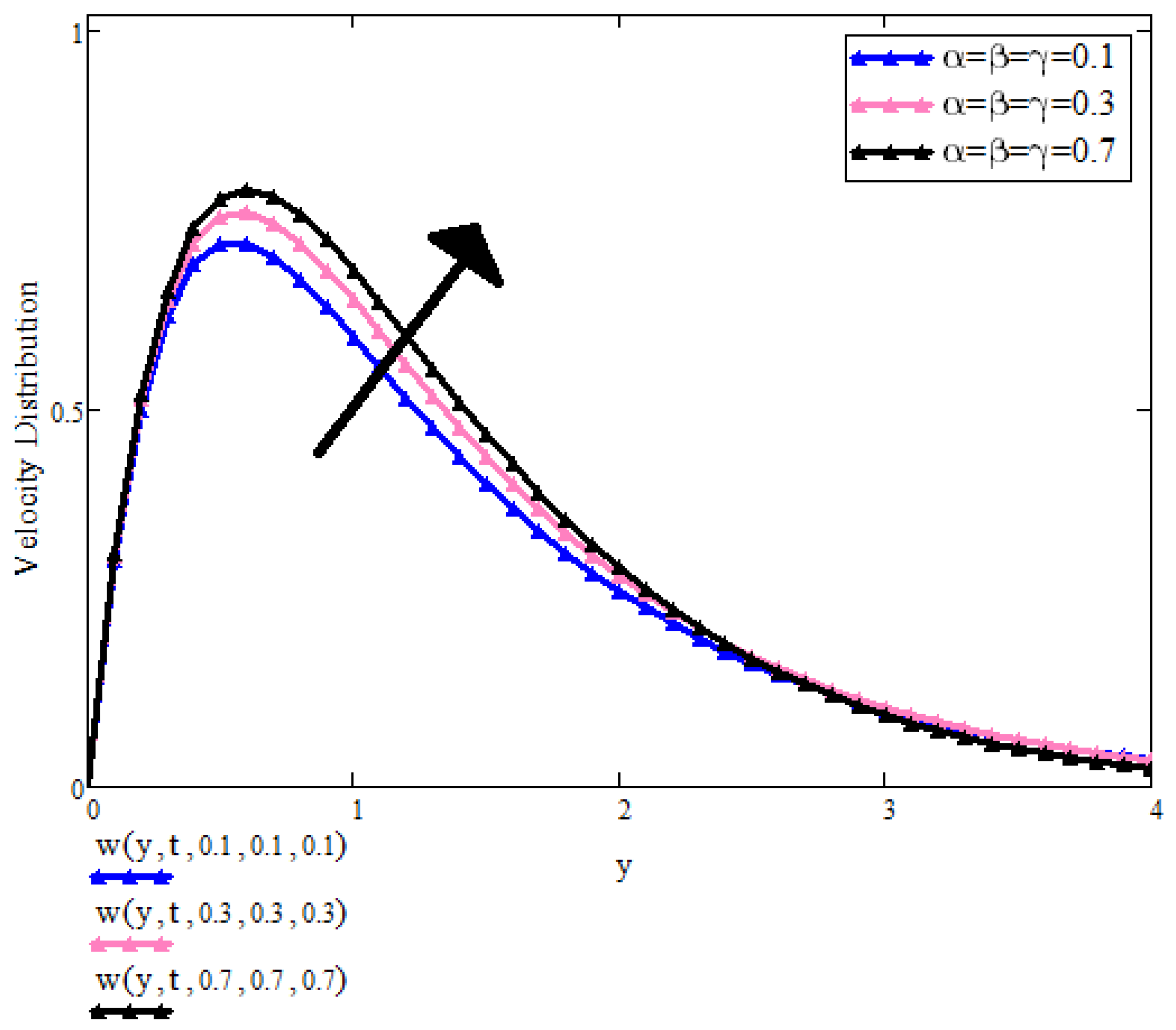
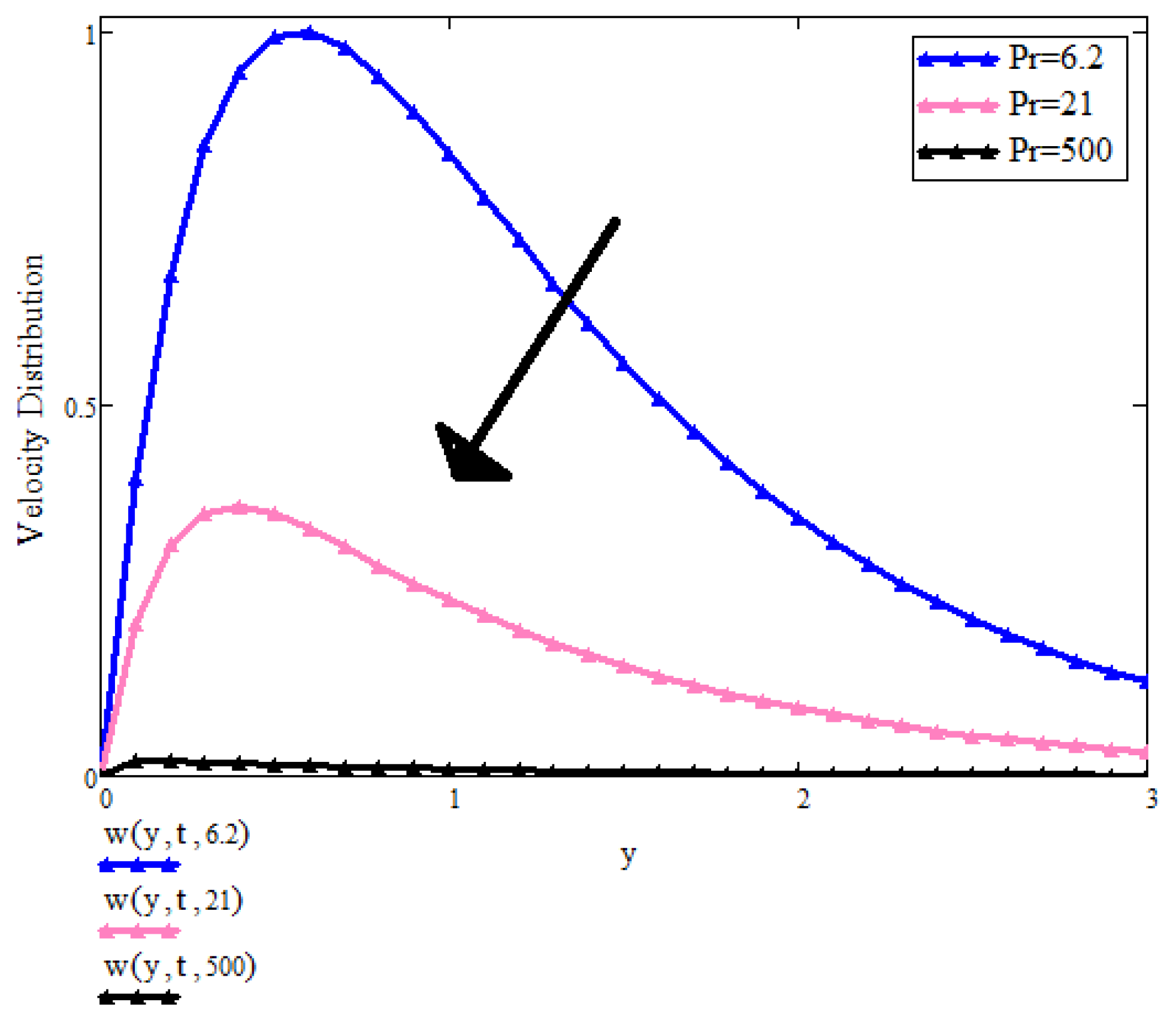
8. Graphical Results and Discussion
9. Conclusions
- The fractional and ternary nanoparticles approach is helpful in improving the exiting results.
- Choosing a specific value of fractional parameters, thermal and momentum boundary layers can be controlled for different time. Such a fractional approach is very helpful in handling the experimental data by using theoretical information.
- The rate of heat transfer for ternary nanoparticles is greater in comparison of hybrid and mono nanoparticles, respectively.
- The obtained results are also useful in the sense of choosing base fluids (water, kerosene and Engin oil) for three types of naoparticles to achieved the desired targets in any transport problem.
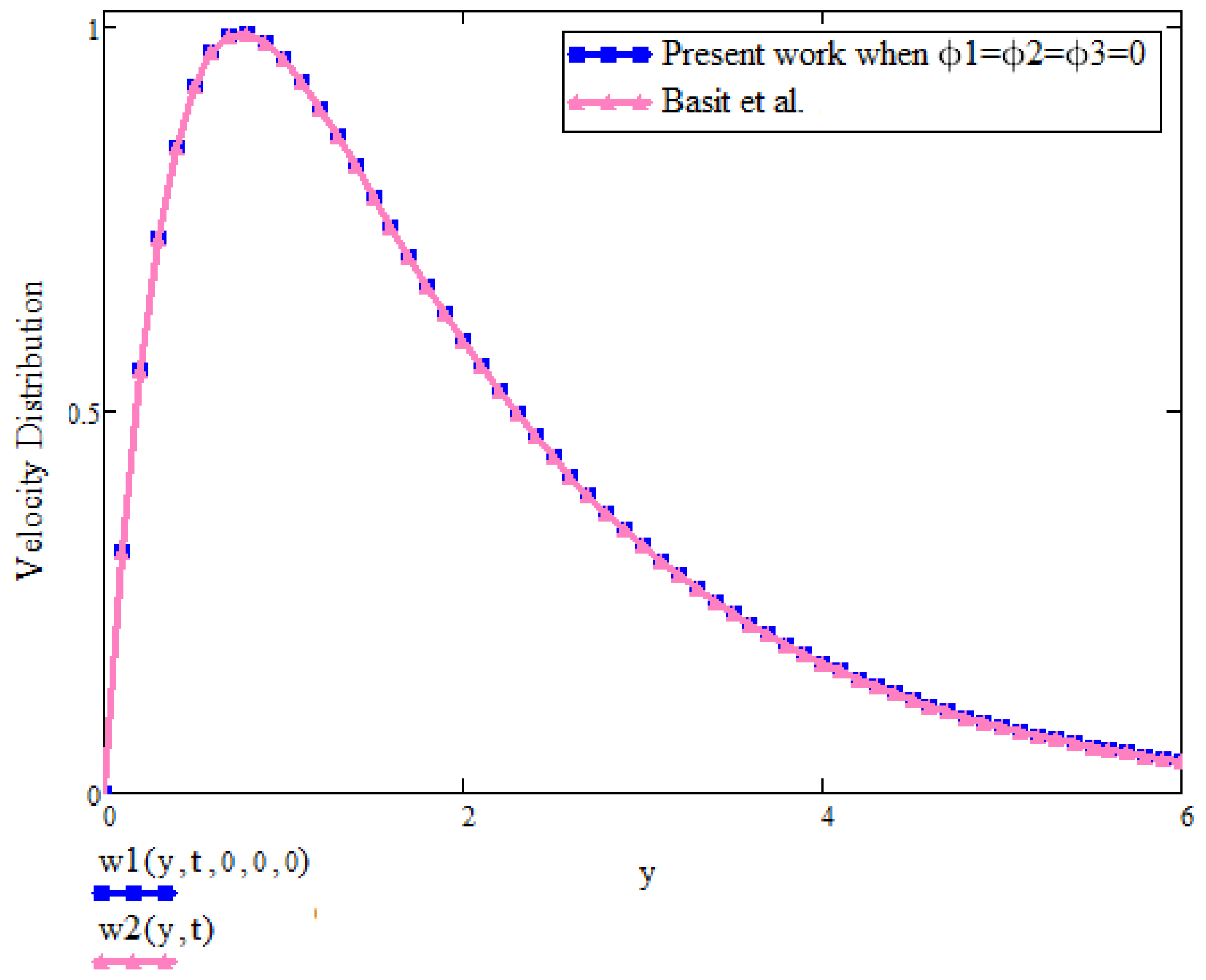
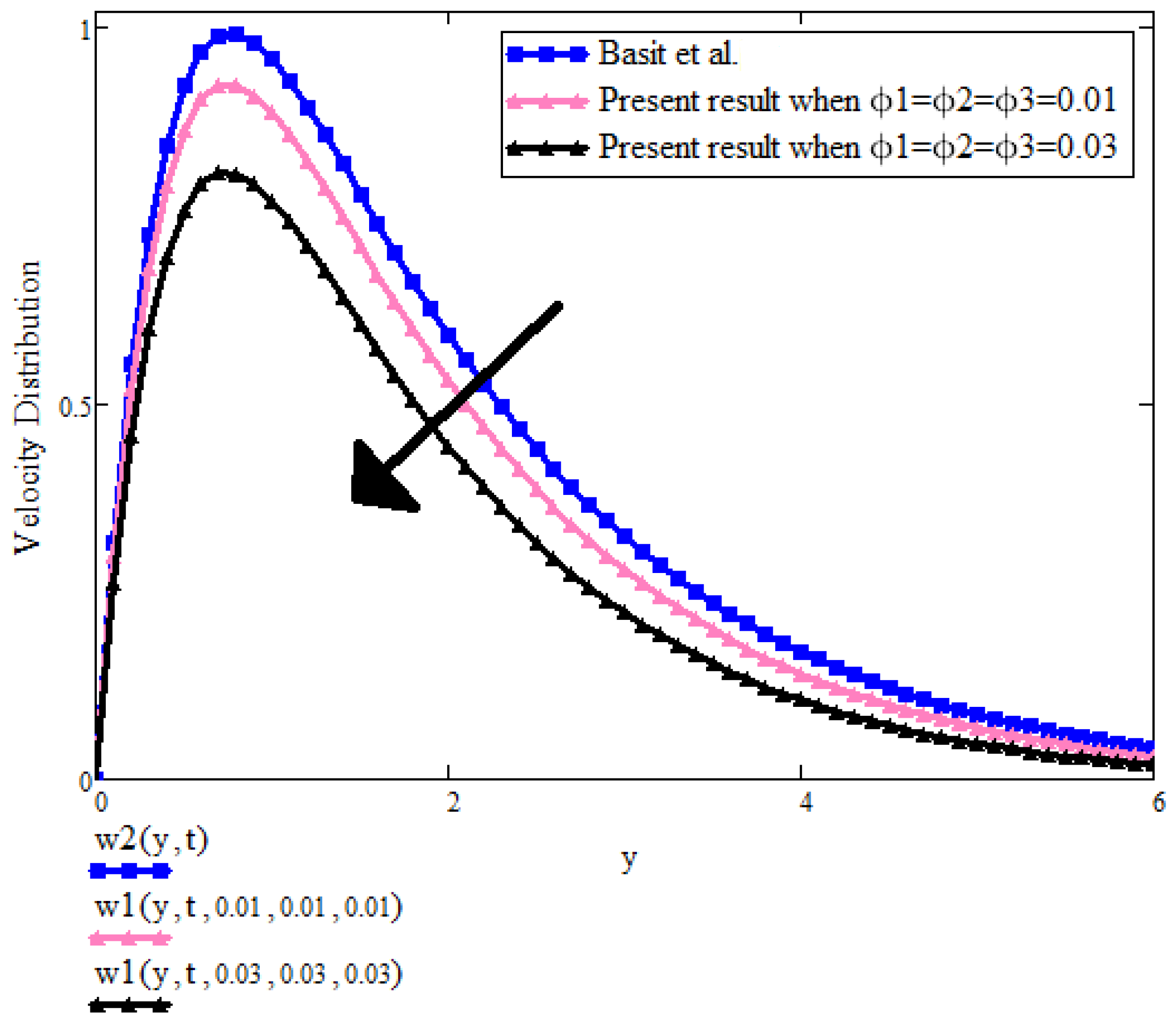
- The new approach with ternary nanoparticles is more reliable and effective, and was validated with the existing literature.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Names |
| Density of fluid | |
| Heat capacity of fluid | |
| Viscosity of fluid | |
| G | Gravitational acceleration |
| Prandtl number | |
| Kinematic viscosity | |
| t | Time |
| Temperature at plate | |
| Temperature at infinity | |
| k | Thermal conductivity |
| Thermal expansion | |
| Fractional parameters | |
| Specific heat for solid nanoparticles of type one, two, three | |
| Thermal heat expansion for temperature one, two, three | |
| Solid volume fraction of type one, two, three | |
| a | Constant between zero and one |
References
- Chen, C.; Rehman, A.U.; Riaz, M.B.; Jarad, F.; Sun, X.E. Impact of Newtonian Heating via Fourier and Fick’s Laws on Thermal Transport of Oldroyd-B Fluid by Using Generalized Mittag-Leffler Kernel. Symmetry 2022, 14, 766. [Google Scholar] [CrossRef]
- Asjad, M.I.; Basit, A.; Akgül, A.; Muhammad, T. Generalized thermal flux flow for Jeffrey fluid with fourier law over an infinite plate. Math. Probl. Eng. 2021, 2021, 5403879. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A. Heat transfer analysis of Jeffrey fluid flow over a stretching sheet with suction/injection and magnetic dipole effect. Alex. Eng. J. 2016, 55, 2171–2181. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Khan, W.A.; Khan, I.; Alharbi, S.O. Numerical solution of non-Newtonian fluid flow due to rotatory rigid disk. Symmetry 2019, 11, 699. [Google Scholar] [CrossRef]
- Ali, M.; Al-Yousef, F. Laminar mixed convection boundary layers induced by a linearly stretching permeable surface. Int. J. Heat Mass Transf. 2002, 45, 4241–4250. [Google Scholar] [CrossRef]
- Mohd Zin, N.A.; Khan, I.; Shafie, S. Influence of thermal radiation on unsteady MHD free convection flow of Jeffrey fluid over a vertical plate with ramped wall temperature. Math. Probl. Eng. 2016, 2016, 6257071. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. Convective boundary conditions effect on peristaltic flow of a MHD Jeffrey nanofluid. Appl. Nanosci. 2016, 6, 323–335. [Google Scholar] [CrossRef]
- Ali, F.; Murtaza, S.; Khan, I.; Sheikh, N.A.; Nisar, K.S. Atangana–Baleanu fractional model for the flow of Jeffrey nanofluid with diffusion-thermo effects: Applications in engine oil. Adv. Differ. Equ. 2019, 2019, 1–21. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Akhtar, R.; Chaudhary, N.I.; Zhiyu, Z.; Khan, Q.; Rehman, A.U.; Zaman, F. A new computing paradigm for the optimization of parameters in adaptive beamforming using fractional processing. Eur. Phys. J. Plus 2019, 134, 275. [Google Scholar] [CrossRef]
- Shahid, N. A study of heat and mass transfer in a fractional MHD flow over an infinite oscillating plate. SpringerPlus 2015, 4, 1–21. [Google Scholar] [CrossRef]
- Murtaza, S.; Ali, F.; Aamina, N.A.; Sheikh, N.A.; Khan, I.; Nisar, K.S. Exact analysis of non-linear fractionalized Jeffrey fluid. A novel approach of Atangana–Baleanu fractional model. Comput. Mater. Contin. 2020, 65, 2033–2047. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Thumma, T.; Yook, S.J. Heat transfers thermodynamic activity of a second-grade ternary nanofluid flow over a vertical plate with Atangana-Baleanu time-fractional integral. Alex. Eng. J. 2022, 61, 10045–10053. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Jan, S.A.A. Exact solutions for free convection flow of generalized Jeffrey fluid: A Caputo-Fabrizio fractional model. Alex. Eng. J. 2018, 57, 1849–1858. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer–Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Abdulrazzaq, T.; Togun, H.; Alsulami, H.; Goodarzi, M.; Safaei, M.R. Heat transfer improvement in a double backward-facing expanding channel using different working fluids. Symmetry 2020, 12, 1088. [Google Scholar] [CrossRef]
- Adun, H.; Adedeji, M.; Dagbasi, M.; Bamisile, O.; Senol, M.; Kumar, R. A numerical and exergy analysis of the effect of ternary nanofluid on performance of Photovoltaic thermal collector. J. Therm. Anal. Calorim. 2021, 145, 1413–1429. [Google Scholar] [CrossRef]
- Valizade, M.; Heyhat, M.M.; Maerefat, M. Experimental comparison of optical properties of nanofluid and metal foam for using in direct absorption solar collectors. Sol. Energy Mater. Sol. Cells 2019, 195, 71–80. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic flow of SWCNT/MWCNT suspensions in two immiscible water-and engine-oil-based Newtonian fluids through porous media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Dezfulizadeh, A.; Aghaei, A.; Joshaghani, A.H.; Najafizadeh, M.M. An experimental study on dynamic viscosity and thermal conductivity of water-Cu-SiO2-MWCNT ternary hybrid nanofluid and the development of practical correlations. Powder Technol. 2021, 389, 215–234. [Google Scholar] [CrossRef]
- Yang, X.; Boroomandpour, A.; Wen, S.; Toghraie, D.; Soltani, F. Applying Artificial Neural Networks (ANNs) for prediction of the thermal characteristics of water/ethylene glycol-based mono, binary and ternary nanofluids containing MWCNTs, titania, and zinc oxide. Powder Technol. 2021, 388, 418–424. [Google Scholar] [CrossRef]
- Agrwal, A.; Kumar, V.; Kasana, V. Preparation and application of highly efficient and reusable TBAPIL@Si(CH2)3@nano-silica-based nano-catalyst for preparation of benzoxanthene derivatives. J. Iran. Chem. Soc. 2021, 18, 2583–2595. [Google Scholar] [CrossRef]
- Salata, O.V. Applications of nanoparticles in biology and medicine. J. Nanobiotechnol. 2004, 2, 1–6. [Google Scholar] [CrossRef]
- Baetke, S.C.; Lammers, T.G.G.M.; Kiessling, F. Applications of nanoparticles for diagnosis and therapy of cancer. Br. J. Radiol. 2015, 88, 20150207. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, W.; Kazi, S.N.; Chowdhury, Z.Z.; Johan, M.R.B.; Soudagar, M.E.M.; Mujtaba, M.A.; Gul, M.; Badruddin, I.A.; Kamangar, S. Ultrasonic assisted new Al2O3@TiO2-ZnO/DW ternary composites nanofluids for enhanced energy transportation in a closed horizontal circular flow passage. Int. Commun. Heat Mass Transf. 2021, 120, 105018. [Google Scholar] [CrossRef]
- Sahoo, R.R.; Kumar, V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int. Commun. Heat Mass Transf. 2020, 111, 104451. [Google Scholar] [CrossRef]
- Garia, R.; Rawat, S.K.; Kumar, M.; Yaseen, M. Hybrid nanofluid flow over two different geometries with Cattaneo–Christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chin. J. Phys. 2021, 74, 421–439. [Google Scholar] [CrossRef]
- Ahmed, W.; Kazi, S.N.; Chowdhury, Z.Z.; Johan, M.R.B.; Mehmood, S.; Soudagar, M.E.M.; Mujtaba, M.A.; Gul, M.; Ahmad, M.S. Heat transfer growth of sonochemically synthesized novel mixed metal oxide ZnO+Al2O3+TiO2/DW based ternary hybrid nanofluids in a square flow conduit. Renew. Sustain. Energy Rev. 2021, 145, 111025. [Google Scholar] [CrossRef]
- Adun, H.; Mukhtar, M.; Adedeji, M.; Agwa, T.; Ibrahim, K.H.; Bamisile, O.; Dagbasi, M. Synthesis and application of ternary nanofluid for photovoltaic-thermal system: Comparative analysis of energy and exergy performance with single and hybrid nanofluids. Energies 2021, 14, 4434. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Animasaun, I.L.; Shah, N.A. Ternary-hybrid nanofluids: Significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with various shapes and densities. Z. Naturforschung A 2021, 76, 231–243. [Google Scholar] [CrossRef]
- Xuan, Z.; Zhai, Y.; Ma, M.; Li, Y.; Wang, H. Thermo-economic performance and sensitivity analysis of ternary hybrid nanofluids. J. Mol. Liq. 2021, 323, 114889. [Google Scholar] [CrossRef]
- Cao, W.; Animasaun, I.L.; Yook, S.J.; Oladipupo, V.A.; Ji, X. Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid. Int. Commun. Heat Mass Transf. 2022, 135, 106069. [Google Scholar] [CrossRef]
- Dezfulizadeh, A.; Aghaei, A.; Hassani Joshaghani, A.; Najafizadeh, M.M. Exergy efficiency of a novel heat exchanger under MHD effects filled with water-based Cu–SiO2-MWCNT ternary hybrid nanofluid based on empirical data. J. Therm. Anal. Calorim. 2022, 147, 4781–4804. [Google Scholar] [CrossRef]
- Chaudhary, P.; Agrwal, A.; Sharma, D.K.; Kumar, V. Synthesis and screen-printing of sol-gel developed pure and Yb-doped ZnO films towards optoelectronic analysis. J. Sol-Gel Sci. Technol. 2022, 104, 425–433. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Shafiq, A.; Kumar, M.; Nonlaopon, K. Analysis of Heat Transfer of Mono and Hybrid Nanofluid Flow between Two Parallel Plates in a Darcy Porous Medium with Thermal Radiation and Heat Generation/Absorption. Symmetry 2022, 14, 1943. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Falkner–Skan Problem for a Stretching or Shrinking Wedge With Nanoparticle Aggregation. J. Heat Transf. 2022, 144, 102501. [Google Scholar] [CrossRef]
- Agrwal, A.; Kasana, V. [Fesipmim] Cl as highly efficient and reusable catalyst for solventless synthesis of dihydropyridine derivatives through Hantzsch reaction. J. Chem. Sci. 2020, 132, 1–11. [Google Scholar] [CrossRef]
- Azam, M. Effects of Cattaneo-Christov heat flux and nonlinear thermal radiation on MHD Maxwell nanofluid with Arrhenius activation energy. Case Stud. Therm. Eng. 2022, 34, 102048. [Google Scholar] [CrossRef]
- Azam, M. Bioconvection and nonlinear thermal extrusion in development ofchemically reactive Sutterby nano-material due to gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2022, 130, 105820. [Google Scholar]
- Azam, M.; Abbas, N.; Ganesh Kumar, K.; Wali, S. Transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and nonlinear radiation. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Azam, M.; Nayak, M.K.; Khan, W.A.; Khan, M. Significance of bioconvection and variable thermal properties on dissipative Maxwell nanofluid due to gyrotactic microorganisms and partial slip. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Azam, M.; Xu, T.; Nayak, M.K.; Khan, W.A.; Khan, M. Gyrotactic microorganisms and viscous dissipation features on radiative Casson nanoliquid over a moving cylinder with activation energy. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Microscale Heat Transfer: The Lagging Behavior; John Wiley Sons: New York, NY, USA, 2014. [Google Scholar]





| Thermodynamics Properties | (kgm) | (JkgK) | K (WmK) | (s/m) |
|---|---|---|---|---|
| Titanium oxide () | 4250 | 686.2 | 8.9538 | |
| Sliver (Ag) | 10,500 | 235 | 418 | 6.3 |
| Base fluid | 997.1 | 4179 | 0.163 | 0.05 |
| Aluminum oxide | 3970 | 765 | 40 | 35 |
| Ternary nanofluid |
| Hybrid nanoparticles |
| Mono nanoparticles |
| Nu for Ternary | Nu for Hybrid | Nu for Mono | ||||
|---|---|---|---|---|---|---|
| 3.123 | 2.466 | 2.958 | 2.356 | 2.802 | 2.213 | |
| 2.92 | 2.46 | 2.765 | 2.33 | 2.62 | 2.207 | |
| 2.704 | 2.418 | 2.561 | 2.391 | 2.426 | 2.17 | |
| 2.486 | 2.352 | 2.355 | 2.227 | 2.231 | 2.11 | |
| 2.275 | 2.267 | 2.155 | 2.148 | 2.042 | 2.035 | |
| 2.075 | 2.173 | 1.963 | 2.058 | 1.861 | 1.949 | |
| 1.886 | 2.072 | 1.768 | 1.962 | 1.692 | 1.859 | |
| for Ternary | for Hybrid | for Mono | ||||
|---|---|---|---|---|---|---|
| 0.325 | 1.249 | 0.312 | 1.247 | 0.299 | 1.183 | |
| 0.379 | 1.45 | 0.377 | 1.447 | 0.359 | 1.363 | |
| 0.469 | 1.727 | 0.467 | 1.721 | 0.441 | 1.602 | |
| 0.698 | 2.327 | 0.6 | 2.127 | 0.559 | 1.943 | |
| 0.845 | 2.822 | 0.825 | 2.812 | 0.751 | 2.481 | |
| 1.299 | 4.33 | 1.293 | 4.274 | 1.123 | 3.492 | |
| 2.375 | 12.934 | 2.34 | 12.227 | 1.975 | 6.693 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asjad, M.I.; Riaz, A.; Alnahdi, A.S.; Eldin, S.M. New Solutions of Fractional Jeffrey Fluid with Ternary Nanoparticles Approach. Micromachines 2022, 13, 1963. https://doi.org/10.3390/mi13111963
Asjad MI, Riaz A, Alnahdi AS, Eldin SM. New Solutions of Fractional Jeffrey Fluid with Ternary Nanoparticles Approach. Micromachines. 2022; 13(11):1963. https://doi.org/10.3390/mi13111963
Chicago/Turabian StyleAsjad, Muhammad Imran, Ayesha Riaz, Abeer S. Alnahdi, and Sayed M. Eldin. 2022. "New Solutions of Fractional Jeffrey Fluid with Ternary Nanoparticles Approach" Micromachines 13, no. 11: 1963. https://doi.org/10.3390/mi13111963
APA StyleAsjad, M. I., Riaz, A., Alnahdi, A. S., & Eldin, S. M. (2022). New Solutions of Fractional Jeffrey Fluid with Ternary Nanoparticles Approach. Micromachines, 13(11), 1963. https://doi.org/10.3390/mi13111963






