Design and Load Kinematics Analysis of Rollover Rehabilitation Mechanism Fitting Human Motion Curve
Abstract
1. Introduction
2. Experimental Analysis of Assisted Rollover Movement
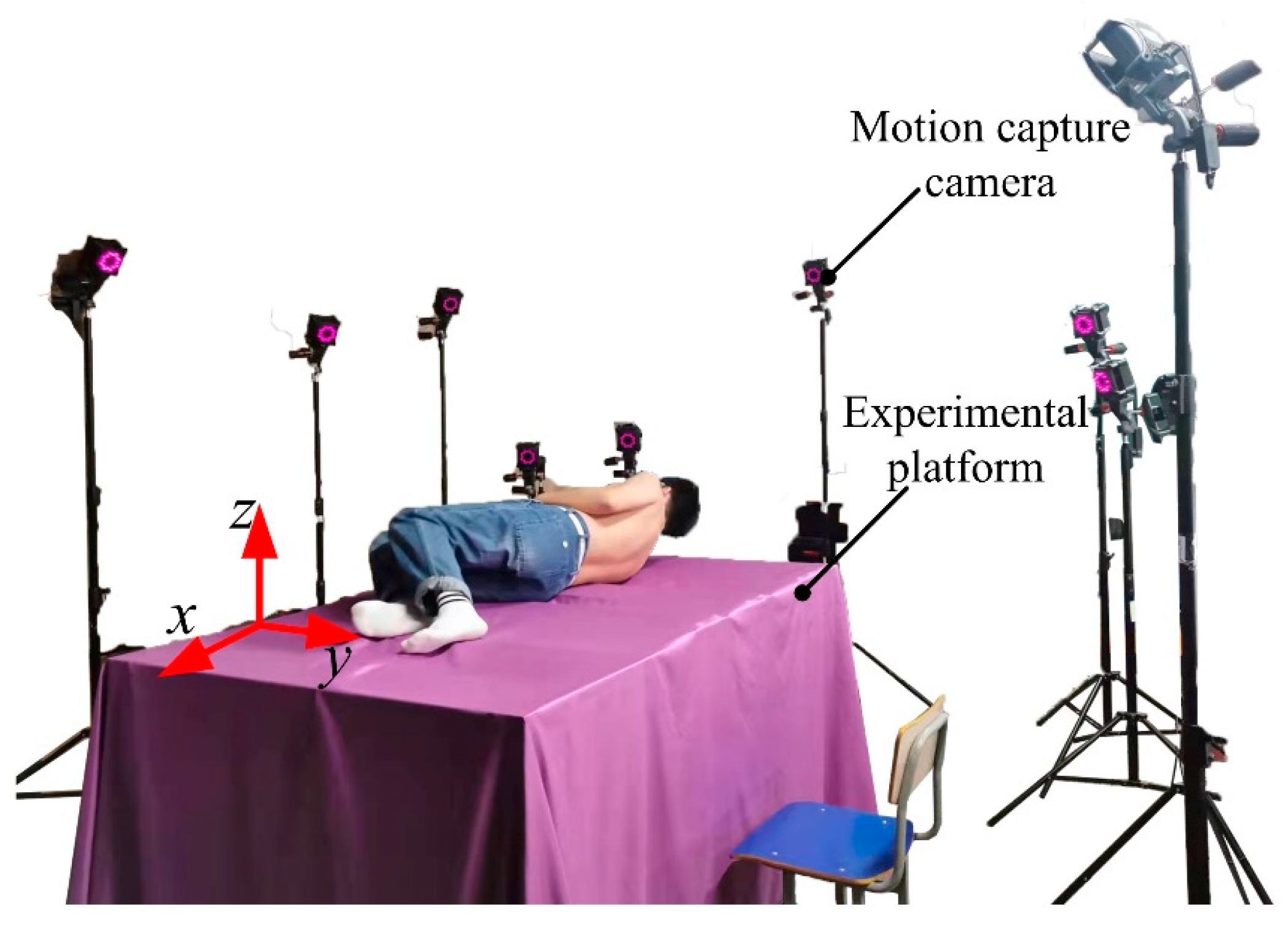
2.1. Motion Information Acquisition Experiment Based on Optical Motion Capture
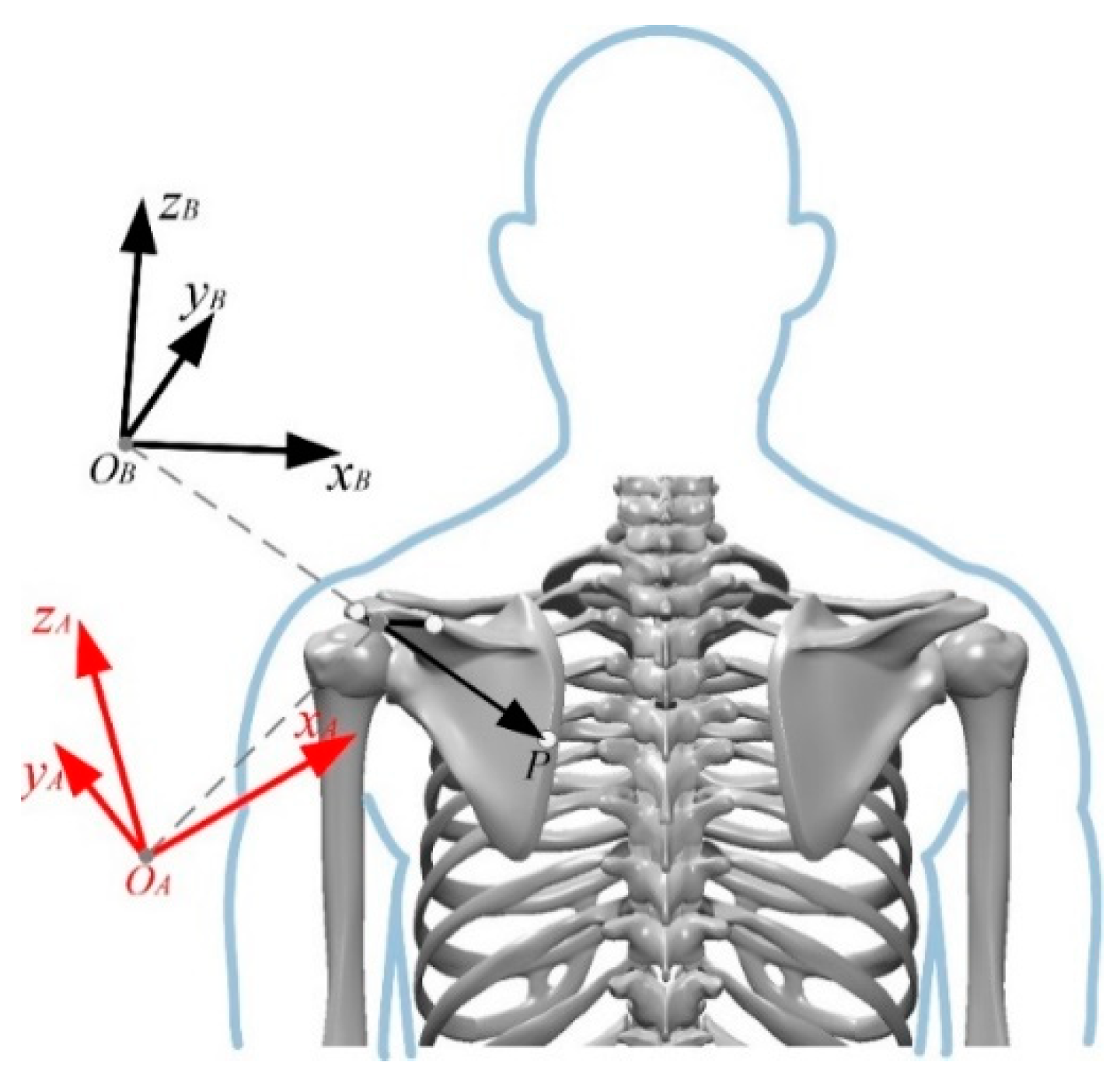
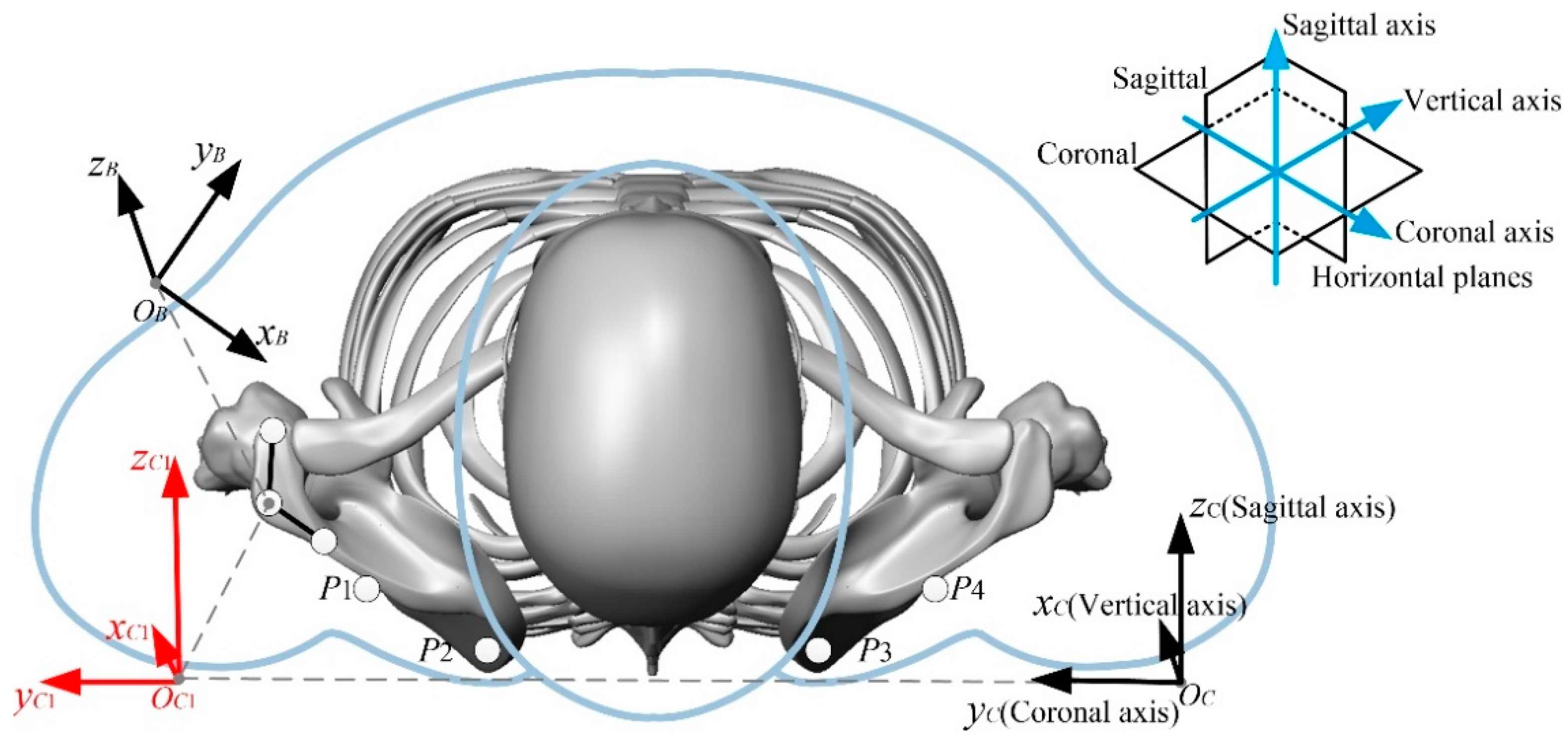
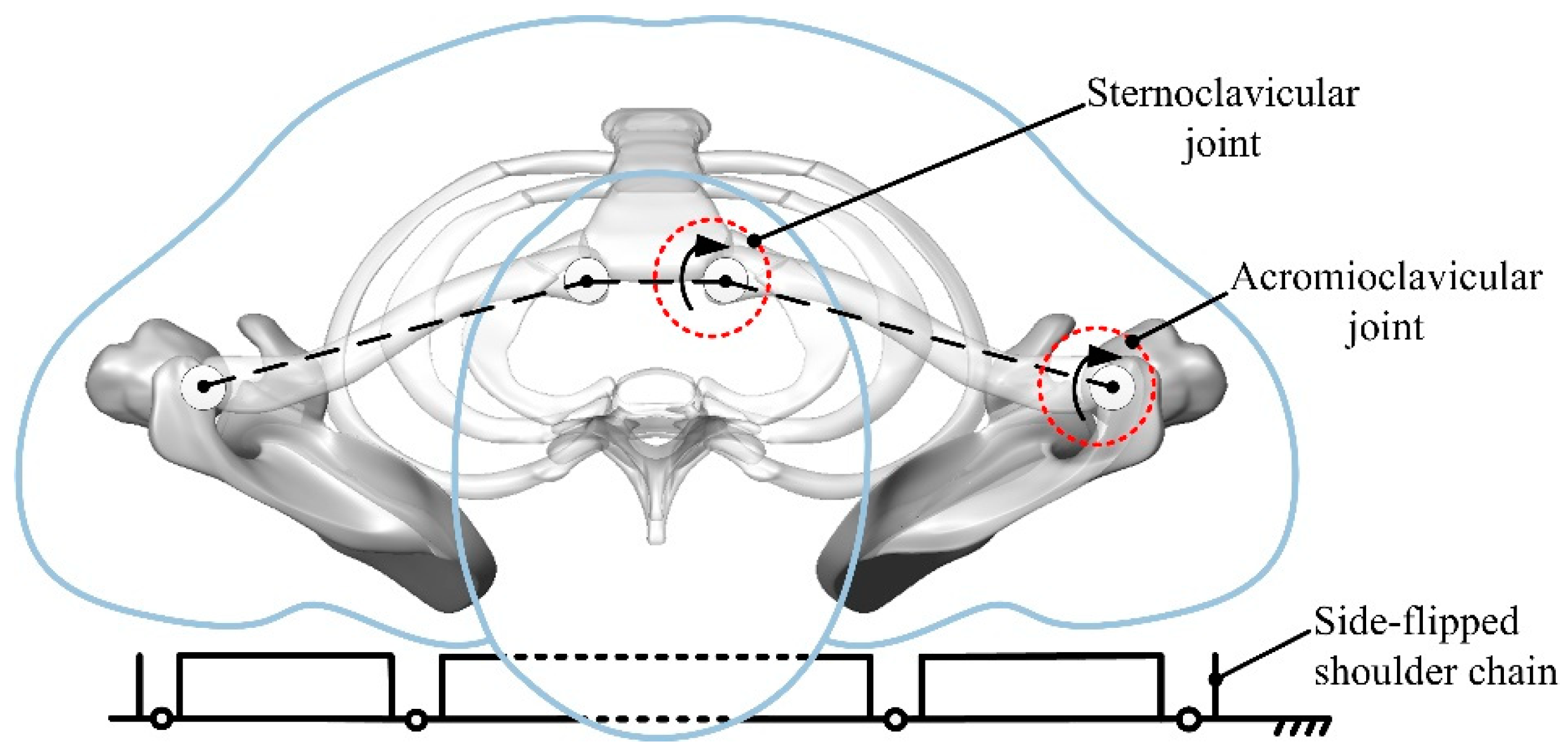
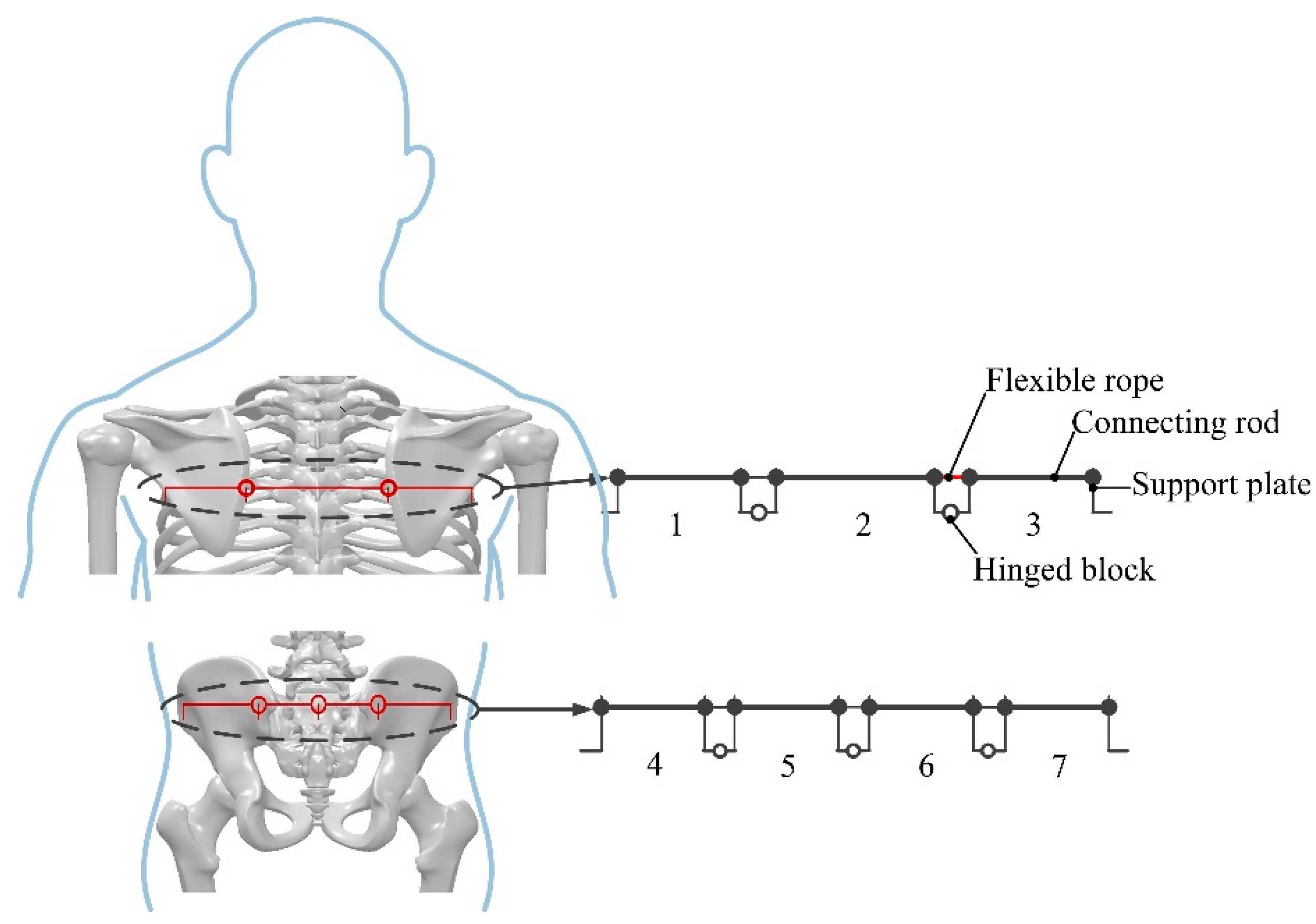
2.2. Rehabilitation Kinematic Modeling of Key Parts
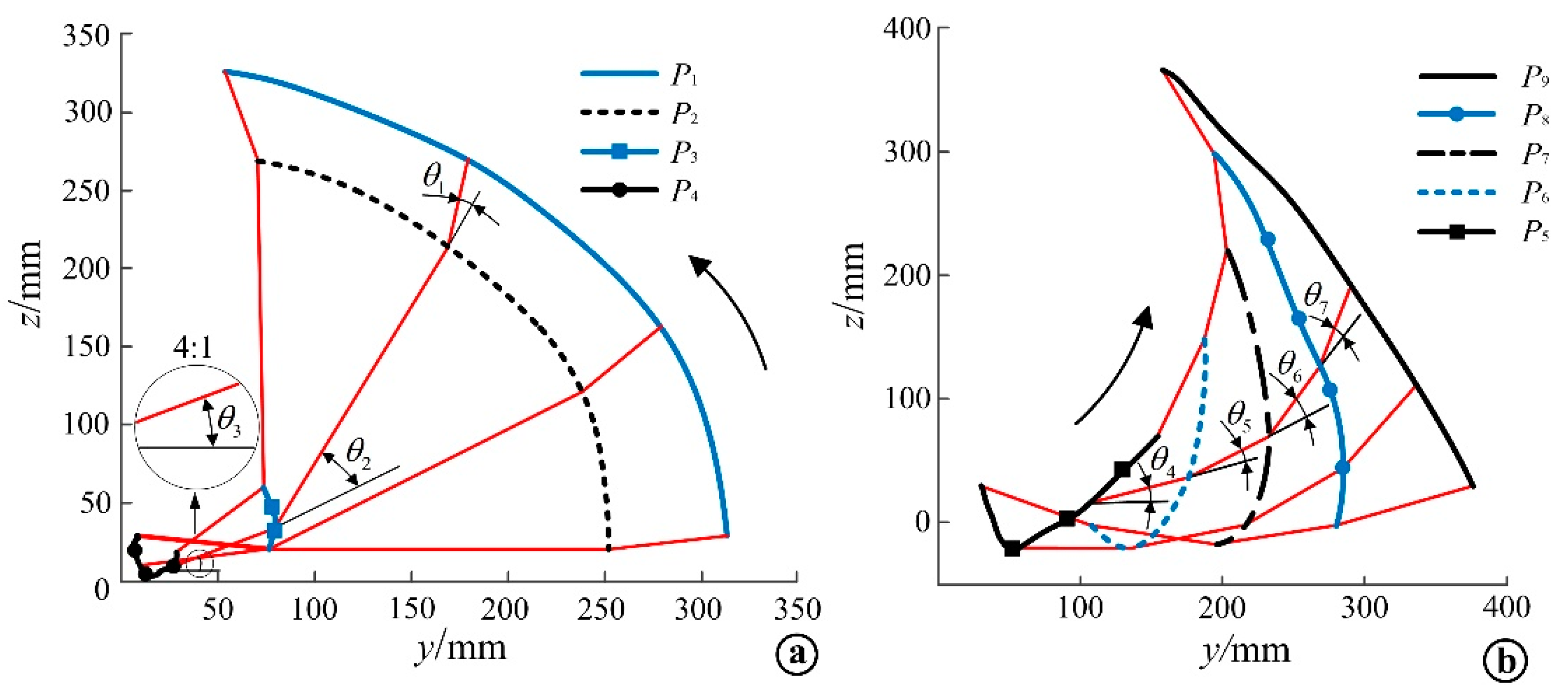
2.3. Results Were Calculated from the Kinematic Model
3. Design of Rehabilitation Assistance Mechanism for Rollover
3.1. Design of Rollover Assist Mechanism
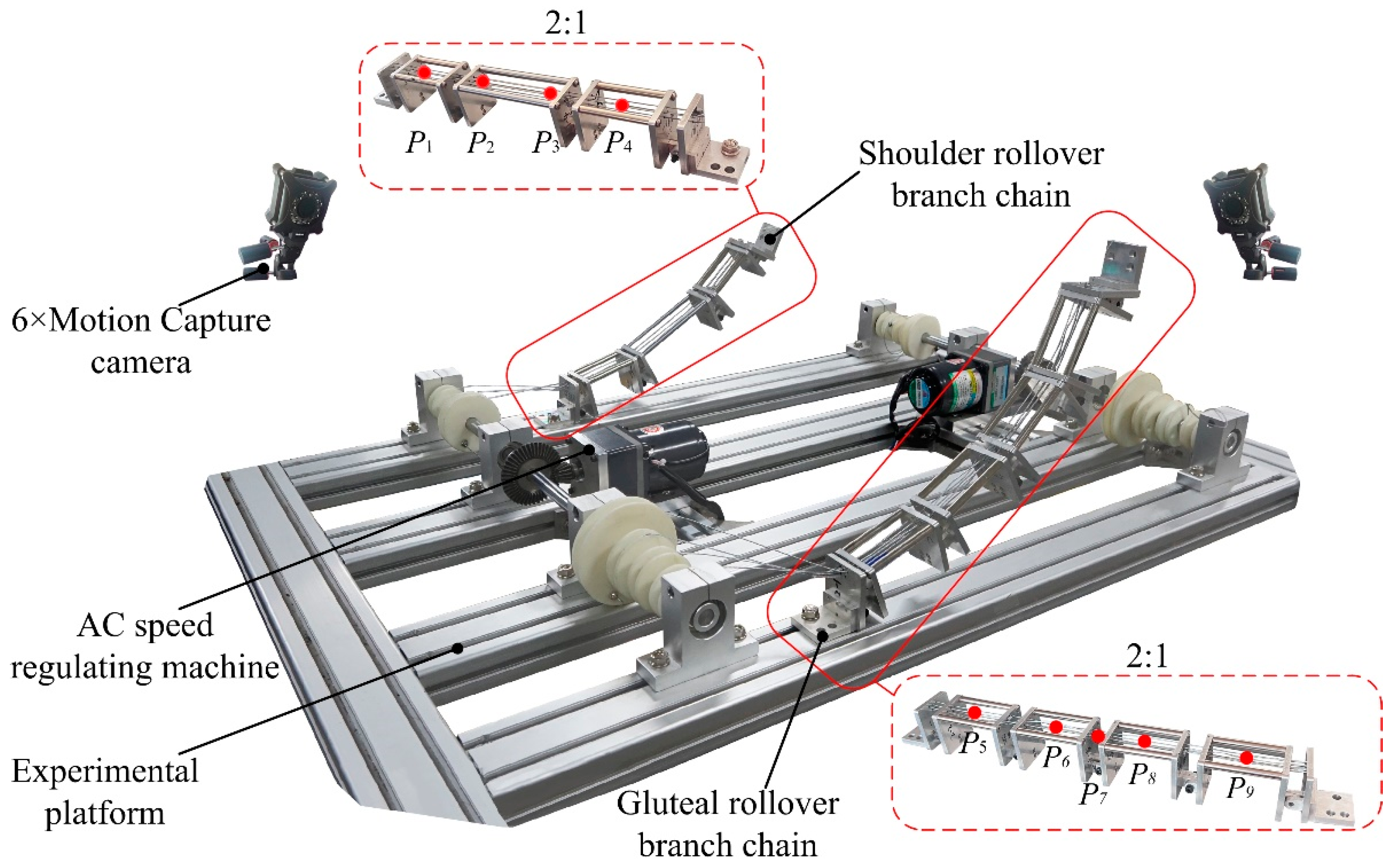
3.2. Key Mechanism Module Design
3.3. Key Mechanism Performance Analysis and Experimental Verification
4. Modeling and Analysis of Load Kinematics
5. The Discussion
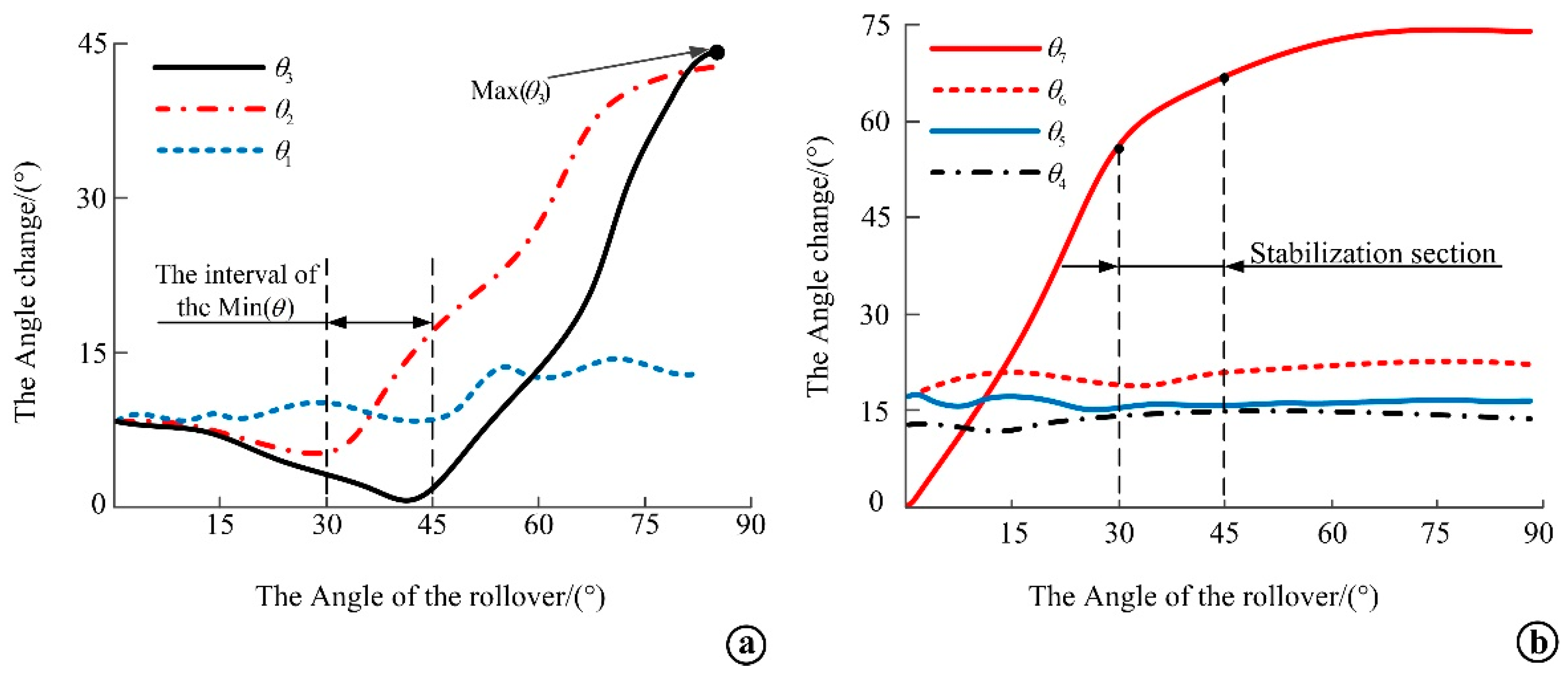
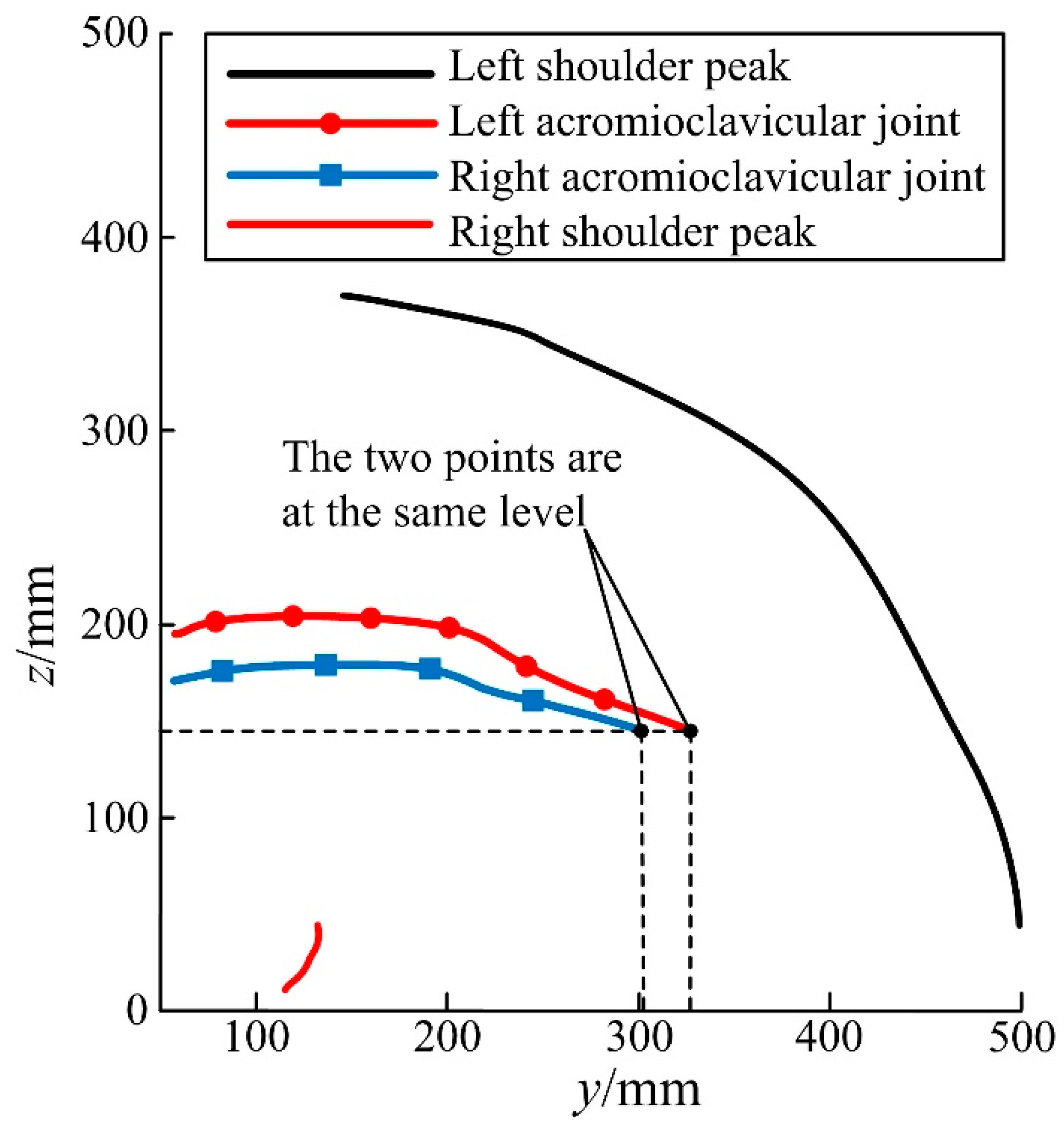
5.1. Analysis of Experimental Data
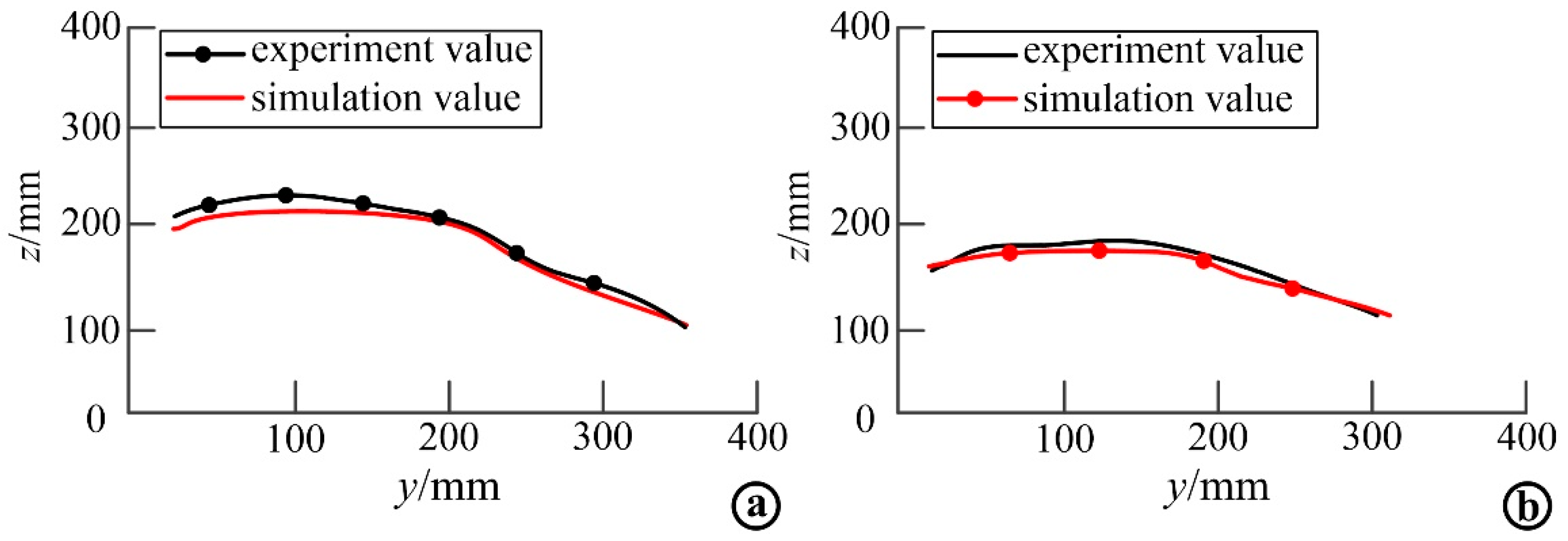
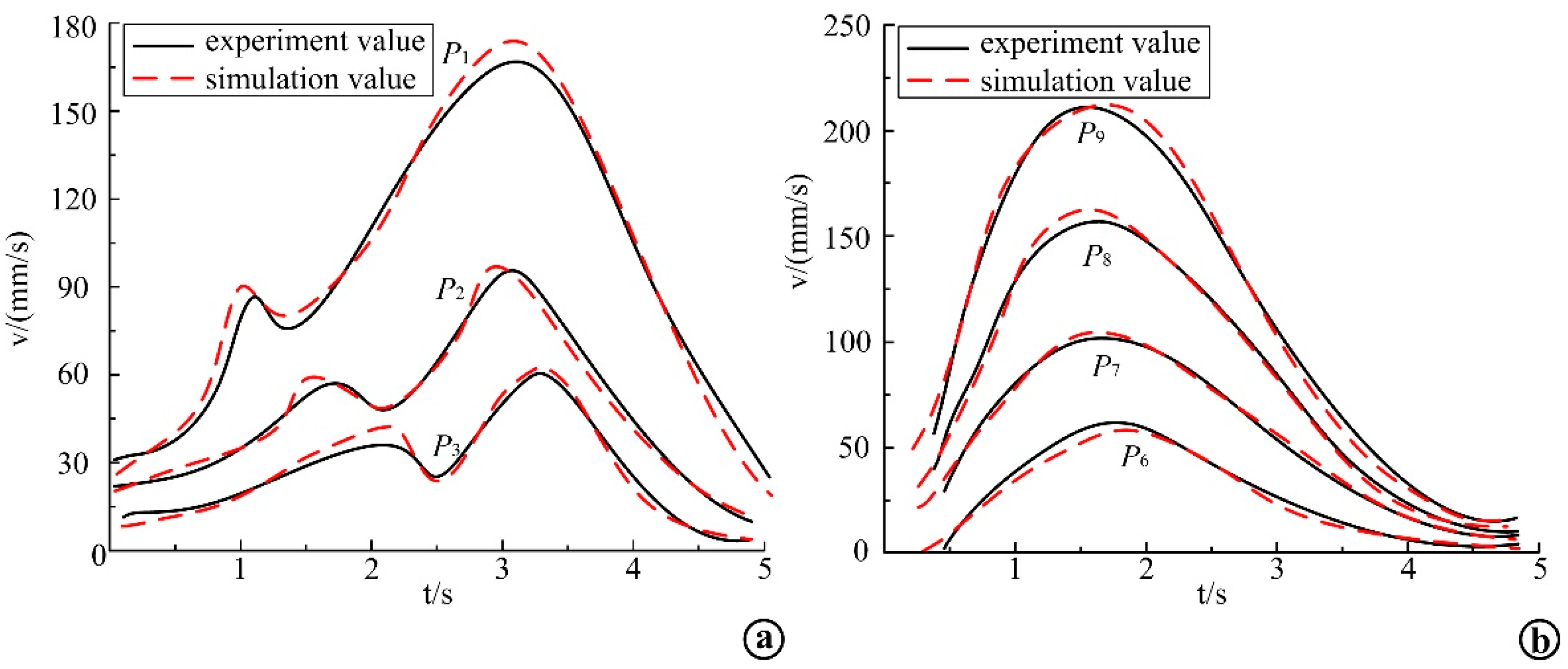
5.2. Load Kinematic Analysis and Comparison with Experimental Results
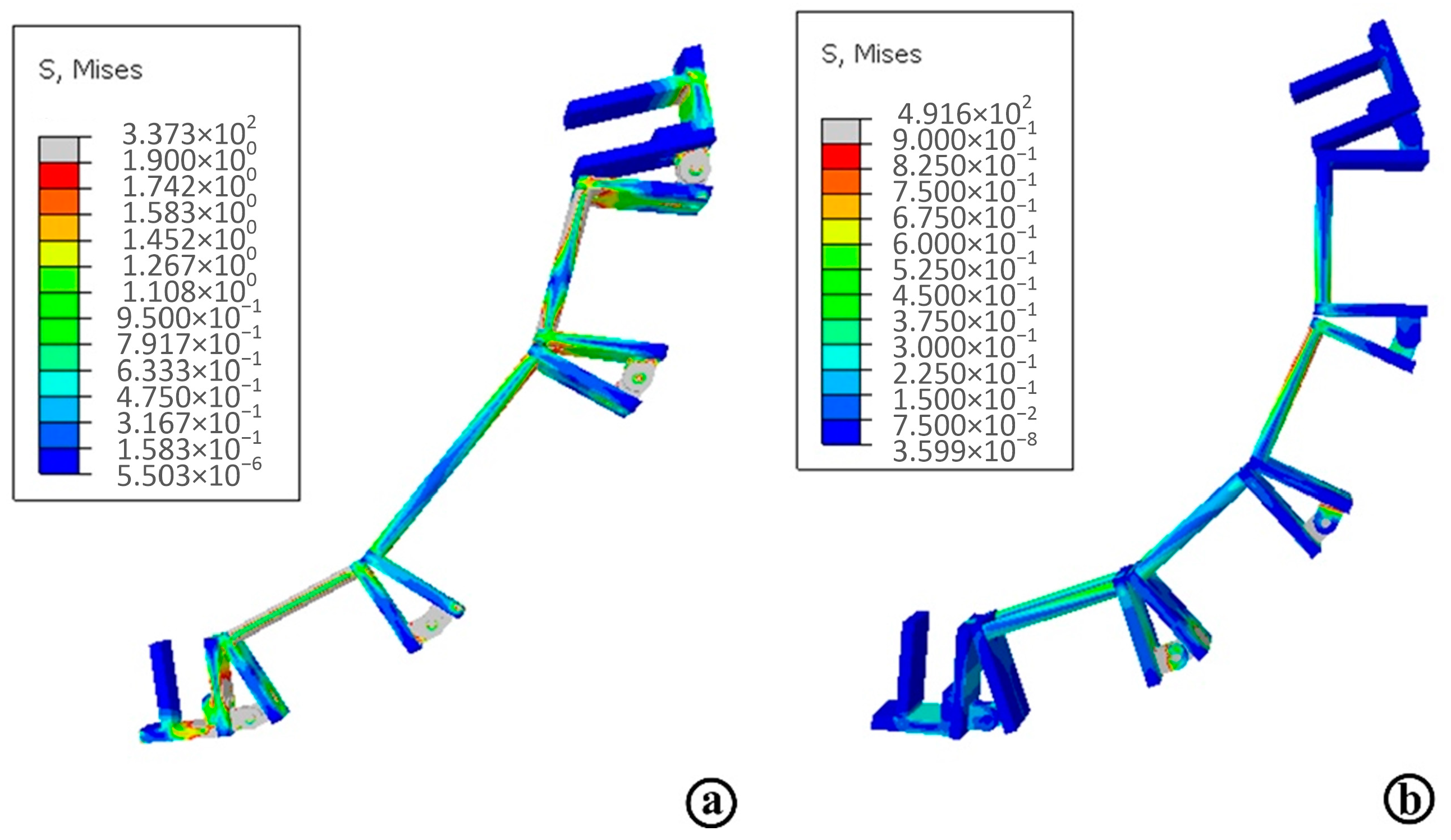
5.3. Mechanism Strength and Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gefen, A.; Brienza, D.M.; Cuddigan, J.; Haesler, E.; Kottner, J. Our contemporary understanding of the aetiology of pressure ulcers/pressure injuries. Int. Wound J. 2021, 19, 692–704. [Google Scholar] [CrossRef] [PubMed]
- Haesler, E. Prevention and Treatment of Pressure Ulcers/injuries: Clinical Practice Guideline. Int. Guidel. 2019, 17, 16–38. [Google Scholar]
- Zhang, S. New progress of pressure ulcers research. Foreign Med. Nurs. Vol. 2013, 14, 193–195. [Google Scholar]
- Xun, J. Research on Intelligent Nursing Bed Control System; Anhui University of Science and Technology: Huainan, China, 2018. [Google Scholar]
- Liu, J.; Zhu, L.; Gou, X. Current situation and trend of multifunctional nursing bed development. Med. Health Equip. 2019, 40, 94–98+103. [Google Scholar]
- Wang, Y.; Li, Z.; Wang, X.; Yu, H.; Liao, W.; Arifoglu, D. Human Gait Data Augmentation and Trajectory Prediction for Lower-Limb Rehabilitation Robot Control Using GANs and Attention Mechanism. Machines 2021, 9, 367. [Google Scholar] [CrossRef]
- Meng, Q.; Yue, Y.; Li, S.; Yu, H. Electromyogram-based motion compensation control for the upper limb rehabilitation robot in active training. Mech. Sci. 2022, 13, 675–685. [Google Scholar] [CrossRef]
- Gao, M.; Wang, Z.; Pang, Z.; Sun, J.; Li, J.; Li, S.; Zhang, H. Electrically Driven Lower Limb Exoskeleton Rehabilitation Robot Based on Anthropomorphic Design. Machines 2022, 10, 266. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Zuo, G.; Feng, G.; Zhang, X. Assist-As-Needed Control Strategy of Bilateral Upper Limb Rehabilitation Robot Based on GMM. Machines 2022, 10, 76. [Google Scholar] [CrossRef]
- Xie, Q.; Meng, Q.; Zeng, Q.; Yu, H.; Shen, Z. An innovative equivalent kinematic model of the human upper limb to improve the trajectory planning of exoskeleton rehabilitation robots. Mech. Sci. 2021, 12, 661–675. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H. Gait Learning for Lower Limb Rehabilitation Exoskeleton using Dynamical Movement Primitives based on General Regression Neural Networks. In Proceedings of the Chinese Automation Congress (CAC) 2020, Shanghai, China, 6–8 November 2020. [Google Scholar]
- Zhao, J.; Zhou, X.; Yang, X.; Yao, Z. Research of Wire-driven Parallel Lower Limb Rehabilitation Robot. J. Phys. Conf. Ser. 2022, 2229, 012025. [Google Scholar] [CrossRef]
- Xu, N.; Peng, X.; Peng, L.; Hou, Z.; Gui, M. Modeling and Kinematics Analysis of a Novel 5-DOF Upper Limb Exoskeleton Rehabilitation Robot. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar]
- Wang, Y.; Wang, K.; Chai, Y.; Mo, Z.; Wang, K. Research on mechanical optimization methods of cable-driven lower limb rehabilitation robot. Robotica 2021, 40, 154–169. [Google Scholar] [CrossRef]
- Chen, C.T.; Lien, W.Y.; Chen, C.T.; Twu, M.J.; Wu, Y.C. Dynamic Modeling and Motion Control of a Cable-Driven Robotic Exoskeleton with Pneumatic Artificial Muscle Actuators. IEEE Access 2020, 8, 149796–149807. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Z.; Wang, Q. On the Design of Rigid-Soft Hybrid Exoskeleton Based on Remote Cable Actuator for Gait Rehabilitation. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020. [Google Scholar]
- Chen, Y.; Li, G.; Zhu, Y.; Zhao, J.; Cai, H. Design of a 6-DOF upper limb rehabilitation exoskeleton with parallel actuated joints. Bio-Med. Mater. Eng. 2014, 24, 2527–2535. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, C.; Fang, Z.; Sun, X.; Chen, W. Design of an Underactuated Body Fixture for a 7-DOF Cable-Driven Upper Limb Exoskeleton. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020. [Google Scholar]
- Tan, J.; Zhou, J. Surgical Nursing; People’s Medical Publishing House: Beijing, China, 2008; p. 281. [Google Scholar]
- Su, P.; Lun, Q.; Lu, D.; Wu, Q.; Liu, T.; Zhang, L. Biomechanical changes on the typical sites of pressure ulcers in the process of turning over from supine position: Theoretical analysis, simulation, and experiment. Ann. Bio-Med. Eng. 2022, 50, 654–665. [Google Scholar] [CrossRef] [PubMed]
- Lang, A.E.; Kim, S.Y.; Milosavljevic, S.; Dickerson, C.R. The utility of the acromion marker cluster (AMC) in a clinical population. J. Electromyogr. Kinesiol. 2019, 62, 102298. [Google Scholar] [CrossRef] [PubMed]
- Wu, T. Kinematic Analysis of Human Shoulder Joint and Research on Shoulder-Humeral Rhythm Based on Optical Motion Capture System; Shanghai Jiao Tong University: Shanghai, China, 2016. [Google Scholar]
- Su, P.; Lu, D.; Lun, Q.; Li, J.; Xu, X.; Fan, Y. Research on the Design of Human Body Rollover Mechanism Based on motion trajectory graph Fitting. J. Graph. 2020, 41, 993–1000. [Google Scholar]
- Wu, S.; Zhang, Q.; Xiao, B.; Wei, X. An effective data processing method for optical motion capture. J. Basic Sci. Eng. 2009, 17, 9. [Google Scholar]
- Lu, D.; Su, P.; Ji, R.; Li, H.; Hao, Y.; Fan, Y. Dynamic simulation and experimental verification of human supine rollover. J. Biomed. Eng. 2019, 36, 777–784. [Google Scholar]





| Adjacent Feature Point Number | Distance between Two Points/mm |
|---|---|
| P1–P2 | 69.2 |
| P2–P3 | 176.6 |
| P3–P4 | 68.4 |
| P5–P6 | 67.9 |
| P6–P7 | 70.4 |
| P7–P8 | 69.8 |
| P8–P9 | 68.5 |
| Feature Points | x | y | z | Two-Point Distance/mm | |
|---|---|---|---|---|---|
| P1 | 51.745 | 474.431 | 25.450 | ||
| 69.2 | |||||
| P2 | 52.803 | 406.060 | 35.957 | ||
| 176.3 | |||||
| P3 | 53.346 | 229.817 | 36.543 | ||
| 68.4 | |||||
| P4 | 51.753 | 162.150 | 26.526 | ||
| Coordinate System Transformation | αi−1/(°) | ai−1/mm | di/mm | θi/(°) |
|---|---|---|---|---|
| O0–O1 | 0 | 0 | 0 | −(π − θ1) |
| O1–O10 | 0 | l1 | 0 | −(π − θ10) |
| O10–O9 | 0 | l7 | l10 | π − θ9 |
| O9–O8 | 0 | l6 | −l11 | 0 |
| Coordinates the i | αi−1/(°) | ai−1/mm | di/mm | θi/(°) |
|---|---|---|---|---|
| O0–O1 | 0 | 0 | 0 | −(π − θ1) |
| O1–O2 | 0 | l1 | 0 | −(π − θ2) |
| O2–O5 | 0 | l2 | 0 | −θ5 |
| O5–O6 | 0 | l4 | l8 | −(π − θ6) |
| O6–O7 | 0 | l5 | −l9 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, P.; Zhang, Y.; Lun, Q.; Ma, C.; Liu, Y.; Zhang, L.; Huang, L. Design and Load Kinematics Analysis of Rollover Rehabilitation Mechanism Fitting Human Motion Curve. Micromachines 2022, 13, 2064. https://doi.org/10.3390/mi13122064
Su P, Zhang Y, Lun Q, Ma C, Liu Y, Zhang L, Huang L. Design and Load Kinematics Analysis of Rollover Rehabilitation Mechanism Fitting Human Motion Curve. Micromachines. 2022; 13(12):2064. https://doi.org/10.3390/mi13122064
Chicago/Turabian StyleSu, Peng, Yuelin Zhang, Qinglong Lun, Chao Ma, Yi Liu, Leiyu Zhang, and Long Huang. 2022. "Design and Load Kinematics Analysis of Rollover Rehabilitation Mechanism Fitting Human Motion Curve" Micromachines 13, no. 12: 2064. https://doi.org/10.3390/mi13122064
APA StyleSu, P., Zhang, Y., Lun, Q., Ma, C., Liu, Y., Zhang, L., & Huang, L. (2022). Design and Load Kinematics Analysis of Rollover Rehabilitation Mechanism Fitting Human Motion Curve. Micromachines, 13(12), 2064. https://doi.org/10.3390/mi13122064








