Experimental Investigation: Vibration Measurement of a Rotating Blade with Digital Image Correlation and Blade Tip-Timing
Abstract
:1. Introduction
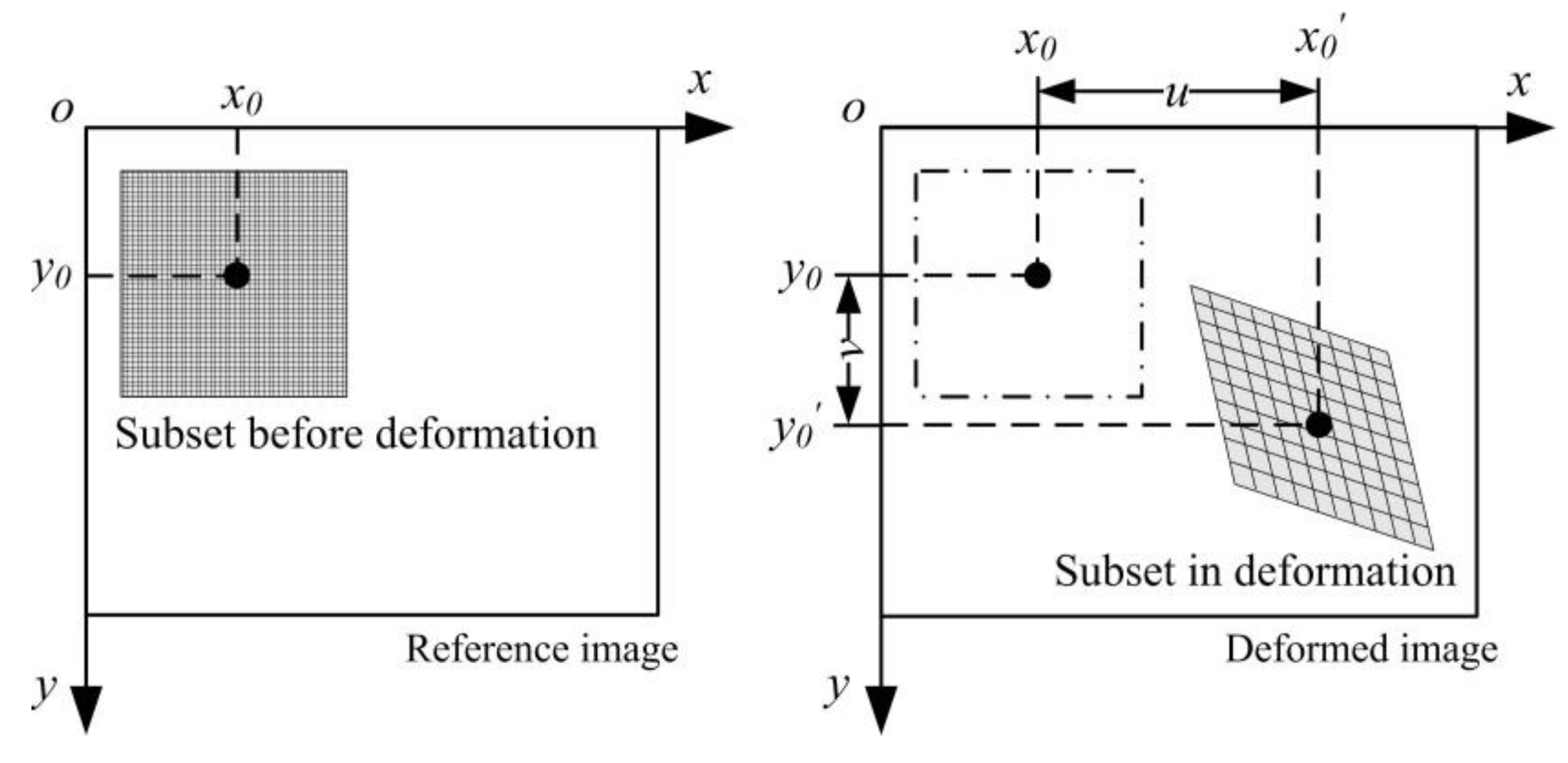
2. Methodology
3. Experimental Set-Ups
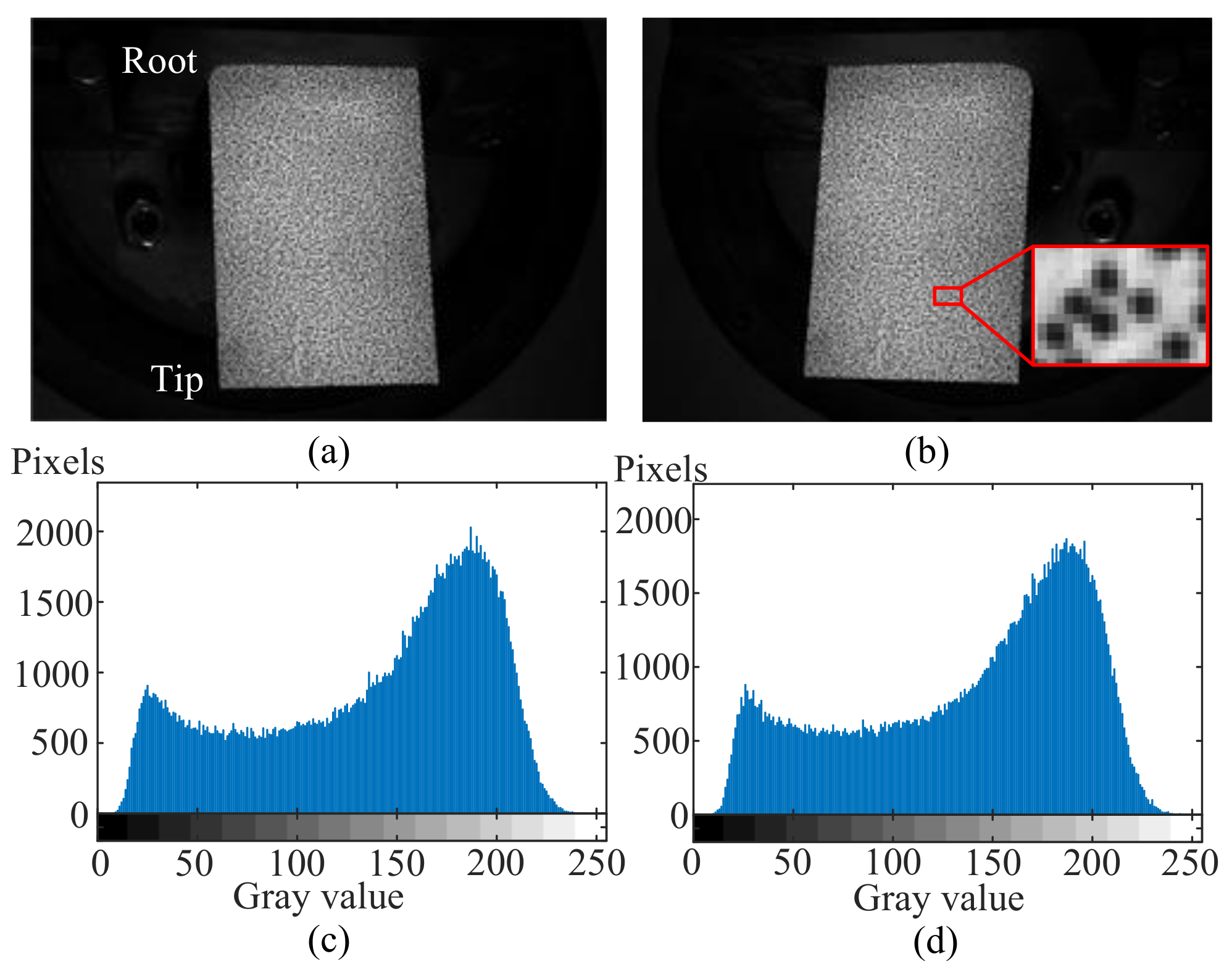
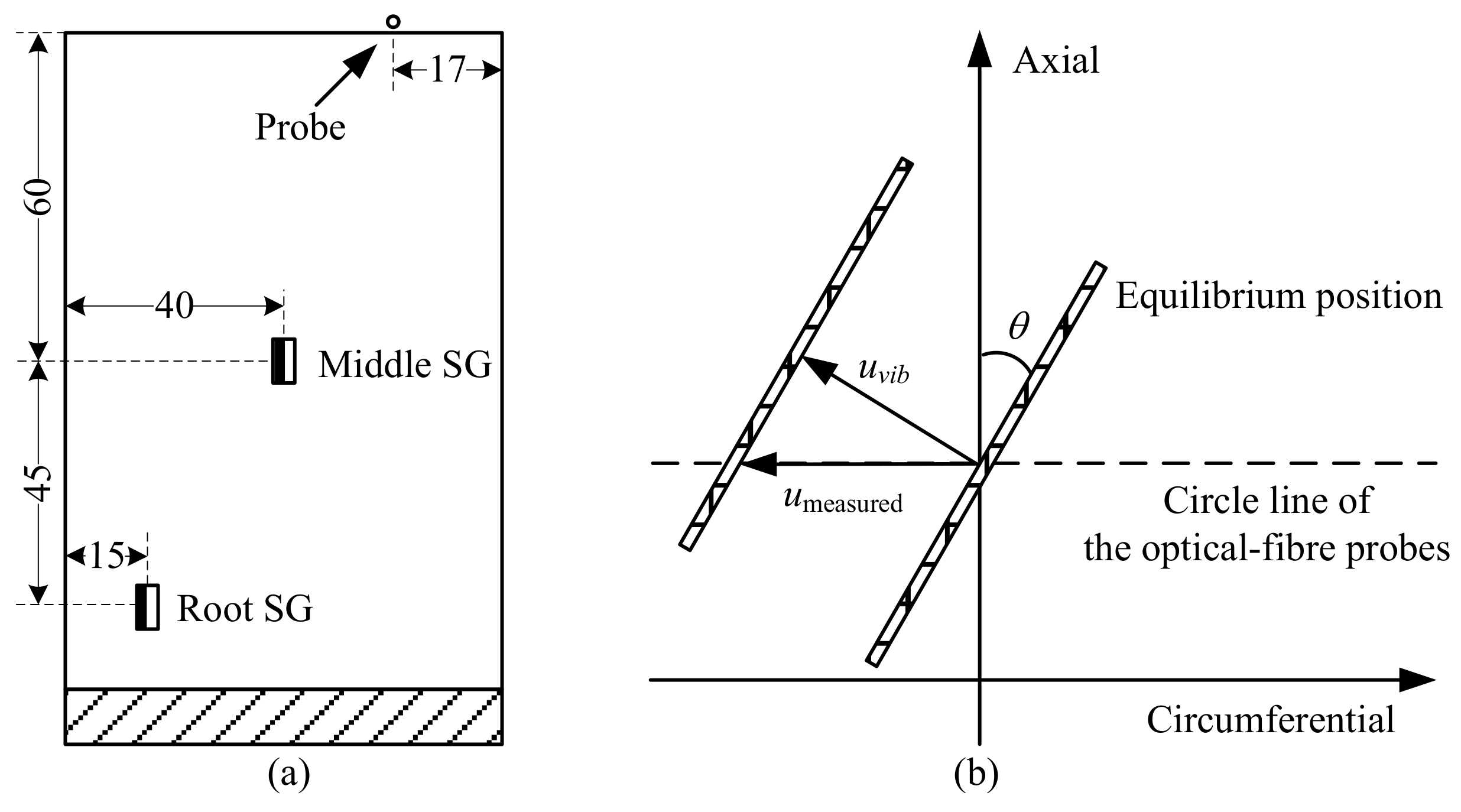
3.1. Stereo-DIC Experimental Setups
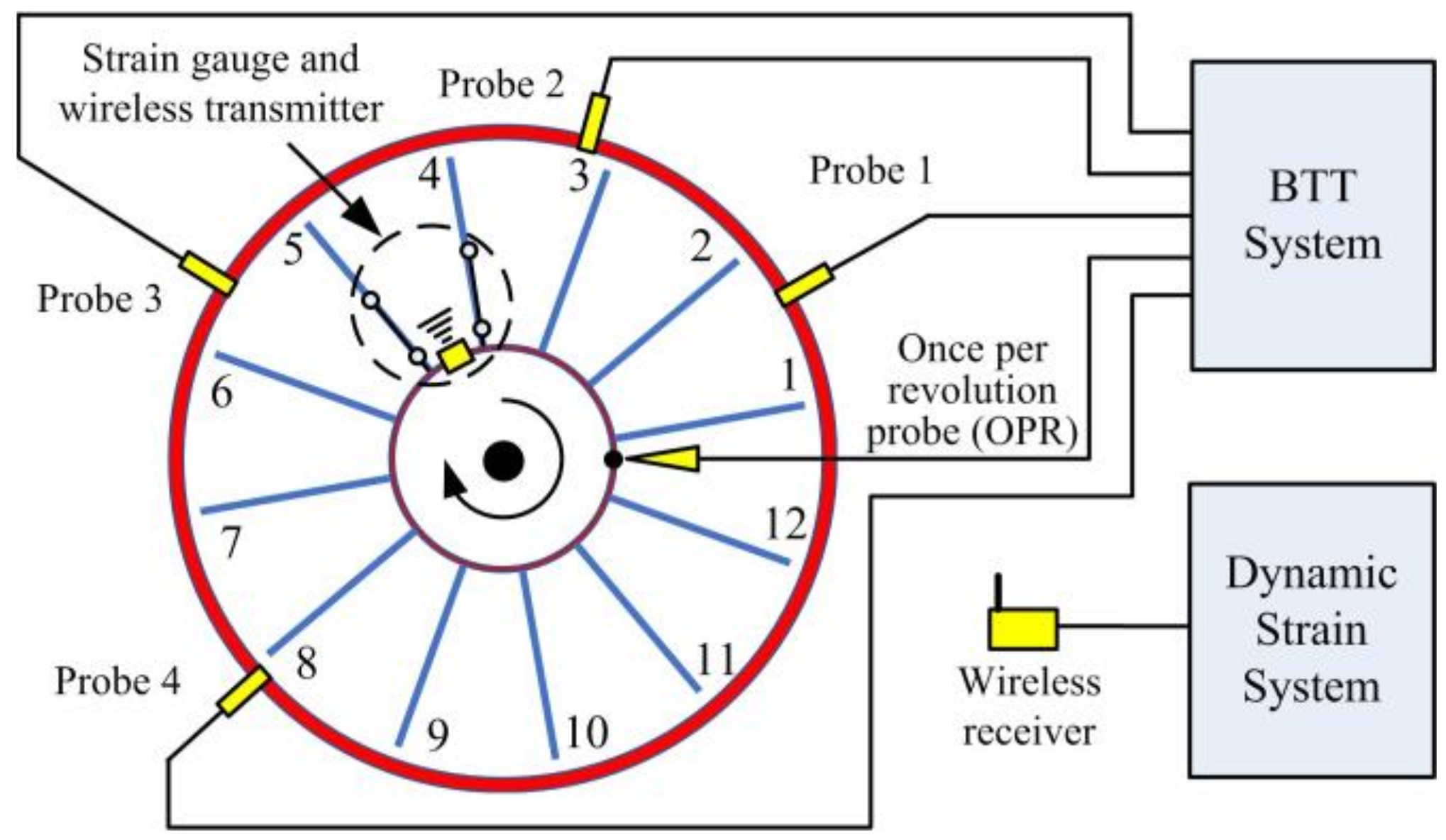
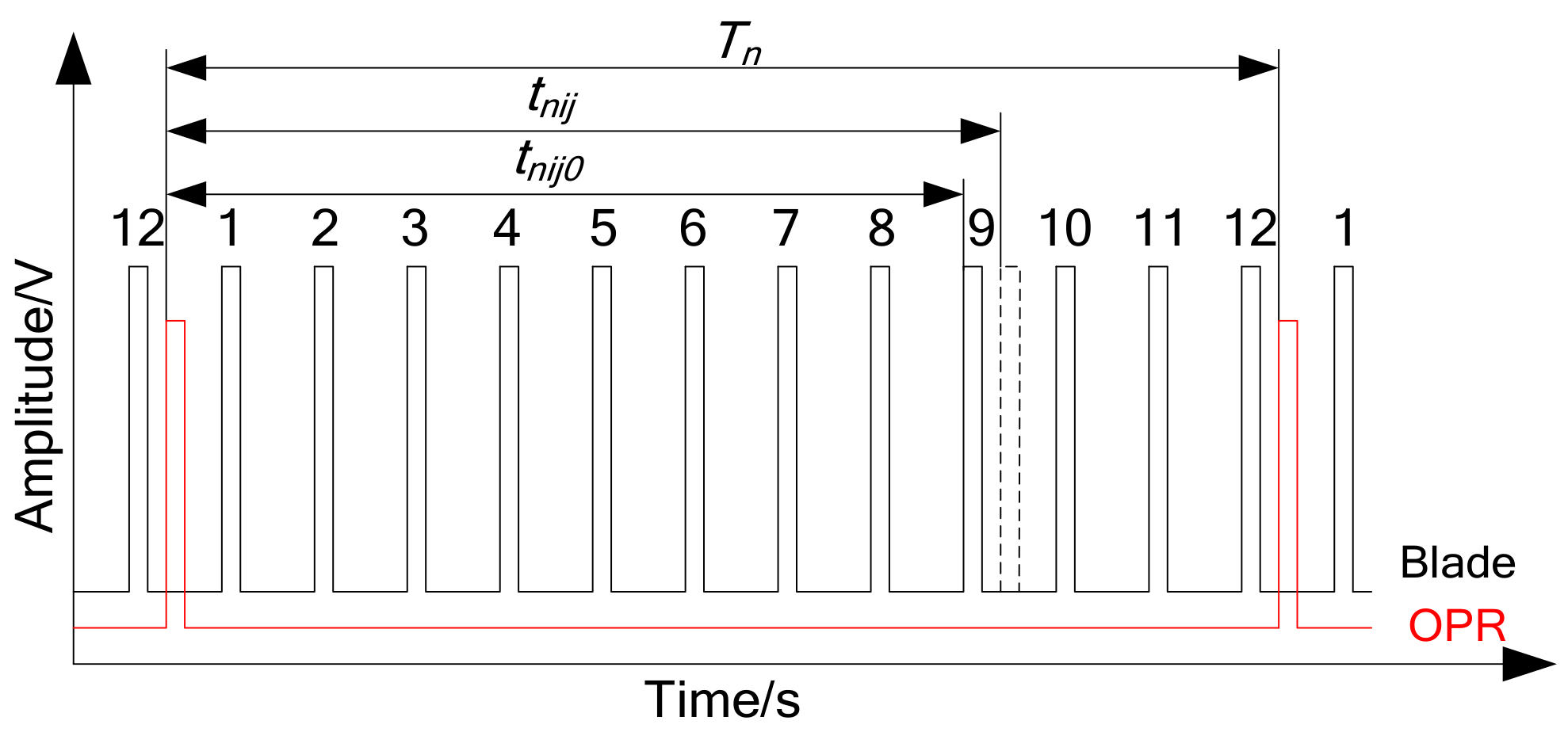
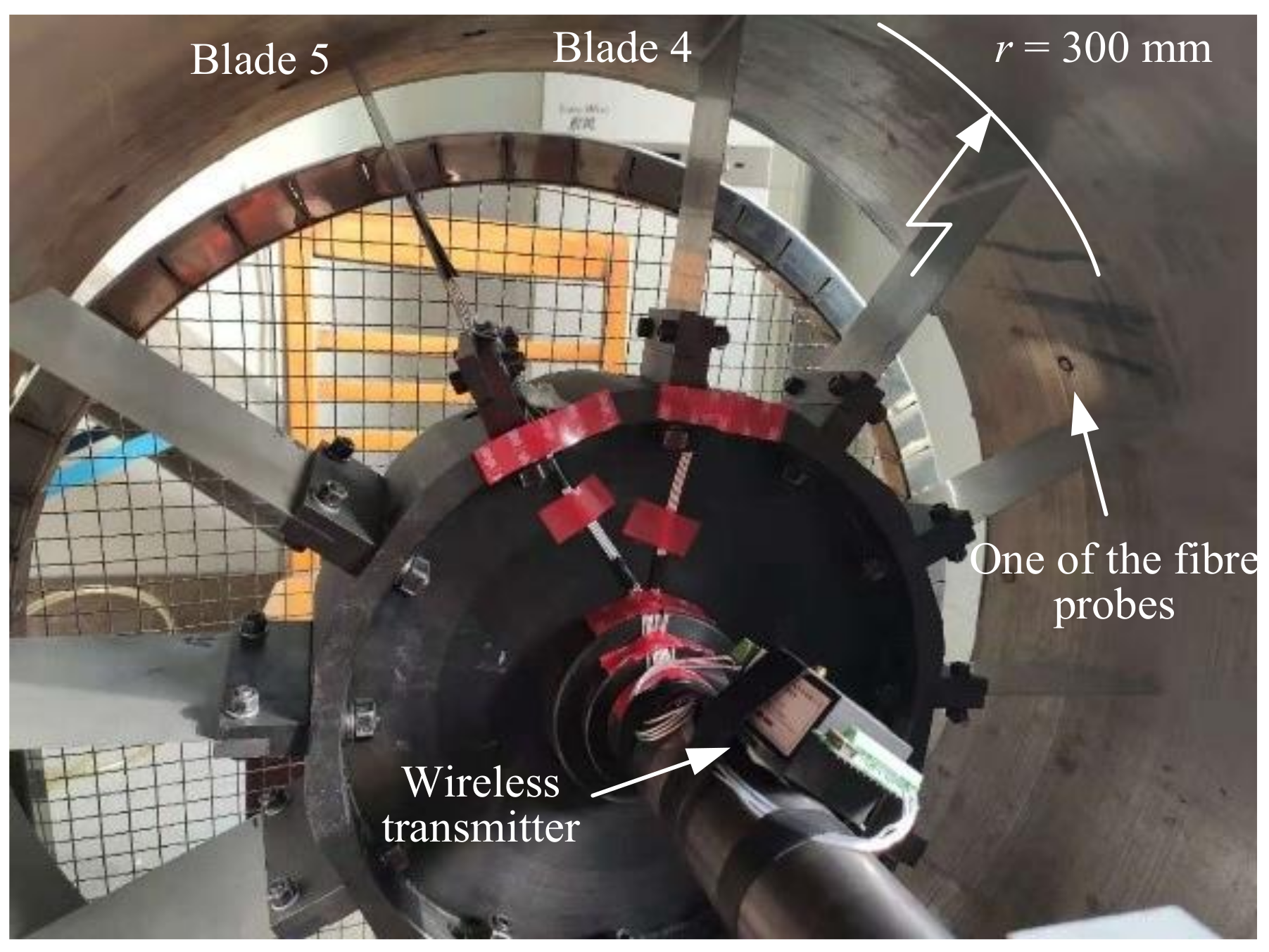
3.2. BTT Experimental Setups
4. Results and Analysis
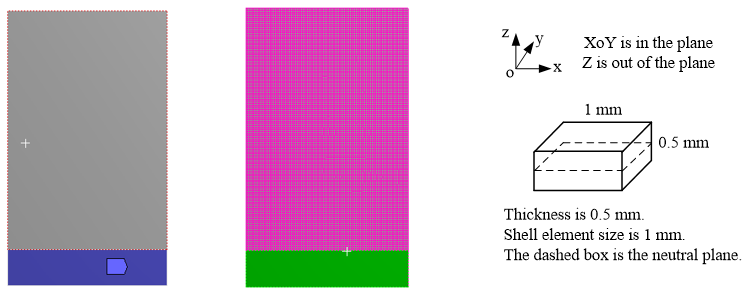
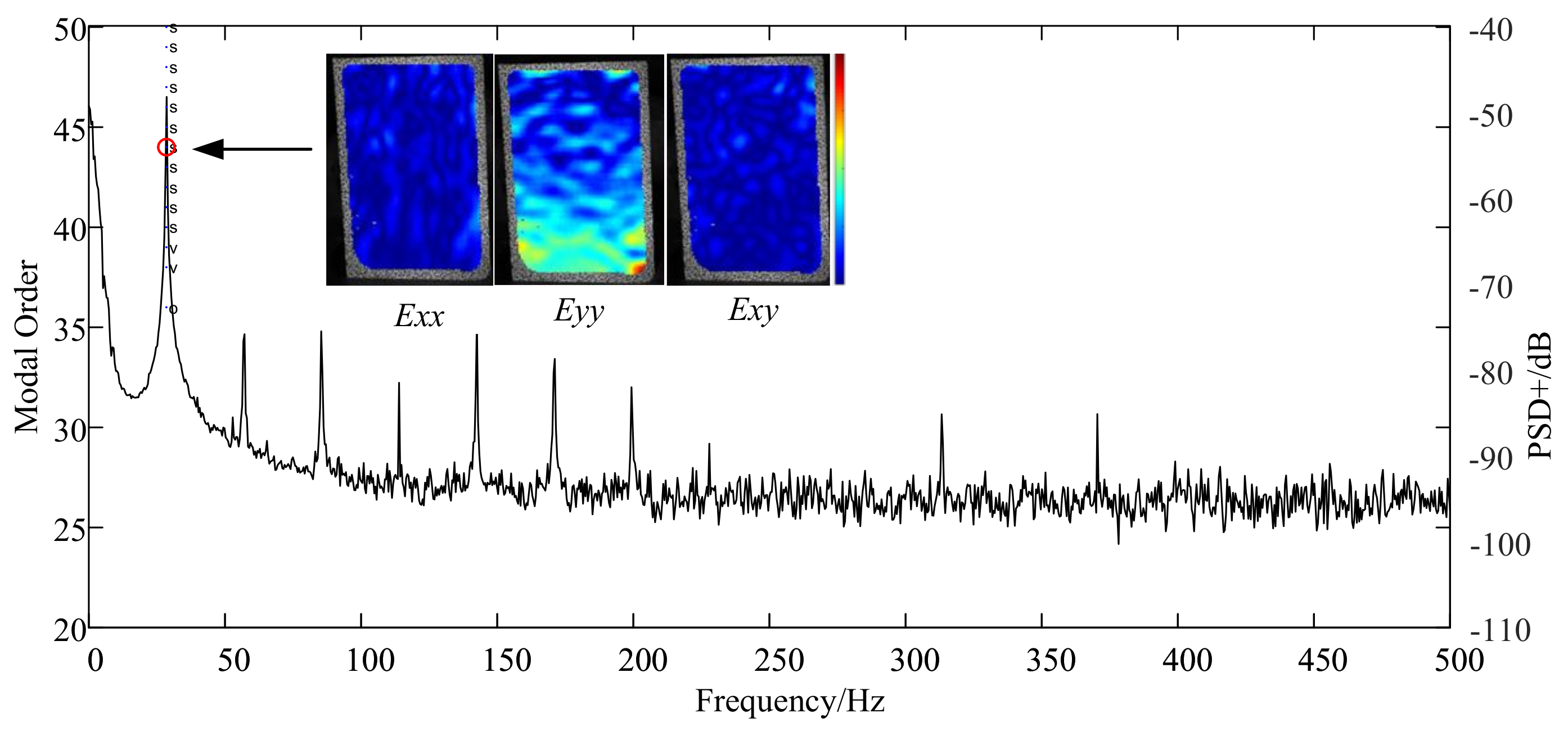
4.1. DIC Results and Validation with FE Model
4.2. Comparisons of the Dynamic Strain at the First Order of Mode Frequency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zielinski, M.; Ziller, G. Noncontact vibration measurements on compressor rotor blades. Meas. Sci. Technol. 2000, 11, 847. [Google Scholar] [CrossRef]
- Battiato, G.; Firrone, C.M.; Berruti, T.M. Forced response of rotating bladed disks: Blade tip-timing measurements. Mech. Syst. Signal Process. 2017, 85, 912–926. [Google Scholar] [CrossRef]
- Gallego-Garrido, J.; Dimitriadis, G.; Carrington, I.B.; Wright, J.R. A class of methods for the analysis of blade tip timing data from bladed assemblies undergoing simultaneous resonances—Part II: Experimental validation. Int. J. Rotating Mach. 2007, 2007, 73624. [Google Scholar] [CrossRef] [Green Version]
- Heath, S.; Imregun, M. An improved single-parameter tip-timing method for turbomachinery blade vibration measurements using optical laser probes. Int. J. Mech. Sci. 1996, 38, 1047–1058. [Google Scholar] [CrossRef]
- Heath, S.; Imregun, M. A survey of blade tip-timing measurement techniques for turbomachinery vibration. J. Eng. Gas. Turbines Power 1998, 120, 784–791. [Google Scholar] [CrossRef]
- Carrington, I.B.; Wright, J.R.; Cooper, J.E.; Dimitriadis, G. A comparison of blade tip timing data analysis methods. Proc. Inst. Mech. Eng. Part G—J. Aerosp. Eng. 2001, 215, 301–312. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Carrington, I.B.; Wright, J.R.; Cooper, J.E. Blade-tip timing measurement of synchronous vibrations of rotating bladed assemblies. Mech. Syst. Signal Process. 2002, 16, 599–622. [Google Scholar] [CrossRef]
- Przysowa, R.; Russhard, P. Non-contact measurement of blade vibration in an axial compressor. Sensors 2020, 20, 68. [Google Scholar] [CrossRef] [Green Version]
- Knappett, D.; Garcia, J. Blade tip timing and strain gauge correlation on compressor blades. Proc. Inst. Mech. Eng. Part G—J. Aerosp. Eng. 2008, 222, 497–506. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H.W. Image Correlation for Shape, Motion, and Deformation Measurements: Basic Concepts, Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.M.; Xie, H.M.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Sutton, M.A.; Hild, F. Recent advances and perspectives in digital image correlation. Exp. Mech. 2015, 55, 1–8. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances, and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Srivastava, V.; Baqersad, J. A multi-view optical technique to extract the operating deflection shapes of a full vehicle using digital image correlation. Thin Wall Struct. 2019, 145, 106426. [Google Scholar] [CrossRef]
- Huňady, R.; Hagara, M. A new procedure of modal parameter estimation for high-speed digital image correlation. Mech. Syst. Signal Process. 2017, 93, 66–79. [Google Scholar] [CrossRef]
- Beberniss, T.J.; Ehrhardt, D.A. High-speed 3D digital image correlation vibration measurement: Recent advancements and noted limitations. Mech. Syst. Signal Process. 2017, 86, 35–48. [Google Scholar] [CrossRef]
- Bharadwaj, K.; Sheidaei, A.; Afshar, A.; Baqersad, J. Full-field strain prediction using mode shapes measured with digital image correlation. Measurement 2019, 139, 326–333. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Baqersad, J.; Bharadwaj, K. Strain expansion-reduction approach. Mech. Syst. Signal Process. 2018, 101, 156–167. [Google Scholar] [CrossRef]
- Patron, S.R.; Sirohi, J. Operational modal analysis of a helicopter rotor blade using digital image correlation. Exp. Mech. 2017, 57, 367–375. [Google Scholar] [CrossRef]
- Uehara, D.; Sirohi, J.; Feil, R.; Rauleder, J. Measurement of transient blade passage loads of a coaxial counter-rotating rotor in hover. In Proceedings of the 44th European Rotorcraft Forum, Delft, The Netherlands, 18–21 September 2018; Available online: https://www.researchgate.net/publication/319618062 (accessed on 12 October 2022).
- Ao, C.Y.; Qiao, B.J.; Liu, M.R.; Fu, S.G.; Yang, Z.B. Dynamic strain reconstruction of rotating blades based on tip timing and response transmissibility. J. Eng. Gas. Turbines Power-Trans. ASME 2022, 144, 061011. [Google Scholar] [CrossRef]
- Ao, C.Y.; Qiao, B.J.; Liu, M.R.; Zhu, W.D.; Zhu, Y.D.; Wang, Y.N.; Chen, X.F. Non-contact full-field dynamic strain reconstruction of rotating blades under multi-mode vibration. Mech. Syst. Signal Proc. 2022, 186, 109840. [Google Scholar] [CrossRef]
- Ehrhardt, D.A.; Allen, M.S.; Yang, S.F.; Beberniss, T.J. Full-field linear and nonlinear measurements using continuous-scan laser Doppler vibrometry and high speed three-dimensional digital image correlation. Mech. Syst. Signal Proc. 2016, 86, 82–97. [Google Scholar] [CrossRef]
- Galeazzi, S.; Chiariotti, P.; Martarelli, M.; Tomasini, E.P. 3D digital image correlation for vibration measurement on rolling tire: Procedure development and comparison with laser Doppler vibrometer. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1149, 012010. [Google Scholar] [CrossRef]
- Reu, P.L.; Rohe, D.P.; Jacobs, L.D. Comparison of DIC and LDV for practical vibration and modal measurements. Mech. Syst. Signal Proc. 2017, 86, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Zanarini, A. Broad frequency band full field measurements for advanced applications: Point-wise comparisons between optical technologies. Mech. Syst. Signal Proc. 2018, 98, 968–999. [Google Scholar] [CrossRef]
- Zanarini, A. Chasing the high-resolution mapping of rotational and strain FRFs as receptance processing from different full-field optical measuring technologies. Mech. Syst. Signal Proc. 2022, 166, 108428. [Google Scholar] [CrossRef]
- Reu, P.L. All about speckles: Speckle size measurement. Exp. Tech. 2015, 38, 1–2. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust, and accurate digital image correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Shao, X.X.; Dai, X.J.; He, X.Y. Noise robustness and parallel computation of the inverse compositional Gauss-Newton algorithm in digital image correlation. Opt. Lasers Eng. 2015, 71, 9–19. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Wang, T.Y.; Jiang, Z.Y.; Qian, K.M.; Liu, Y.P.; Liu, Z.J.; Tang, L.Q.; Dong, S.B. High accuracy digital image correlation powered by GPU-based parallel computing. Opt. Lasers Eng. 2015, 69, 7–12. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, G.C.; Ma, S.P.; Meng, L.B. Application of an improved subpixel registration algorithm on digital speckle correlation measurement. Opt. Laser Technol. 2003, 35, 533–542. [Google Scholar] [CrossRef]
- Bruck, H.A.; McNeill, S.R.; Sutton, M.A.; Peters, W.H. Digital image correlation using Newton-Raphson method of partial differential correction. Exp. Mech. 1989, 29, 261–267. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Lucas-Kanade 20 years on: A unifying framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Available online: http://www.ncorr.com/index.php/dic-algorithms (accessed on 12 October 2022).
- Pan, M.H.; Yang, Y.M.; Guan, F.J.; Hu, H.F.; Xu, H.L. Sparse representation based frequency detection and uncertainty reduction in blade tip timing measurement for multi-mode blade vibration monitoring. Sensors 2017, 17, 1745. [Google Scholar] [CrossRef] [Green Version]
- Joung, K.K.; Kang, S.C.; Paeng, K.S.; Park, N.G.; Choi, H.J.; You, Y.J. Analysis of vibration of the turbine blades using non-intrusive stress measurement system. In Proceedings of the ASME 2006 Power Conference, Atlanta, GA, America, 2–4 May 2006. [Google Scholar] [CrossRef]
- Garrido, J.G.; Dimitriadis, G.; Wright, J.R. A class of methods for the analysis of blade tip timing data from bladed assemblies undergoing simultaneous resonances—Part I: Theoretical development. Int. J. Rotating Mach. 2007, 2007, 27247. [Google Scholar] [CrossRef]
- Heath, S. A new technique for identifying synchronous resonances using tip-timing. J. Eng. Gas. Turbines Power 2000, 122, 219–225. [Google Scholar] [CrossRef]
- Yue, L.; Liu, H.; Zang, C.P.; Wang, D.; Hu, W.; Wang, L. The parameter identification method of blade asynchronous vibration under sweep speed excitation. J. Phys. Conf. Ser. 2016, 744, 012051. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.H.; Yue, L. Vibration measurement of a metal sheet using single-camera digital image correlation with projection components. Shock Vib. 2022, 2022, 1098337. Available online: https://www.hindawi.com/journals/sv/2022/1098337/ (accessed on 12 October 2022). [CrossRef]
- Liang, Z.H.; Yue, L. Vibration modes measurement of defective plate using high-speed digital image correlation. In Proceedings of the 9th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018; Available online: https://www.ndt.net/search/docs.php3?id=23453 (accessed on 12 October 2022).
- Guillaume, P.; Verboven, P.; Vanlanduit, S.; Auweraer, H.V.; Peeters, B. A ploy-reference implementation of the least-squares complex frequency-domain estimator. In Proceedings of the International Modal Analysis Conference; 2003; pp. 395–409. Available online: https://www.researchgate.net/publication/265423092 (accessed on 12 October 2022).



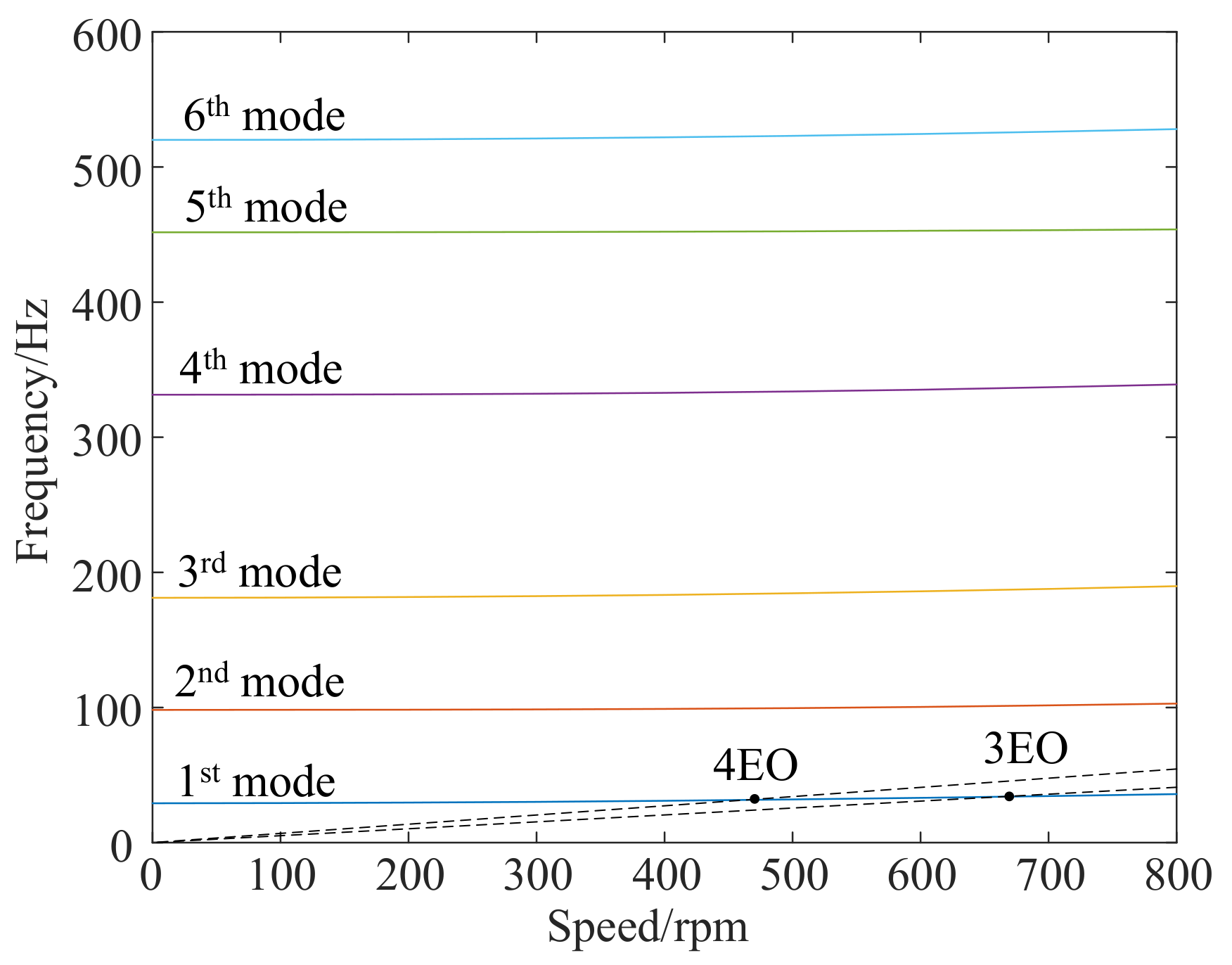
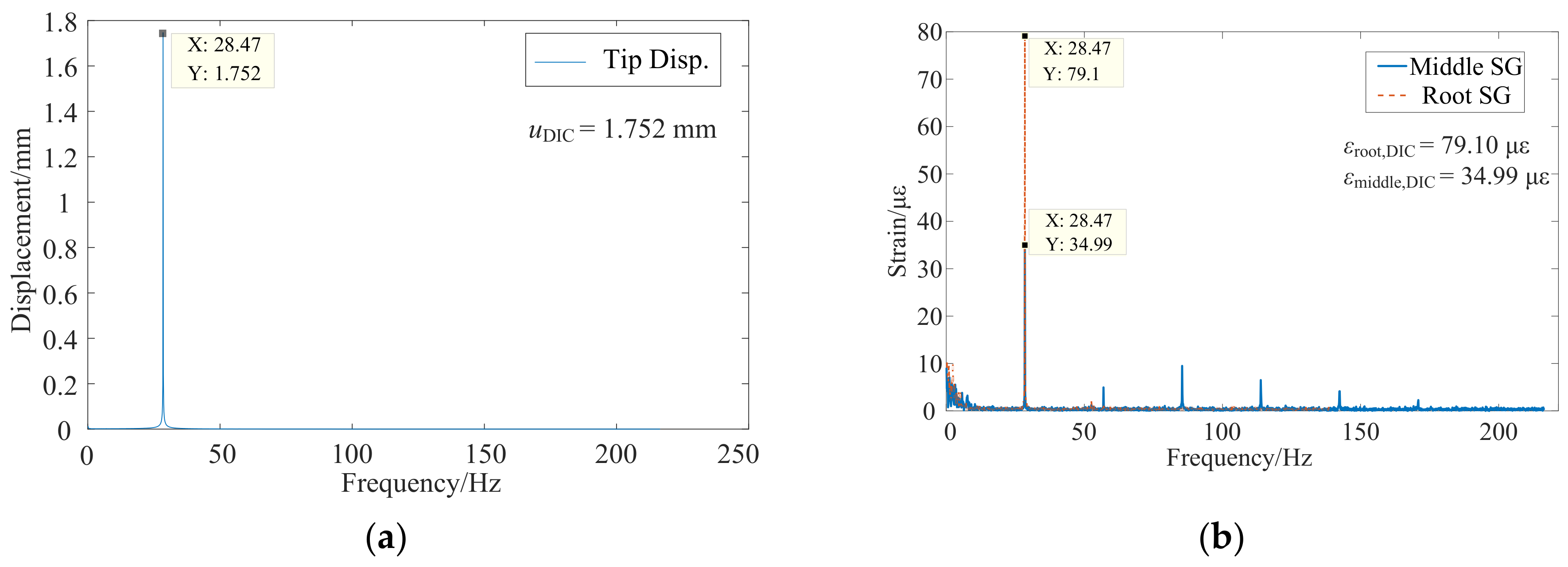
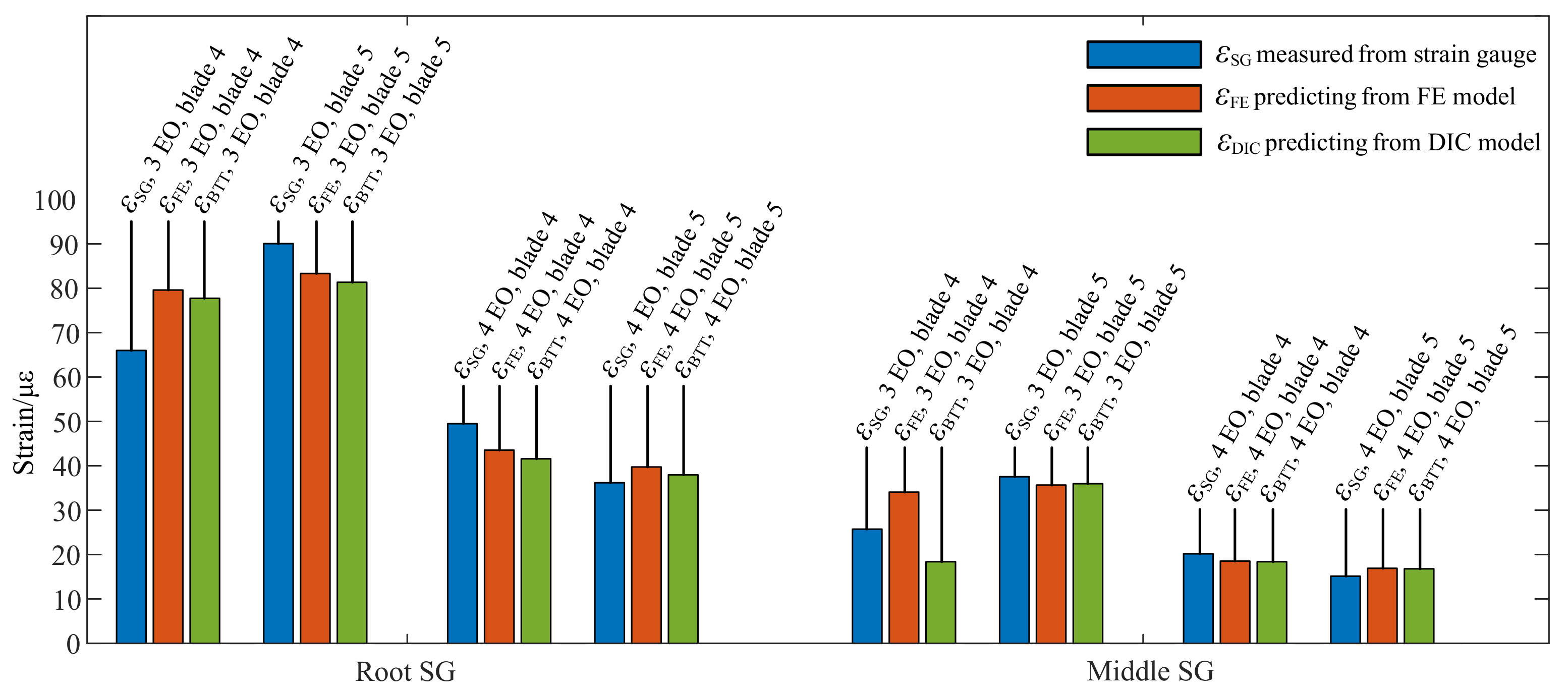

| No Speed | 4 EO @ 479.7 rpm | 3 EO @ 682.8 rpm | |
|---|---|---|---|
| 49.27 | 48.17 | 47.13 | |
| 20.85 | 20.50 | 20.17 |
| 1.752 | 79.10 | 46.02 | 6.59% | |||
| 34.99 | 20.35 | 1.12% | ||||
| Relative Errors | Relative Errors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Blade 4 | 1.6892 | 65.99 | 79.61 | 20.64% | 77.74 | 17.81% | |||
| 25.73 | 34.07 | 32.41% | 18.39 | 28.53% | |||||
| Blade 5 | 1.7678 | 90.05 | 83.32 | 7.47% | 81.35 | 9.66% | |||
| 37.54 | 35.66 | 5.01% | 35.97 | 4.18% | |||||
| Relative Errors | Relative Errors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Blade 4 | 0.9035 | 49.49 | 43.52 | 12.06% | 41.58 | 15.98% | |||
| 20.18 | 18.52 | 8.23% | 18.39 | 8.87% | |||||
| Blade 5 | 0.8250 | 36.18 | 39.74 | 9.84% | 37.97 | 4.95% | |||
| 15.14 | 16.91 | 11.69% | 16.79 | 10.90% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Zhang, Y.; Yue, L. Experimental Investigation: Vibration Measurement of a Rotating Blade with Digital Image Correlation and Blade Tip-Timing. Micromachines 2022, 13, 2156. https://doi.org/10.3390/mi13122156
Liang Z, Zhang Y, Yue L. Experimental Investigation: Vibration Measurement of a Rotating Blade with Digital Image Correlation and Blade Tip-Timing. Micromachines. 2022; 13(12):2156. https://doi.org/10.3390/mi13122156
Chicago/Turabian StyleLiang, Zhonghan, Yuxiang Zhang, and Lin Yue. 2022. "Experimental Investigation: Vibration Measurement of a Rotating Blade with Digital Image Correlation and Blade Tip-Timing" Micromachines 13, no. 12: 2156. https://doi.org/10.3390/mi13122156
APA StyleLiang, Z., Zhang, Y., & Yue, L. (2022). Experimental Investigation: Vibration Measurement of a Rotating Blade with Digital Image Correlation and Blade Tip-Timing. Micromachines, 13(12), 2156. https://doi.org/10.3390/mi13122156





