Numerical Modeling of the Effect of Cutting-Edge Radius on Cutting Force and Stress Concentration during Machining
Abstract
:1. Introduction
2. Simulation Modeling
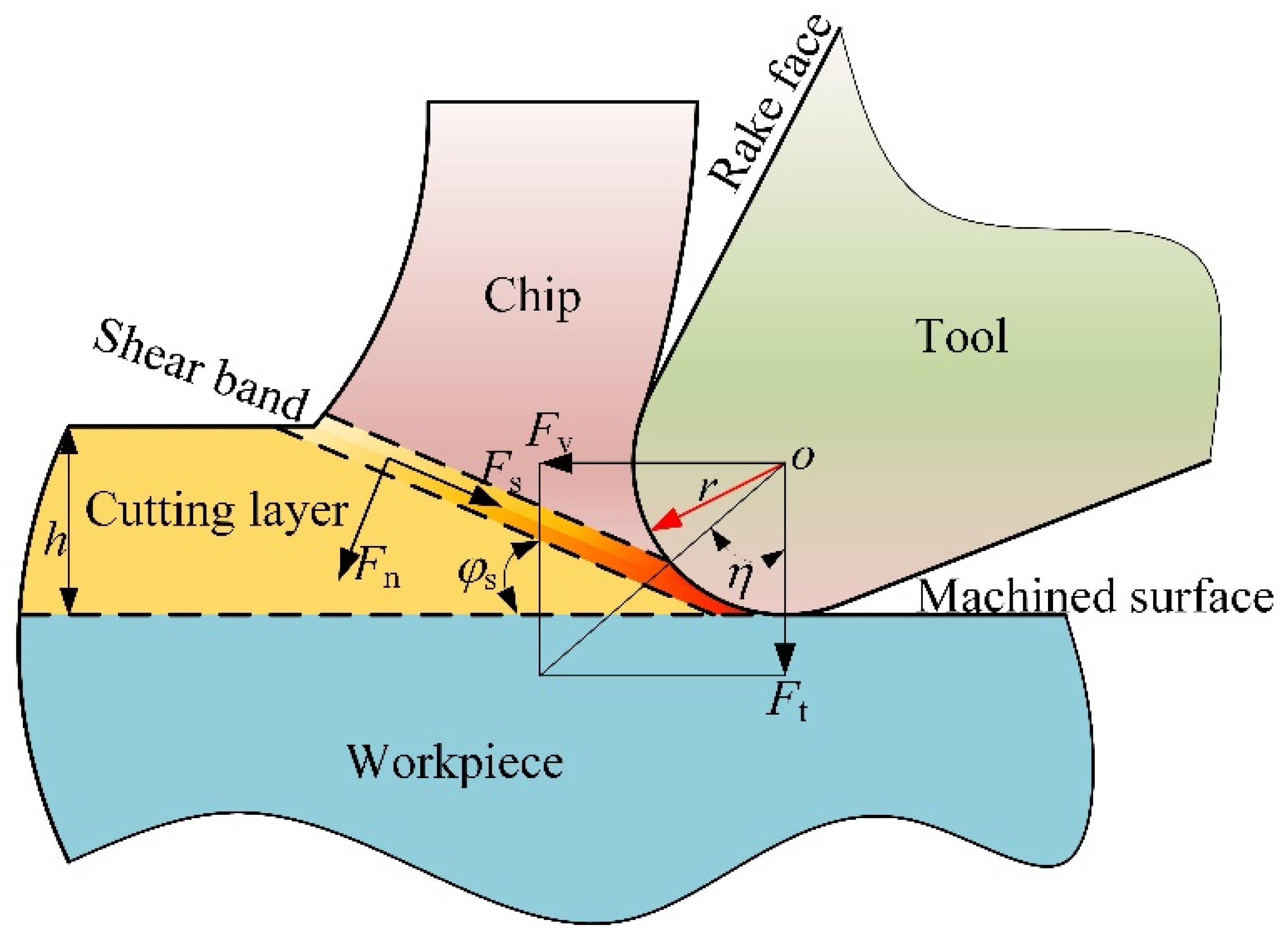
2.1. Tool Geometry and Mechanical Model
2.2. Workpiece Property
3. Results and Discussion
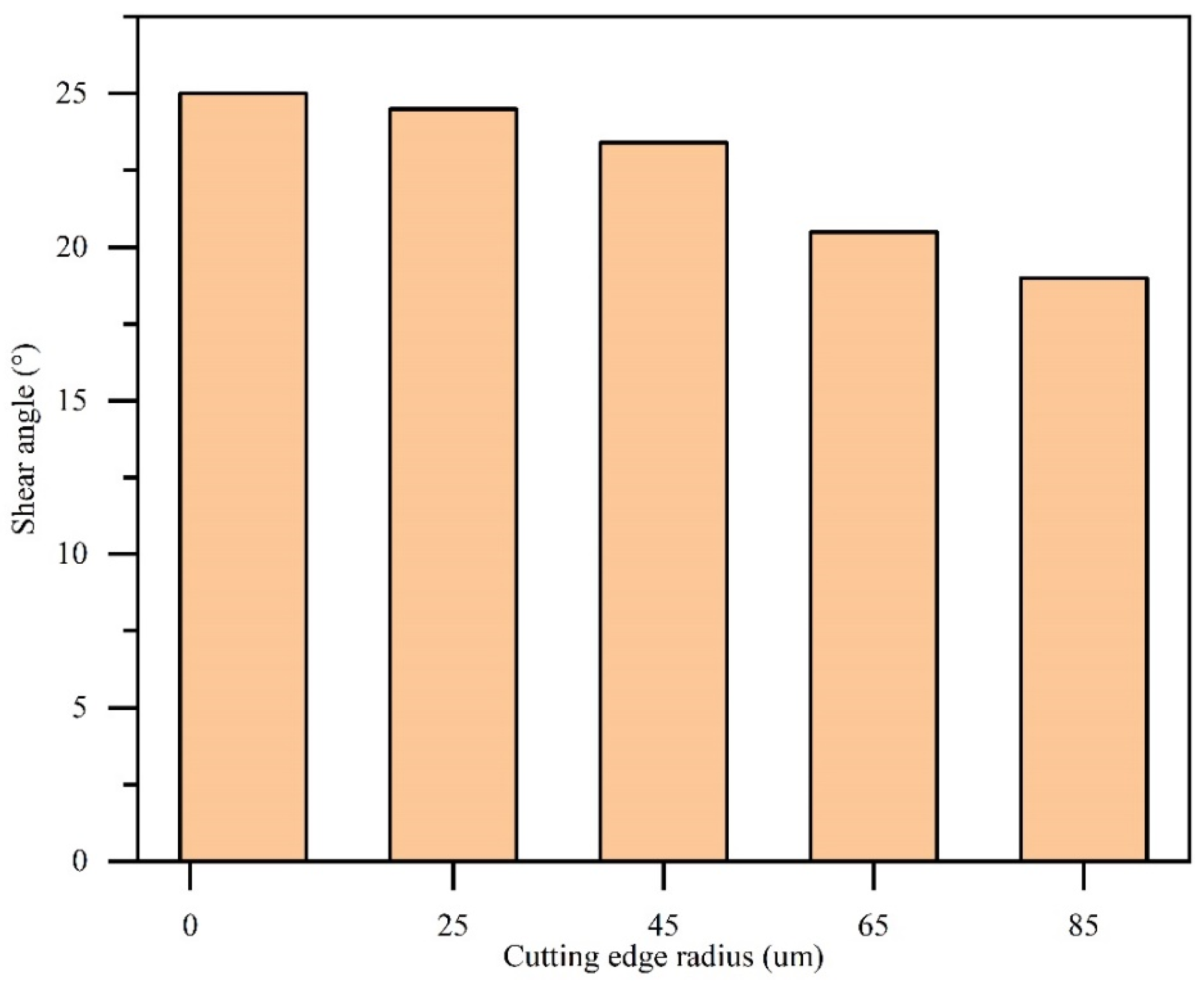
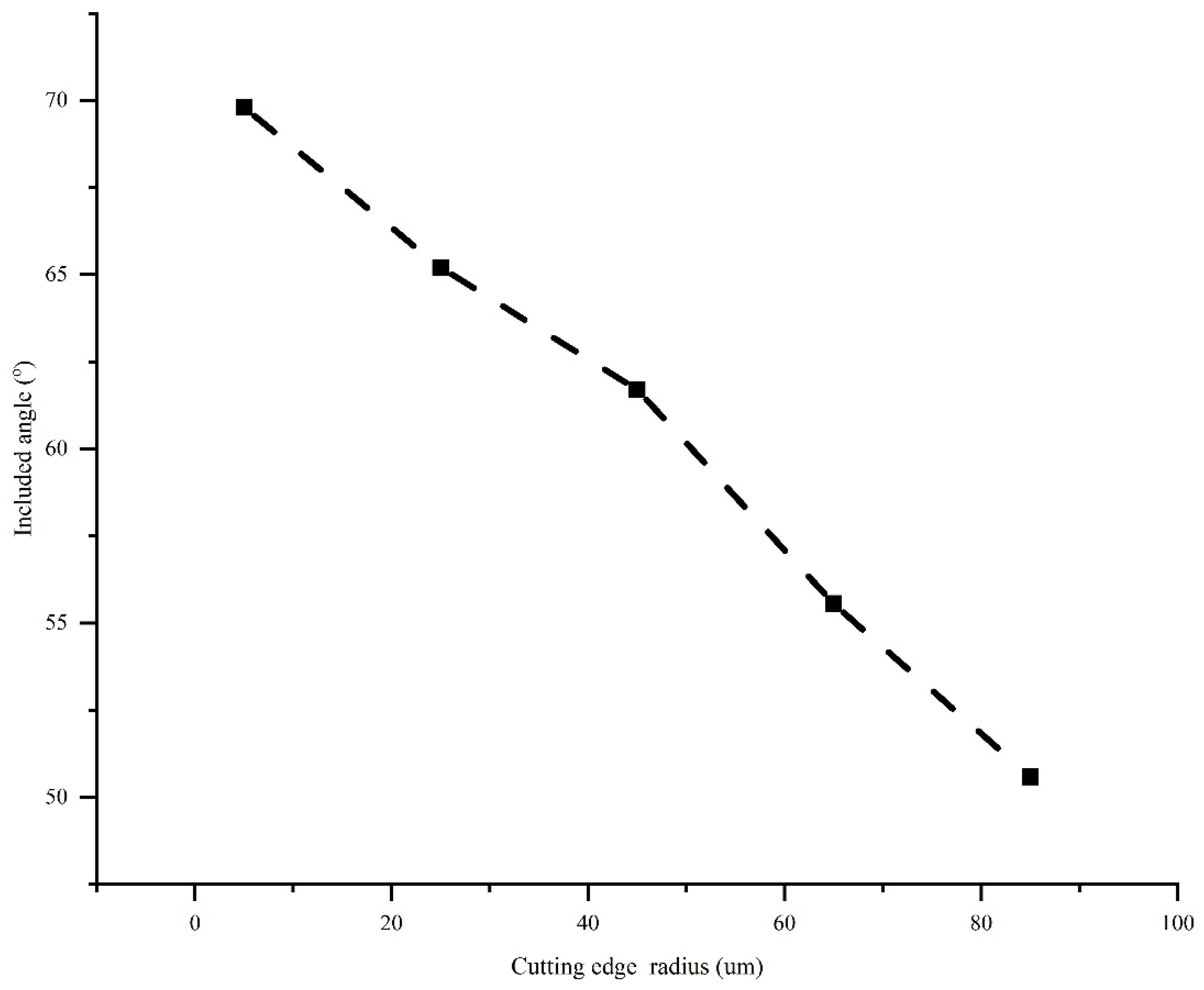
3.1. Evolution of Shear Angle
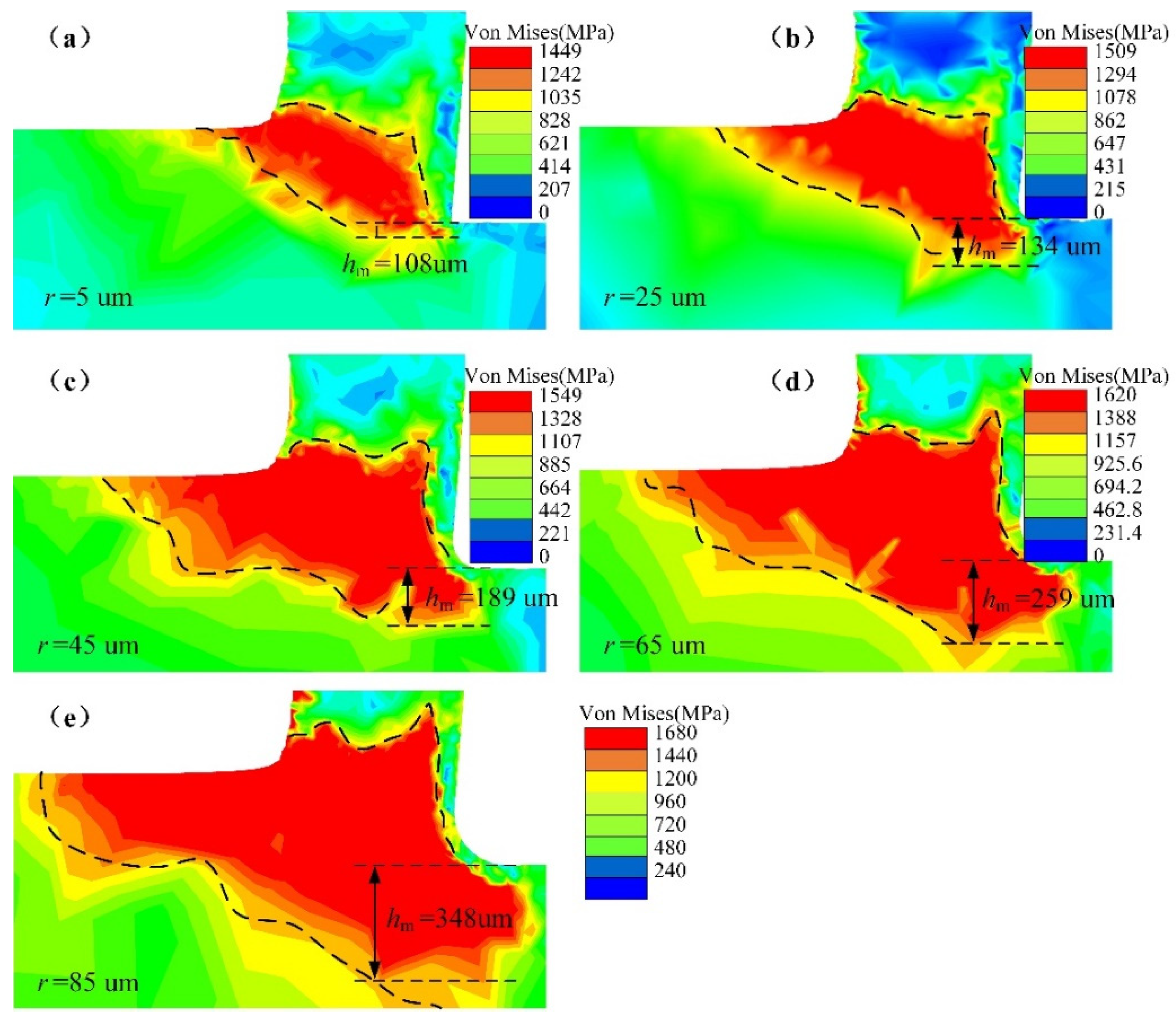
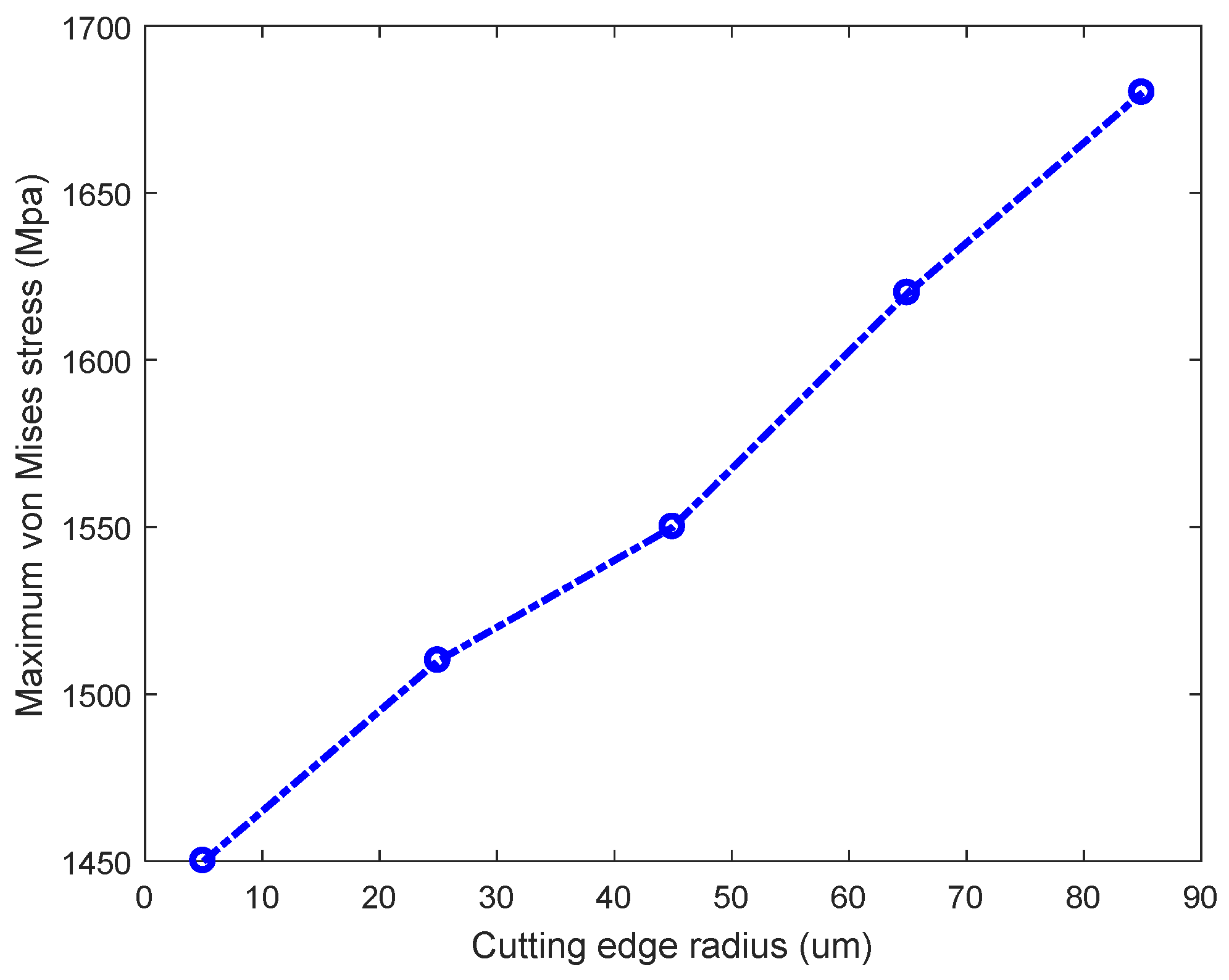
3.2. Von Mises Stress of the Machined Surface
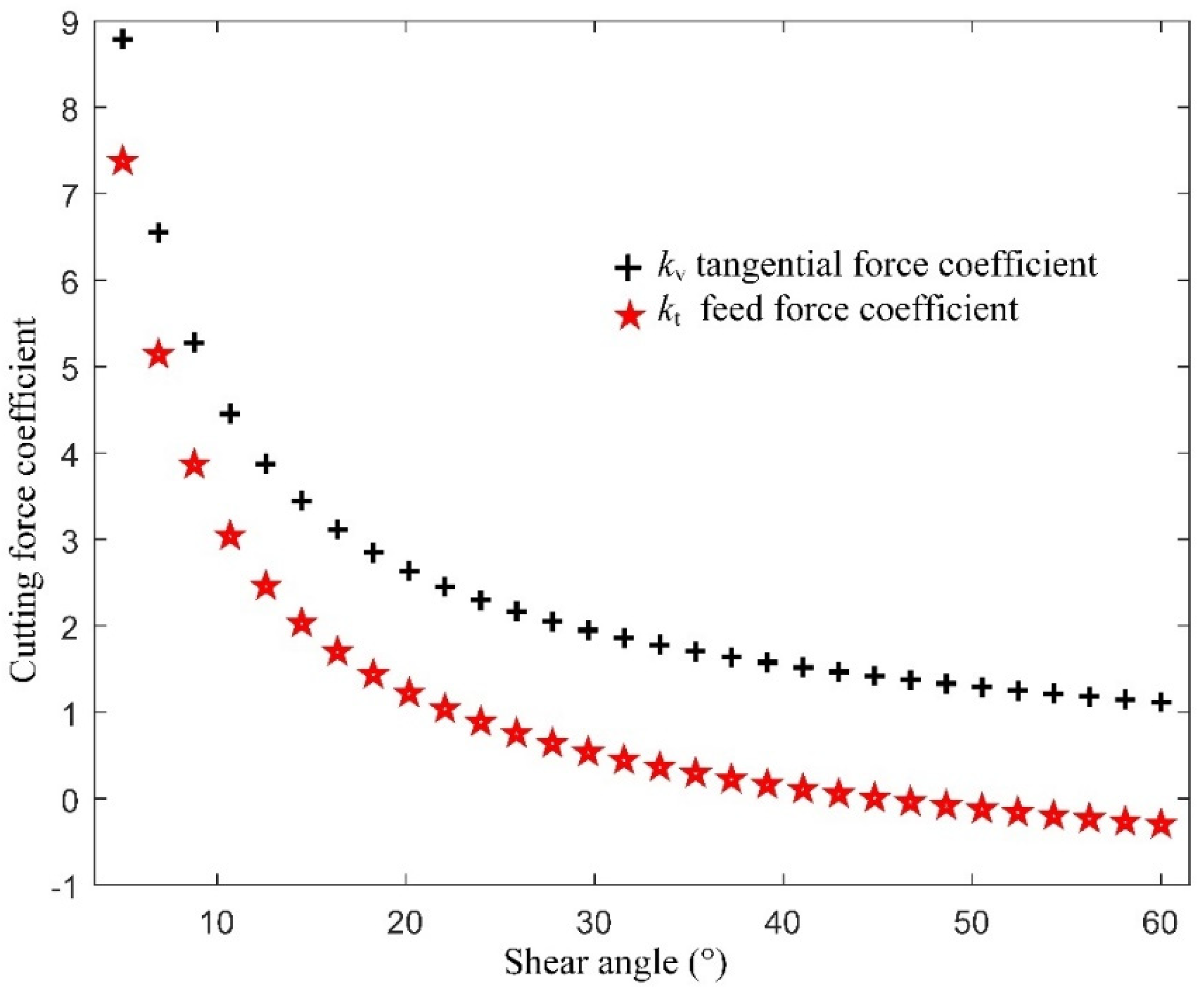
3.3. Effect of the CER on Cutting Forces
4. Conclusions
- The cutting force increased with the CER. The simulation analysis showed that the cutting force coefficient decreased as the shear angle increased, which was consistent with the analytical cutting force model. As the CER increased, the shear angle decreased, which caused the cutting force to increase.
- The increase in the feed force was quicker than the increase in the tangential force with increasing CER. With enhanced CER, the rate of feed force growth was much higher than that of the tangential force, unlike the behavior of traditional sharp cutter. The effect of the CER on the feed force must be considered in order to understand tool life and the quality of machined parts.
- The stress concentration range of the workpiece gradually expanded with increasing CER. Simulation experiments showed that the stress concentration area extended from the shear band to the cutting layer and the subsurface of the workpiece, resulting in a substantial increase in the stress concentration depth, which affected the surface and integrity of the workpiece. Additionally, the maximum stress in the workpiece increased with the CER.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, S.; Zhang, H.J.; Zong, W.J. Modeling and simulation on the effect of tool rake angle in diamond turning of KDP crystal. J. Mater. Process. Technol. 2019, 273, 116259. [Google Scholar] [CrossRef]
- Liu, C.; Wan, M.; Yang, Y. Simulation of the chip morphology together with its evolution in machining of Inconel 718 by considering widely spread cutting speed. Int. J. Adv. Manuf. Technol. 2021, 116, 175–195. [Google Scholar] [CrossRef]
- Sun, W.; Duan, C.; Yin, W. Modeling of force and temperature in cutting of particle reinforced metal matrix composites considering particle effects. J. Mater. Process. Technol. 2021, 290, 116991. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.; Garg, A.; Gao, L.; Vijayaraghavan, R.; Lu, G. A finite element based data analytics approach for modeling turning process of Inconel 718 alloys. J. Clean. Prod. 2016, 137, 1619–1627. [Google Scholar] [CrossRef]
- Zhuang, K.; Weng, J.; Zhu, D.; Ding, H. Analytical Modeling and Experimental Validation of Cutting Forces Considering Edge Effects and Size Effects with Round Chamfered Ceramic Tools. J. Manuf. Sci. Eng. 2018, 140, 081012. [Google Scholar] [CrossRef]
- Davis, B.; Dabrow, D.; Ifju, P.; Xiao, G.; Liang, S.Y.; Huang, Y. Study of the Shear Strain and Shear Strain Rate Progression During Titanium Machining. J. Manuf. Sci. Eng. 2018, 140, 051007. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Piao, Y.; Hu, Y.; Wei, Z.; Li, L.; Zhang, F. Modelling and experimental investigation of temperature field during fly-cutting of KDP crystals. Int. J. Mech. Sci. 2021, 210, 106751. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Matuszak, M.; Powałka, B.; Madajewski, M.; Maruda, R.W.; Królczyk, G.M. Prediction of cutting forces during micro end milling considering chip thickness accumulation. Int. J. Mach. Tools Manuf. 2019, 147, 103466. [Google Scholar] [CrossRef]
- Wu, F.; Liu, Z.; Guo, B.; Sun, Y.; Chen, J. Research on the burr-free interrupted cutting model of metals. J. Mater. Process. Technol. 2021, 295, 117190. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Mrozek, K. Mechanical and technological aspects of micro ball end milling with various tool inclinations. Int. J. Mech. Sci. 2017, 134, 424–435. [Google Scholar] [CrossRef]
- Son, S.M.; Lim, H.S.; Ahn, J.H. Effects of the friction coefficient on the minimum cutting thickness in micro cutting. Int. J. Mach. Tools Manuf. 2005, 45, 529–535. [Google Scholar] [CrossRef]
- Fang, F.Z.; Wu, H.; Liu, Y.C. Modelling and experimental investigation on nanometric cutting of monocrystalline silicon. Int. J. Mach. Tools Manuf. 2005, 45, 1681–1686. [Google Scholar] [CrossRef]
- Woon, K.S.; Rahman, M.; Fang, F.Z.; Neo, K.S.; Liu, K. Investigations of tool edge radius effect in micromachining: A FEM simulation approach. J. Mater. Process. Technol. 2008, 195, 204–211. [Google Scholar] [CrossRef]
- Woon, K.S.; Rahman, M.; Neo, K.S.; Liu, K. The effect of tool edge radius on the contact phenomenon of tool-based micromachining. Int. J. Mach. Tools Manuf. 2008, 48, 1395–1407. [Google Scholar] [CrossRef]
- Özel, T. Computational modelling of 3D turning: Influence of edge micro-geometry on forces, stresses, friction and tool wear in PcBN tooling. J. Mater. Process. Technol. 2009, 209, 5167–5177. [Google Scholar] [CrossRef]
- Mir, A.; Luo, X.; Siddiq, A. Smooth particle hydrodynamics study of surface defect machining for diamond turning of silicon. Int. J. Adv. Manuf. Technol. 2017, 88, 2461–2476. [Google Scholar] [CrossRef] [Green Version]
- Lai, M.; Zhang, X.D.; Fang, F.Z. Study on critical rake angle in nanometric cutting. Appl. Phys. A Mater. Sci. Process. 2012, 108, 809–818. [Google Scholar] [CrossRef]
- Yang, S.; Tong, X.; Liu, X.; Ji, W.; Zhang, Y. Investigation on the characteristic of forces of the tool edge in finish machining of titanium alloys. Int. J. Adv. Manuf. Technol. 2018, 96, 2431–2441. [Google Scholar] [CrossRef]
- Dai, X.; Zhuang, K.; Ding, H. A systemic investigation of tool edge geometries and cutting parameters on cutting forces in turning of Inconel 718. Int. J. Adv. Manuf. Technol. 2019, 105, 531–543. [Google Scholar] [CrossRef]
- Aramcharoen, A.; Mativenga, P.T. Size effect and tool geometry in micromilling of tool steel. Precis. Eng. 2009, 33, 402–407. [Google Scholar] [CrossRef]
- Arefin, S.; Zhang, X.Q.; Neo, D.W.K.; Kumar, A.S. Effects of cutting edge radius in vibration assisted micro machining. Int. J. Mech. Sci. 2021, 208, 106673. [Google Scholar] [CrossRef]
- Yusuf, A. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. Appl. Mech. Rev. 2001, 54, B84. [Google Scholar]
- Albrecht, P. New Developments in the Theory of the Metal-Cutting Process: Part I. The Ploughing Process in Metal Cutting. J. Eng. Ind. 1960, 82, 348–357. [Google Scholar] [CrossRef]
- Ozel, T.; Llanos, I.; Soriano, J.; Arrazola, P.-J. 3D Finite Element Modelling of Chip Formation Process for Machining Inconel 718: Comparison of FE Software Predictions. Mach. Sci. Technol. 2011, 15, 21–46. [Google Scholar] [CrossRef]
- Li, P.; Chang, Z. Accurate modeling of working normal rake angles and working inclination angles of active cutting edges and application in cutting force prediction. Micromachines 2021, 12, 1207. [Google Scholar] [CrossRef]


| Test No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Cutting-edge radius r (µm) | 5 | 25 | 45 | 65 | 85 |
| Element | Ni | Cr | Nb | Mo | Ti | Al | Co | Mn | Cu | Si | C | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wt % | 52.15 | 19.26 | 5.03 | 3.03 | 1.08 | 0.56 | 0.5 | 0.22 | 0.1 | 0.26 | 0.052 | 17.75 |
| Tensile Strength (MPa) | Yield Strength (MPa) | Young’s Modulus (GPa) | Density (g∙cm−3) | Poisson’s Ratio | Thermal Conductivity (W/m∙K) |
|---|---|---|---|---|---|
| 1430 | 1300 | 204 | 8.24 | 0.3 | 14.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Chang, Z. Numerical Modeling of the Effect of Cutting-Edge Radius on Cutting Force and Stress Concentration during Machining. Micromachines 2022, 13, 211. https://doi.org/10.3390/mi13020211
Li P, Chang Z. Numerical Modeling of the Effect of Cutting-Edge Radius on Cutting Force and Stress Concentration during Machining. Micromachines. 2022; 13(2):211. https://doi.org/10.3390/mi13020211
Chicago/Turabian StyleLi, Peng, and Zhiyong Chang. 2022. "Numerical Modeling of the Effect of Cutting-Edge Radius on Cutting Force and Stress Concentration during Machining" Micromachines 13, no. 2: 211. https://doi.org/10.3390/mi13020211
APA StyleLi, P., & Chang, Z. (2022). Numerical Modeling of the Effect of Cutting-Edge Radius on Cutting Force and Stress Concentration during Machining. Micromachines, 13(2), 211. https://doi.org/10.3390/mi13020211





