Characteristics of Cracking Failure in Microbump Joints for 3D Chip-on-Chip Interconnections under Drop Impact
Abstract
:1. Introduction
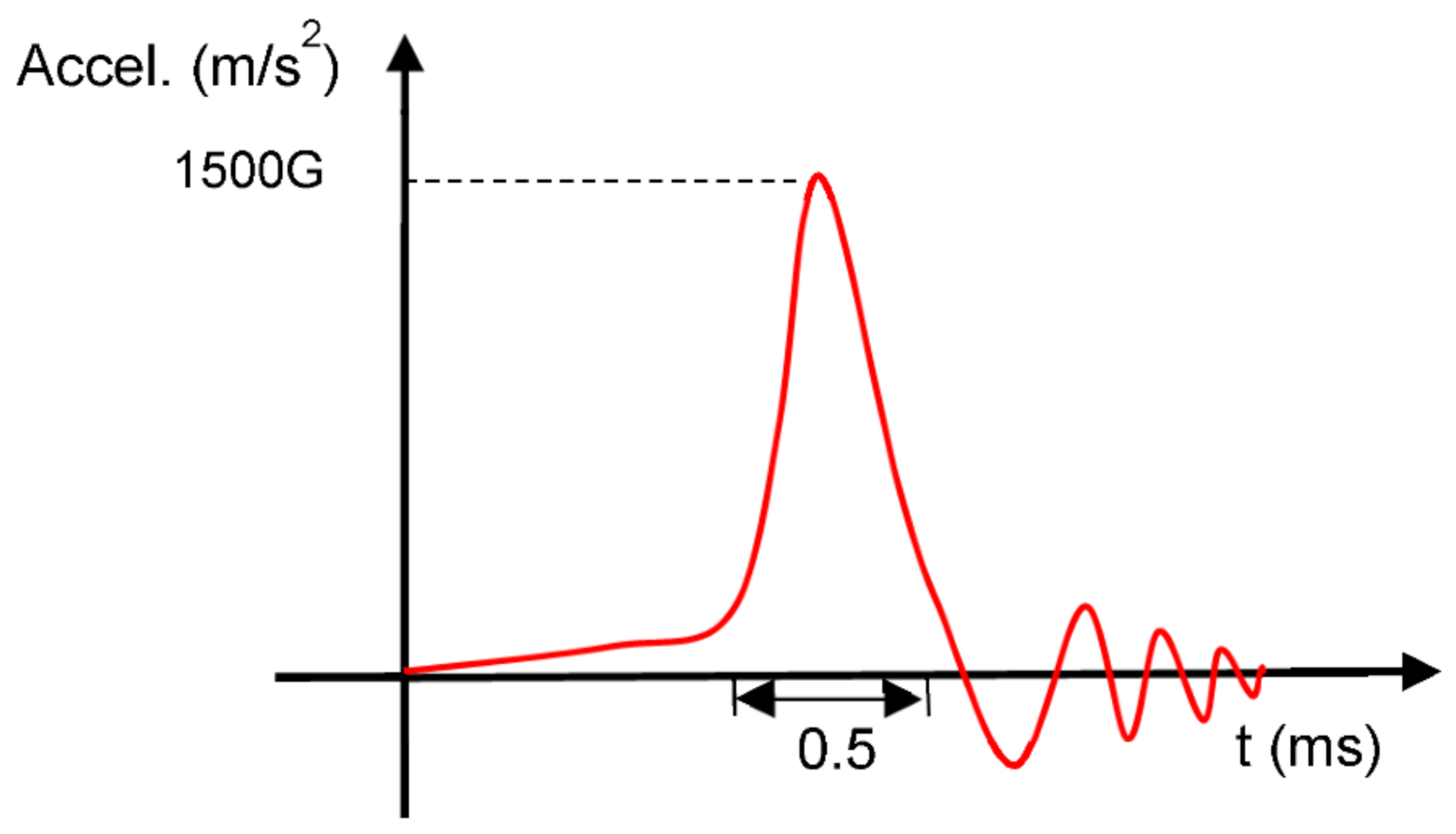
2. Setup for Drop Experiment
3. Set up for Simulation and Experiment
4. Results and Discussion
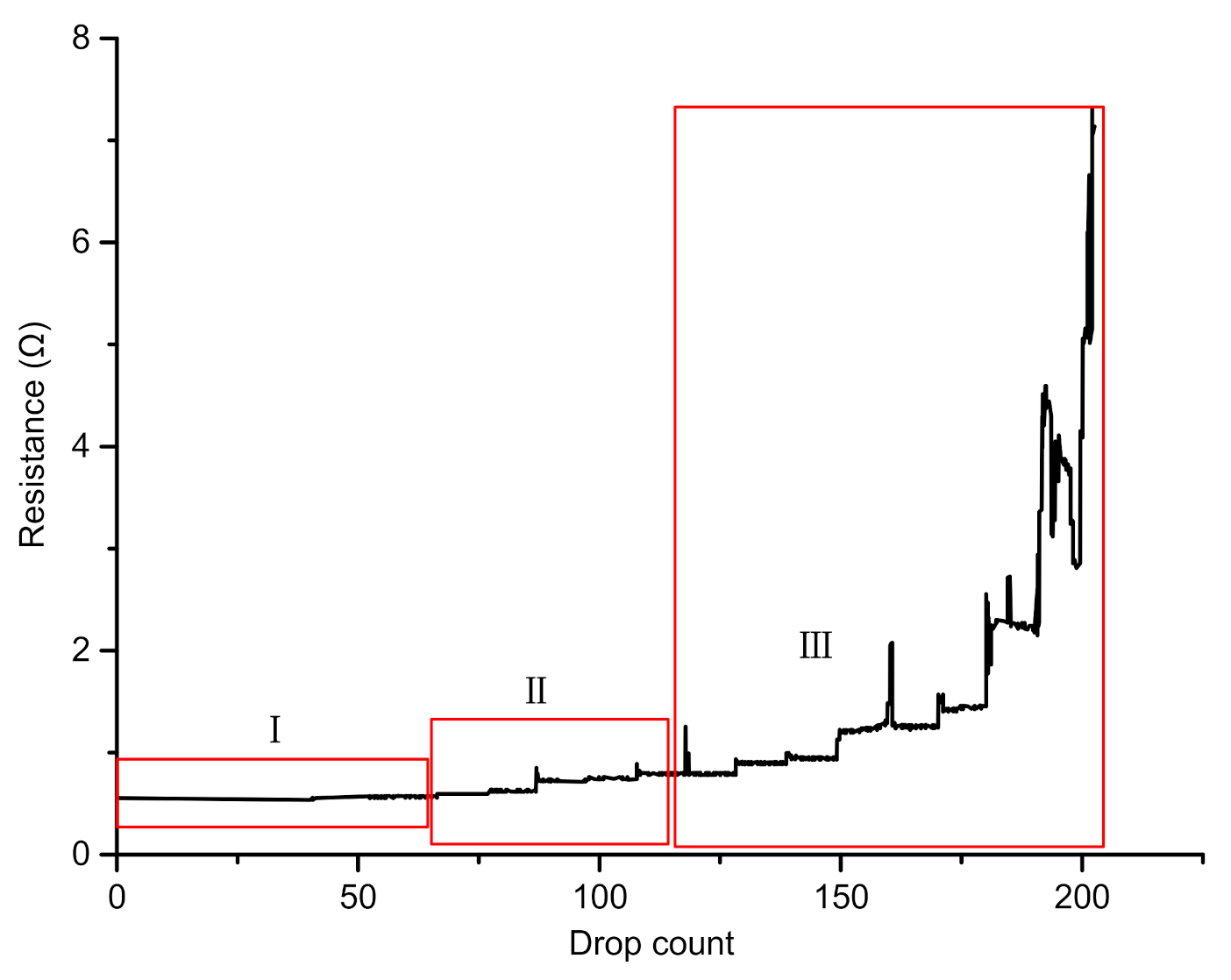
4.1. Failure Mode and Mechanism of Microbumps
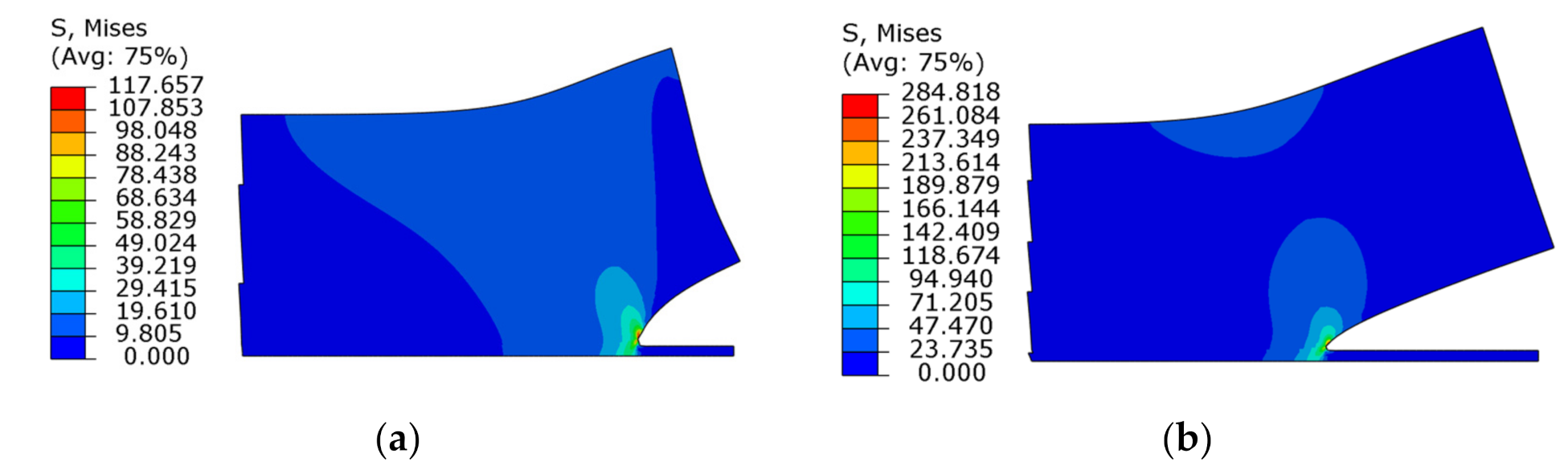
4.2. Stress Intensity Factor Analysis of Solder–IMC Interface Crack under Quasi-Static Load
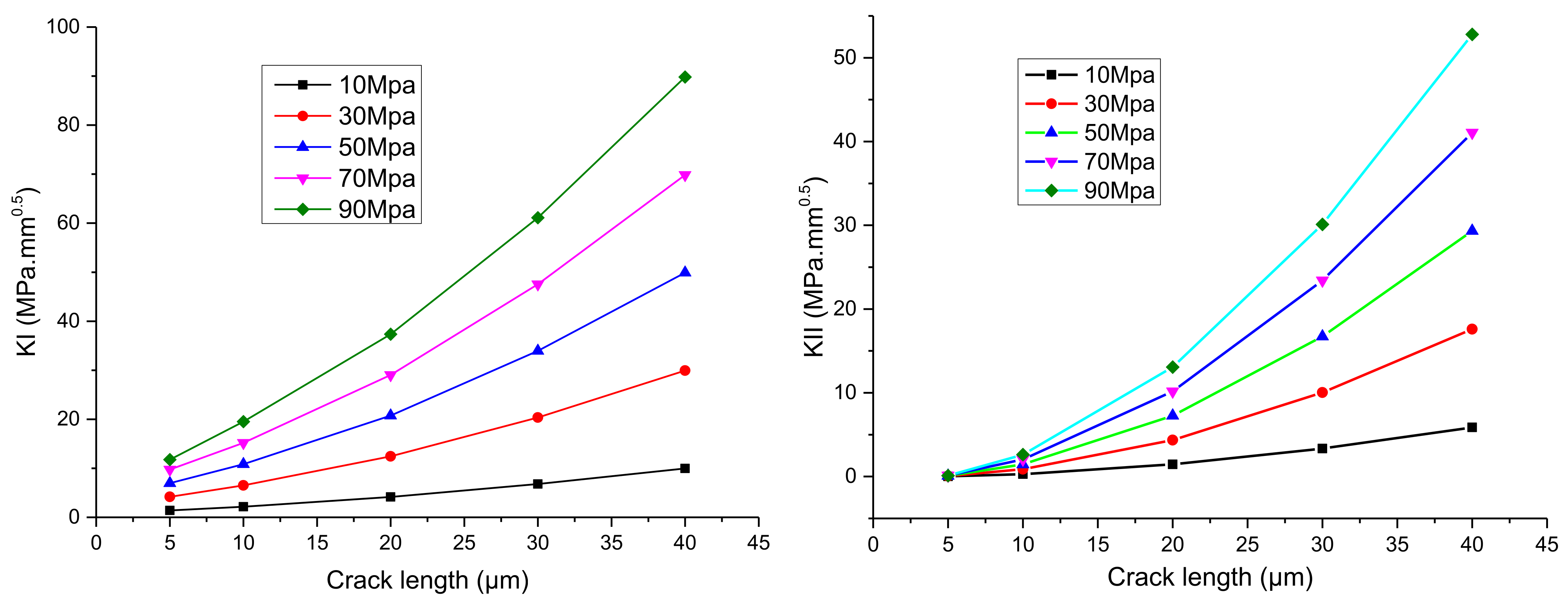
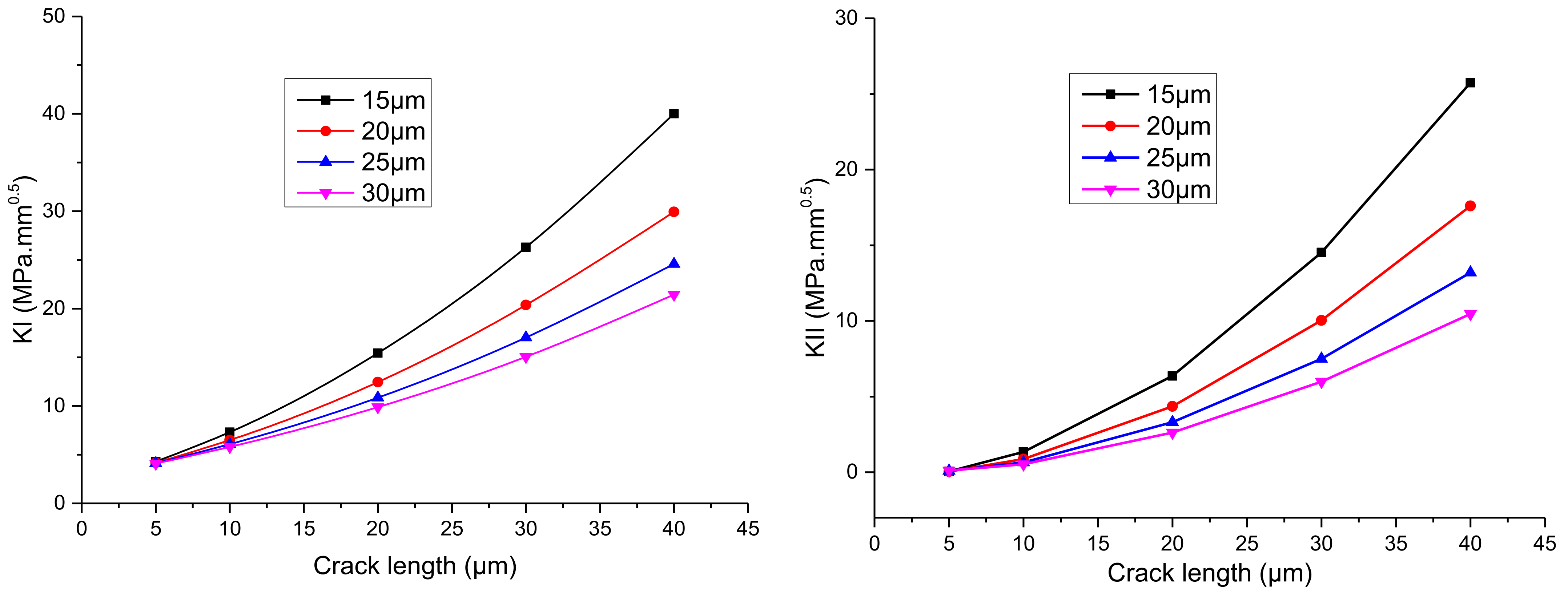
4.2.1. Relationship between Stress Intensity Factor at Interface Crack Tip and Crack Length
4.2.2. Influence of Solder Thickness on Stress Intensity Factor of Interface Crack
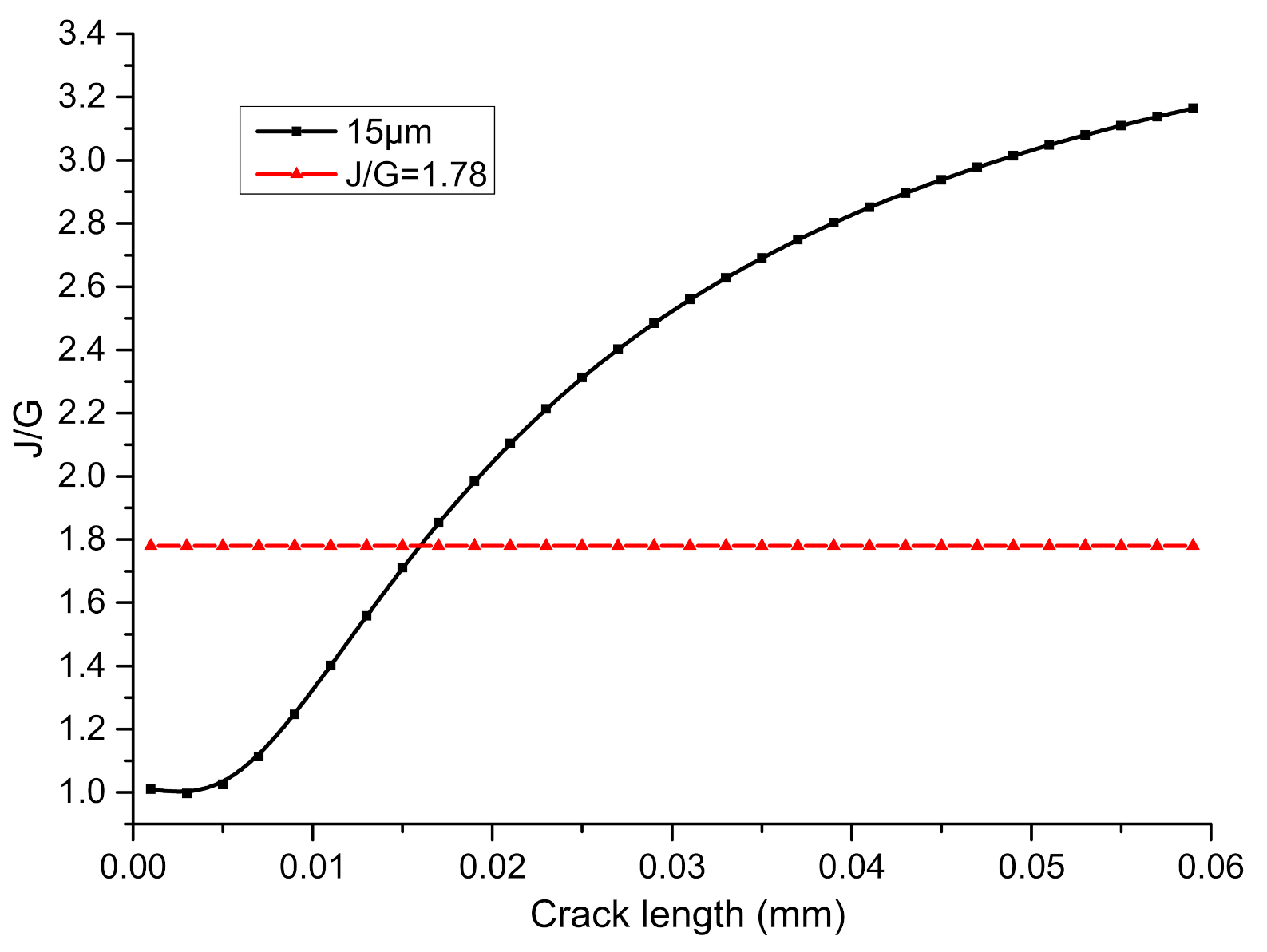
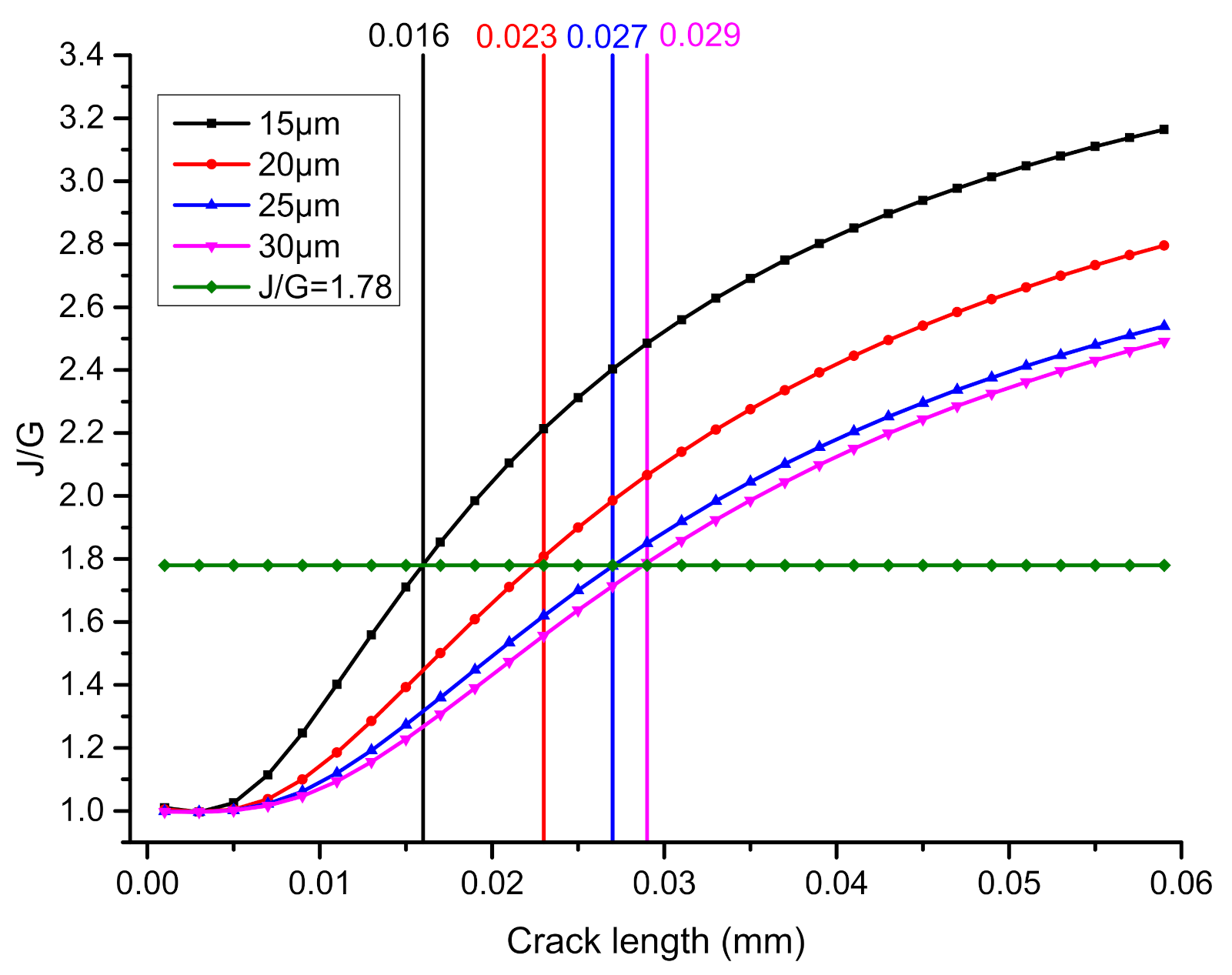
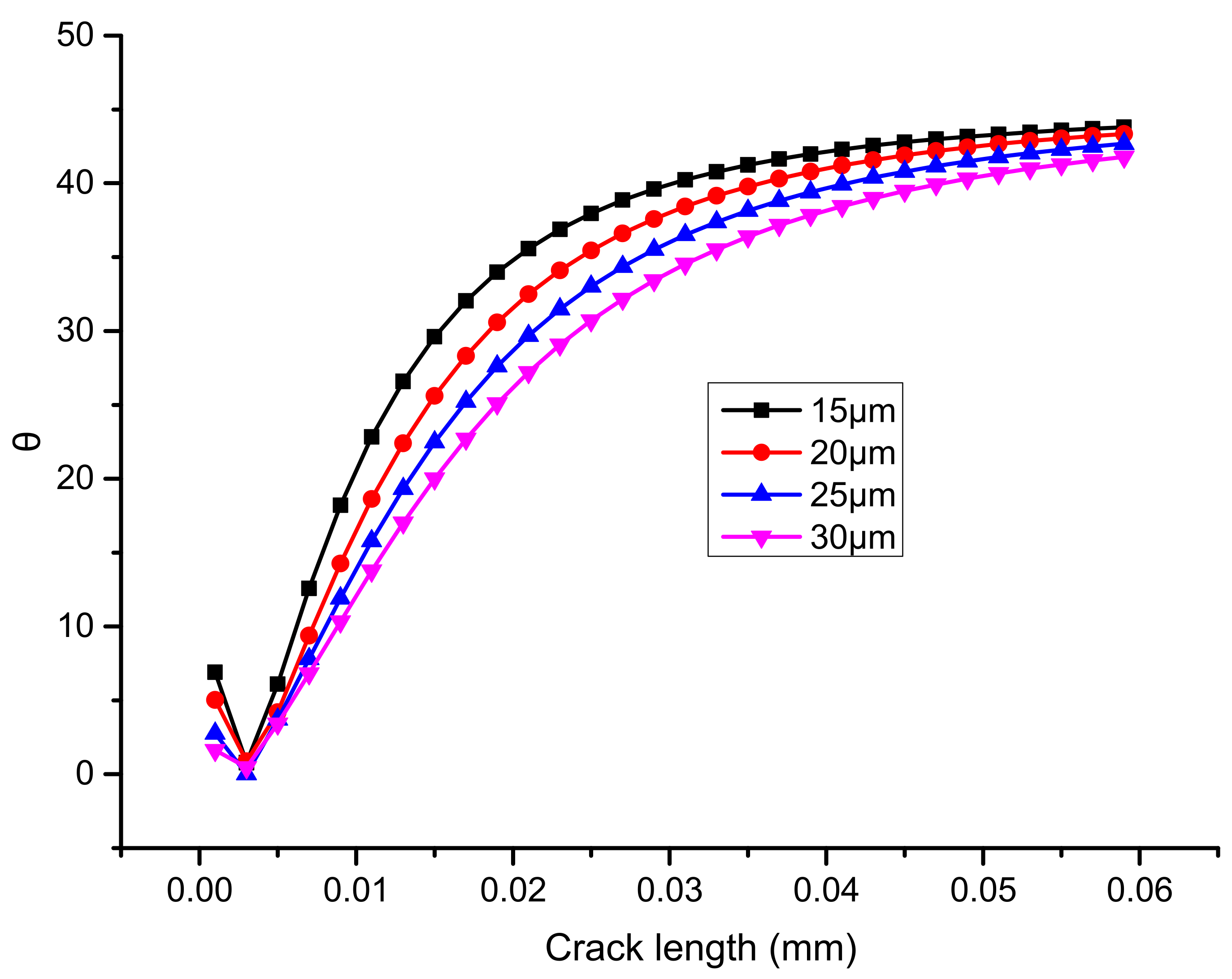
4.3. Investigation on Crack Growth Behavior
5. Experimental Validation and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, J.; Chiou, W.; Yang, K.; Chang, H.; Lin, Y.; Liao, E.; Hung, J.; Tsai, P.; Shih, Y.; Wu, T.; et al. High density 3D integration using CMOS foundry technologies for 28 nm node and beyond. In Proceedings of the 2010 International Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 2.1.1–2.1.4. [Google Scholar] [CrossRef]
- Yu, A.; Lau, J.H.; Ho, S.W.; Kumar, A.; Hnin, W.Y.; Yu, D.-Q.; Jong, M.C.; Kripesh, V.; Pinjala, D.; Kwong, D.-L. Study of 15 μm pitch solder microbumps for 3D IC integration. In Proceedings of the 2009 59th Electronic Components and Technology Conference, San Diego, CA, USA, 26–29 May 2009; pp. 6–10. [Google Scholar] [CrossRef]
- Suh, D.; Kim, D.W.; Liu, P.; Kim, H.; Weninger, J.A.; Kumar, C.M.; Prasad, A.; Grimsley, B.W.; Tejada, H.B. Effects of Ag content on fracture resistance of Sn–Ag–Cu lead-free solders under high-strain rate conditions. Mater. Sci. Eng. A 2007, 460–461, 595–603. [Google Scholar] [CrossRef]
- Kim, D.; Suh, D.; Millard, T.; Kim, H.; Kumar, C.; Zhu, M.; Xu, Y. Evaluation of High Compliant Low Ag Solder Alloys on OSP as a Drop Solution for the 2nd Level Pb-Free Interconnection. In Proceedings of the 57th Electronic Components and Technology Conference, Sparks, NV, USA, 29 May–1 June 2007; pp. 1614–1619. [Google Scholar] [CrossRef]
- Tee, T.Y.; Ng, H.S.; Lim, C.T.; Pek, E.; Zhong, Z. Impact life prediction modeling of TFBGA packages under board level drop test. Microelectron. Reliab. 2004, 44, 1131–1142. [Google Scholar] [CrossRef]
- Tee, T.Y.; Ng, H.S.; Lim, C.T.; Pek, E.; Zhong, Z. Board level drop test and simulation of TFBGA packages for telecommunication applications. In Proceedings of the 53rd Electronic Components and Technology Conference, New Orleans, LA, USA, 27–30 May 2003; pp. 121–129. [Google Scholar] [CrossRef]
- Pang, J.H.L.; Che, F. Drop impact analysis of Sn-Ag-Cu solder joints using dynamic high-strain rate plastic strain as the impact damage driving force. In Proceedings of the 56th Electronic Components and Technology Conference, San Diego, CA, USA, 30 May–2 June 2006; p. 6. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Liu, Y.; Liu, S. Drop test simulation of 3D stacked-die packaging with Input-G finite element method. In Proceedings of the 2010 11th International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, China, 16–19 August 2010; pp. 742–746. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Cheng, H.-K.; Lu, S.-T.; Juang, J.-Y.; Chen, W.-H. Drop Impact Reliability Analysis of 3-D Chip-on-Chip Packaging: Numerical Modeling and Experimental Validation. IEEE Trans. Device Mater. Reliab. 2014, 14, 499–511. [Google Scholar] [CrossRef]
- Cheng, T.-H.; Cheng, H.-C.; Chen, W.-H.; Huang, H.-Y.; Chang, T.-C. Reliability characterization of 2.5D multi-chip module on board under drop impact. In Proceedings of the 2014 International Conference on Electronics Packaging (ICEP), Toyama, Japan, 23–25 April 2014; pp. 215–218. [Google Scholar] [CrossRef]
- Tee, T.Y.; Luan, J.-E.; Pek, E.; Lim, C.T.; Zhong, Z. Novel numerical and experimental analysis of dynamic responses under board level drop test. In Proceedings of the 5th International Conference on Thermal and Mechanical Simulation and Experiments in Microelectronics and Microsystems, 2004. EuroSimE 2004, Brussels, Belgium, 10–12 May 2004; pp. 133–140. [Google Scholar] [CrossRef]
- Yu, H.-H.; He, M.; Hutchinson, J. Edge effects in thin film delamination. Acta Mater. 2001, 49, 93–107. [Google Scholar] [CrossRef]
- Chong, D.Y.; Che, F.; Pang, J.H.; Ng, K.; Tan, J.Y.; Low, P.T. Drop impact reliability testing for lead-free and lead-based soldered IC packages. Microelectron. Reliab. 2006, 46, 1160–1171. [Google Scholar] [CrossRef]
- Ghosh, G. Elastic properties, hardness, and indentation fracture toughness of intermetallics relevant to electronic packaging. J. Mater. Res. 2004, 19, 1439–1454. [Google Scholar] [CrossRef]
- Ming-Yuan, H.; Hutchinson, J.W. Crack deflection at an interface between dissimilar elastic materials. Int. J. Solids Struct. 1989, 25, 1053–1067. [Google Scholar] [CrossRef]
- Loo, S.Z.Y.; Lee, P.C.; Lim, Z.X.; Yantara, N.; Tee, T.Y.; Tan, C.M.; Chen, Z. Interface fracture toughness assessment of solder joints using double cantilever beam test. Int. J. Mod. Phys. B 2010, 24, 164–174. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, C.; Li, M. Scanning electron microscope in-situ investigation of fracture behavior in 96.5Sn3.5Ag lead-free solder. J. Electron. Mater. 2005, 34, 1324–1335. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Miyashita, Y.; Mutoh, Y. Low-cycle fatigue behavior and mechanisms of a lead-free solder 96.5Sn/3.5Ag. J. Electron. Mater. 2002, 31, 142–151. [Google Scholar] [CrossRef]
- Chen, H.; Mueller, M.; Mattila, T.T.; Li, J.; Liu, X.; Wolter, K.-J.; Paulasto-Kröckel, M. Localized recrystallization and cracking of lead-free solder interconnections under thermal cycling. J. Mater. Res. 2011, 26, 2103–2116. [Google Scholar] [CrossRef]
- Le, V.-N.; Benabou, L.; Tao, Q.-B.; Etgens, V. Modeling of intergranular thermal fatigue cracking of a lead-free solder joint in a power electronic module. Int. J. Solids Struct. 2017, 106–107, 1–12. [Google Scholar] [CrossRef]
- Chang, Z.Y.; Zhao, N.; Wu, C.M.L. Effects of cooling rate and joint size on Sn grain features in Cu/Sn–3.5Ag/Cu solder joints. Materialia 2020, 14, 100929. [Google Scholar] [CrossRef]
- Darbandi, P.; Bieler, T.R.; Pourboghrat, F.; Lee, T.-K. The Effect of Cooling Rate on Grain Orientation and Misorientation Microstructure of SAC105 Solder Joints Before and After Impact Drop Tests. J. Electron. Mater. 2014, 43, 2521–2529. [Google Scholar] [CrossRef]








| Part | Density (g/cm3) | Elastic Modulus (MPa) | Poisson Ratio |
|---|---|---|---|
| SAC305 | 0.00736 | 81,000 | 0.347 |
| IMC | 0.00855 | 114,000 | 0.318 |
| Ni | 0.0089 | 199,000 | 0.312 |
| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Values | 6.06 × 1010 | −0.028 | 0.088 | 3.59 × 1010 | 0.314 | 1.388 × 1010 | 0.347 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Fang, M.; Shi, L.; Gu, Y.; Chen, Z.; Zhu, W. Characteristics of Cracking Failure in Microbump Joints for 3D Chip-on-Chip Interconnections under Drop Impact. Micromachines 2022, 13, 281. https://doi.org/10.3390/mi13020281
Liu Z, Fang M, Shi L, Gu Y, Chen Z, Zhu W. Characteristics of Cracking Failure in Microbump Joints for 3D Chip-on-Chip Interconnections under Drop Impact. Micromachines. 2022; 13(2):281. https://doi.org/10.3390/mi13020281
Chicago/Turabian StyleLiu, Zhen, Mingang Fang, Lei Shi, Yu Gu, Zhuo Chen, and Whenhui Zhu. 2022. "Characteristics of Cracking Failure in Microbump Joints for 3D Chip-on-Chip Interconnections under Drop Impact" Micromachines 13, no. 2: 281. https://doi.org/10.3390/mi13020281
APA StyleLiu, Z., Fang, M., Shi, L., Gu, Y., Chen, Z., & Zhu, W. (2022). Characteristics of Cracking Failure in Microbump Joints for 3D Chip-on-Chip Interconnections under Drop Impact. Micromachines, 13(2), 281. https://doi.org/10.3390/mi13020281






