Determination of the Dielectrophoretic Force Induced by the Photovoltaic Effect on Lithium Niobate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fe-Doped Lithium Niobate Samples
2.2. Dielectrophoretic Force on a Water Droplet Generated by Photovoltaic and Electrostatic Charges
3. Results and Discussion
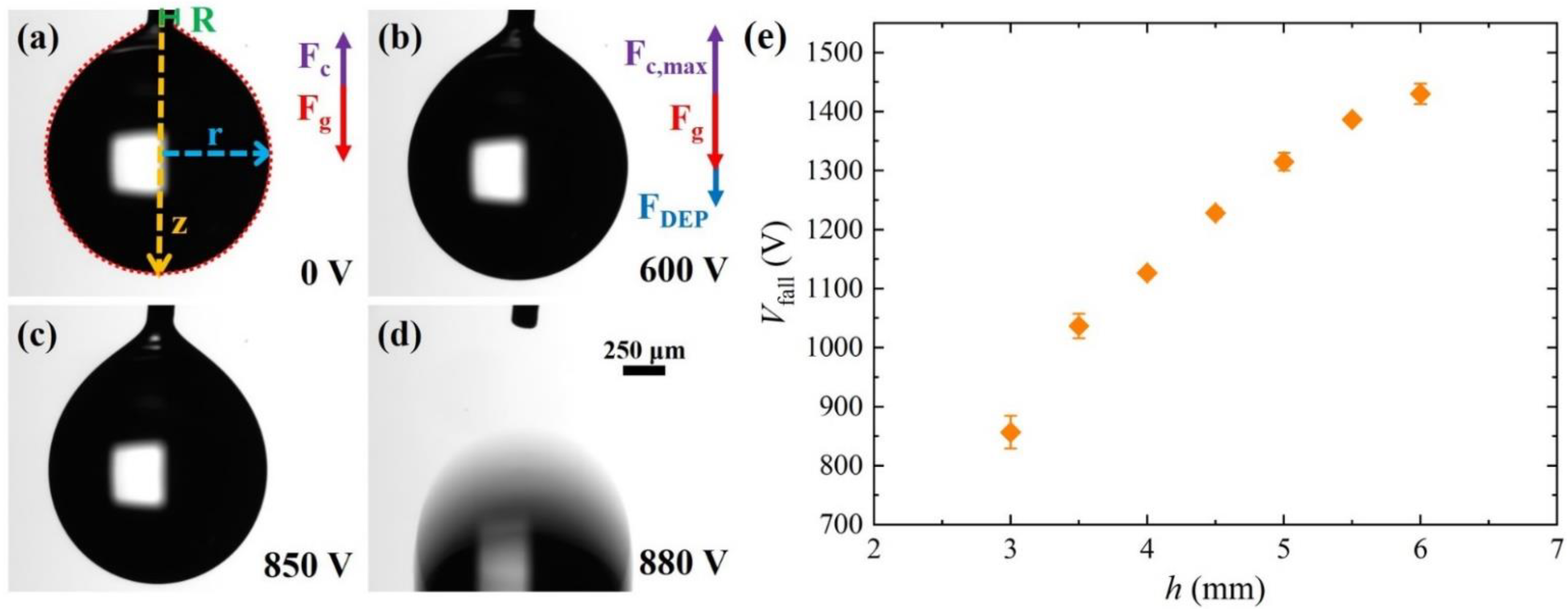
3.1. Dielectrophoretic Force on Pendant Droplet: Electrostatic Effect (E–DEP)
3.2. Dielectrophoretic Force on the Pendant Droplet: Photovoltaic Effect (P–DEP)
3.3. Dynamics of the Dielectrophoretic Force by the Photovoltaic Effect (P–DEP)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mistura, G.; Pierno, M. Drop mobility on chemically heterogeneous and lubricant-impregnated surfaces. Adv. Phys. X 2017, 2, 591–607. [Google Scholar] [CrossRef] [Green Version]
- Malinowski, R.; Parkin, I.P.; Volpe, G. Advances towards programmable droplet transport on solid surfaces and its applications. Chem. Soc. Rev. 2020, 49, 7879–7892. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.K.; Moon, H.J.; Kim, C.J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromech. Syst. 2003, 12, 70–80. [Google Scholar] [CrossRef] [Green Version]
- McHale, G.; Brown, C.V.; Newton, M.I.; Wells, G.G.; Sampara, N. Dielectrowetting driven spreading of droplets. Phys. Rev. Lett. 2011, 107, 186101. [Google Scholar] [CrossRef] [Green Version]
- Khalil, K.S.; Mahmoudi, S.R.; Abu-dheir, N.; Varanasi, K.K. Active surfaces: Ferrofluid-impregnated surfaces for active manipulation of droplets. Appl. Phys. Lett. 2014, 105, 041604. [Google Scholar] [CrossRef]
- Rigoni, C.; Ferraro, D.; Carlassara, M.; Filippi, D.; Varagnolo, S.; Pierno, M.; Talbot, D.; Abou-Hassan, A.; Mistura, G. Dynamics of ferrofluid drops on magnetically patterned surfaces. Langmuir 2018, 34, 8917–8922. [Google Scholar] [CrossRef]
- Ichimura, K.; Oh, S.K.; Nakagawa, M. Light-driven motion of liquids on a photoresponsive surface. Science 2000, 288, 1624–1626. [Google Scholar] [CrossRef] [Green Version]
- Dattilo, D.; Armelao, L.; Fois, G.; Mistura, G.; Maggini, M. Wetting properties of flat and porous silicon surfaces coated with a spiropyran. Langmuir 2007, 23, 12945–12950. [Google Scholar] [CrossRef]
- Xia, F.; Feng, L.; Wang, S.T.; Sun, T.L.; Song, W.L.; Jiang, W.H.; Jiang, L. Dual-responsive surfaces that switch superhydrophilicity and superhydrophobicity. Adv. Mater. 2006, 18, 432–436. [Google Scholar] [CrossRef]
- Wixforth, A.; Strobl, C.; Gauer, C.; Toegl, A.; Scriba, J.; von Guttenberg, Z. Acoustic manipulation of small droplets. Anal. Bioanal. Chem. 2004, 379, 982–991. [Google Scholar] [CrossRef]
- Sartori, P.; Guglielmin, E.; Ferraro, D.; Filippi, D.; Zaltron, A.; Pierno, M.; Mistura, G. Motion of Newtonian drops deposited on liquid-impregnated surfaces induced by vertical vibrations. J. Fluid Mech. 2019, 876, R4. [Google Scholar] [CrossRef]
- Li, J.S.; Ueda, E.; Paulssen, D.; Levkin, P.A. Slippery lubricant-infused surfaces: Properties and emerging applications. Adv. Funct. Mater. 2019, 29, 1802317. [Google Scholar] [CrossRef] [Green Version]
- Lou, X.D.; Huang, Y.; Yang, X.; Zhu, H.; Heng, L.P.; Xia, F. External stimuli responsive liquid-infused surfaces switching between slippery and nonslippery states: Fabrications and applications. Adv. Funct. Mater. 2020, 30, 1901130. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Hao, C.L.; Liu, Y.H.; Chen, X.M.; He, Y.C.; Li, Q.S.; Li, K.Y.; Wang, Z.K. Electrowetting on liquid-infused film (EWOLF): Complete reversibility and controlled droplet oscillation suppression for fast optical imaging. Sci. Rep. 2014, 4, 6846. [Google Scholar] [CrossRef] [Green Version]
- Buse, K. Light-induced charge transport processes in photorefractive crystals. 1. Models and experimental methods. Appl. Phys. B Lasers Opt. 1997, 64, 273–291. [Google Scholar] [CrossRef]
- Frejlich, J. Photorefractive Materials: Fundamental Concepts, Holographic Recording and Materials Characterization; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Puerto, A.; Coppola, S.; Miccio, L.; Vespini, V.; Garcia-Cabanes, A.; Carrascosa, M.; Ferraro, P. Droplet ejection and liquid jetting by visible laser irradiation in pyro-photovoltaic Fe-doped LiNbO3 platforms. Adv. Mater. Interfaces 2021, 8, 2101164. [Google Scholar] [CrossRef]
- Glass, A.M.; Linde, D.v.d.; Negran, T.J. High-voltage bulk photovoltaic effect and the photorefractive process in LiNbO3. Appl. Phys. Lett. 1974, 25, 233–235. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Wang, J.Q.; Tang, B.Q.; Tan, X.H.; Rupp, R.A.; Pan, L.T.; Kong, Y.F.; Sun, Q.; Xu, J.J. Optical trapping and manipulation of metallic micro/nanoparticles via photorefractive crystals. Opt. Express 2009, 17, 9981–9988. [Google Scholar] [CrossRef]
- Carrascosa, M.; Garcia-Cabanes, A.; Jubera, M.; Ramiro, J.B.; Agullo-Lopez, F. LiNbO3: A photovoltaic substrate for massive parallel manipulation and patterning of nano-objects. Appl. Phys. Rev. 2015, 2, 040605. [Google Scholar] [CrossRef] [Green Version]
- Esseling, M.; Zaltron, A.; Horn, W.; Denz, C. Optofluidic droplet router. Laser Photon. Rev. 2015, 9, 98–104. [Google Scholar] [CrossRef]
- Gazzetto, M.; Nava, G.; Zaltron, A.; Cristiani, I.; Sada, C.; Minzioni, P. Numerical and experimental study of optoelectronic trapping on iron-doped lithium niobate substrate. Crystals 2016, 6, 123. [Google Scholar] [CrossRef] [Green Version]
- Munoz-Martinez, J.F.; Alcazar, A.; Carrascosa, M. Time evolution of photovoltaic fields generated by arbitrary light patterns in z-cut LiNbO3:Fe: Application to optoelectronic nanoparticle manipulation. Opt. Express 2020, 28, 18085–18102. [Google Scholar] [CrossRef] [PubMed]
- Villarroel, J.; Burgos, H.; Garcia-Cabanes, A.; Carrascosa, M.; Blazquez-Castro, A.; Agullo-Lopez, F. Photovoltaic versus optical tweezers. Opt. Express 2011, 19, 24320–24330. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.P.; Li, S.B.; Fan, B.L.; Yan, W.B.; Wang, D.H.; Shi, L.H.; Chen, H.J.; Ban, D.C.; Sun, S.H. Dielectrophoretic behaviours of microdroplet sandwiched between LN substrates. Sci. Rep. 2016, 6, 29166. [Google Scholar] [CrossRef] [Green Version]
- Eggert, H.A.; Kuhnert, F.Y.; Buse, K.; Adleman, J.R.; Psaltis, D. Trapping of dielectric particles with light-induced space-charge fields. Appl. Phys. Lett. 2007, 90, 241909. [Google Scholar] [CrossRef] [Green Version]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Lucchetti, L.; Kushnir, K.; Zaltron, A.; Simoni, F. Liquid crystal cells based on photovoltaic substrates. J. Eur. Opt. Soc. Rapid Publ. 2016, 11, 16007. [Google Scholar] [CrossRef] [Green Version]
- Fan, B.L.; Li, F.F.; Chen, L.P.; Shi, L.H.; Yan, W.B.; Zhang, Y.Q.; Li, S.B.; Wang, X.L.; Wang, X.; Chen, H.J. Photovoltaic manipulation of water microdroplets on a hydrophobic LiNbO3 substrate. Phys. Rev. Appl. 2017, 7, 064010. [Google Scholar] [CrossRef]
- Puerto, A.; Mendez, A.; Arizmendi, L.; Garcia-Cabanes, A.; Carrascosa, M. Optoelectronic manipulation, trapping, splitting, and merging of water droplets and aqueous biodroplets based on the bulk photovoltaic effect. Phys. Rev. Appl. 2020, 14, 024046. [Google Scholar] [CrossRef]
- Tang, X.; Li, W.; Wang, L.Q. Furcated droplet motility on crystalline surfaces. Nat. Nanotechnol. 2021, 16, 1106–1112. [Google Scholar] [CrossRef]
- Zhang, X.; Mugisha, E.R.; Mi, Y.H.; Liu, X.H.; Wang, M.T.; Gao, Z.X.; Gao, K.F.; Shi, L.H.; Chen, H.J.; Yan, W.B. Photovoltaic cycling to-and-fro actuation of a water-microdroplet for automatic repeatable solute acquisition on oil-infused hydrophobic LN:Fe surface. ACS Photonics 2021, 8, 639–647. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, D.; Serra, M.; Filippi, D.; Zago, L.; Guglielmin, E.; Pierno, M.; Descroix, S.; Viovy, J.L.; Mistura, G. Controlling the distance of highly confined droplets in a capillary by interfacial tension for merging on-demand. Lab Chip 2019, 19, 136–146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ciampolillo, M.V.; Zaltron, A.; Bazzan, M.; Argiolas, N.; Sada, C. Quantification of iron (Fe) in lithium niobate by optical absorption. Appl. Spectrosc. 2011, 65, 216–220. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2004. [Google Scholar]
- Lee, B.B.; Ravindra, P.; Chan, E.S. A critical review: Surface and interfacial tension measurement by the drop weight method. Chem. Eng. Commun. 2008, 195, 889–924. [Google Scholar] [CrossRef]
- Rigoni, C.; Pierno, M.; Mistura, G.; Talbot, D.; Massart, R.; Bacri, J.C.; Abou-Hassan, A. Static magnetowetting of ferrofluid drops. Langmuir 2016, 32, 7639–7646. [Google Scholar] [CrossRef]
- Daerr, A.; Mogne, A. Pendent_Drop: An ImageJ plugin to measure the surface tension from an image of a pendent drop. J. Open Res. Softw. 2016, 4, e3. [Google Scholar] [CrossRef] [Green Version]



| h (mm) | (μN) | (μN) |
|---|---|---|
| 3.0 ± 0.1 | 14.9 ± 1.5 | 14.2 ± 1.5 |
| 4.0 ± 0.1 | 15.8 ± 1.5 | 12.0 ± 1.4 |
| 5.0 ± 0.1 | 12.2 ± 1.4 | 12.0 ± 1.4 |
| 6.0 ± 0.1 | 11.9 ± 1.4 | 15.0 ± 1.5 |
| 14 ± 2 | 13.3 ± 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meggiolaro, A.; Cremaschini, S.; Ferraro, D.; Zaltron, A.; Carneri, M.; Pierno, M.; Sada, C.; Mistura, G. Determination of the Dielectrophoretic Force Induced by the Photovoltaic Effect on Lithium Niobate. Micromachines 2022, 13, 316. https://doi.org/10.3390/mi13020316
Meggiolaro A, Cremaschini S, Ferraro D, Zaltron A, Carneri M, Pierno M, Sada C, Mistura G. Determination of the Dielectrophoretic Force Induced by the Photovoltaic Effect on Lithium Niobate. Micromachines. 2022; 13(2):316. https://doi.org/10.3390/mi13020316
Chicago/Turabian StyleMeggiolaro, Alessio, Sebastian Cremaschini, Davide Ferraro, Annamaria Zaltron, Mattia Carneri, Matteo Pierno, Cinzia Sada, and Giampaolo Mistura. 2022. "Determination of the Dielectrophoretic Force Induced by the Photovoltaic Effect on Lithium Niobate" Micromachines 13, no. 2: 316. https://doi.org/10.3390/mi13020316
APA StyleMeggiolaro, A., Cremaschini, S., Ferraro, D., Zaltron, A., Carneri, M., Pierno, M., Sada, C., & Mistura, G. (2022). Determination of the Dielectrophoretic Force Induced by the Photovoltaic Effect on Lithium Niobate. Micromachines, 13(2), 316. https://doi.org/10.3390/mi13020316











