Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams
Abstract
:1. Introduction
2. Design and Simulation
2.1. Design and Working Principle
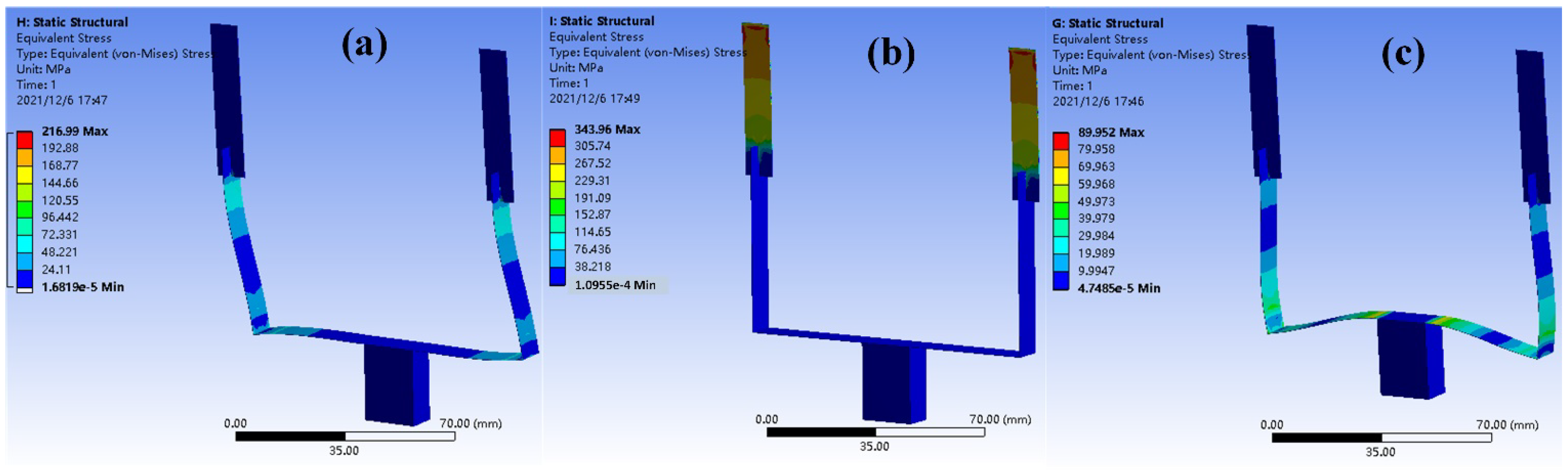
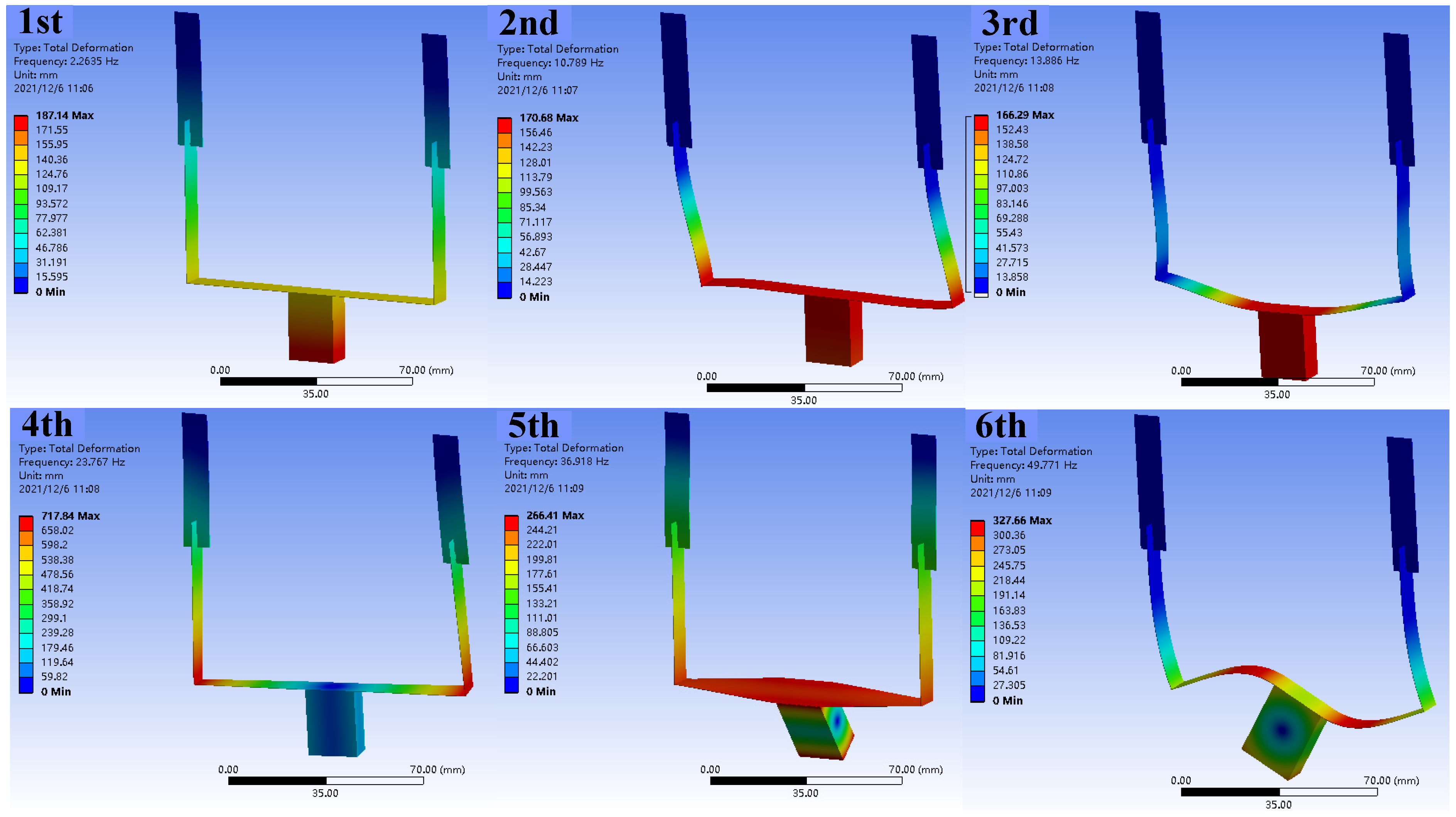
2.2. Analysis for Proof-of-Concept
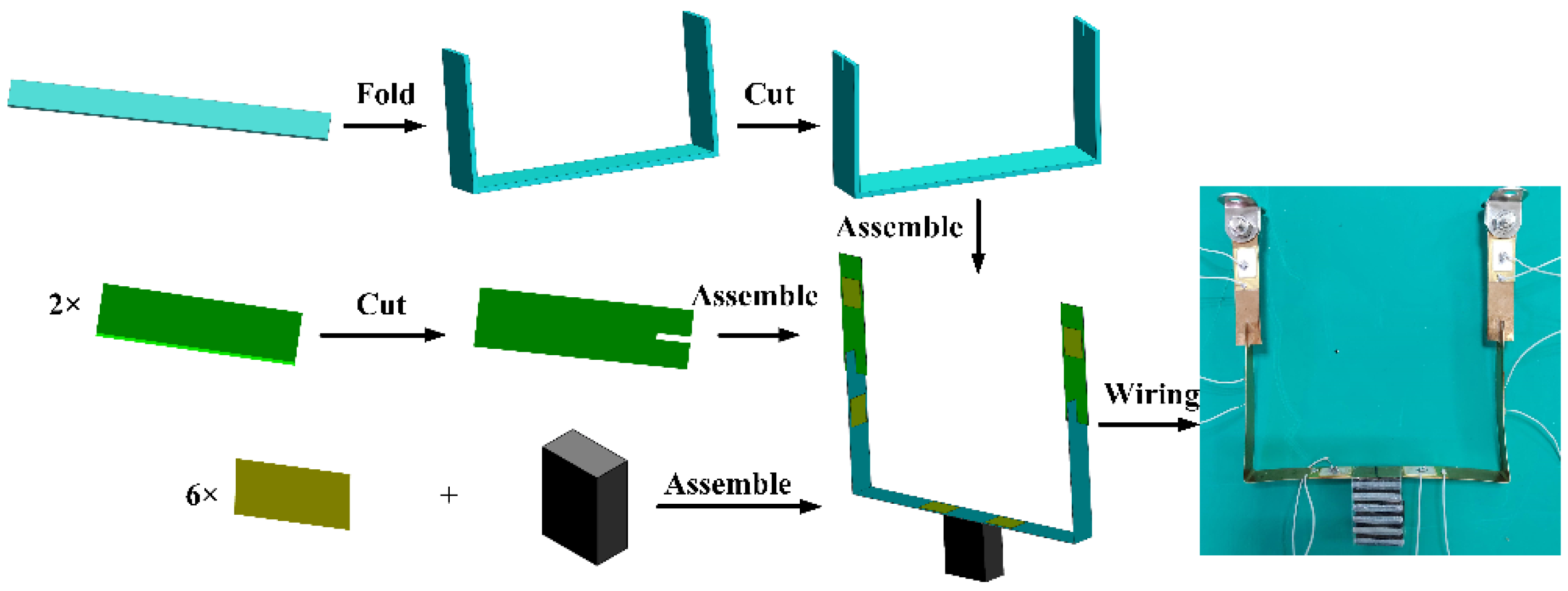
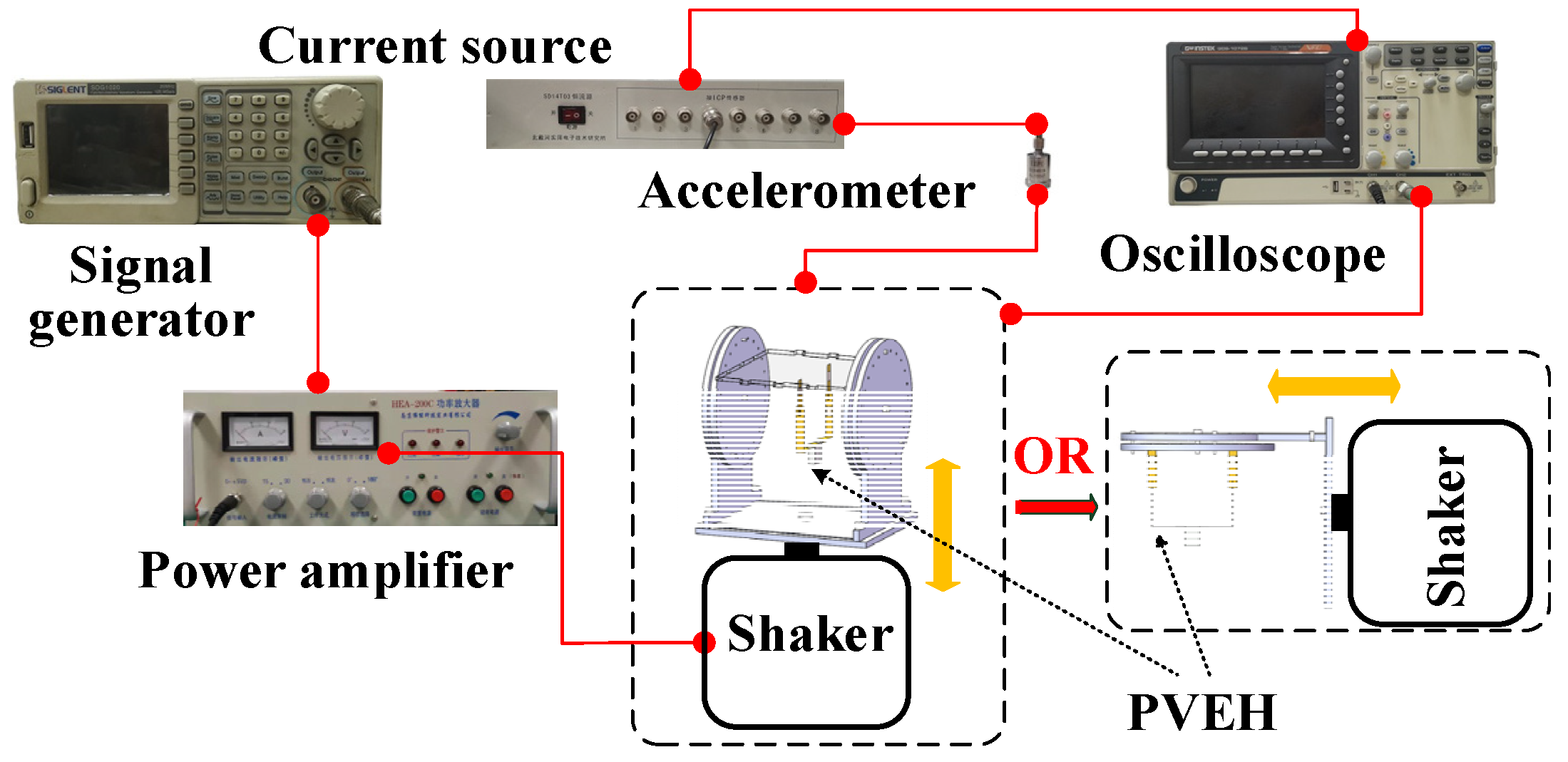
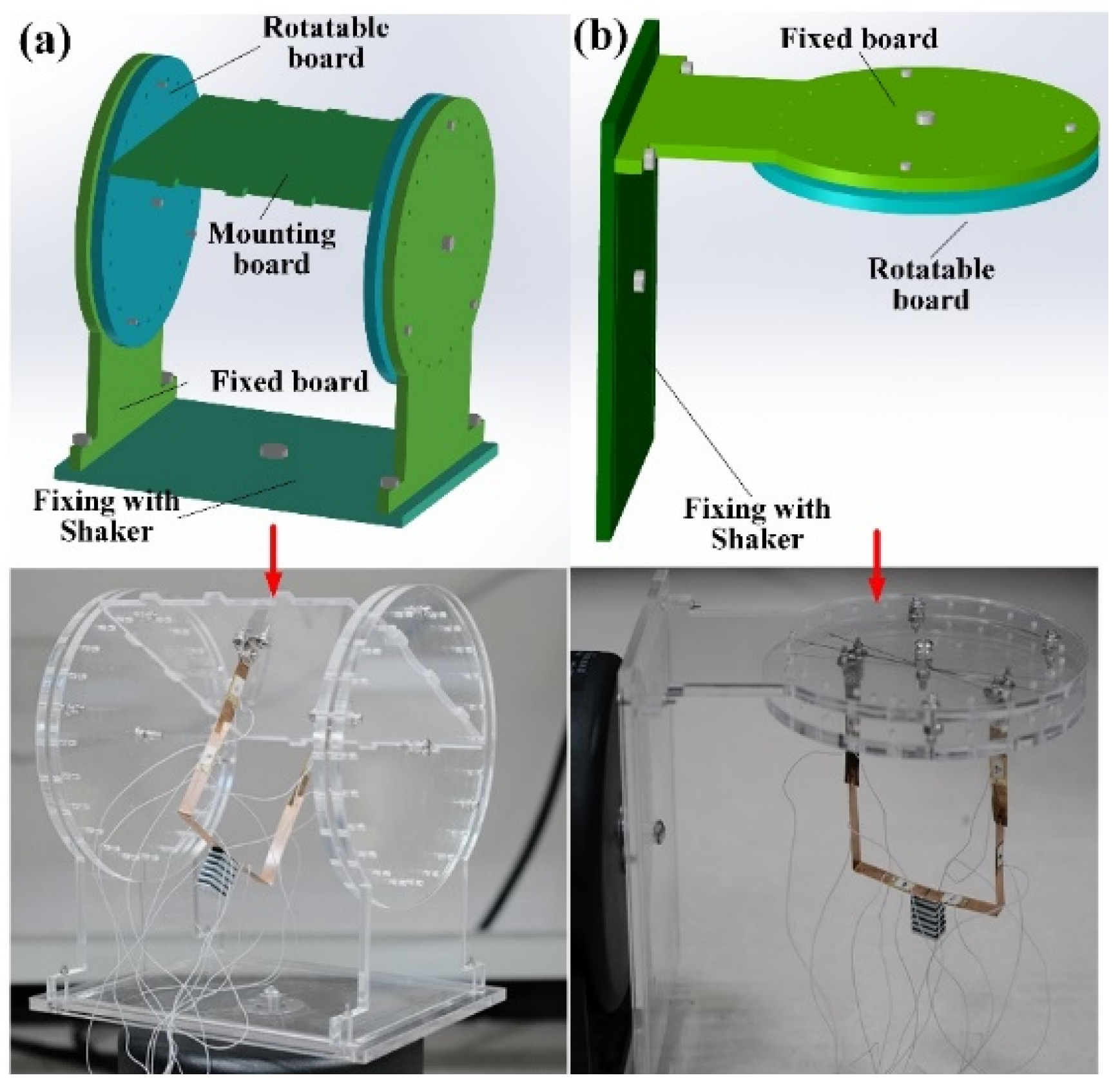
3. Prototype and Experimental Setup
4. Results and Discussions
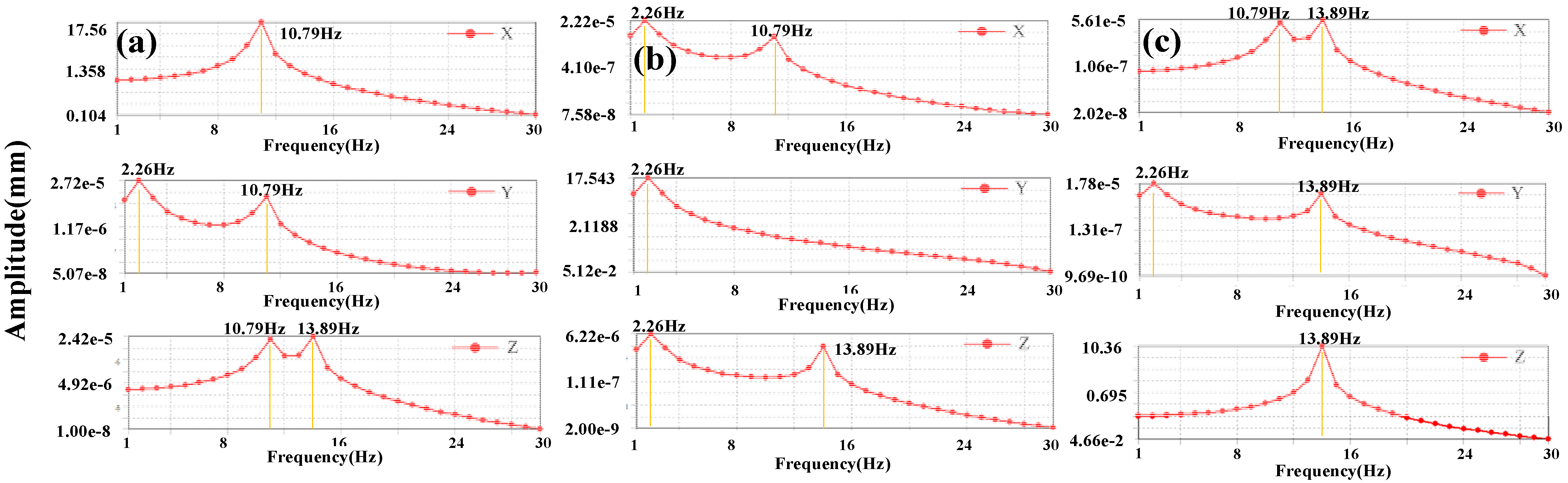
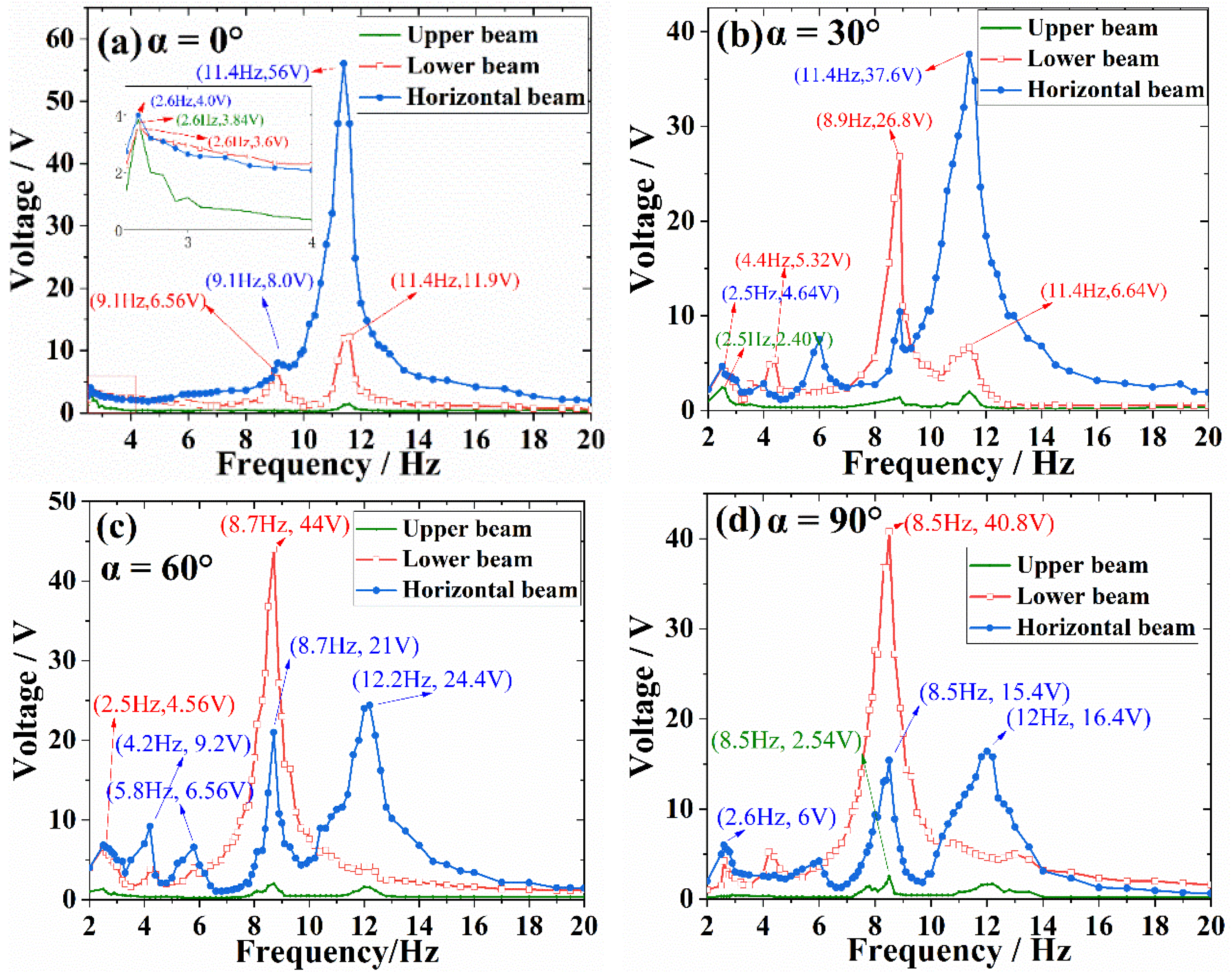
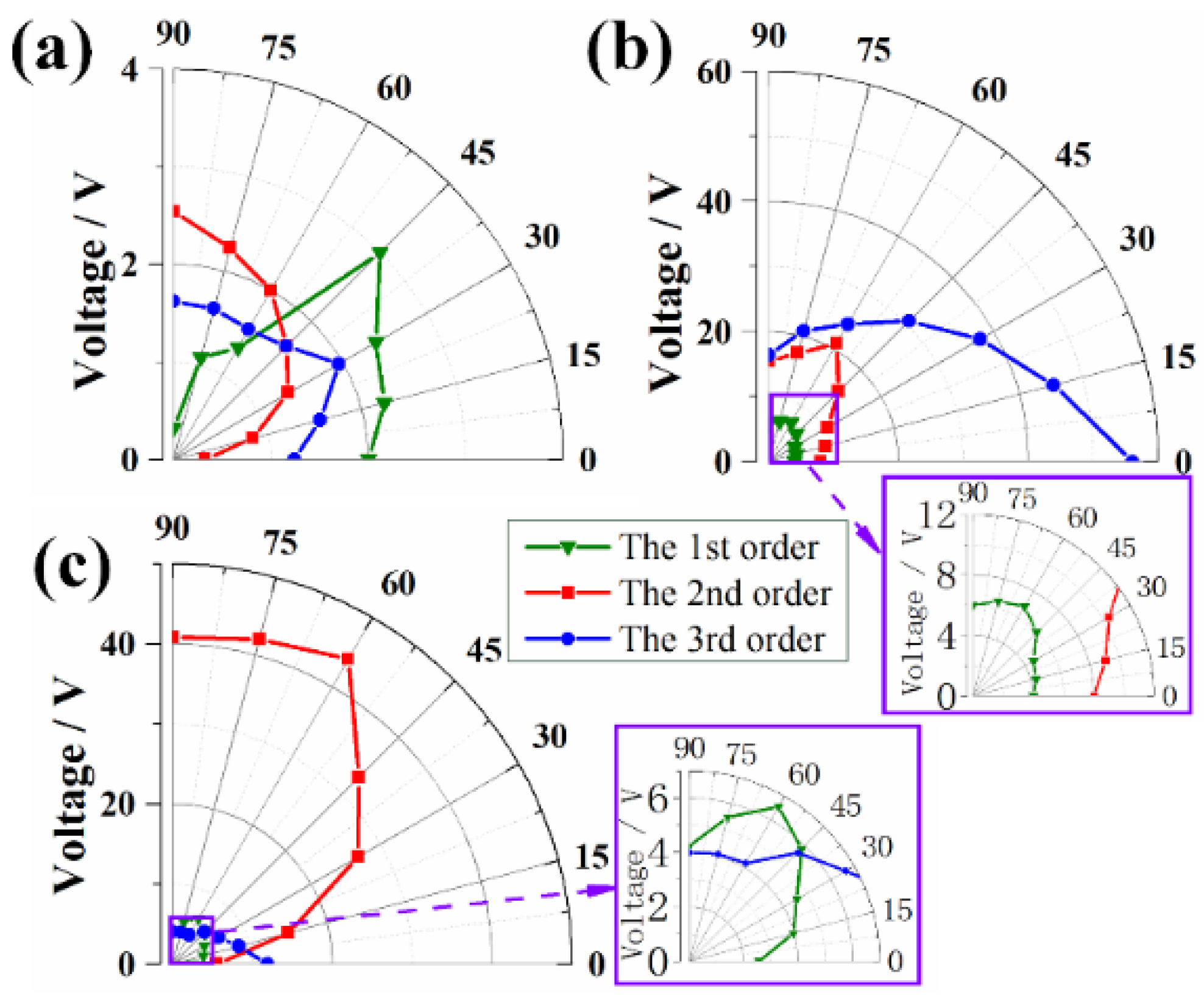
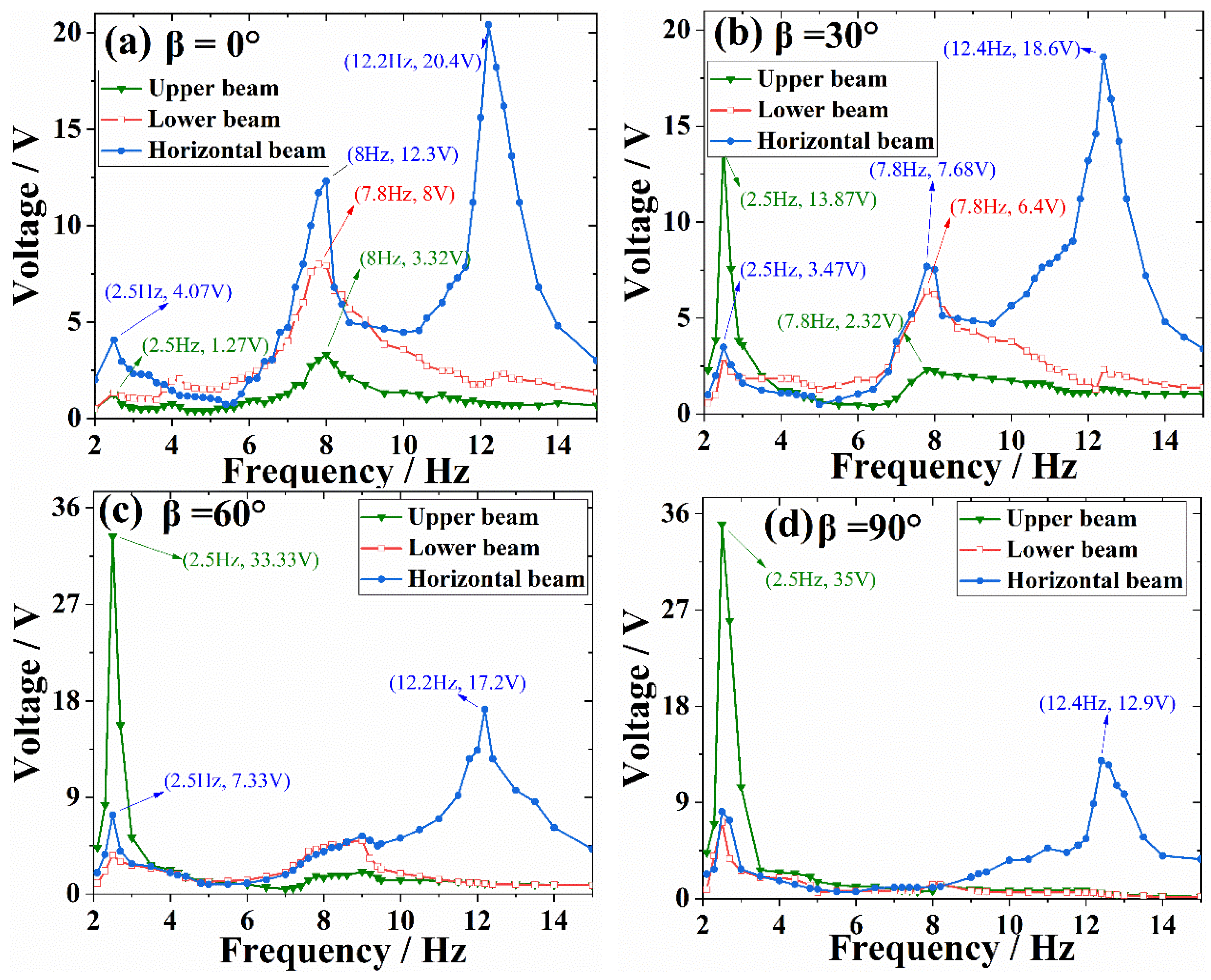
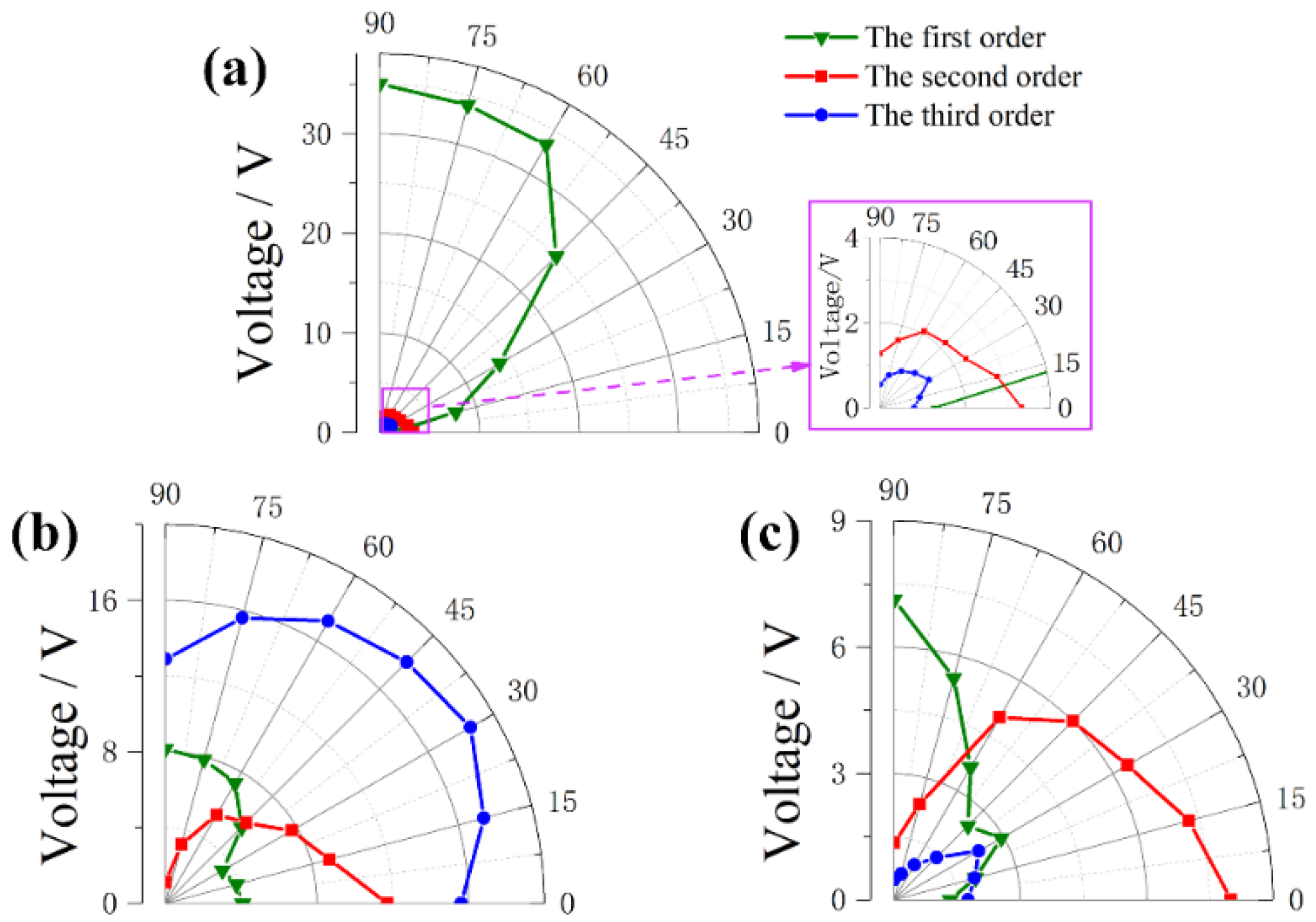
4.1. Experimental Results
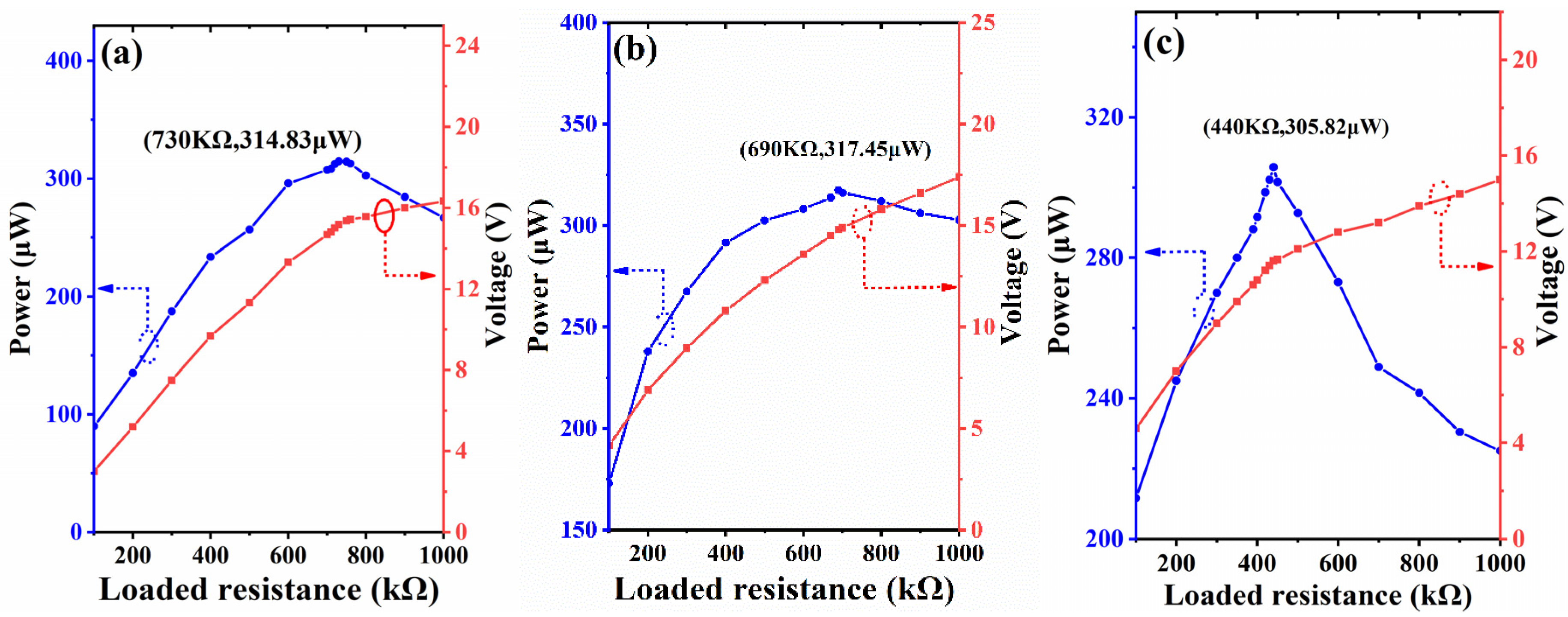
4.2. Discussions
4.3. Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of piezoelectric energy harvesting system and application of optimization techniques to enhance the performance of the harvesting system. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Zhao, W.; Zhang, M.; Qin, H.; Xie, Y. Flexible, Stretchable Sensors for Wearable Health Monitoring: Sensing Mechanisms, Materials, Fabrication Strategies and Features. Sensors 2018, 18, 645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ong, Z.C.; Ooi, Y.X.; Khoo, S.Y.; Huang, Y.H. Two-stage multi-modal system for low frequency and wide bandwidth vibration energy harvesting. Measurement 2020, 149, 106981. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Ding, L.; Zhu, H.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Yan, G.; Liu, F.-R.; Tan, T.; Wei, K.-X.; Zhang, W.-M. Magnetic coupling and flextensional amplification mechanisms for high-robustness ambient wind energy harvesting. Energy Convers. Manag. 2019, 201, 112166. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, S.; Zhang, Z.; Yurchenko, D. High-performance piezoelectric wind energy harvester with Y-shaped attachments. Energy Convers. Manag. 2019, 181, 645–652. [Google Scholar] [CrossRef]
- Fan, K.; Cai, M.; Wang, F.; Tang, L.; Liang, J.; Wu, Y.; Qu, H.; Tan, Q. A string-suspended and driven rotor for efficient ultra-low frequency mechanical energy harvesting. Energy Convers. Manag. 2019, 198, 111820. [Google Scholar] [CrossRef]
- Miao, G.; Fang, S.; Wang, S.; Zhou, S. A low-frequency rotational electromagnetic energy harvester using a magnetic plucking mechanism. Appl. Energy 2022, 305, 117838. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Zhang, A.; Peng, Z.; Luo, D.; Chen, R.; Wang, F. Electrostatic energy harvesting device with dual resonant structure for wideband random vibration sources at low frequency. Rev. Sci. Instrum. 2016, 87, 125001. [Google Scholar] [CrossRef]
- He, L.; Zhao, D.; Li, W.; Wu, X.; Cheng, G. A dual piezoelectric energy harvester with contact and non-contact driven by inertial wheel. Mech. Syst. Signal Process. 2021, 146, 106994. [Google Scholar] [CrossRef]
- Chen, K.; Gao, F.; Liu, Z.; Liao, W.-H. A nonlinear M-shaped tri-directional piezoelectric energy harvester. Smart Mater. Struct. 2021, 30, 045017. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Hao, G.; Olszewski, O.Z. A review on vibration-based piezoelectric energy harvesting from the aspect of compliant mechanisms. Sens. Actuators A Phys. 2021, 331, 112743. [Google Scholar] [CrossRef]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar] [CrossRef] [Green Version]
- Tran, N.; Ghayesh, M.H.; Arjomandi, M. Ambient vibration energy harvesters: A review on nonlinear techniques for performance enhancement. Int. J. Eng. Sci. 2018, 127, 162–185. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Liu, Y.; Zhao, W. Low-frequency, broadband piezoelectric vibration energy harvester with folded trapezoidal beam. Rev. Sci. Instrum. 2019, 90, 035001. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, Y.; Wang, Y.; Luo, C.; Li, G.; Hu, J.; Liu, W.; Zhang, W. Low-frequency and wideband vibration energy harvester with flexible frame and interdigital structure. AIP Adv. 2015, 5, 047151. [Google Scholar] [CrossRef]
- Cha, Y. Energy harvesting using flexible piezoelectric materials from human walking motion: Theoretical analysis. J. Intell. Mater. Syst. Struct. 2017, 28, 3006–3015. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Fan, K.; Ji, H.; Qiu, J. Investigation of an ultra-low frequency piezoelectric energy harvester with high frequency up-conversion factor caused by internal resonance mechanism. Mech. Syst. Signal Process. 2022, 162, 108038. [Google Scholar] [CrossRef]
- Pyo, S.; Kwon, D.-S.; Ko, H.-J.; Eun, Y.; Kim, J. Frequency up-Conversion Hybrid Energy Harvester Combining Piezoelectric and Electromagnetic Transduction Mechanisms. Int. J. Precis. Eng. Manuf.-Green Technol. 2022, 9, 241–251. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Du, Y.; Yan, Z.; Tan, T. Nonlinear broadband piezoelectric vibration energy harvesting enhanced by inter-well modulation. Energy Convers. Manag. 2021, 246, 114661. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Y.; Li, T.; Yan, Z.; Tan, T. A flute-inspired broadband piezoelectric vibration energy harvesting device with mechanical intelligent design. Appl. Energy 2021, 303, 117577. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, L.; Zhao, L.; Luo, G.; Yang, P.; Ning, S.; Lu, D.; Lin, Q. Modeling and design of V-shaped piezoelectric vibration energy harvester with stopper for low-frequency broadband and shock excitation. Sens. Actuators A Phys. 2021, 317, 112458. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, S. Tunable multi-source energy harvesting via frequency selective structures. Eng. Res. Express 2019, 1, 015001. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Wang, S.; Wei, T.; Chen, R. A wide band nonlinear dual piezoelectric cantilever energy harvester coupled by origami. Smart Mater. Struct. 2021, 30, 025025. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Dane Quinn, D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Chen, R.; Ren, L.; Xia, H.; Yuan, X.; Liu, X. Energy harvesting performance of a dandelion-like multi-directional piezoelectric vibration energy harvester. Sens. Actuators A Phys. 2015, 230, 1–8. [Google Scholar] [CrossRef]
- Wang, H.; Hu, F.; Wang, K.; Liu, Y.; Zhao, W. Three-dimensional piezoelectric energy harvester with spring and magnetic coupling. Appl. Phys. Lett. 2017, 110, 163905. [Google Scholar] [CrossRef]
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Multi-directional energy harvesting by piezoelectric cantilever-pendulum with internal resonance. Appl. Phys. Lett. 2015, 107, 213902. [Google Scholar] [CrossRef]
- Mo, S.; Liu, Y.; Shang, S.; Wang, H.; Yang, K. Tri-directional piezoelectric energy harvester based on U-shaped beam-pendulum structure. Rev. Sci. Instrum. 2021, 92, 015002. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Liang, J.; Lan, C.; Tang, L. A twist piezoelectric beam for multi-directional energy harvesting. Smart Mater. Struct. 2020, 29, 11LT01. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, H.; Soh, C.K. Experiment and modeling of a two-dimensional piezoelectric energy harvester. Smart Mater. Struct. 2015, 24, 125011. [Google Scholar] [CrossRef]
- Brenes, A.; Morel, A.; Gibus, D.; Yoo, C.S.; Gasnier, P.; Lefeuvre, E.; Badel, A. Large-bandwidth piezoelectric energy harvesting with frequency-tuning synchronized electric charge extraction. Sens. Actuators A Phys. 2020, 302, 111759. [Google Scholar] [CrossRef]
- Wang, L.; Ding, J.; Jiang, Z.; Luo, G.; Zhao, L.; Lu, D.; Yang, X.; Ryutaro, M. A packaged piezoelectric vibration energy harvester with high power and broadband characteristics. Sens. Actuators A Phys. 2019, 295, 629–636. [Google Scholar] [CrossRef]
- Ju, S.; Ji, C.-H. Impact-based piezoelectric vibration energy harvester. Appl. Energy 2018, 214, 139–151. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
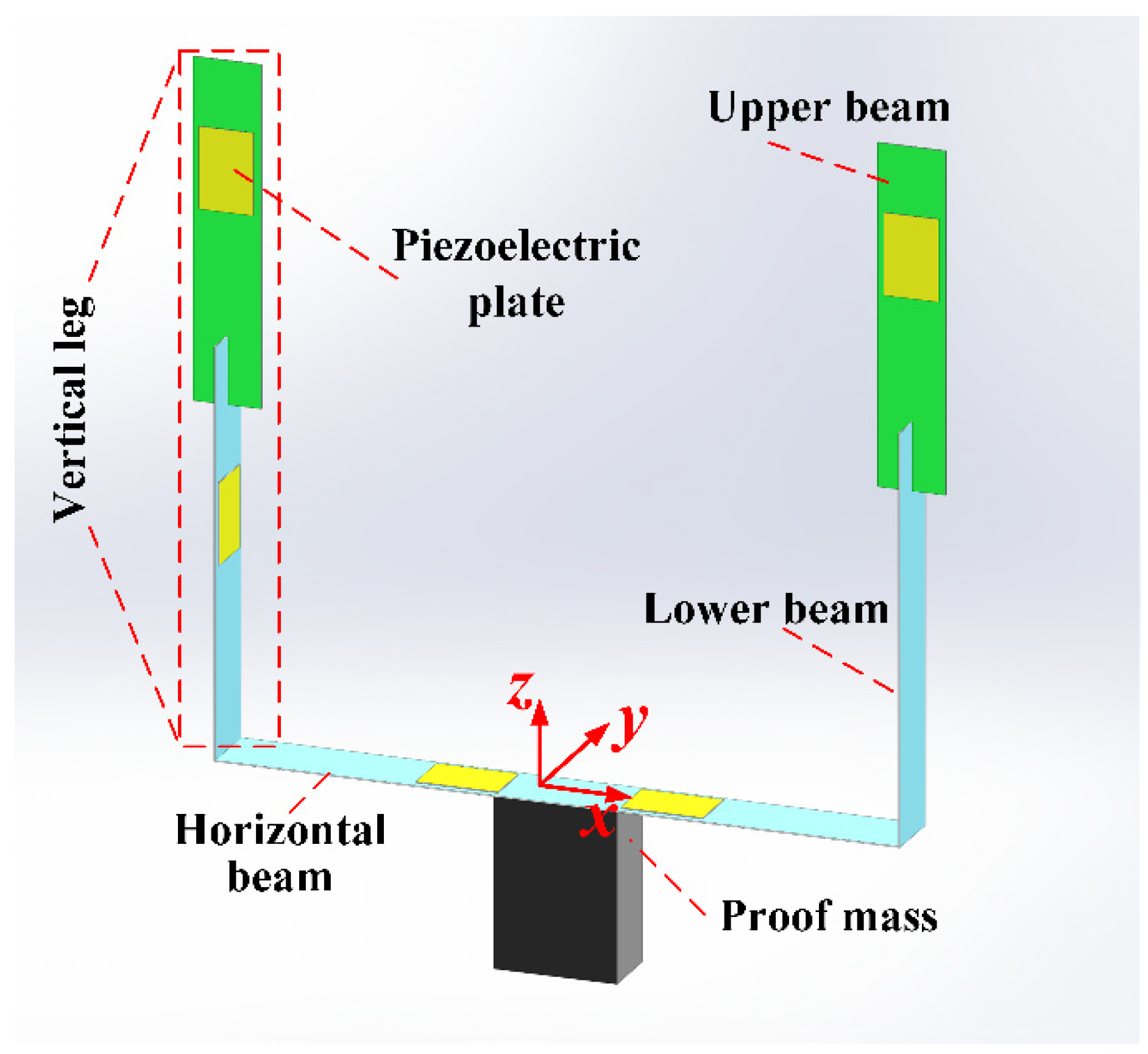
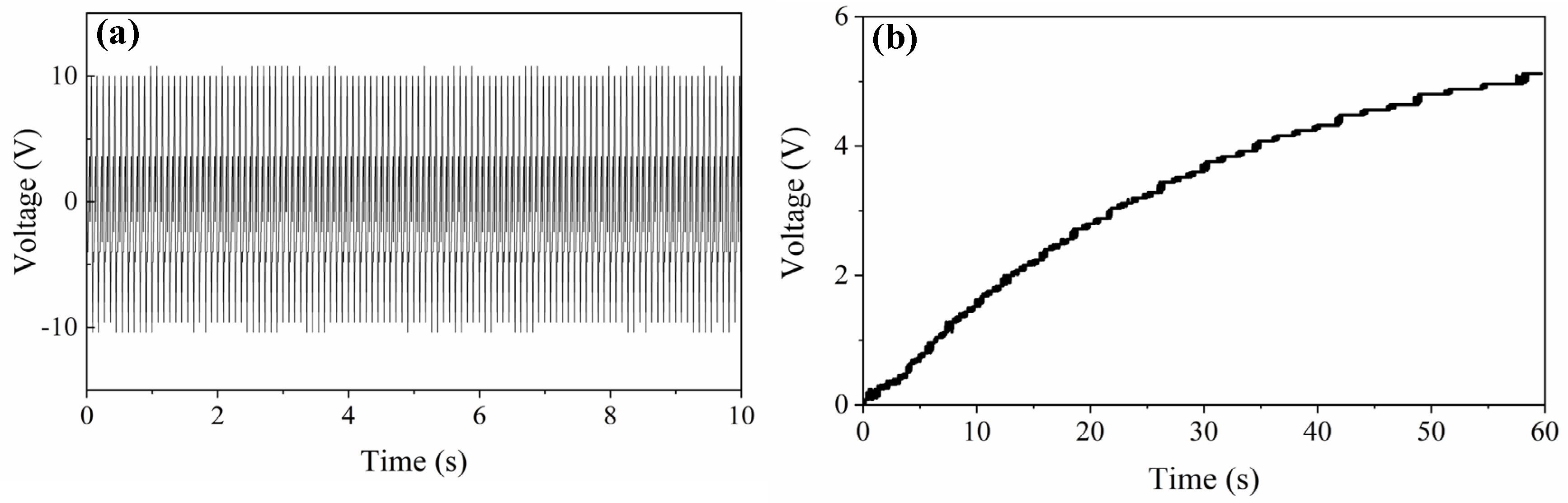
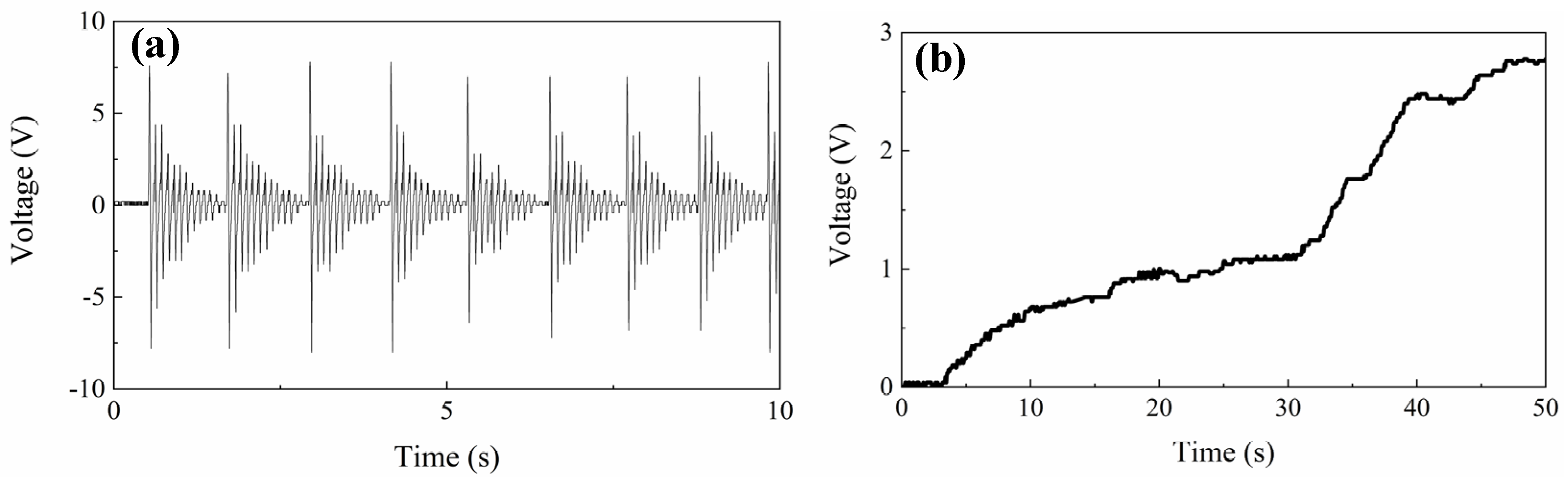
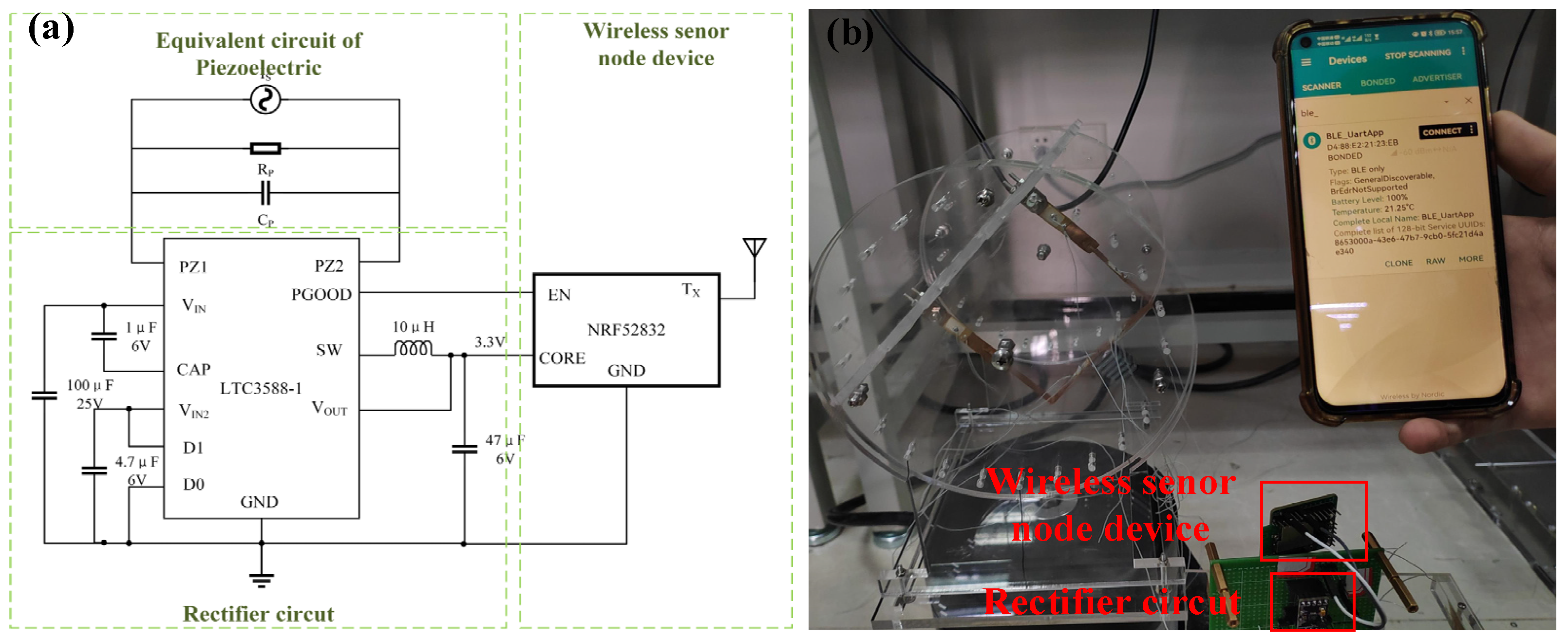
| Components | Valid Length | Width | Thickness |
|---|---|---|---|
| PZT-5A | 12 | 8 | 0.2 |
| Horizontal beam | 100 | 10 | 0.2 |
| Lower beam | 50 | 10 | 0.2 |
| Upper beam | 40 | 10 | 0.2 |
| Orders | Measured | Simulated | Deviation |
|---|---|---|---|
| 1st | 2.6 | 2.26 | 0.34 |
| 2nd | 9.1 | 10.79 | 1.69 |
| 3rd | 11.4 | 13.89 | 2.35 |
| Works | Excitations (1D/2D/3D) | Acc. (g) | Fre. (Hz) | Power (µW) | Volu. (mm3) | NVPD (µW/(mm3g2Hz)) |
|---|---|---|---|---|---|---|
| [34] | 1D | 0.041 | 27.5 | 93 | 6300 | 0.3139 |
| [35] | 1D | 1 | 160 | 2490 | 880 | 0.0177 |
| [23] | 1D | 0.1 | 12 | 442 | 8400 | 0.4383 |
| [36] | 2D | 3 | 18 | 963.9 | 3120 | 0.00191 |
| [32] | 3D | 0.5 | 23.7 | 9.2 | 4256 | 0.00036 |
| [30] | 3D | 0.008 | 4.56 | - | 982 | - |
| [28] | 3D | 0.5 | 8 | 110.3 | 3480 | 0.0158 |
| [31] | 3D | 1 | 2.9 | 306 | 4507 | 0.0234 |
| This work | 3D | 0.5 | 2.5 | 314 | 4586 | 0.1115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Mo, S.; Jiang, X.; Shang, S.; Wang, P.; Liu, Y. Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines 2022, 13, 396. https://doi.org/10.3390/mi13030396
Qin H, Mo S, Jiang X, Shang S, Wang P, Liu Y. Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines. 2022; 13(3):396. https://doi.org/10.3390/mi13030396
Chicago/Turabian StyleQin, Hongbo, Shuting Mo, Xin Jiang, Siyao Shang, Peng Wang, and Yan Liu. 2022. "Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams" Micromachines 13, no. 3: 396. https://doi.org/10.3390/mi13030396
APA StyleQin, H., Mo, S., Jiang, X., Shang, S., Wang, P., & Liu, Y. (2022). Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines, 13(3), 396. https://doi.org/10.3390/mi13030396






