Robust Optimal Control Design for Performance Enhancement of PWM Voltage Source Inverter
Abstract
1. Introduction
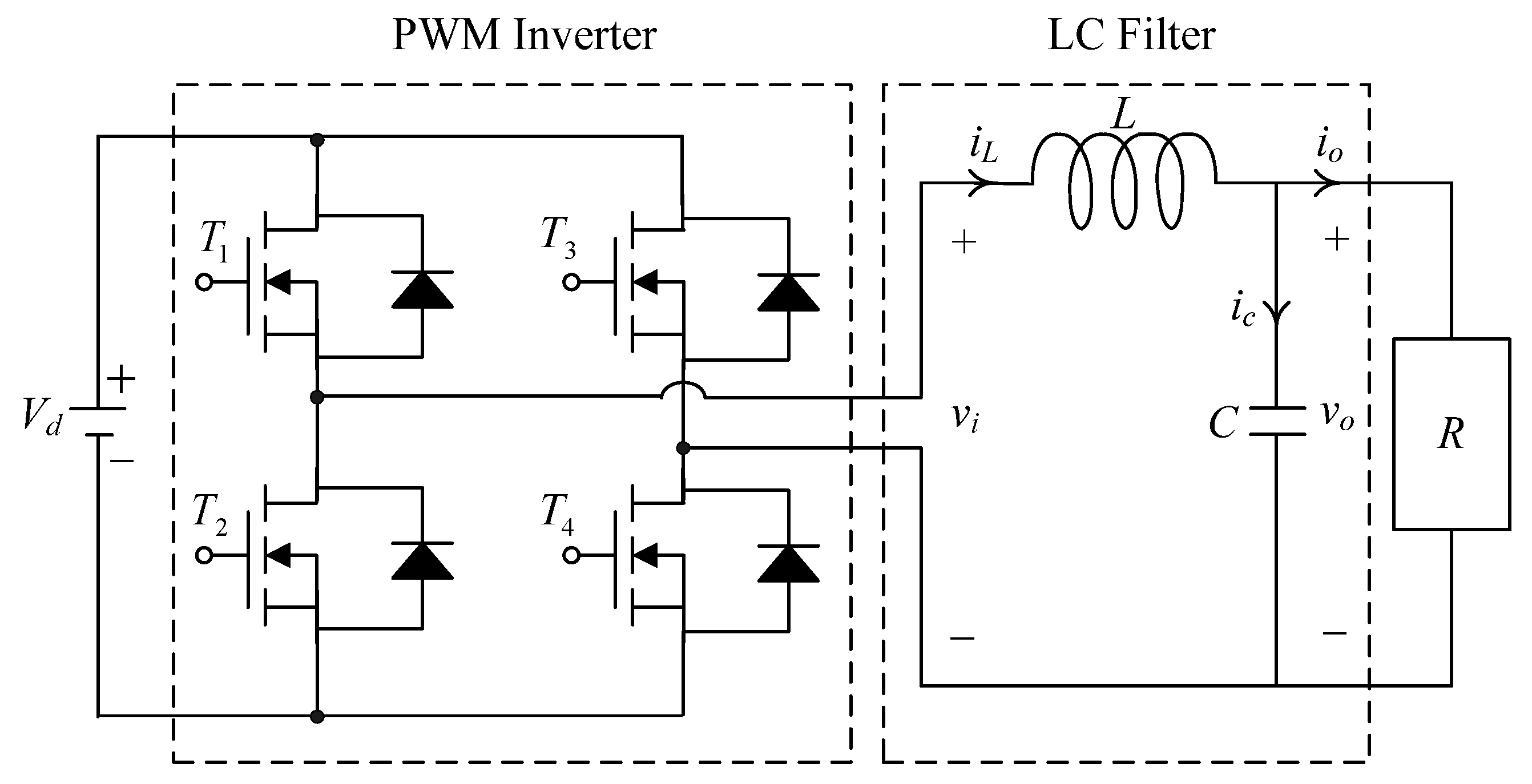
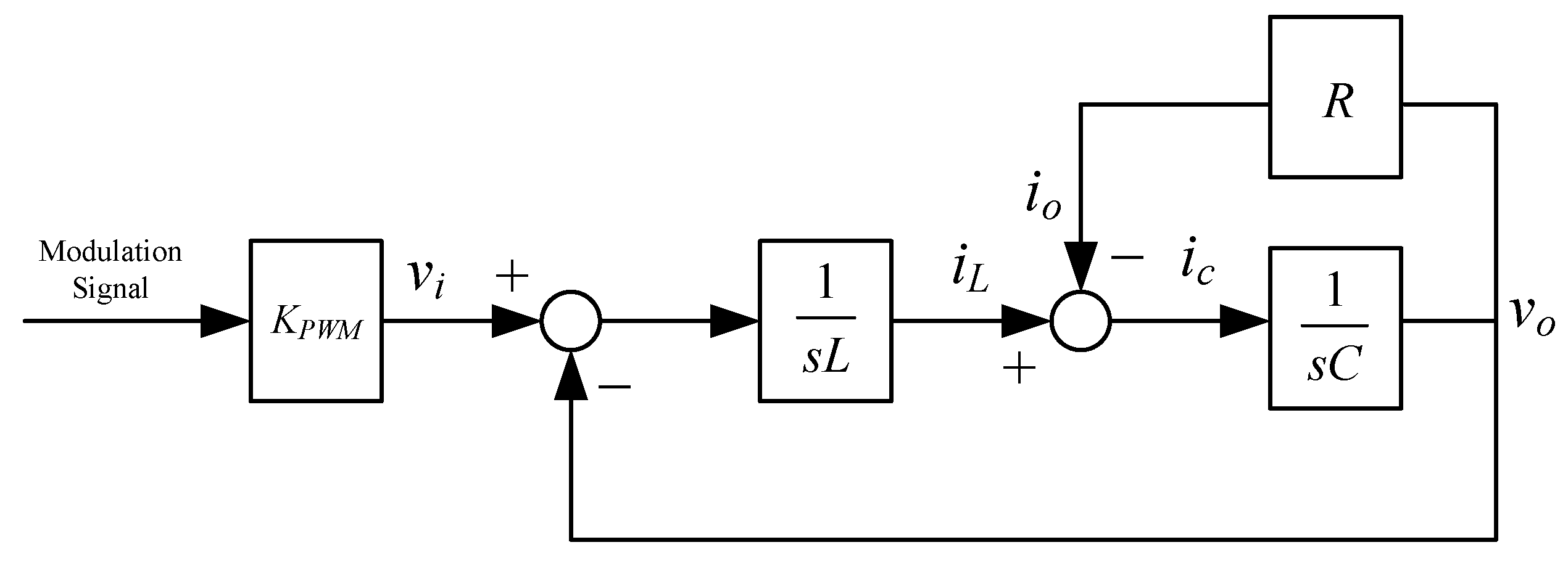
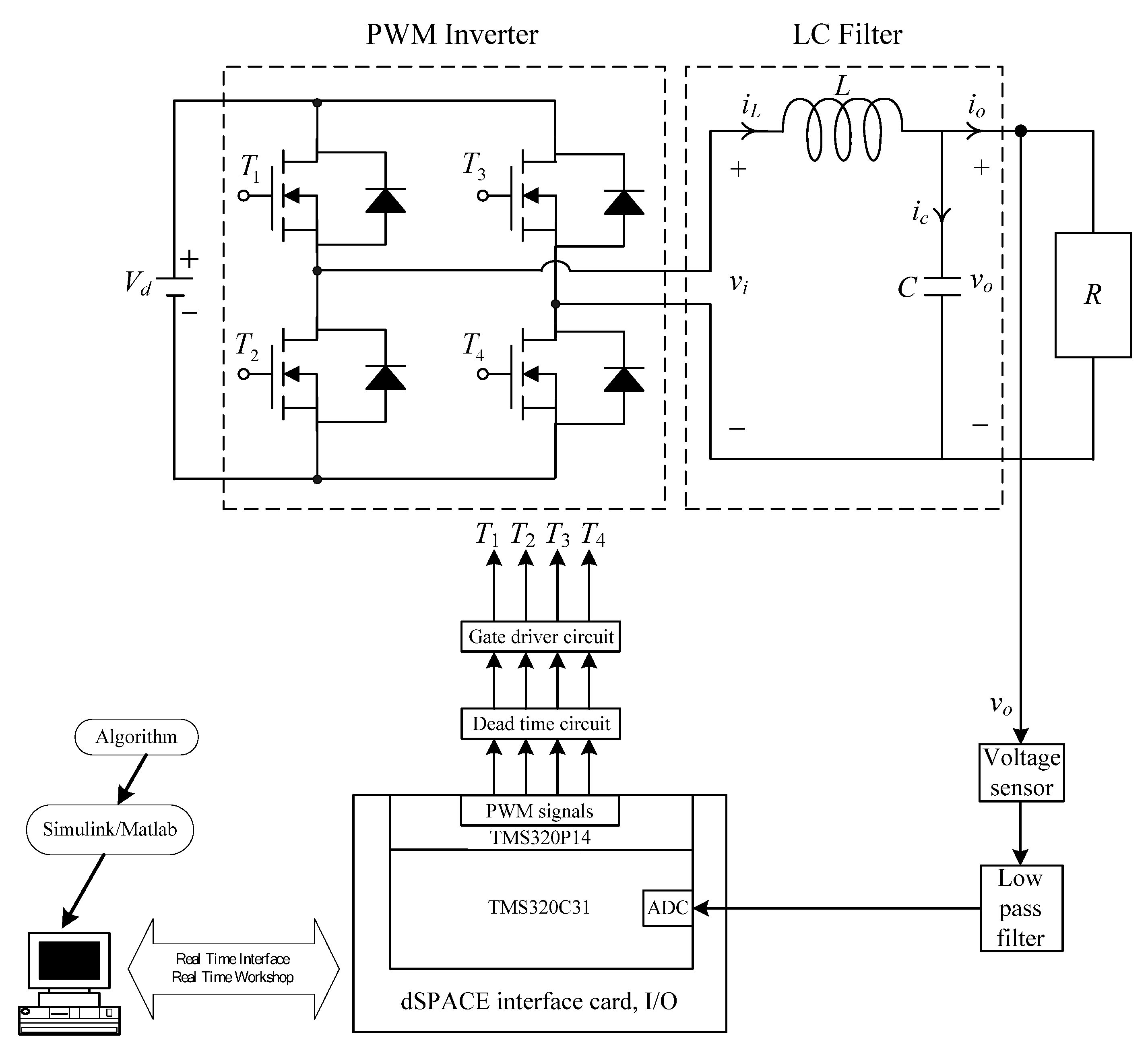
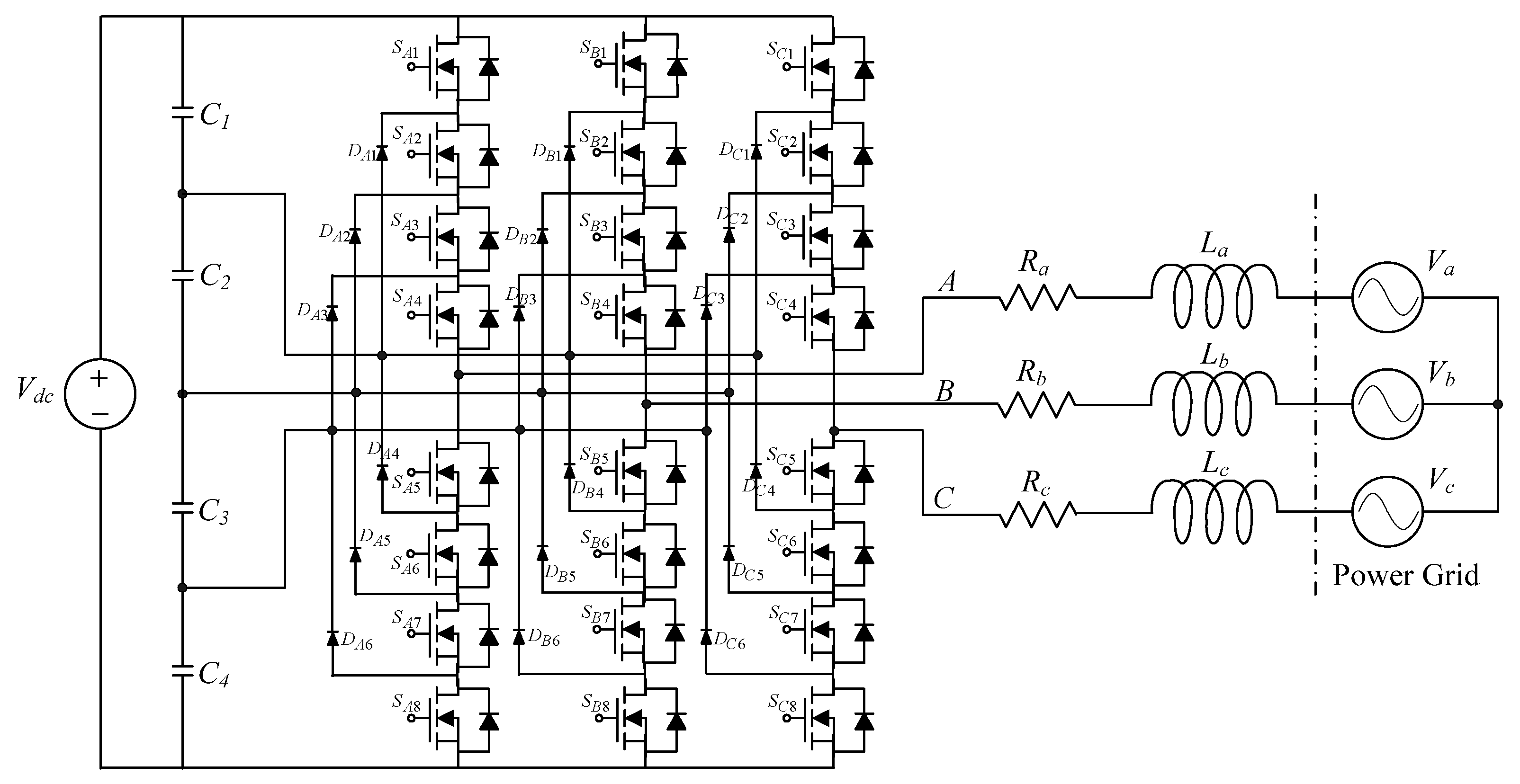
2. Modeling of PWM Voltage Source Inverter
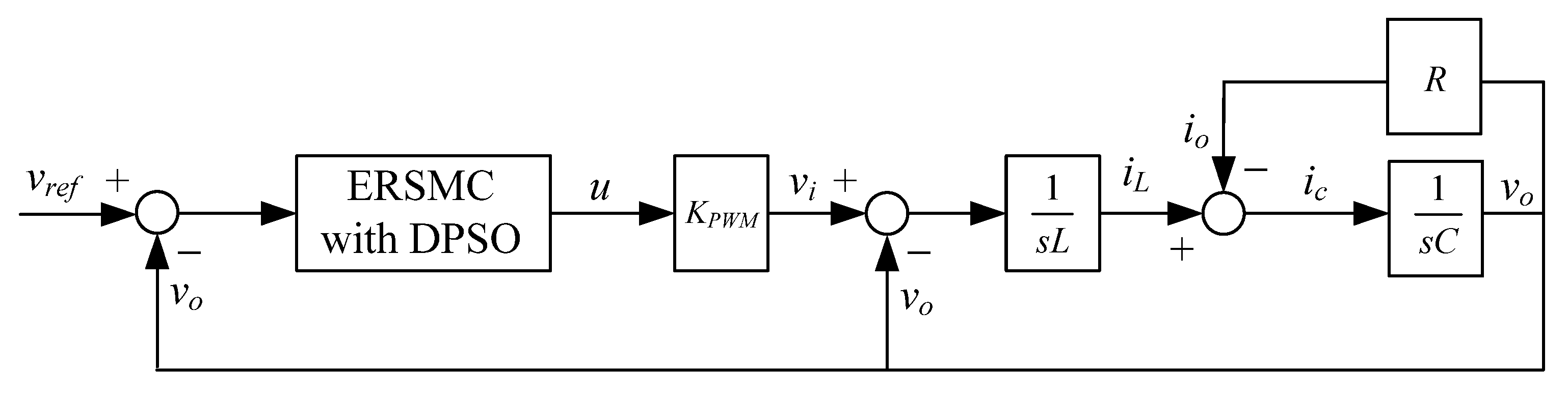
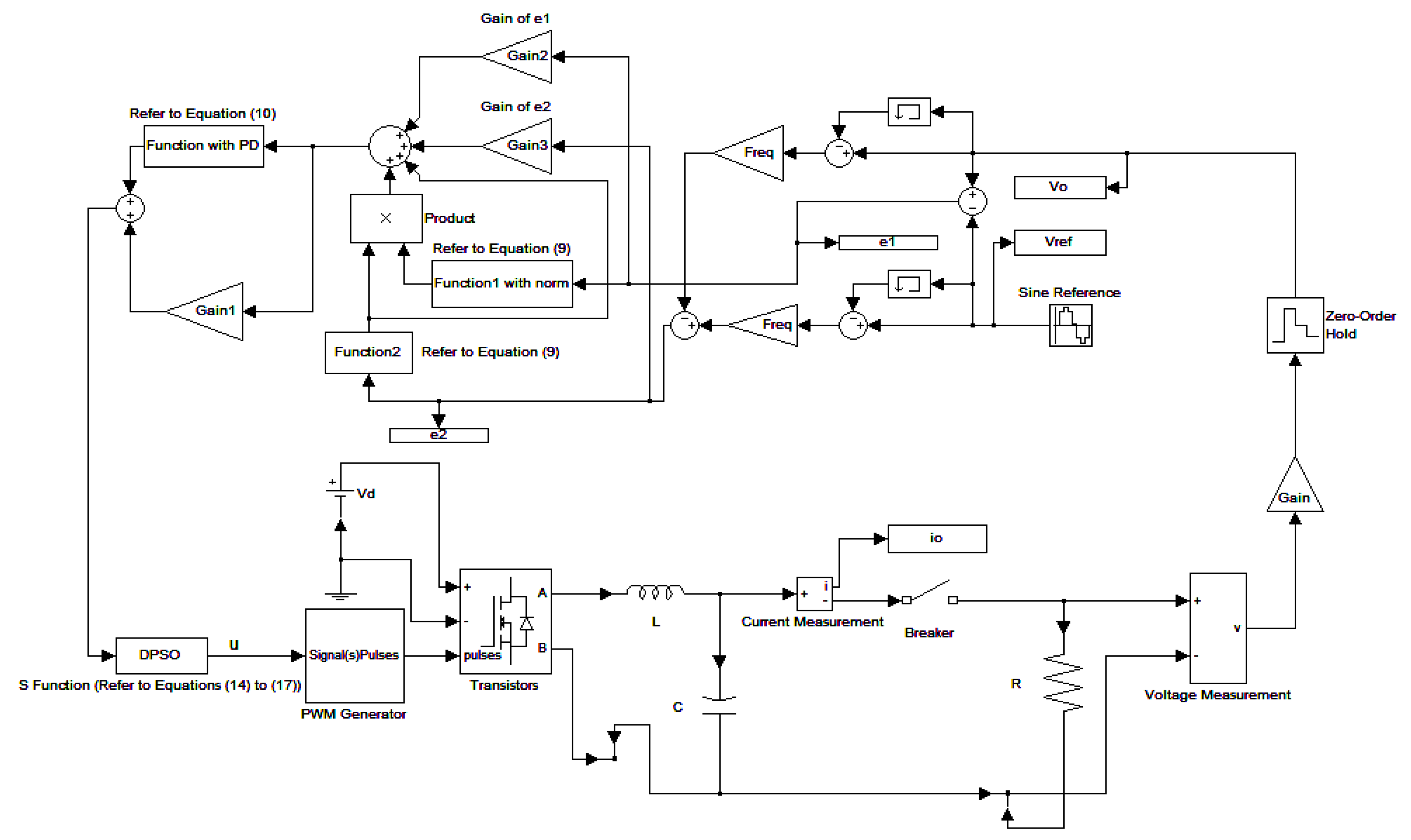
3. Control Design
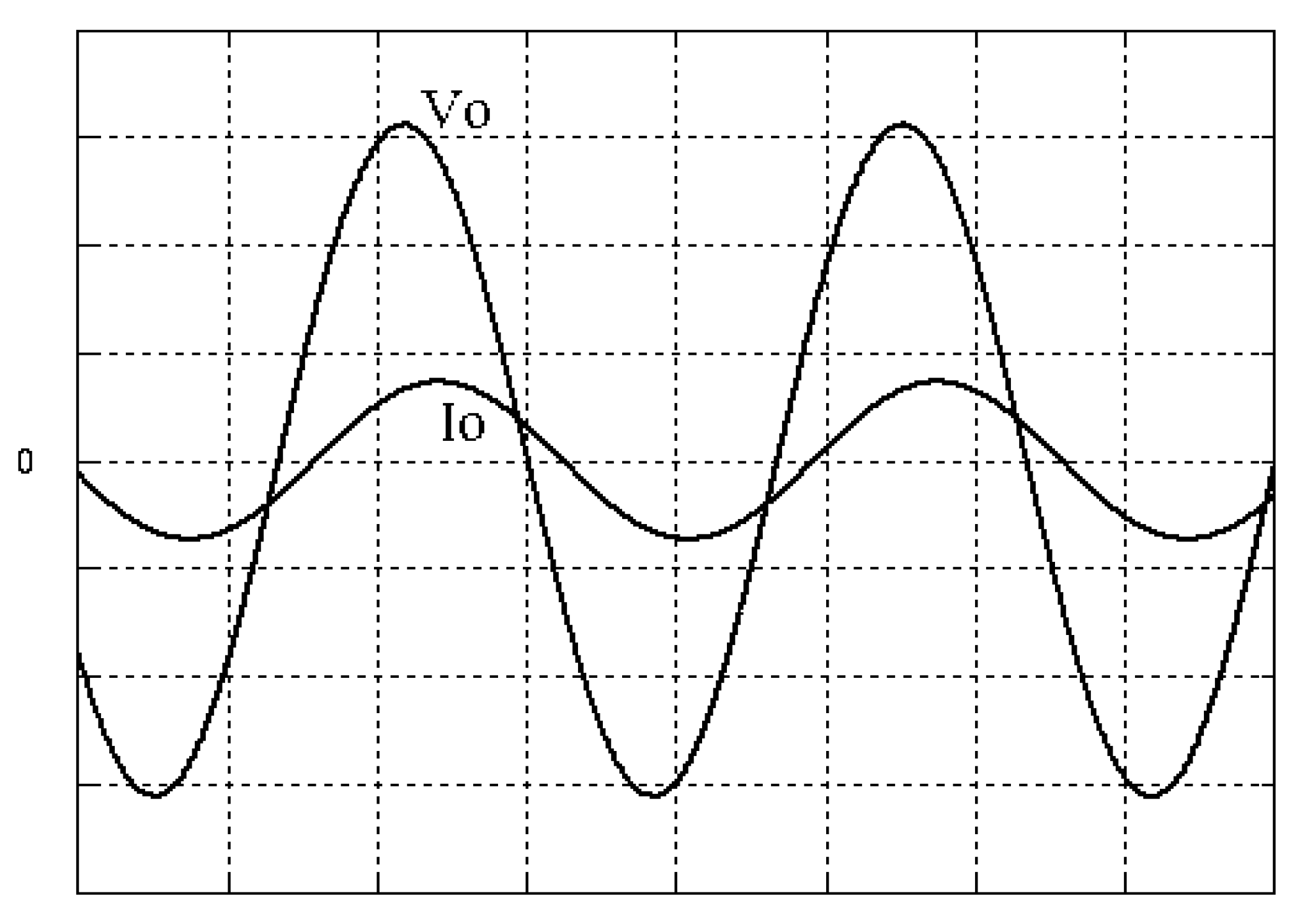
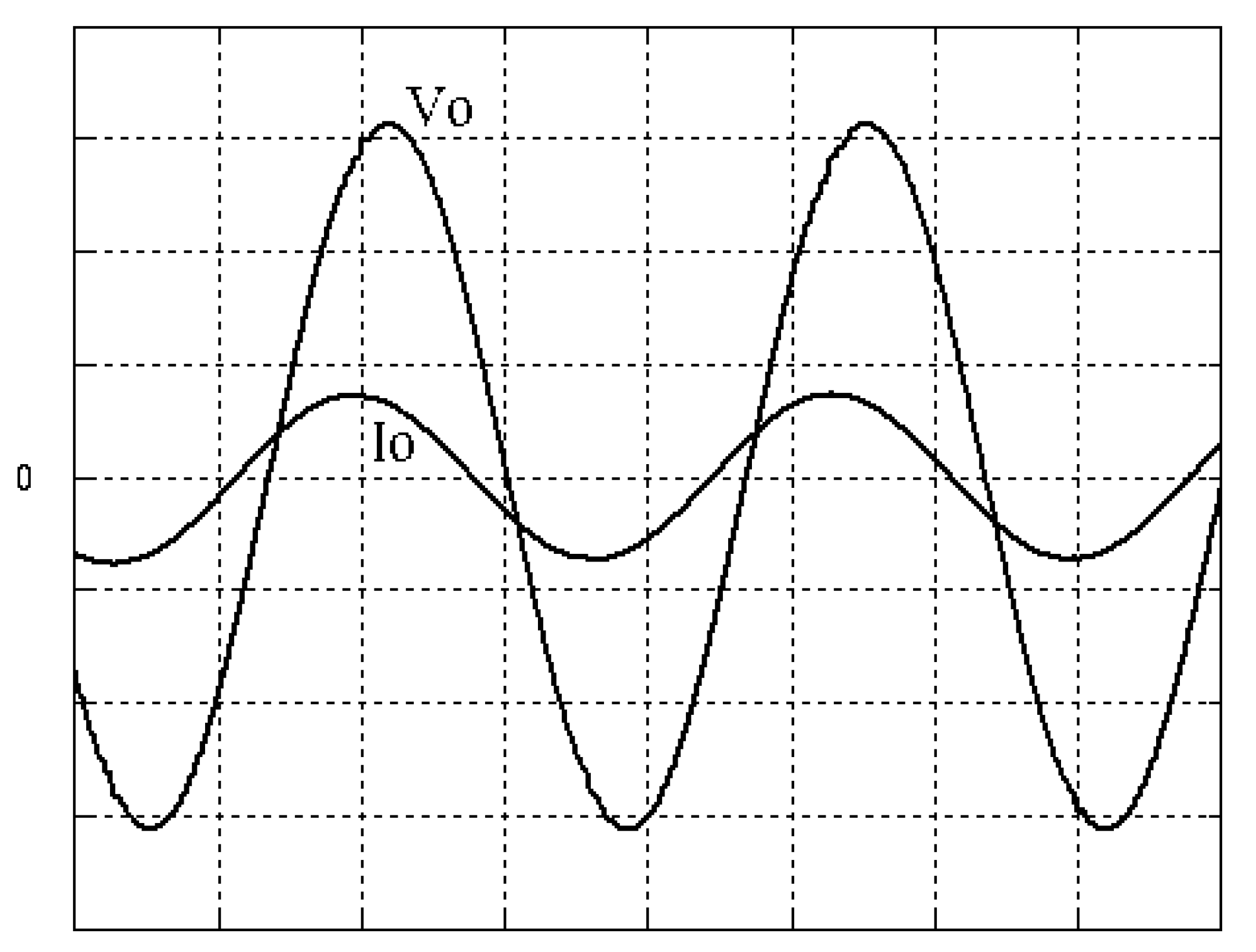
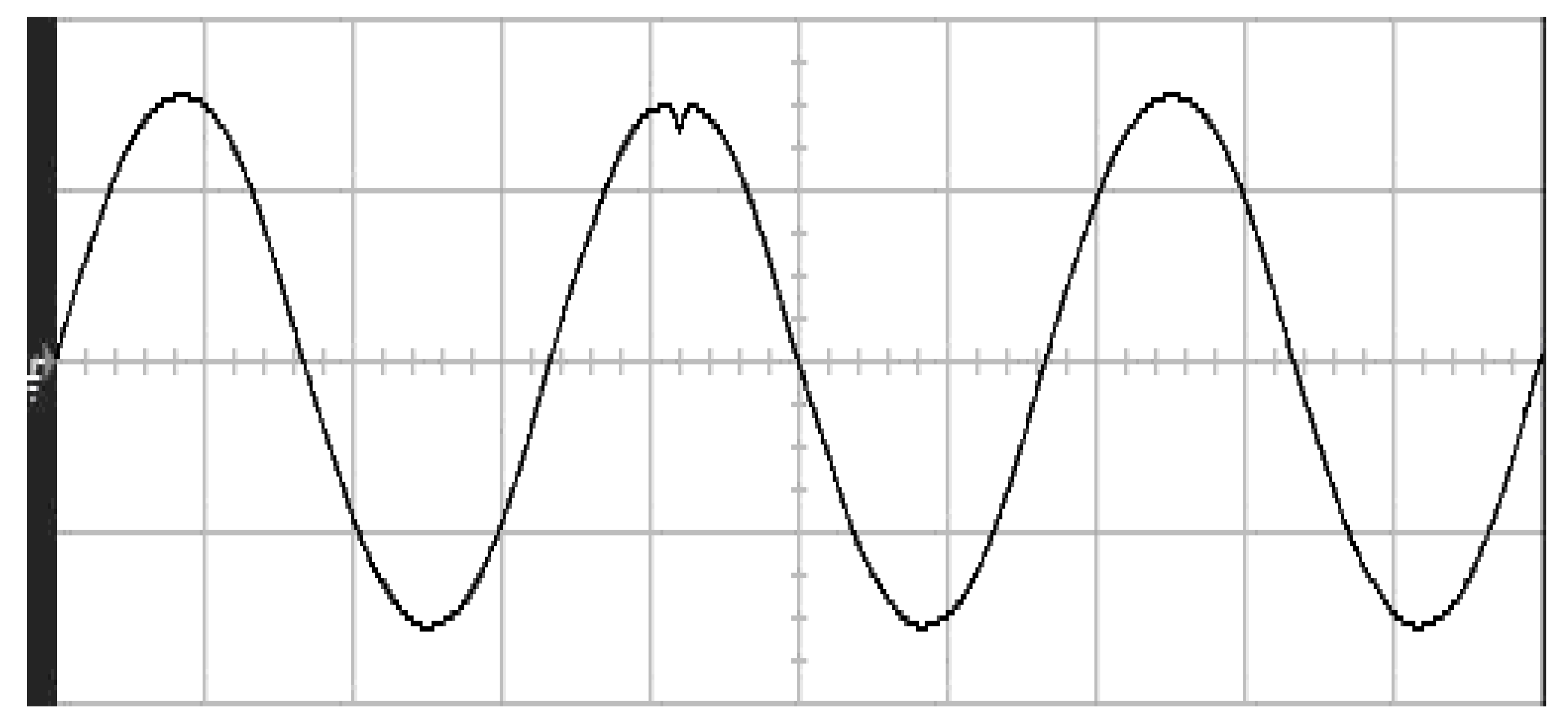
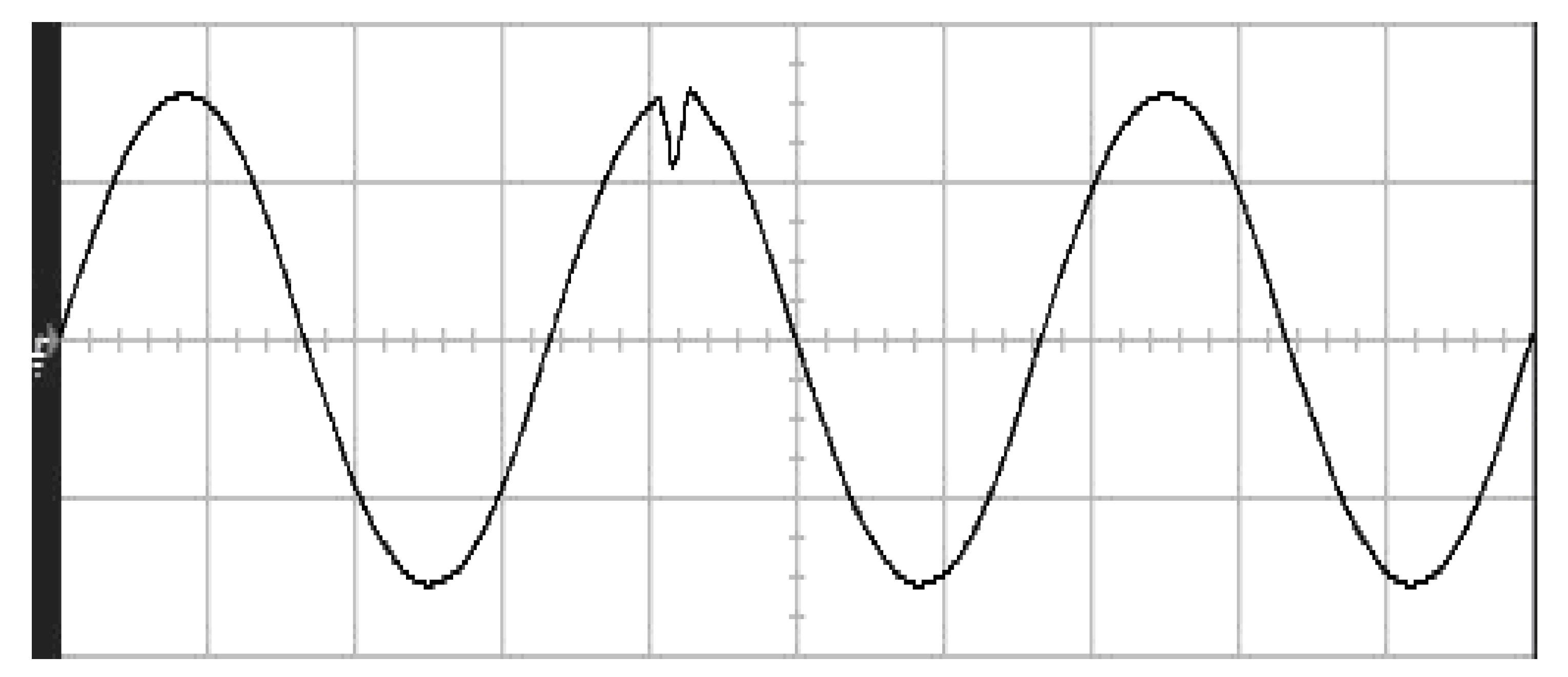
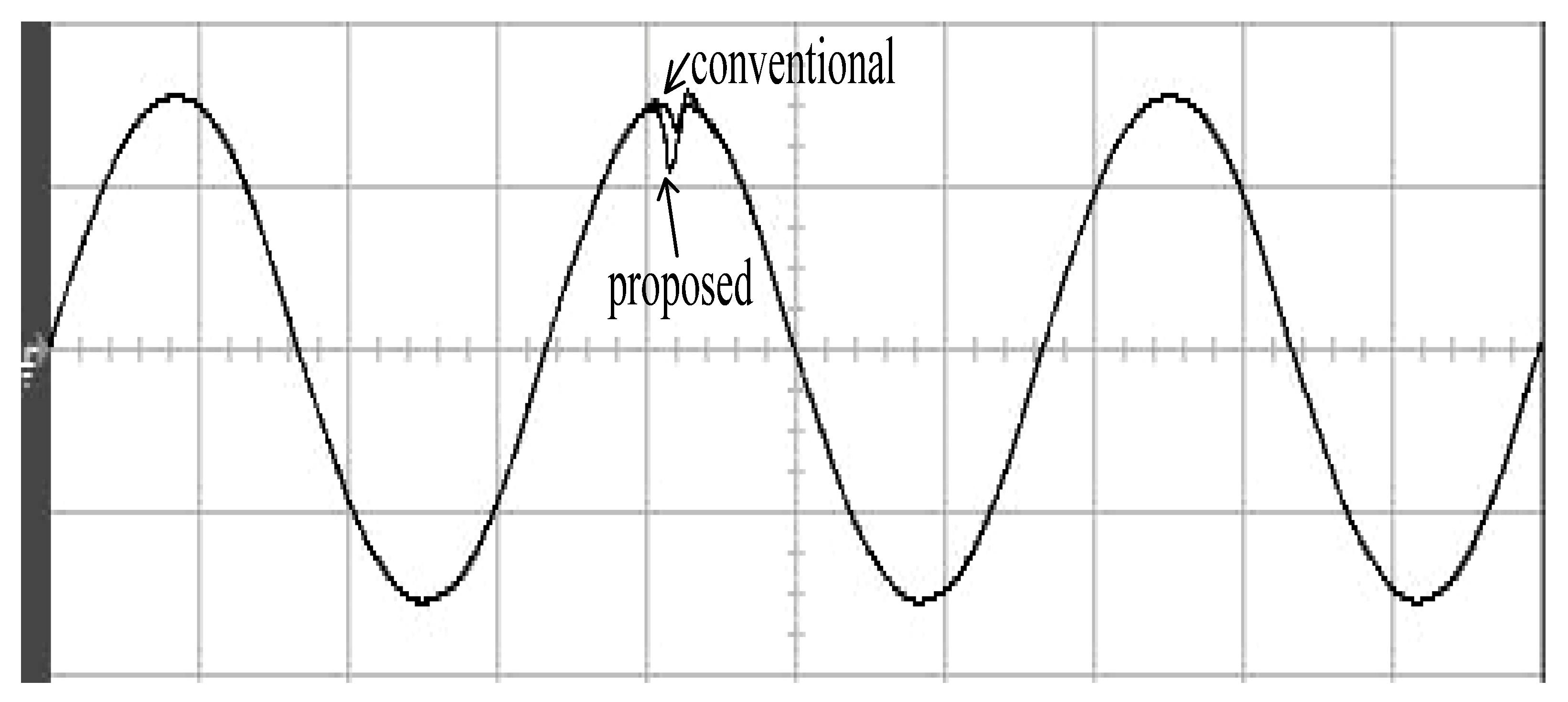
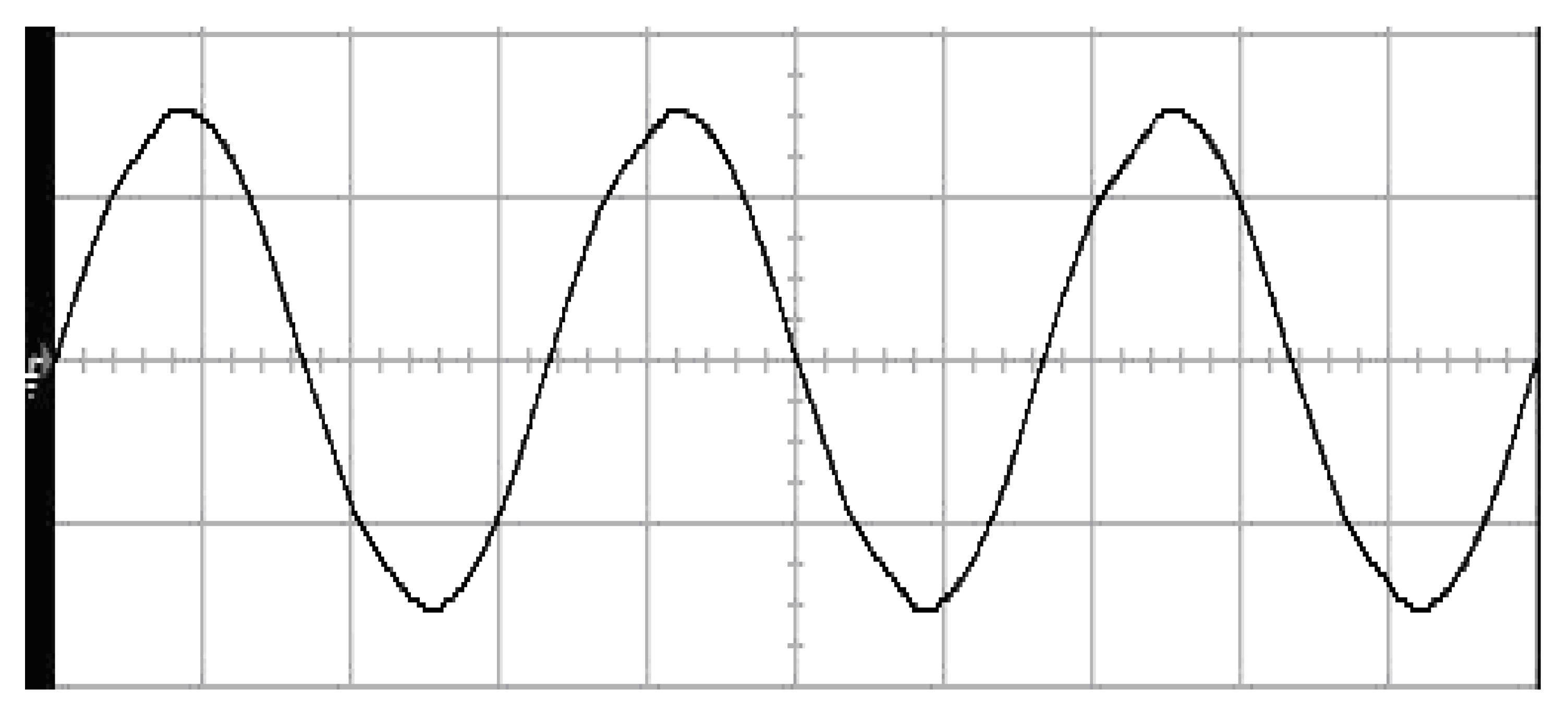
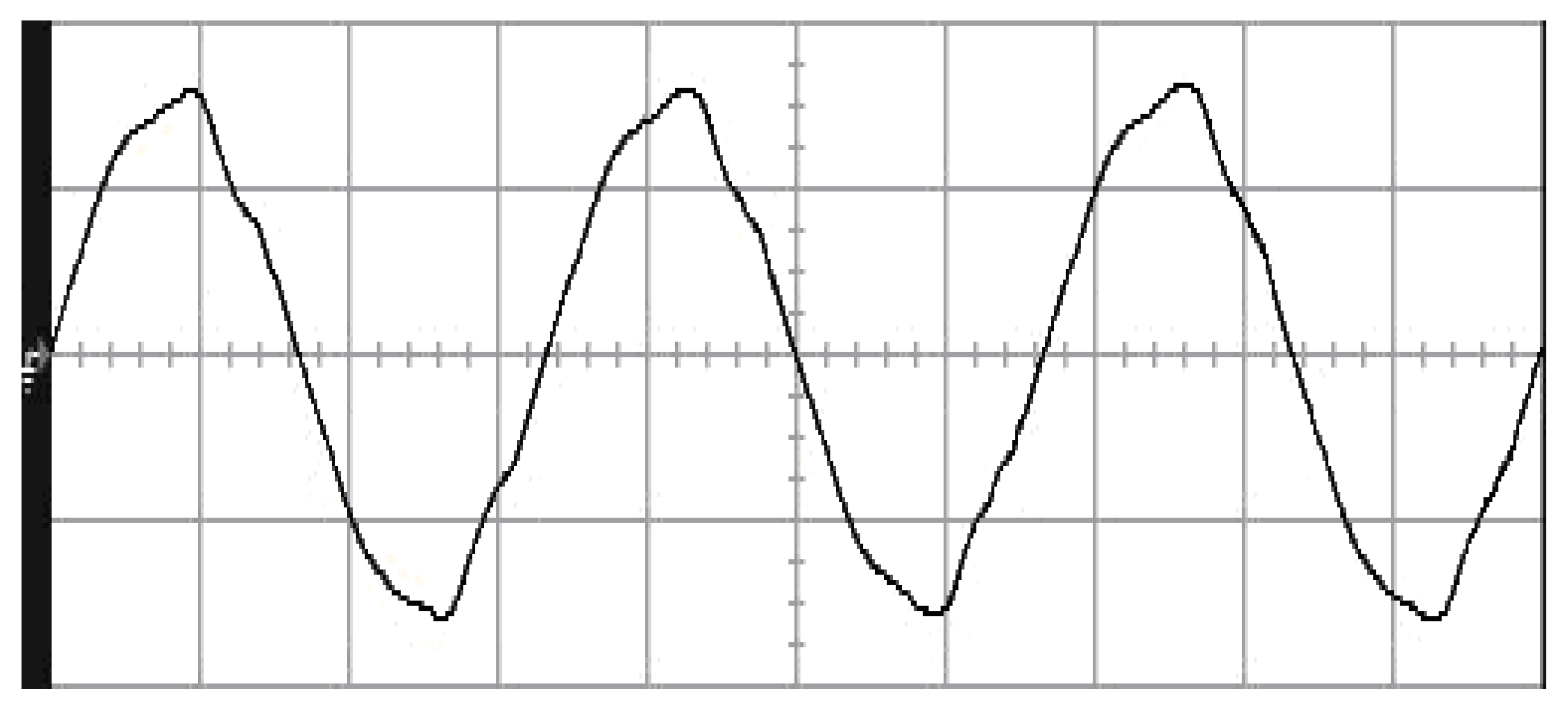
4. Results and Analysis
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Lam, C.S.; Wong, M.C. Analysis, Control, and Design of a Hybrid Grid-Connected Inverter for Renewable Energy Generation with Power Quality Conditioning. IEEE Trans. Power Electron. 2018, 33, 6755–6768. [Google Scholar] [CrossRef]
- Yang, Z.X.; Zeng, J.W.; Zhang, Q.; Zhang, Z.; Winstead, V.; Yu, D.Z. A Composite Power Decoupling Method for a PV Inverter With Optimized Energy Buffer. IEEE Trans. Ind. Appl. 2021, 57, 3877–3887. [Google Scholar] [CrossRef]
- Soares-Ramos, P.P.; Oliveira-Assís, L.D.; Sarrias-Mena, R.; García-Triviño, P.; García-Vázquez, C.A.; Fernández-Ramírez, L.A. Averaged Dynamic Modeling and Control of a Quasi-Z-Source Inverter for Wind Power Applications. IEEE Access 2021, 9, 114348–114358. [Google Scholar] [CrossRef]
- Kumar, M.; Tyagi, B.A. Robust Adaptive Decentralized Inverter Voltage Control Approach for Solar PV and Storage-Based Islanded Microgrid. IEEE Trans. Ind. Appl. 2021, 57, 5356–5371. [Google Scholar] [CrossRef]
- He, Y.; Chung, H.S.; Ho, C.N.; Wu, W.M. Direct Current Tracking Using Boundary Control With Second-Order Switching Surface for Three-Phase Three-Wire Grid-Connected Inverter. IEEE Trans. Power Electron. 2017, 32, 5723–5740. [Google Scholar] [CrossRef]
- Julian, A.L.; Oriti, G.; Ji, C.; Zanchetta, P. Single-Phase Energy Management System Operating in Islanding Mode With Repetitive Control and Active Damping. IEEE Trans. Ind. Appl. 2018, 54, 5163–5172. [Google Scholar] [CrossRef]
- Montanari, G.C. Time behavior of partial discharges and life of type II turn insulation specimens under repetitive impulse and sinusoidal waveforms. IEEE Electr. Insul. Mag. 2017, 33, 17–26. [Google Scholar] [CrossRef]
- Xia, C.Y.; Wang, W.; Chen, G.P.; Wu, X.J.; Zhou, S.J.; Sun, Y.J. Robust Control for the Relay ICPT System Under External Disturbance and Parametric Uncertainty. IEEE Trans. Control. Syst. 2017, 25, 2168–2175. [Google Scholar] [CrossRef]
- Azar, A.T.; Zhu, Q.M. Advances and Applications in Sliding Mode Control Systems; Springer: New York, NY, USA, 2015. [Google Scholar]
- Vaidyanathan, S.; Lien, C.H. Applications of Sliding Mode Control in Science and Engineering; Springer: New York, NY, USA, 2017. [Google Scholar]
- Utkin, V.I. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Contr. 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Tabart, Q.; Vechiu, I.; Etxeberria, A.; Bacha, S. Hybrid Energy Storage System Microgrids Integration for Power Quality Improvement Using Four-Leg Three-Level NPC Inverter and Second-Order Sliding Mode Control. IEEE Trans. Ind. Electron. 2018, 65, 424–435. [Google Scholar] [CrossRef]
- Rezkallah, M.; Sharma, S.K.; Chandra, A.; Singh, B.; Rousse, D.R. Lyapunov Function and Sliding Mode Control Approach for the Solar-PV Grid Interface System. IEEE Trans. Ind. Electron. 2017, 64, 785–795. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wang, J.; Li, H.; Zheng, T.Q.; Lai, J.S.; Li, J.G.; Wang, J.H.; Chen, Q. Dynamic Performance Improving Sliding-Mode Control-Based Feedback Linearization for PV System Under LVRT Condition. IEEE Trans. Power Electron. 2020, 35, 11745–11757. [Google Scholar] [CrossRef]
- Bi, G.D.; Zhang, G.Q.; Wang, G.L.; Wang, Q.W.; Hu, Y.H.; Xu, D.G. Adaptive Iterative Learning Control Based Rotor Position Harmonic Error Suppression Method for Sensorless PMSM Drives. IEEE Trans. Ind. Electron. 2021, 1, (Early Access Article). [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Xue, R.N.; Li, G.J.; Chen, Y.M. Active Damping Adaptive Controller for Grid-Connected Inverter Under Weak Grid. IEEE Access. 2021, 9, 132442–132454. [Google Scholar] [CrossRef]
- Guo, W.F.; Du, H.; Cheong, J.W.; Southwell, B.J.; Dempster, A.G. GNSS-R Wind Speed Retrieval of Sea Surface Based on Particle Swarm Optimization Algorithm. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4202414. [Google Scholar] [CrossRef]
- Song, M.M.; Liu, S.X.; Li, W.Q.; Chen, S.Z.; Li, W.W.; Zhang, K.K.; Yu, D.F.; Liu, L.; Liu, X.Y. A Continuous Space Location Model and a Particle Swarm Optimization-Based Heuristic Algorithm for Maximizing the Allocation of Ocean-Moored Buoys. IEEE Access 2021, 9, 32249–32262. [Google Scholar] [CrossRef]
- Yousaf, S.; Mughees, A.; Khan, M.G.; Amin, A.A.; Adnan, M. A Comparative Analysis of Various Controller Techniques for Optimal Control of Smart Nano-Grid Using GA and PSO Algorithms. IEEE Access 2020, 8, 205696–205711. [Google Scholar] [CrossRef]
- Mercangöz, B.A. Applying Particle Swarm Optimization: New Solutions and Cases for Optimized Portfolios; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Alswaitti, M.; Albughdadi, M.; Isa, A.M. Density-based particle swarm optimization algorithm for data clustering. Expert Syst. Appl. 2018, 91, 170–186. [Google Scholar] [CrossRef]
- Tan, Y.; Xiao, Z.M. Clonal Particle Swarm Optimization and Its Applications. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation (CEC 2007), Singapore, 25–28 September 2007; pp. 2303–2309. [Google Scholar]
- Ma, L.H.; Zhang, Y.; Lu, Z.M.; Li, H. Research of Particle Filter Based on Immune Particle Swarm Optimization. Inf. Technol. J. 2013, 12, 155–161. [Google Scholar] [CrossRef][Green Version]
- Ge, X.C. The Application of Particle Immune Algorithm in Soccer Equipment Training. MATEC Web Conf. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Du, H.; Liu, D.C.; Zhang, M.H. A Hybrid Algorithm Based on Particle Swarm Optimization and Artificial Immune for an Assembly Job Shop Scheduling Problem. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Zhang, Q.R.; Luo, M.; Wang, H.X.; Tan, J.H. A Hyperlipemia Information Analysis System based on immune algorithm. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; pp. 421–424. [Google Scholar]
- Liu, L.P.; Jia, W.S. An Intelligent Algorithm for Solving the Efficient Nash Equilibrium of a Single Leader Multi-Follower Game. Mathematics 2021, 9, 454. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Abrishamifar, A.; Farzi, M. A New Design Procedure for Output LC Filter of Single Phase Inverters. In Proceedings of the 2010 Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 13–14 November 2010; pp. 86–91. [Google Scholar]
- Dahono, P.A.; Purwadi, A.; Qamaruzzaman. An LC filter Design Method for Single-Phase PWM Inverters. In Proceedings of the 1995 Power Electronics and Drive Systems, Singapore, 21–24 February 1995; pp. 571–576. [Google Scholar]
- Kim, H.S.; Sul, S.K. A Novel Filter Design for Output LC Filters of PWM Inverters. J. Power Electron. 2011, 11, 74–81. [Google Scholar] [CrossRef]
- Huynh, A.T.; Ho, A.V.; Chun, T.W. Three-Phase Embedded Modified-Z-Source Three-Level T-Type Inverters. IEEE Access 2020, 8, 130740–130750. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Z.D.; Xu, L.; Li, Y.D. A Generalized Carrier-Overlapped PWM Method for Neutral-Point-Clamped Multilevel Converters. IEEE Trans. Power Electron. 2020, 35, 9095–9106. [Google Scholar] [CrossRef]
- Pratheesh, K.J.; Jagadanand, G.; Ramchand, R. A Generalized-Switch-Matrix-Based Space Vector Modulation Technique Using the Nearest Level Modulation Concept for Neutral-Point-Clamped Multilevel Inverters. IEEE Trans. Ind. Electron. 2018, 65, 4542–4552. [Google Scholar] [CrossRef]
- Ye, Y.M.; Hua, T.K.; Chen, S.J.; Wang, X.L. Neutral-Point-Clamped Five-Level Inverter with Self-Balanced Switched Capacitor. IEEE Trans. Ind. Electron. 2022, 69, 2202–2215. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| ) | 200 V |
| ) | 110 Vrms |
| Frequency of sine output voltage | 60 Hz |
| 0.25 mH | |
| 20 μF | |
| 12 Ω | |
| Switching frequency | 30 kHz |
| Proposed Controller | ||
| Experiments | Step changing in load | Nonlinear load |
| Voltage sag | %THD | |
| 8.73 Vrms | 0.61% | |
| Conventional RSMC | ||
| Experiments | Step changing in load | Nonlinear load |
| Voltage sag | %THD | |
| 37.12 Vrms | 14.12% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, E.-C.; Cheng, H.-L.; Chang, C.-H.; Wu, R.-C.; Cheng, C.-A.; Xiao, Z.-K.; Lu, W.-J.; Wei, Z.-Y. Robust Optimal Control Design for Performance Enhancement of PWM Voltage Source Inverter. Micromachines 2022, 13, 435. https://doi.org/10.3390/mi13030435
Chang E-C, Cheng H-L, Chang C-H, Wu R-C, Cheng C-A, Xiao Z-K, Lu W-J, Wei Z-Y. Robust Optimal Control Design for Performance Enhancement of PWM Voltage Source Inverter. Micromachines. 2022; 13(3):435. https://doi.org/10.3390/mi13030435
Chicago/Turabian StyleChang, En-Chih, Hung-Liang Cheng, Chien-Hsuan Chang, Rong-Ching Wu, Chun-An Cheng, Zheng-Kai Xiao, Wen-Jie Lu, and Zhi-Yu Wei. 2022. "Robust Optimal Control Design for Performance Enhancement of PWM Voltage Source Inverter" Micromachines 13, no. 3: 435. https://doi.org/10.3390/mi13030435
APA StyleChang, E.-C., Cheng, H.-L., Chang, C.-H., Wu, R.-C., Cheng, C.-A., Xiao, Z.-K., Lu, W.-J., & Wei, Z.-Y. (2022). Robust Optimal Control Design for Performance Enhancement of PWM Voltage Source Inverter. Micromachines, 13(3), 435. https://doi.org/10.3390/mi13030435










