Assessment of Blood Biophysical Properties Using Pressure Sensing with Micropump and Microfluidic Comparator
Abstract
:1. Introduction
2. Materials and Methods
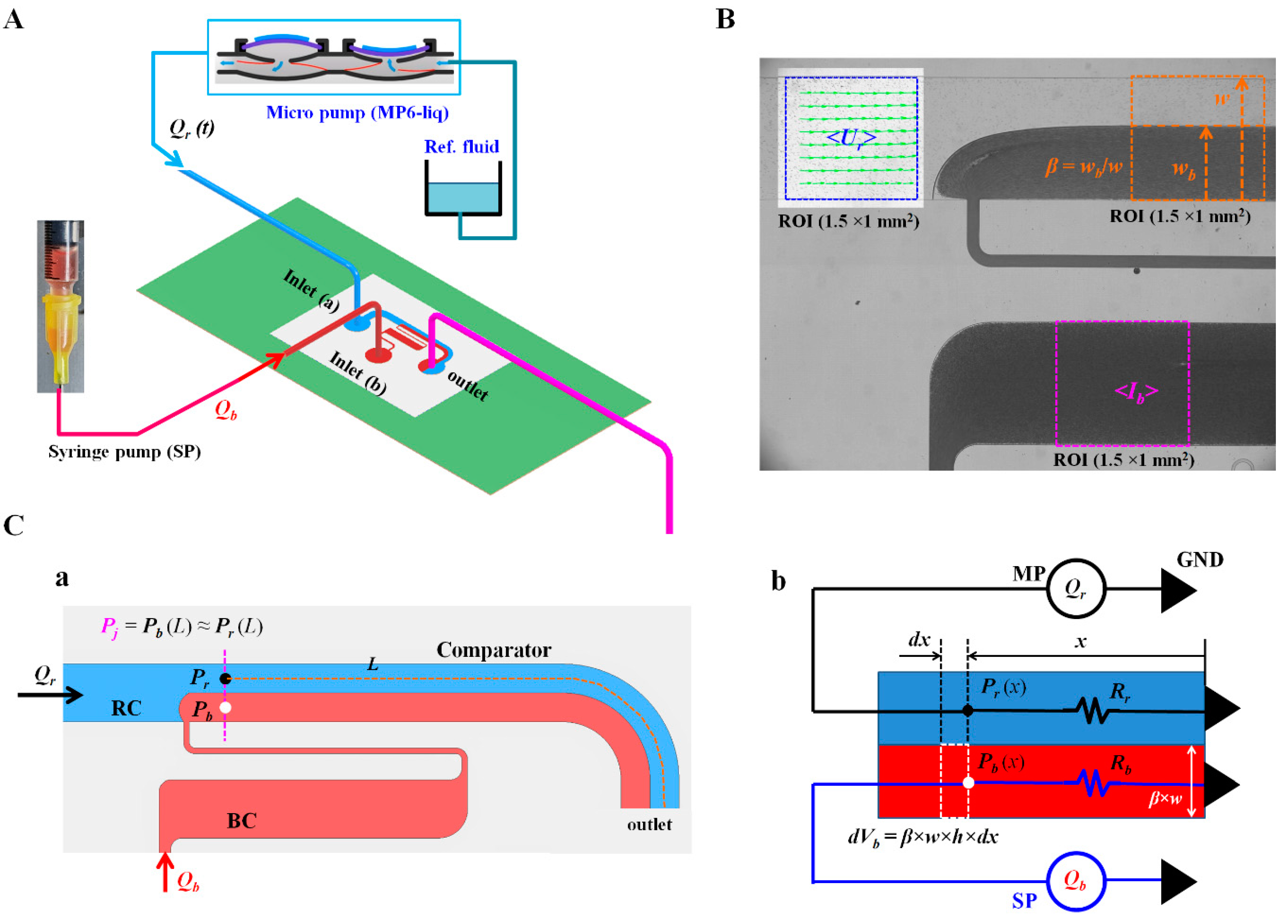
2.1. Design and Fabrication of Microfluidic Device, and Experimental Procedure
2.2. Image Acquisition and Processing for Quantifying Three Parameters
2.3. Quantification of Blood Biophysical Properties
2.4. Blood Sample Preparation
3. Results and Discussion
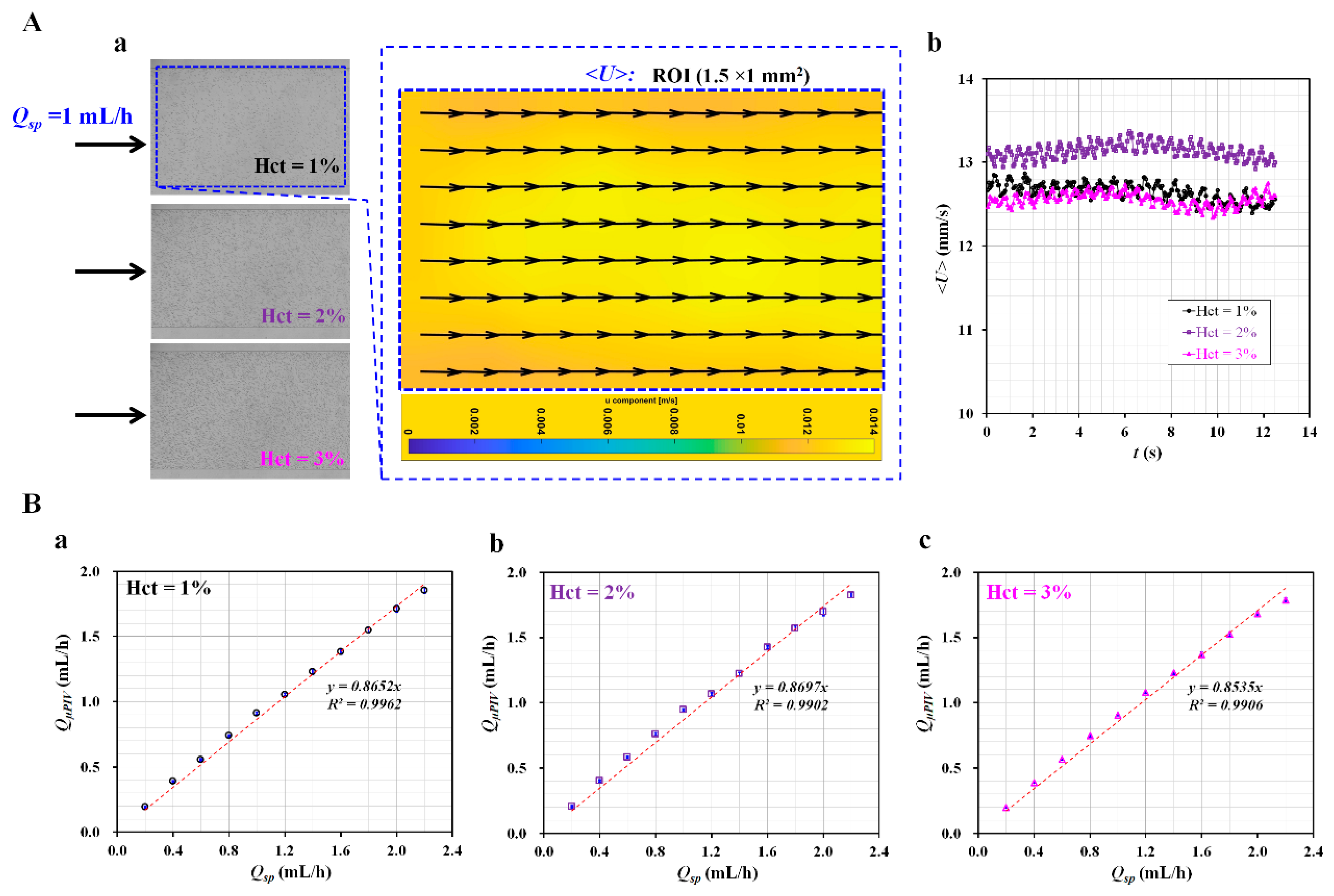
3.1. Validation of Flow Rate of Reference Fluid Using Micro-PIV
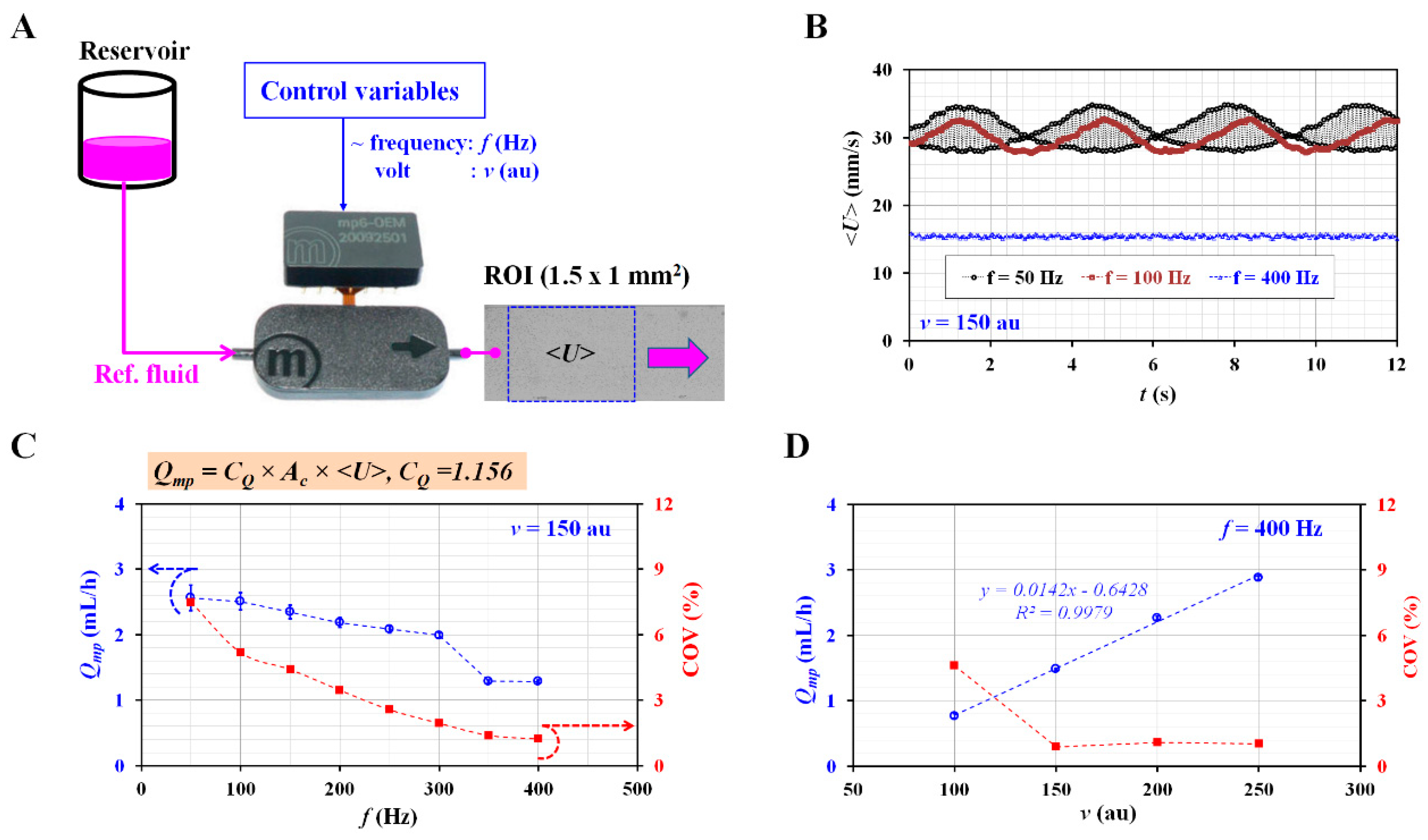
3.2. Selection of Control Variables for Consistent Flow Rate with Micropump
3.3. Quantitative Comparison between the Present Method and Previous Method for Measuring Biophysical Properties of Blood Sample
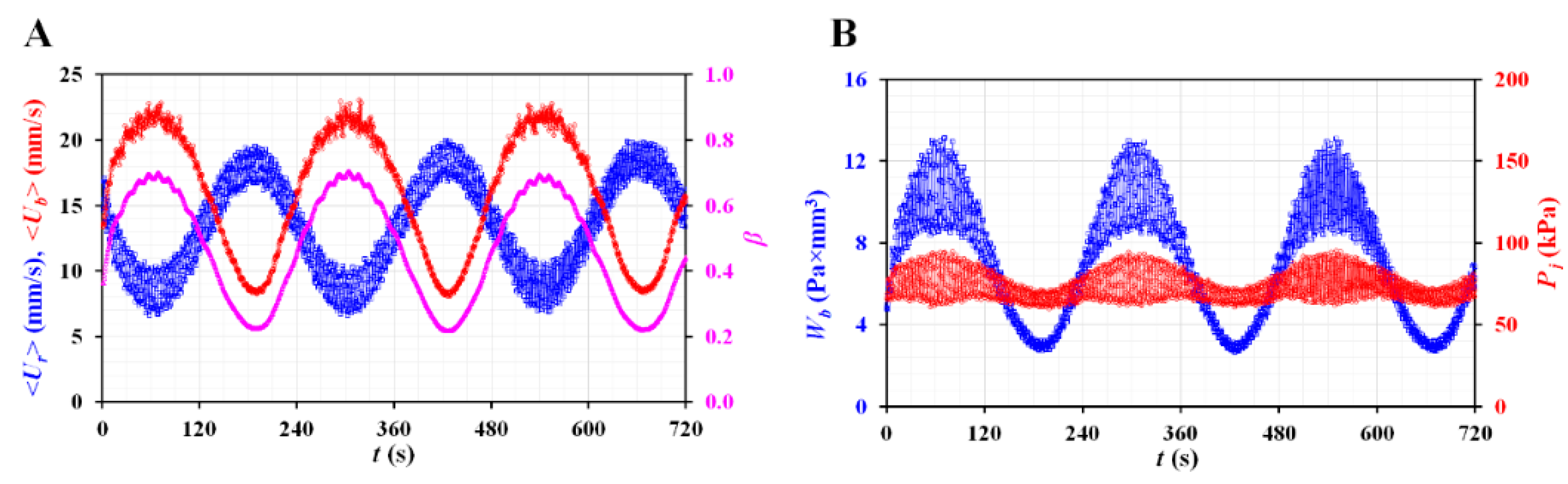
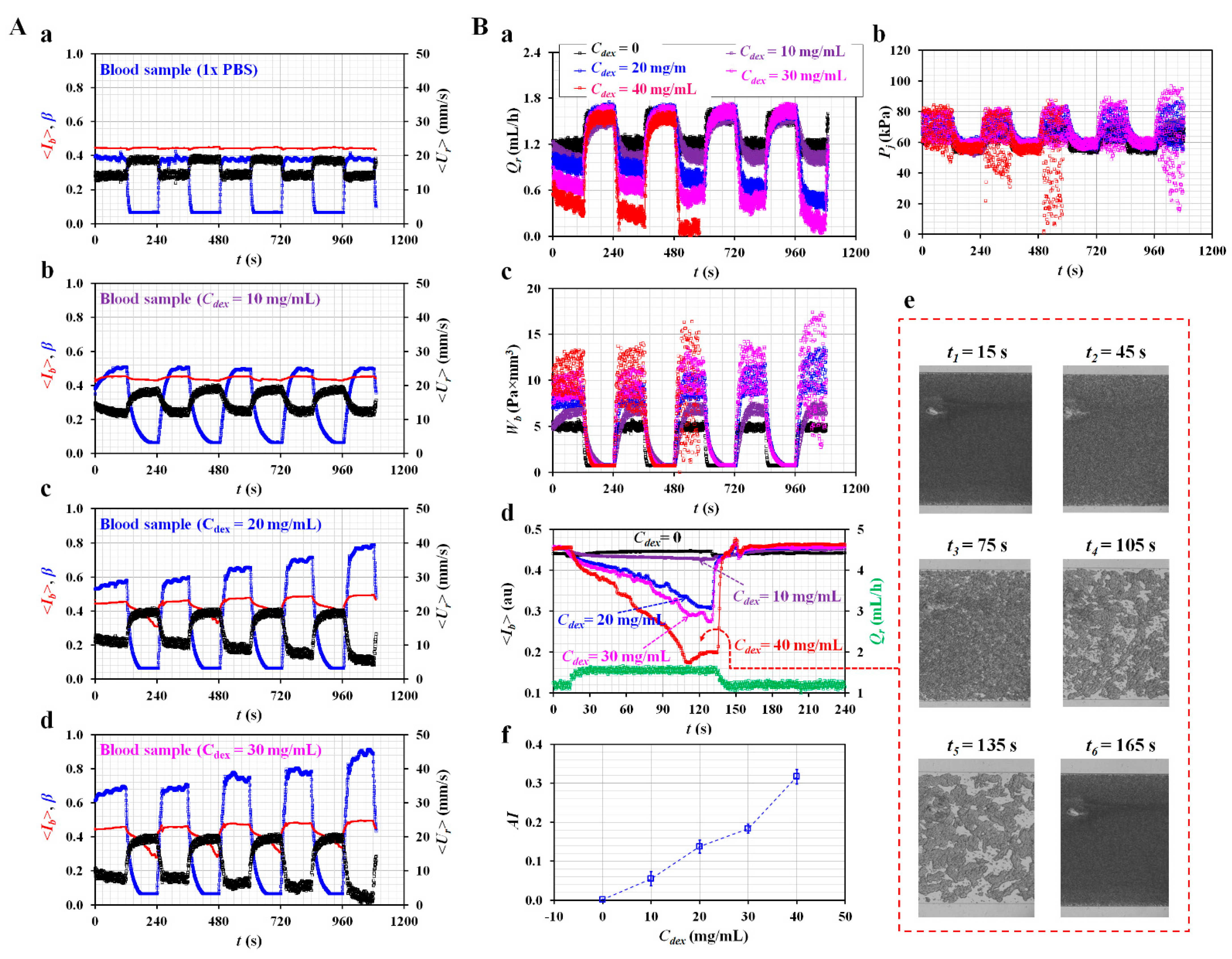
3.4. Quantitative Evaluations of Biophysical Properties of Blood Sample
4. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Experimental Estimation of Correction Factor (CR)
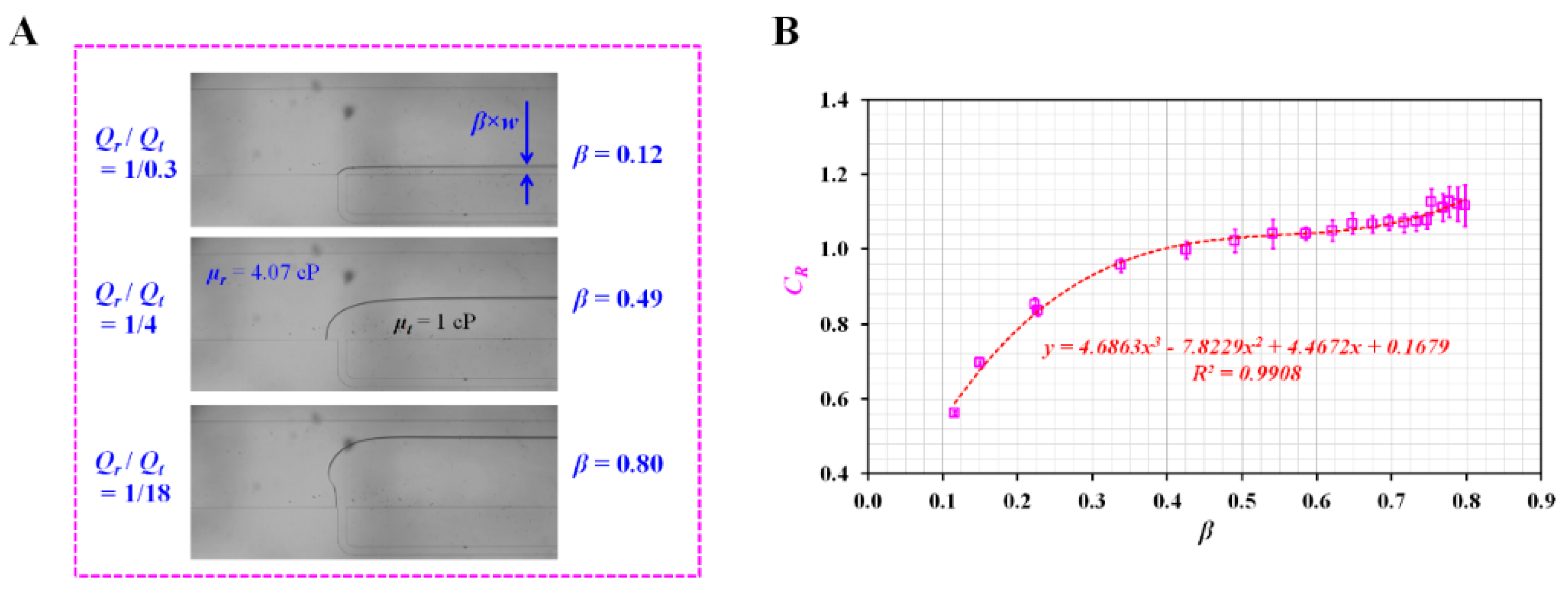
Appendix A.2. Validation of Red Blood Cell (RBC) Sedimentation in Reference Fluid
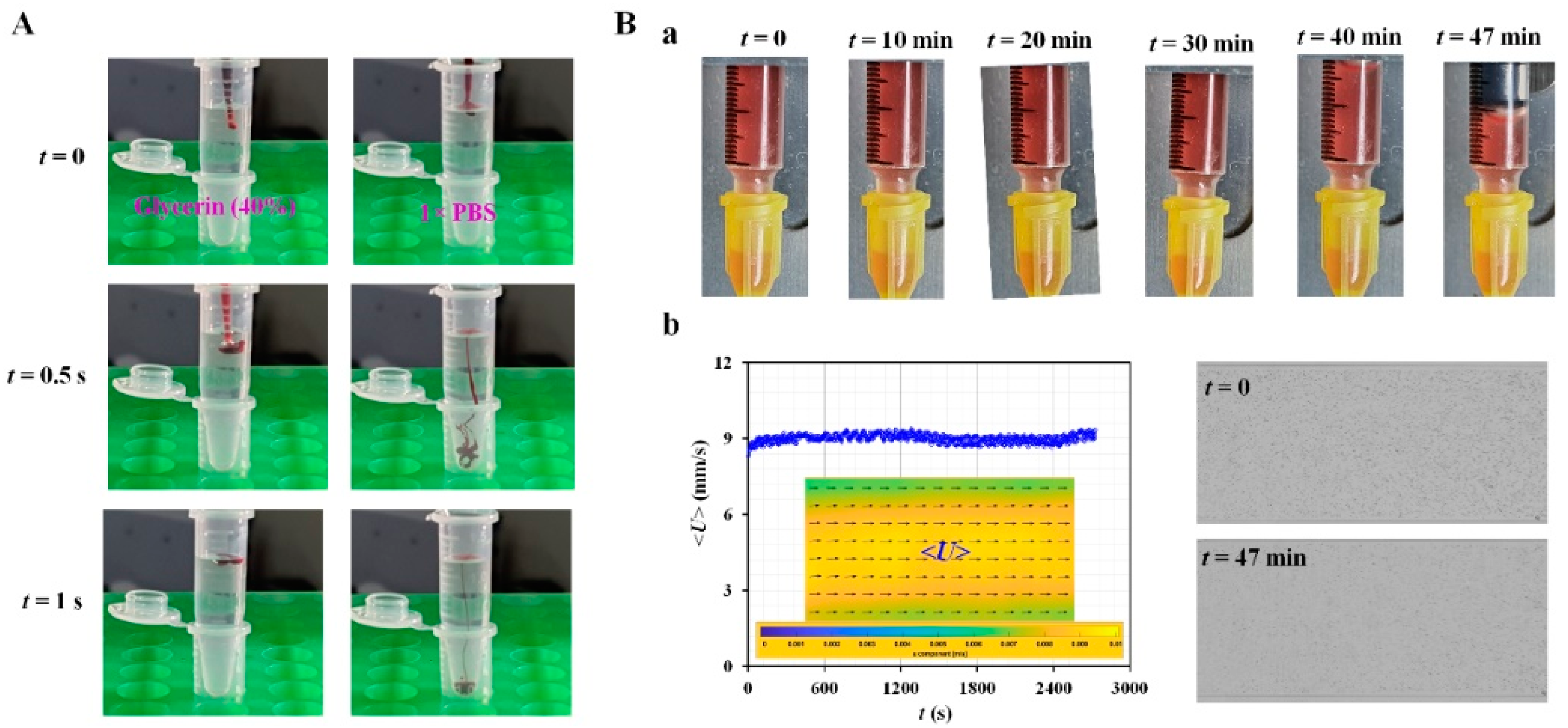
Appendix A.3. Quantification of Tree Blood Properties Obtained by Analyzing Blood Flows as Controlled by Syringe Pump
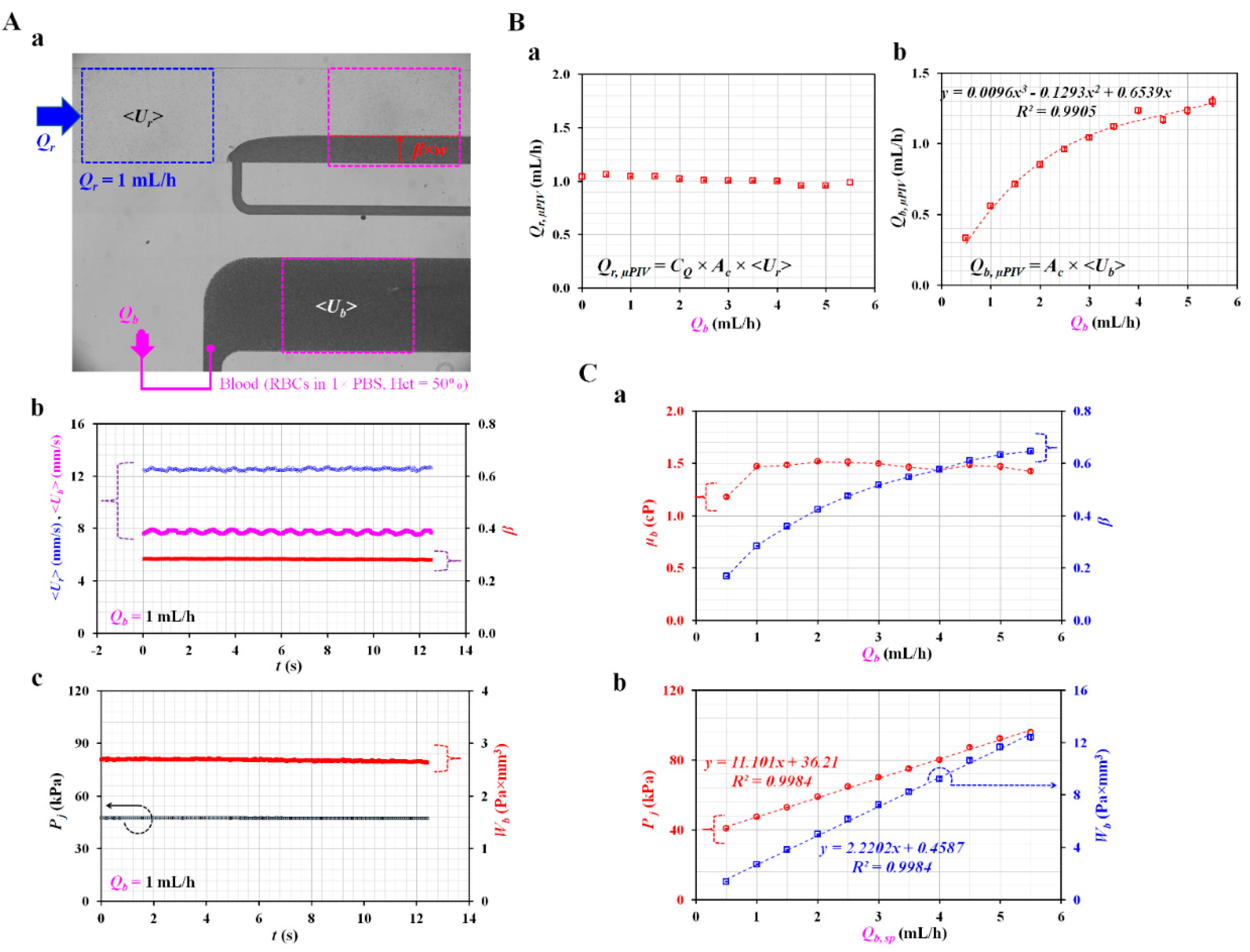
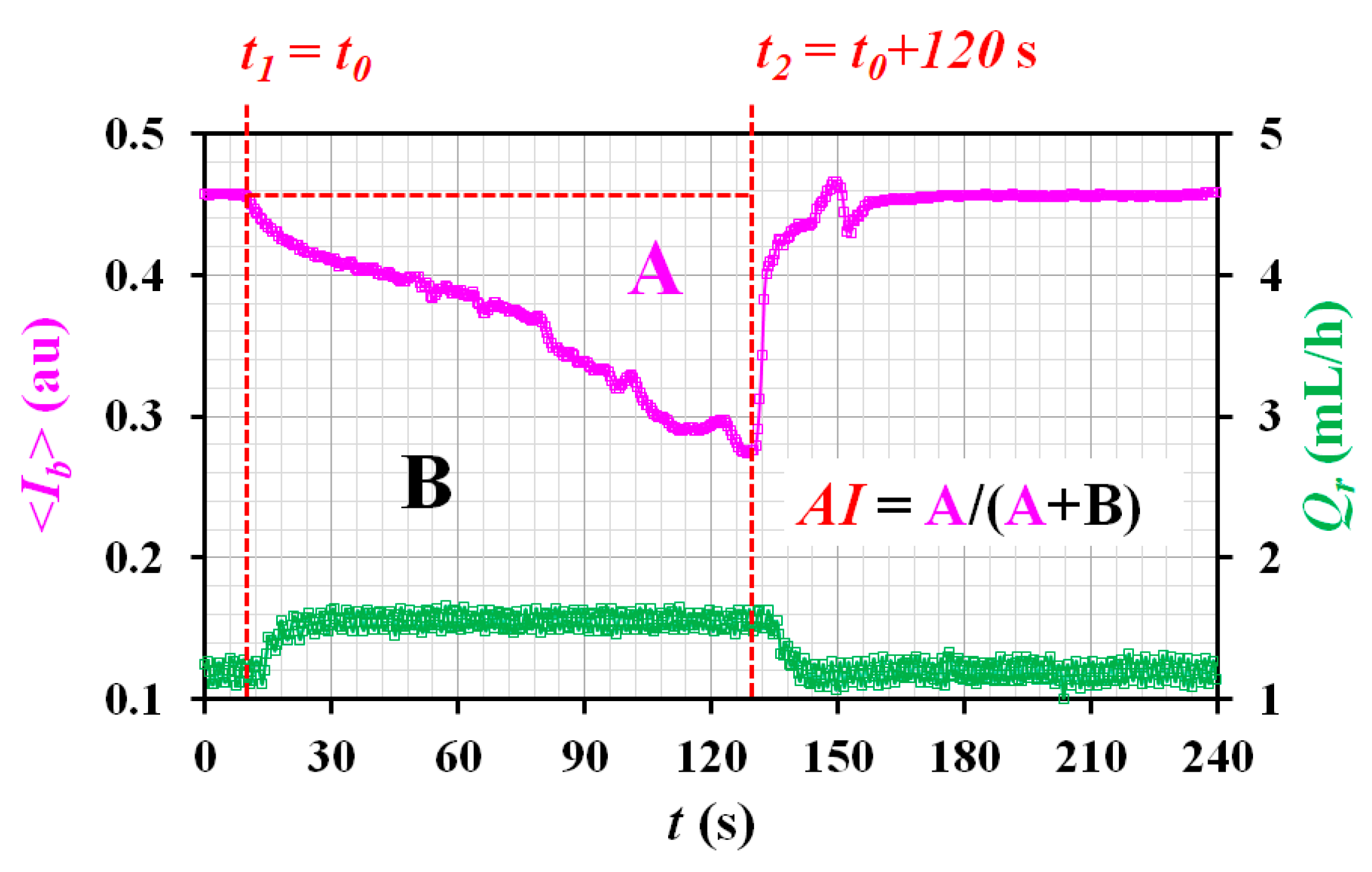
Appendix A.4. Quantification of RBC Aggregation Index (AI)
References
- Trejo-Soto, C.; Lázaro, G.R.; Pagonabarraga, I.; Hernández-Machado, A. Microfluidics approach to the mechanical properties of red blood cell membrane and their effect on blood rheology. Membranes 2022, 12, 217. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, K.; Yeom, E. Microfluidic method for measuring viscosity using images from smartphone. Opt. Lasers Eng. 2018, 104, 237–243. [Google Scholar] [CrossRef]
- Oh, S.; Kim, B.; Lee, J.K.; Choi, S. 3D-printed capillary circuits for rapid, low-cost, portable analysis of blood viscosity. Sens. Actuator B-Chem. 2018, 259, 106–113. [Google Scholar] [CrossRef]
- Khnouf, R.; Karasneh, D.; Abdulhay, E.; Abdelhay, A.; Sheng, W.; Fan, Z.H. Microfluidics-based device for the measurement of blood viscosity and its modeling based on shear rate, temperature, and heparin concentration. Biomed. Microdevices 2019, 21, 80. [Google Scholar] [CrossRef]
- Kang, H.; Jang, I.; Song, S.; Bae, S.-C. Development of a paper-based viscometer for blood plasma using colorimetric analysis. Anal. Chem. 2019, 91, 4868–4875. [Google Scholar] [CrossRef]
- Kang, Y.J. Blood viscoelasticity measurement using interface variations in coflowing streams under pulsatile blood flows. Micromachines 2020, 11, 245. [Google Scholar] [CrossRef] [Green Version]
- Urbanska, M.; Muñoz, H.E.; Bagnall, J.S.; Otto, O.; Manalis, S.R.; Carlo, D.D.; Guck, J. A comparison of microfluidic methods for high-throughput cell deformability measurements. Nat. Methods 2020, 17, 587–593. [Google Scholar] [CrossRef]
- Kang, Y.J. Simultaneous measurement method of erythrocyte sedimentation rate and erythrocyte deformability in resource-limited settings. Physiol. Meas. 2020, 41, 025009. [Google Scholar] [CrossRef]
- Huisjes, R.; Makhro, A.; Llaudet-Planas, E.; Hertz, L.; Petkova-Kirova, P.; Verhagen, L.P.; Pignatelli, S.; Rab, M.A.; Schiffelers, R.M.; Seiler, E.; et al. Density, heterogeneity and deformability of red cells as markers of clinical severity in hereditary spherocytosis. Haematologica 2020, 105, 338–347. [Google Scholar] [CrossRef]
- Kim, B.J.; Lee, Y.S.; Zhbanov, A.; Yang, S. A physiometer for simultaneous measurement of whole blood viscosity and its determinants: Hematocrit and red blood cell deformability. Analyst 2019, 144, 3144–3157. [Google Scholar] [CrossRef]
- Huisjes, R.; Bogdanova, A.; Van Solinge, W.W.; Schiffelers, R.M.; Kaestner, L.; Van Wijk, R. Squeezing for life—properties of red blood cell deformability. Front. Physiol. 2018, 9, 656. [Google Scholar] [CrossRef]
- Boas, L.V.; Faustino, V.; Lima, R.; Miranda, J.M.; Minas, G.; Fernandes, C.S.V.; Catarino, S.O. Assessment of the deformability and velocity of healthy and artificially impaired red blood cells in narrow polydimethylsiloxane (PDMS) microchannels. Micromachines 2018, 9, 384. [Google Scholar] [CrossRef] [Green Version]
- Pasias, D.; Passos, A.; Constantinides, G.; Balabani, S.; Kaliviotis, E. Surface tension driven flow of blood in a rectangular microfluidic channel: Effect of erythrocyte aggregation. Phys. Fluids 2020, 32, 071903. [Google Scholar] [CrossRef]
- Namgung, B.; Lee, T.; Tan, J.K.S.; Poh, D.K.H.; Park, S.; Chng, K.Z.; Agrawal, R.; Park, S.-Y.; Leo, H.L.; Kim, S. Vibration motor-integrated low-cost, miniaturized system for rapid quantification of red blood cell aggregation. Lab Chip 2020, 20, 3930–3937. [Google Scholar] [CrossRef] [PubMed]
- Ermolinskiy, P.; Lugovtsov, A.; Yaya, F.; Lee, K.; Kaestner, L.; Wagner, C.; Priezzhev, A. Effect of red blood cell aging in vivo on their aggregation properties in vitro: Measurements with laser tweezers. App. Sci. 2020, 10, 7581. [Google Scholar] [CrossRef]
- Wen, J.; Wan, N.; Bao, H.; Li, J. Quantitative measurement and evaluation of red blood cell aggregation in normal blood based on a modified hanai equation. Sensors 2019, 19, s19051095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, H.; Song, J.M.; Yeom, E. Micro-vibrational erythrocyte sedimentation rate (ESR) for sensitive measurement of erythrocyte aggregation. J. Vis. 2021, 24, 749–760. [Google Scholar] [CrossRef]
- Forchelet, D.; Béguin, S.; Sajic, T.; Bararpour, N.; Pataky, Z.; Frias, M.; Grabherr, S.; Augsburger, M.; Liu, Y.; Charnley, M.; et al. Separation of blood microsamples by exploiting sedimentation at the microscale. Sci. Rep. 2018, 8, 14101. [Google Scholar] [CrossRef] [PubMed]
- Mehri, R.; Mavriplis, C.; Fenech, M. Red blood cell aggregates and their effect on non-Newtonian blood viscosity at low hematocrit in a two-fluid low shear rate microfluidic system. PLoS ONE 2018, 13, e0199911. [Google Scholar] [CrossRef]
- Lee, H.; Na, W.; Lee, S.B.; Ahn, C.W.; Moon, J.S.; Won, K.C.; Shin, S. Potential Diagnostic Hemorheological Indexes for Chronic Kidney Disease in Patients With Type 2 Diabetes. Front. Physiol. 2019, 10, 1062. [Google Scholar] [CrossRef] [PubMed]
- Rab, M.A.E.; Van Oirschot, B.A.; Bos, J.; Merkx, T.H.; van Wesel, A.C.W.; Abdulmalik, O.; Safo, M.K.; Versluijs, B.A.; Houwing, M.E.; Cnossen, M.H.; et al. Rapid and reproducible characterization of sickling during automated deoxygenation in sickle cell disease patients. Am. J. Hematol. 2019, 94, 575–584. [Google Scholar] [CrossRef] [PubMed]
- Nader, E.; Skinner, S.; Romana, M.; Fort, R.; Lemonne, N.; Guillot, N.; Gauthier, A.; Antoine-Jonville, S.; Renoux, C.; Hardy-Dessources, M.-D.; et al. Blood rheology: Key parameters, impact on blood flow, role in sickle cell disease and effects of exercise. Front. Physiol. 2019, 10, 1329. [Google Scholar] [CrossRef] [Green Version]
- Isiksacan, Z.; Serhatlioglu, M.; Elbuken, C. In vitro analysis of multiple blood flow determinants using red blood cell dynamics under oscillatory flow. Anayst 2020, 148, 5996–6005. [Google Scholar] [CrossRef] [PubMed]
- Giudice, F.D. A review of microfluidic devices for rheological characterisation. Micromachines 2022, 13, 167. [Google Scholar] [CrossRef]
- Christov, I.C.; Cognet, V.; Shidhore, T.C.; Stone, H.A. Flow rate pressure drop relation for deformable shallow microuidic channels. J. Fluid Mech. 2018, 841, 267–286. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.J.; Lee, S.Y.; Jee, S.; Atajanov, A.; Yang, S. Micro-viscometer for measuring shear-varying blood viscosity over a wide-ranging shear rate. Sensors 2017, 17, 1442. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Microfluidic-based measurement of RBC aggregation and the ESR using a driving syringe system. Anal. Methods 2018, 10, 1805–1816. [Google Scholar] [CrossRef]
- Kang, Y.J. Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System. Micromachines 2020, 11, 215. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Microfluidic-based effective monitoring of bloods by measuring RBC aggregation and blood viscosity under stepwise varying shear rates. Korea-Aust. Rheol. J. 2020, 32, 15–27. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Quantitative monitoring of dynamic blood flows using coflowing laminar streams in a sensorless approach. App. Sci. 2021, 11, 7260. [Google Scholar] [CrossRef]
- Norouzi, N.; Bhakta, H.C.; Grover, W.H. Sorting cells by their density. PLoS ONE 2017, 7, e0180520. [Google Scholar] [CrossRef] [Green Version]
- McDonald, J.C.; Duffy, D.C.; Anderson, J.R.; Chiu, D.T.; Wu, H.; Schueller, O.J.A.; Whitesides, G.M. Fabrication of microfluidic systems in poly (dimethylsioxane). Electrophoresis 2000, 21, 27–40. [Google Scholar] [CrossRef]
- Kang, Y.J. Continuous and simultaneous measurement of the biophysical properties of blood in a microfluidic environment. Analyst 2016, 141, 6583–6597. [Google Scholar] [CrossRef]
- Kang, Y.J.; Ryu, J.; Lee, S.-J. Label-free viscosity measurement of complex fluids using reversal flow switching manipulation in a microfluidic channel. Biomicrofluidics 2013, 7, 044106. [Google Scholar] [CrossRef] [Green Version]
- Cheng, N.-S. Formula for the viscosity of a glycerol-water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Bourdon, C.J.; Olsen, M.G.; Gorby, A.D. The depth of correction in miciro-PIV for high numerical aperaure and immersion objectives. J. Fluid Eng. T. ASME 2006, 128, 883–886. [Google Scholar] [CrossRef]
- Passos, A.; Sherwood, J.M.; Kaliviotis, E.; Agrawal, R.; Pavesio, C.; Balabani, S. The effect of deformability on the microscale flow behavior of red blood cell suspensions. Biomicrofluidics 2019, 31, 091903. [Google Scholar] [CrossRef]
- Dincau, B.; Dressaire, E.; Sauret, A. Pulsatile flow in microfluidic systems. Small 2019, 16, 1904032. [Google Scholar] [CrossRef]
- Munas, F.R.; Melroy, G.; Abeynayake, C.B.; Chathuranga, H.L.; Amarasinghe, R.; Kumarage, P.; Dau, V.T.; Dao, D.V. Development of PZT actuated valveless micropump. Sensors 2018, 18, 1302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Q.; Yin, Y.; Sun, W.; Fu, J. Advances in valveless piezoelectric pumps. Appl. Sci. 2021, 11, 7061. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J.; Yan, J.; Zhu, T.; Guo, S.; Li, S.; Li, T. Standing air bubble-based micro-hydraulic capacitors for flow stabilization in syringe pump-driven systems. Micromachines 2020, 11, 396. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.H.; Kim, I.C.; Kang, Y.J.; Ryu, J.; Lee, S.J. Effect of phase shift on optimal operation of serial-connected valveless micropumps. Sens. Actuator A-Phys. 2014, 209, 133–139. [Google Scholar] [CrossRef]
- Kang, Y.J.; Yang, S. Integrated microfluidic viscometer equipped with fluid temperature controller for measurement of viscosity in complex fluids. Microfluid. Nanofluid. 2013, 14, 657–668. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Caswell, B.; Popel, A.S.; Karniadakis, G.E. Blood Flow and Cell-Free Layer in Microvessels. Microcirculation 2010, 17, 615–628. [Google Scholar] [CrossRef] [Green Version]
- Bauersachs, R.M.; Wenby, R.B.; Meiselman, H.J. Determination of specific red blood cell aggregation indices via an automated system. Clin. Hemorheol. Microcirc. 1989, 9, 1–25. [Google Scholar] [CrossRef]
- Sherwood, J.M.; Dusting, J.; Kaliviotis, E.; Balabani, S. The effect of red blood cell aggregation on velocity and cell-depleted layer characteristics of blood in a bifurcating microchannel. Biomicrofluidics 2012, 6, 024119. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Blood rheometer based on microflow manipulation of continuous blood flows using push-and-back mechanism. Anal. Methods 2021, 13, 4871–4883. [Google Scholar] [CrossRef]
- Buchanan, B.C.; Yoon, J.-Y. Microscopic imaging methods for organ-on-a-chip platforms. Micromachines 2022, 13, 328. [Google Scholar] [CrossRef]
- Solomon, D.E.; Abdel-Raziq, A.; Vanapalli, S.A. A stress-controlled microfluidic shear viscometer based on smartphone imaging. Rheol. Acta 2016, 55, 727–738. [Google Scholar] [CrossRef]
- Yang, K.; Wu, J.; Peretz-Soroka, H.; Zhu, L.; Sang, Y.; Hipolito, J.; Zhang, M.; Santos, S.; Hillier, C.; de Faria, R.L.; et al. Mkit: A Cell Migration Assay Based on Microfluidic Device and Smartphone. Biosens. Bioelectron. 2018, 99, 259–267. [Google Scholar] [CrossRef] [Green Version]
- Hassan, S.-u.; Tariq, A.; Noreen, Z.; Donia, A.; Zaidi, S.Z.J.; Bokhari, H.; Zhang, X. Capillary-driven flow microfluidics combined with smartphone detection: An emerging tool for point-of-care diagnostics. Diagnostics 2020, 10, 509. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Chai, H.H.; Yu, L.; Fang, C. Smartphone supported backlight illumination and image acquisition for microfluidic-based point-of-care testing. Biomed. Opt. Express 2018, 9, 4604. [Google Scholar] [CrossRef] [PubMed]
- Narayanamurthy, V.; Jeroish, Z.E.; Bhuvaneshwari, K.S.; Bayat, P.; Premkumar, R.; Samsuri, F.; Yusoff, M.M. Advances in passively driven microfluidics and labon-chip devices: A comprehensive literature review and patent analysis. RSC Adv. 2020, 10, 11652–11680. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.J. Assessment of Blood Biophysical Properties Using Pressure Sensing with Micropump and Microfluidic Comparator. Micromachines 2022, 13, 438. https://doi.org/10.3390/mi13030438
Kang YJ. Assessment of Blood Biophysical Properties Using Pressure Sensing with Micropump and Microfluidic Comparator. Micromachines. 2022; 13(3):438. https://doi.org/10.3390/mi13030438
Chicago/Turabian StyleKang, Yang Jun. 2022. "Assessment of Blood Biophysical Properties Using Pressure Sensing with Micropump and Microfluidic Comparator" Micromachines 13, no. 3: 438. https://doi.org/10.3390/mi13030438
APA StyleKang, Y. J. (2022). Assessment of Blood Biophysical Properties Using Pressure Sensing with Micropump and Microfluidic Comparator. Micromachines, 13(3), 438. https://doi.org/10.3390/mi13030438





