Electrocapillary Actuation of Liquid Metal in Microchannels
Abstract
:1. Introduction
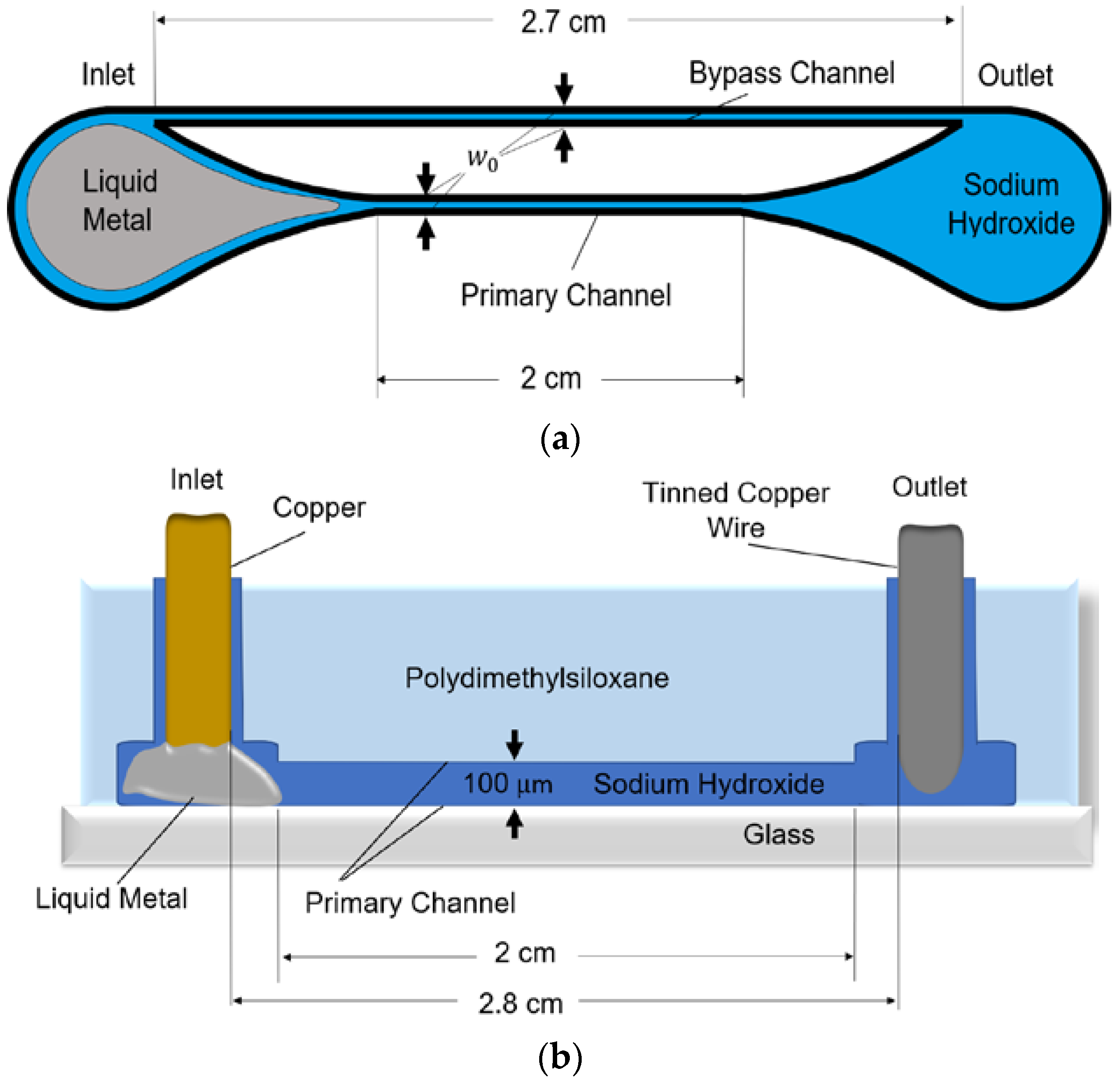
2. Materials and Methods
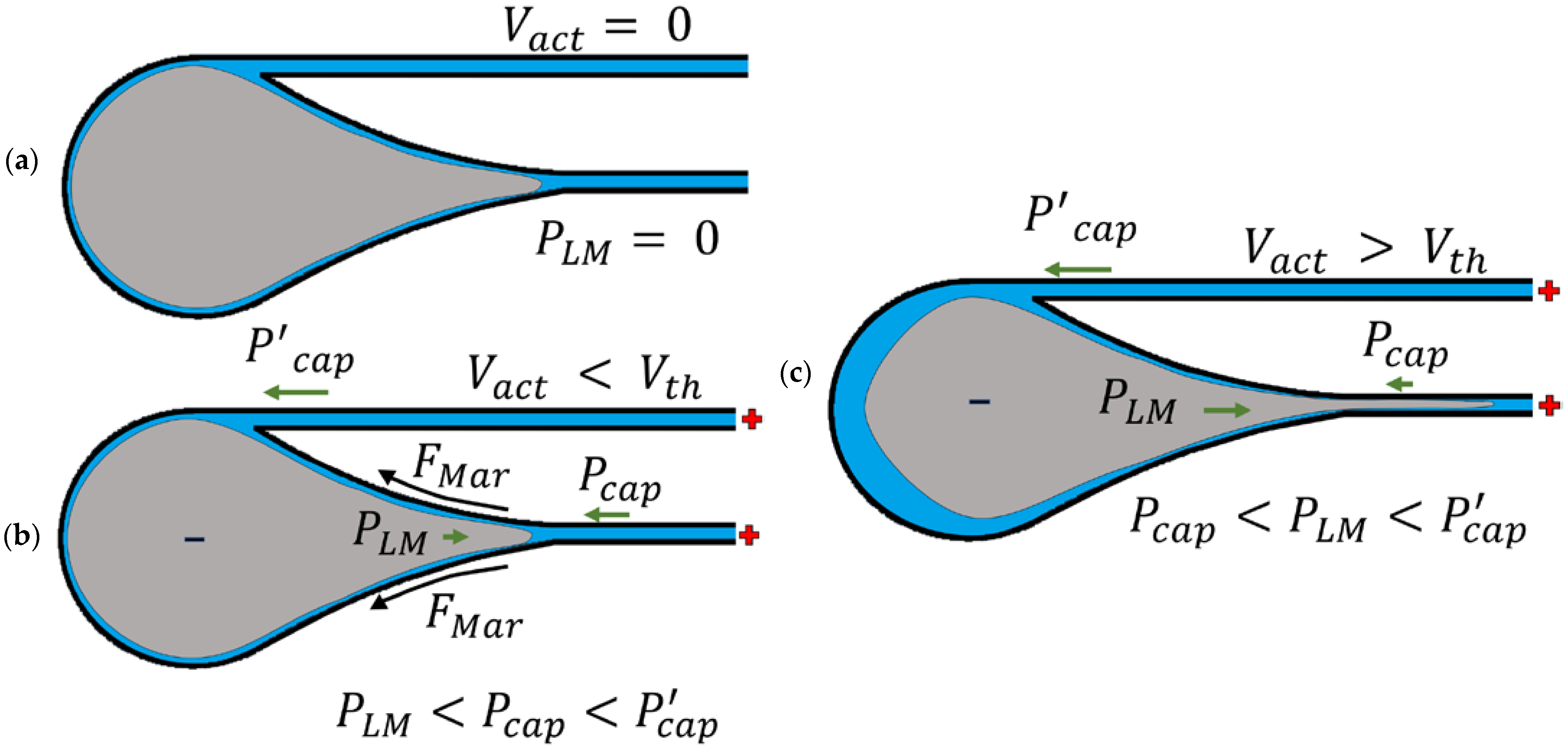
3. Concept
4. Results and Discussion
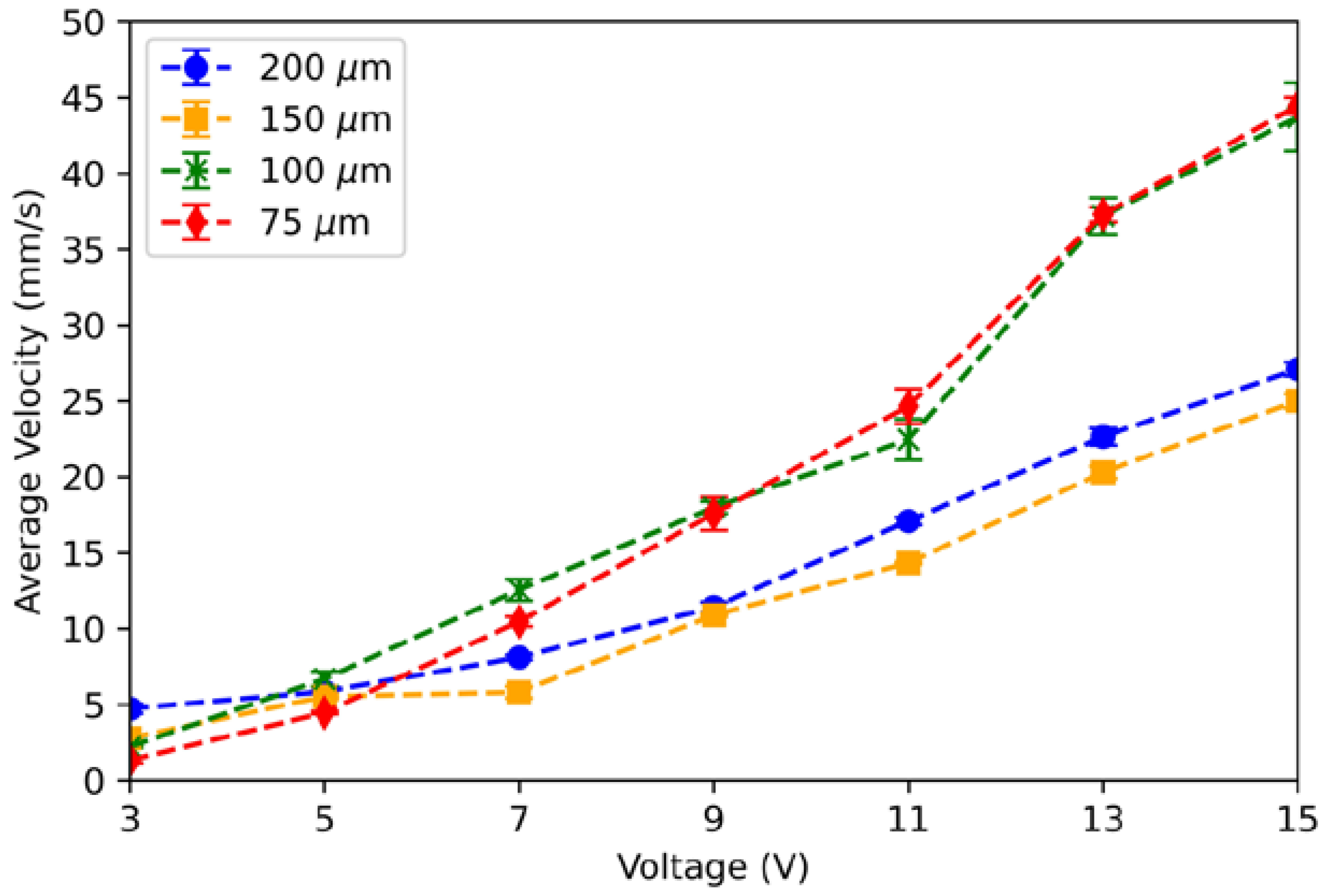
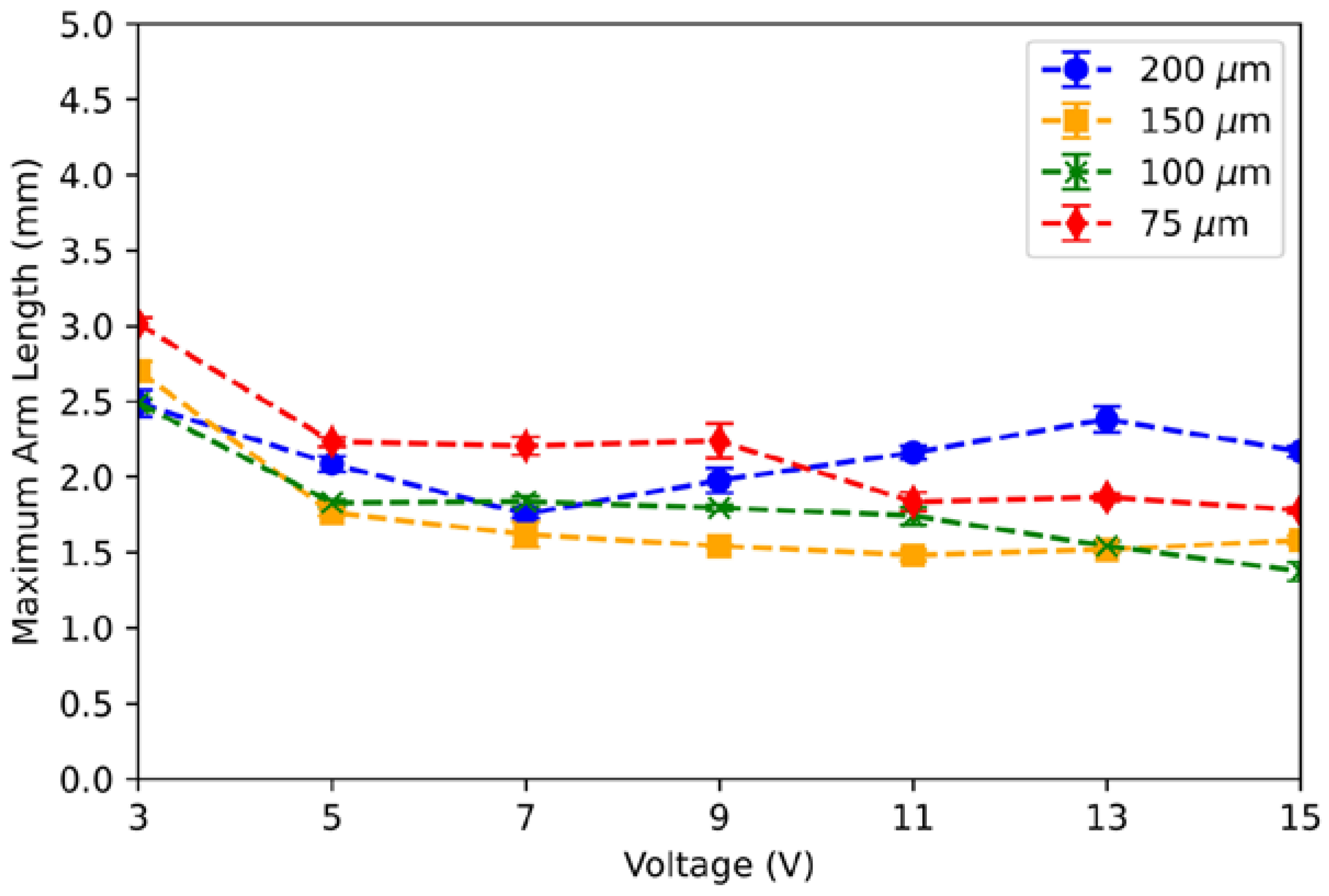
4.1. Elongation of Liquid Metal
4.2. Occupation Ratio
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khoshmanesh, K.; Tang, S.-Y.; Zhu, J.Y.; Schaefer, S.; Mitchell, A.; Kalantar-zadeh, K.; Dickey, M.D. Liquid metal enabled microfluidics. Lab Chip 2017, 17, 974–993. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sheng, L.; He, Z.-Z. Liquid Metal Soft Machines, 1st ed.; Springer: Singapore, 2019. [Google Scholar]
- Park, S.; Yoon, H.-J. New approach for large-area thermoelectric junctions with a liquid eutectic gallium-indium electrode. Nano Lett. 2018, 18, 7715–7718. [Google Scholar] [CrossRef] [PubMed]
- Alqurashi, K.Y.; Kelly, J.R.; Wang, Z.; Crean, C.; Mittra, R.; Khalily, M.; Gao, Y. Liquid metal bandwidth-reconfigurable antenna. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 218–222. [Google Scholar] [CrossRef]
- Gough, R.C.; Dang, J.H.; Morishita, A.M.; Ohta, A.T.; Shiroma, W.A. Frequency-tunable slot antenna using continuous electrowetting of liquid metal. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS 2014), Tampa, FL, USA, 1–6 June 2014. [Google Scholar]
- Wang, M.; Trlica, C.; Khan, M.R.; Dickey, M.D.; Adams, J.J. A reconfigurable liquid metal antenna driven by electrochemically controlled capillarity. J. Appl. Phys. 2015, 117, 194901. [Google Scholar] [CrossRef]
- Peng, K.; Yao, J.; Cho, S.; Cho, Y.; Kim, H.S.; Park, J. Liquid metal embedded real time microfluidic flow pressure monitoring sensor. Sens. Actuators A 2020, 305, 111909. [Google Scholar] [CrossRef]
- Varga, M.; Ladd, C.; Ma, S.; Holbery, J.; Tröster, G. On-skin liquid metal inertial sensor. Lab Chip 2017, 17, 3272–3278. [Google Scholar] [CrossRef]
- Dacuycuy, S.J.; Shiroma, W.A.; Ohta, A.T. Two-dimensional actuation of liquid-metal droplets for hot-spot cooling. In Proceedings of the IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (iTherm), San Diego, CA, USA, 1–4 June 2021. [Google Scholar]
- Yang, T.; Kwon, B.; Weisensee, P.B.; Kang, J.G.; Li, X.; Braun, P.; Miljkovic, N.; King, W.P. Millimeter-scale liquid metal droplet thermal switch. Appl. Phys. Lett. 2018, 112, 063505. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Tang, S.-Y.; Khoshmanesh, K.; Ghorbani, K. An integrated liquid cooling system based on Galinstan liquid metal droplets. ACS Appl. Mater. Interfaces 2015, 8, 2173–2180. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Thurgood, P.; Nguyen, N.; Ghorbani, K.; Khoshmanesh, K. Customised spatiotemporal temperature gradients created by a liquid metal enabled vortex generator. Lab Chip 2017, 17, 3862. [Google Scholar] [CrossRef]
- Tang, S.-Y.; Khoshmanesh, K.; Sivan, V.; Kalantar-zadeh, K. Liquid metal enabled pump. Proc. Natl. Acad. Sci. USA 2014, 111, 3304–3309. [Google Scholar] [CrossRef] [Green Version]
- Chiechi, R.C.; Weiss, E.A.; Dickey, M.D.; Whitesides, G.M. Eutectic gallium–indium (EGaIn): A moldable liquid metal for electrical characterization of self-assembled monolayers. Angew. Chem. Int. Ed. 2007, 47, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Simeone, F.C.; Yoon, H.-J.; Thuo, M.M.; Barber, J.R.; Smith, B.; Whitesides, G.M. Defining the value of injection current and effective electrical contact area for EGaIn-based molecular tunneling junctions. J. Am. Chem. Soc. 2013, 135, 18131–18144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.; Kang, S.; Yoon, H.-J. Power factor of one molecule thick films and length dependence. ACS Cent. Sci. 2019, 5, 1975–1982. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, H.; Kim, T.; Kang, S.; Jin, H.; Lee, K.; Yoon, H.-J. Ga-based liquid metal micro/nanoparticles: Recent advances and applications. Small 2019, 16, 1903391. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Vardeny, Z.-V.; Nahata, A. Liquid metal-based plasmonics. Opt. Express 2012, 20, 2346–2353. [Google Scholar] [CrossRef]
- Zuraiqi, K.; Zavabeti, A.; Allioux, F.-M.; Tang, J.; Nguyen, C.-K.; Tafazolymotie, P.; Mayyas, M.; Ramarao, A.V.; Spencer, M.; Shah, K.; et al. Liquid metals in catalysis for energy applications. Joule 2020, 4, 2290–2321. [Google Scholar] [CrossRef]
- Gough, R.C.; Morishita, A.M.; Dang, J.H.; Moorefield, M.R.; Shiroma, W.A.; Ohta, A.T. Rapid electrocapillary deformation of liquid metal with reversible shape retention. Micro Nano Syst. Lett. 2015, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Lin, Z.; Zhou, C.; Gao, C.; He, Q. Liquid metal gallium micromachines speed up in confining channels. Adv. Intell. Syst. 2019, 1, 1970070. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Liu, J.; Guo, H.; Qi, M.; Kato, N. Envisioning device-to-device communications in 6G. IEEE Netw. 2020, 34, 86–91. [Google Scholar] [CrossRef] [Green Version]
- Gambino, J.P.; Adderly, S.A.; Knickerbocker, J.U. An overview of through-silicon-via technology and manufacturing challenges. Microelectron. Eng. 2015, 135, 73–106. [Google Scholar] [CrossRef]
- Liu, T.; Sen, P.; Kim, C.-J. Characterization of nontoxic liquid-metal alloy Galinstan for applications in microdevices. J. Microelectromech. Syst. 2012, 21, 443–450. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dacuycuy, S.J.; Shiroma, W.A.; Ohta, A.T. Electrocapillary Actuation of Liquid Metal in Microchannels. Micromachines 2022, 13, 572. https://doi.org/10.3390/mi13040572
Dacuycuy SJ, Shiroma WA, Ohta AT. Electrocapillary Actuation of Liquid Metal in Microchannels. Micromachines. 2022; 13(4):572. https://doi.org/10.3390/mi13040572
Chicago/Turabian StyleDacuycuy, Saige J., Wayne A. Shiroma, and Aaron T. Ohta. 2022. "Electrocapillary Actuation of Liquid Metal in Microchannels" Micromachines 13, no. 4: 572. https://doi.org/10.3390/mi13040572
APA StyleDacuycuy, S. J., Shiroma, W. A., & Ohta, A. T. (2022). Electrocapillary Actuation of Liquid Metal in Microchannels. Micromachines, 13(4), 572. https://doi.org/10.3390/mi13040572







