Efficient Water-Assisted Glass Cutting with 355 nm Picosecond Laser Pulses
Abstract
:1. Introduction
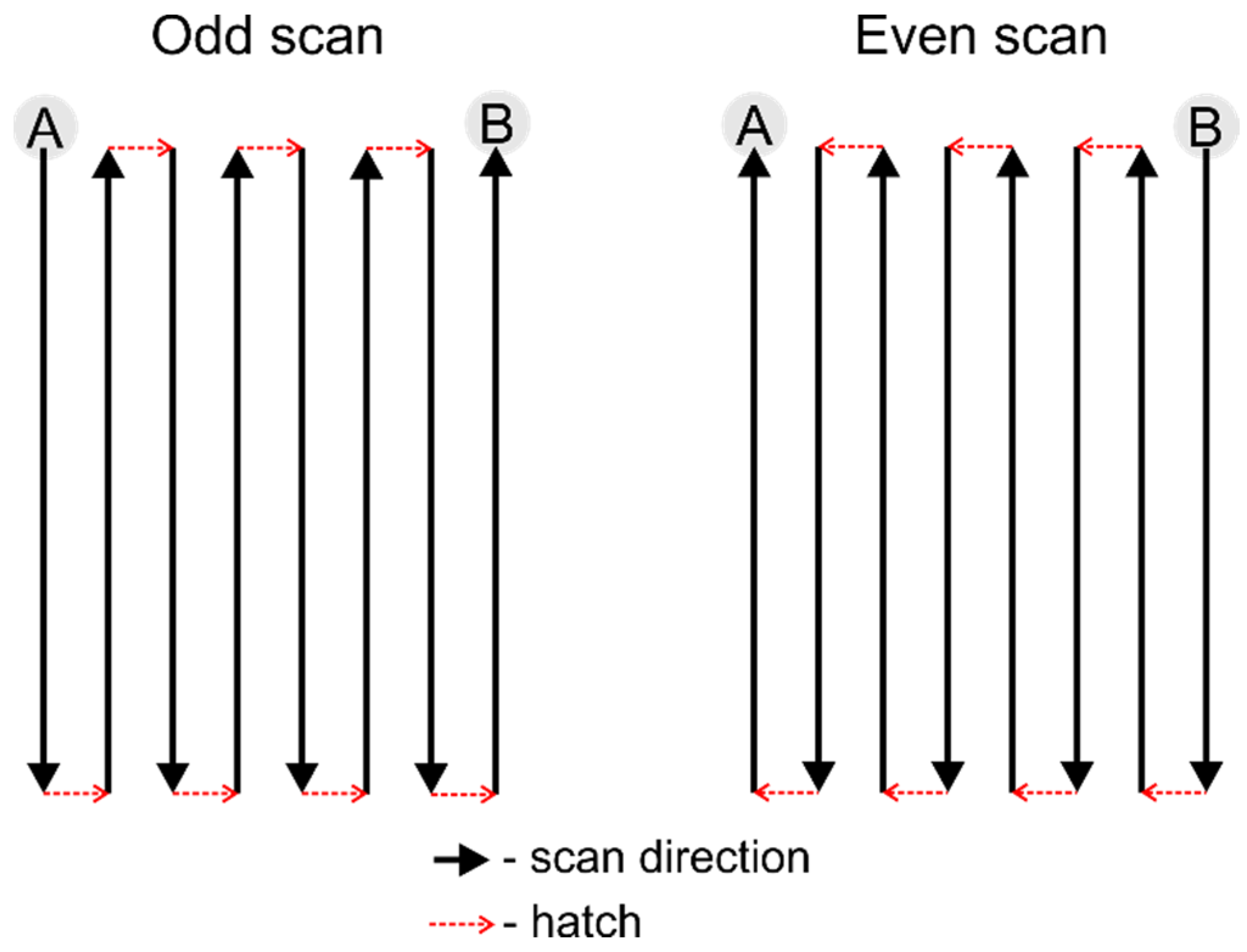
2. Materials and Methods
3. Results and Discussion
3.1. Low-Laser-Power Cutting Regime
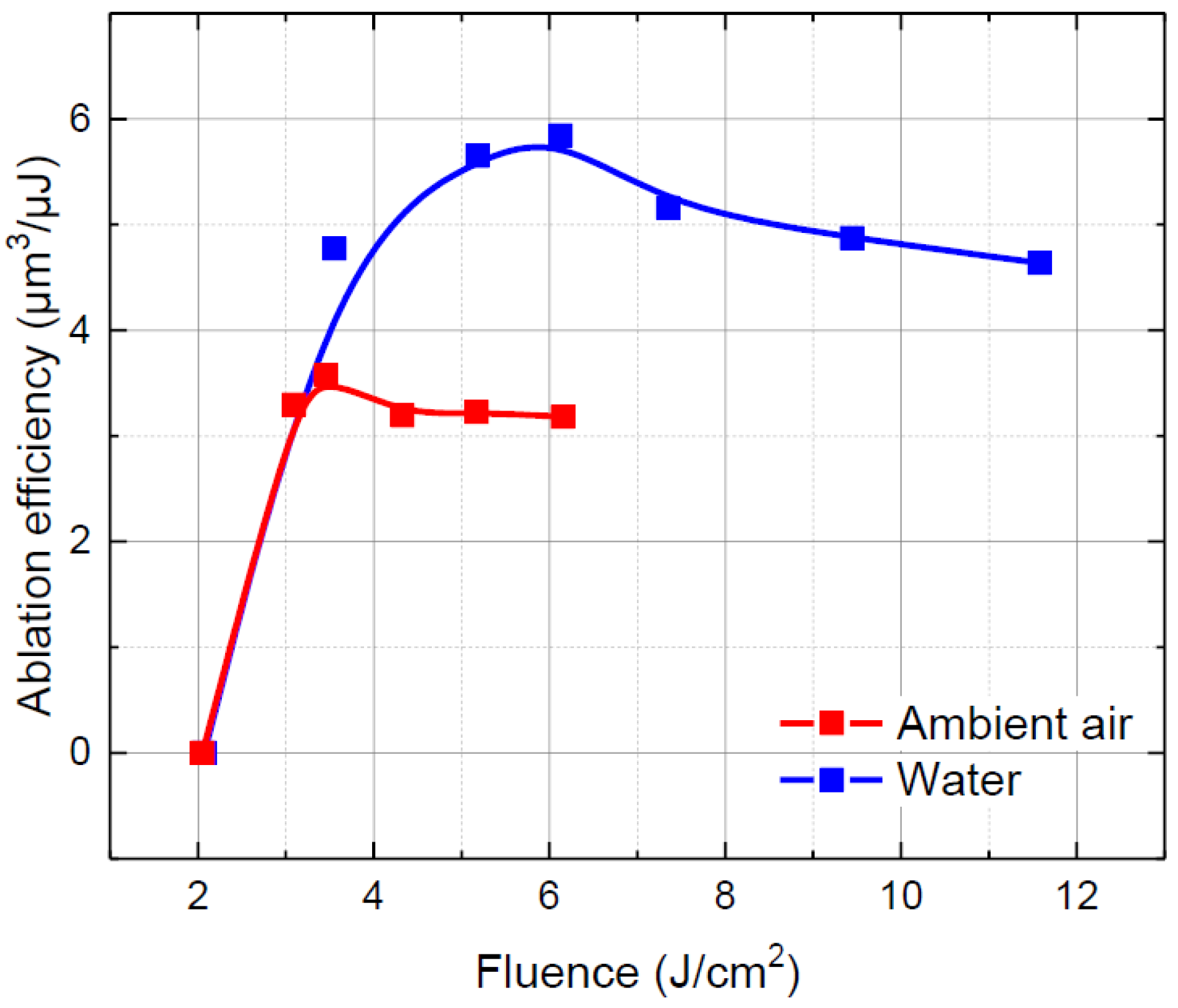
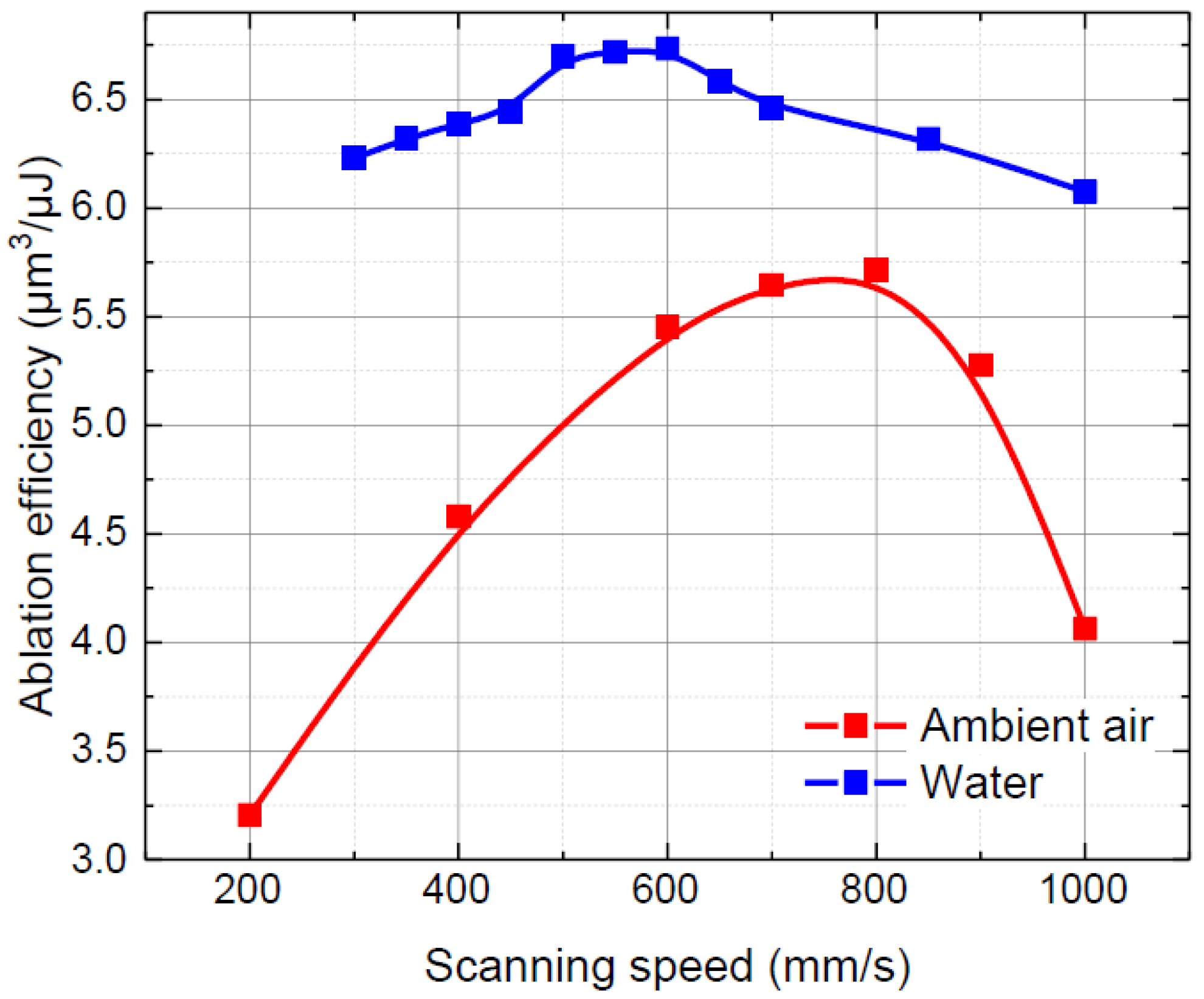
3.1.1. Cutting Process Optimisation
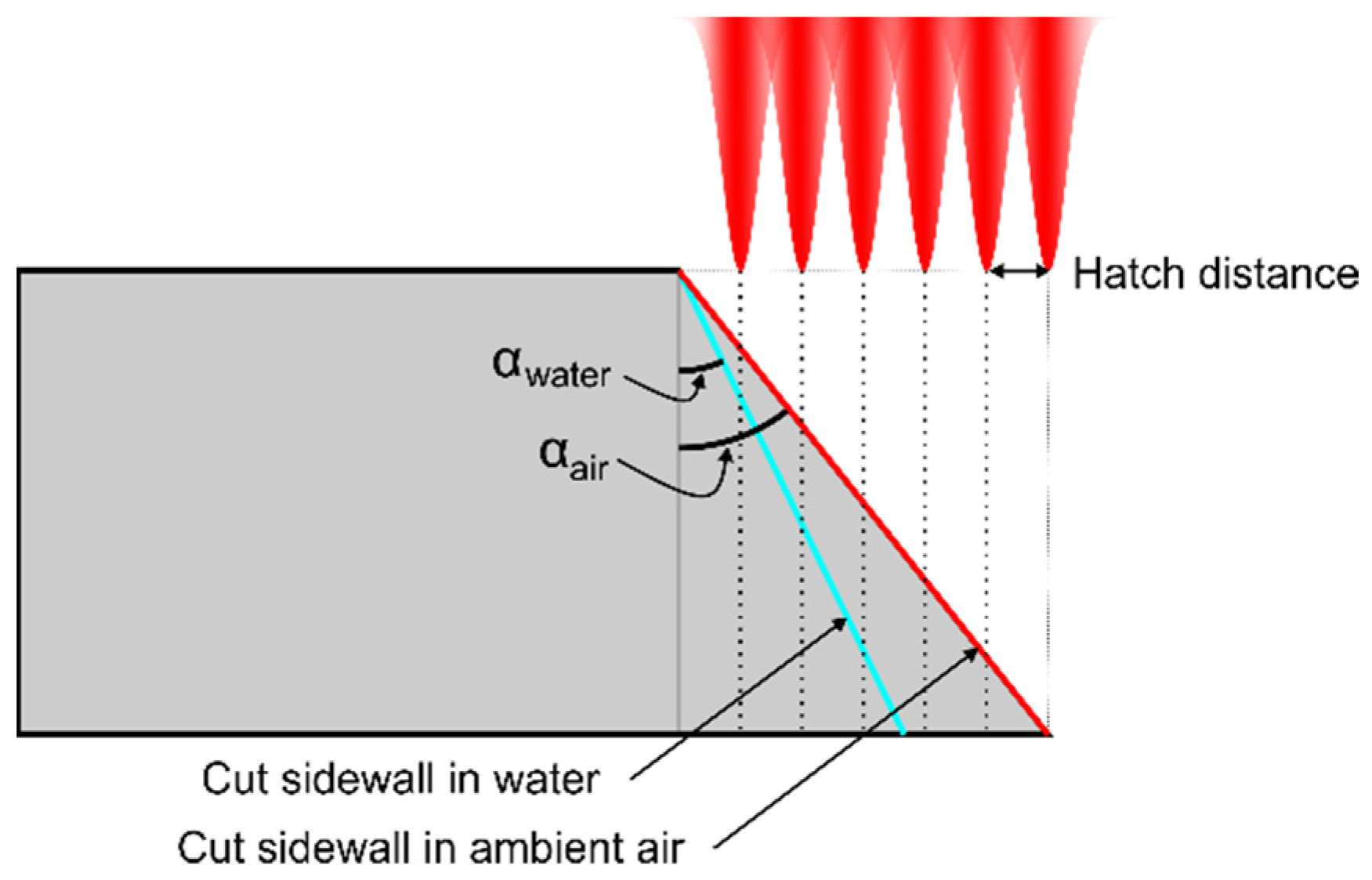
3.1.2. Cut Sidewall Quality
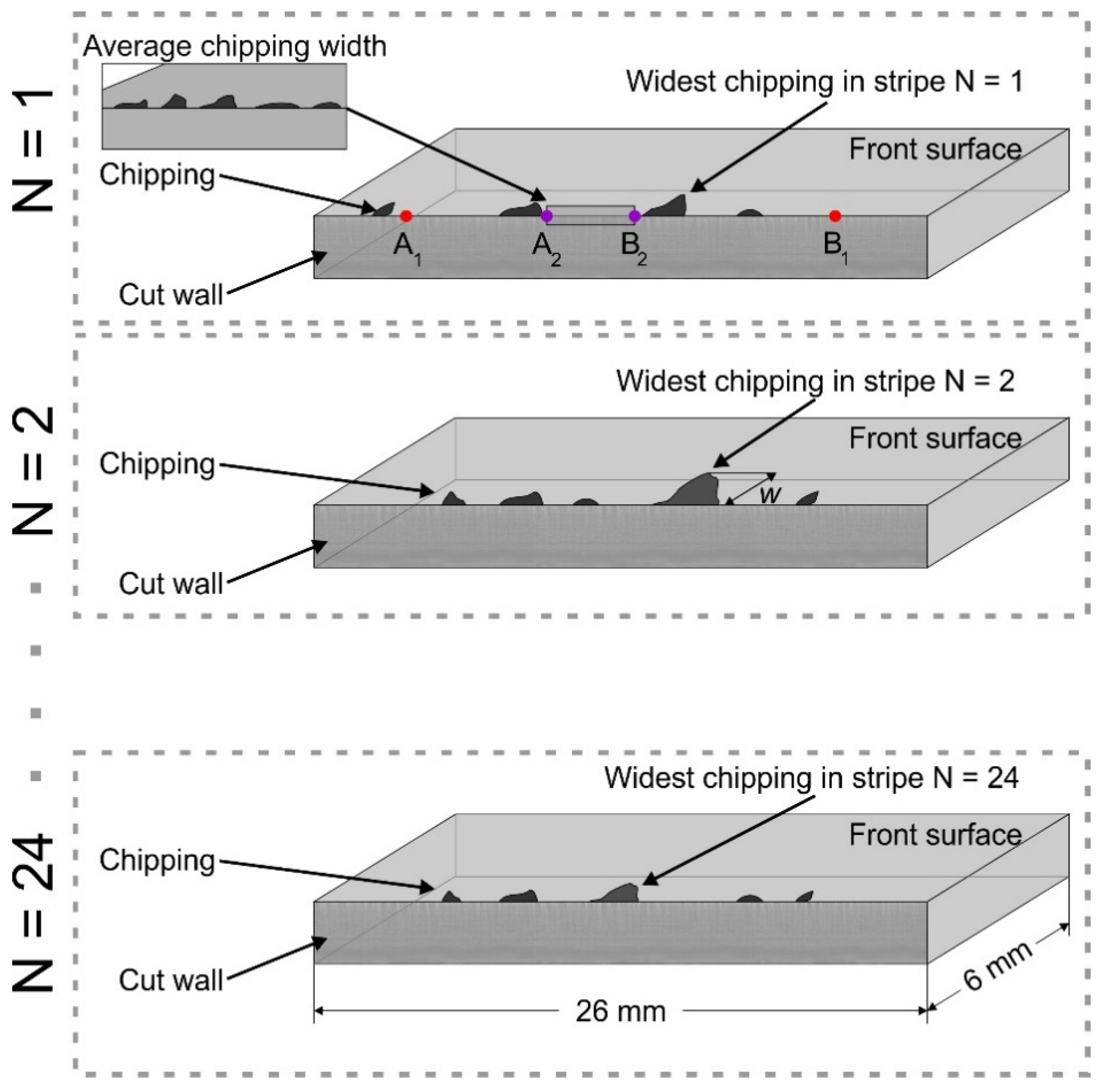
3.1.3. Cut Edge Quality
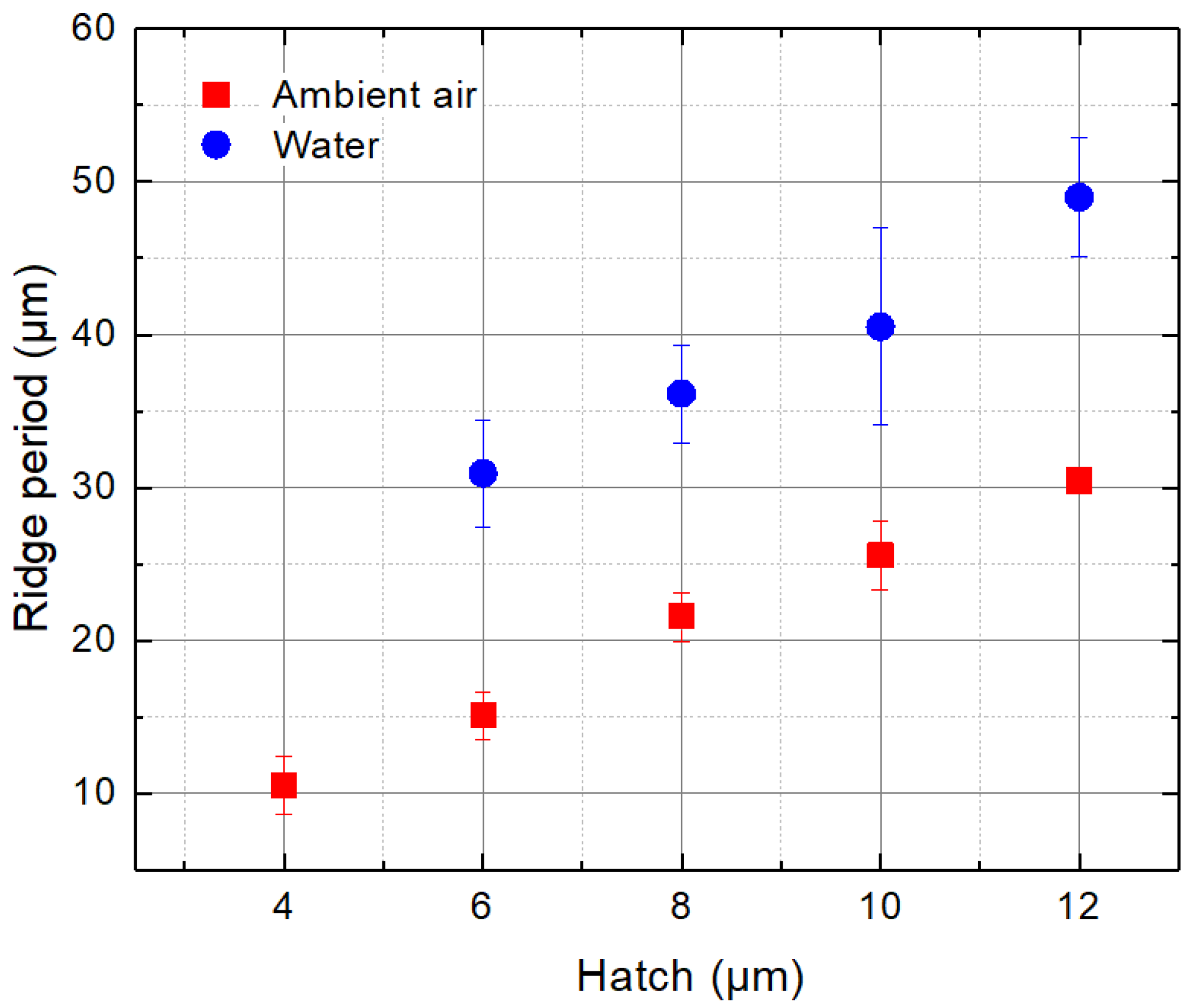
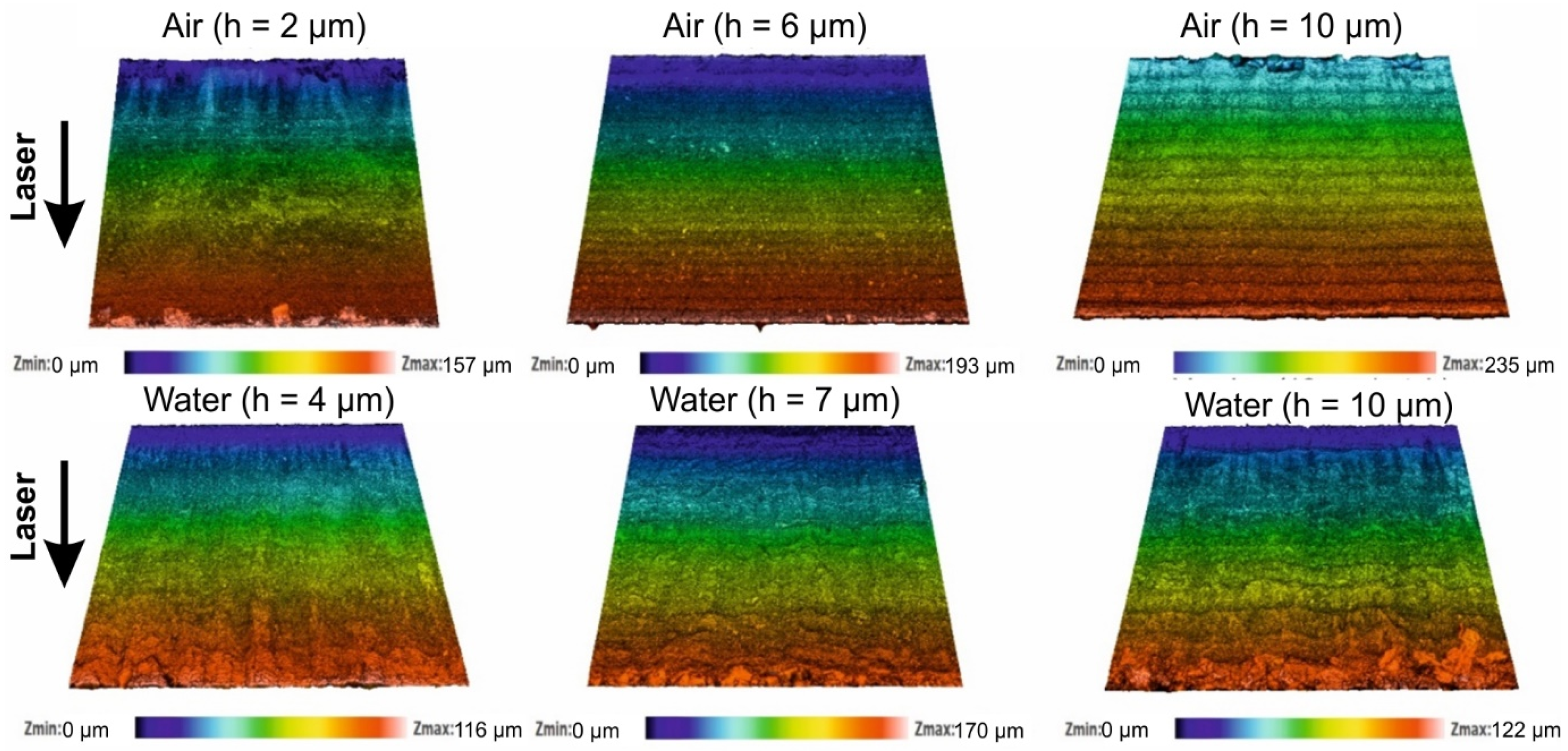
3.1.4. Cut Wall Roughness
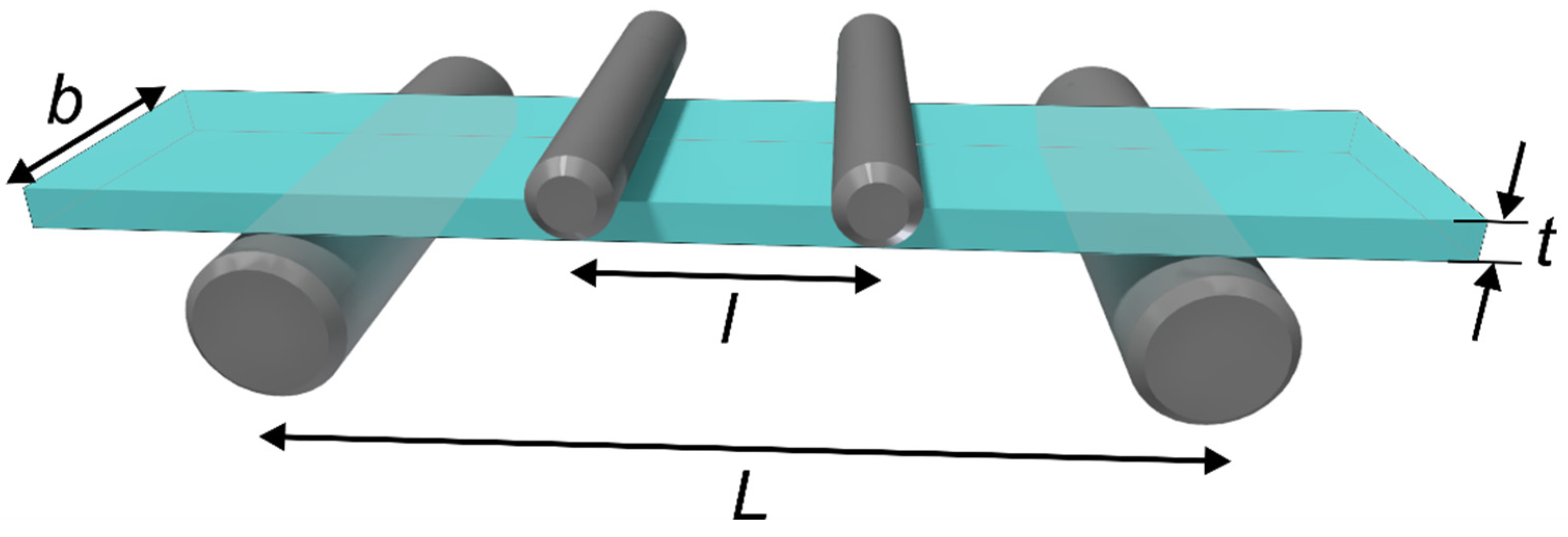
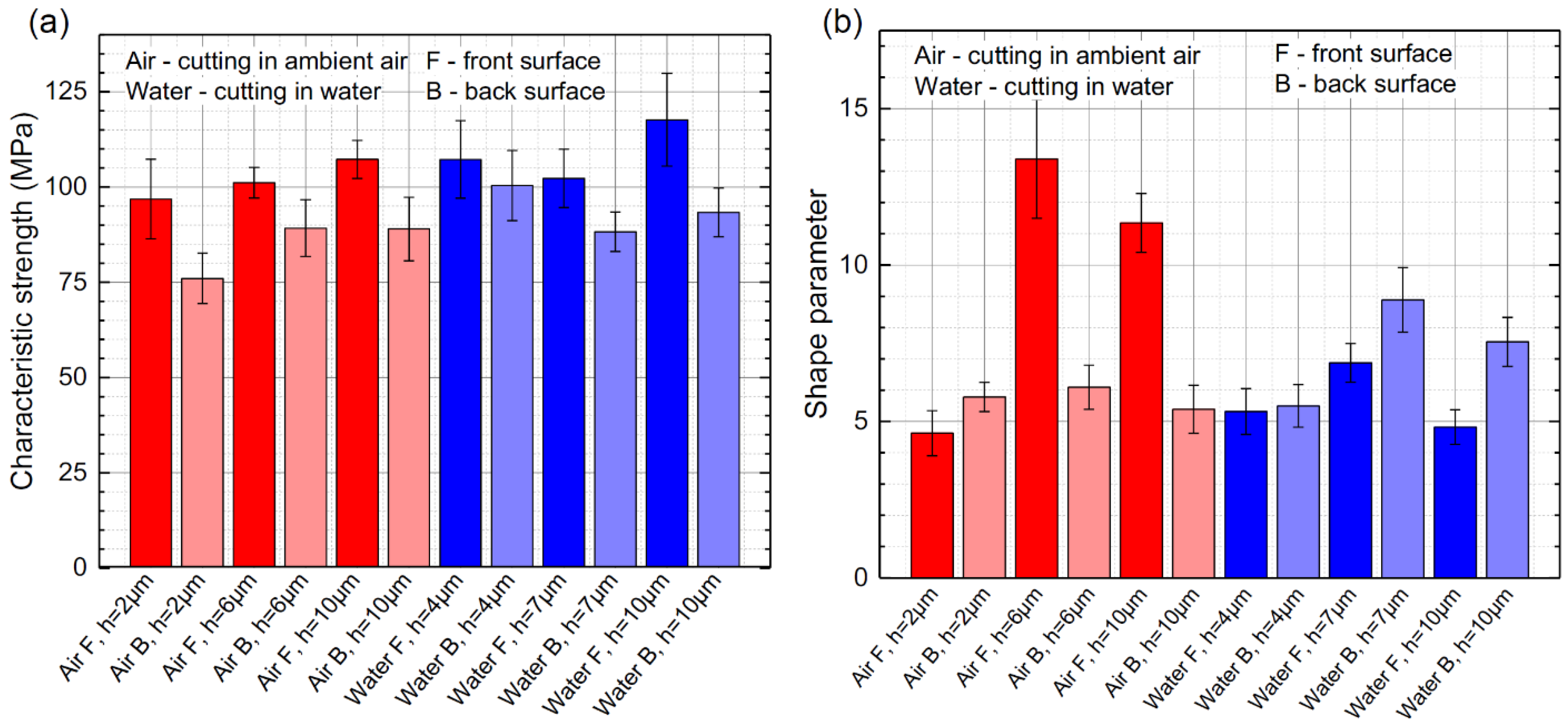
3.1.5. Flexural Strength
3.2. High-Laser-Power Cutting Regime
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kahr, M.; Domke, M.; Steiner, H.; Hortschitz, W.; Stifter, M. Borosilicate Glass MEMS Lorentz Force Magnetometer. Proceedings 2018, 2, 788. [Google Scholar]
- Okamoto, Y.; Miyamoto, I.; Cvecek, K.; Okada, A.; Takahashi, K.; Schmidt, M. Evaluation of Molten Zone in Micro-welding of Glass by Picosecond Pulsed Laser. JLMN J. Laser Micro Nanoeng. 2013, 8, 65–69. [Google Scholar] [CrossRef]
- Plat, K.; von Witzendorff, P.; Suttmann, O.; Overmeyer, L. Process strategy for drilling of chemically strengthened glass with picosecond laser radiation. J. Laser Appl. 2016, 28, 022201. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.; Li, S.; Guo, C.; Wei, Z. Experimental Study of Micro ElectrochemicalDischarge Machining of Ultra-Clear Glass witha Rotating Helical Tool. Processes 2019, 7, 195. [Google Scholar] [CrossRef] [Green Version]
- Axinte, E. Glasses as engineering materials: A review. Mater. Des. 2011, 32, 1717–1732. [Google Scholar] [CrossRef]
- Nisar, S.; Li, L.; Sheikh, M.A. Laser glass cutting techniques—A review. J. Laser Appl. 2013, 25, 042010. [Google Scholar] [CrossRef]
- Sun, M.; Eppelt, U.; Russ, S.; Hartmann, C.; Siebert, C.; Zhu, J.; Schulz, W. Numerical analysis of laser ablation and damage in glass with multiple picosecond laser pulses. Opt. Express 2013, 21, 7858–7867. [Google Scholar] [CrossRef]
- Yan, Y.; Ji, L.; Bao, Y.; Chen, X.; Jiang, Y. CO2 laser high-speed crack-free cutting of thick-section alumina based on close-piercing lapping technique. Int. J. Adv. Manuf. Technol. 2013, 64, 1611–1624. [Google Scholar] [CrossRef]
- Shin, H.; Kim, D. Strength of ultra-thin glass cut by internal scribing using a femtosecond Bessel beam. Opt. Laser Technol. 2020, 129, 106307. [Google Scholar] [CrossRef]
- Kumkar, M.; Bauer, L.; Russ, S.; Wendel, M.; Kleiner, J.; Grossmann, D.; Bergner, K.; Nolte, S. Comparison of Different Processes for Separation of Glass and Crystals Using Ultrashort Pulsed Lasers; SPIE: Bellingham, WA, USA, 2014; Volume 8972. [Google Scholar]
- Gečys, P.; Dudutis, J.; Račiukaitis, G. Nanosecond Laser Processing of Soda-Lime Glass. J. Laser Micro Nanoeng. 2015, 10, 254–258. [Google Scholar] [CrossRef]
- Dudutis, J.; Stonys, R.; Račiukaitis, G.; Gečys, P. Glass dicing with elliptical Bessel beam. Opt. Laser Technol. 2019, 111, 331–337. [Google Scholar] [CrossRef]
- Shin, J. Investigation of the surface morphology in glass scribing with a UV picosecond laser. Opt. Laser Technol. 2019, 111, 307–314. [Google Scholar] [CrossRef]
- Tamura, A.; Kiyokawa, S.; Nakamura, Y.; Fushinobu, K. Picosecond laser ablation on glass using wavelength of 1064, 532, and 355 nm. Opt. Eng. 2020, 59, 075102. [Google Scholar] [CrossRef]
- Sun, M.; Eppelt, U.; Hartmann, C.; Schulz, W.; Zhu, J.; Lin, Z. Damage morphology and mechanism in ablation cutting of thin glass sheets with picosecond pulsed lasers. Opt. Laser Technol. 2016, 80, 227–236. [Google Scholar] [CrossRef]
- Markauskas, E.; Zubauskas, L.; Gečys, P. Efficient milling and cutting of borosilicate glasses through a thin flowing water film with a picosecond laser. J. Manuf. Process. 2021, 68, 898–909. [Google Scholar] [CrossRef]
- Dudutis, J.; Zubauskas, L.; Daknys, E.; Markauskas, E.; Gvozdaitė, R.; Račiukaitis, G.; Gečys, P. Quality and flexural strength of laser-cut glass: Classical top-down ablation versus water-assisted and bottom-up machining. Opt. Express 2022, 30, 4564–4582. [Google Scholar] [CrossRef]
- Markauskas, E.; Gečys, P. Thin water film assisted glass ablation with a picosecond laser. Procedia CIRP 2018, 74, 328–332. [Google Scholar] [CrossRef]
- Tangwarodomnukun, V.; Wuttisarn, T. Evolution of milled cavity in the multiple laser scans of titanium alloy under a flowing water layer. Int. J. Adv. Manuf. Technol. 2017, 92, 293–302. [Google Scholar] [CrossRef]
- Charee, W.; Tangwarodomnukun, V.; Dumkum, C. Laser ablation of silicon in water under different flow rates. Int. J. Adv. Manuf. Technol. 2015, 78, 19–29. [Google Scholar] [CrossRef]
- Wee, L.M.; Ng, E.Y.K.; Prathama, A.H.; Zheng, H. Micro-machining of silicon wafer in air and under water. Opt. Laser Technol. 2011, 43, 62–71. [Google Scholar] [CrossRef]
- Garcia-Giron, A.; Sola, D.; Peña, J.I. Liquid-assisted laser ablation of advanced ceramics and glass-ceramic materials. Appl. Surf. Sci. 2016, 363, 548–554. [Google Scholar] [CrossRef]
- Kang, H.W.; Lee, H.; Chen, S.; Welch, A.J. Enhancement of bovine bone ablation assisted by a transparent liquid Layer on a target surface. IEEE J. Quantum Electron. 2006, 42, 633–642. [Google Scholar] [CrossRef]
- Parmar, M.; James, S. Experimental and Modeling Study of Liquid-Assisted—Laser Beam Micromachining of Smart Ceramic Materials. J. Manuf. Mater. Process. 2018, 2, 28. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Lu, M.; Wang, W.; Hong, Z.; Chen, Z.; Zhang, W.; Pan, S.; Shui, L.; Zhang, C. Sucrose solution assisted femtosecond laser ablation of aluminum film to induce nanospikes for efficient and stable oil-water separation. Surf. Coat. Technol. 2021, 417, 127182. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, H.J.; Lin, D.T.; Zuo, F.; Zhao, Z.X.; Lin, H.T. Characterization of hole taper in laser drilling of silicon nitride ceramic under water. Ceram. Int. 2018, 44, 13449–13452. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Li, C.-C. Investigation of underwater laser drilling for brittle substrates. J. Mater. Process. Technol. 2009, 209, 2838–2846. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, Y.X.; Zhao, Y.W.; Jiao, H.; Liu, Q.Y.; Long, Y.H. Study on water-assisted laser ablation mechanism based on water layer characteristics. Opt. Commun. 2019, 450, 112–121. [Google Scholar] [CrossRef]
- Butkus, S.; Gaižauskas, E.; Mačernytė, L.; Jukna, V.; Paipulas, D.; Sirutkaitis, V. Femtosecond Beam Transformation Effects in Water, Enabling Increased Throughput Micromachining in Transparent Materials. Appl. Sci. 2019, 9, 2405. [Google Scholar] [CrossRef] [Green Version]
- Butkus, S.; Alesenkov, A.; Paipulas, D.; Gaižauskas, E.; Melninkaitis, A.; Kaškelytė, D.; Barkauskas, M.; Sirutkaitis, V. Analysis of the Micromachining Process of Dielectric and Metallic Substrates Immersed in Water with Femtosecond Pulses. Micromachines 2015, 6, 2010–2022. [Google Scholar] [CrossRef] [Green Version]
- Wee, L.M.; Khoong, L.E.; Tan, C.W.; Lim, G.C. Solvent-Assisted Laser Drilling of Silicon Carbide. Int. J. Appl. Ceram. Technol. 2011, 8, 1263–1276. [Google Scholar] [CrossRef]
- Butkus, S.; Paipulas, D.; Sirutkaitis, R.; Gaizauskas, E.; Sirutkaitis, V. Rapid Cutting and Drilling of Transparent Materials via Femtosecond Laser Filamentation. JLMN J. Laser Micro Nanoeng. 2014, 9, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Han, F.; Ying, W. The experimental investigation of water jet–guided laser cutting of CFRP. Int. J. Adv. Manuf. Technol. 2019, 102, 719–729. [Google Scholar] [CrossRef]
- Mullick, S.; Madhukar, Y.K.; Roy, S.; Nath, A.K. Performance optimization of water-jet assisted underwater laser cutting of AISI 304 stainless steel sheet. Opt. Lasers Eng. 2016, 83, 32–47. [Google Scholar] [CrossRef]
- Tangwarodomnukun, V.; Wang, J.; Mathew, P. A Comparison of Dry and Underwater Laser Micromachining of Silicon Substrates. Key Eng. Mater. 2010, 443, 693–698. [Google Scholar] [CrossRef]
- Kruusing, A. Underwater and water-assisted laser processing: Part 1—General features, steam cleaning and shock processing. Opt. Lasers Eng. 2004, 41, 307–327. [Google Scholar] [CrossRef]
- Liu, J.M. Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef]
- Zhao, L.; Maynadier, A.; Nelias, D. Stiffness and fracture analysis of photovoltaic grade silicon plates. Int. J. Solids Struct. 2016, 97–98, 355–369. [Google Scholar] [CrossRef]
- Fuegl, M.; Mackh, G.; Meissner, E.; Frey, L. Analytical stress characterization after different chip separation methods. Microelectron. Reliab. 2014, 54, 1735–1740. [Google Scholar] [CrossRef]
- Przybilla, C.; Fernández-Canteli, A.; Castillo, E. An iterative method to obtain the specimen-independent three-parameter Weibull distribution of strength from bending tests. Procedia Eng. 2011, 10, 1414–1419. [Google Scholar] [CrossRef]
- Khalili, K.; Kromp, K. Statistical Properties of Weibull estimators. J. Mater. Sci. 1991, 26, 6741–6752. [Google Scholar] [CrossRef]
- Bergman, B. On the estimation of the Weibull modulus. J. Matter. Sci. Lett. 1984, 3, 689–692. [Google Scholar] [CrossRef]
- Martan, J.; Prokešová, L.; Moskal, D.; de Faria, B.F.; Honner, M.; Lang, V. Heat accumulation temperature measurement in ultrashort pulse laser micromachining. Int. J. Heat Mass Transf. 2021, 168, 120866. [Google Scholar] [CrossRef]
- Guarino, S.; Ponticelli, G.S.; Giannini, O.; Genna, S.; Trovalusci, F. Laser milling of yttria-stabilized zirconia by using a Q-switched Yb:YAG fiber laser: Experimental analysis. Int. J. Adv. Manuf. Technol. 2018, 94, 1373–1385. [Google Scholar] [CrossRef]
- Leone, C.; Genna, S.; Tagliaferri, F. Multiobjective optimisation of nanosecond fiber laser milling of 2024 T3 aluminium alloy. J. Manuf. Process. 2020, 57, 288–301. [Google Scholar] [CrossRef]
- Žemaitis, A.; Gaidys, M.; Gečys, P.; Račiukaitis, G.; Gedvilas, M. Rapid high-quality 3D micro-machining by optimised efficient ultrashort laser ablation. Opt. Lasers Eng. 2019, 114, 83–89. [Google Scholar] [CrossRef]
- Wu, B.; Liu, P.; Zhang, F.; Duan, J.; Wang, X.; Zeng, X. Effect of parameters on picosecond laser ablation of Cr12MoV cold work mold steel. Appl. Phys. A 2017, 124, 11. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, K.; Shen, H.; Yao, Z. Experimental study on direct fabrication of micro channel on fused silica by picosecond laser. J. Manuf. Process. 2020, 55, 87–95. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, B.; Zhao, Q.; Liu, W.; Zheng, Q. Optimisation of spray-mist-assisted laser machining of micro-structures on CVD diamond coating surfaces. Ceram. Int. 2021, 47, 22108–22120. [Google Scholar] [CrossRef]
- Charee, W.; Tangwarodomnukun, V. Dynamic features of bubble induced by a nanosecond pulse laser in still and flowing water. Opt. Laser Technol. 2018, 100, 230–243. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Tinguely, M.; Kobel, P.; Dorsaz, N.; Farhat, M. Scaling laws for jets of single cavitation bubbles. J. Fluid Mech. 2016, 802, 263–293. [Google Scholar] [CrossRef] [Green Version]
- Adelmann, B.; Hellmann, R. Investigation on Flexural Strength Changes of Alumina Caused by Cutting using Fiber Laser. JLMN J. Laser Micro Nanoeng. 2014, 9, 153–160. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.; Kim, D. Cutting thin glass by femtosecond laser ablation. Opt. Laser Technol. 2018, 102, 1–11. [Google Scholar] [CrossRef]
- Indrišiūnas, S.; Svirplys, E.; Jorudas, J.; Kašalynas, I. Laser Processing of Transparent Wafers with a AlGaN/GaN Heterostructures and High-Electron Mobility Devices on a Backside. Micromachines 2021, 12, 407. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Zheng, J.; Liang, C.; Hu, Y.; Zhong, H.; Duan, J. Improvement of rear damage of thin fused silica by liquid-assisted femtosecond laser cutting. Appl. Phys. A 2019, 125, 1–8. [Google Scholar] [CrossRef]
- Collins, A.; Rostohar, D.; Prieto, C.; Chan, Y.K.; O’Connor, G.M. Laser scribing of thin dielectrics with polarised ultrashort pulses. Opt. Lasers Eng. 2014, 60, 18–24. [Google Scholar] [CrossRef]
- Lu, J.; Xu, R.Q.; Chen, X.; Shen, Z.H.; Ni, X.W.; Zhang, S.Y.; Gao, C.M. Mechanisms of laser drilling of metal plates underwater. J. Appl. Phys. 2004, 95, 3890–3894. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Akhtar, S.S.; Karatas, C. Laser straight cutting of alumina tiles: Thermal stress analysis. Int. J. Adv. Manuf. Technol. 2012, 58, 1019–1030. [Google Scholar] [CrossRef]

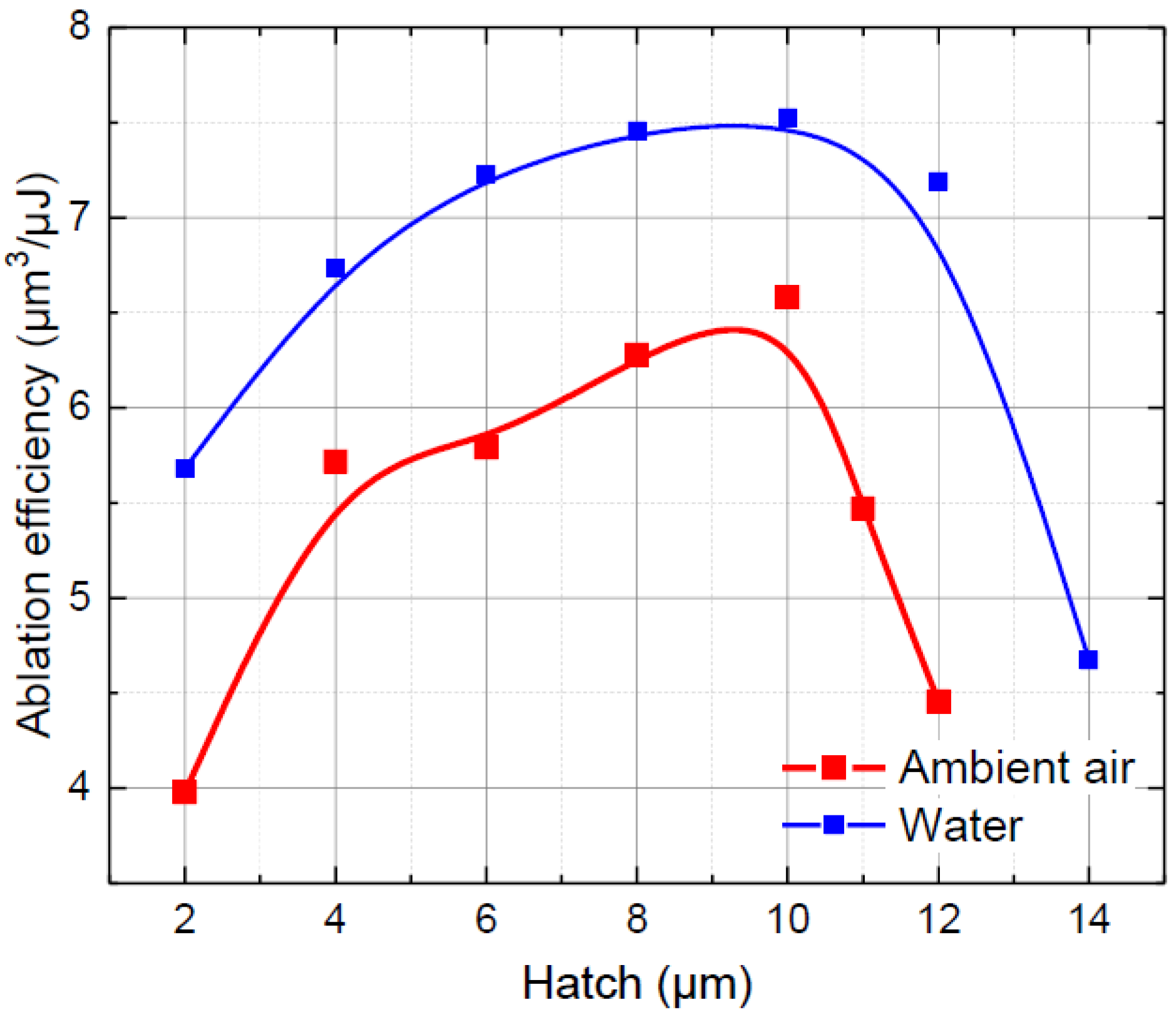







| Cutting Environment | Average Laser Power, W | Ablation Efficiency, µm3/µJ | Fluence, J/cm2 | Scan Speed, mm/s | Pulse Energy, μJ | Pulse Repetition Rate, kHz | Hatch, µm | Cut Width, µm |
|---|---|---|---|---|---|---|---|---|
| Air | 2.1 | 6.6 | 3.5 | 800 | 3.2 | 653 | 10 | 300 |
| Water (low power) | 2.75 | 7.5 | 6.1 | 600 | 5.2 | 529 | 10 | 300 |
| Cutting in Ambient Air | Cutting in Water | |||||
|---|---|---|---|---|---|---|
| Hatch, μm | 2 μm | 6 μm | 10 μm | 4 μm | 7 μm | 10 μm |
| Front surface, μm | 6.4 ± 3.7 | 6.2 ± 2.9 | 4.3 ± 1.8 | 0.85 ± 0.4 | 0.8 ± 0.4 | 0.75 ± 0.35 |
| Back surface, μm | 3.9 ± 2.9 | 5.4 ± 3.2 | 6.7 ± 3.3 | 4.4 ± 2.2 | 6.7 ± 2.6 | 6.9 ± 4.3 |
| Cutting Environment | Front Side | Back Side |
|---|---|---|
| Ambient air | 101.7 ± 6 MPa | 84.7 ± 7 MPa |
| Water | 109 ± 8 MPa | 93.9 ± 7 MPa |
| Cutting Environment | Average Laser Power, W | Ablation Efficiency, µm3/µJ | Fluence, J/cm2 | Scan Speed, mm/s | Pulse Energy, μJ | Pulse Repetition Rate, kHz | Hatch, µm | Cut Width, µm |
|---|---|---|---|---|---|---|---|---|
| Water (high power) | 15.5 | 8.7 | 6.1 | 1250 | 21.4 | 725 | 15 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markauskas, E.; Zubauskas, L.; Voisiat, B.; Gečys, P. Efficient Water-Assisted Glass Cutting with 355 nm Picosecond Laser Pulses. Micromachines 2022, 13, 785. https://doi.org/10.3390/mi13050785
Markauskas E, Zubauskas L, Voisiat B, Gečys P. Efficient Water-Assisted Glass Cutting with 355 nm Picosecond Laser Pulses. Micromachines. 2022; 13(5):785. https://doi.org/10.3390/mi13050785
Chicago/Turabian StyleMarkauskas, Edgaras, Laimis Zubauskas, Bogdan Voisiat, and Paulius Gečys. 2022. "Efficient Water-Assisted Glass Cutting with 355 nm Picosecond Laser Pulses" Micromachines 13, no. 5: 785. https://doi.org/10.3390/mi13050785
APA StyleMarkauskas, E., Zubauskas, L., Voisiat, B., & Gečys, P. (2022). Efficient Water-Assisted Glass Cutting with 355 nm Picosecond Laser Pulses. Micromachines, 13(5), 785. https://doi.org/10.3390/mi13050785






