Self-Attention-Augmented Generative Adversarial Networks for Data-Driven Modeling of Nanoscale Coating Manufacturing
Abstract
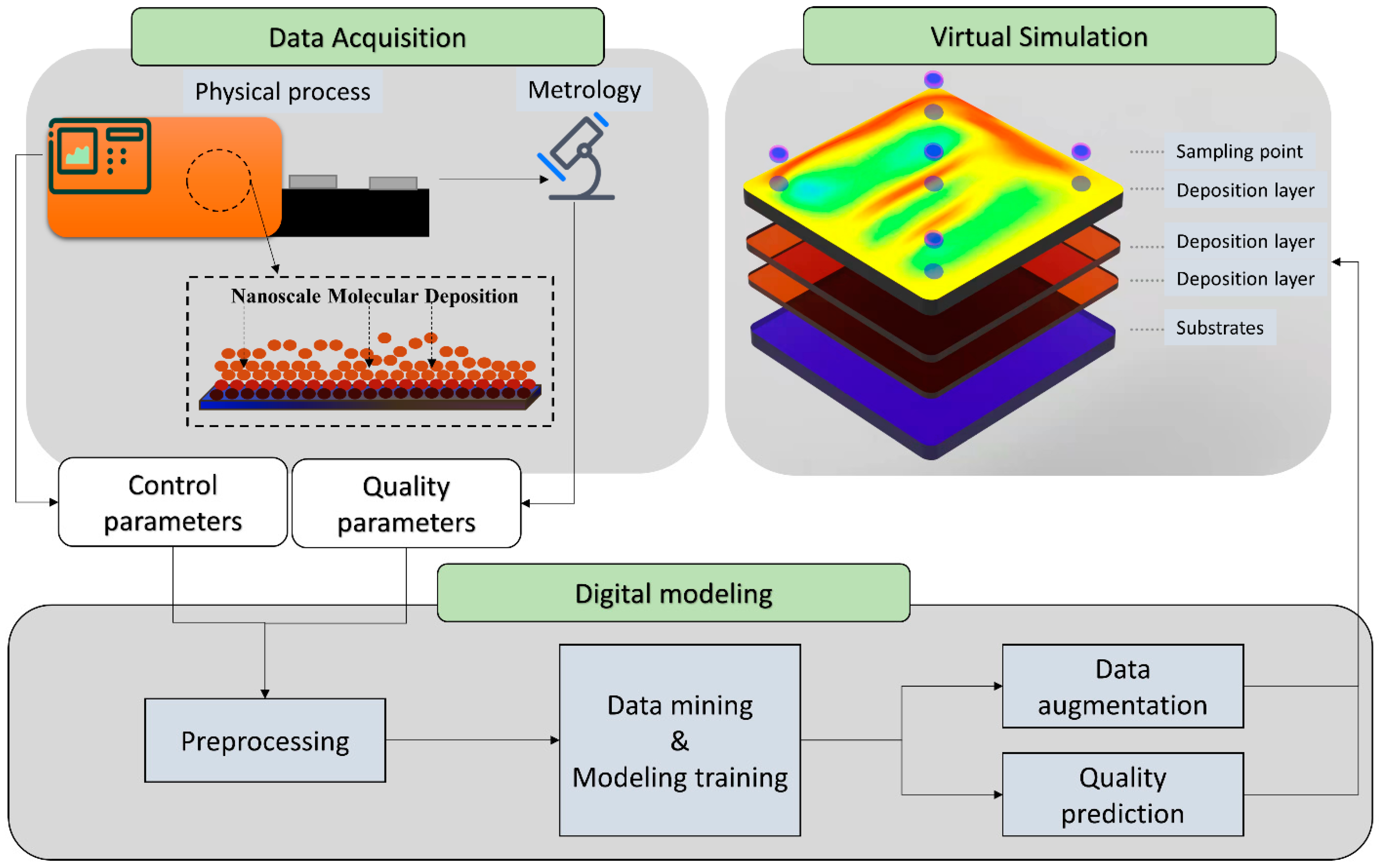
:1. Introduction
- (1)
- The relations among different manufacturing steps are ignored when extracting features from the control recipes;
- (2)
- Data augmentation is an essential technique in DL-based process modeling in industrial manufacturing. Prior works have few studies about recipe augmentation, especially in NCM;
- (3)
- The multivariable quality prediction and data augmentation of NCM are rarely considered simultaneously, as these factors can increase the training cost.
- (1)
- A data-driven NCM process model is proposed in an end-to-end way that can predict coating quality by learning features adaptively from complex industrial process data and can make data augmentation by generating recipes of coating processing.
- (2)
- The data augmentation of the multilayer coating processing is challenging work. The proposed model not only learns the connection information between the NCM output quality and the control parameters, but it also extracts latent knowledge between the former coating steps and the subsequent coating steps from history production data with the assistance of a self-attention technique.
- (3)
- The quality of the NCM output has multiple variables, which may include thickness, refractive index, or other reference values. In addition, there is a coupling relationship between these output values. The proposed framework can predict multivariable quality by sharing feature information of control parameters and regression weights.
2. Background Knowledge
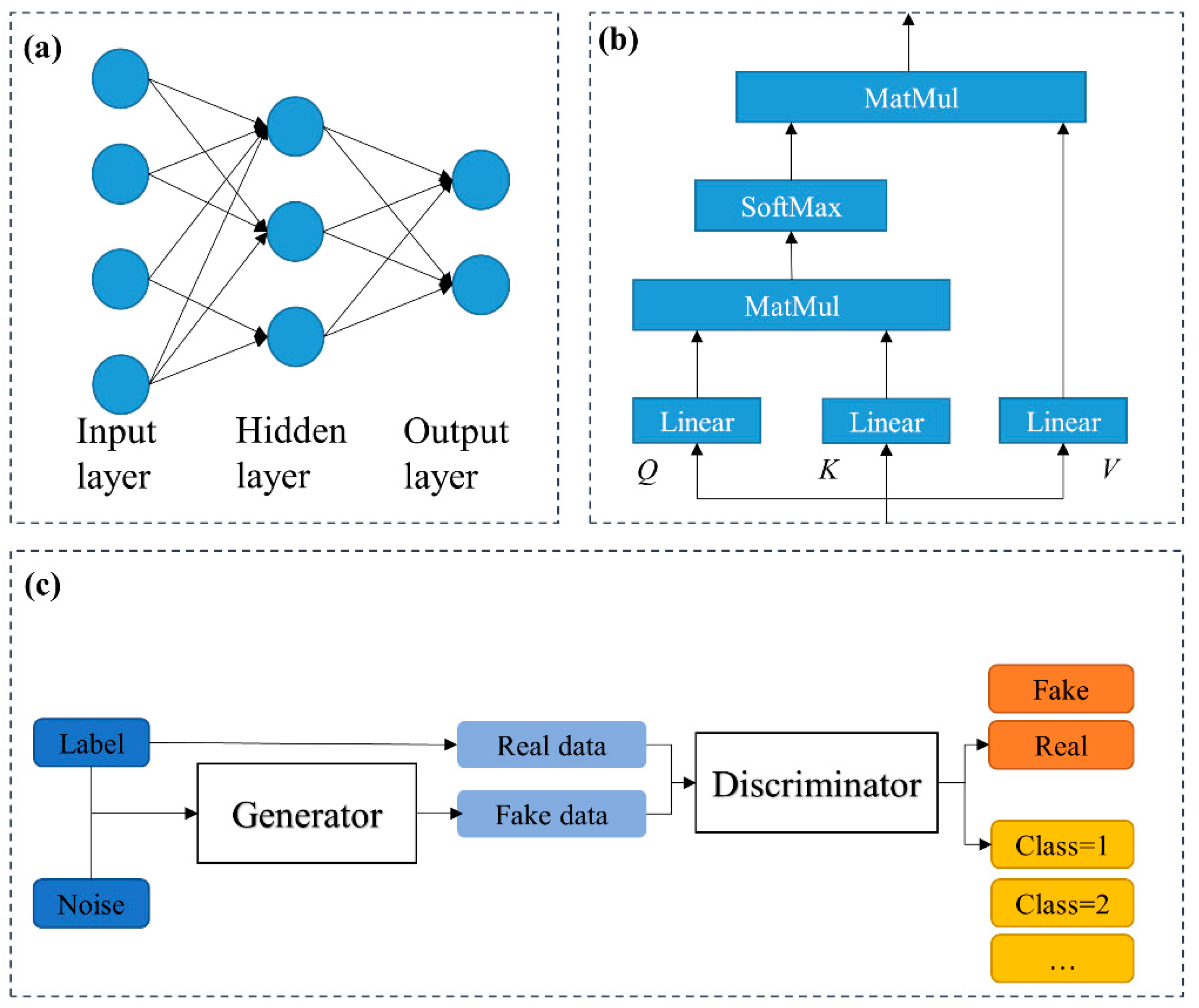
2.1. NCM Process Modeling Using ANNs
2.2. Self-Attention Mechanism
2.3. Basic Generative Adversarial Networks
- (1)
- The generated data for target coating quality;
- (2)
- The discriminator to distinguish between real control parameters and generated parameters;
- (3)
- The regression for quality estimation using the input control parameters.
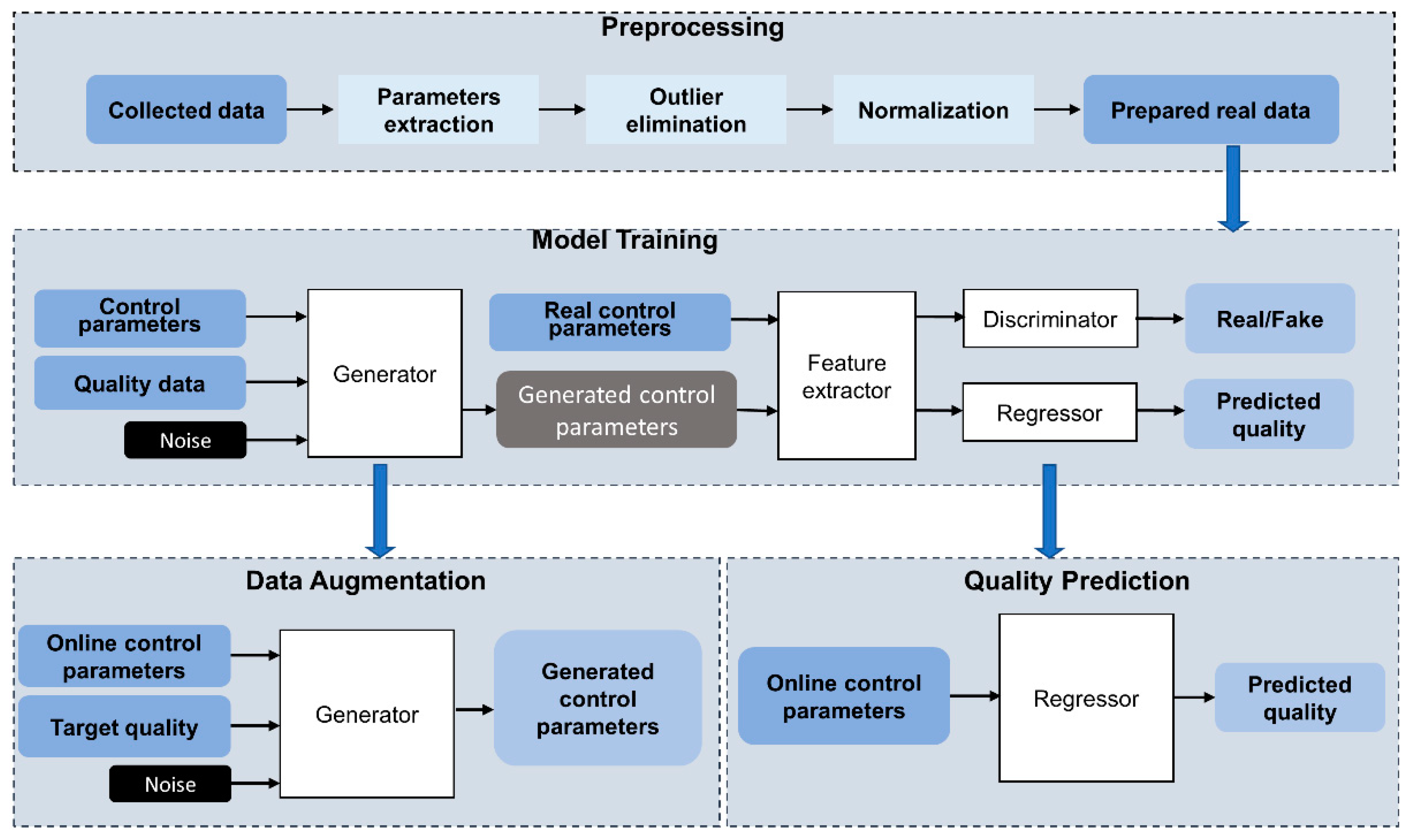
3. Proposed Approach
- (1)
- Preprocessing. The collected data included control data and associated quality data. In addition to deposition time, the raw control data sampled from multiple sensors were continuous and fluctuated around the original control value. Thus, the median values in each coating step were extracted as the feature. After that, outlier elimination and normalization were carried out.
- (2)
- Model training. Our proposed AR-SAGAN was trained using an offline dataset. The AR-SAGAN was periodically trained and updated to adapt the real-time operating conditions.
- (3)
- Quality prediction. The online control parameters were collected, preprocessed, and then input to a regressor, which was trained using AR-SAGAN to predict quality.
- (4)
- Data augmentation. In this step, the online control parameters and the target quality data were preprocessed and input to a generator trained by AR-SAGAN to generate more control recipes.
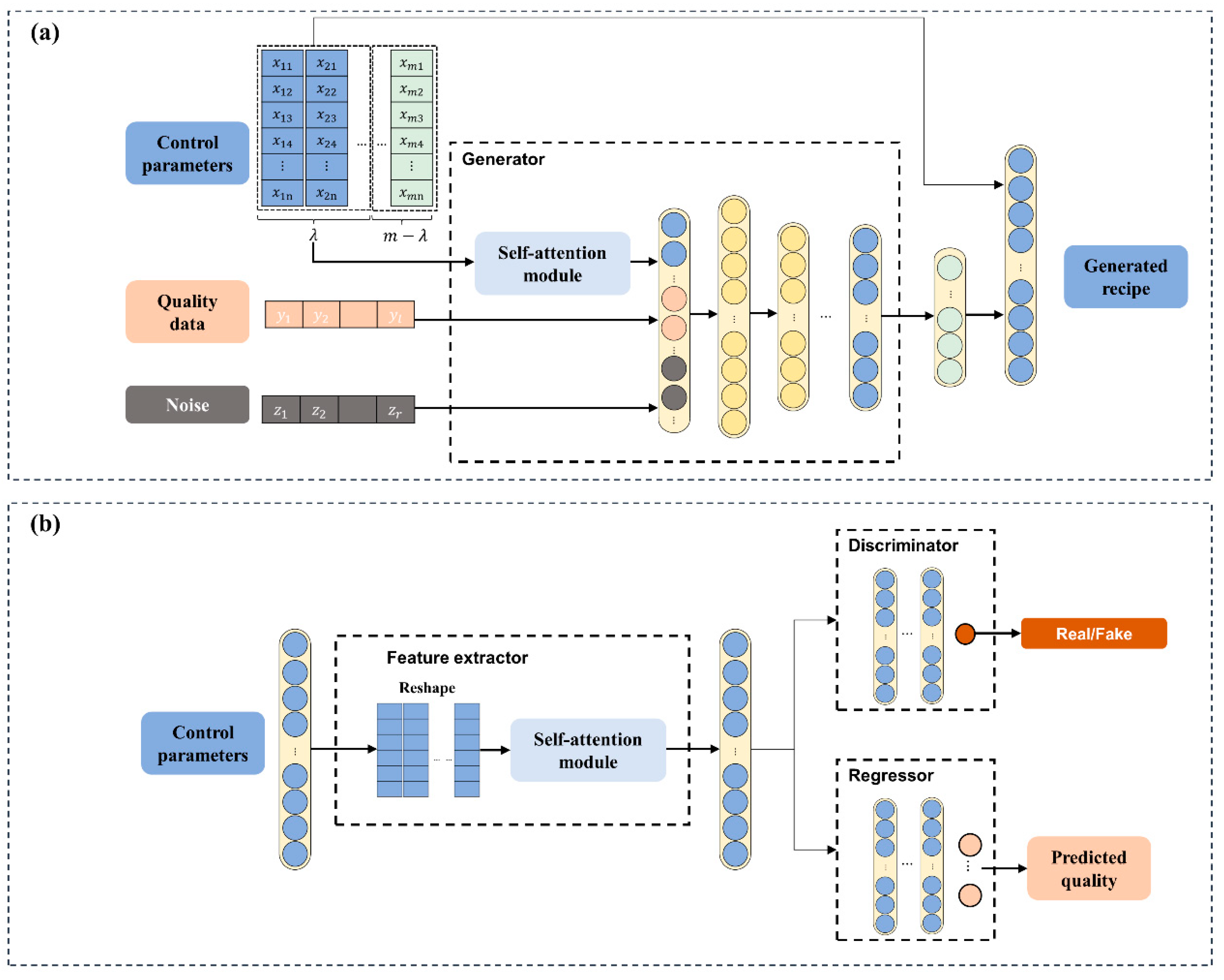
3.1. AR-SAGAN Model
- (1)
- The generator took random noise, desired quality data, and control parameters of the first coating steps as the input. Subsequently, the implied feature of the control parameter matrix was concatenated with quality data and noise via the self-attention module. The output of generator was the last steps of the recipe. Finally, to output the complete recipe, a concatenation operation was employed between the control parameters of the first steps and the generated last steps.
- (2)
- The feature extractor extracted latent information from the complete recipe. The control parameters were reshaped into the size and then passed through the self-attention module. The module output was connected with a flattened layer, which was related with the discriminator and regressor. The discriminator distinguished between the real recipe or fake recipes (generated control parameters). The regressor predicted the coating quality based on the complete coating recipe.
3.2. Loss Function
3.3. Training Algorithms
| Algorithm 1: Training AR-SAGAN based on TC1. |
| Input, Initialize network parameters , , , while not converged do for k steps do end end while |
| Algorithm 2: Training AR-SAGAN based on TC2. |
| Input, Initialize network parameters , , , while not converged do for k steps do end end while |
| Algorithm 3: Training AR-SAGAN based on TC3. |
| Input, Initialize network parameters , , , while not converged do for k steps do end end while |
4. Case Study
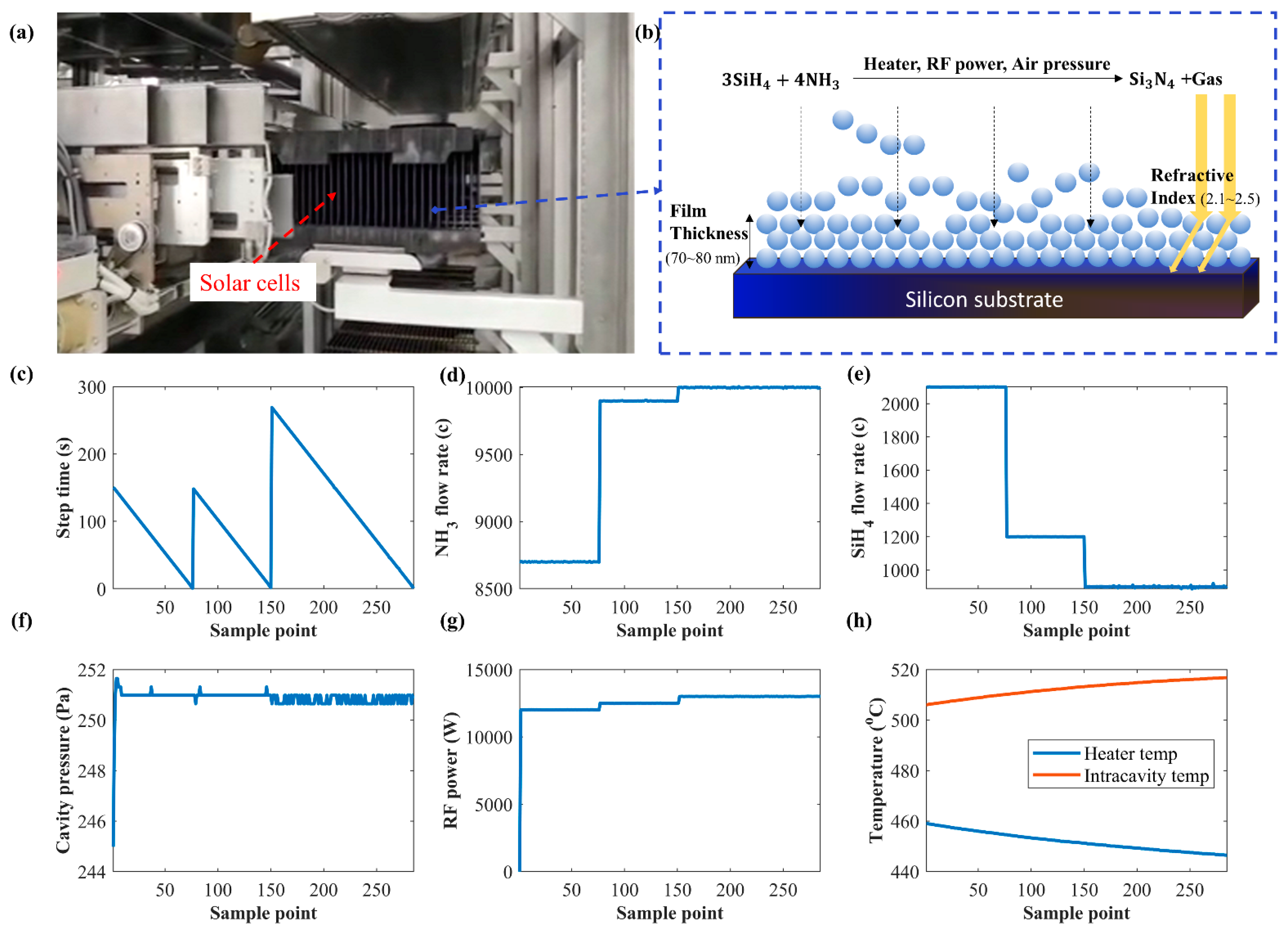
4.1. Experimental Setup and Dataset Description
4.2. Performance of AR-SAGAN
4.3. Practical Application in NCM
4.4. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pogrebnjak, A.D.; A Lisovenko, M.; Turlybekuly, A.; Buranich, V.V. Protective coatings with nanoscale multilayer architecture: Current state and main trends. Physics-Uspekhi 2021, 64, 253–279. [Google Scholar] [CrossRef]
- Sarkın, A.S.; Ekren, N.; Sağlam, Ş. A review of anti-reflection and self-cleaning coatings on photovoltaic panels. Sol. Energy 2020, 199, 63–73. [Google Scholar] [CrossRef]
- van Kampen, A.; Kohlus, R. Statistical modelling of coating layer thickness distributions: Influence of overspray on coating quality. Powder Technol. 2018, 325, 557–567. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Cheruku, S.; Geereddy, S.R. Process modeling and parameter optimization of surface coatings using artificial neural networks (ANNs): State-of-the-art review. Mater. Today Proc. 2020, 38, 2764–2774. [Google Scholar] [CrossRef]
- Shozib, I.A.; Ahmad, A.; Rahaman, S.A.; Abdul-Rani, A.M.; Alam, M.A.; Beheshti, M.; Taufiqurrahman, I. Modelling and optimization of microhardness of electroless Ni–P–TiO2 composite coating based on machine learning approaches and RSM. J. Mater. Res. Technol. 2021, 12, 1010–1025. [Google Scholar] [CrossRef]
- Azam, M.A.; Jahanzaib, M.; Wasim, A.; Hussain, S. Surface roughness modeling using RSM for HSLA steel by coated carbide tools. Int. J. Adv. Manuf. Technol. 2014, 78, 1031–1041. [Google Scholar] [CrossRef]
- Dinh, V.C.; Nguyen, T.H.; Nguyen, K.L. Application of Taguchi Method and Anova Techniques to Maximize HVOF Spraying to WC-12Co. Key Eng. Mater. 2020, 854, 109–116. [Google Scholar] [CrossRef]
- Li, B.; Fan, X.; Li, D.; Jiang, P. Design of Thermal Barrier Coatings Thickness for Gas Turbine Blade Based on Finite Element Analysis. Math. Probl. Eng. 2017, 2017, 2147830. [Google Scholar] [CrossRef] [Green Version]
- Segu, D.Z.; Kim, J.-H.; Choi, S.G.; Jung, Y.-S.; Kim, S.-S. Application of Taguchi techniques to study friction and wear properties of MoS2 coatings deposited on laser textured surface. Surf. Coat. Technol. 2013, 232, 504–514. [Google Scholar] [CrossRef]
- Zhao, L.; Diao, G.; Yao, Y. A Dynamic Process Adjustment Method Based on Residual Prediction for Quality Improvement. IEEE Trans. Ind. Inform. 2015, 12, 41–50. [Google Scholar] [CrossRef]
- Vicente, A.; Wojcik, P.J.; Mendes, M.J.; Águas, H.; Fortunato, E.; Martins, R. A statistics modeling approach for the optimization of thin film photovoltaic devices. Sol. Energy 2017, 144, 232–243. [Google Scholar] [CrossRef]
- Purwins, H.; Nagi, A.; Barak, B.; Hockele, U.; Kyek, A.; Lenz, B.; Pfeifer, G.; Weinzierl, K. Regression Methods for Prediction of PECVD Silicon Nitride Layer Thickness. In Proceedings of the 2011 IEEE International Conference on Automation Science and Engineering, Trieste, Italy, 24–27 August 2011; pp. 387–392. [Google Scholar] [CrossRef]
- Barletta, M.; Gisario, A.; Palagi, L.; Silvestri, L. Modelling the Electrostatic Fluidised Bed (EFB) coating process using Support Vector Machines (SVMs). Powder Technol. 2014, 258, 85–93. [Google Scholar] [CrossRef]
- Liau, L.-K.; Huang, C.-J.; Chen, C.-C.; Lin, S.-C.; Kuo, L.-C. Process modeling and optimization of PECVD silicon nitride coated on silicon solar cell using neural networks. Sol. Energy Mater. Sol. Cells 2002, 71, 169–179. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, W.; Luo, Z.; Sun, X.; Li, Z.; Lin, L. Ultrasonic characterization of thermal barrier coatings porosity through BP neural network optimizing Gaussian process regression algorithm. Ultrasonics 2019, 100, 105981. [Google Scholar] [CrossRef] [PubMed]
- Paturi, U.M.R.; Reddy, N.; Cheruku, S.; Narala, S.K.R.; Cho, K.K.; Reddy, M. Estimation of coating thickness in electrostatic spray deposition by machine learning and response surface methodology. Surf. Coat. Technol. 2021, 422, 127559. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, Z.; Zhou, Y.; Xia, Z.; Zhou, Z.; Zhang, L. Convolution and Long Short-Term Memory Neural Network for PECVD Process Quality Prediction. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Goodfellow, I.; Metaxas, D.; Odena, A. Self-Attention Generative Adversarial Networks. arXiv 2018, arXiv:1805.08318. [Google Scholar]
- Guan, Z.-J.; Li, R.; Jiang, J.-T.; Song, B.; Gong, Y.-X.; Zhen, L. Data mining and design of electromagnetic properties of Co/FeSi filled coatings based on genetic algorithms optimized artificial neural networks (GA-ANN). Compos. Part B Eng. 2021, 226, 109383. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Kim, E.; Cho, S.; Lee, B.; Cho, M. Fault Detection and Diagnosis Using Self-Attentive Convolutional Neural Networks for Variable-Length Sensor Data in Semiconductor Manufacturing. IEEE Trans. Semicond. Manuf. 2019, 32, 302–309. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis with Auxiliary Classifier GANs. arXiv 2017, arXiv:1610.09585. [Google Scholar]
- Rezagholiradeh, M.; Haidar, A. Reg-Gan: Semi-Supervised Learning Based on Generative Adversarial Networks for Regression. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2806–2810. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved Training of Wasserstein GANs. arXiv 2017, arXiv:1704.00028. [Google Scholar]
- Pujahari, R.M. Solar cell technology. In Energy Materials; Elsevier: Amsterdam, The Netherlands, 2021; pp. 27–60. [Google Scholar]
- Wu, X.; Zhang, Z.; Liu, Y.; Chu, X.; Li, Y. Process parameter selection study on SiNx:H films by PECVD method for silicon solar cells. Sol. Energy 2015, 111, 277–287. [Google Scholar] [CrossRef]
- Aggarwal, K.; Kirchmeyer, M.; Yadav, P.; Keerthi, S.S.; Gallinari, P. Regression with Conditional GAN. arXiv 2019, arXiv:1905.12868v1. [Google Scholar]
| Control Parameter | TC1 | TC2 | TC3 |
|---|---|---|---|
| 1 | 0.07353 | 0.05976 | 0.03904 |
| 2 | 0.03534 | 0.02876 | 0.03092 |
| 3 | 0.03125 | 0.02440 | 0.02318 |
| 4 | 0.01832 | 0.01118 | 0.00921 |
| 5 | 0.00370 | 0.00648 | 0.00096 |
| 6 | 0.00607 | 0.00614 | 0.00562 |
| 7 | 0.01228 | 0.01033 | 0.01106 |
| 8 | 0.01398 | 0.00966 | 0.00938 |
| 9 | 0.00921 | 0.00920 | 0.00976 |
| 10 | 0.01981 | 0.01504 | 0.01319 |
| 11 | 0.01209 | 0.01176 | 0.01114 |
| 12 | 0.01481 | 0.01546 | 0.01664 |
| 13 | 0.04192 | 0.05158 | 0.04206 |
| 14 | 0.01348 | 0.02008 | 0.02158 |
| 15 | 0.01931 | 0.01913 | 0.01945 |
| 16 | 0.03966 | 0.02920 | 0.03228 |
| 17 | 0.03939 | 0.03530 | 0.04110 |
| 18 | 0.03316 | 0.02360 | 0.02082 |
| 19 | 0.01759 | 0.02021 | 0.03367 |
| 20 | 0.00813 | 0.00608 | 0.00610 |
| Mean ± Std. | 0.0232 ± 0.0169 | 0.0207 ± 0.0146 | 0.0199 ± 0.0127 |
| Quality Variable | Metrics | TC1 | TC2 | TC3 | |||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | ||
| Thickness (nm) | MSE | 2.0678 | 2.6034 | 1.7089 | 2.0579 | 1.6627 | 2.0111 |
| MAPE | 0.0163 | 0.0185 | 0.0127 | 0.0148 | 0.0128 | 0.0149 | |
| Refractive index | MSE | 6.588 × 10−5 | 6.232 × 10−5 | 6.775 × 10−5 | 6.186 × 10−5 | 7.072 × 10−5 | 6.194 × 10−5 |
| MAPE | 0.0030 | 0.0028 | 0.0031 | 0.0029 | 0.0031 | 0.0029 | |
| Method | SVM | CGAN | AR-SAGAN | |||
|---|---|---|---|---|---|---|
| TN (nm) | RI | TN (nm) | RI | TN (nm) | RI | |
| Train MSE | 3.7215 | 0.0068 | 3.4107 | 8.5 × 10−5 | 1.6627 | 7.1 × 10−5 |
| Test MSE | 4.1665 | 0.0065 | 2.8082 | 8.6 × 10−5 | 2.0111 | 6.2 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.; Zhu, J.; Yang, Y.; Zhang, H.; Zhang, Z.; Xia, Z.; Zhang, Z. Self-Attention-Augmented Generative Adversarial Networks for Data-Driven Modeling of Nanoscale Coating Manufacturing. Micromachines 2022, 13, 847. https://doi.org/10.3390/mi13060847
Ji S, Zhu J, Yang Y, Zhang H, Zhang Z, Xia Z, Zhang Z. Self-Attention-Augmented Generative Adversarial Networks for Data-Driven Modeling of Nanoscale Coating Manufacturing. Micromachines. 2022; 13(6):847. https://doi.org/10.3390/mi13060847
Chicago/Turabian StyleJi, Shanling, Jianxiong Zhu, Yuan Yang, Hui Zhang, Zhihao Zhang, Zhijie Xia, and Zhisheng Zhang. 2022. "Self-Attention-Augmented Generative Adversarial Networks for Data-Driven Modeling of Nanoscale Coating Manufacturing" Micromachines 13, no. 6: 847. https://doi.org/10.3390/mi13060847
APA StyleJi, S., Zhu, J., Yang, Y., Zhang, H., Zhang, Z., Xia, Z., & Zhang, Z. (2022). Self-Attention-Augmented Generative Adversarial Networks for Data-Driven Modeling of Nanoscale Coating Manufacturing. Micromachines, 13(6), 847. https://doi.org/10.3390/mi13060847









