Robust Adaptive Beamforming Algorithm for Sparse Subarray Antenna Array Based on Hierarchical Weighting
Abstract
:1. Introduction
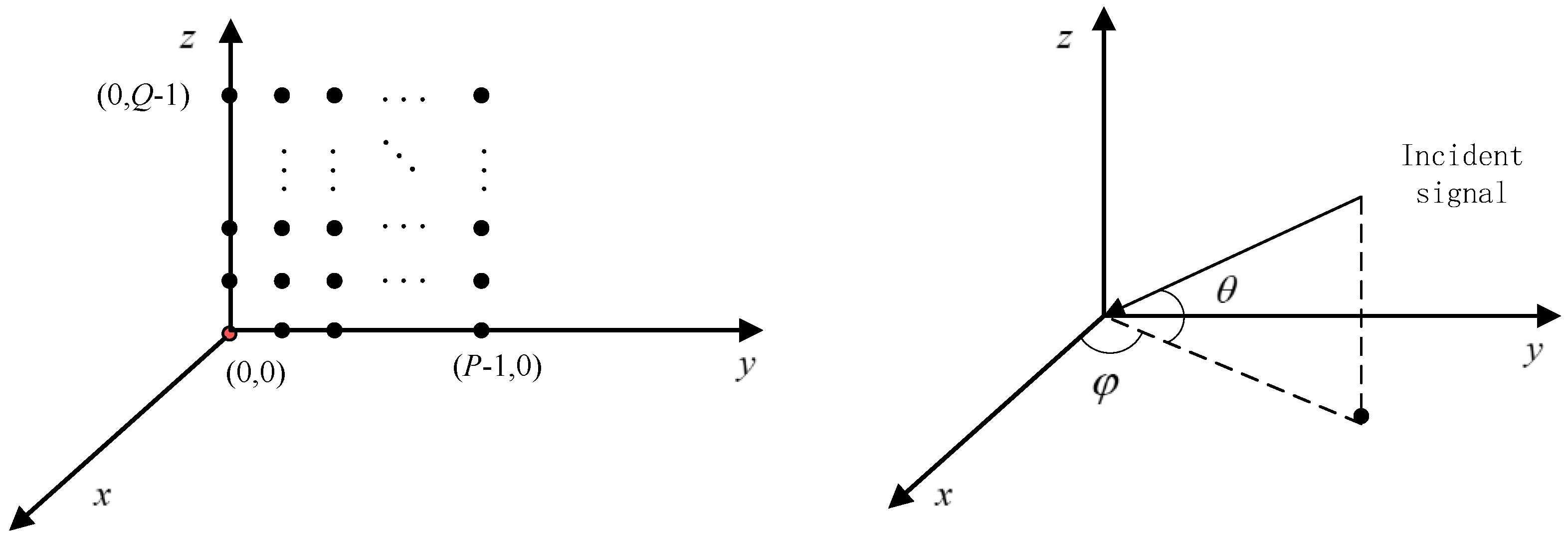
2. Received Signal Model of Two-Dimensional Planar Sparse Subarray
2.1. Two-Dimensional Planar Uniform Sparse Array Signal Model
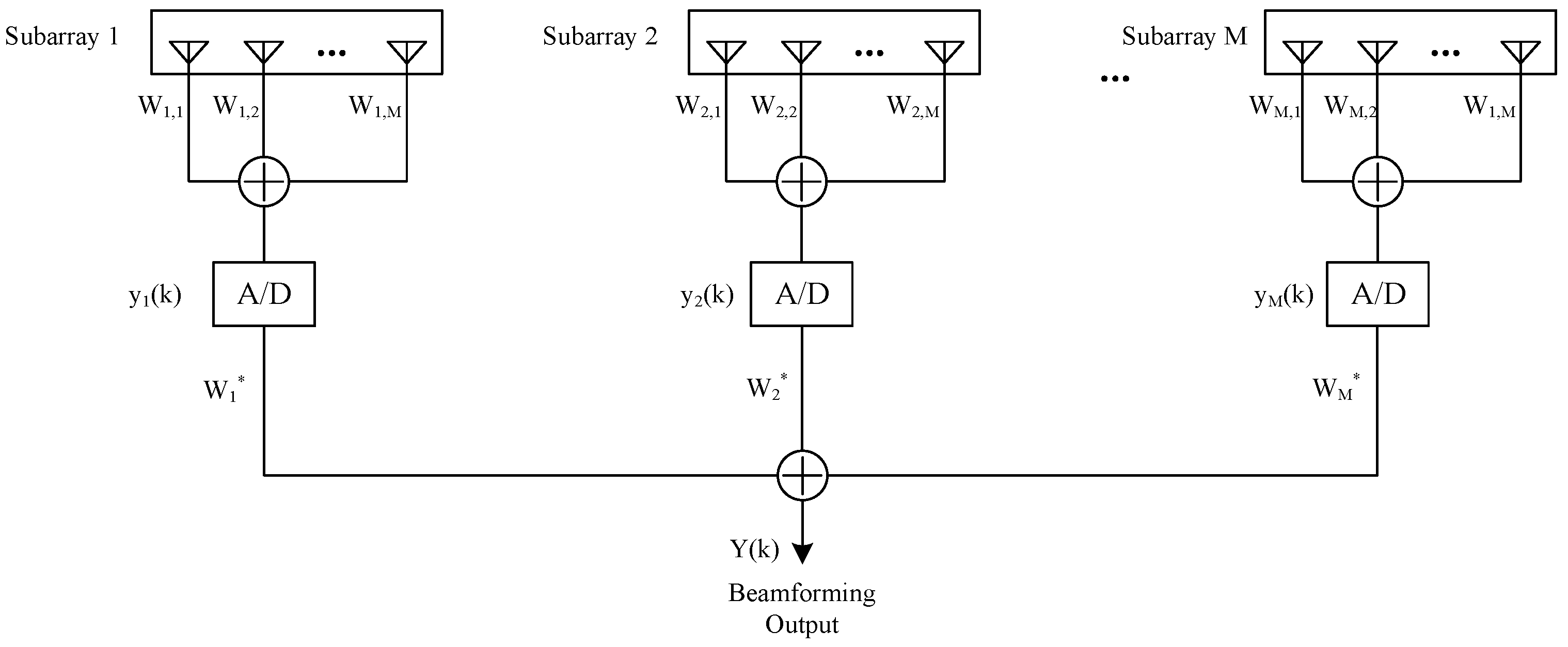
2.2. Two-Dimensional Planar Sparse Subarray Signal Model
3. Algorithm Introduction
- Step 1: According to the sparse subarray antenna array configuration, the array guidance vector is constructed according to Equations (11)–(14);
- Step 2: According to the beam pointing requirements of the antenna array, calculate the weight vector of the antenna elements in the subarray according to Equation (17);
- Step 3: Taking the beamforming output of each subarray as the sparse array element signal, and are calculated according to Equations (28) and (30), respectively;
- Step 4: According to the optimization model (33), estimate the true steering vector ;
- Step 5: According to Equation (34), the weight vector among the subarrays is obtained with and the estimated true steering vector, and the final beamforming output result is obtained by using Equation (20).
4. Simulation Experiment Verification
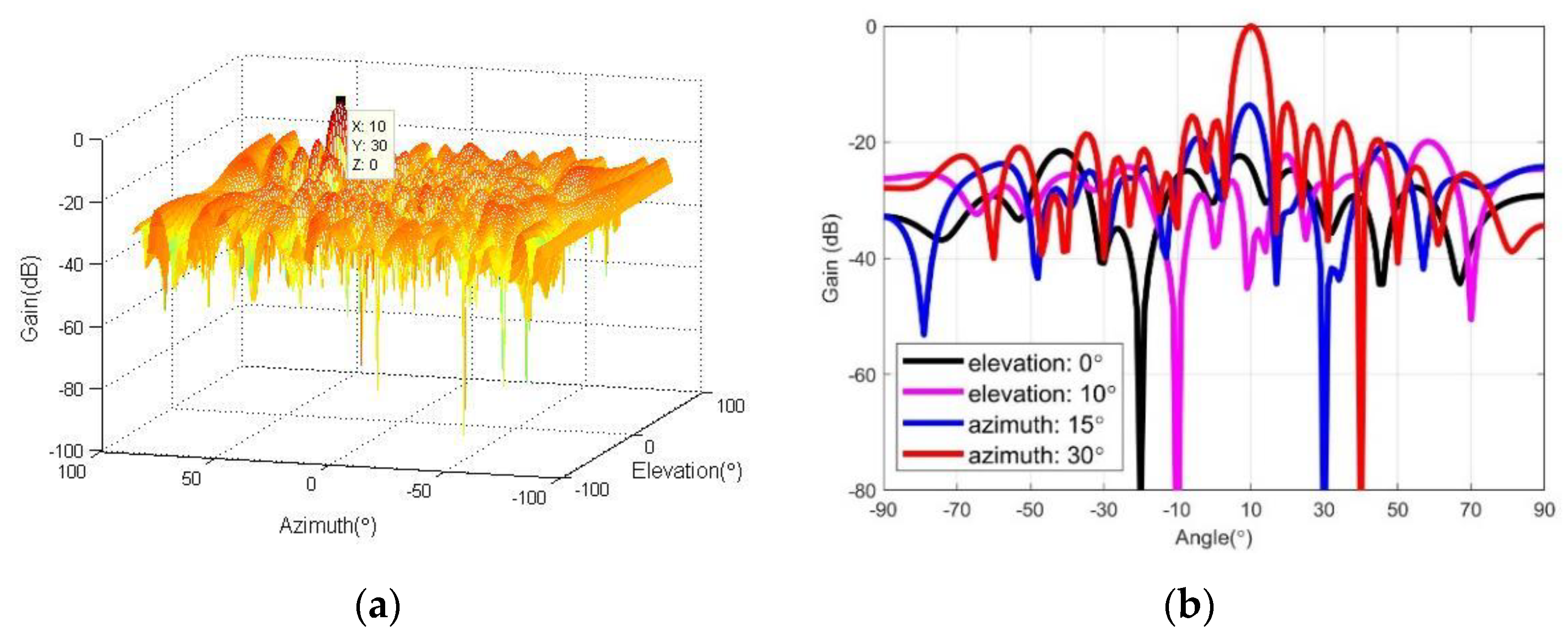
4.1. Simulation for Array Beampattern
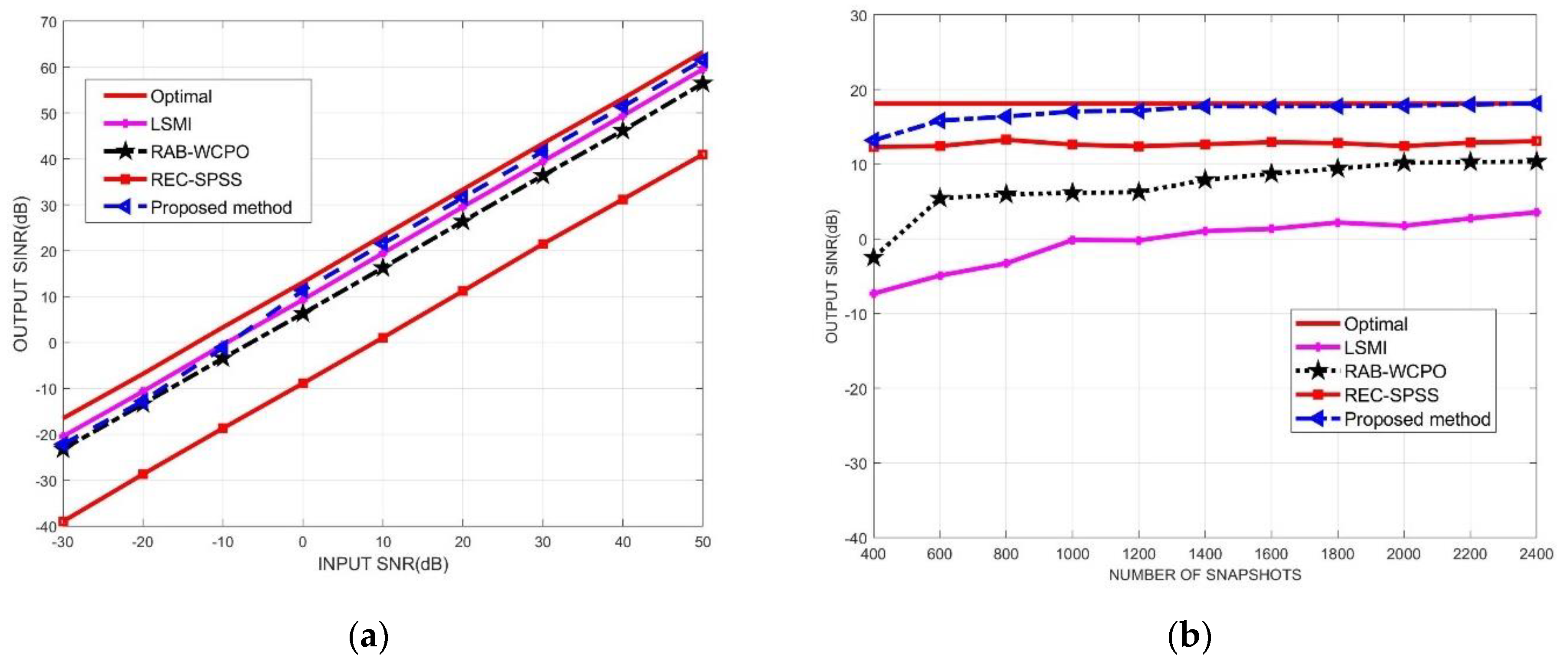
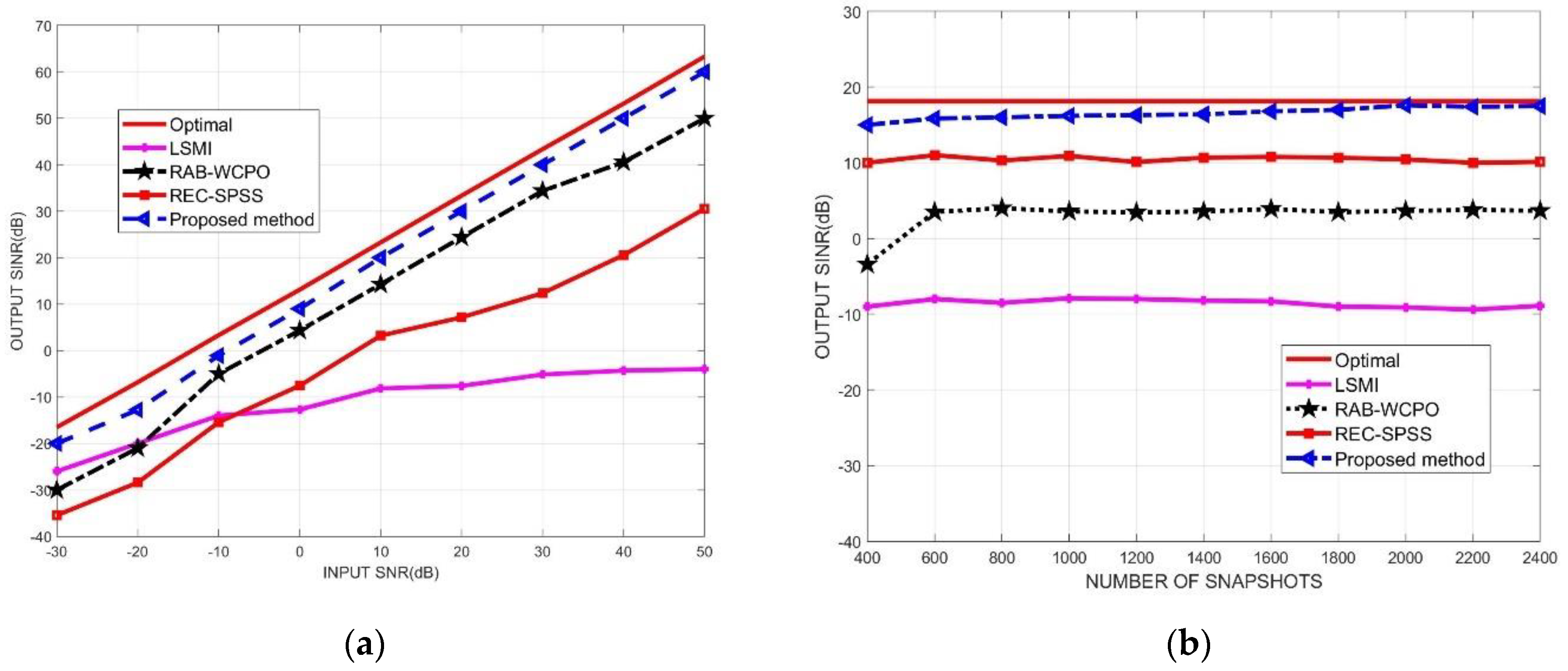
4.2. Beamforming Performance without Direction Mismatch of the Desired Signal
4.3. Beamforming Performance with Direction Mismatch of the Desired Signal
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, A.D. AESA Overview. In Active Electronically Scanned Arrays: Fundamentals and Applications; IEEE: Piscataway, NJ, USA, 2022; pp. 1–17. [Google Scholar] [CrossRef]
- Yang, J.; Lu, J.; Liu, X.; Liao, G. Robust Null Broadening Beamforming Based on Covariance Matrix Reconstruction via Virtual Interference Sources. Sensors 2020, 20, 1865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mestre, X.; Lagunas, M.A. Finite sample size effect on minimum variance beamformers: Optimum diagonal loading factor for large arrays. IEEE Trans. Signal Process. 2006, 54, 69–82. [Google Scholar] [CrossRef]
- Ke, Y.; Zheng, C.; Peng, R.; Li, X. Robust Adaptive Beamforming Using Noise Reduction Preprocessing-Based Fully Automatic Diagonal Loading and Steering Vector Estimation. IEEE Access 2017, 5, 12974–12987. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Amin, M.G. Array processing for nonstationary interference suppression in DS/SS communications using subspace projection techniques. IEEE Trans. Signal Process. 2001, 49, 3005–3014. [Google Scholar] [CrossRef]
- Amin, M.G.; Zhao, L.; Lindsey, A.R. Subspace array processing for the suppression of FM jamming in GPS receivers. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 80–92. [Google Scholar] [CrossRef]
- Sgammini, M.; Antreich, F.; Kurz, L.; Meurer, M.; Noll, T.G. Blind Adaptive Beamformer Based on Orthogonal Projections for GNSS. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 17–22 September 2012; Volume 137, pp. 926–935. [Google Scholar]
- Bao, Y.; Chen, H. Design of robust broadband beamformers using Worst-Case Performance Optimization: A Semidefinite Programming Approach. IEEE ACM Trans. Audio Speech Lang. Process. 2017, 25, 895–907. [Google Scholar] [CrossRef]
- Luo, Y.; Pan, J.; Zhang, J.A.; Huang, S. Worst-Case Performance Optimization beamformer with embedded array’s active pattern. Int. J. Antennas Propag. 2018, 2018, 9237321. [Google Scholar] [CrossRef]
- Huang, Y.; Fu, H.; Vorobyov, S.A.; Luo, Z.Q. Worst-Case SINR maximization based robust adaptive beamforming problem with a nonconvex uncertainty set. In Proceedings of the 2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Le Gosier, Guadeloupe, 15–18 December 2019; pp. 31–35. [Google Scholar]
- Gu, Y.; Leshem, A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steeing vector estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Mohammadzadeh, S.; Nascimento, V.H.; de Lamare, R.C.; Kukrer, O. Maximum entropy-based interference-plus-noise covariance matrix reconstruction for robust adaptive beamforming. IEEE Signal Process. Lett. 2020, 27, 845–849. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, J.; Xu, X.; Ye, Z. Robust adaptive beamforming with a novel interference-plus-noise covariance matrix reconstruction method. IEEE Trans. Signal Process. 2015, 63, 1643–1650. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Liu, F.; Lan, T.; Long, T.; Sarkar, T.K. Robust adaptive beamforming based on covariance matrix reconstruction with annular uncertainty set and vector space projection. IEEE Antennas Wirel. Propag. Lett. 2020, 20, 130–134. [Google Scholar] [CrossRef]
- Yuan, X.; Gan, L. Robust algorithm against large look direction error for interference- plus-noise covariance matrix reconstruction. Electron. Lett. 2016, 52, 448–450. [Google Scholar] [CrossRef]
- Shen, F.; Chen, F.; Song, J. Robust adaptive beamforming based on steering vector estimation and covariance matrix reconstruction. IEEE Commun. Lett. 2015, 19, 1636–1639. [Google Scholar] [CrossRef]
- Ruan, H.; De Lamare, R.C. Robust adaptive beamforming using a low-complexity shrinkage-based mismatch estimation algorithm. IEEE Signal Process. Lett. 2014, 21, 60–64. [Google Scholar] [CrossRef]
- Hou, Y.S.; Liu, X.; Yong, J. Robust adaptive beamforming method based on interference-plus-noise covariance matrix. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Communication and Computing, Kunming, China, 5–8 August 2013. [Google Scholar]
- Liu, J.B.; Xie, W.; Wan, Q.; Gui, G. Robust Widely Linear Beamforming via the Techniques of Iterative QCQP and Shrinkage for Steering Vector Estimation. IEEE Access 2018, 6, 17143–17152. [Google Scholar] [CrossRef]
- Sun, S.C.; Ye, Z.F. Robust adaptive beamforming based on a method for steering vector estimation and interference covariance matrix reconstruction. Signal Process. 2021, 182, 107939. [Google Scholar] [CrossRef]
- Bi, Y.; Feng, X.A.; Guo, T. Robust Adaptive Beamforming Based on Interference-Plus-Noise Covariance Matrix Reconstruction Method. Prog. Electromagn. Res. M 2020, 97, 87–96. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhang, Y.D. Generalized Non-Redundant Sparse Array Designs. IEEE Trans. Signal Process. 2021, 69, 4580–4594. [Google Scholar] [CrossRef]
- Wang, X.; Amin, M.; Wang, X.; Cao, X. Sparse array quiescent beamformer design combining adaptive and deterministic constraints. IEEE Trans. Antennas Propag. 2017, 65, 5808–5818. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, C.; Goodman, N.A.; Song, W.Z.; Shi, Z. Coprime array adaptive beamforming based on compressive sensing virtual array signal. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2981–2985. [Google Scholar]
- Liu, K.; Zhang, Y.D. Coprime array-based robust beamforming using covariance matrix reconstruction technique. IET Commun. 2018, 12, 2206–2212. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.Y.; Li, M.; Tan, W.J. Sparsity-based robust beamforming method using nested array. J. Terahertz Sci. Electron. Inf. Technol. 2019, 17, 462–468. [Google Scholar]
- Zheng, Z.; Yang, T.; Wang, W.Q.; Zhang, S.S. Robust adaptive beamforming via coprime coarray interpolation. Signal Processing 2020, 169, 107382. [Google Scholar] [CrossRef]
- Du, Y.X.; Cui, W.J.; Wang, Y.S.; Jian, C.X.; Zhang, J. Robust Adaptive Beamforming Algorithm for Sparse Array Based on Covariance Matrix Reconstruction Technology. Int. J. Antennas Propag. 2022, 2022, 1442459. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplinedconvex Programming, Version 2.1. March 2017. Available online: http://cvxr.com/cvx (accessed on 20 April 2021).
- Liu, X.X.; Yang, J.; Lu, J. Optimization software for sparse subarray layout based on genetic algorithm. Ordnance Ind. Autom. 2022, 41, 74–79. [Google Scholar]
- Cox, H.; Zeskind, R.M.; Owen, M.M. Robust adaptive beamforming. IEEE Trans. Acoust. Speech Signal Processing 1987, 35, 1365–1376. [Google Scholar] [CrossRef] [Green Version]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, W.; Leng, W.; Wang, A.; Shi, H. Interference-plus-noise covariance matrix reconstruction via spatial power spectrum sampling for robust adaptive beamforming. IEEE Signal Process. Lett. 2016, 23, 121–125. [Google Scholar] [CrossRef] [Green Version]
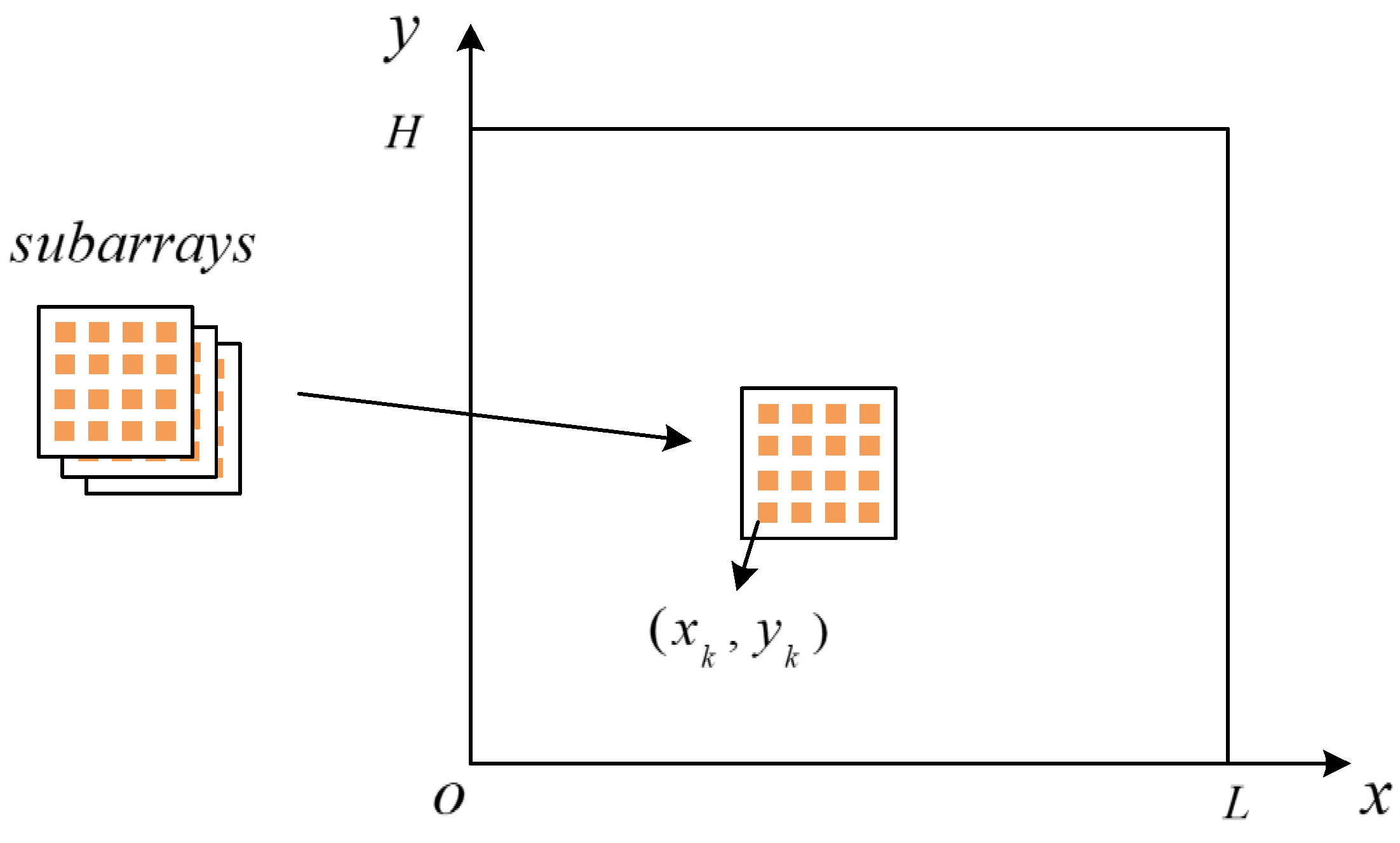
| Position | Subarray 1 | Subarray 2 | Subarray 3 | Subarray 4 | Subarray 5 | Subarray 6 | Subarray 7 | Subarray 8 |
|---|---|---|---|---|---|---|---|---|
| X | 0 | 0 | 0.0794 | 0.1325 | 0.1955 | 0.25 | 0.25 | 0.25 |
| Y | 0.0075 | 0.2349 | 0.1578 | 0.25 | 0.25 | 0.25 | 0.1339 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Liu, X.; Tu, Y.; Li, W. Robust Adaptive Beamforming Algorithm for Sparse Subarray Antenna Array Based on Hierarchical Weighting. Micromachines 2022, 13, 859. https://doi.org/10.3390/mi13060859
Yang J, Liu X, Tu Y, Li W. Robust Adaptive Beamforming Algorithm for Sparse Subarray Antenna Array Based on Hierarchical Weighting. Micromachines. 2022; 13(6):859. https://doi.org/10.3390/mi13060859
Chicago/Turabian StyleYang, Jian, Xinxin Liu, Yuwei Tu, and Weixing Li. 2022. "Robust Adaptive Beamforming Algorithm for Sparse Subarray Antenna Array Based on Hierarchical Weighting" Micromachines 13, no. 6: 859. https://doi.org/10.3390/mi13060859
APA StyleYang, J., Liu, X., Tu, Y., & Li, W. (2022). Robust Adaptive Beamforming Algorithm for Sparse Subarray Antenna Array Based on Hierarchical Weighting. Micromachines, 13(6), 859. https://doi.org/10.3390/mi13060859






