Effect of Substrate-RF on Sub-200 nm Al0.7Sc0.3N Thin Films
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication Flow
2.2. Characterization Method
3. Results
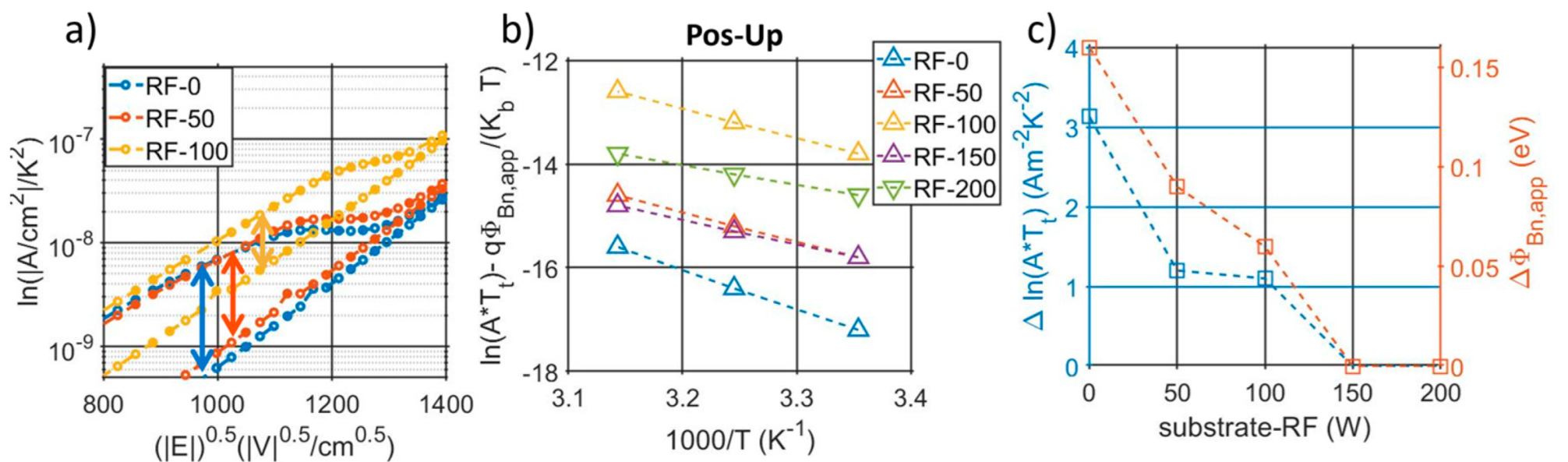
3.1. Material
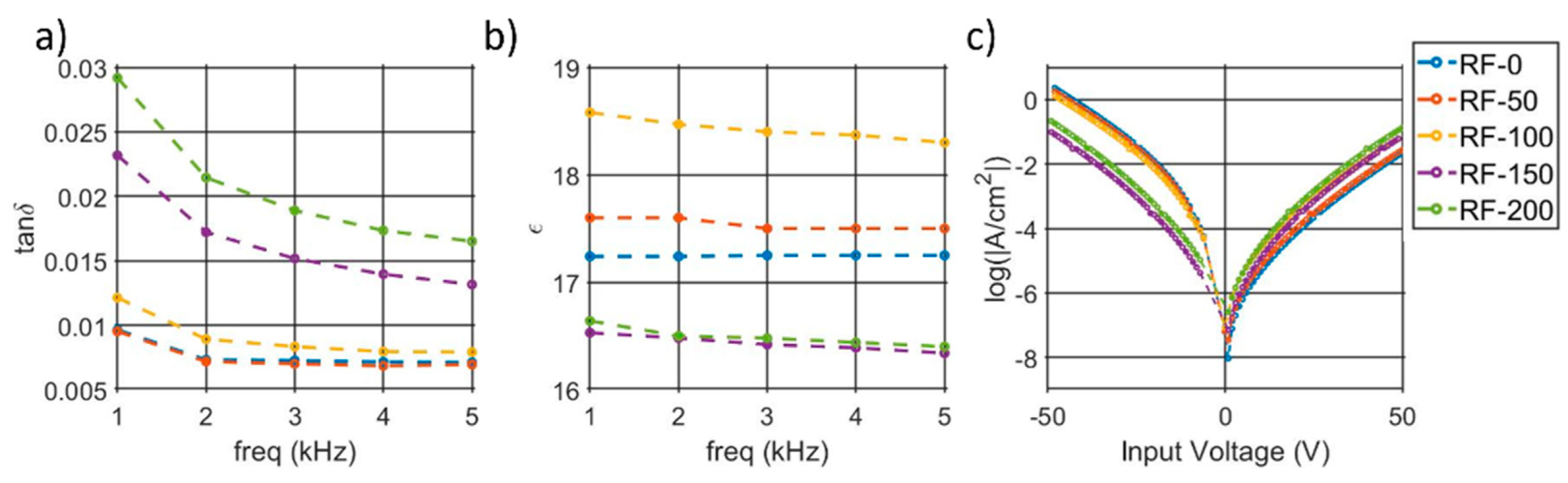
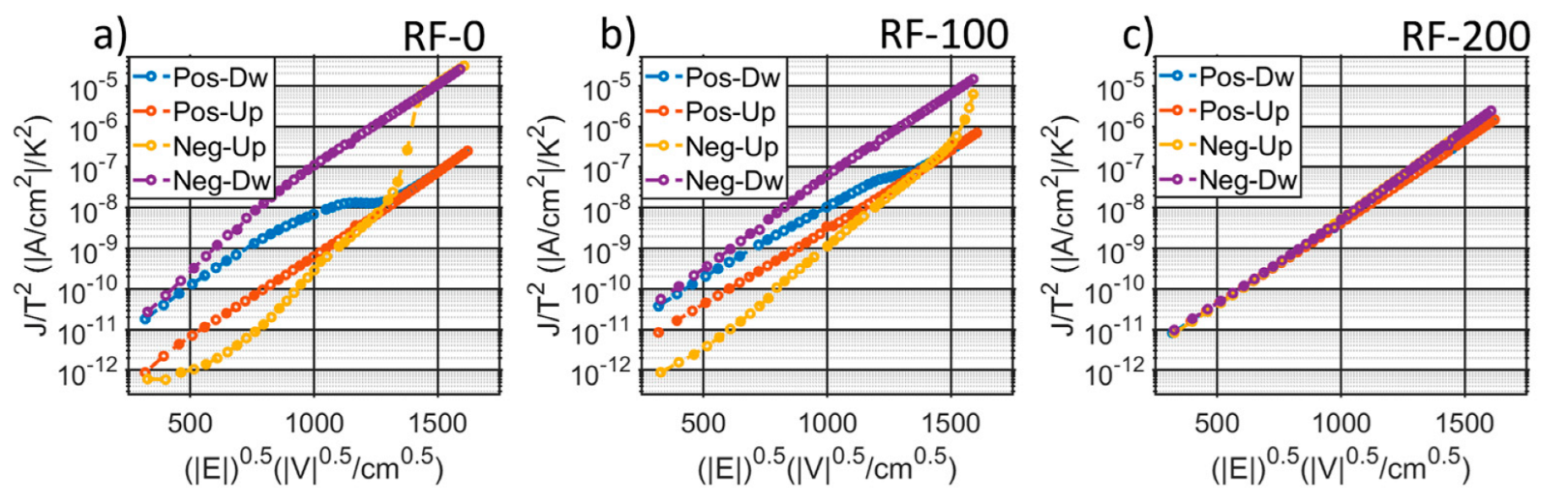
3.2. Dielectric Properties
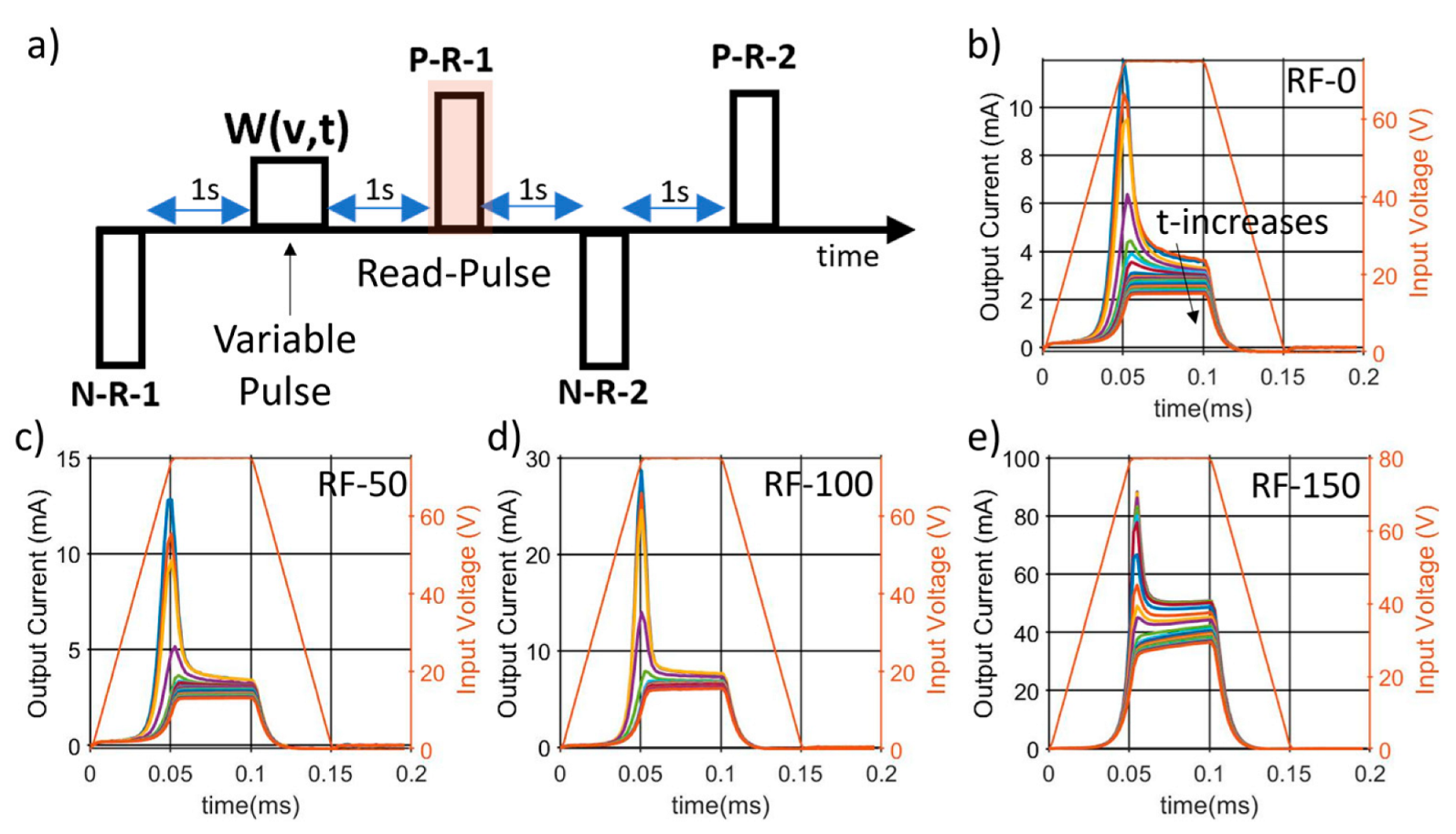
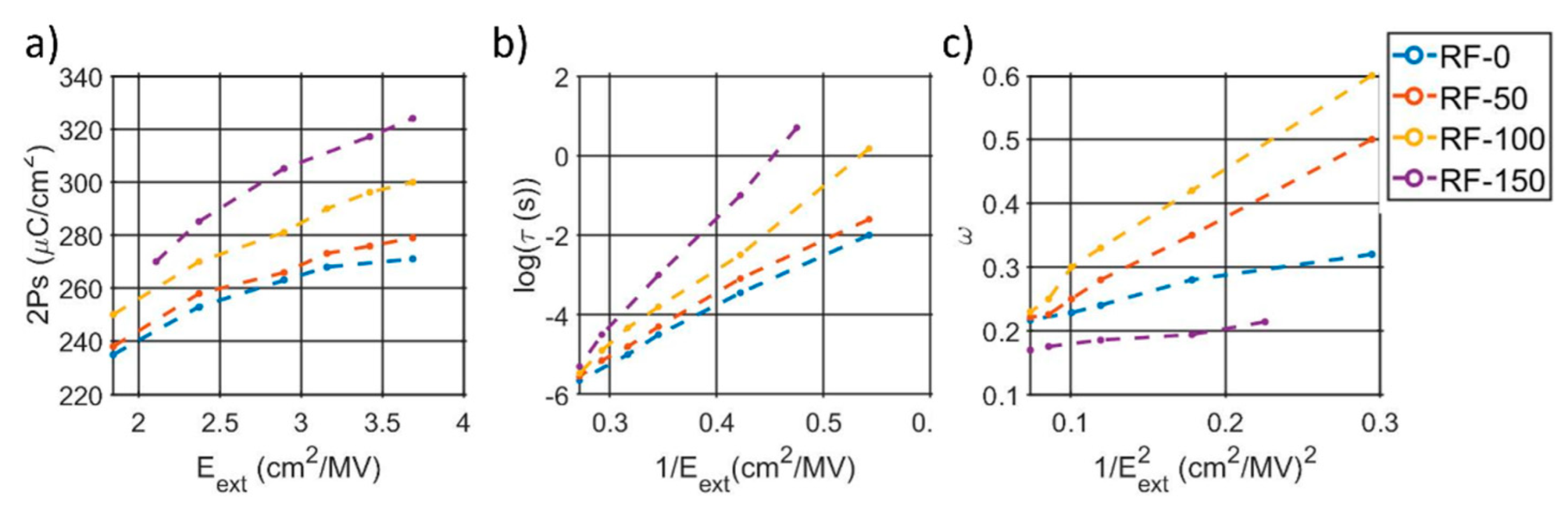
3.3. Ferroelectric Properties
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akiyama, M.; Kamohara, T.; Kano, K.; Teshigahara, A.; Takeuchi, Y.; Kawahara, N. Enhancement of piezoelectric response in scandium aluminum nitride alloy thin films prepared by dual reactive cosputtering. Adv. Mater. 2009, 21, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.Y.; Sato, S.; Teshigahara, A.; Nakamura, T.; Kano, K. High-performance surface acoustic wave resonators inthe 1 to 3 GHz range using a ScAlN/6 H-SiC structure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 637–642. [Google Scholar] [CrossRef] [PubMed]
- Moreira, M.; Bjurström, J.; Katardjev, I.; Yantchev, V. Aluminum scandium nitride thin-film bulk acoustic resonators for wide band applications. Vacuum 2011, 86, 23–26. [Google Scholar] [CrossRef]
- Konno, A.; Sumisaka, M.; Teshigahara, A.; Kano, K.; Hashimo, K.Y.; Hirano, H.; Esashi, M.; Kadota, M.; Tanaka, S. ScAlN Lamb wave resonator in GHz range released by XeF 2 etching. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 1378–1381. [Google Scholar] [CrossRef]
- Yantchev, V.; Katardjiev, I. Thin film Lamb wave resonators in frequency control and sensing applications: A review. J. Micromech. Microeng. 2013, 23, 043001. [Google Scholar] [CrossRef]
- Lozzi, A.; Yen, E.T.T.; Muralt, P.; Villanueva, L.G. Al0.83 Sc0.17 N contour-mode resonators with electromechanical coupling in excess of 4.5%. In IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control; IEEE: Piscataway, NJ, USA, 2018; Volume 66, pp. 146–153. [Google Scholar] [CrossRef]
- Schneider, M.; DeMiguel-Ramos, M.; Flewitt, A.J.; Iborra, E.; Schmid, U. Scandium aluminium nitride-based film bulk acoustic resonators. Multidiscip. Digit. Publ. Inst. Proc. 2017, 1, 305. [Google Scholar] [CrossRef] [Green Version]
- Ghatge, M.; Felmetsger, V.; Tabrizian, R. High kt2*Q Waveguide-Based ScAlN-on-Si UHF and SHF Resonators. In Proceedings of the IEEE International Frequency Control Symposium (IFCS), Olympic Valley, CA, USA, 21–24 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Ansari, A. Single crystalline scandium aluminum nitride: An emerging material for 5 G acoustic filters. In Proceedings of the IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Fichtner, S.; Wolff, N.; Lofink, F.; Kienle, L.; Wagner, B. AlScN: A III-V semiconductor based ferroelectric. J. Appl. Phys. 2019, 125, 114103. [Google Scholar] [CrossRef]
- Wang, J.; Park, M.; Mertin, S.; Pensala, T.; Ayazi, F.; Ansari, A. A High-kt2 Switchable Ferroelectric Al0.7Sc0.3N Film Bulk Acoustic Resonator. In Proceedings of the Joint Conference of the IEEE International Frequency Control Symposium and International Symposium on Applications of Ferroelectrics (IFCS-ISAF), Keystone, CO, USA, 19–23 July 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Rassay, S.; Mo, D.; Li, C.; Choudhary, N.; Forgey, C.; Tabrizian, R. Intrinsically switchable ferroelectric scandium aluminum nitride lamb-mode resonators. IEEE Electron Device Lett. 2021, 42, 1065–1068. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Wang, D.; Musavigharavi, P.; Stach, E.; Olsson, R.; Jariwala, D. Aluminum scandium nitride-based metal–ferroelectric–metal diode memory devices with high on/off ratios. Appl. Phys. Lett. 2021, 118, 202901. [Google Scholar] [CrossRef]
- Herrera, B.; Pirro, M.; Giribaldi, G.; Colombo, L.; Rinaldi, M. AlScN Programmable Ferroelectric Micromachined UltrasonicTransducer (FMUT). In Proceedings of the 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; pp. 38–41. [Google Scholar] [CrossRef]
- Olsson, R.H.; Tang, Z.; D’Agati, M. Non-Kolmogorov-Avrami switching kinetics in ferroelectric thin films. In Proceedings of the IEEE Custom Integrated Circuits Conference (CICC), Boston, MA, USA, 22–25 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kataoka, J.; Tsai, S.L.; Hoshii, T.; Wakabayashi, H.; Tsutsui, K.; Kakushima, K. A possible origin of the large leakage current in ferroelectric Al1 xScxN films. Jpn. J. Appl. Phys. 2021, 60, 030907. [Google Scholar] [CrossRef]
- Tsai, S.L.; Hoshii, T.; Wakabayashi, H.; Tsutsui, K.; Chung, T.K.; Chang, E.Y.; Kakushima, K. Field cycling behavior and breakdown mechanism of ferroelectric Al0.78Sc0.22N films. Jpn. J. Appl. Phys. 2022. [Google Scholar] [CrossRef]
- Yasuoka, S.; Shimizu, T.; Tateyama, A.; Uehara, M.; Yamada, H.; Akiyama, M.; Hiranaga, Y.; Cho, Y.; Funakubo, H. Effectsof deposition conditions on the ferroelectric properties of (Al1 x Sc x) N thin films. J. Appl. Phys. 2020, 128, 114103. [Google Scholar] [CrossRef]
- Yazawa, K.; Drury, D.; Zakutayev, A.; Brennecka, G.L. Reduced coercive field in epitaxial thin film of ferroelectric wurtzite Al0.7Sc0.3N. Appl. Phys. Lett. 2021, 118, 162903. [Google Scholar] [CrossRef]
- Zhu, W.; Hayden, J.; He, F.; Yang, J.I.; Tipsawat, P.; Hossain, M.D.; Maria, J.P.; Trolier-McKinstry, S. Strongly temperature dependent ferroelectric switching in AlN, Al1-xScxN, and Al1-xBxN thin films. Appl. Phys. Lett. 2021, 119, 062901. [Google Scholar] [CrossRef]
- Fichtner, S.; Reimer, T.; Chemnitz, S.; Lofink, F.; Wagner, B. Stress controlled pulsed direct current co-sputtered Al1 xScxN as piezoelectric phase for micromechanical sensor applications. APL Mater. 2015, 3, 116102. [Google Scholar] [CrossRef] [Green Version]
- Dubois, M.A.; Muralt, P. Stress and piezoelectric properties of aluminum nitride thin films deposited onto metal electrodes by pulsed direct current reactive sputtering. J. Appl. Phys. 2001, 89, 6389–6395. [Google Scholar] [CrossRef]
- Iborra, E.; Olivares, J.; Clement, M.; Vergara, L.; Sanz-Hervás, A.; Sangrador, J. Piezoelectric properties and residual stress of sputtered AlN thin films for MEMS applications. Sens. Actuators A Phys. 2004, 115, 501–507. [Google Scholar] [CrossRef]
- Zhang, S.; Holec, D.; Fu, W.Y.; Humphreys, C.J.; Moram, M.A. Tunable optoelectronic and ferroelectric properties in Sc-based III-nitrides. J. Appl. Phys. 2013, 114, 133510. [Google Scholar] [CrossRef] [Green Version]
- Garino, T.J.; Harrington, M. Residual Stress in Pzt Thin Films and its Effect on Ferroelectric Properties. In MRS Online Proceedings Library (OPL); Springer Nature Switzerland AG: Cham, Switzerland, 1999; Volume 243, pp. 341–347. [Google Scholar] [CrossRef]
- Berfield, T.A.; Ong, R.J.; Payne, D.A.; Sottos, N.R. Residual stress effects on piezoelectric response of sol-gel derived lead zirconate titanate thin films. J. Appl. Phys. 2007, 101, 024102. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Zhou, J.; Chen, W.; Shen, J.; Lv, C. Effects of residual stress on the electrical properties in PbZr0.52Ti0.48O3 thin films. J. Sol-Gel Sci. Technol. 2015, 75, 551–556. [Google Scholar] [CrossRef]
- Lee, J.W.; Park, C.S.; Kim, M.; Kim, H.E. Effects of residual stress on the electrical properties of PZT films. J. Am. Ceram. Soc. 2007, 90, 1077–1080. [Google Scholar] [CrossRef]
- Rassay, S.; Hakim, F.; Li, C.; Forgey, C.; Choudhary, N.; Tabrizian, R. A Segmented-Target Sputtering Process for Growth of Sub-50 nm Ferroelectric Scandium–Aluminum–Nitride Films with Composition and Stress Tuning. Phys. Status Solidi (RRL)-Rapid Res. Lett. 2021, 15, 2100087. [Google Scholar] [CrossRef]
- Gong, N.; Sun, X.; Jiang, H.; Chang-Liao, K.S.; Xia, Q.; Ma, T.P. Nucleation limited switching (NLS) model for HfO2-based metal-ferroelectric-metal (MFM) capacitors: Switching kinetics and retention characteristics. Appl. Phys. Lett. 2018, 112, 262903. [Google Scholar] [CrossRef]
- Tagantsev, A.K.; Stolichnov, I.; Setter, N.; Cross, J.S.; Tsukada, M. Non-Kolmogorov-Avrami switching kinetics in ferroelectric thin films. Phys. Rev. B 2002, 66, 214109. [Google Scholar] [CrossRef]
- Anders, A. Physics of arcing, and implications to sputter deposition. Thin Solid Films 2006, 502, 22–28. [Google Scholar] [CrossRef] [Green Version]
- Berg, S.; Nyberg, T. Fundamental understanding and modeling of reactive sputtering processes. Thin Solid Films 2005, 476, 215–230. [Google Scholar] [CrossRef]
- Zheng, J.X.; Wang, D.; Musavigharavi, P.; Fiagbenu, M.M.A.; Jariwala, D.; Stach, E.A.; Olsson, R.H., III. Electrical breakdown strength enhancement in aluminum scandium nitride through a compositionally modulated periodic multilayer structure. J. Appl. Phys. 2021, 130, 144101. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, W.; Tai, L.; Zhao, G.; Sang, P.; Wang, Q.; Chen, F.; Tang, M.; Feng, Y.; Zhan, X.; et al. In-depth Understanding of Polarization Switching Kinetics in Polycrystalline Hf0.5Zr0.5O2 Ferroelectric Thin Film: A Transition From NLS to KAI. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–16 December 2021; pp. 19.1.1–19.1.4. [Google Scholar] [CrossRef]
- Ishibashi, Y.; Takagi, Y. Note on ferroelectric domain switching. J. Phys. Soc. Jpn. 1971, 31, 506–510. [Google Scholar] [CrossRef]
- Dimmler, K.; Parris, M.; Butler, D.; Eaton, S.; Pouligny, B.; Scott, J.F.; Ishibashi, Y. Switching kinetics in KNO3 ferroelectric thin-film memories. J. Appl. Phys. 1987, 61, 5467–5470. [Google Scholar] [CrossRef]
- Pabst, G.W.; Martin, L.M.; Chu, Y.M.; Ramesh, R. Leakage mechanisms in thin BiFeO3 films. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
- Jo, J.Y.; Han, H.S.; Yoon, J.G.; Song, T.K.; Kim, S.H.; Noh, T.W. Domain switching kinetics in disordered ferroelectric thin films. Phys. Rev. Lett. 2007, 99, 267602. [Google Scholar] [CrossRef] [Green Version]
- Moram, M.A.; Vickers, M.E. X-ray diffraction of III-nitrides. Rep. Prog. Phys. 2009, 72, 036502. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirro, M.; Zhao, X.; Herrera, B.; Simeoni, P.; Rinaldi, M. Effect of Substrate-RF on Sub-200 nm Al0.7Sc0.3N Thin Films. Micromachines 2022, 13, 877. https://doi.org/10.3390/mi13060877
Pirro M, Zhao X, Herrera B, Simeoni P, Rinaldi M. Effect of Substrate-RF on Sub-200 nm Al0.7Sc0.3N Thin Films. Micromachines. 2022; 13(6):877. https://doi.org/10.3390/mi13060877
Chicago/Turabian StylePirro, Michele, Xuanyi Zhao, Bernard Herrera, Pietro Simeoni, and Matteo Rinaldi. 2022. "Effect of Substrate-RF on Sub-200 nm Al0.7Sc0.3N Thin Films" Micromachines 13, no. 6: 877. https://doi.org/10.3390/mi13060877
APA StylePirro, M., Zhao, X., Herrera, B., Simeoni, P., & Rinaldi, M. (2022). Effect of Substrate-RF on Sub-200 nm Al0.7Sc0.3N Thin Films. Micromachines, 13(6), 877. https://doi.org/10.3390/mi13060877





