Peripheral-Free Calibration Method for Redundant IMUs Based on Array-Based Consumer-Grade MEMS Information Fusion
Abstract
:1. Introduction
1.1. Background
1.2. Related Works
1.3. Purpose of This Research
- (1)
- The IMU achieves peripheral-free real-time calibration [31] of a single IMU based on the elimination of its own random errors using ALLAN variance [32], which is achieved by calibrating a single IMU in real time in the attitude transformation of the inertial module, and recording the currently calibrated deterministic error parameters, and calculating the extremes of the deterministic error parameters of the single IMU through an iterative optimization algorithm. The iterative optimization algorithm calculates the extreme value of the deterministic error parameter of the individual IMU, thus obtaining a highly accurate individual IMU.
- (2)
- Based on the calibrated individual IMU, the multi-sensor fusion algorithm [33,34,35] is referenced to obtain the fusion calibration algorithm proposed in this thesis, which is used to calculate the deterministic error parameters of the MEMS array, thus enabling pure inertial navigation without auxiliary equipment in complex outdoor environments in a short time.
2. Error Modelling of M-IMU and Cost Functions
2.1. Error Models for M-IMU
2.2. Constructing Cost Functions for Accelerometers
2.3. Constructing the Cost Function of the Gyroscope
2.3.1. Constructing the Attitude Transformation Matrix
2.3.2. The Cost Function of the Gyroscope
2.4. Optimization Algorithm for Minimizing the Cost Function
2.5. Algorithm for Fusing Calibration Parameters
3. MEMS Array Calibration Experiments
3.1. Calibration Experimental Procedure
3.1.1. Static and Dynamic Filters
3.1.2. Calibration Procedure
3.2. Calibration of MEMS Data Parameters for Real Experiments
| Parameters | Accelerometers | Gyroscope | ||||
|---|---|---|---|---|---|---|
| White Noise | Bias Instability | Random Walk | White Noise | Bias Instability | Random Walk | |
| X-axis | 0.0012 | 1.5702 × 10−5 | 3.3759 × 10−4 | 0.1219 | 5.6467 × 10−4 | 0.0119 |
| Y-axis | 0.0015 | 5.0196 × 10−6 | 1.3451 × 10−4 | 0.1219 | 5.6467 × 10−4 | 0.0119 |
| Z-axis | 0.0011 | 3.5621 × 10−6 | 1.0334 × 10−4 | 0.1526 | 0.6689 | 0.2182 |
4. Validation and Discussion
- (1)
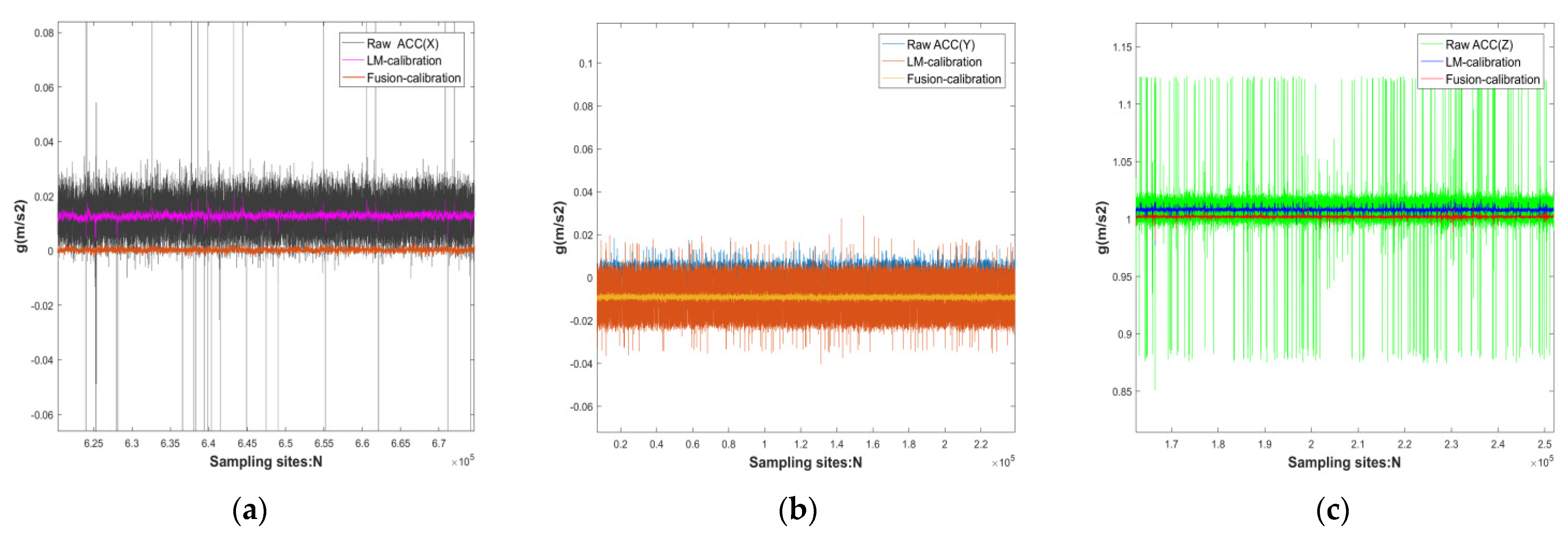
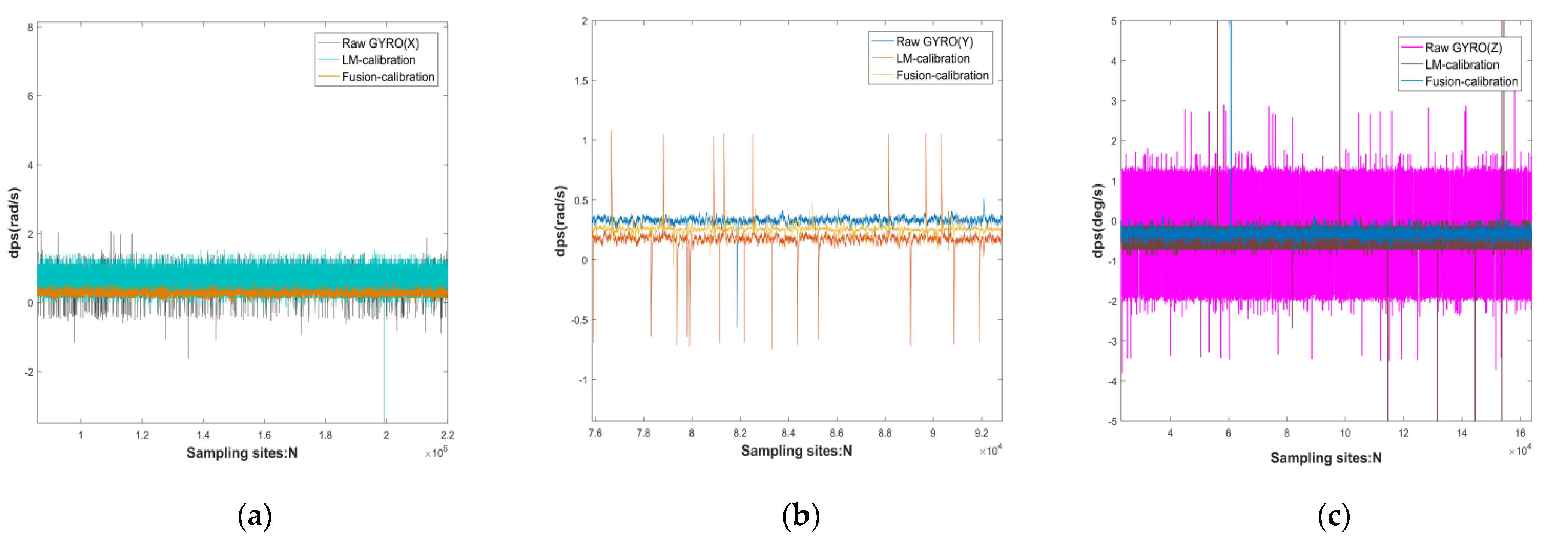
- Static measurements: compare the static output of the original data [36], the static output after calibration by the LM-calibration algorithm, the static output of the fusion-calibration algorithm, compare the estimated value of the output data with the measured value, and simultaneously measure the RMSE of the above three sets of data per unit of time.
- (2)
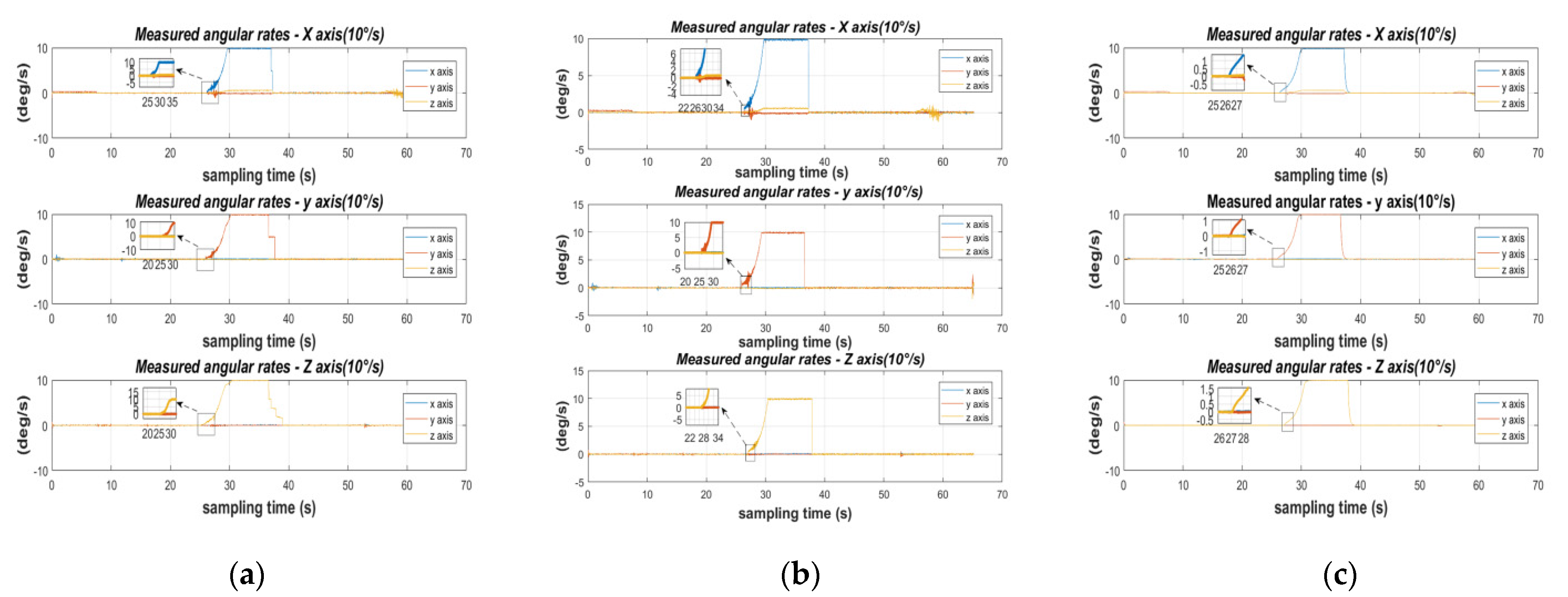
- Dynamic measurements: for accelerometers, uniform acceleration motion in the X-O-Y plane at a certain acceleration to measure the accuracy of the acceleration; for gyroscopes, rotation at a fixed angular rate using a single axis turntable to compare the accuracy of the angular rate after LM-calibration, and then after fusion-calibration.
- (3)
- Integrated measurement: the GPS prescribed path as a benchmark, the planned trajectory is in the width of 2 m, the total length of 4 km road vehicle travel route, the vehicle in the first 10 s uniform speed straight line walking, 10–100 s accelerated curve walking, after deceleration to the end of the actual environment there are trees, tall buildings shade, obstacles road stalls and other interference, in the vehicle speed and road conditions complex The GPS planned path, the inertial guidance path of LM calibration algorithm and the inertial guidance path of fusion calibration algorithm are observed in the situation. The path coincidence, planar displacement error and skyward displacement error of these three solutions are analysed.
4.1. Static Validation
4.2. Dynamic Validation
4.3. Integrated Validation
5. Conclusions
- (1)
- Building a high-precision static and dynamic screener for M-IMU: for the M-IMU calibration, we do not use high-cost calibration instruments as experimental equipment, rather, on the basis of a redundant consumer-grade MEMS composition array using the original data of the MEMS array multi-position attitude rotation and stationary interval for accurate estimation of the error parameters of the array MEMS, this subject uses ALLAN variance to calculate the stationary state of the initialization time and defines the variance of the output data of the MEMS array as a covariate during the period of for weighted average. Its weighted average value is the threshold value for judging the static and dynamic of this M-IMU system, which is greater than the threshold value per unit of time as dynamic, and less than the threshold value as static, and this filter can accurately distinguish the different state intervals required for different sensors.
- (2)
- Construction of a calibration parameter optimization algorithm for individual MEMS: For individual MEMS arrays subject to fixed errors, a non-linear calibration factor based on the LM-calibration algorithm is proposed, which optimizes the deterministic error parameters by calculating a non-linear cost function constructed according to the IMU error model and using the LM algorithm to iteratively optimize the cost function in different state intervals. The method is able to guarantee the reliability of the data on the premise of faster convergence; that is, the sensor cost function in multiple targets can quickly converge to the optimal value.
- (3)
- Constructing a fusion calibration algorithm for MEMS arrays: For MEMS arrays affected by the error of autocorrelation and intercorrelation of MEMSi and MEMSj, this paper uses the gravity coordinate system of MEMS0 as the reference, and the angular rates of the remaining MEMS sensitive axes are mapped with the reference as the system coordinate system. Each MEMS after coordinate transformation is calibrated with fixed error parameters, and the fixed error parameters of the obtained MEMS arrays are subjected to a fusion algorithm for improving adaptive support based on a priori information. The fusion-calibration algorithm’s support quotes an exponential function that efficiently and accurately quantifies the support of the sensor observations, allowing the MEMS array fixed error parameters to be fused into the error parameters of a “high precision virtual inertial guidance” MEMS0 along the way.
- (4)
- The feasibility of the calibration algorithm is verified in a practical environment from multiple perspectives: the traditional validations of calibration results are: validation of the data set, validation of the variance of the fixed error parameters, and validation of the static output of the sensor. The above-mentioned validation methods are carried out at the system level in an ideal laboratory environment, and the non-linearity of the calibration factor cannot be accurately verified in real-world situations. The dispersion of the fused and calibrated sensor data converges exponentially. The fusion-calibrated M_IMU outdoor navigation trajectory in the real environment also overlaps well with the GPS-planned trajectory [39], and the horizontal orientation error is small. By comparing the calibrated trajectories of different calibration algorithms, it is verified that the proposed fusion calibration algorithm has a high robustness in the real environment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, Q.; Deng, W.H.; Bebek, O.; Cavusoglu, M.C.; Mastrangelo, C.H.; Young, D.J. Personal Inertial Navigation System Assisted by MEMS Ground Reaction Sensor Array and Interface ASIC for GPS-Denied Environment. IEEE J. Solid-State Circuits 2018, 53, 3039–3049. [Google Scholar] [CrossRef]
- Zhao, T.; Ahamed, M.J. Pseudo-Zero Velocity Re-Detection Double Threshold Zero-Velocity Update (ZUPT) for Inertial Sensor-Based Pedestrian Navigation. IEEE Sens. J. 2021, 21, 13772–13785. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Y.; Li, S.; Zhang, T.; Niu, X. Mounting Parameter Estimation from Velocity Vector Observations for Land Vehicle Navigation. IEEE Trans. Ind. Electron. 2022, 69, 4234–4244. [Google Scholar] [CrossRef]
- Jung, J.H.; Cha, J.; Chung, J.Y.; Kim, T.I.; Seo, M.H.; Park, S.Y.; Yeo, J.Y.; Park, C.G. Monocular Visual-Inertial-Wheel Odometry Using Low-Grade IMU in Urban Areas. IEEE Trans. Intell. Transp. Syst. 2022, 23, 925–938. [Google Scholar] [CrossRef]
- Otegui, J.; Bahillo, A.; Lopetegi, I.; Díez, L.E. Simulation Framework for Testing Train Navigation Algorithms Based on 9-DOF-IMU and Tachometers. IEEE Trans. Instrum. Meas. 2020, 69, 5260–5273. [Google Scholar] [CrossRef]
- Deka, N.; Subramanian, V. On-Chip Fully Integrated Field Emission Arrays for High-Voltage MEMS Applications. IEEE Trans. Electron Devices 2020, 67, 3753–3760. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Jin, Y. A Passive Wireless Switching Array Based on MEMS Switches. J. Microelectromech. Syst. 2019, 28, 1013–1018. [Google Scholar] [CrossRef]
- Yao, S.S.; Cheng, Y.J.; Zhou, M.M.; Wu, Y.F.; Fan, Y. D-Band Wideband Air-Filled Plate Array Antenna with Multistage Impedance Matching Based on MEMS Micromachining Technology. IEEE Trans. Antennas Propag. 2020, 68, 4502–4511. [Google Scholar] [CrossRef]
- Xu, C.; Chen, J.; Zhu, H.; Liu, H.; Lin, Y. Experimental Research on Seafloor Mapping and Vertical Deformation Monitoring for Gas Hydrate Zone Using Nine-Axis MEMS Sensor Tapes. IEEE J. Ocean. Eng. 2019, 44, 1090–1101. [Google Scholar] [CrossRef]
- Mohammad, T.; He, S.; Mrad, R.B. A MEMS Optical Phased Array Based on Pitch Tunable Silicon Micromirrors for LiDAR Scanners. J. Microelectromech. Syst. 2021, 30, 712–724. [Google Scholar] [CrossRef]
- Liu, S.; Li, S.; Zheng, J.; Fu, Q. Benefits of Using Carrier Phase Tracking Errors for Ultratight GNSS/INS Integration: Precise Velocity Estimation and Fine IMU Calibration. IEEE Trans. Instrum. Meas. 2022, 71, 8500912. [Google Scholar] [CrossRef]
- Refai, M.I.M.; Van Beijnum, B.J.F.; Buurke, J.H.; Veltink, P.H. Portable Gait Lab: Estimating 3D GRF Using a Pelvis IMU in a Foot IMU Defined Frame. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1308–1316. [Google Scholar] [CrossRef]
- Baziw, J.; Leondes, C.T. In-Flight Alignment and Calibration of Inertial Measurement Units—Part I: General Formulation. IEEE Trans. Aerosp. Electron. Syst. 1972, AES-8, 439–449. [Google Scholar] [CrossRef]
- Baziw, J.; Leondes, C.T. In-Flight Alignment and Calibration of Inertial Measurement Units—Part II: Experimental Results. IEEE Trans. Aerosp. Electron. Syst. 1972, AES-8, 450–465. [Google Scholar] [CrossRef]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A robust and easy to implement method for IMU calibration without external equipments. In Proceedings of the International Conference on Robotics and Automation (ICRA), 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–5 June 2014. [Google Scholar]
- Zhang, X.; Zhou, C.; Chao, F.; Lin, C.M.; Yang, L.; Shang, C.; Shen, Q. Low-Cost Inertial Measurement Unit Calibration with Nonlinear Scale Factors. IEEE Trans. Ind. Inform. 2022, 18, 1028–1038. [Google Scholar] [CrossRef]
- Blocher, L.; Mayer, W.; Arena, M.; Radović, D.; Hiller, T.; Gerlach, J.; Bringmann, O. Purely Inertial Navigation with a Low-Cost MEMS Sensor Array. In Proceedings of the Inertial Sensors and Systems (INERTIAL), 2021 IEEE International Symposium on Inertial Sensors and Systems, Kailua-Kona, HI, USA, 22–25 March 2021. [Google Scholar]
- Hu, P.; Xu, P.; Chen, B.; Wu, Q. A Self-Calibration Method for the Installation Errors of Rotation Axes Based on the Asynchronous Rotation of Rotational Inertial Navigation Systems. IEEE Trans. Ind. Electron. 2018, 65, 3550–3558. [Google Scholar] [CrossRef]
- Rohac, J.; Sipos, M.; Simanek, J. Calibration of low-cost triaxial inertial sensors. IEEE Instrum. Meas. Mag. 2015, 18, 32–38. [Google Scholar] [CrossRef]
- Feynman, R.P. There’s plenty of room at the bottom [data storage]. J. Microelectromech. Syst. 1992, 1, 60–66. [Google Scholar] [CrossRef]
- Qureshi, U.; Golnaraghi, F. An Algorithm for the In-Field Calibration of a MEMS IMU. IEEE Sens. J. 2017, 17, 7479–7486. [Google Scholar] [CrossRef]
- Munoz Poblete, C.; Roa Munoz, N.; Huircan Quilaqueo, J.I. Caw’s Walking State Recognition Based on Accelerometers and Gyroscopes Installed on Ear-Tags and Collar-Tags. IEEE Lat. Am. Trans. 2018, 16, 2490–2495. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, X.; Chen, Y.; Li, M. A Lightweight and Accurate Localization Algorithm Using Multiple Inertial Measurement Units. IEEE Robot. Autom. Lett. 2020, 5, 1508–1515. [Google Scholar] [CrossRef] [Green Version]
- Eckenhoff, K.; Geneva, P.; Huang, G. MIMC-VINS: A Versatile and Resilient Multi-IMU Multi-Camera Visual-Inertial Navigation System. IEEE Trans. Robot. 2021, 37, 1360–1380. [Google Scholar] [CrossRef]
- Lee, J.; Hanley, D.; Bretl, T. Extrinsic Calibration of Multiple Inertial Sensors from Arbitrary Trajectories. IEEE Robot. Autom. Lett. 2022, 7, 2055–2062. [Google Scholar] [CrossRef]
- Vigne, M.; El Khoury, A.; Di Meglio, F.; Petit, N. State Estimation for a Legged Robot with Multiple Flexibilities Using IMUs: A Kinematic Approach. IEEE Robot. Autom. Lett. 2020, 5, 195–202. [Google Scholar] [CrossRef]
- Takayasu, M. Acoustic MEMS Sensor Array for Quench Detection of CICC Superconducting Cables. IEEE Trans. Appl. Supercond. 2020, 30, 4702705. [Google Scholar] [CrossRef]
- Song, J.; Shi, Z.; Du, B.; Wang, H. The Filtering Technology of Virtual Gyroscope Based on Taylor Model in Low Dynamic State. IEEE Sens. J. 2019, 19, 5204–5212. [Google Scholar] [CrossRef]
- Nilsson, J.; Skog, I.; Händel, P. Aligning the Forces—Eliminating the Misalignments in IMU Arrays. IEEE Trans. Instrum. Meas. 2014, 63, 2498–2500. [Google Scholar] [CrossRef]
- Lu, J.; Hu, M.; Yang, Y.; Dai, M. On-Orbit Calibration Method for Redundant IMU Based on Satellite Navigation & Star Sensor Information Fusion. IEEE Sens. J. 2020, 20, 4530–4543. [Google Scholar]
- Wang, L.; Hao, Y.; Wei, Z.; Wang, F. A calibration procedure and testing of MEMS inertial sensors for an FPGA-based GPS/INS system. In Proceedings of the Mechatronics and Automation, 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010. [Google Scholar]
- Chikovani, V.V. Performance parameters comparison of ring laser, coriolis vibratory and fiber-optic gyros based on Allan variance analysis. In Proceedings of the Actual Problems of Unmanned Air Vehicles Developments Proceedings (APUAVD), 2013 IEEE 2nd International Conference Actual Problems of Unmanned Air Vehicles Developments Proceedings, Kiev, Ukraine, 15–17 October 2013. [Google Scholar]
- Liu, Y.; Zhang, J.; Li, M. A spatial-temporal fusion algorithm based support degree and self-adaptive weighted theory for multi-senso. In Proceedings of the Machine Learning and Cybernetics, 2010 International Conference on Machine Learning and Cybernetics, Qingdao, China, 11–14 July 2010. [Google Scholar]
- Wang, C.; Zhu, Y.; Han, Z. The application of data-level fusion algorithm based on adaptive-weighted and support degree in intelligent household greenhouse. In Proceedings of the Modelling, Identification and Control (ICMIC), 2017 9th International Conference on Modelling, Identification and Control, Kunming, China, 10–12 July 2017. [Google Scholar]
- Jia, P.; Zhao, Z. Research on data fusion of surrounding rock mass in mine based on support degree and adaptive weighted. In Proceedings of the Intelligent Computing and Signal Processing (ICSP), 2021 6th International Conference on Intelligent Computing and Signal Processing, Xi’an, China, 15–17 April 2021. [Google Scholar]
- Gao, P.; Li, K.; Song, T.; Liu, Z. An Accelerometers-Size-Effect Self-Calibration Method for Triaxis Rotational Inertial Navigation System. IEEE Trans. Ind. Electron. 2018, 65, 1655–1664. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Chen, Y. Common Frame Based Unscented Quaternion Estimator for Inertial-Integrated Navigation. IEEE/ASME Trans. Mechatron. 2018, 23, 2413–2423. [Google Scholar] [CrossRef]
- Elsheikh, M.; Noureldin, A.; Korenberg, M. Integration of GNSS Precise Point Positioning and Reduced Inertial Sensor System for Lane-Level Car Navigation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2246–2261. [Google Scholar] [CrossRef]
- Wang, L.; Tang, H.; Zhang, T.; Chen, Q.; Shi, J.; Niu, X. Improving the Navigation Performance of the MEMS IMU Array by Precise Calibration. IEEE Sens. J. 2021, 21, 26050–26058. [Google Scholar] [CrossRef]
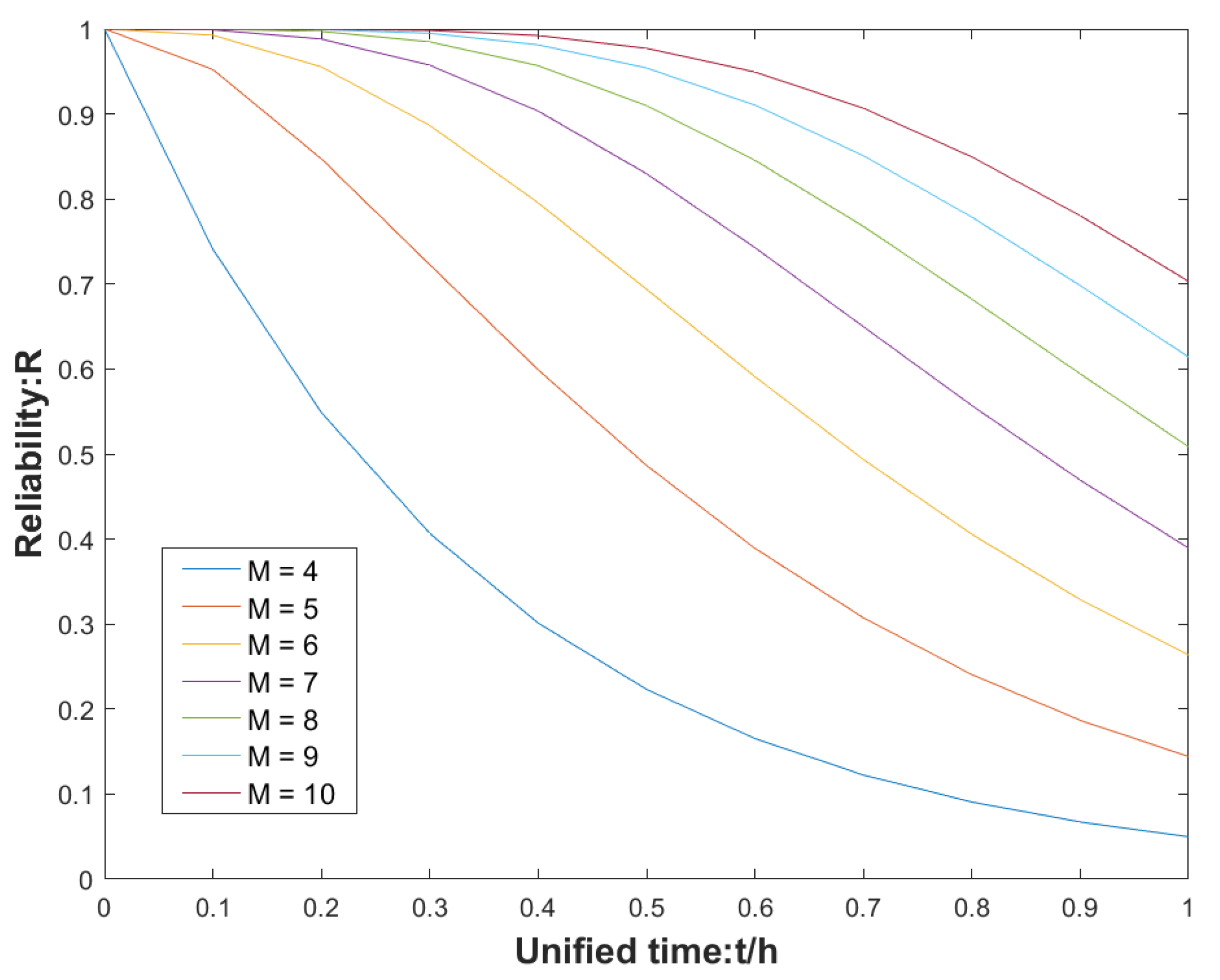


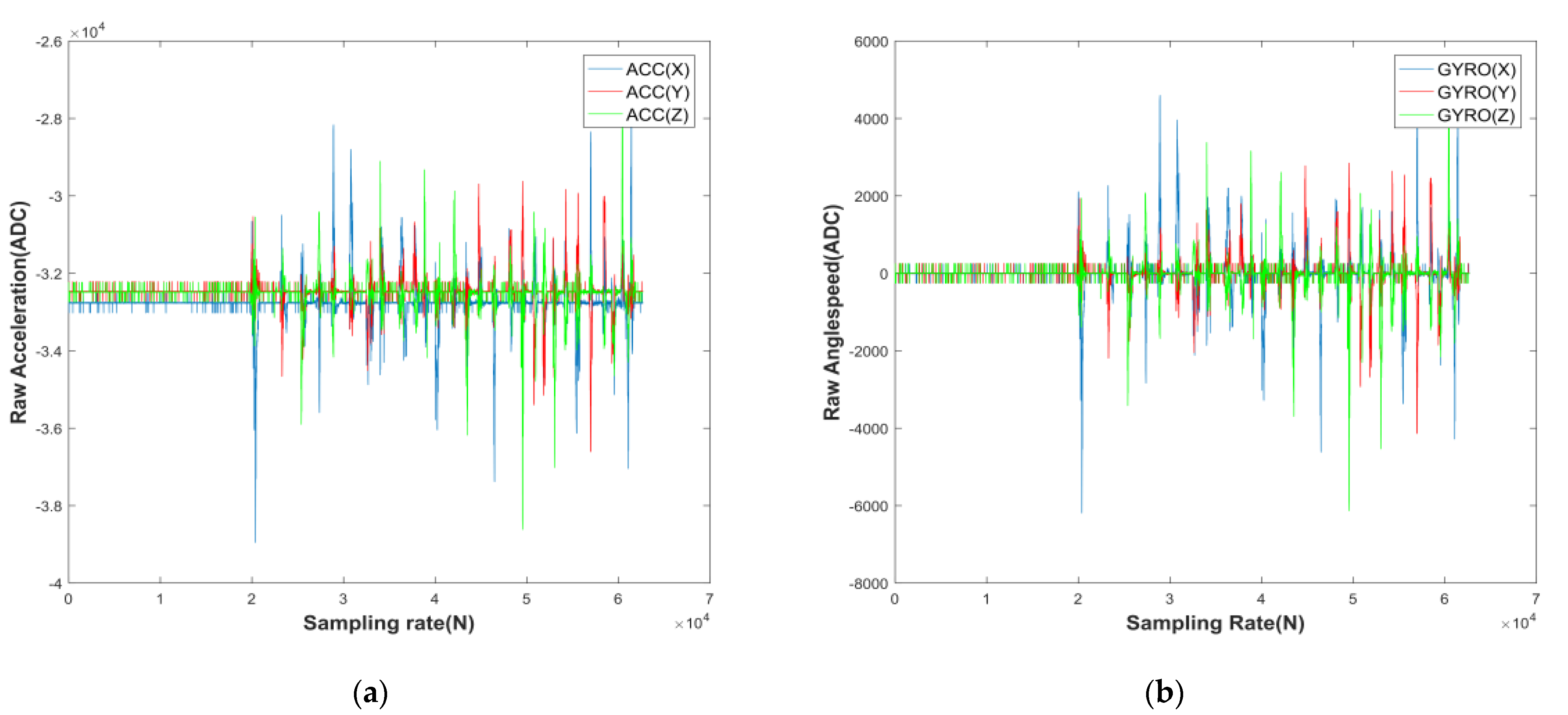
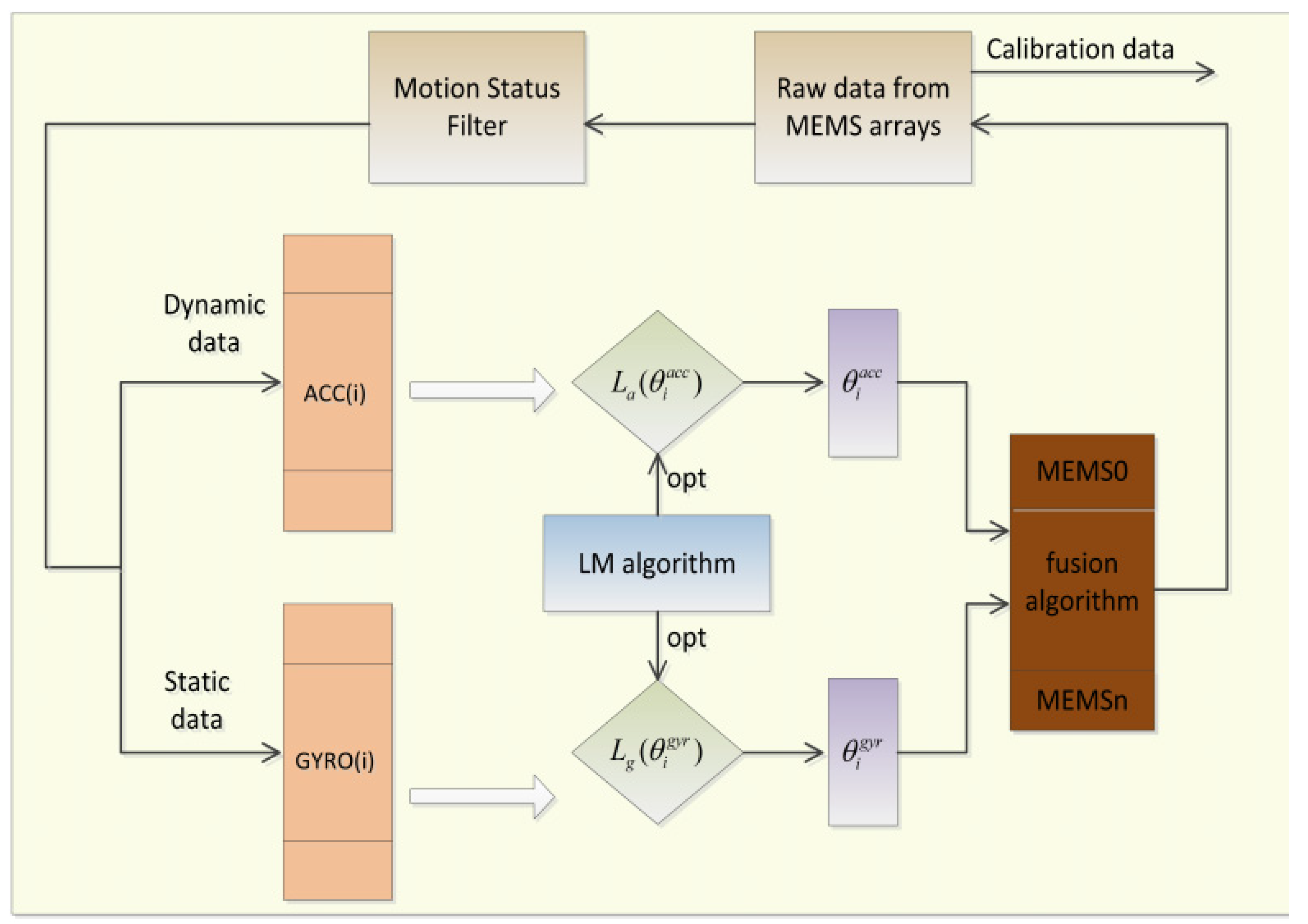
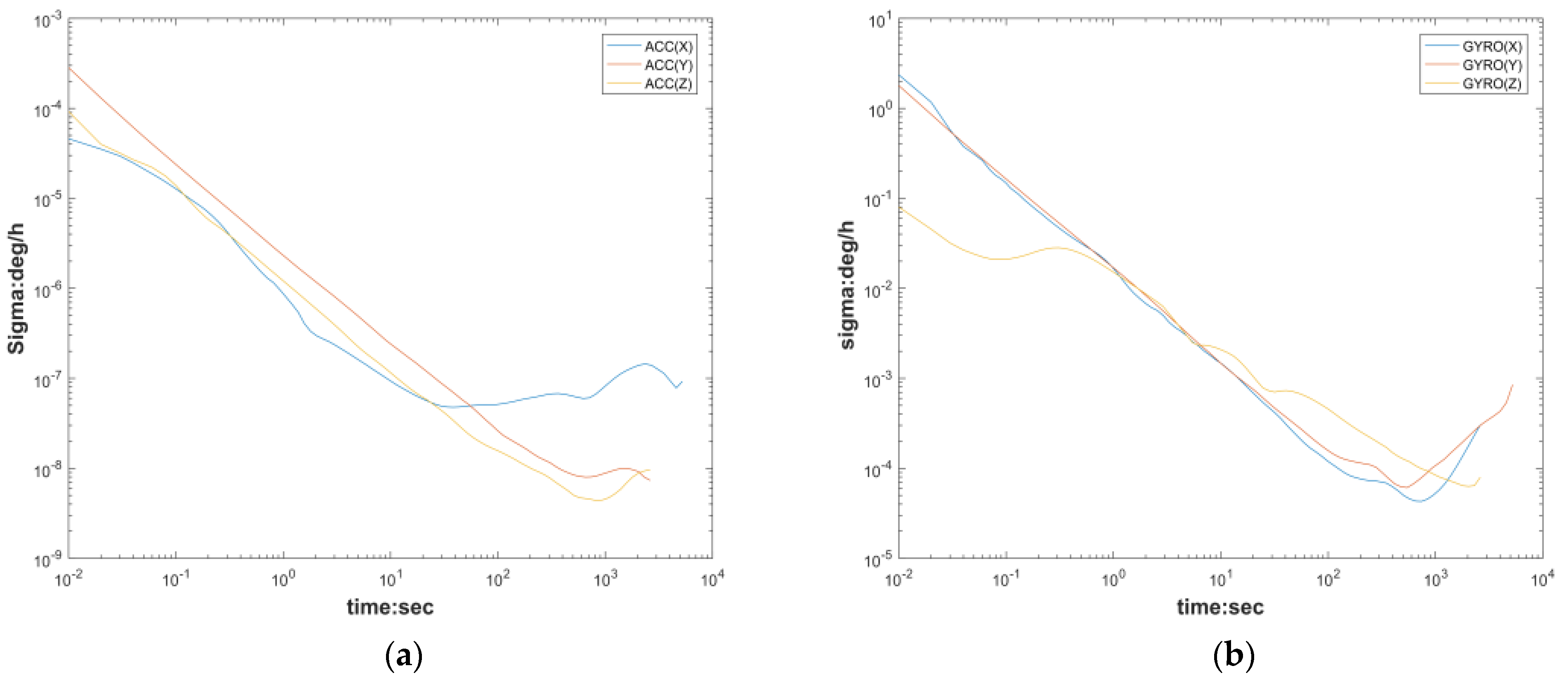



| Simultaneous Calibration of MEMS Arrays | Duration of Calibration (Min) | Real-Time Calibration | Auxiliary Equipment | Accuracy of Calibration | |
|---|---|---|---|---|---|
| Multi-position swing | Not applicable | 20 | Not applicable | YES | Excellence |
| Multi-rate rotation | Not applicable | 20 | Not applicable | YES | Excellence |
| Traditional LM-calibration | Not applicable | 5 | Applicable | NO | Good |
| Fusion- calibration | Applicable | 7 | Applicable | NO | Excellence |
| MEMS0 | MEMS1 | MEMS2 | MEMS3 | MEMS4 | MEMS5 | MEMS6 | MEMS7 | MEMS8 | MEMS9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| βyz | 0.0156 | 0.0129 | −0.0087 | −0.0098 | −0.0098 | 0.0045 | 0.0073 | 0.0118 | 0.0063 | −0.0078 |
| βzy | 0.3246 | 0.1244 | 0.0501 | 0.0440 | 0.0440 | −0.0415 | −0.0558 | −0.1911 | −0.1737 | −0.0478 |
| βxz | 0.0134 | 0.0127 | 0.0098 | 0.0100 | 0.0119 | 0.0100 | 0.0098 | 0.0103 | 0.0135 | 0.0103 |
| βzx | −0.1703 | −0.1345 | 0.0116 | 0.0010 | 0.0010 | −0.0017 | 0.0119 | 0.0166 | −0.1746 | 0.0135 |
| βxy | −0.0201 | −0.0201 | −0.0201 | −0.0201 | −0.0201 | −0.0201 | −0.0201 | −0.0201 | 0.0201 | 0.0201 |
| βyx | 0.0098 | 0.0098 | 0.0098 | 0.0098 | 0.0098 | 0.0098 | 0.0098 | 0.0098 | −0.0098 | 0.0098 |
| αyz | 0.4074 | 0.1613 | −0.9850 | −0.2787 | 0.0978 | −0.3137 | −0.7320 | −0.0314 | 0.0600 | 0.0963 |
| αzy | 0.3176 | −0.0346 | −0.0255 | 2.3920 | 0.0872 | −3.1487 | 1.2964 | 0.1114 | 0.0658 | −1.4672 |
| αxz | 0.5530 | 0.1421 | −0.4196 | −2.0693 | −0.2942 | −1.8412 | −1.5592 | 0.0224 | 0.0534 | −1.9963 |
| αzx | −0.3486 | −0.3173 | 0.6723 | −0.1927 | −0.1102 | 0.6250 | 1.4246 | −0.0464 | 0.1800 | 0.2984 |
| αxy | −0.1713 | 0.1323 | 0.9803 | −0.2584 | 0.7119 | 2.1076 | 0.7412 | −0.1229 | −0.0744 | 0.0173 |
| αyx | 0.2140 | 0.6368 | −0.2490 | −2.6332 | −0.6268 | −3.3696 | −1.6540 | 0.1367 | 0.1282 | −1.7084 |
| Sax | 1.1774 | 0.9793 | −1.0370 | −0.9737 | 1.1470 | −0.9557 | 0.9467 | 0.9770 | 0.9515 | 0.9571 |
| Say | 0.9009 | 0.9881 | −0.9203 | 1.0206 | 0.9232 | −1.0450 | 0.9548 | 1.1411 | 1.1741 | 0.9739 |
| Saz | 0.9775 | 1.1296 | −1.1527 | −1.1377 | −0.8155 | −1.1217 | 0.9822 | 0.9771 | −0.9602 | 1.1010 |
| Sgx | 1.4908 | 1.7746 | −2.9116 | 2.8745 | 3.0908 | −1.3875 | −1.4758 | 0.5557 | −1.3609 | −0.5601 |
| Sgy | −3.0940 | −3.0137 | −0.5167 | −1.6659 | 1.3196 | 3.1842 | 2.9777 | −1.6535 | −3.0783 | 3.0474 |
| Sgz | −0.5662 | 0.5544 | 1.6354 | 0.5374 | 0.5623 | 0.5511 | 0.5471 | 3.0038 | 0.5633 | 0.5968 |
| bax | 0.0125 | 0.0013 | 0.0071 | 0.0183 | −0.0029 | −0.0180 | 0.0006 | 0.0034 | −0.0231 | 0.0028 |
| bay | 0.0016 | −0.0146 | 0.0072 | −0.0037 | −0.0065 | 0.0013 | −0.0264 | −0.0123 | −0.0154 | −0.0235 |
| baz | 0.0078 | 0.0025 | −0.0073 | −0.0098 | 0.0040 | −0.0065 | 0.0151 | 0.0011 | −0.0107 | 0.0097 |
| bgx | 0.4659 | 0.2948 | 0.5430 | 0.7256 | −0.3401 | 0.0263 | 0.6740 | −0.4590 | 0.0745 | 0.6452 |
| bgy | 0.1180 | 0.4999 | 0.7233 | 0.0607 | 0.3091 | −0.1212 | 0.6842 | −0.3417 | −0.7949 | 0.2644 |
| bgz | −0.3766 | −0.1295 | 0.0336 | −0.0817 | −0.0485 | −0.5892 | −0.6529 | −0.3511 | 0.7438 | −0.6763 |
| Parameters | X-Axis | Y-Axis | Z-Axis |
|---|---|---|---|
| Accelerometers | 1.0659 | 0.9485 | 1.0356 |
| Gyroscope | 1.2683 | 3.0275 | 0.5551 |
| Parameters | X-Axis | Y-Axis | Z-Axis |
|---|---|---|---|
| Accelerometers | 0.0090 | −0.0112 | 0.0074 |
| Gyroscope | 0.4254 | 0.3912 | −0.3682 |
| Parameters | X-Axis | Y-Axis | Z-Axis | |
|---|---|---|---|---|
| Accelerometers | X-axis | 0.9990 | 0.0089 | −0.0453 |
| Y-axis | 0.0112 | 1.0001 | 0.0451 | |
| Z-axis | 0.0201 | 0.0098 | 0.9998 | |
| Gyroscope | X-axis | 1.6206 | −0.2243 | −0.6300 |
| Y-axis | −0.6494 | 1.5533 | −0.1190 | |
| Z-axis | −0.3780 | −0.6812 | 1.4497 |
| Axial | X-Axis | Y-Axis | Z-Axis | |||
|---|---|---|---|---|---|---|
| Parameters | Average | RMSE | Average | RMSE | Average | RMSE |
| Raw data | 0.0125 | 2.3559 × 10−4 | −0.0235 | 3.7514 × 10−5 | 0.9903 | 9.2439 × 10−5 |
| LM-calibration | 0.0028 | 2.9632 × 10−6 | −0.0182 | 5.9399 × 10−6 | 1.0078 | 3.0600 × 10−6 |
| Fusion-calibration | 0.0002 | 5.0428 × 10−7 | −0.0092 | 2.7991 × 10−7 | 1.0019 | 9.4217 × 10−7 |
| Axial | X-Axis | Y-Axis | Z-Axis | |||
|---|---|---|---|---|---|---|
| Parameters | Average | RMSE | Average | RMSE | Average | RMSE |
| Raw data | 0.6452 | 2.1370 | 0.2644 | 0.0425 | −0.3766 | 0.3137 |
| LM-calibration | 0.4659 | 0.0385 | 0.2466 | 0.0054 | −0.3341 | 0.1371 |
| Fusion-calibration | 0.2703 | 0.0021 | 0.1180 | 0.0034 | −0.3118 | 0.0105 |
| The Axis of Rotation | MEMSO Accelerometer (m/s2) | ||||||
|---|---|---|---|---|---|---|---|
| Axial | Raw Data | LM-Calibration | Fusion-Calibration | ||||
| Parameters | Average | RMSE | Average | RMSE | Average | RMSE | |
| X-axis | X-axis | 9.7673 | 0.1246 | 9.7674 | 0.0312 | 9.8226 | 0.0081 |
| Y-axis | −0.0858 | 0.9835 | −0.0820 | 0.2060 | −0.0715 | 5.2899 × 10−5 | |
| Z-axis | 0.7076 | 1.3006 | 0.7070 | 0.4738 | −0.0751 | 6.8966 × 10−5 | |
| Y-axis | X-axis | 0.0111 | 2.5050 | 0.0110 | 0.4441 | −0.0090 | 6.3637 × 10−5 |
| Y-axis | 9.6402 | 1.1647 | 9.7401 | 0.5740 | 9.8221 | 0.0205 | |
| Z-axis | 0.3766 | 2.4213 | 0.3655 | 0.3364 | −0.0199 | 1.1143 × 10−4 | |
| Z-axis | X-axis | −0.1488 | 0.6900 | −0.1486 | 0.0206 | −0.0005 | 5.4024 × 10−5 |
| Y-axis | 0.0138 | 0.1337 | 0.0100 | 0.0028 | 0.0110 | 5.4158 × 10−5 | |
| Z-axis | 9.8309 | 0.6390 | 9.8306 | 0.5420 | 9.8009 | 0.4667 | |
| The Axis of Rotation | MEMSO Gyroscope (dps) | ||||||
|---|---|---|---|---|---|---|---|
| Status | Raw Data | LM-Calibration | Fusion-Calibration | ||||
| Parameters | Average | RMSE | Average | RMSE | Average | RMSE | |
| Stationary | 0.0759 | 0.0966 | 0.0073 | 1.1726 × 10−4 | 0.0020 | 3.5822 × 10−5 | |
| X-axis | Rotation | 9.7167 | 0.0031 | 9.8170 | 1.1910 × 10−4 | 9.9348 | 4.4647 × 10−5 |
| Stationary | 0.0210 | 0.0035 | 0.0032 | 1.8668 × 10−4 | 0.0014 | 1.5160 × 10−4 | |
| Stationary | 0.4177 | 2.0450 | 0.0199 | 6.9120 × 10−4 | 0.0113 | 2.1360 × 10−4 | |
| Y-axis | Rotation | 9.7987 | 0.0044 | 9.8999 | 1.3235 × 10−4 | 9.9829 | 1.0088 × 10−4 |
| Stationary | 0.0100 | 0.0847 | 0.0108 | 0.0016 | 0.0019 | 4.6261 × 10−4 | |
| Stationary | 0.4534 | 2.6219 | 0.0014 | 8.3999 × 10−5 | −0.0004 | 3.6236 × 10−5 | |
| Z-axis | Rotation | 9.8063 | 0.0046 | 9.9052 | 3.3486 × 10−4 | 9.9886 | 3.2120 × 10−5 |
| Stationary | 0.1740 | 0.0048 | 0.0400 | 1.7718 × 10−4 | 0.0025 | 3.4964 × 10−5 | |
| Calibration Algorithms | RMSE in North Direction (m) | RMSE in East Direction (m) | Initial Gravity Misalignment Angle Error (°) |
|---|---|---|---|
| GPS | 0 | 0 | 0 |
| LM-calibration | 1.0637 | 1.2263 | 2.56 |
| Fusion-calibration | 0.9856 | 0.8541 | 0.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Dong, X.; Guo, T.; Zhao, F.; Zhang, Y. Peripheral-Free Calibration Method for Redundant IMUs Based on Array-Based Consumer-Grade MEMS Information Fusion. Micromachines 2022, 13, 1214. https://doi.org/10.3390/mi13081214
Liang S, Dong X, Guo T, Zhao F, Zhang Y. Peripheral-Free Calibration Method for Redundant IMUs Based on Array-Based Consumer-Grade MEMS Information Fusion. Micromachines. 2022; 13(8):1214. https://doi.org/10.3390/mi13081214
Chicago/Turabian StyleLiang, Siyuan, Xiaochao Dong, Tianyu Guo, Feng Zhao, and Yuhua Zhang. 2022. "Peripheral-Free Calibration Method for Redundant IMUs Based on Array-Based Consumer-Grade MEMS Information Fusion" Micromachines 13, no. 8: 1214. https://doi.org/10.3390/mi13081214
APA StyleLiang, S., Dong, X., Guo, T., Zhao, F., & Zhang, Y. (2022). Peripheral-Free Calibration Method for Redundant IMUs Based on Array-Based Consumer-Grade MEMS Information Fusion. Micromachines, 13(8), 1214. https://doi.org/10.3390/mi13081214





