Performance Evaluation of Different Coating Materials in Delamination for Micro-Milling Applications on High-Speed Steel Substrate
Abstract
:1. Introduction
2. Research Objective
- Objective 1: to model delamination of the coating from the substrate for micro-milling applications and find out factors on which delamination depends.
- Objective 2: to evaluate the performance of different coating materials for delamination and report the best coating material for micro-milling applications and their corresponding thickness.
3. CAD Model of Coating and Substrate Design to Study Delamination (Objective 1)
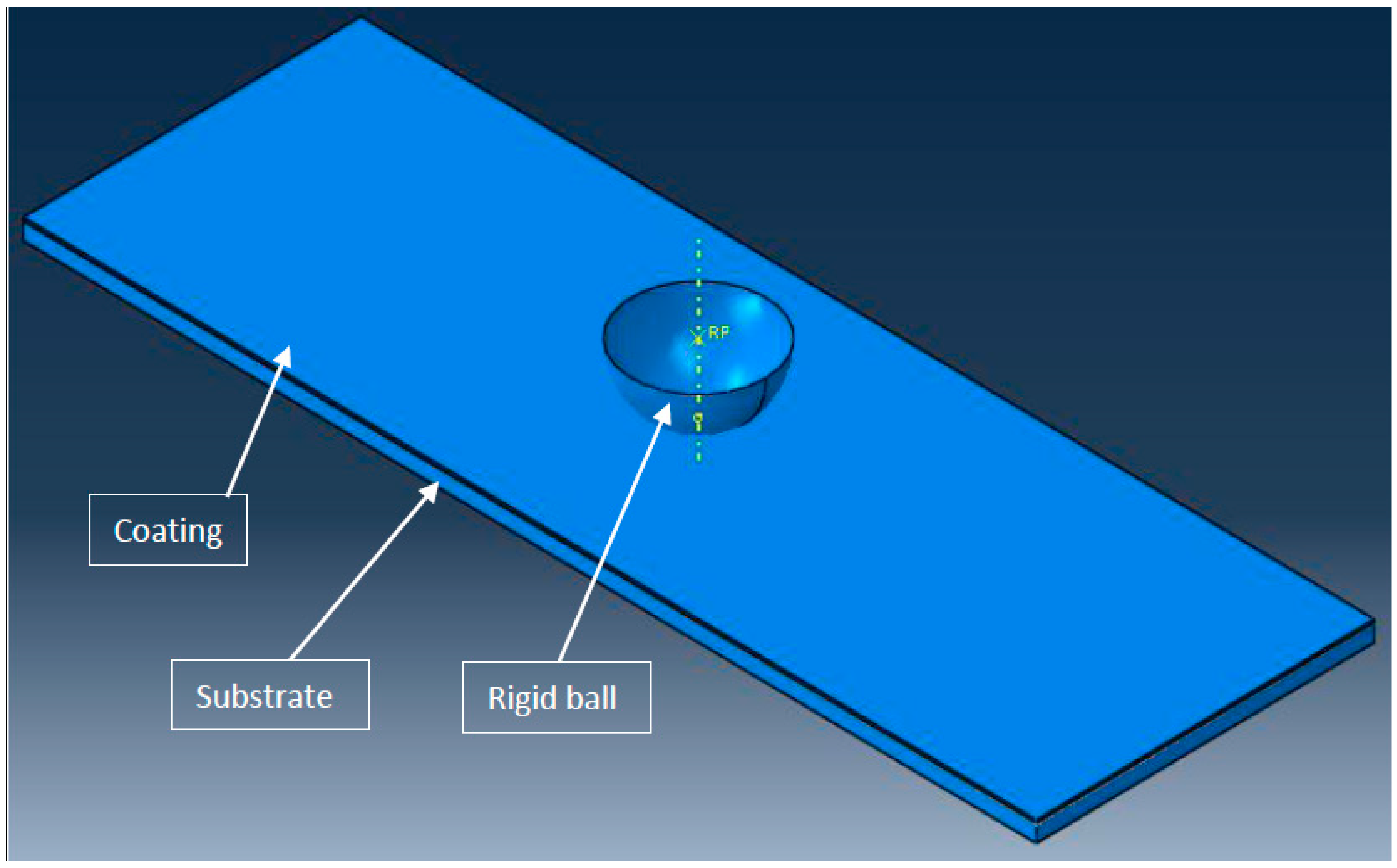
3.1. Designing of Coating and Substrate Assembly
3.2. Mechanical Properties of Different Coatings and the Substrate
3.3. Assumptions in the Present Study
- The deformation behaviour of the substrate was characterized as elastic–plastic with isotropic hardening.
- The deformation behaviour of the coating materials was modelled as linear–elastic.
- The hemispherical ball was modelled as analytical rigid.
- For the surface interaction between the ball and coating material, the outer surface of the hemispherical ball was considered as the master surface and the top surface of the coating material was considered as the slave surface. This was done because the hemispherical ball was modelled as analytical rigid [37].
- For the surface interaction between the coating material and substrate, the bottom surface of the coating was considered as the master surface and the top surface of the substrate was modelled as the slave surface as the coating material was harder than the substrate.
- The interaction property for the junction of the coating and substrate was modelled as a ‘tie’ such that there was no slip, separation and penetration.
- Brick elements were taken for both the coating and substrate, and the element type was taken as the quadratic with the hybrid formulation and reduced integration. The structured type of mesh control is used.
3.4. Dimensioning and Boundary Conditions
- Along the length and width, the coating and substrate both were divided into 26 equal parts. Along the thickness, the coating material was divided into two equal parts and the substrate was divided into five parts with single bias with the bias ratio as five. Along the length, the mesh size of the coating material and substrate was 115 µm; along the width, the mesh size of the coating material and substrate was 38 µm; along the thickness, the mesh size for the coating material was 1.5 µm; and for the substrate, the mesh size ranged from 4 µm to 19 µm. The interaction property for the junction of the coating and substrate was modelled as a ‘tie’ such that there was no slip, separation and penetration.
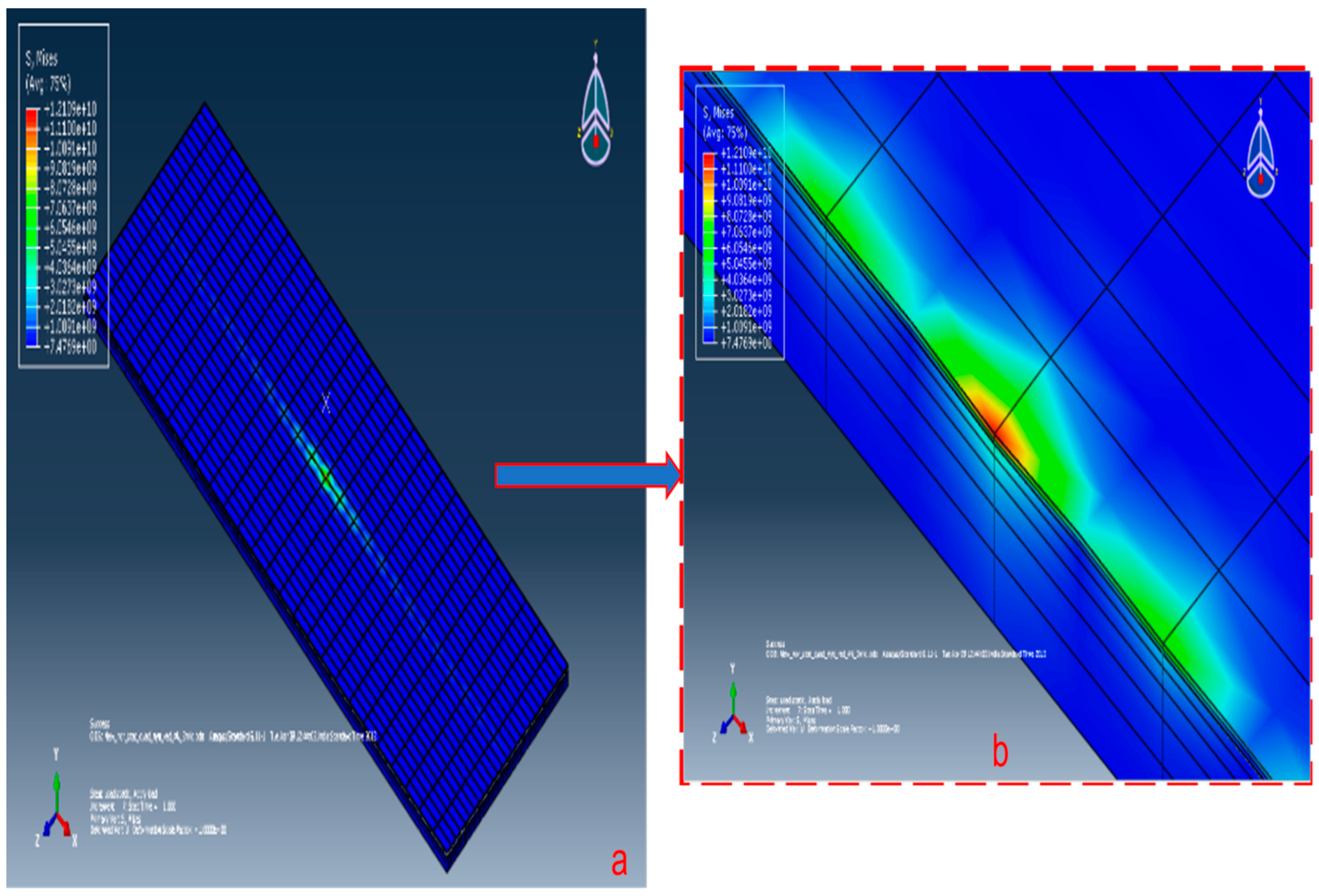
- The bottom of the substrate was given a rigid support and a normal load of 4 N was applied at the reference point of the rigid ball. The stress contour thus obtained is shown in Figure 3a,b.
3.5. Surface-Based Cohesive Behaviour
4. Analytical Calculation for Hertzian Normal Stress
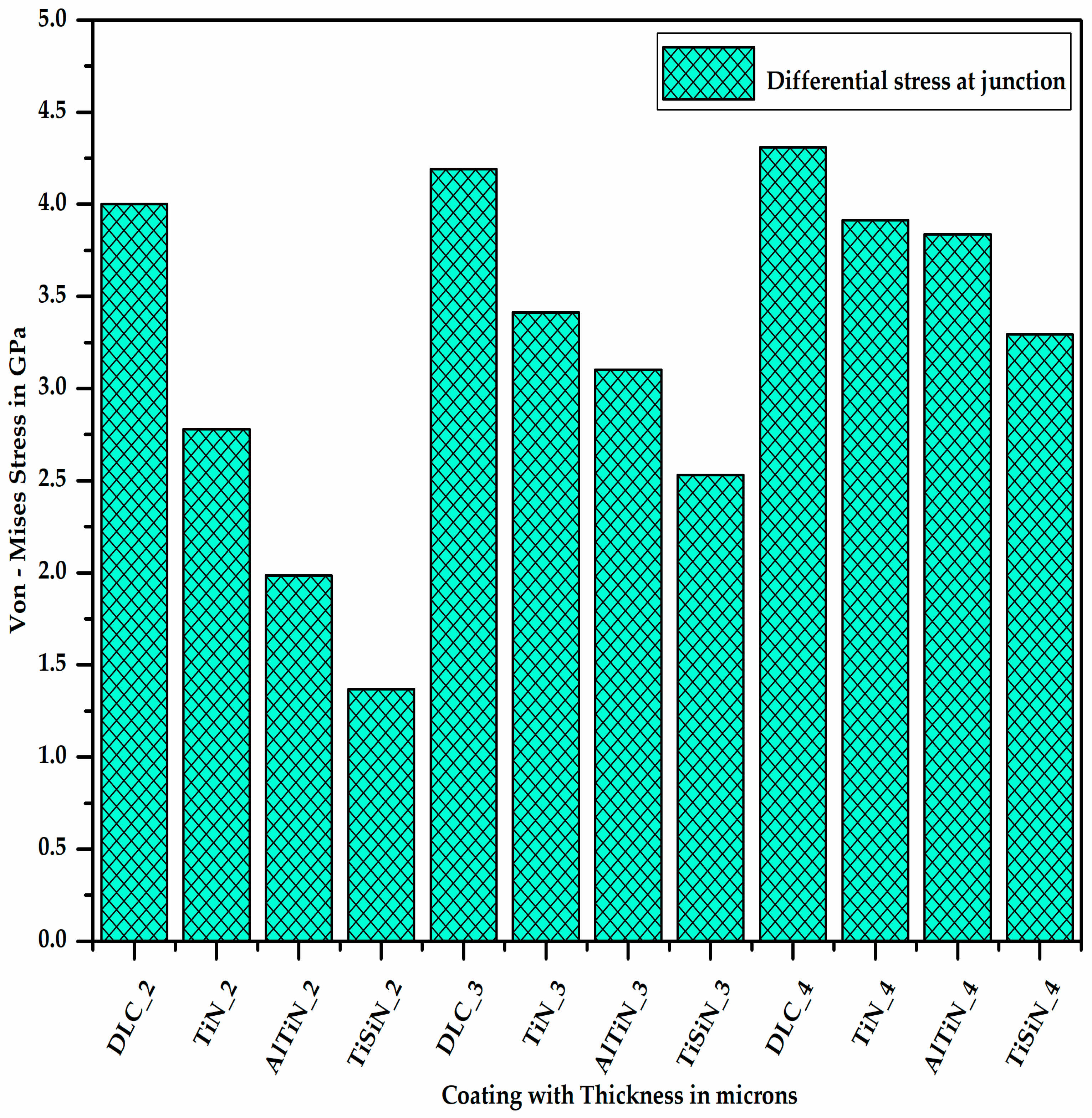
5. Results and Discussion: Performance Evaluation of Different Coating Materials in Delamination (Objective 2)
6. Conclusions
- Using a 3D modelling approach, the coating and substrate assembly was modelled and studied for delamination. Various factors were evaluated which impacted the delamination in micro-milling.
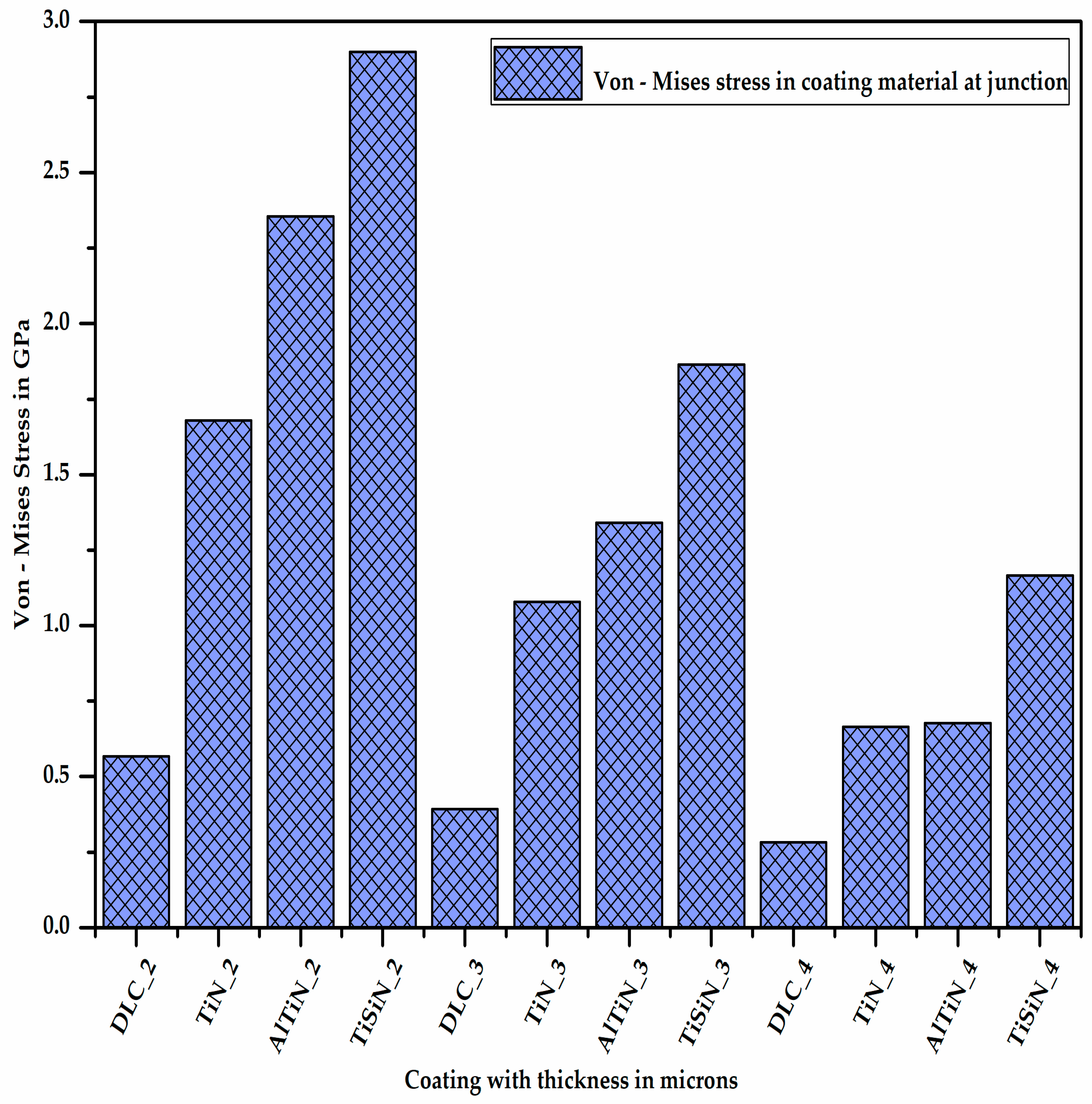
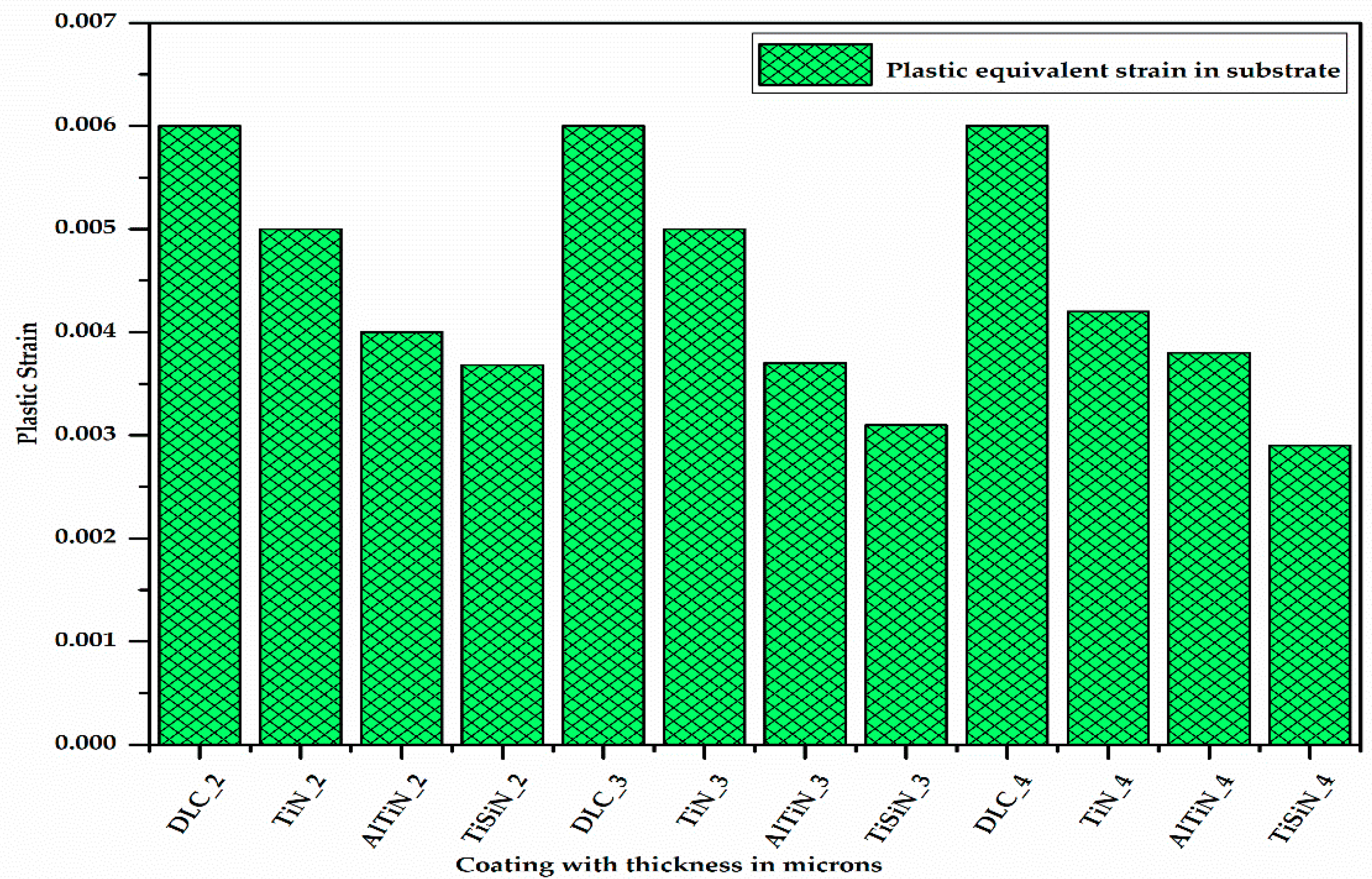
- On the basis of the plastic equivalent strain occurring in the substrate material, the TiSiN and AlTiN coatings are the best since the plastic equivalent strain occurring in the substrate with the TiSiN and AlTiN coating materials is less (Appendix A). Between these two, the TiSiN coating shows the least plastic equivalent strain in the substrate, which serves the purpose of protecting the substrate from plastic deformation. The plastic equivalent strain in the substrate decreases with increase in the thickness of the coating material.
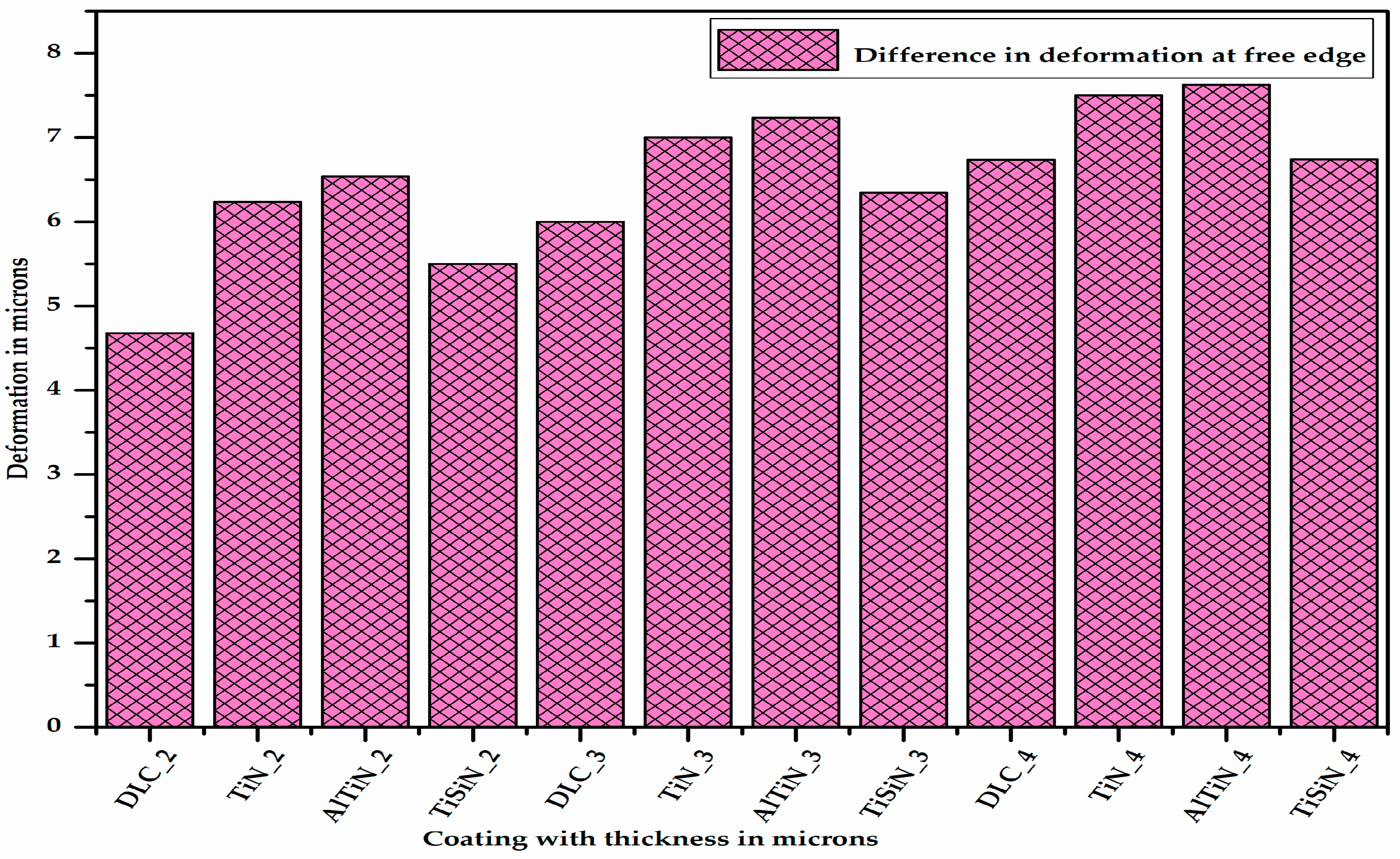
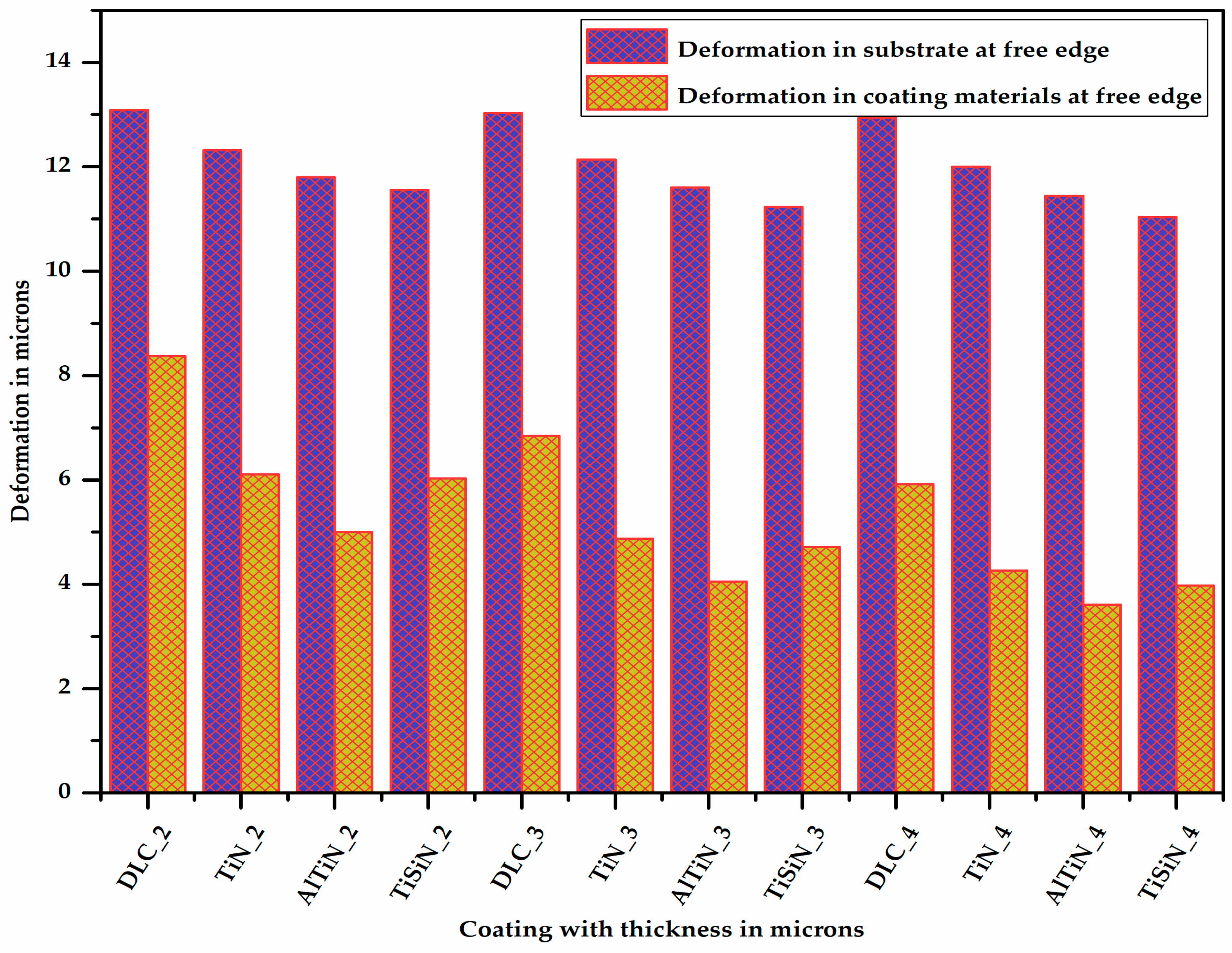
- On the basis of the difference in deformation, i.e., delamination, the TiSiN coating is better than the AlTiN coating since delamination in the coating–substrate assembly with the TiSiN coating is less than that of the AlTiN coating. The delamination of the coating material from the substrate increases with increase in the thickness of the coating material.
- By combining the plastic equivalent strain in the substrate and the delamination of the coating from the substrate, we can conclude that the TiSiN coating of 3 micron thickness is the most optimum coating thickness for micro-milling applications. These results fulfill the requirements of objectives 1 and 2.
- The higher the interface stiffness coefficient of the coating–substrate assembly is, the less the delamination of the coating material from the substrate is.
- The delamination depends on the Young’s modulus and the hardness of both the coating material and substrate.
Author Contributions
Funding
Conflicts of Interest
Appendix A





References
- Aramcharoen, A.; Mativenga, P.T.; Yang, S.; Cooke, K.E.; Teer, D.G. Evaluation and selection of hard coatings for micro milling of hardened tool steel. Int. J. Mach. Tools Manuf. 2008, 48, 1578–1584. [Google Scholar] [CrossRef]
- Dornfeld, D.; Min, S.; Takeuchi, Y. Recent advances in mechanical micromachining. CIRP Ann.—Manuf. Technol. 2006, 55, 745–768. [Google Scholar] [CrossRef] [Green Version]
- Masuzawa, T. State of the art of micromachining. CIRP Ann.—Manuf. Technol. 2000, 49, 473–488. [Google Scholar] [CrossRef]
- Weule, H.; Huntrup, V.; Tritschler, H. Micro-cutting of steel to meet new requirements in miniaturization. CIRP Ann.—Manuf. Technol. 2001, 50, 61–64. [Google Scholar] [CrossRef]
- Liu, X.; de Vor, R.E.; Kapoor, S.G.; Ehmann, K.F. The mechanics of machining at the microscale: Assessment of the current state of the science. J. Manuf. Sci. Eng. 2004, 126, 666–678. [Google Scholar] [CrossRef]
- Min, S.; Sangermann, H.; Mertens, C.; Dornfeld, D. A study on initial contact detection for precision micro-mold and surface generation of vertical side walls in micromachining. CIRP Ann.—Manuf. Technol. 2008, 57, 109–112. [Google Scholar] [CrossRef]
- Masuzawa, T.; Toenshoff, H.K. Three-dimensional micromachining by machine tools. CIRP Ann. —Manuf. Technol. 1997, 46, 621–628. [Google Scholar] [CrossRef]
- Bissacco, G.; Hansen, H.N.; de Chiffre, L. Micromilling of hardened tool steel for mould making applications. J. Mater. Process. Technol. 2005, 167, 201–207. [Google Scholar] [CrossRef]
- Bissacco, G.; Hansen, H.N.; de Chiffre, L. Size effects on surface generation in micro milling of hardened tool steel. CIRP Ann.—Manuf. Technol. 2006, 55, 593–596. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Oosterling, J.A.J.; Hoogstrate, A.M. Performance evaluation of micromilling of hardened tool steel. In Proceedings of the ICOMM, Greenville, NC, USA, 11–13 September 2007; pp. 219–224. [Google Scholar]
- Aramcharoen, A.; Mativenga, P.T.; Yang, S. The effect of AlCrTiN coatings on product quality in micro-milling of 45 HRC hardened H13 die steel. In Proceedings of the 35th International Matador Conference, Taipei, Taiwan, 27 July 2007; pp. 203–206. [Google Scholar]
- Maekawa, K.; Obikawa, T.; Yamane, Y.; Childs, T.H.C. Metal Machining—Theory and Applications; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Kobayashi, A. The features and application of UPC nano-micro forming tools. Ind. Diam. Rev. 2005, 65, 28–30. [Google Scholar]
- Kim, C.J.; Bono, M.; Ni, J. Experimental Analysis of Chip Formation in Micro-Milling; Technical Papers Society of Manufacturing Engineers-All Series; NAMRIA: Manila, Philippines, 2002. [Google Scholar]
- Jun, M.B.G.; DeVor, R.E.; Kapoor, S.G. Investigation of the dynamics of microend milling-Part II: Model validation and interpretation. J. Manuf. Sci. Eng. 2006, 128, 901–912. [Google Scholar] [CrossRef]
- Torres, C.D.; Heaney, P.J.; Sumant, A.V.; Hamilton, M.A.; Carpick, R.W.; Pfefferkorn, F.E. Analyzing the performance of diamond-coated micro end mills. Int. J. Mach. Tools Manuf. 2009, 49, 599–612. [Google Scholar] [CrossRef]
- Ozel, T.; Lui, X.; Dhanorker, A. Modelling and simulation of micro-milling process. In Proceedings of the 4th International Conference and Exhibition on Design and Production of Machines and Dies/Molds, Cesme, Turkey, 21–23 June 2007. [Google Scholar]
- Tansel, I.; Rodriguez, O.; Trujillo, M.; Paz, E.; Li, W. Micro-end-milling-I. Wear and breakage. Int. J. Mach. Tools Manuf. 1998, 38, 1419–1436. [Google Scholar] [CrossRef]
- Baharudin, B.T.H.T.; Dimou, N.; Hon, K.K.B. Tool wear behaviour of micro-tools in high speed CNC machining. In Proceedings of the 34th International MATADOR Conference, Manchester, UK, 7 July 2004; Springer: London, UK; pp. 111–118. [Google Scholar]
- Uhlmann, E.; Schauer, K. Dynamic load and strain analysis for the optimization of micro end mills. CIRP Ann.—Manuf. Technol. 2005, 54, 75–78. [Google Scholar] [CrossRef]
- Rahman, M.; Kumar, A.S.; Prakash, J.R.S. Micro milling of pure copper. J. Mater. Process. Technol. 2001, 116, 39–43. [Google Scholar] [CrossRef]
- Bissacco, G.; Hansen, H.N.; Chiffre, L.D. Wear of micro end mills. In Proceedings of the 5th EUSPEN International Conference, Montpellier, France, 8–11 May 2005; pp. 561–564. [Google Scholar]
- Zaman, M.T.; Kumar, A.S.; Rahman, M.; Sreeram, S. A three-dimension analytical cutting force model for micro end milling operation. Int. J. Mach. Tools Manuf. 2006, 46, 353–366. [Google Scholar] [CrossRef]
- Uriarte, L.; Zatarian, M.; Albizuri, J.; Lacalle, L.N.L.d.; Lamikiz, A. Effect of the tool wear in micro-milling cutting forces. In Proceedings of the 2nd International Conference on High Performance Cutting, Tirupati, India, 4–5 December 2020. [Google Scholar]
- Takacs, M.; Vero, B.; Meszaros, I. Micromilling of metallic materials. J. Mater. Process. Technol. 2003, 138, 152–155. [Google Scholar] [CrossRef]
- Tansel, I.N.; Arkan, T.T.; Bao, W.Y.; Mahendrakar, N.; Shisler, B.; Smith, D.; McCool, M. Tool wear estimation in micro-machining, part II: Neural network-based periodic inspector for non-metals. Int. J. Mach. Tools Manuf. 2000, 40, 609–620. [Google Scholar] [CrossRef]
- Schmidt, J.; Tritschler, H. Micro cutting of steel. Microsyst. Technol. 2004, 10, 167–174. [Google Scholar] [CrossRef]
- Uhlmann, E.; Piltz, S.; Schauer, K. Micro milling of sintered tungsten-copper composite materials. J. Mater. Process. Technol. 2005, 167, 402–407. [Google Scholar] [CrossRef]
- Vogler, M.P.; DeVor, R.E.; Kapoor, S.G. On the modeling and analysis of machining performance in micro-endmilling, Part I: Surface generation. J. Manuf. Sci. Eng. 2004, 126, 685–694. [Google Scholar] [CrossRef]
- Weinert, K.; Petzoldt, V. Machining NiTi micro-parts by micro-milling. Mater. Sci. Eng. A 2008, 481, 672–675. [Google Scholar] [CrossRef]
- Aramcharoen, A.; Mativenga, P.T.; Yang, S. The contribution of CrTiAlN coatings in micro milling of hardened die steel. In Proceedings of the 40th CIRP International Seminar on Manufacturing Systems, Liverpool, UK, 30 May–1 June 2007. [Google Scholar]
- Bin Saedon, J. Micromilling of Hardened (62 HRC) AISI D2 Cold Work Tool Steel. Ph.D. Thesis, The University of Birmingham, Edgbaston, UK, October 2011. [Google Scholar]
- Dobrzanski, L.A.; Golombek, K.; Kopac, J.; Sokovic, M. Effect of depositing the hard surface coatings on properties of the selected cemented carbides and tool cermets. J. Mater. Process. Technol. 2004, 157, 304–311. [Google Scholar] [CrossRef]
- Talib, R.J.; Ariff, H.M.; Fazira, M.F. Machining performance and wear mechanism of TiAlN-coated insert. Int. J. Mech. Mater. Eng. (IJMME) 2011, 6, 414–418. [Google Scholar]
- Kumar, M. Laser Assisted Micro Milling of Hard Materials. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2011. [Google Scholar]
- Scherzer, M.; Glaser, H. Mechanical Modelling of Failure Patterns in TiN-Coatings Loaded by Homogenous Stresses of a Bending Specimen. Int. J. Fract. 2002, 114, 291–306. [Google Scholar] [CrossRef]
- Holmberg, K.; Laukkanen, A.; Ronkainen, H.; Wallin, K.; Varjus, S.; Koskinen, J. Tribological contact analysis of a rigid ball sliding on a hard coated surface. Part II: Material deformations, influence of coating thickness and Young’s modulus. Surf. Coat. Technol. 2006, 200, 3810–3823. [Google Scholar] [CrossRef]
- Holmberg, K.; Laukkanen, A.; Ronkainen, H.; Wallin, K.; Hogmark, S.; Jacobson, S.; Wiklund, U.; Souza, R.M.; Stahle, P. Residual stresses in TiN, DLC and MoS2 coated surfaces with regard to their tribological fracture behaviour. Wear 2009, 267, 2142–2156. [Google Scholar] [CrossRef]
- Wu, T.; Cheng, K. Micro milling performance assessment of diamond-like carbon coatings on a micro-end mill. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 1038–1046. [Google Scholar] [CrossRef] [Green Version]
- Ucun, I.; Aslantas, K.; Bedir, F. An experimental investigation of the effect of coating material on tool wear in micro milling of Inconel 718 super alloy. Wear 2013, 300, 8–19. [Google Scholar] [CrossRef]
- Tao Wu, T. Tooling Performance in Micro Milling: Modelling, Simulation and Experimental Study. Ph.D. Thesis, Brunel University, Uxbridge, UK, December 2012. [Google Scholar]
- Cselle, T.; Coddet, O.; Galamand, C.; Holubar, P.; Jilek, M.; Jilek, J.; Luemkemann, A.; Morstein, M. Triple coatings—New Generation of PVD-Coatings for Cutting Tools. J. Mach. Manuf. 2009, 49, 19–25. [Google Scholar]
- Lille, H.; Koo, J.; Gregor, A.; Ryabchikov, A.; Sergejev, F.; Traksmaa, R.; Kulu, P. Comparison of Curvature and X-Ray Methods for Measuring of Residual Stresses in Hard PVD Coatings. Mater. Sci. Forum 2011, 681, 455–460. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Munroe, P.; Jiang, Z.T.; Rickard, W.; Xie, Z. Corrosion behaviour of nano-composite TiSiN coatings on steel substrates. Corros. Sci. 2011, 53, 3678–3687. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.Y.; Yang, S.J.; Wang, D.Y. Structural and mechanical properties of AlTiN/CrN coatings synthesized by a cathodic-arc deposition process. Surf. Coat. Technol. 2006, 201, 4209–4214. [Google Scholar] [CrossRef]
- Trent, E.M.; Paul, K. Metal Cutting, 4th ed.; Wright: Bristol, UK, 2000; p. 145. [Google Scholar]
- Surface Based Cohesive Behaviour 35.1.10; 6.11 Documentation; Abaqus: Providence, RI, USA.
- Lesage, J.; Chicot, D. Role of residual stresses on interface toughness of thermally sprayed coatings. Thin Solid Films 2002, 415, 143–150. [Google Scholar] [CrossRef]
- Zhang, J.; Cho, Y.; Kim, J.; Malikov, A.K.; Kim, Y.H.; Yi, J.-H.; Li, W. Non-Destructive Evaluation of Coating Thickness Using Water Immersion Ultrasonic Testing. Coatings 2021, 11, 1421. [Google Scholar] [CrossRef]
- Šporin, J.; Mrvar, P.; Janc, B.; Vukelić, Ž. Expression of the Self-Sharpening Mechanism of a Roller Cone Bit during Wear Due to the Influence of the Erosion Protection Carbide Coating. Coatings 2021, 11, 1308. [Google Scholar] [CrossRef]
- Dettlaff, A.; Brodowski, M.; Kowalski, M.; Stranak, V.; Prysiazhnyi, V.; Klugmann-Radziemska, E.; Ryl, J.; Bogdanowicz, R. Highly oriented zirconium nitride and oxynitride coatings deposited via high-power impulse magnetron sputtering: Crystal-facet-driven corrosion behavior in domestic wastewater. Adv. Eng. Mater. 2021, 23, 2001349. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Huo, D. Investigation on the Tool Wear Suppression Mechanism in Non-Resonant Vibration-Assisted Micro Milling. Micromachines 2020, 11, 380. [Google Scholar] [CrossRef] [Green Version]
- Kino, H.; Imada, T.; Ogawa, K.; Nakagawa, H.; Kojima, H. An Experimental Investigation on Micro End Milling with High-Speed Up Cut Milling for Hardened Die Steel. Materials 2020, 13, 4745. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Migranov, M.S.; Melnik, Y.A.; Okunkova, A.A.; Fedorov, S.V.; Gurin, V.D.; Volosova, M.A. Application of Adaptive Materials and Coatings to Increase Cutting Tool Performance: Efficiency in the Case of Composite Powder High Speed Steel. Coatings 2021, 11, 855. [Google Scholar] [CrossRef]
- Asghar, O.; Lou, L.Y.; Yasir, M.; Li, C.J.; Li, C.X. Enhanced Tribological Properties of LA43M Magnesium Alloy by Ni60 Coating via Ultra-High-Speed Laser Cladding. Coatings 2020, 10, 638. [Google Scholar] [CrossRef]





| Sl No. | Type | Material | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|---|
| 1 | Coating | TiN | 300 GPa | 0.22 |
| 2 | Substrate | High-speed steel | 200 GPa | 0.29 |
| S. No. | Type | Material | Young’s Modulus (GPa) | Hardness (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| 1 | Coating | TiN | 300 | 27 | 0.22 |
| 2 | Coating | DLC | 70 | 10.5 | 0.22 |
| 3 | Coating | AlTiN | 560 | 35 | 0.22 |
| 4 | Coating | TiSiN | 510 | 56 | 0.20 |
| 5 | Substrate | HSS | 200 | 7.5 | 0.29 |
| Sl No. | Type | Material | Length | Width | Thickness |
|---|---|---|---|---|---|
| 1 | Coating | Titanium Nitride | 3 mm | 1 mm | 2, 3 and 4 µm |
| 2 | Coating | Diamond-like Carbon | 3 mm | 1 mm | 2, 3 and 4 µm |
| 3 | Coating | Aluminium Titanium Nitride | 3 mm | 1 mm | 2, 3 and 4 µm |
| 4 | Coating | Titanium Silicon Nitride | 3 mm | 1 mm | 2, 3 and 4 µm |
| 5 | Substrate | High-speed Steel | 3 mm | 1 mm | 50 µm |
| Sl No. | Coating–Substrate Assembly | Ec (GPa) | Hc (GPa) | Es (GPa) | Hs (GPa) | Hi = (Hs + Hc)/2 (GPa) | Ei or Knn, Kss, Ktt (GPa) |
|---|---|---|---|---|---|---|---|
| 1 | TiN-HSS | 300 | 27 | 200 | 7.5 | 17.25 | 357 |
| 2 | DLC-HSS | 70 | 10.5 | 200 | 7.5 | 9 | 143 |
| 3 | AlTiN-HSS | 560 | 35 | 200 | 7.5 | 21.25 | 487 |
| 4 | TiSiN-HSS | 510 | 56 | 200 | 7.5 | 31.75 | 665 |
| S. N. | Particulars | Symbol | Equation Number Used | Value |
|---|---|---|---|---|
| 1 | Composite elastic modulus | Ec | 3.2 | 315.26 GPa |
| 2 | Mean normal stress | pm | 3.6 | 8290.64 MPa |
| 3 | Maximum normal stress | po | 3.7 | 12,435.97 MPa |
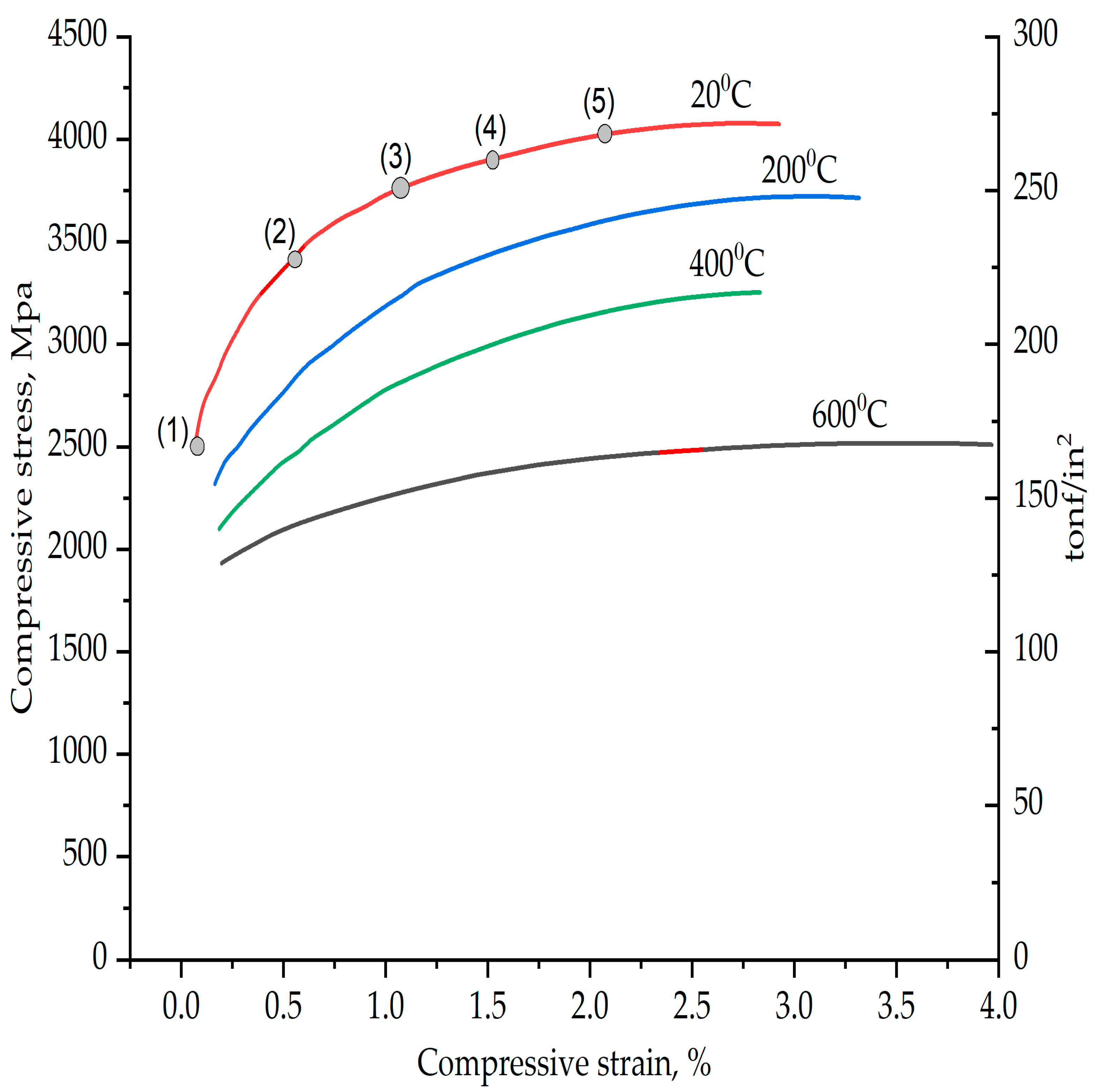
| Data Point | Compressive Stress (MPa) | Compressive Strain |
|---|---|---|
| 1 | 2450 | 0 |
| 2 | 3470 | 0.005 |
| 3 | 3750 | 0.01 |
| 4 | 3820 | 0.015 |
| 5 | 4000 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhoi, S.; Kumar, A.; Prasad, A.; Meena, C.S.; Sarkar, R.B.; Mahto, B.; Ghosh, A. Performance Evaluation of Different Coating Materials in Delamination for Micro-Milling Applications on High-Speed Steel Substrate. Micromachines 2022, 13, 1277. https://doi.org/10.3390/mi13081277
Bhoi S, Kumar A, Prasad A, Meena CS, Sarkar RB, Mahto B, Ghosh A. Performance Evaluation of Different Coating Materials in Delamination for Micro-Milling Applications on High-Speed Steel Substrate. Micromachines. 2022; 13(8):1277. https://doi.org/10.3390/mi13081277
Chicago/Turabian StyleBhoi, Sandeep, Ashwani Kumar, Arbind Prasad, Chandan Swaroop Meena, Rudra Bubai Sarkar, Bidyanand Mahto, and Aritra Ghosh. 2022. "Performance Evaluation of Different Coating Materials in Delamination for Micro-Milling Applications on High-Speed Steel Substrate" Micromachines 13, no. 8: 1277. https://doi.org/10.3390/mi13081277
APA StyleBhoi, S., Kumar, A., Prasad, A., Meena, C. S., Sarkar, R. B., Mahto, B., & Ghosh, A. (2022). Performance Evaluation of Different Coating Materials in Delamination for Micro-Milling Applications on High-Speed Steel Substrate. Micromachines, 13(8), 1277. https://doi.org/10.3390/mi13081277










