Utilizing the Intrinsic Mode of Weakly Coupled Resonators for Temperature Compensation
Abstract
:1. Introduction
2. Theory Analysis and Method of Temperature Compensation
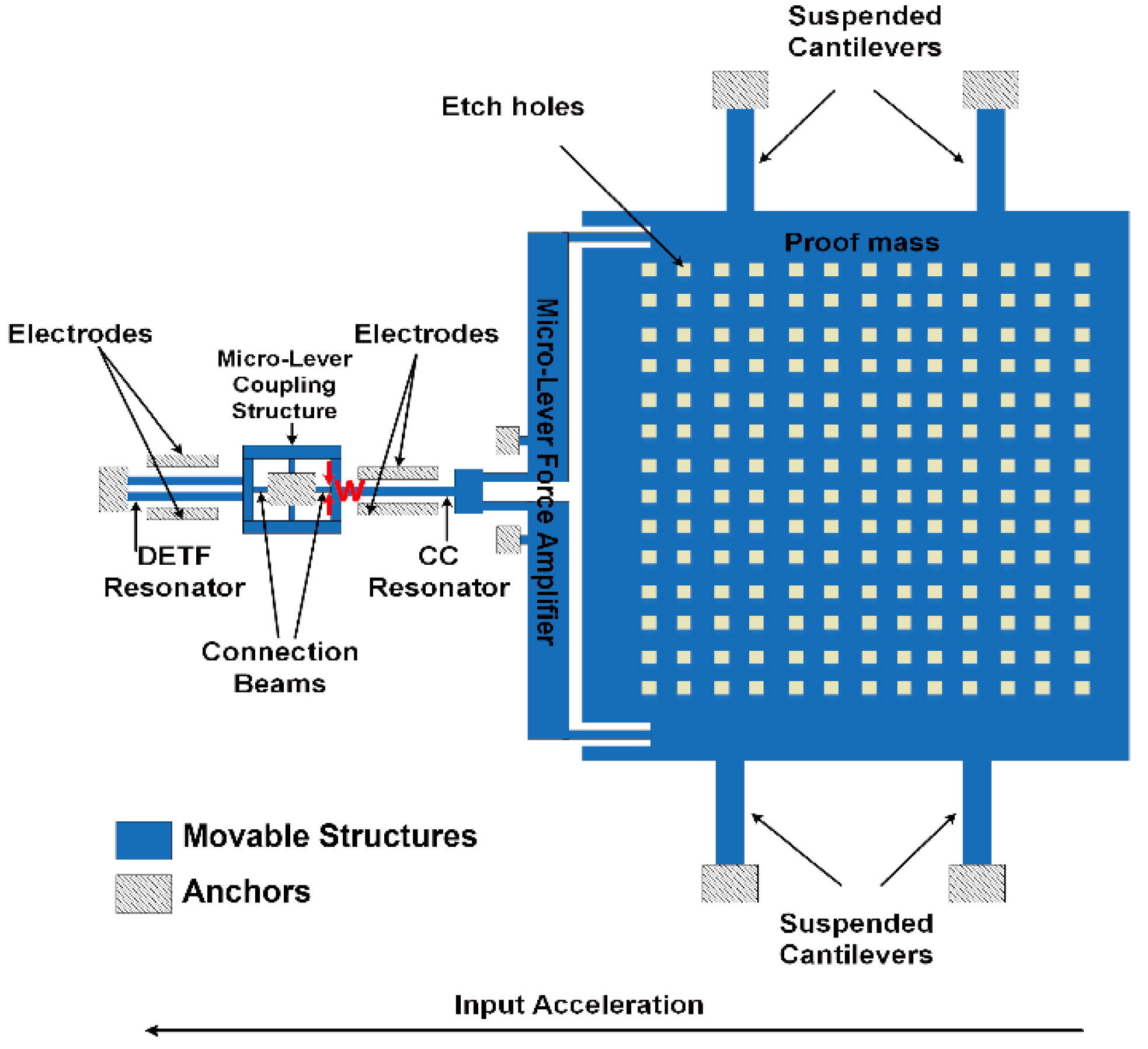
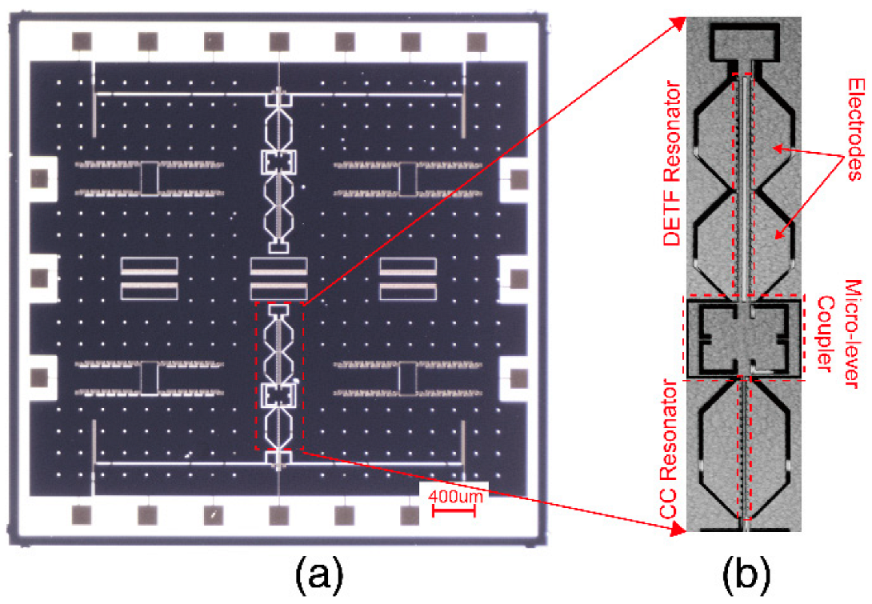
2.1. Structure Design
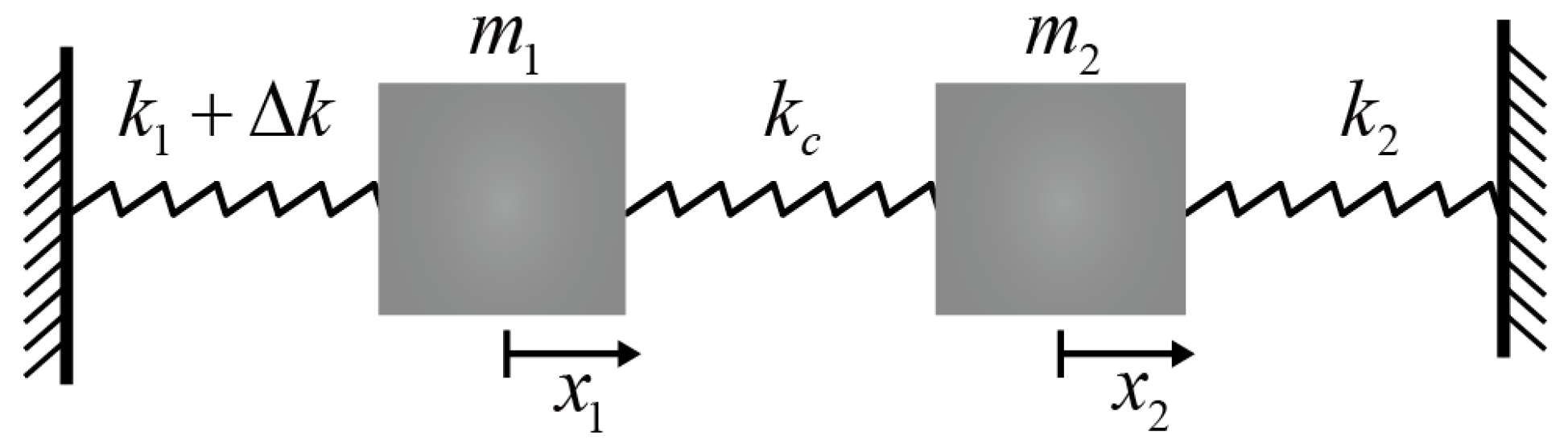
2.2. Theory Analysis
2.3. Simulation and Temperature Compensation
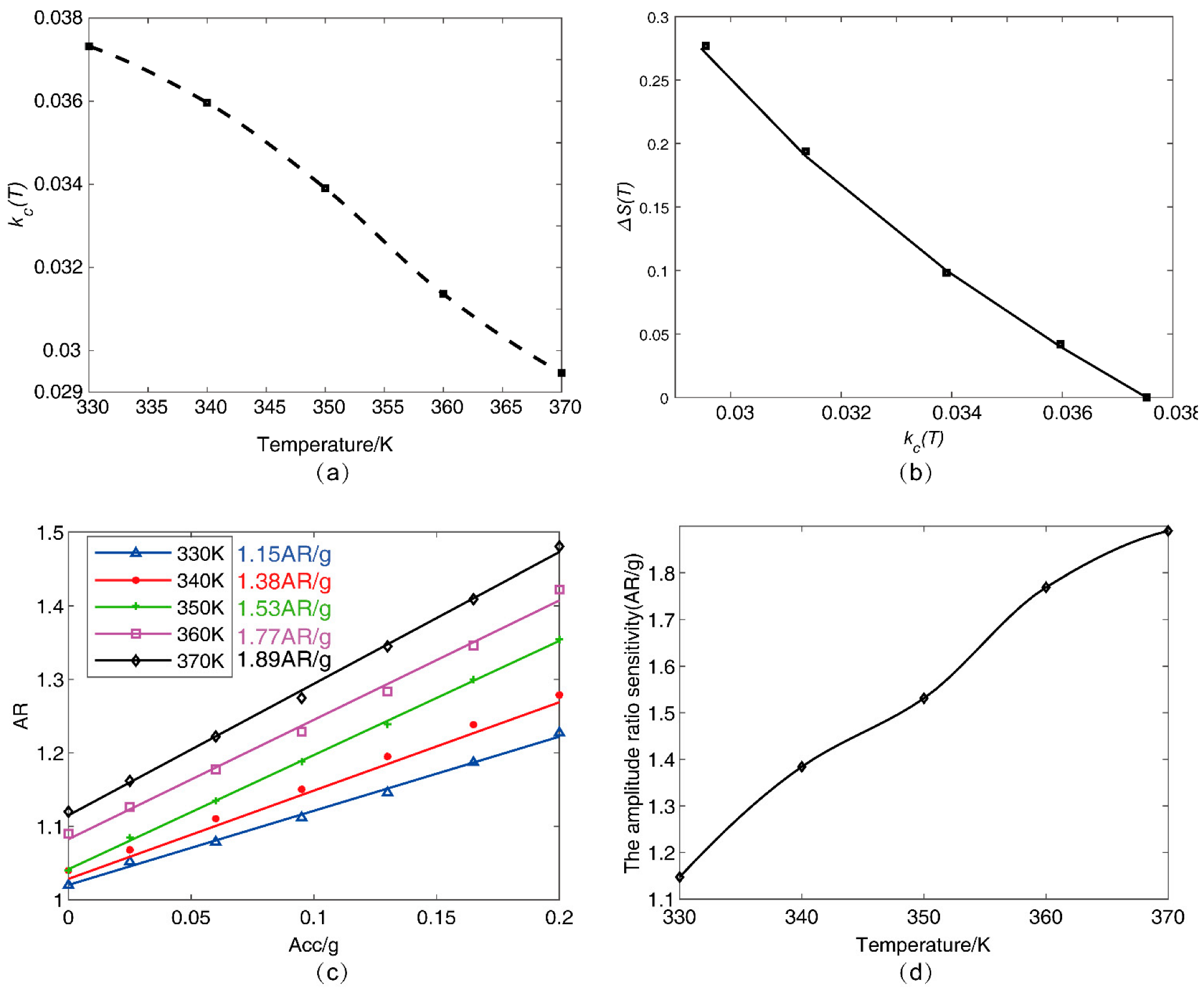
2.3.1. Simulation of the Mode Localized Accelerometer Temperature Characteristic
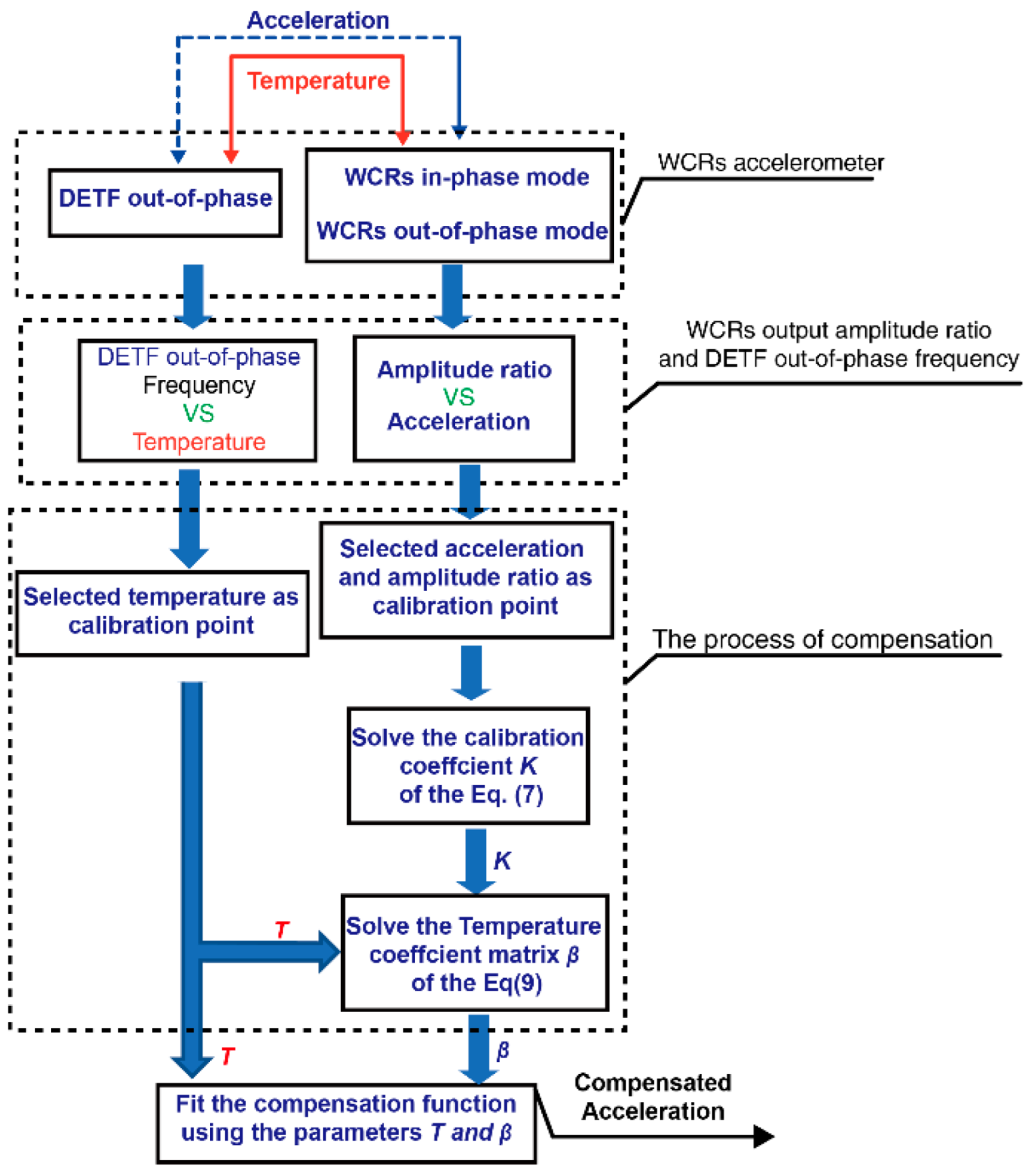
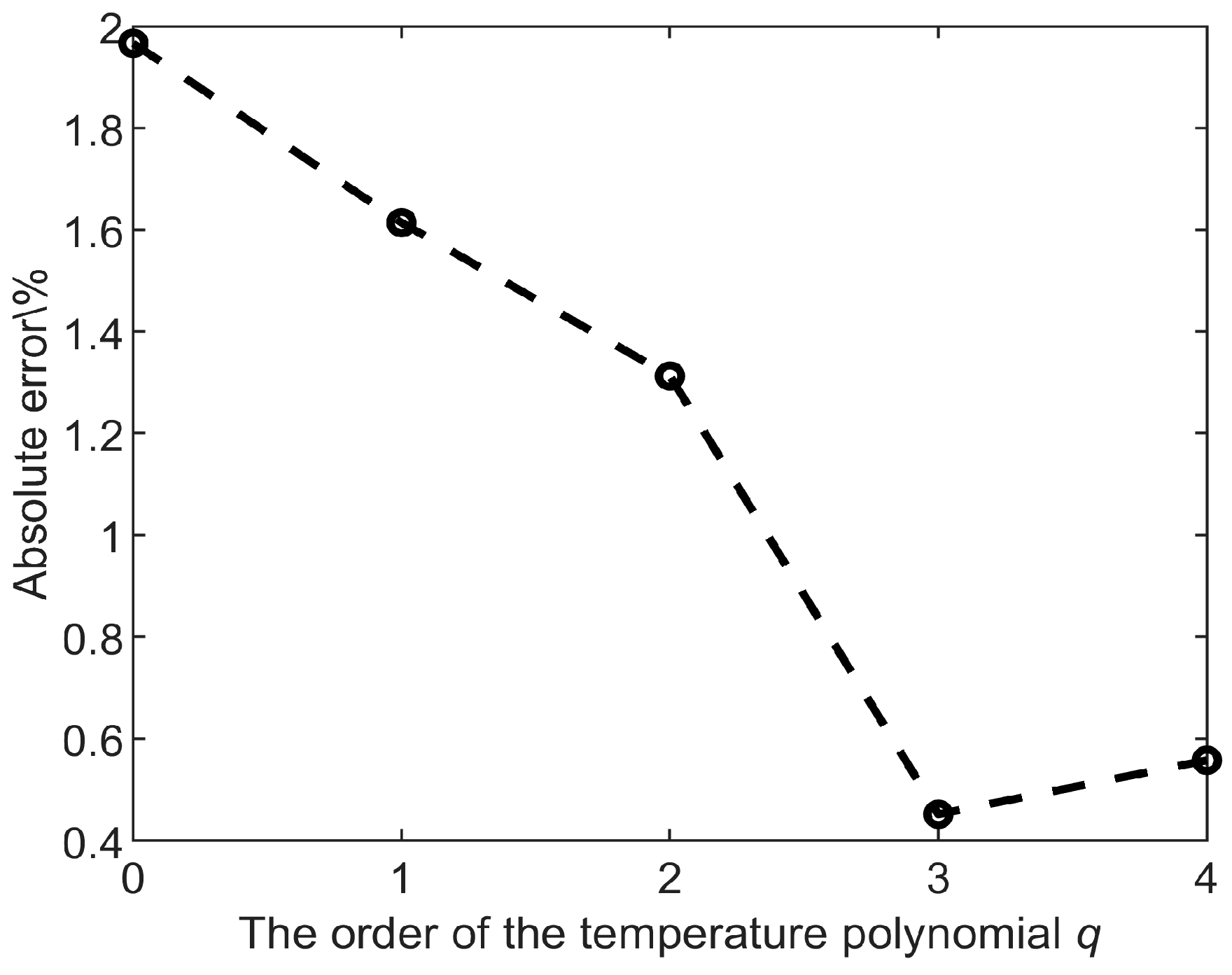
2.3.2. Temperature Compensation Mechanism and Algorithm Implementation
3. Experimental Results
3.1. Experimental Setup
3.2. Experimental Results
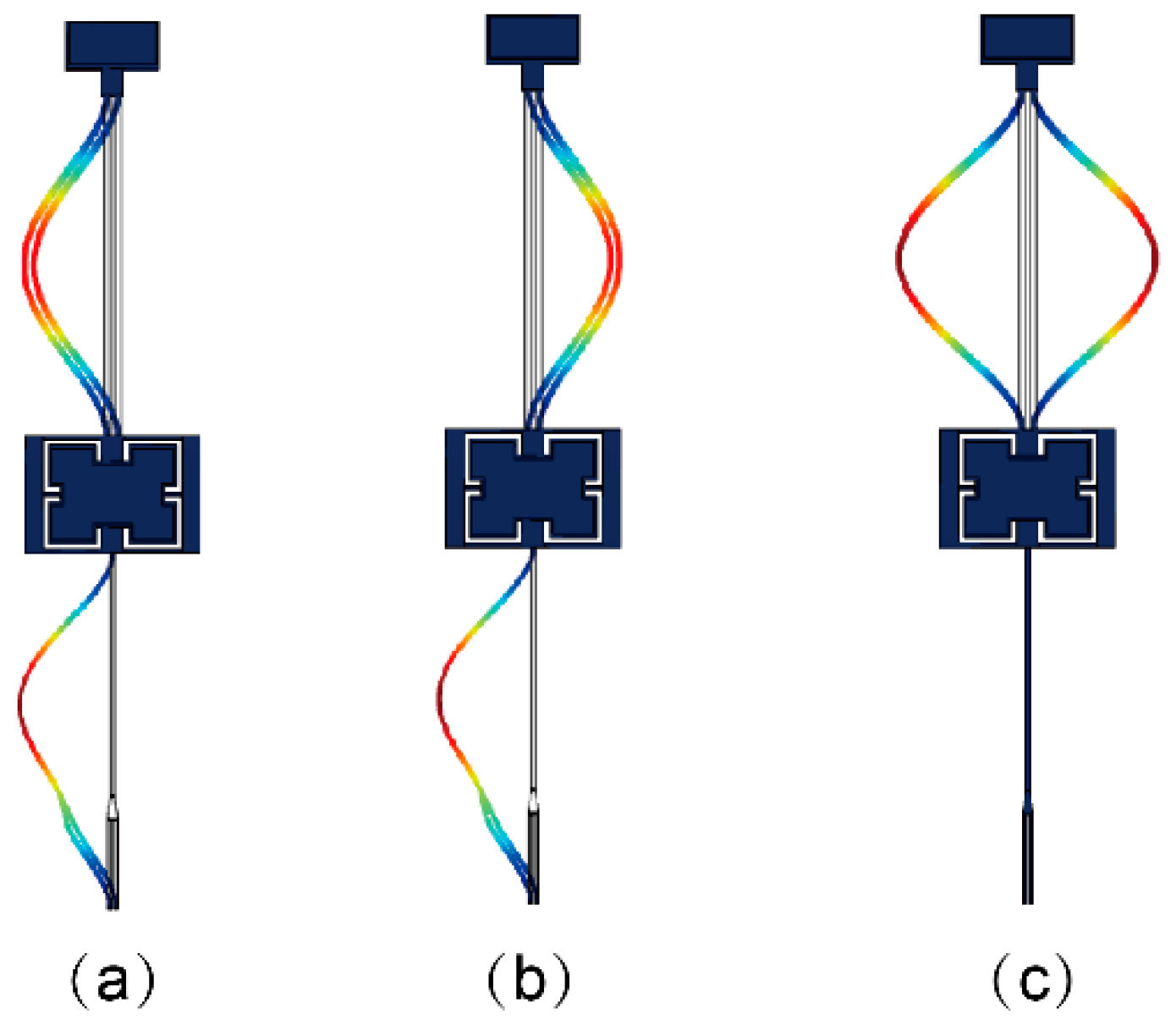
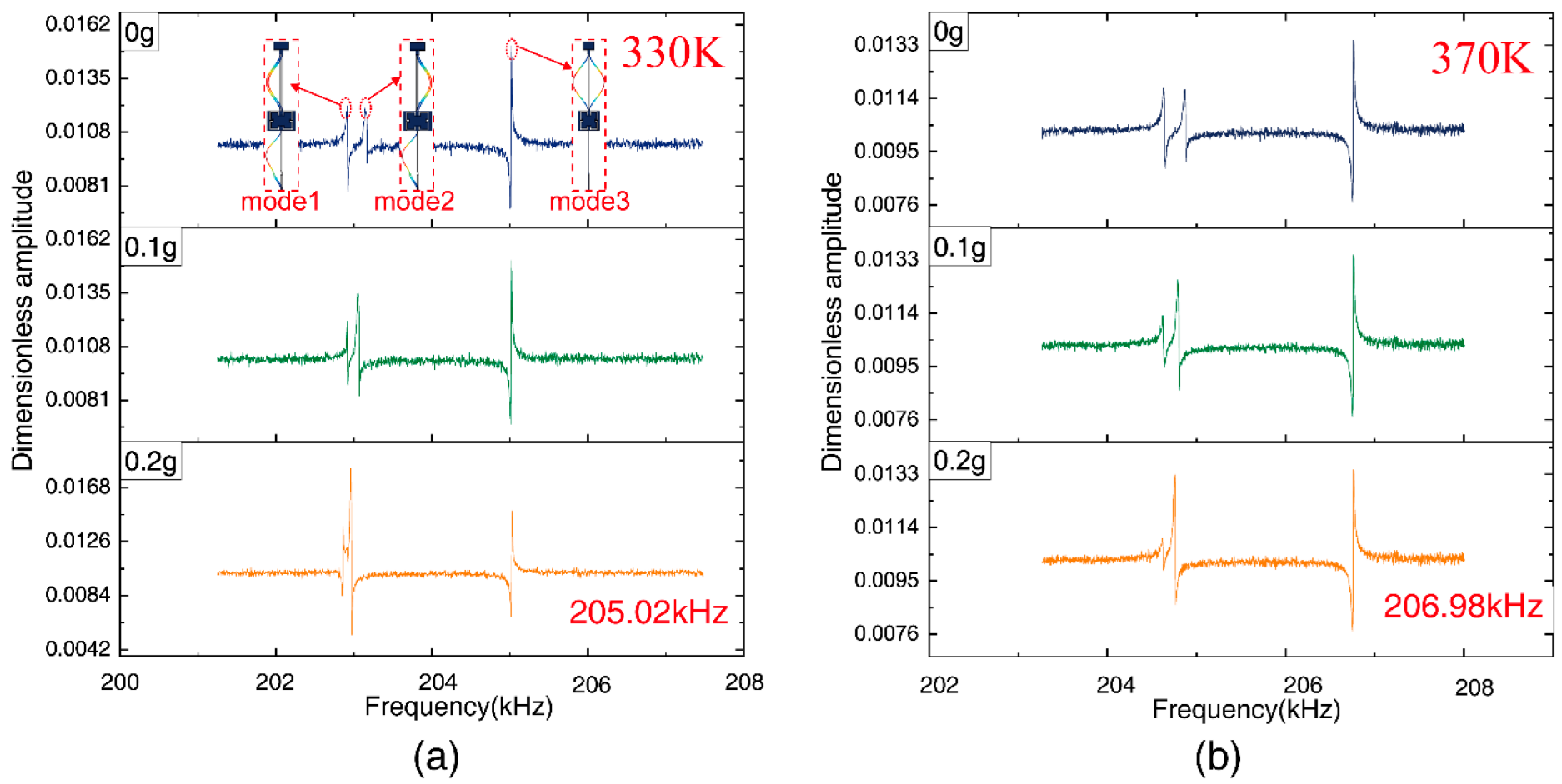
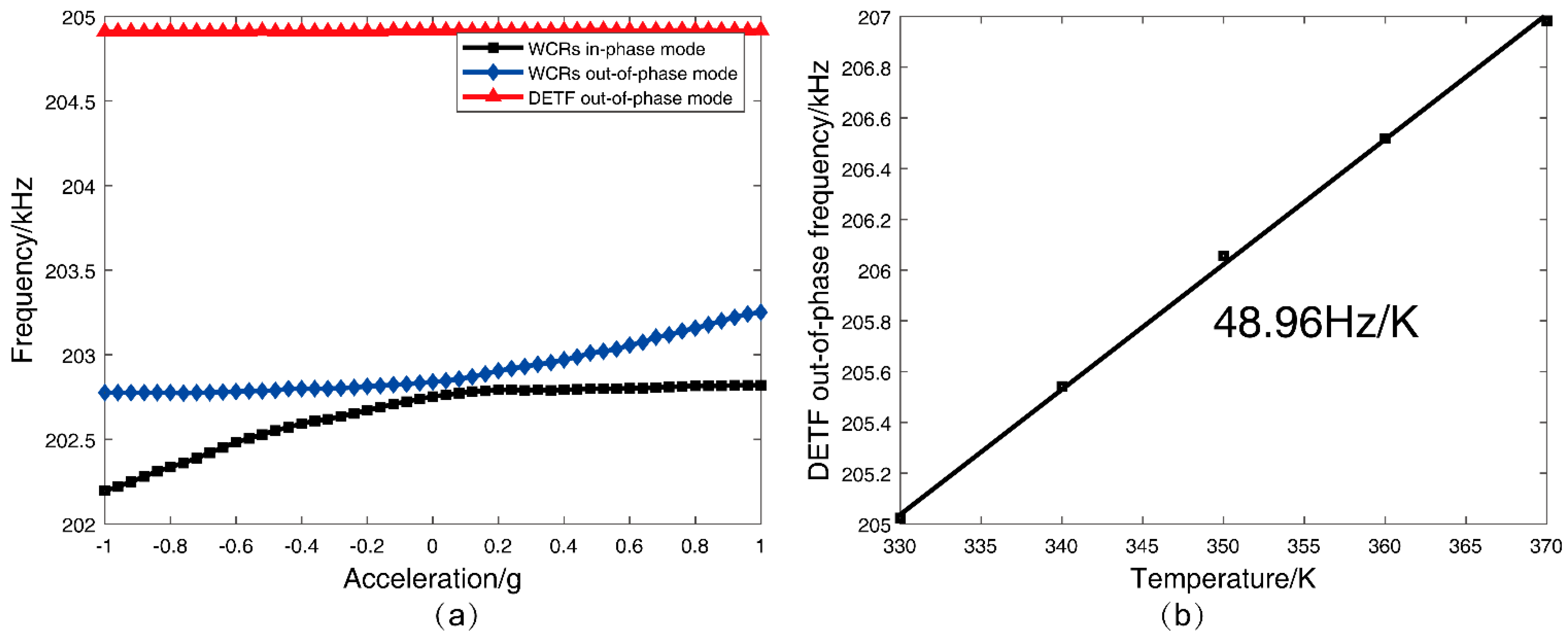
3.2.1. Mode Analysis and Sensitivity
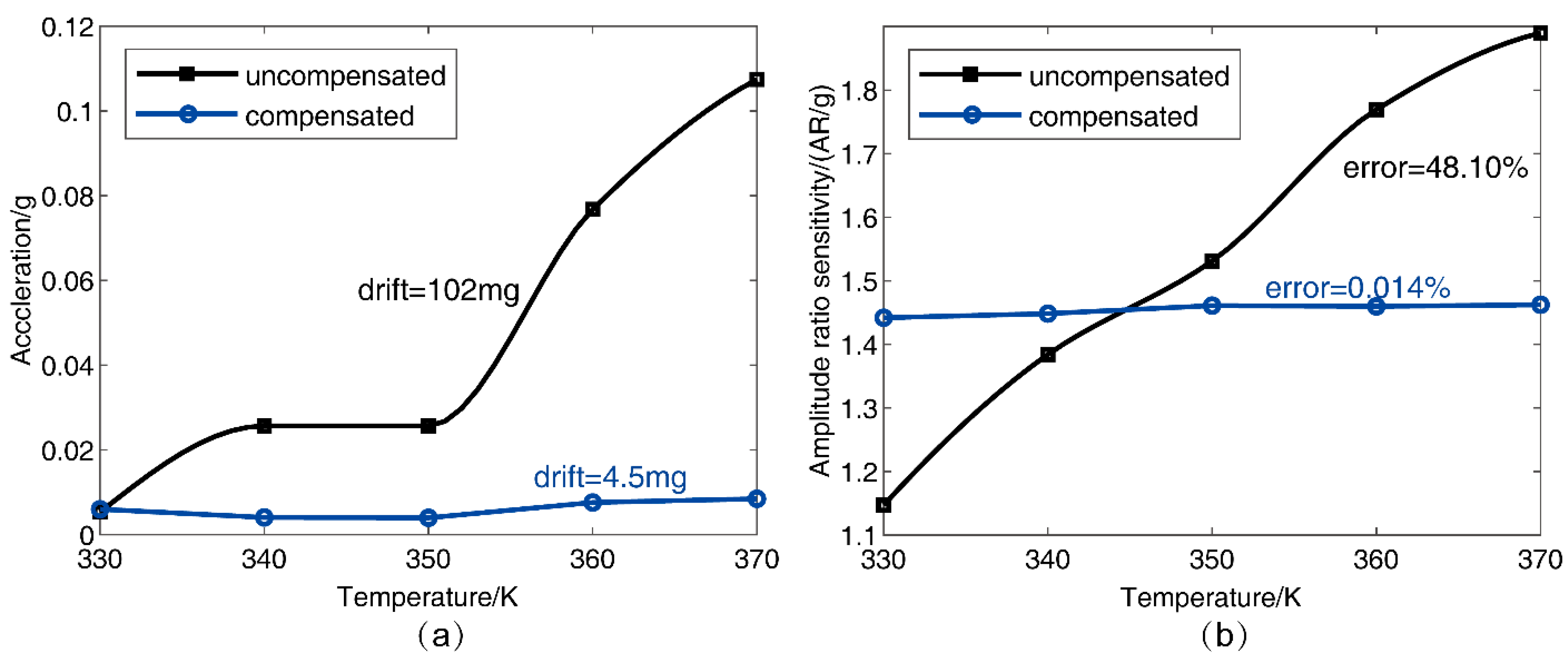
3.2.2. Temperature Compensation Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromechanical Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Zhao, Y.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A 0.23-μg Bias Instability and 1-μg/√Hz Acceleration Noise Density Silicon Oscillating Accelerometer with Embedded Frequency-to-Digital Converter in PLL. IEEE J. Solid-State Circuits 2017, 52, 1053–1065. [Google Scholar] [CrossRef]
- Xudong, Z.; Thiruvenkatanathan, P.; Seshia, A.A. A Seismic-Grade Resonant MEMS Accelerometer. J. Microelectromechanical Syst. 2014, 23, 768–770. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Qin, L.; Liu, J.; Li, M. Multiparameter Modeling of Piezoelectric Six-Degree-of-Freedom Accelerometer About Sensitivity Characteristics. IEEE Sens. J. 2020, 20, 7129–7137. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, K.; Shang, C.; Zhang, G.; Liu, G.J.M.J. MEMS inclinometer based on a novel piezoresistor structure. Microelectron. J. 2009, 40, 78–82. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, T. Parasitic Resistance-Based High Precision Capacitive MEMS Accelerometer Phase Shift and Its Usage for Temperature Compensation. IEEE Sens. J. 2018, 18, 629–634. [Google Scholar] [CrossRef]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Zou, X.; Seshia, A. A High Resolution Differential Mode-Localized MEMS Accelerometer. J. Microelectromechanical Syst. 2019, 28, 782–789. [Google Scholar] [CrossRef]
- Thiruvenkatanathan, P.; Jize, Y.; Woodhouse, J.; Seshia, A.A. Enhancing Parametric Sensitivity in Electrically Coupled MEMS Resonators. J. Microelectromechanical Syst. 2009, 18, 1077–1086. [Google Scholar] [CrossRef]
- Manav, M.; Reynen, G.; Sharma, M.; Cretu, E.; Phani, A.S. Ultrasensitive resonant MEMS transducers with tunable coupling. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 996–999. [Google Scholar]
- Hao, Y.; Liang, J.; Kang, H.; Yuan, W.; Chang, H. A Micromechanical Mode-Localized Voltmeter. IEEE Sens. J. 2021, 21, 4325–4332. [Google Scholar] [CrossRef]
- Li, B.; Zhang, H.; Zhong, J.; Chang, H. A mode localization based resonant MEMS tilt sensor with a linear measurement range of 360°. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar]
- Wood, G.S.; Zhao, C.; Pu, S.H.; Boden, S.A.; Sari, I.; Kraft, M. Mass sensor utilising the mode-localisation effect in an electrostatically-coupled MEMS resonator pair fabricated using an SOI process. Microelectron. Eng. 2016, 159, 169–173. [Google Scholar] [CrossRef] [Green Version]
- Thiruvenkatanathan, P.; Yan, J.; Woodhouse, J.; Aziz, A.; Seshia, A.A. Ultrasensitive mode-localized mass sensor with electrically tunable parametric sensitivity. Appl. Phys. Lett. 2010, 96, 081913. [Google Scholar] [CrossRef]
- Spletzer, M.; Raman, A.; Wu, A.Q.; Xu, X.; Reifenberger, R. Ultrasensitive mass sensing using mode localization in coupled microcantilevers. Appl. Phys. Lett. 2006, 88, 254102. [Google Scholar] [CrossRef]
- Peng, B.; Hu, K.M.; Shao, L.; Yan, H.; Li, L.; Wei, X.; Zhang, W.M. A Sensitivity Tunable Accelerometer Based on Series-Parallel Electromechanically Coupled Resonators Using Mode Localization. J. Microelectromechanical Syst. 2020, 29, 3–13. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, X.; Pandit, M.; Sobreviela, G.; Du, S.; Zou, X.; Seshia, A. Toward High-Resolution Inertial Sensors Employing Parametric Modulation in Coupled Micromechanical Resonators. Phys. Rev. Appl. 2019, 12, 044005. [Google Scholar] [CrossRef]
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A Three Degree-of-Freedom Weakly Coupled Resonator Sensor With Enhanced Stiffness Sensitivity. J. Microelectromechanical Syst. 2016, 25, 38–51. [Google Scholar] [CrossRef]
- Zheng, W.; Xiong, X.; Li, Z.; Wang, K.; Yang, W.; Zou, X. Enhancing Parametric Sensitivity Using Micro-Lever Coupler in Mechanical Coupling Mode-Localized Mems Accelerometer. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 1846–1849. [Google Scholar]
- Zhang, H.; Sobreviela, G.; Pandit, M.; Chen, D.; Sun, J.; Parajuli, M.; Zhao, C.; Seshia, A.A. A Low-Noise High-Order Mode-Localized MEMS Accelerometer. J. Microelectromechanical Syst. 2021, 30, 178–180. [Google Scholar] [CrossRef]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Seshia, A. Practical Limits to Common Mode Rejection in Mode Localized Weakly Coupled Resonators. IEEE Sens. J. 2020, 20, 6818–6825. [Google Scholar] [CrossRef]
- Kang, H.; Ruan, B.; Hao, Y.; Chang, H. A Mode-Localized Resonant Accelerometer with Self-Temperature Drift Suppression. IEEE Sens. J. 2020, 20, 12154–12165. [Google Scholar] [CrossRef]
- Watanabe, H.; Yamada, N.; Okaji, M. Linear Thermal Expansion Coefficient of Silicon from 293 to 1000 K. Int. J. Thermophys. 2004, 25, 221–236. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromechanical Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef] [Green Version]
- Li, M.-H.; Chen, C.-Y.; Li, C.-S.; Chin, C.-H.; Li, S.-S. A Monolithic CMOS-MEMS Oscillator Based on an Ultra-Low-Power Ovenized Micromechanical Resonator. J. Microelectromechanical Syst. 2015, 24, 360–372. [Google Scholar] [CrossRef]
- Xu, C.; Segovia-Fernandez, J.; Kim, H.J.; Piazza, G. Temperature-Stable Piezoelectric MEMS Resonators Using Integrated Ovens and Simple Resistive Feedback Circuits. J. Microelectromechanical Syst. 2017, 26, 187–195. [Google Scholar] [CrossRef]
- Yang, D.; Woo, J.-K.; Lee, S.; Mitchell, J.; Challoner, A.D.; Najafi, K. A Micro Oven-Control System for Inertial Sensors. J. Microelectromechanical Syst. 2017, 26, 507–518. [Google Scholar] [CrossRef]
- Ortiz, L.C.; Flader, I.B.; Vukasin, G.D.; Gerrard, D.D.; Chandorkar, S.A.; Rodriguez, J.; Shin, D.D.; Kwon, R.; Heinz, D.B.; Chen, Y.; et al. Thermal effects of ovenized clocks on episeal encapsulated inertial measurement units. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 980–983. [Google Scholar]
- Li, B.; Li, C.; Zhao, Y.; Han, C.; Zhang, Q. An integrated packaged resonant accelerometer with temperature compensation. Rev. Sci. Instrum. 2020, 91, 105004. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, J.; Luo, Z.; Chen, D.; Chen, J. A resonant pressure microsensor capable of self-temperature compensation. Sensors 2015, 15, 10048–10058. [Google Scholar] [CrossRef]
- Shi, R.; Zhao, J.; Qiu, A.P.; Xia, G.M. Temperature Self-Compensation of Micromechanical Silicon Resonant Accelerometer. Appl. Mech. Mater. 2013, 373, 373–381. [Google Scholar] [CrossRef]
- Zotov, S.A.; Simon, B.R.; Trusov, A.A.; Shkel, A.M. High Quality Factor Resonant MEMS Accelerometer with Continuous Thermal Compensation. IEEE Sens. J. 2015, 15, 5045–5052. [Google Scholar] [CrossRef]
- Kose, T.; Azgin, K.; Akin, T. Temperature compensation of a capacitive MEMS accelerometer by using a MEMS oscillator. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems, Laguna Beach, CA, USA, 22–25 February 2016; pp. 33–36. [Google Scholar]
- Lee, J.; Rhim, J. Temperature compensation method for the resonant frequency of a differential vibrating accelerometer using electrostatic stiffness control. J. Micromechanics Microengineering 2012, 22, 095016. [Google Scholar] [CrossRef]
- Pachkawade, V. State-of-the-Art in Mode-Localized MEMS Coupled Resonant Sensors: A Comprehensive Review. IEEE Sens. J. 2021, 21, 8751–8779. [Google Scholar] [CrossRef]
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Yuan, W.; Kraft, M.; Chang, H. An Acceleration Sensing Method Based on the Mode Localization of Weakly Coupled Resonators. J. Microelectromechanical Syst. 2016, 25, 286–296. [Google Scholar] [CrossRef]
- Zhao, C.; Li, M.; Yin, M.; Liu, Z. Micro-Raman spectroscopy analysis of residual stress in polysilicon MEMS resonators. In Proceedings of the 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Suzhou, China, 7–10 April 2013; pp. 570–573. [Google Scholar] [CrossRef]
- Cai, P.; Xiong, X.; Wang, K.; Wang, J.; Zou, X. An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers. Micromachines 2021, 12, 1022. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Value |
|---|---|
| Total chip size | 20 mm3 |
| Structure thickness | 40 μm |
| Anchor thickness | 20 μm |
| Glass thickness | 50 μm |
| Length of CC resonator | 400 μm |
| Width of CC resonator | 7 μm |
| Length of DETF resonator | 600 μm |
| Width of DETF resonator | 9.5 μm |
| Lever amplification ratio | 23 |
| Gap of parallel-plate capacitor | 2 μm |
| Coupling stiffness at room temperature | 0.037 N/m |
| The effective stiffness of CC resonator | 335.23 N/m |
| The effective stiffness of DETF resonator | 486.06 N/m |
| The effective mass of CC resonator | 0.20 μg |
| The effective mass of DETF resonator | 0.29 μg |
| Proof mass | 1.5 mg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Xiong, X.; Wang, Z.; Cai, P.; Ma, L.; Zou, X. Utilizing the Intrinsic Mode of Weakly Coupled Resonators for Temperature Compensation. Micromachines 2022, 13, 1447. https://doi.org/10.3390/mi13091447
Wang K, Xiong X, Wang Z, Cai P, Ma L, Zou X. Utilizing the Intrinsic Mode of Weakly Coupled Resonators for Temperature Compensation. Micromachines. 2022; 13(9):1447. https://doi.org/10.3390/mi13091447
Chicago/Turabian StyleWang, Kunfeng, Xingyin Xiong, Zheng Wang, Pengcheng Cai, Liangbo Ma, and Xudong Zou. 2022. "Utilizing the Intrinsic Mode of Weakly Coupled Resonators for Temperature Compensation" Micromachines 13, no. 9: 1447. https://doi.org/10.3390/mi13091447
APA StyleWang, K., Xiong, X., Wang, Z., Cai, P., Ma, L., & Zou, X. (2022). Utilizing the Intrinsic Mode of Weakly Coupled Resonators for Temperature Compensation. Micromachines, 13(9), 1447. https://doi.org/10.3390/mi13091447






