Structural Optimization and MEMS Implementation of the NV Center Phonon Piezoelectric Device
Abstract
:1. Introduction
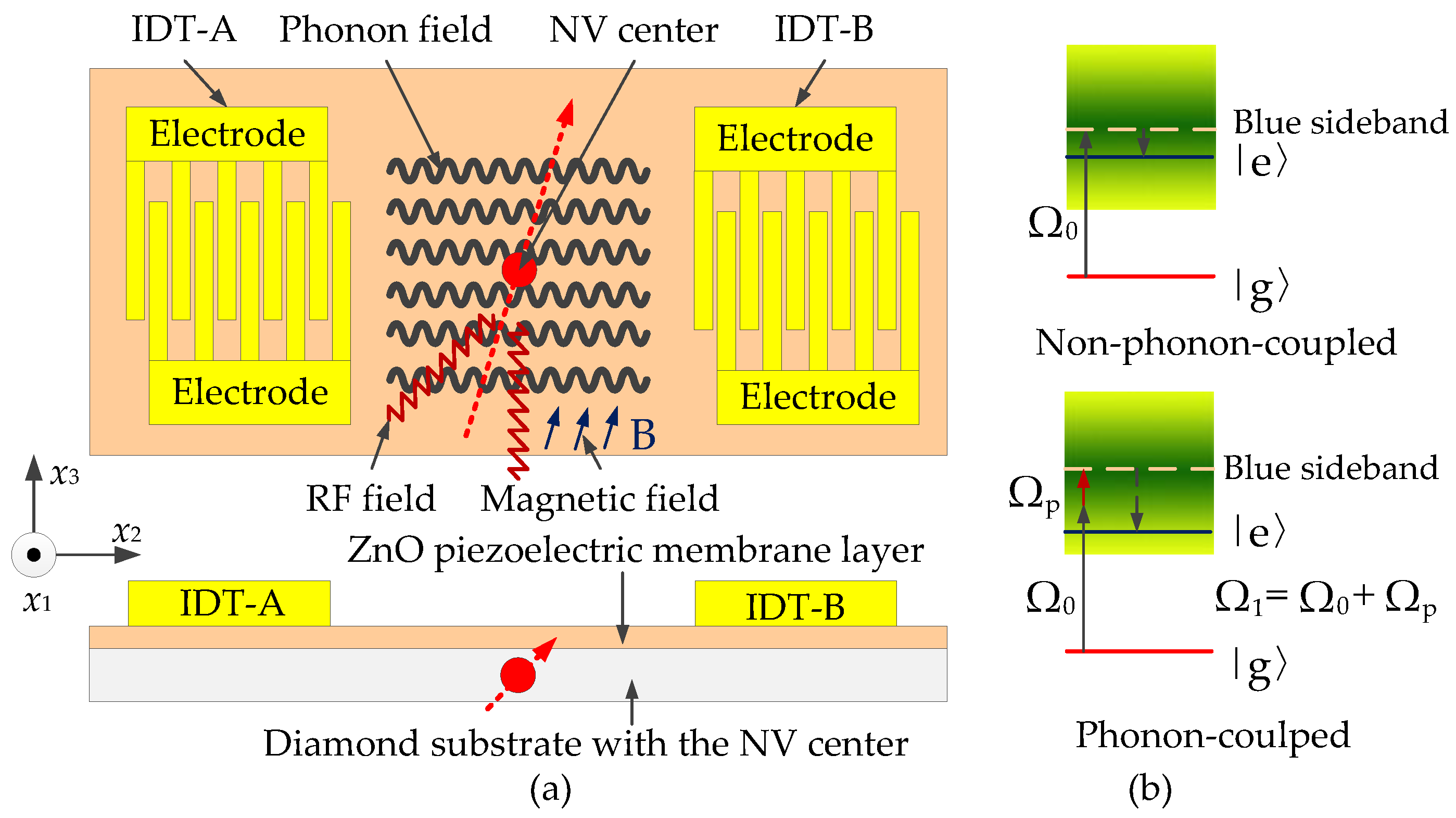
2. Phonon-Coupled Manipulation Mechanism and Acoustic Characteristics of the Phonon Piezoelectric Device of the NV Center
2.1. Phonon Resonance Structure and Acoustic Manipulation Mechanism of the NV Center
2.2. Acoustic Characteristics Model of Phonon Piezoelectric Devices
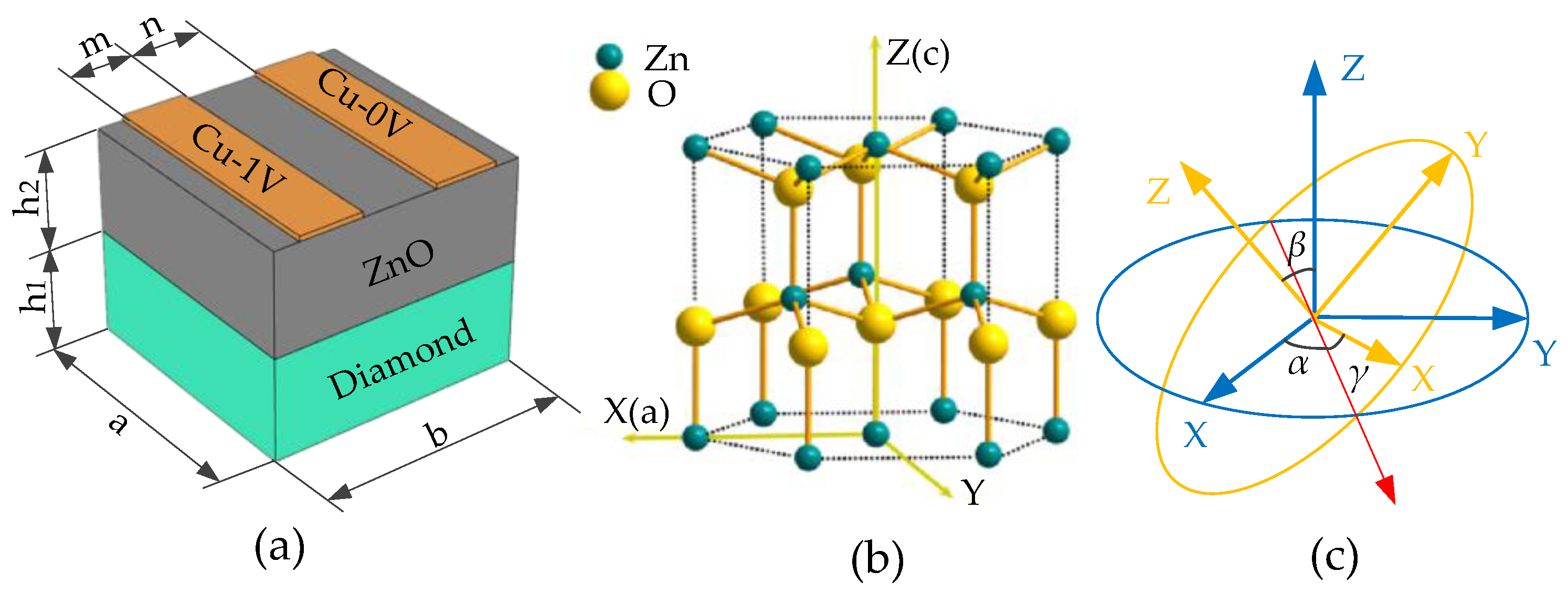
2.3. Mathematical Construction of the Phonon Piezoelectric Device of the NV Center
- (1)
- Model construction of the IDT of the phonon piezoelectric device
- (2)
- Structural unit analysis of the phonon piezoelectric device
3. Structural Optimization of Phonon Piezoelectric Device of the NV Center
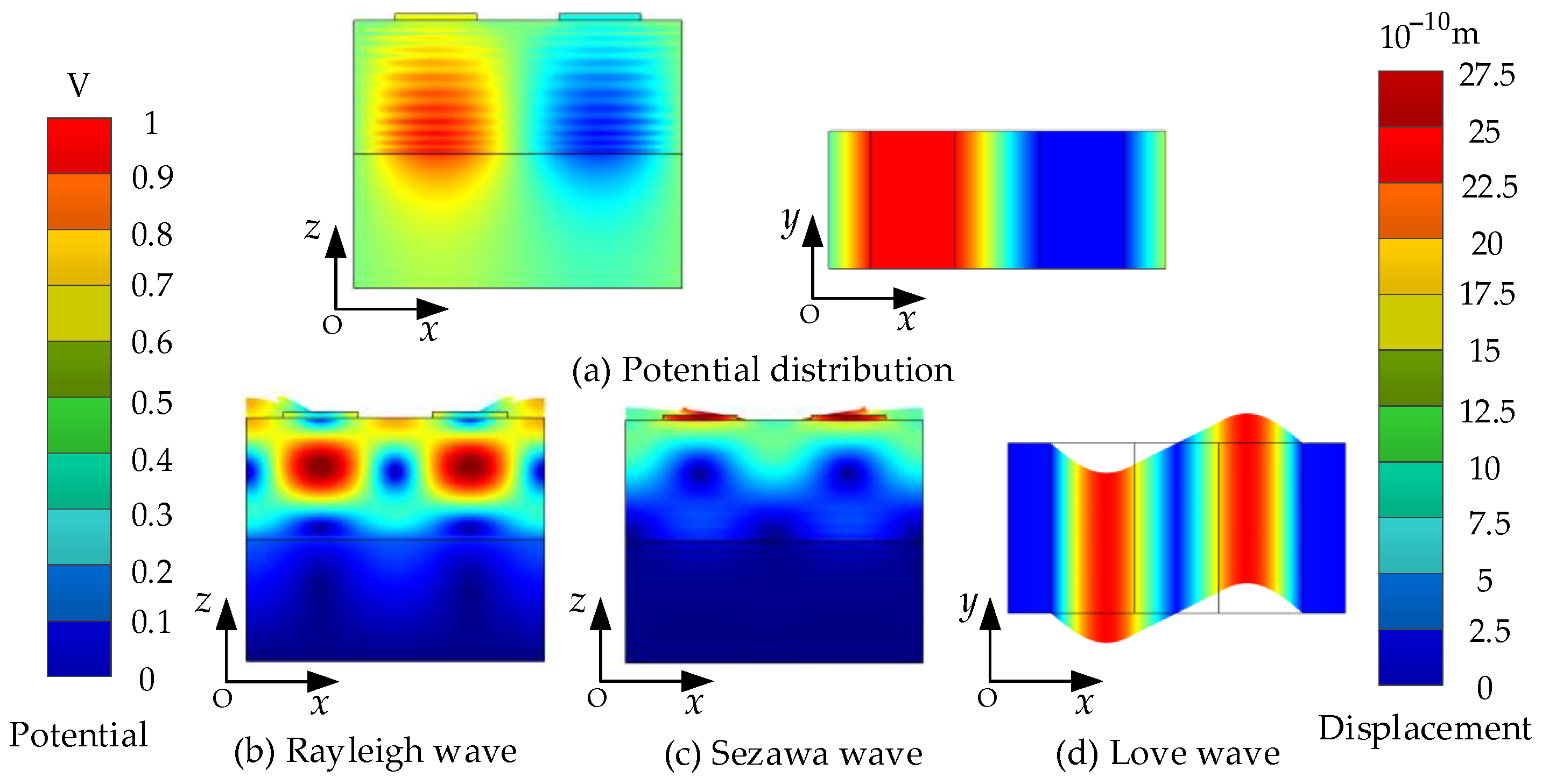
3.1. Finite Element Model of the Phonon Piezoelectric Device
- (1)
- Mathematical model
- (2)
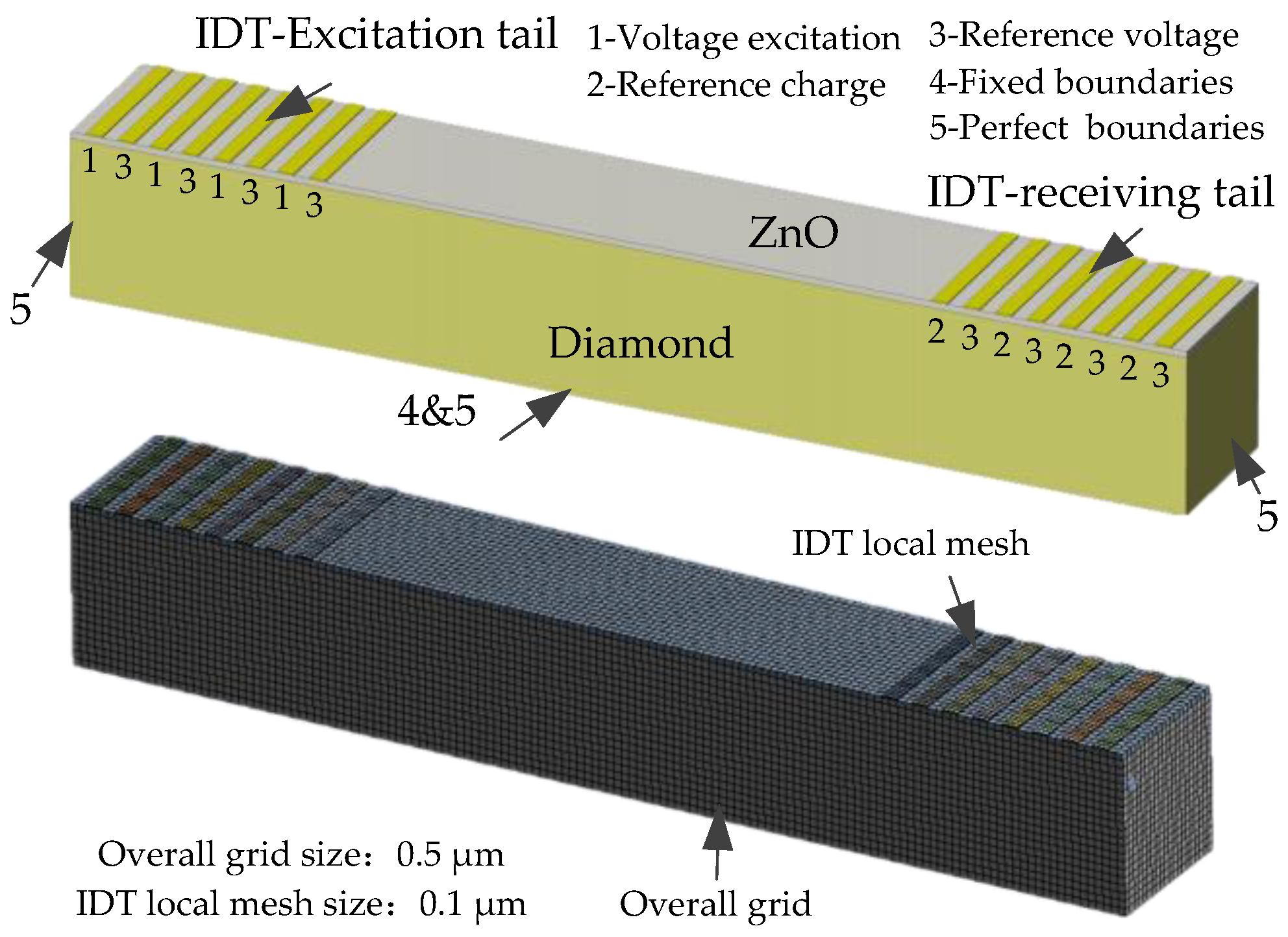
- Finite element model and boundary conditions
- (3)
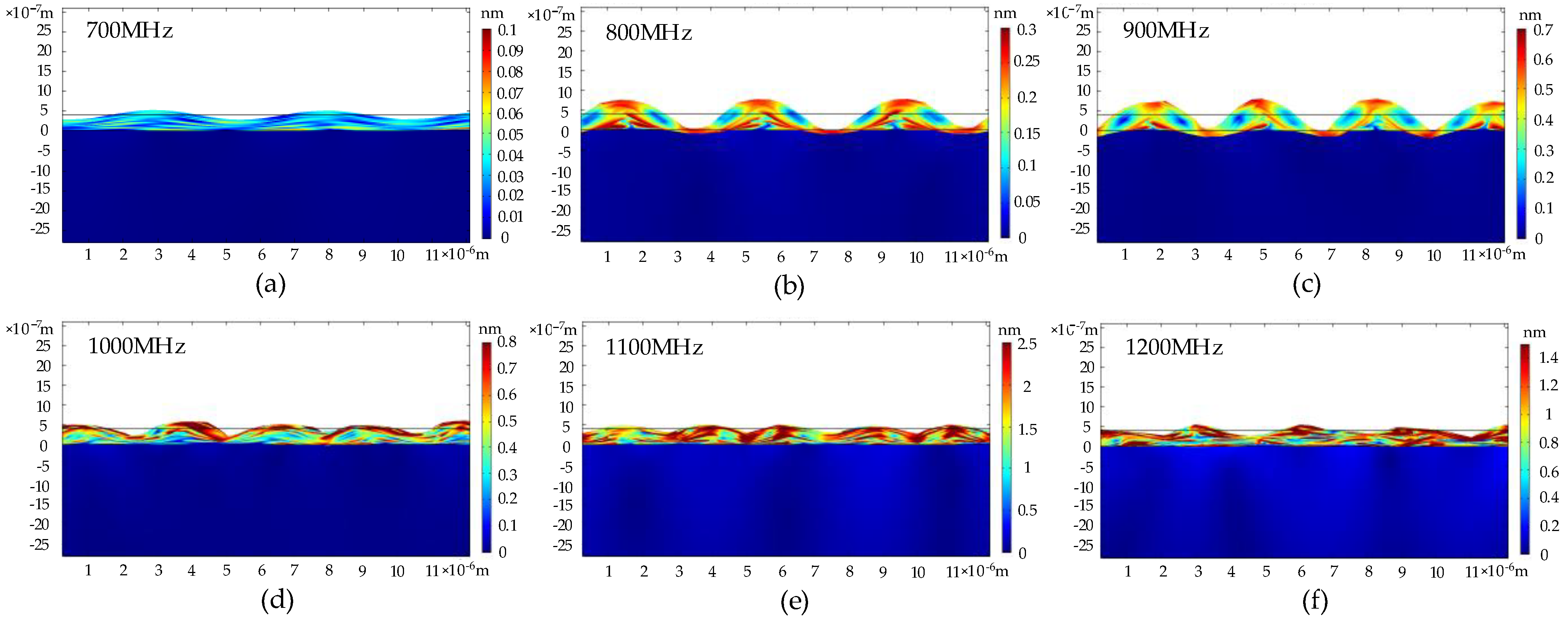
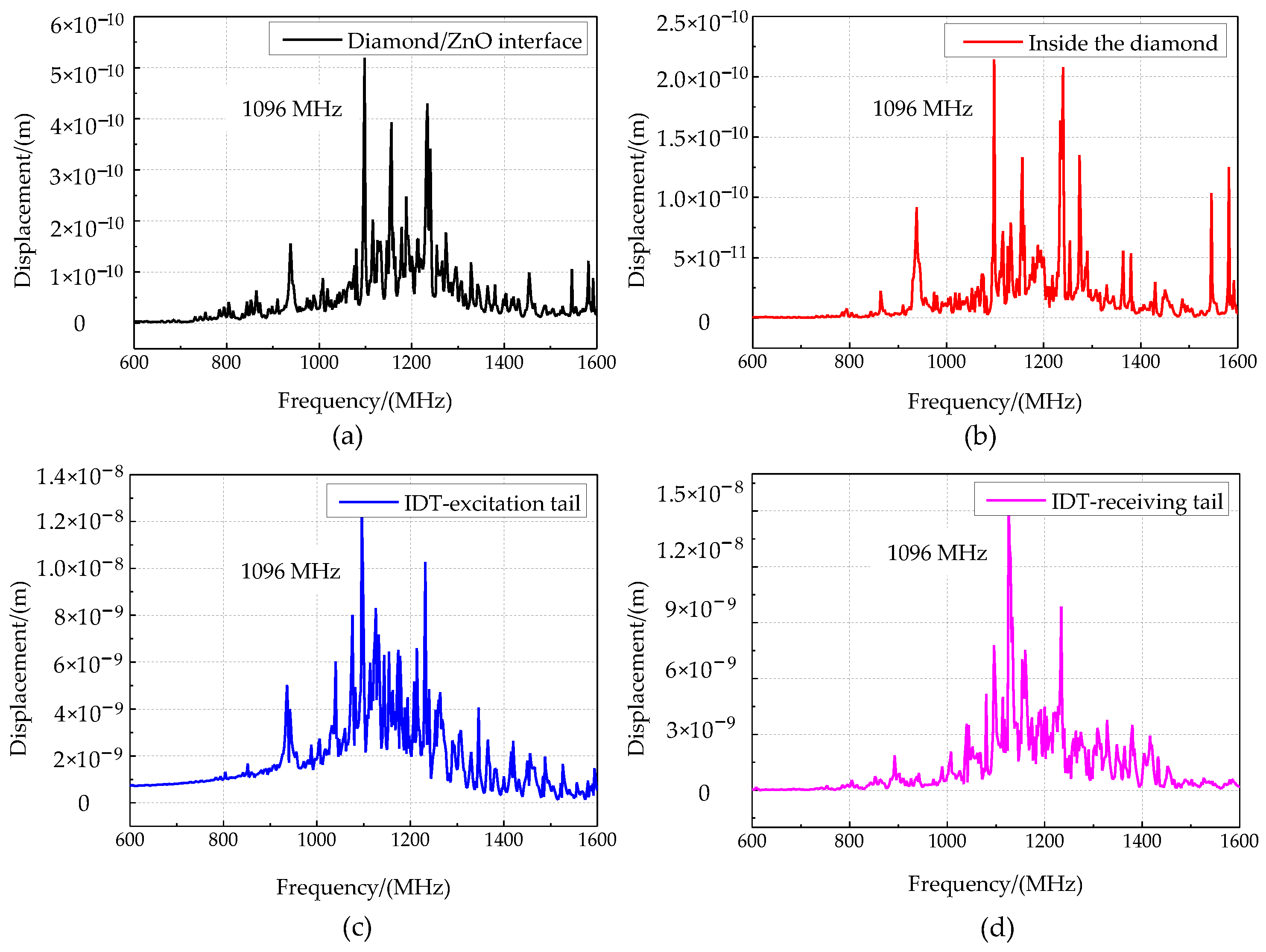
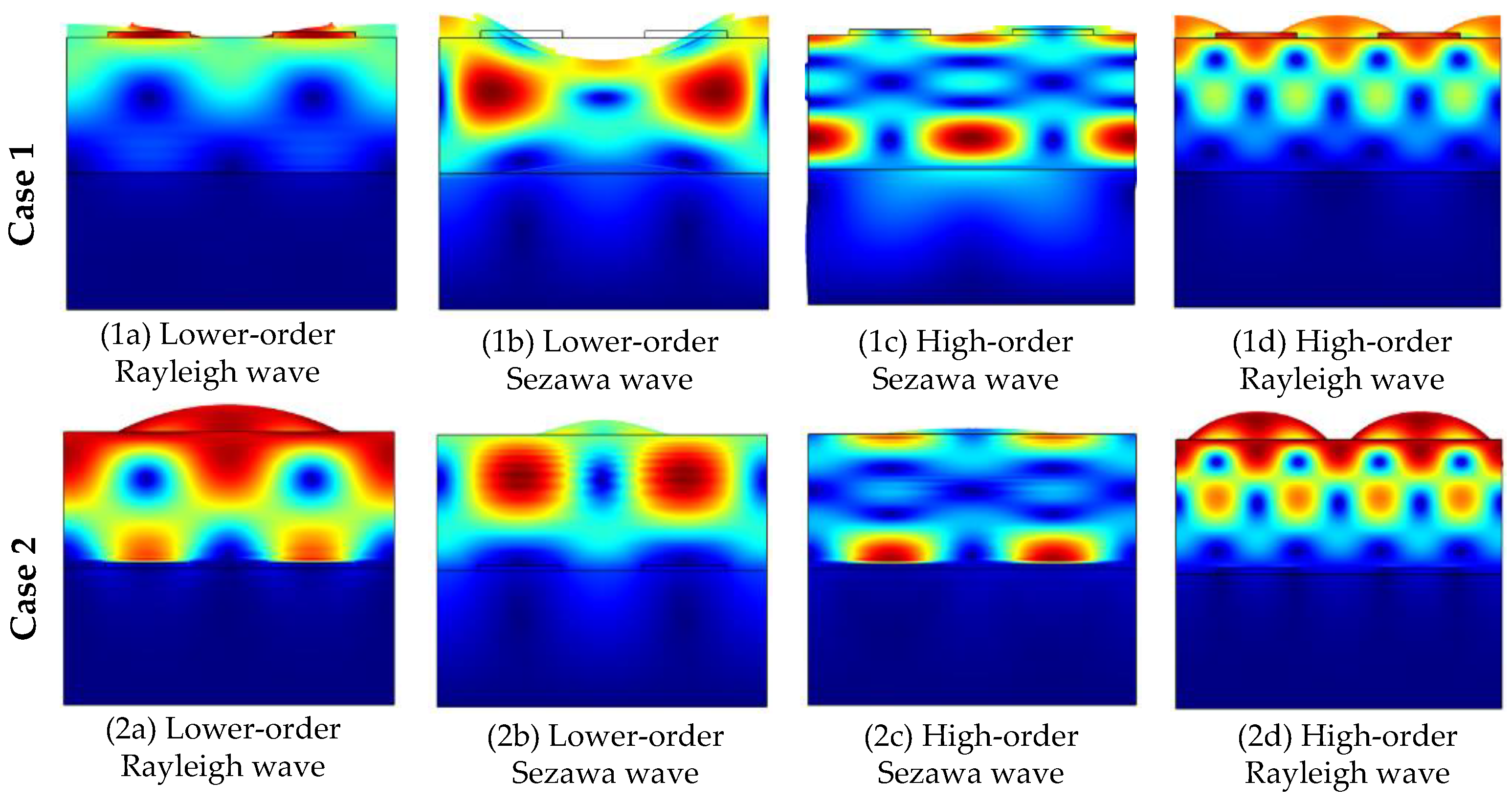
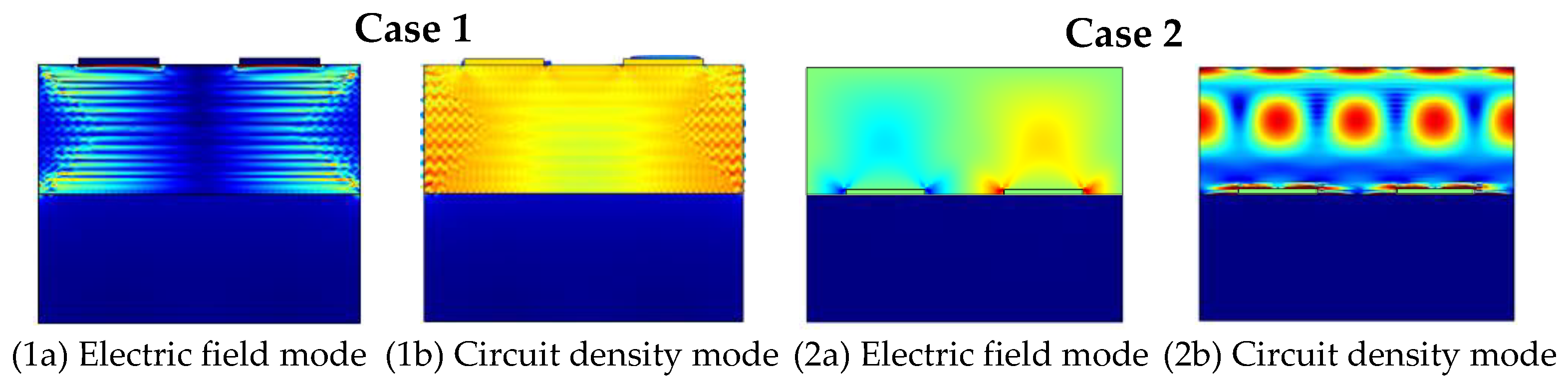
- Simulation results of phonon field characteristics
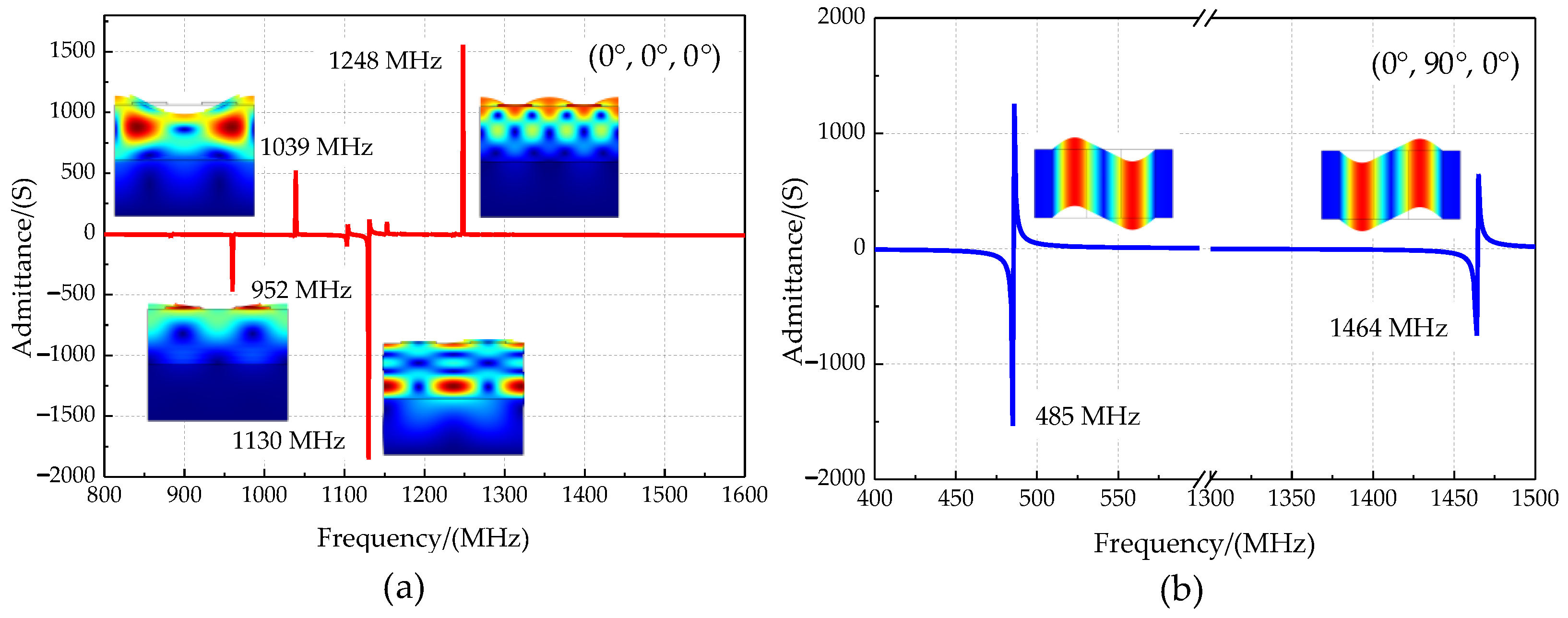
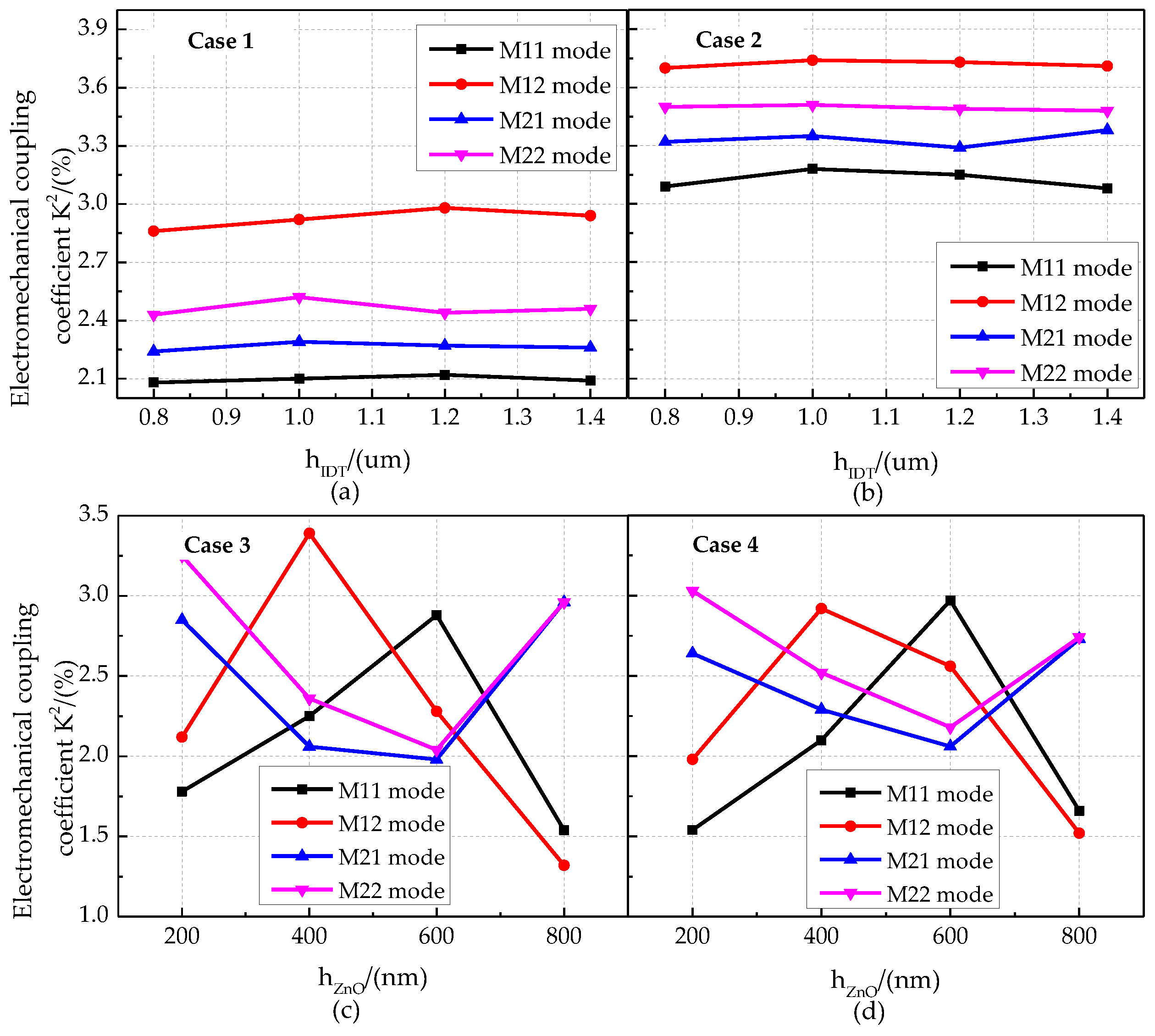
3.2. Structural Optimization of the Phonon Piezoelectric Device
- (1)
- Geometry parameters
- (2)
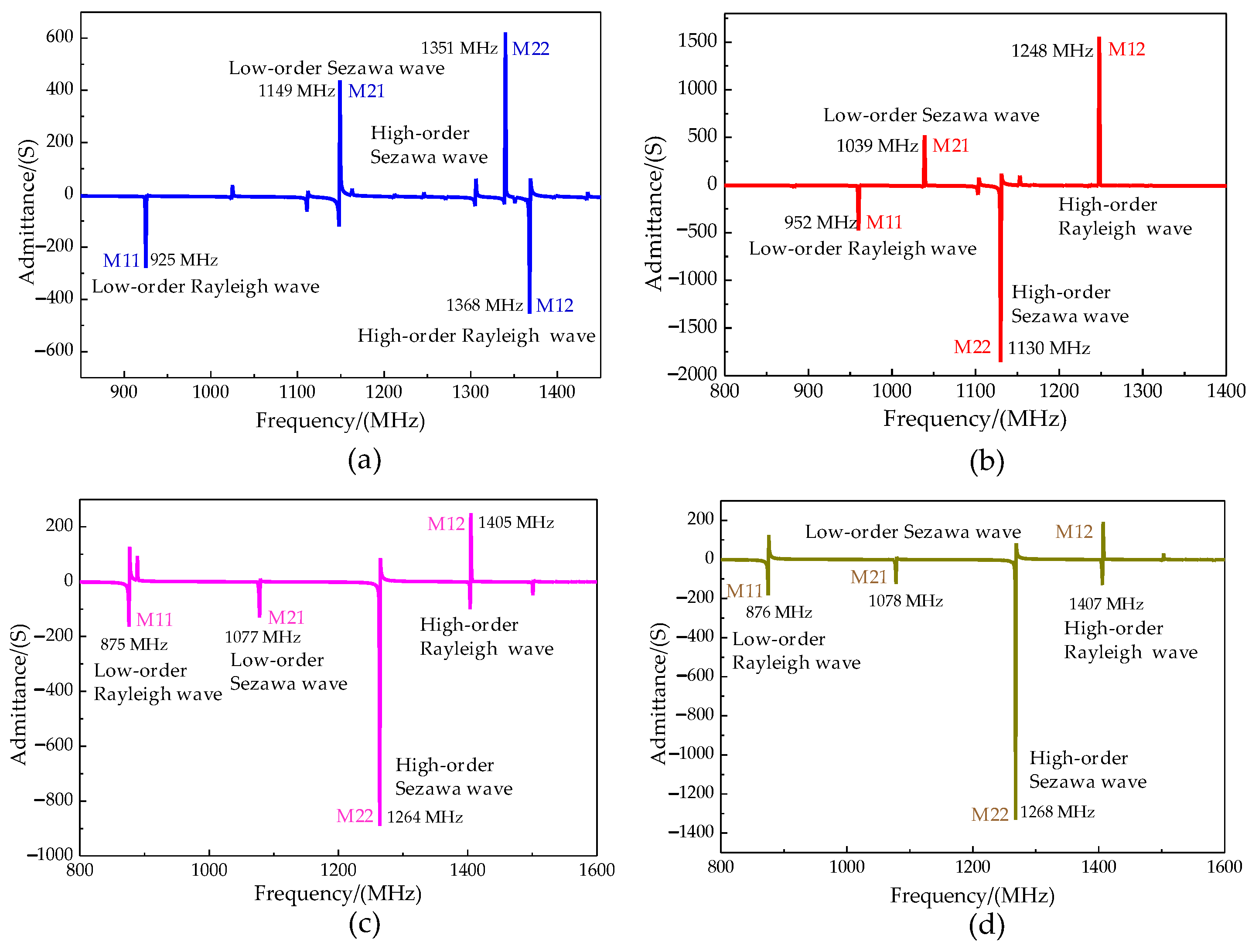
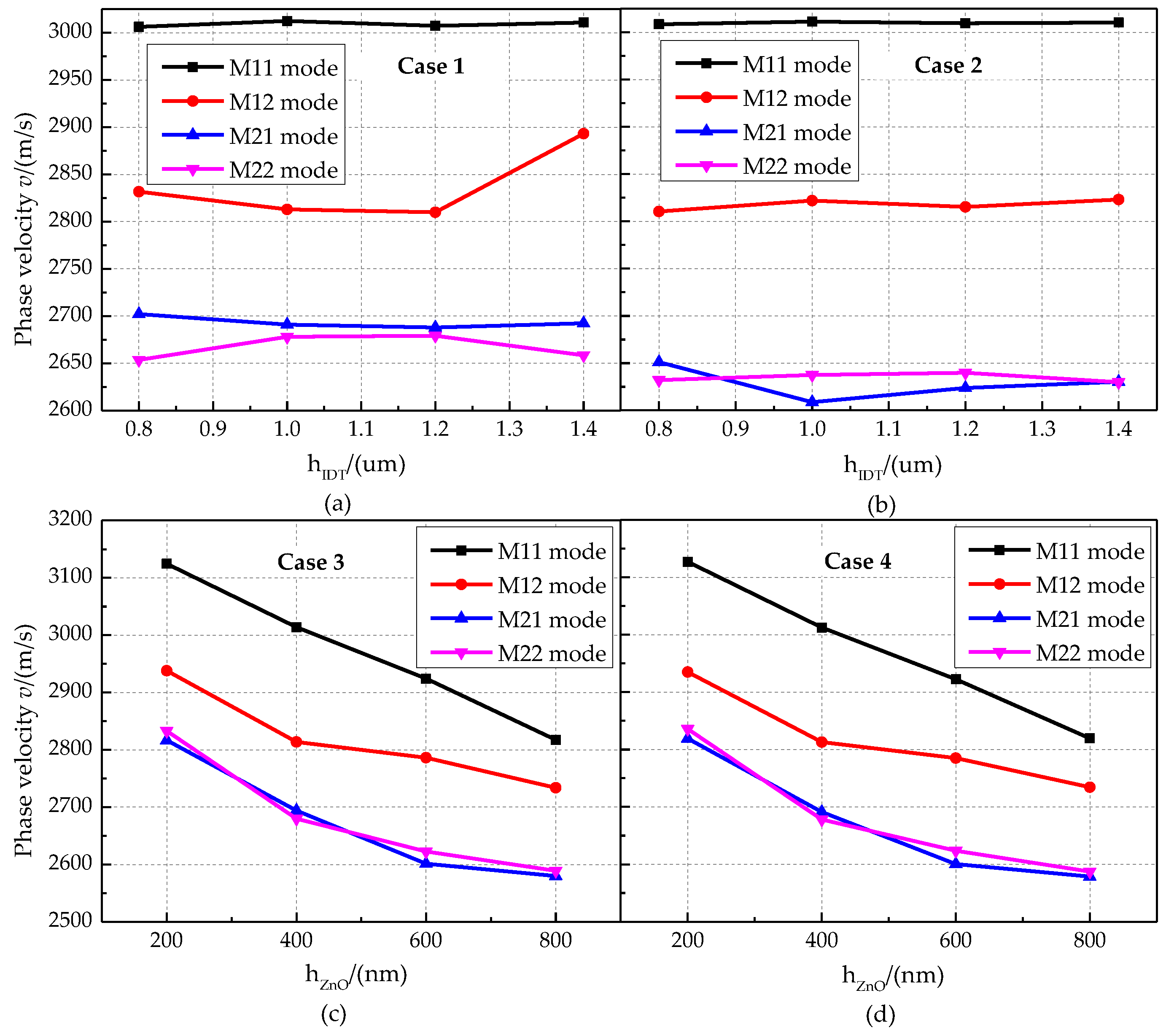
- Optimization results
4. Phonon-Coupled Manipulation Experiment of the NV Center
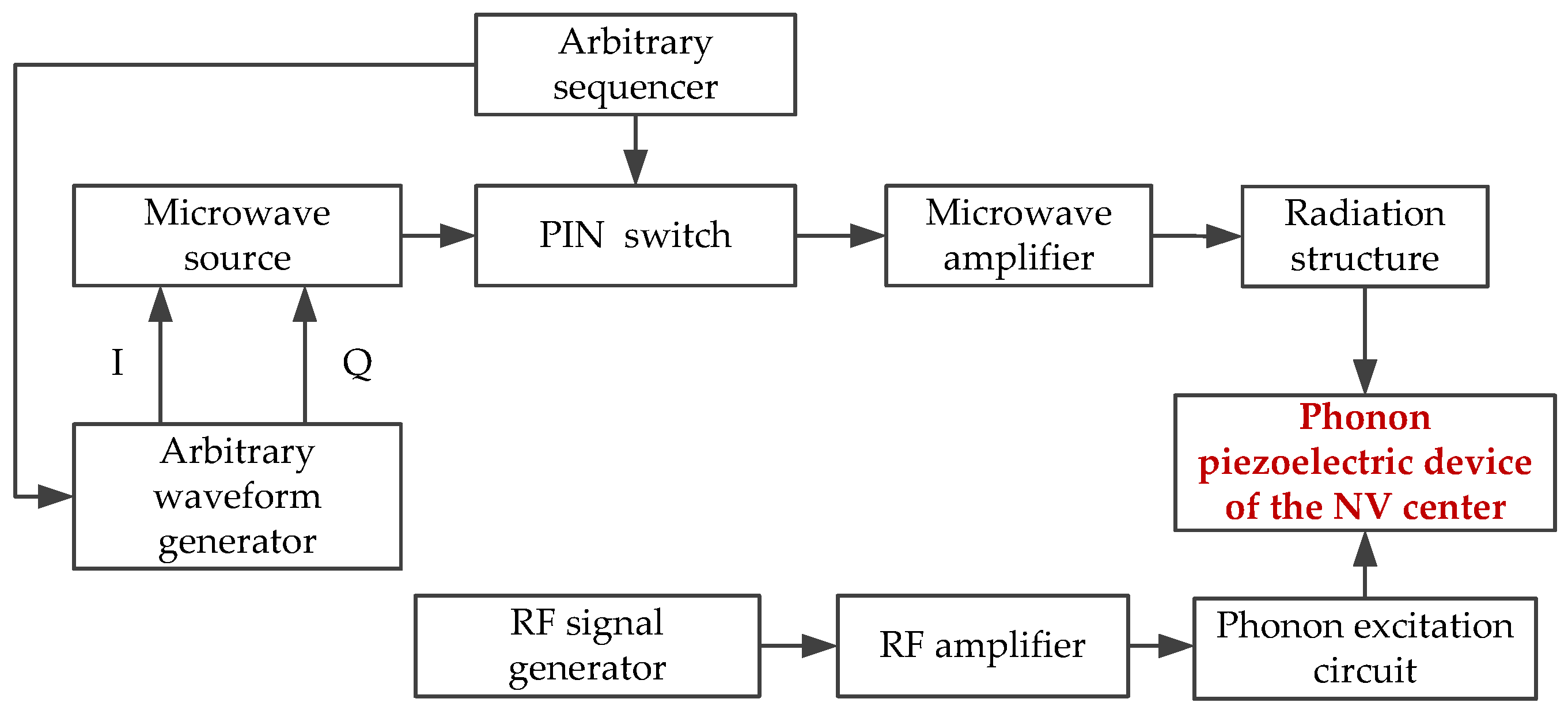
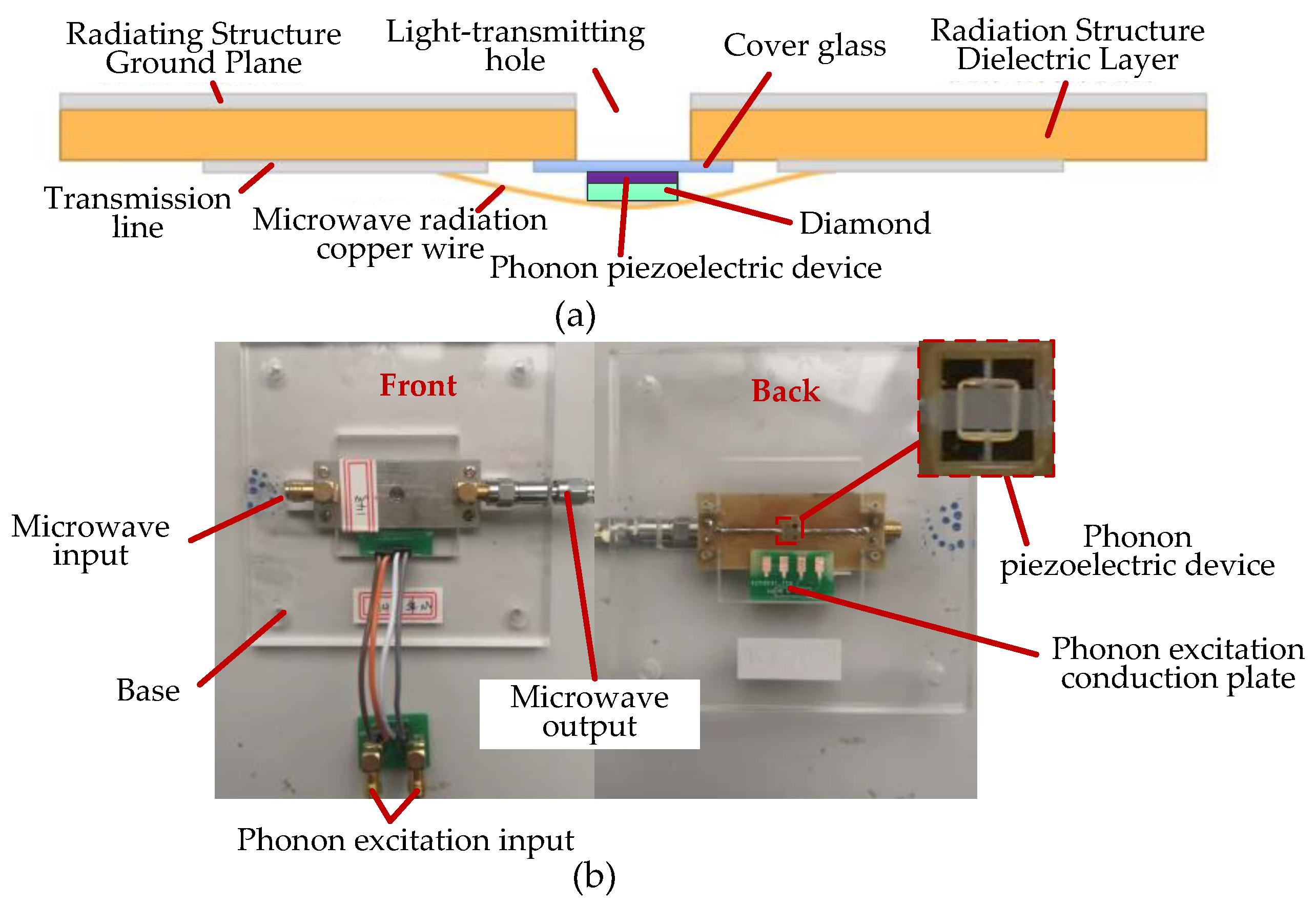
4.1. MEMS Implement of the Phonon Piezoelectric Device of the NV Center
4.2. Phonon-Coupled Manipulation Experiment
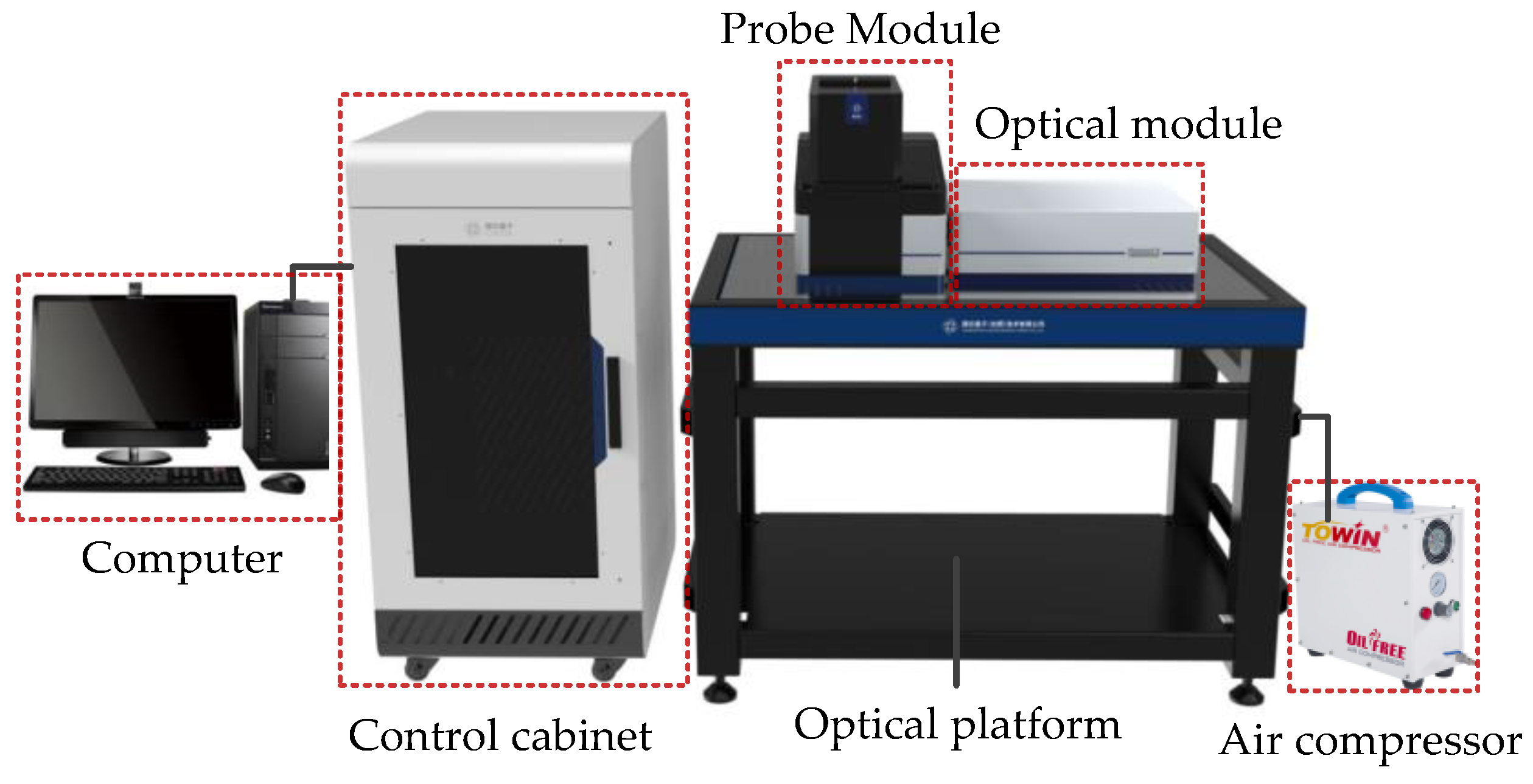
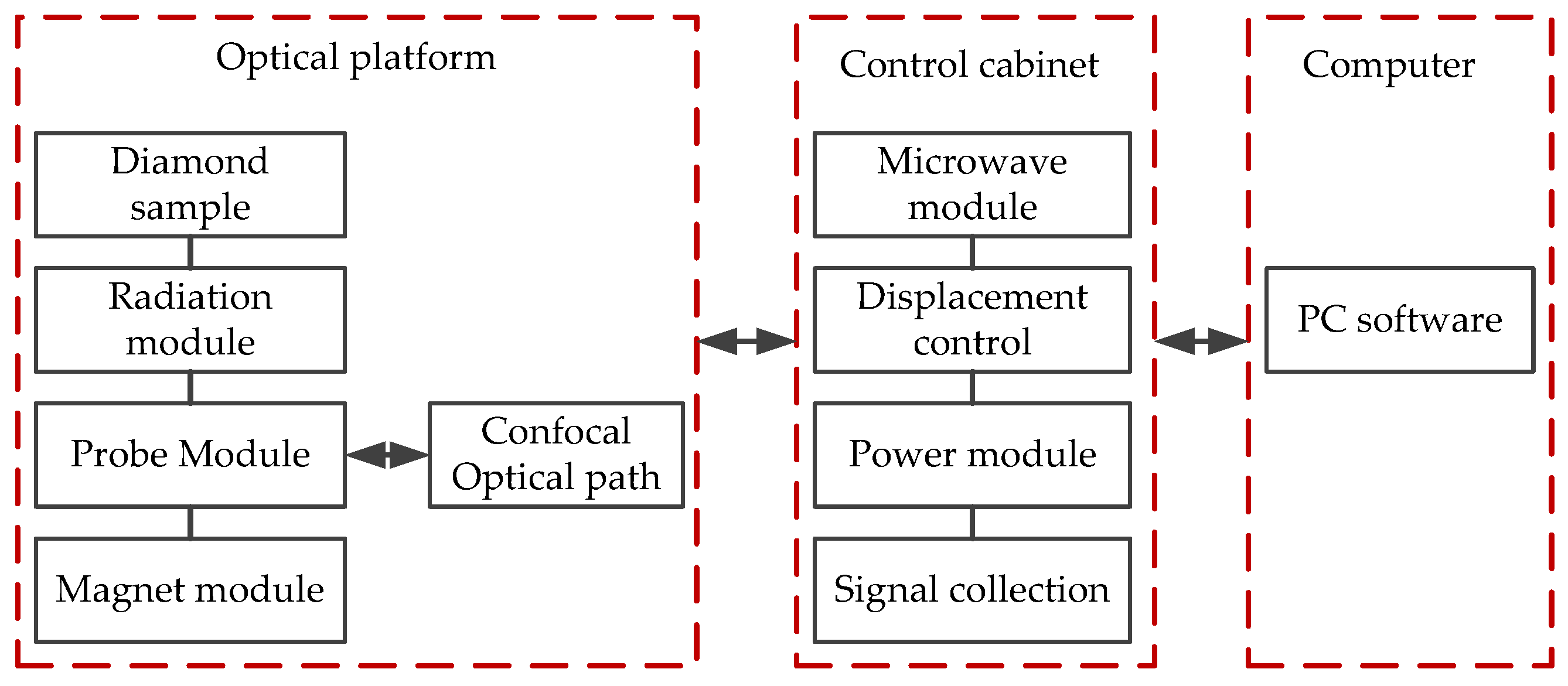
- (1)
- Experimental environment and platform
- (2)
- Experimental method
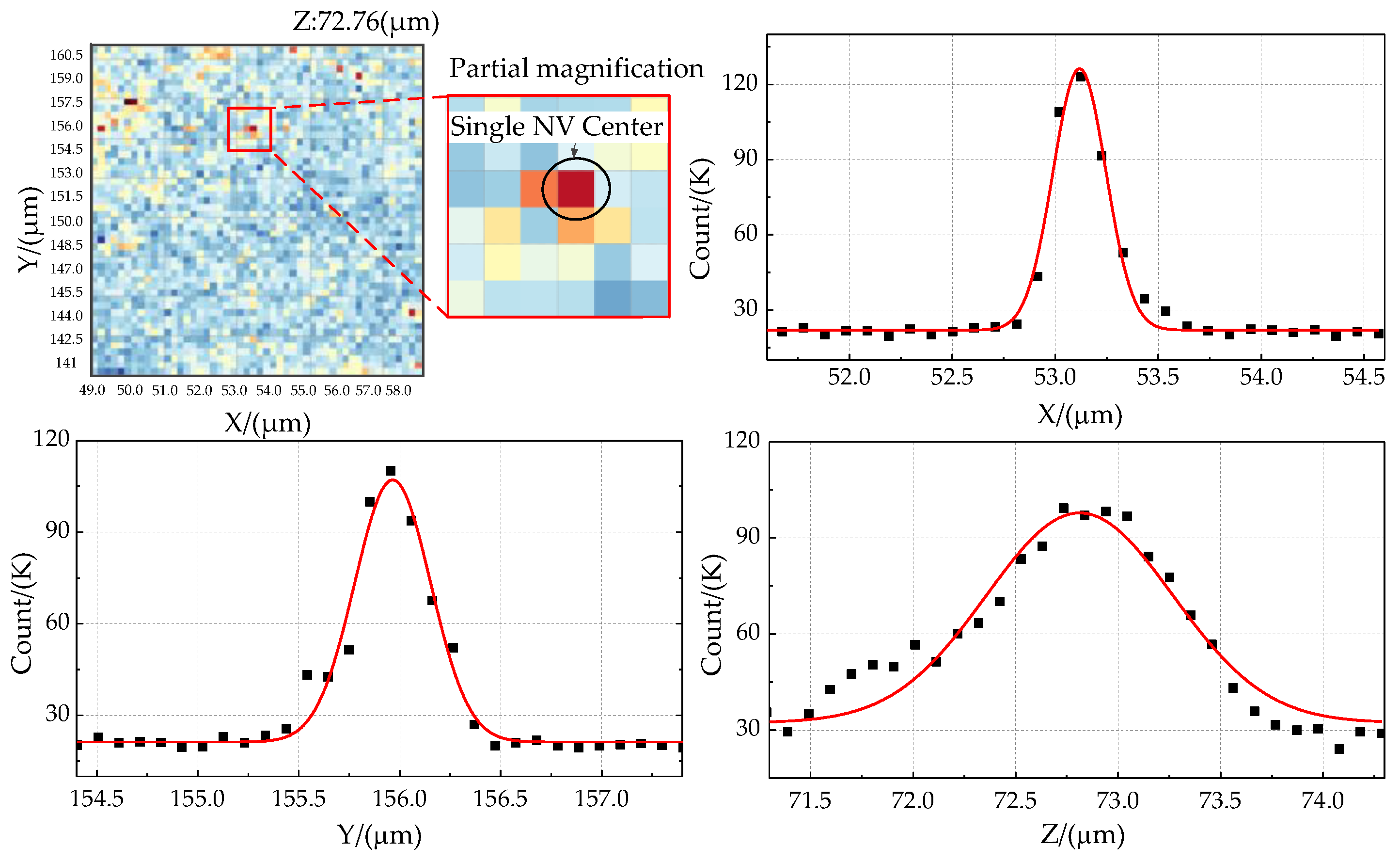
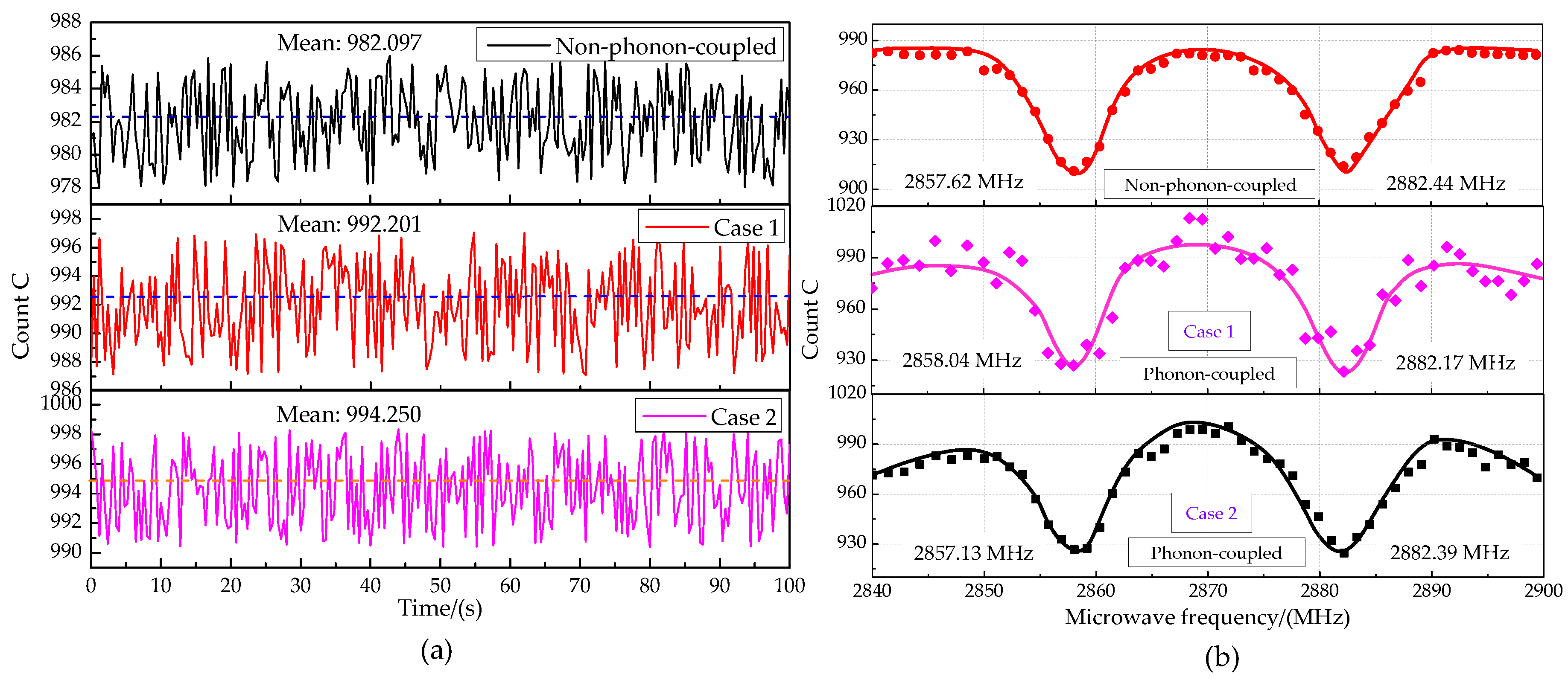
- (3)
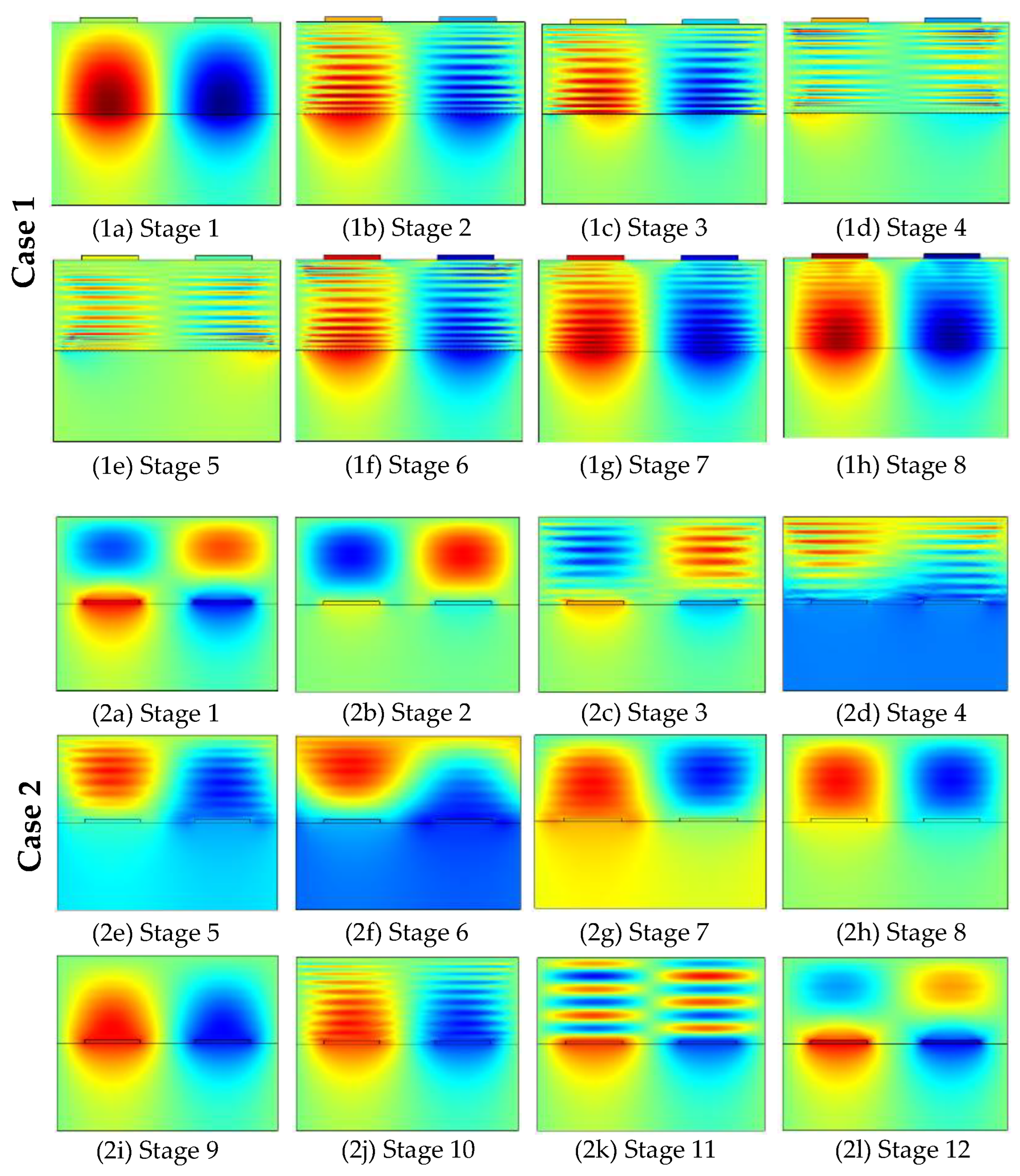
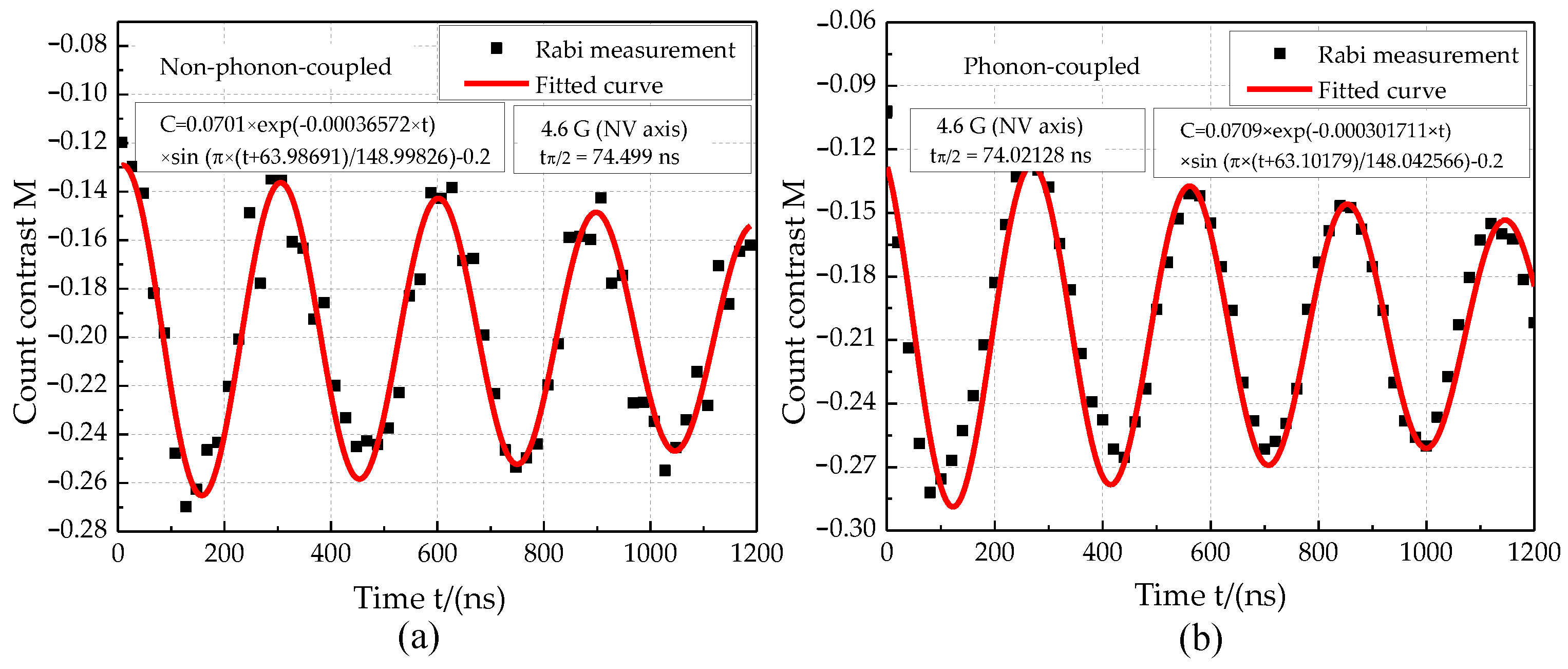
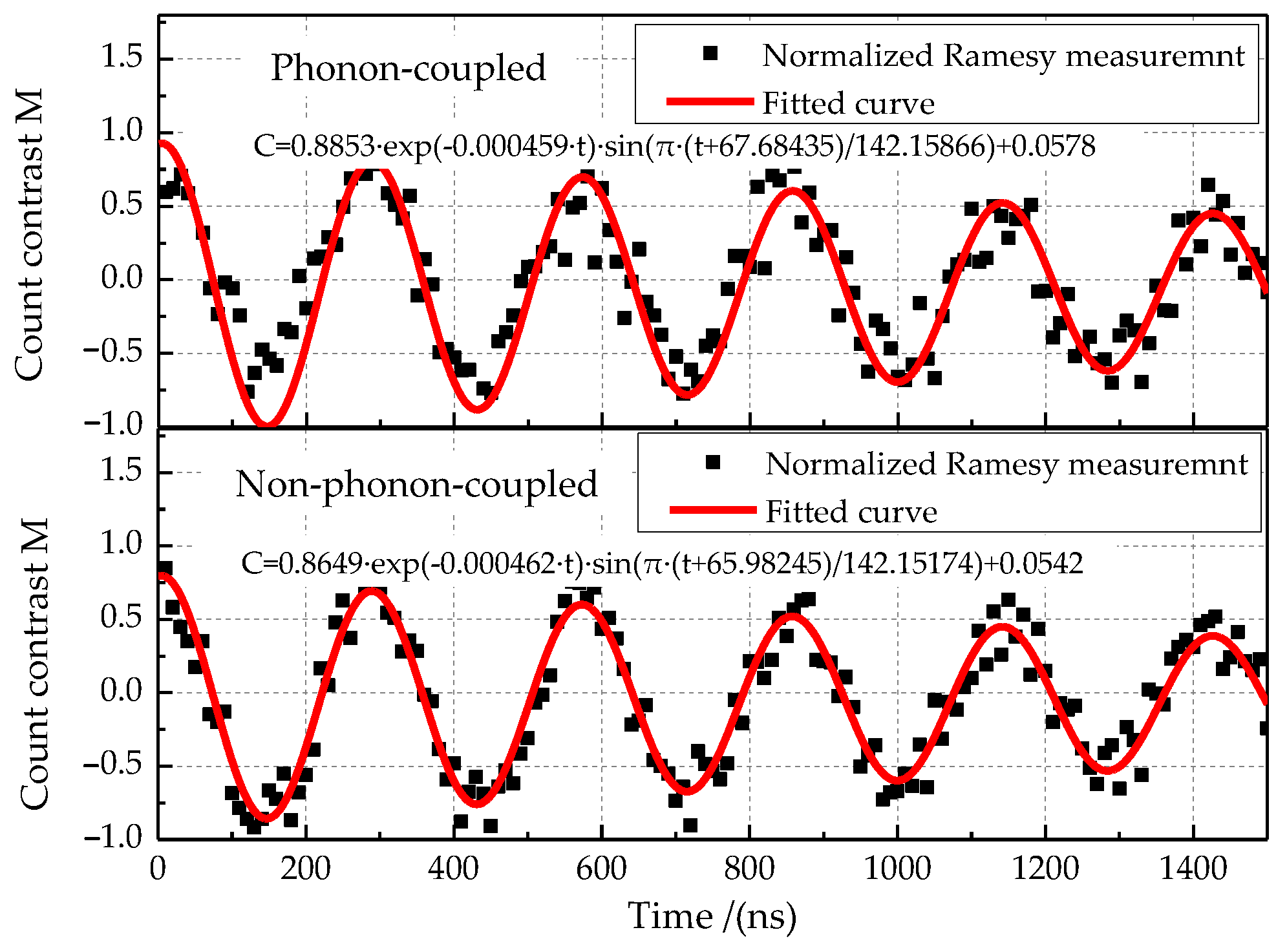
- Experimental results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gardill, A.; Cambria, M.C.; Kolkowitz, S. Fast relaxation on qutrit transitions of nitrogen-vacancy centers in nanodiamonds. Phys. Rev. Appl. 2020, 13, 034010. [Google Scholar] [CrossRef]
- Gali, A. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics 2019, 8, 1907–1943. [Google Scholar] [CrossRef]
- Rong, X.; Lu, D.; Kong, X.; Geng, J.P.; Wang, Y.; Shi, F.Z.; Duan, C.K.; Du, J.F. Harnessing the power of quantum systems based on spin magnetic resonance: From ensembles to single spins. Adv. Phys. X 2017, 2, 125–168. [Google Scholar] [CrossRef]
- Hopper, D.A.; Shulevitz, H.J.; Bassett, L.C. Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond. Micromachines 2018, 9, 437. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hellenberg, L.C.L. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Boss, J.M.; Chang, K.; Armijo, J.; Cujia, K.; Rosskopf, T.; Maze, J.R.; Degen, C.L. One- and two-dimensional nuclear magnetic resonance spectroscopy with a diamond quantum sensor. Phys. Rev. Lett. 2016, 116, 197601. [Google Scholar] [CrossRef]
- Staudacher, T.; Shi, F.; Pezzagna, S.; Meijer, J.; Du, J.; Meriles, C.A.; Reinhard, F.; Wrachtrup, J. Nuclear magnetic resonance spectroscopy on a (5-Nanometer) (3) sample volume. Science 2013, 339, 561–563. [Google Scholar] [CrossRef]
- Fortman, B.; Takahashi, S. Understanding the Linewidth of the ESR Spectrum Detected by a Single NV Center in Diamond. J. Phys. Chem. A 2019, 123, 6350–6355. [Google Scholar] [CrossRef]
- Gustafsson, M.V.; Aref, T.; Kockum, A.F.; Kkstrom, M.K.; Johansson, G.; Delsing, P. Propagating phonons coupled to an artificial atom. Science 2014, 346, 207–211. [Google Scholar] [CrossRef]
- Schuetz, M.J.A.; Kessler, E.M.; Giedke, G.; Vandersypen, L.M.K.; Lukin, M.D.; Cirac, J.I. Universal quantum transducers based on surface acoustic waves. Phys. Rev. X 2015, 5, 031031. [Google Scholar] [CrossRef] [Green Version]
- Kervinen, M.; Rissanen, I.; Sillanpää, M. Interfacing planar superconducting qubits with high overtone bulk acoustic phonons. Phys. Rev. B 2018, 97, 205443. [Google Scholar] [CrossRef]
- Moores, B.A.; Sletten, L.R.; Viennot, J.J.; Lehnert, K.W. Cavity quantum acoustic device in the multimode strong coupling regime. Phys. Rev. Lett. 2018, 120, 227701. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, A.; Yamazaki, R.; Tabuchi, Y.; Nakamura, Y. Qubit-assisted transduction for a detection of surface acoustic waves near the quantum limit. Phy. Rev. Lett. 2017, 119, 180505. [Google Scholar] [CrossRef]
- Kepesidis, K.V.; Bennett, S.D.; Portolan, S.; Lukin, M.D.; Rabl, P. Phonon cooling and lasing with nitrogen-vacancy centers in diamond. Phys. Rev. B 2013, 88, 064105. [Google Scholar] [CrossRef]
- Pirkkalainen, J.M.; Cho, S.U.; Li, J.; Paraoanu, G.S.; Hakonen, P.J.; Sillanpaa, M.A. Hybrid circuit cavity quantum electrodynamics with a micromechanical resonator. Nature 2013, 494, 211–215. [Google Scholar] [CrossRef] [PubMed]
- Basso, L.; Sacco, M.; Bazzanella, N.; Cazzanelli, M.; Barge, A.; Orlandi, M.; Bifone, A.; Miotello, A. Laser-Synthesis of NV-Centers-Enriched Nanodiamonds: Effect of Different Nitrogen Sources. Micromachines 2020, 11, 579. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, A.; Retzker, A.; Jelezko, F.; Plenio, M.B. Coupling of nitrogen vacancy centers in nanodiamonds by means of phonons. New J. Phys. 2013, 15, 083014. [Google Scholar] [CrossRef]
- Bennett, S.D.; Yao, N.Y.; Otterbach, J.; Zoller, P.; Rabl, P.; Lukin, M.D. Phonon-induced spin-spin interactions in diamond nanostructures: Application to spin squeezing. Phys. Rev. Lett. 2013, 110, 156402. [Google Scholar] [CrossRef]
- Wang, H.; Burkard, G. Mechanically induced two-qubit gates and maximally entangled states for single electron spins in a carbon nanotube. Phys. Rev. B 2015, 92, 195432. [Google Scholar] [CrossRef]
- Shen, X.; Zhao, L.Y.; Huang, P.; Rong, X.; Ji, L.M. Atomic spin and phonon coupling mechanism of nitrogen-vacancy center. Acta Phys. Sin. 2021, 70, 068501. [Google Scholar] [CrossRef]
- Schulein, F.J.R.; Zallo, E.; Atkinson, P.; Zallo, E.; Atkinson, P.; Schmidt, O.G.; Trotta, R.; Rastelli, A.; Wixforth, A.; Krenner, H.J. Fourier synthesis of radiofrequency nanomechanical pulses with different shapes. Nat. Nanotechnol. 2015, 10, 512–516. [Google Scholar] [CrossRef] [PubMed]
- Arcizet, O.; Jacques, V.; Siria, A.; Poncharal, P.; Vincent, P.; Seidelin, S. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 2011, 7, 879–883. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Jayich, A.C.B.; Unterreithmeier, Q.P.; Bennett, S.D.; Rabl, P.; Harris, J.G.E.; Lukin, M.D. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 2012, 335, 1603–1606. [Google Scholar] [CrossRef] [PubMed]
- MacQuarrie, E.R.; Gosavi, T.A.; Jungwirth, N.R.; Bhave, S.A.; Fuchs, G.D. Mechanical spin control of nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2013, 111, 227602. [Google Scholar] [CrossRef]
- Teissier, J.; Barfuss, A.; Appel, P.; Neu, E.; Maletinsky, P. Strain coupling of a nitrogen-vacancy center spin to a diamond mechanical oscillator. Phys. Rev. Lett. 2014, 113, 020503. [Google Scholar] [CrossRef]
- Ovartchaiyapong, P.; Lee, K.W.; Myers, B.A.; Jayich, A.C.B. Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator. Nat. Commun. 2014, 5, 4429. [Google Scholar] [CrossRef]
- MacQuarrie, E.R.; Gosavi, T.A.; Bhave, S.A.; Fuchs, G.D. Continuous dynamical decoupling of a single diamond nitrogen-vacancy center spin with a mechanical resonator. Phys. Rev. B 2015, 92, 224419. [Google Scholar] [CrossRef]
- Barfuss, A.; Teissier, J.; Neu, E.; Nunnenkamp, A.; Maletinsky, P. Strong mechanical driving of a single electron spin. Nat. Phys. 2015, 11, 820–824. [Google Scholar] [CrossRef]
- MacQuarrie, E.R.; Gosavi, T.A.; Moehle, A.M.; Jungwirth, N.R.; Bhave, S.A.; Fuchs, G.D. Coherent control of a nitrogen-vacancy center spin ensemble with a diamond mechanical resonator. Optica 2015, 2, 233–238. [Google Scholar] [CrossRef]
- Meesala, S.; Sohn, Y.I.; Atikian, H.A.; Kim, S.; Burek, M.J.; Choy, J.T.; Loncar, M. Enhanced strain coupling of nitrogen-vacancy spins to nanoscale diamond cantilevers. Phys. Rev. Appl. 2016, 5, 034010. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.B.; Imamoglu, A.; Bernien, H.; Hanson, R. Coherent manipulation, measurement and entanglement of individual solid-state spins using optical fields. Nat. Photonics 2015, 9, 363–373. [Google Scholar] [CrossRef]
- Rath, P.; Ummethala, S.; Nebel, C.; Pernice, W.H.P. Diamond as a material for monolithically integrated optical and optomechanical devices. Phys. Status Solidi A Appl. Mater. Sci. 2015, 212, 2385–2399. [Google Scholar] [CrossRef]
- Khanaliloo, B.; Jayakumar, H.; Hryciw, A.C.; Lake, D.P.; Kaviani, H.; Barclay, P.E. Single crystal diamond nanobeam waveguide optomechanics. Phys. Rev. X 2015, 5, 041051. [Google Scholar] [CrossRef]
- Golter, D.A.; Oo, T.; Amezcua, M.; Lekavicius, I.; Stewart, K.A.; Wang, H.L. Coupling a surface acoustic wave to an electron spin in diamond via a dark state. Phys. Rev. X 2016, 6, 041060. [Google Scholar] [CrossRef]
- Müller, C.; Kong, X.; Cai, J.M.; Melentijević, K.; Stacey, A.; Markham, M.; Twitchen, D.; Isoya, J.; Pezzagna, S.; Meijer, J.; et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 2014, 5, 4703. [Google Scholar] [CrossRef] [PubMed]
- Plessky, V.; Koskela, J. Coupling-of-modes analysis of SAW devices. Int. J. High Speed Electron. Syst. 2000, 10, 867–947. [Google Scholar] [CrossRef]


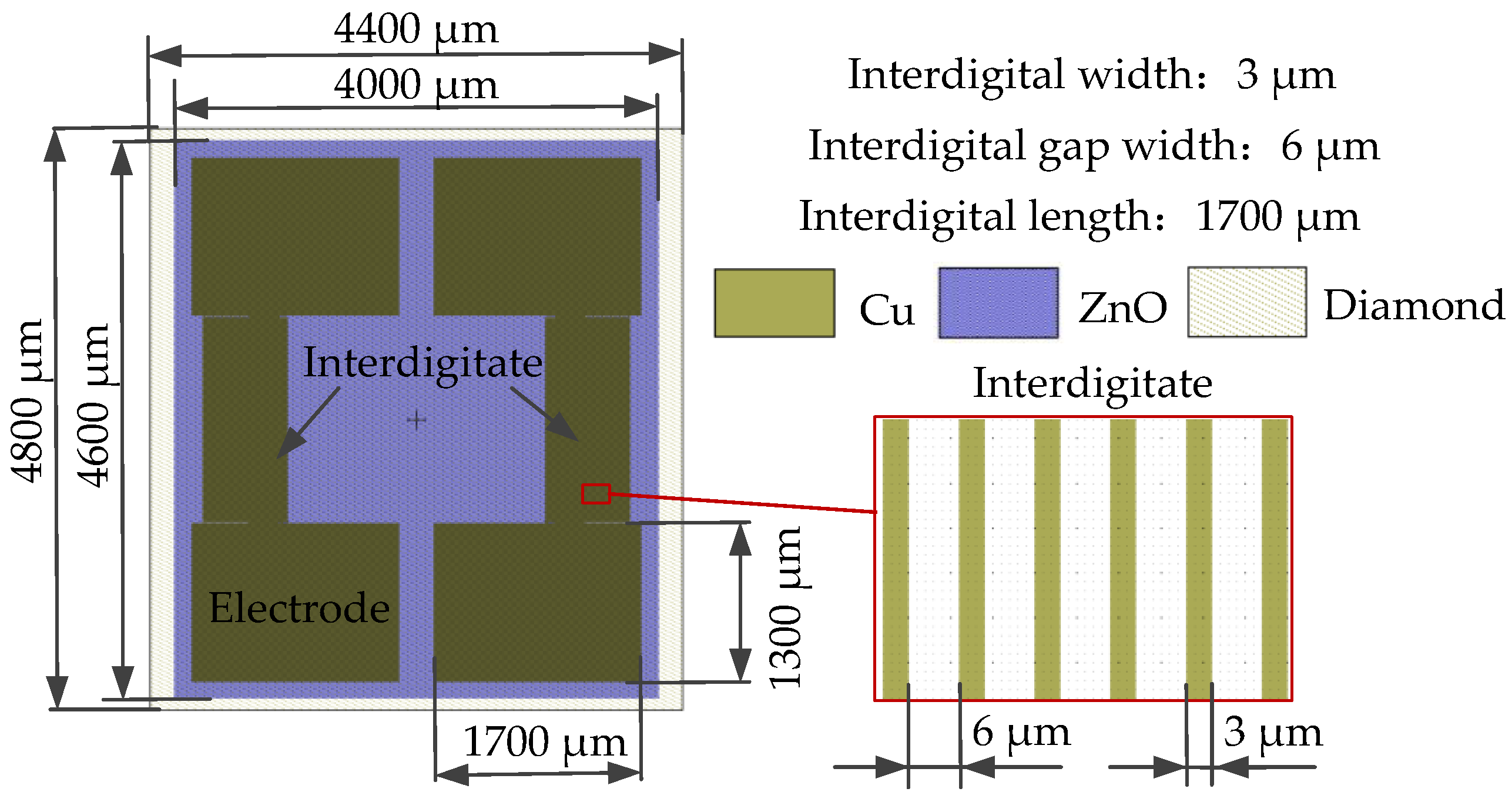


| Layer | Size | Value |
|---|---|---|
| IDT | Length/(μm) | 10 |
| Width/(μm) | 1 | |
| Thickness/(μm) | 0.1 | |
| Spacing/(μm) | 1 | |
| ZnO | Length/(μm) | 70 |
| Width/(μm) | 10 | |
| Thickness/(μm) | 0.4 | |
| Diamond | Length/(μm) | 70 |
| Width/(μm) | 10 | |
| Thickness/(μm) | 10 |
| Parameters | Symbol | Diamond | (100) ZnO | (002) ZnO |
|---|---|---|---|---|
| Elasticity coefficient (1011 N/m2) | c11 | 11.531 | 2.096 | 2.096 |
| c12 | 0.864 | 1.205 | 1.205 | |
| c13 | 0.864 | 1.046 | 1.046 | |
| c33 | 11.531 | 2.106 | 2.106 | |
| c44 | 5.333 | 0.423 | 0.423 | |
| Temperature Coefficient (10−4/°C) | Tc11 | −0.14 | −1.12 | −1.12 |
| Tc12 | −0.57 | −1.61 | −1.61 | |
| Tc33 | −0.14 | −1.23 | −1.23 | |
| Tc44 | −0.125 | −0.70 | −0.70 | |
| Piezoelectric constant (C/m2) | e15 | --- | −0.48 | — |
| e31 | --- | −0.573 | — | |
| e33 | --- | 1.321 | — | |
| Relative permittivity | ε11/ε0 | 5.67 | 8.55 | −0.48 |
| ε33/ε0 | 5.67 | 10.2 | — | |
| Density (103 kg/m3) | Ρ | 3.512 | 5.665 | −0.573 |
| Density Temperature Coefficient (10−6/°C) | Tρ | −3.6 | −10.1 | 1.321 |
| Cases | The Thickness of the IDT/(nm) | Cases | The Thickness of the ZnO/(nm) | ||
|---|---|---|---|---|---|
| Case 1 | a | 80 | Case 3 | a | 200 |
| b | 100 | b | 400 | ||
| c | 120 | c | 600 | ||
| d | 140 | d | 800 | ||
| Case 2 | a | 80 | Case 4 | a | 200 |
| b | 100 | b | 400 | ||
| c | 120 | c | 600 | ||
| d | 140 | d | 800 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Zhao, L.; Ge, F. Structural Optimization and MEMS Implementation of the NV Center Phonon Piezoelectric Device. Micromachines 2022, 13, 1628. https://doi.org/10.3390/mi13101628
Shen X, Zhao L, Ge F. Structural Optimization and MEMS Implementation of the NV Center Phonon Piezoelectric Device. Micromachines. 2022; 13(10):1628. https://doi.org/10.3390/mi13101628
Chicago/Turabian StyleShen, Xiang, Liye Zhao, and Fei Ge. 2022. "Structural Optimization and MEMS Implementation of the NV Center Phonon Piezoelectric Device" Micromachines 13, no. 10: 1628. https://doi.org/10.3390/mi13101628
APA StyleShen, X., Zhao, L., & Ge, F. (2022). Structural Optimization and MEMS Implementation of the NV Center Phonon Piezoelectric Device. Micromachines, 13(10), 1628. https://doi.org/10.3390/mi13101628





