High-Level Vibration for Single-Frequency and Multi-Frequency Excitation in Macro-Composite Piezoelectric (MFC) Energy Harvesters, Nonlinearity, and Higher Harmonics
Abstract
1. Introduction
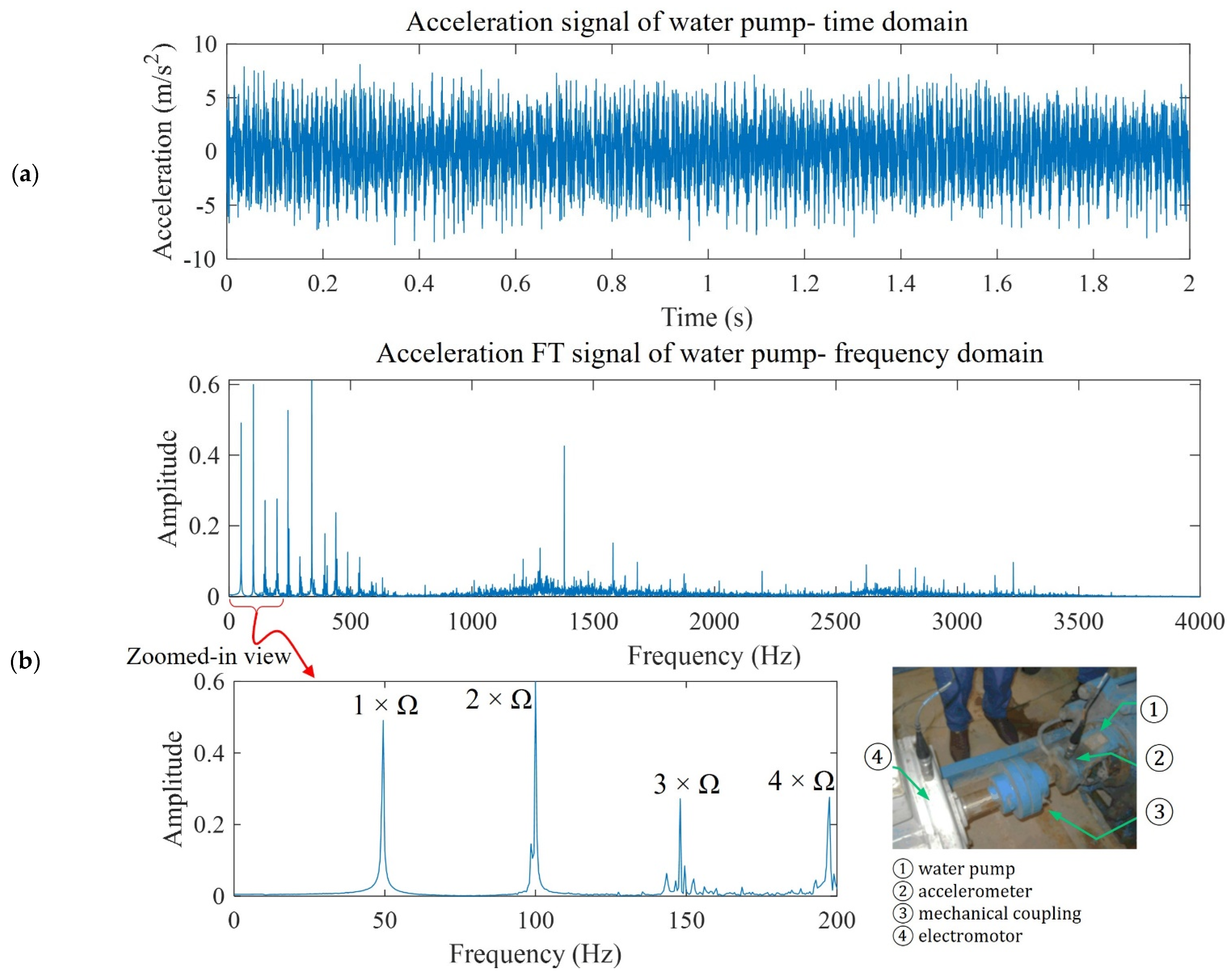
2. The Need for Multi-Frequency Harmonic Analysis
3. Closed-Form Solutions for Mechanical and Electrical Responses
- (1)
- The total output power is calculated using two series over the frequency range and the modal mode shapes for general input acceleration. Therefore, parameters such as and are mode-shape dependent, in addition to being dependent on the external frequency, which is . The interaction between the external excitation frequency and the mode shapes is a complex research object, specifically when an electrode covers the piezoelectric layer.
- (2)
- Moreover, there is a linear relationship between the output power and the external square acceleration amplitude. This linear dependency over different frequencies needs to be researched, since excitation and modal mode interactions can be nonlinear.
4. Experimental Setup and Initial MFC Harvester Characterisation
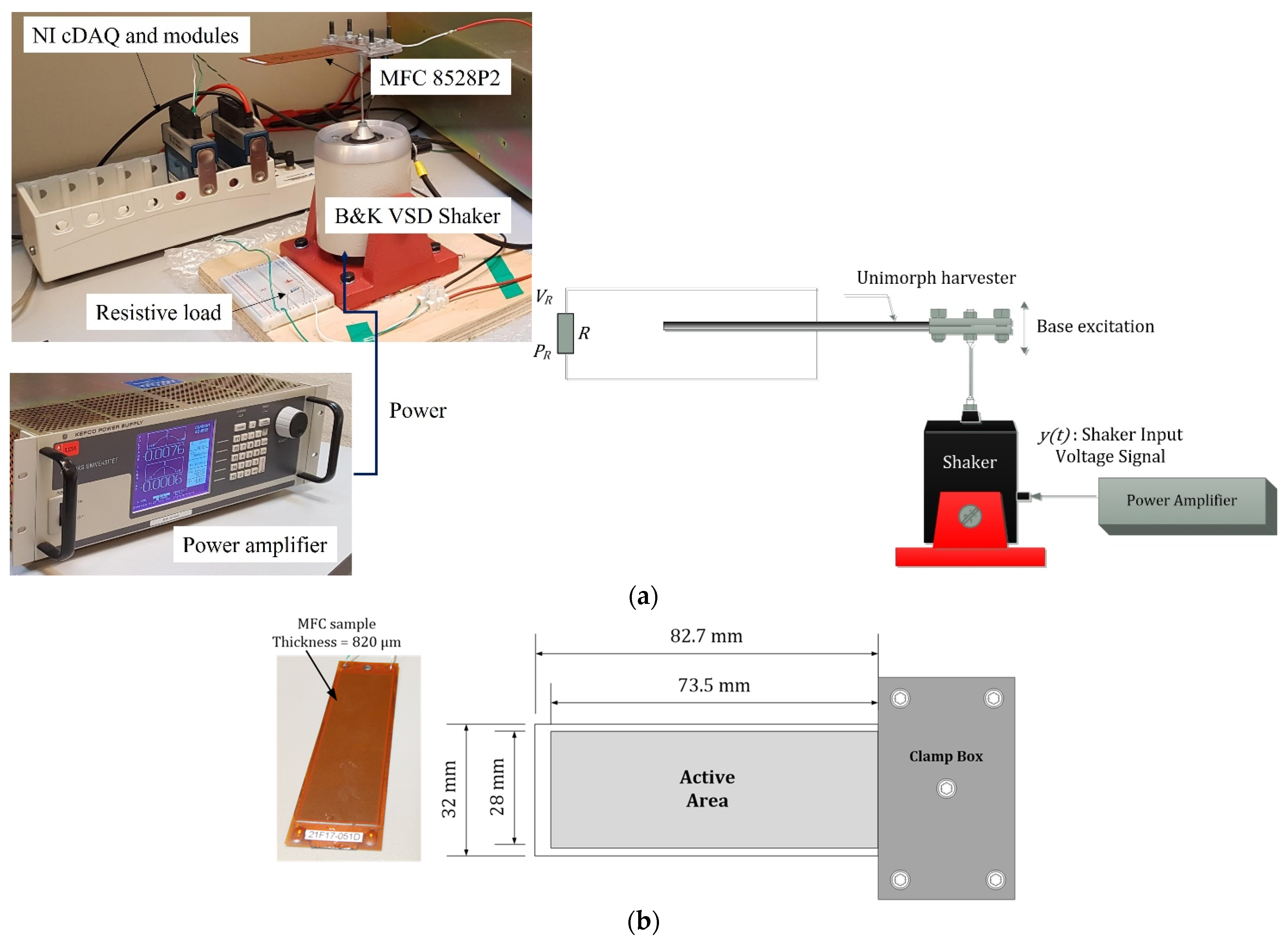
4.1. Experimental Setup
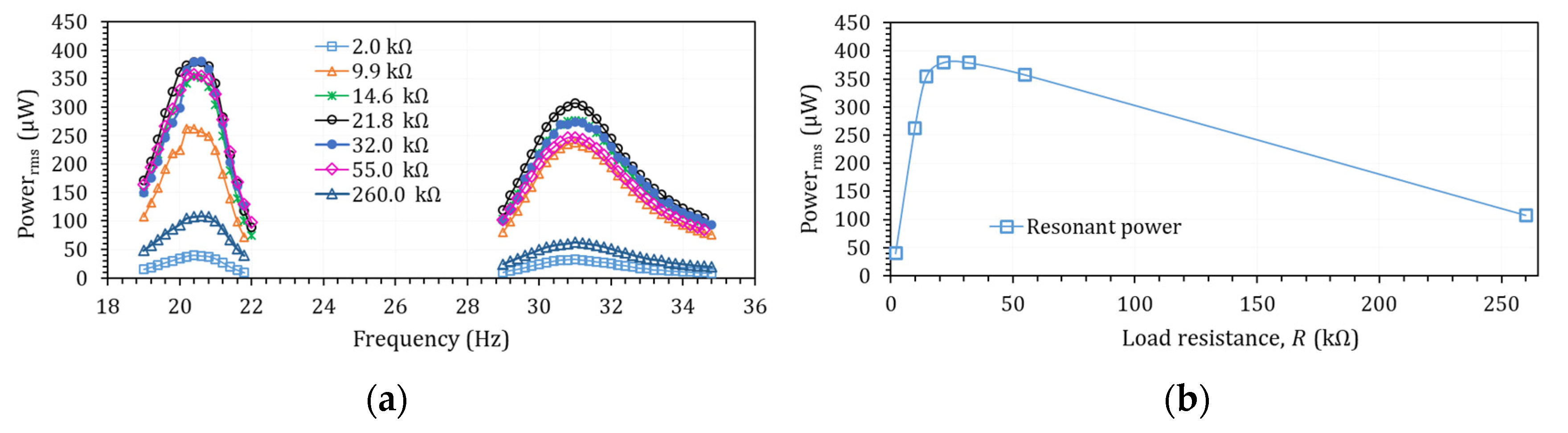
4.2. PVEH Device Optimum Characterisation
5. Results and Discussion
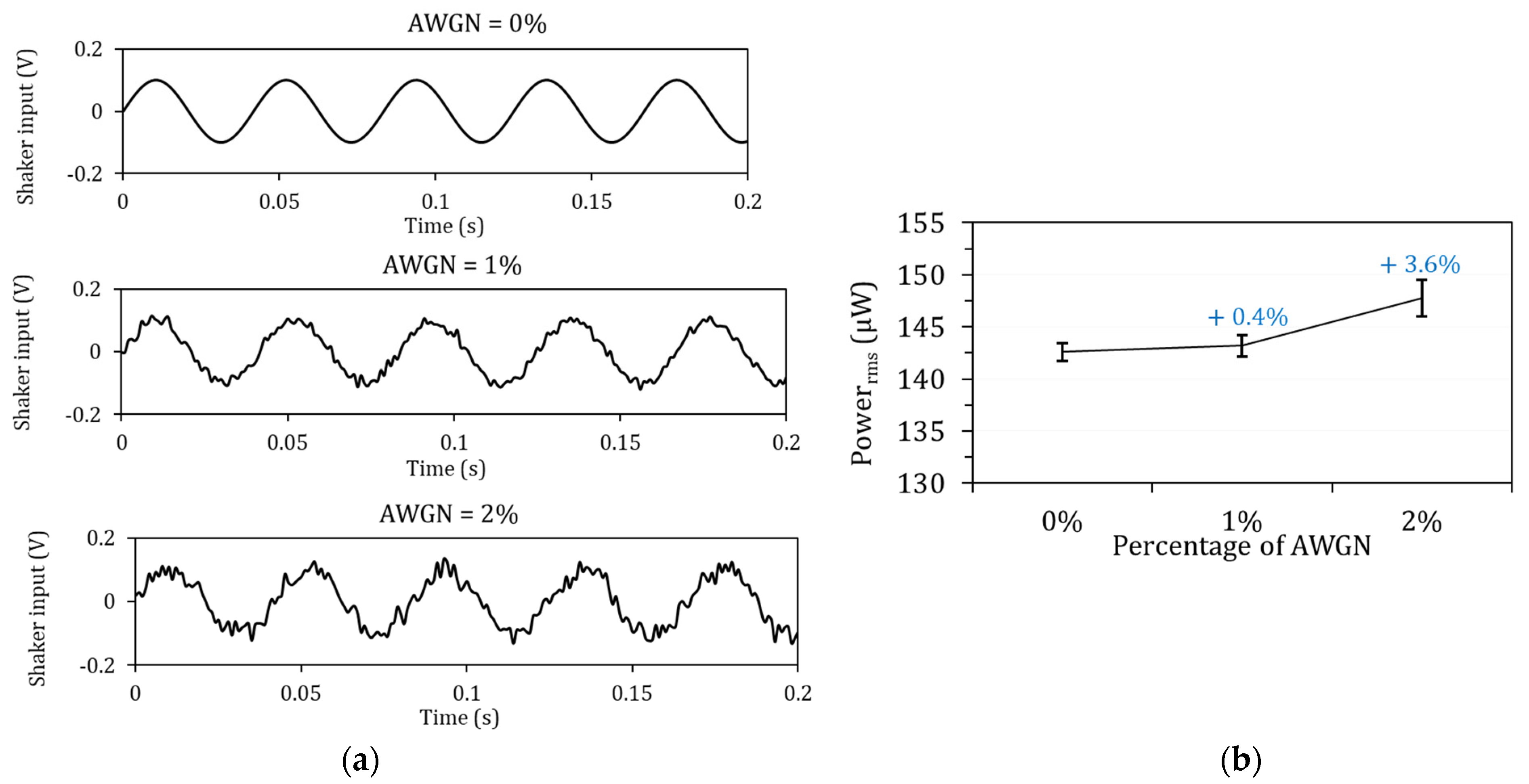
5.1. Effects of Adding White Noise to the Excitation Signal
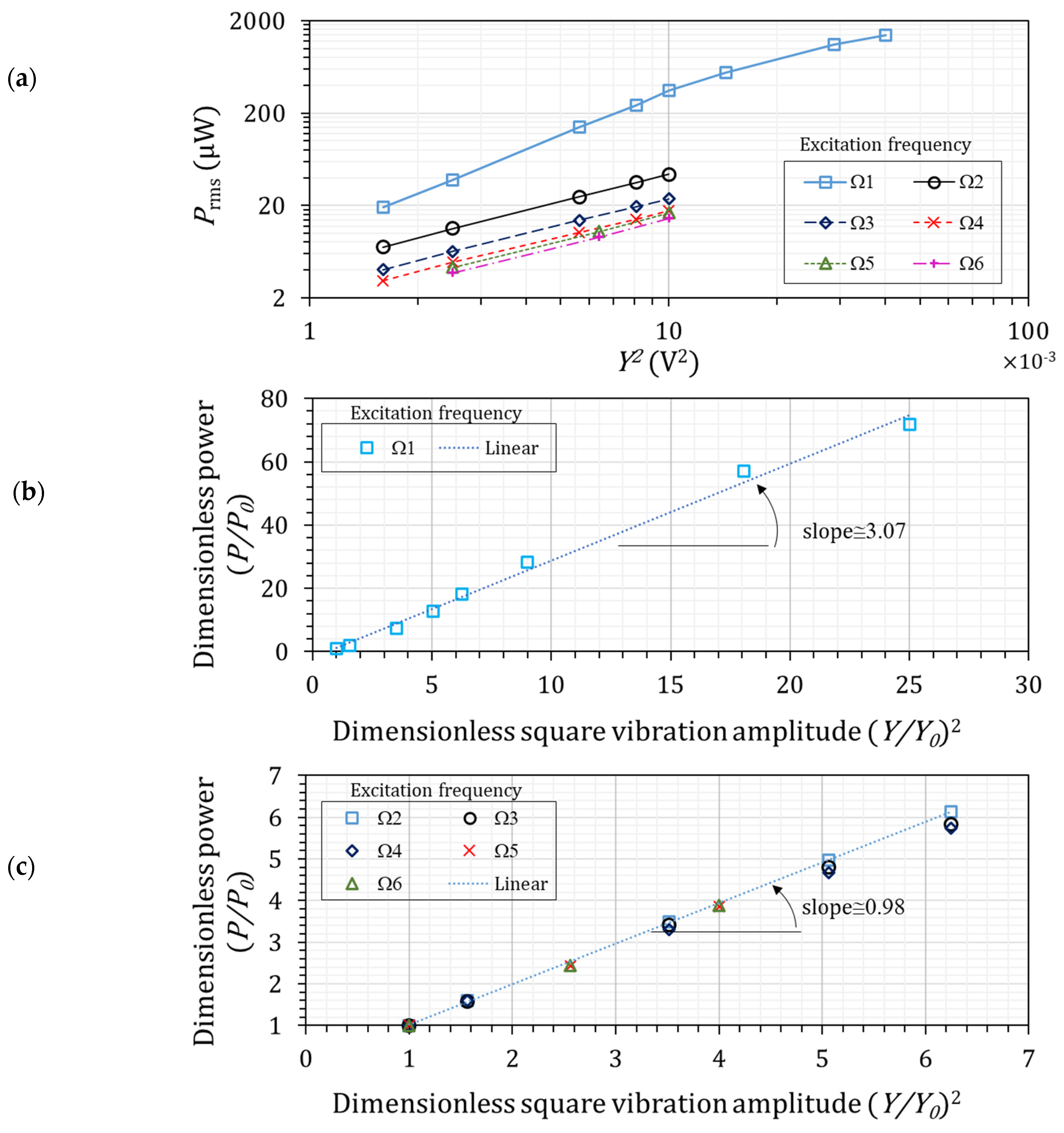
5.2. Effects of Increasing the Vibration Level with Single-Frequency Harmonics
5.3. Effects of Increasing the Vibration Level with Multi-Frequency Harmonics
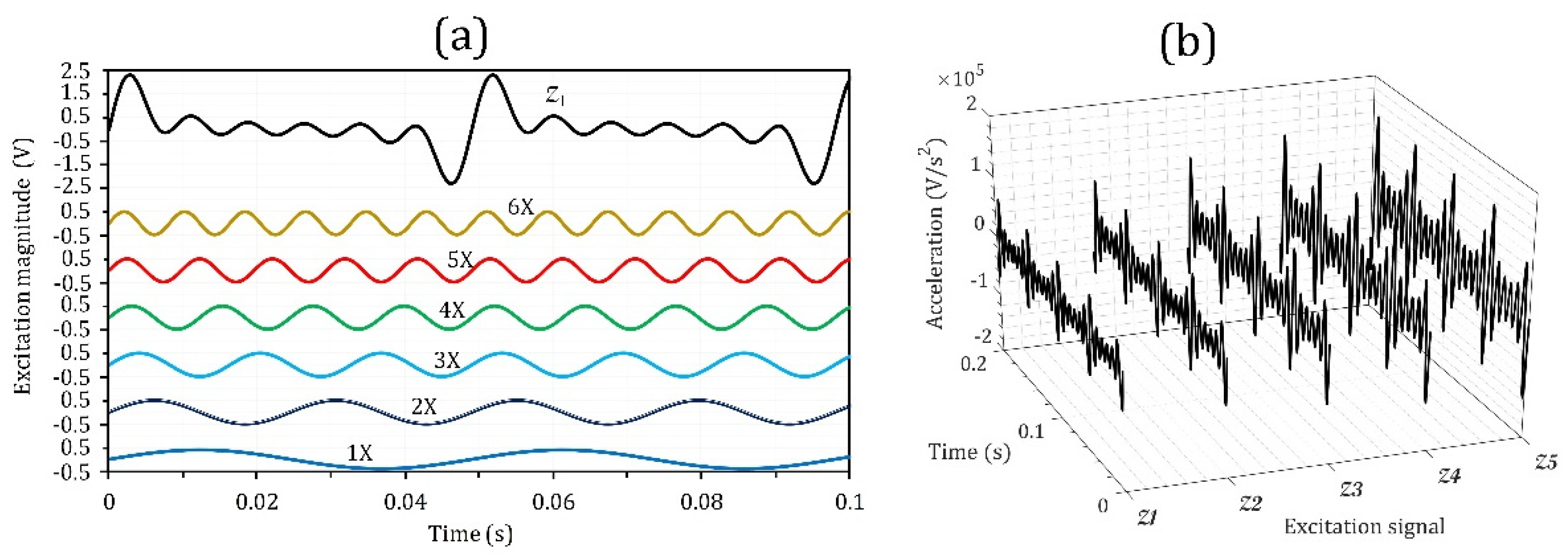
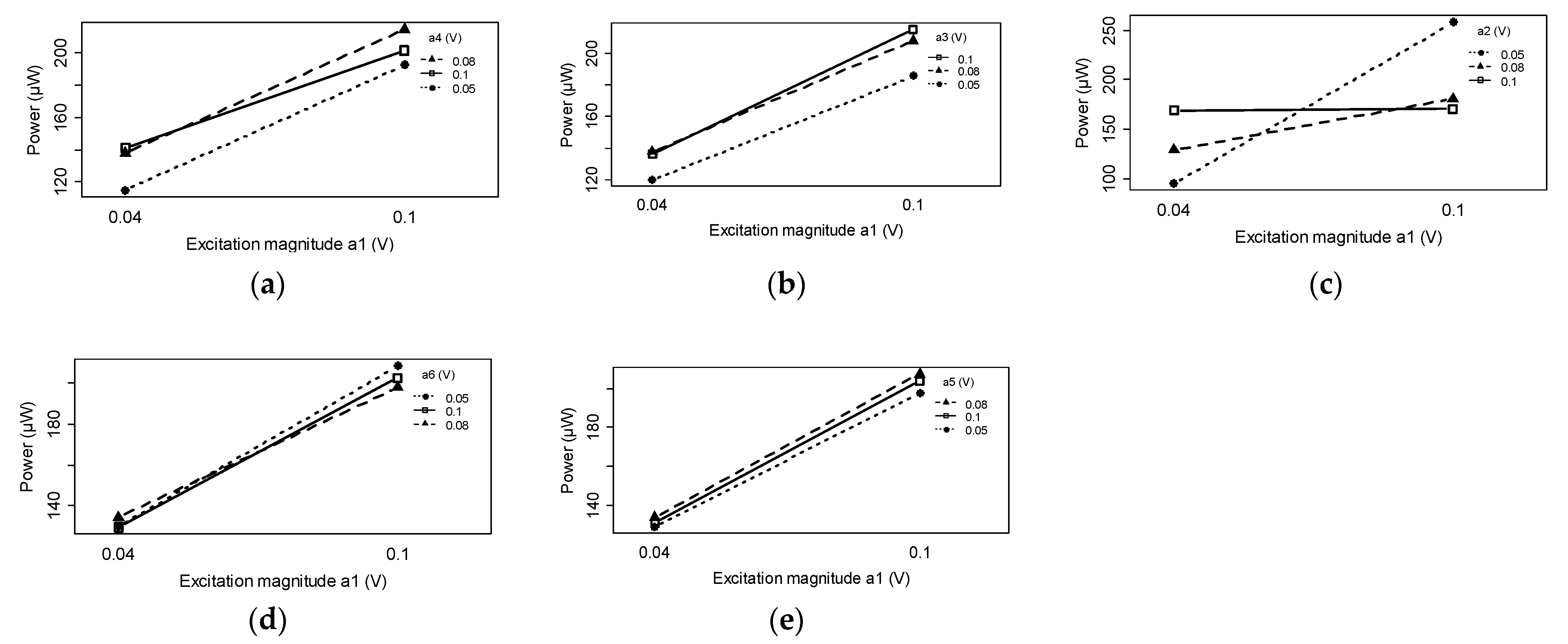
5.4. Interaction Effects between Different Excitation Harmonics
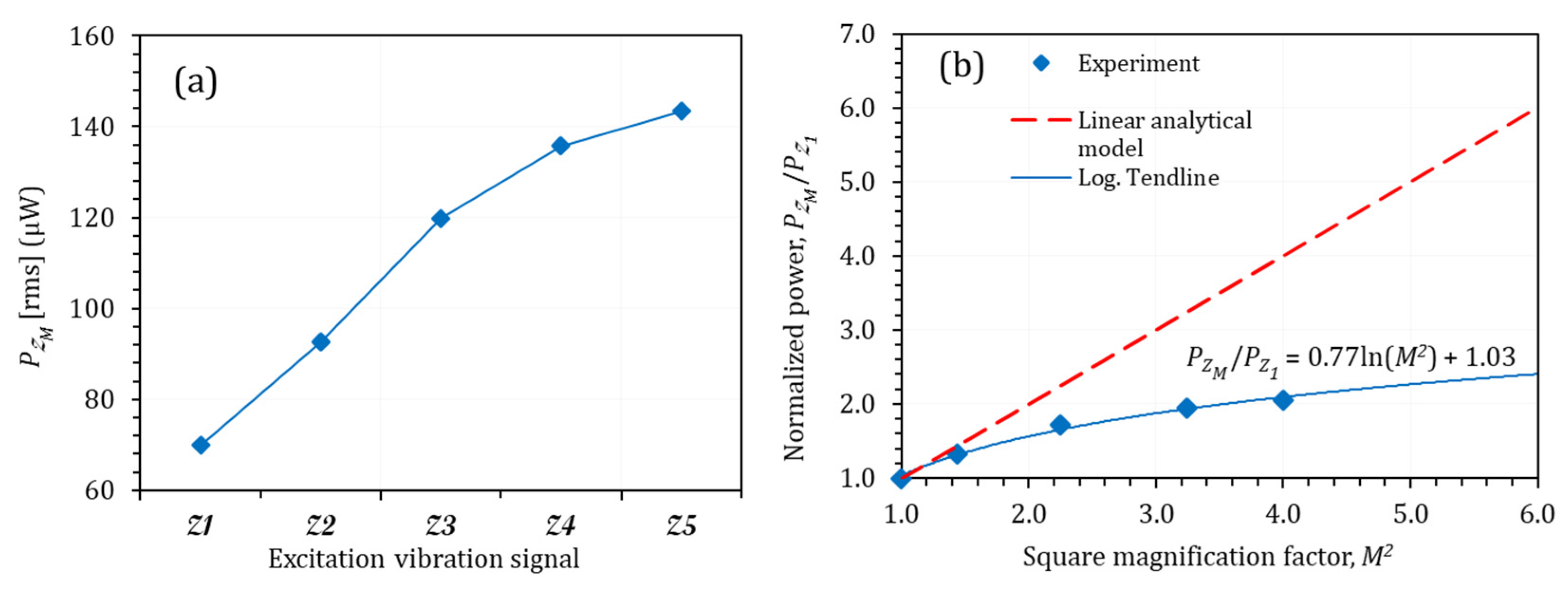
5.5. Proposing a Nonlinear Model
6. Concluding Remarks and Future Works
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khazaee, M.; Rosendahl, L.; Rezania, A. Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations. Sensors 2022, 22, 3395. [Google Scholar] [CrossRef] [PubMed]
- Ali, F.; Raza, W.; Li, X.; Gul, H.; Kim, K.H. Piezoelectric Energy Harvesters for Biomedical Applications. Nano Energy 2019, 57, 879–902. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of Piezoelectric Energy Harvesting System and Application of Optimization Techniques to Enhance the Performance of the Harvesting System. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezania, A.; Rosendahl, L. Piezoelectric Resonator Design and Analysis from Stochastic Car Vibration Using an Experimentally Validated Finite Element with Viscous-Structural Damping Model. Sustain. Energy Technol. Assess. 2022, 52, 102228. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I.; Inman, D.J. Piezoelectric Energy Harvesting from Broadband Random Vibrations. Smart Mater. Struct. 2009, 18. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, Z.; Duan, X.; Xu, Y. Stochastic Dynamics of a Piezoelectric Energy Harvester with Fractional Damping under Gaussian Colored Noise Excitation. Appl. Math. Model. 2021, 97, 268–280. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Grabowski, Ł.; Czyż, Z.; Karpiński, P.; Staczek, P.; Litak, G. Ceramic-Based Piezoelectric Material for Energy Harvesting Using Hybrid Excitation. Material 2021, 14. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance Tuning of Piezoelectric Vibration Energy Scavenging Generators Using Compressive Axial Preload. Smart Mater. Struct. 2006, 15, 1413–1420. [Google Scholar] [CrossRef]
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Wright, P.K.; Sundararajan, V. Improving Power Output for Vibration-Based Energy Scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezaniakolaei, A.; Rosendahl, L.A. A Study on Interaction Effects of Different Harmonics in Translational Base Excitation for Piezoelectric Vibration Energy Harvesters. In Proceedings of the ECCOMAS Smart 2019, Paris, France, 8–11 July 2019. [Google Scholar]
- Noel, A.B.; Abdaoui, A.; Elfouly, T.; Ahmed, M.H.; Badawy, A.; Shehata, M.S. Structural Health Monitoring Using Wireless Sensor Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2017, 19, 1403–1423. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy Harvesting from Low Frequency Applications Using Piezoelectric Materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezania, A.; Rosendahl, L. An Experimental Study to Determine Damping of Piezoelectric Harvesters Using Transient Analysis of Unified Electromechanical Voltage Equation. Energy Convers. Manag. 2021, 227, 113567. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezaniakolaei, A.; Rosendahl, L. A Broadband Macro-Fiber-Composite Piezoelectric Energy Harvester for Higher Energy Conversion from Practical Wideband Vibrations. Nano Energy 2020, 76, 104978. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A Comprehensive Review on Vibration Energy Harvesting: Modelling and Realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A Study of Low Level Vibrations as a Power Source for Wireless Sensor Nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezania, A.; Rosendahl, L. Effect of Damage and Support Damping Mechanisms on Unimorph Piezoelectric Energy Harvester. J. Vib. Control 2019, 107754631985516. [Google Scholar] [CrossRef]
- Evensen, D.A. Nonlinear Vibrations of Beams with Various Boundary Conditions. AIAA J. 1968, 6, 370–372. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A Review of Energy Harvesting Using Piezoelectric Materials: State-of-the-Art a Decade Later (2008–2018). Smart Mater. Struct. 2019, 28. [Google Scholar] [CrossRef]
- Khazaee, M.; Rezaniakolaie, A.; Moosavian, A.; Rosendahl, L. A Novel Method for Autonomous Remote Condition Monitoring of Rotating Machines Using Piezoelectric Energy Harvesting Approach. Sens. Actuators A Phys. 2019, 295, 37–50. [Google Scholar] [CrossRef]
- Jovanović, D.; Raos, M.; Jovanović, M.; Stanković, M.; Živković, L.; Protić, M. Vibration Analysis of the Boiler Supply Air Fan—A Case Study. Springer Proc. Phys. 2018, 198, 227–237. [Google Scholar] [CrossRef]
- Yang, P.; Yuan, Q.; Huang, C.; Zhou, Y.; Li, H.; Zhou, Y. Analysis of the Impacts of Bearing on Vibration Characteristics of Rotor. Shock Vib. 2017, 2017, 8098591. [Google Scholar] [CrossRef]
- Khazaee, M.; Huber, J.E.; Rosendahl, L.; Rezania, A. The Investigation of Viscous and Structural Damping for Piezoelectric Energy Harvesters Using Only Time-Domain Voltage Measurements. Appl. Energy 2021, 285, 116427. [Google Scholar] [CrossRef]
- Khazaee, M.; Huber, J.E.; Rosendahl, L.; Rezania, A. On the Determination of Viscous and Structural Damping Coefficients for Piezoelectric Energy Harvesters Using Only Time-Domain Voltage Measurements. Appl. Energy 2021, 285, 116427. [Google Scholar] [CrossRef]
- Smart Material GmbH Company, Dresden, Germany. Available online: https://www.smart-material.com/13CompOverviewV2.html (accessed on 9 December 2022).
- Smart Materials Datasheet. Available online: https://www.Smart-Material.Com (accessed on 9 December 2022).
- Khazaee, M.; Rezaniakolaei, A.; Rosendahl, L. An Experimental Study on Macro Piezoceramic Fiber Composites for Energy Harvesting. Mater. Sci. Forum 2019, 951 MSF, 3–8. [Google Scholar] [CrossRef]
- Yi, J.W.; Shih, W.Y.; Shih, W.H. Effect of Length, Width, and Mode on the Mass Detection Sensitivity of Piezoelectric Unimorph Cantilevers. J. Appl. Phys. 2002, 91, 1680–1686. [Google Scholar] [CrossRef]
- Kim, M.; Hoegen, M.; Dugundji, J.; Wardle, B.L. Modeling and Experimental Verification of Proof Mass Effects on Vibration Energy Harvester Performance. Smart Mater. Struct. 2010, 19, 045023. [Google Scholar] [CrossRef]
- Lawson, J. Design and Analysis of Experiments with R; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9781498728485. [Google Scholar]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Effects of Nonlinear Piezoelectric Coupling on Energy Harvesters under Direct Excitation. Nonlinear Dyn. 2012, 67, 1221–1232. [Google Scholar] [CrossRef]
- Firoozy, P.; Khadem, S.E.; Pourkiaee, S.M. Power Enhancement of Broadband Piezoelectric Energy Harvesting Using a Proof Mass and Nonlinearities in Curvature and Inertia. Int. J. Mech. Sci. 2017, 133, 227–239. [Google Scholar] [CrossRef]
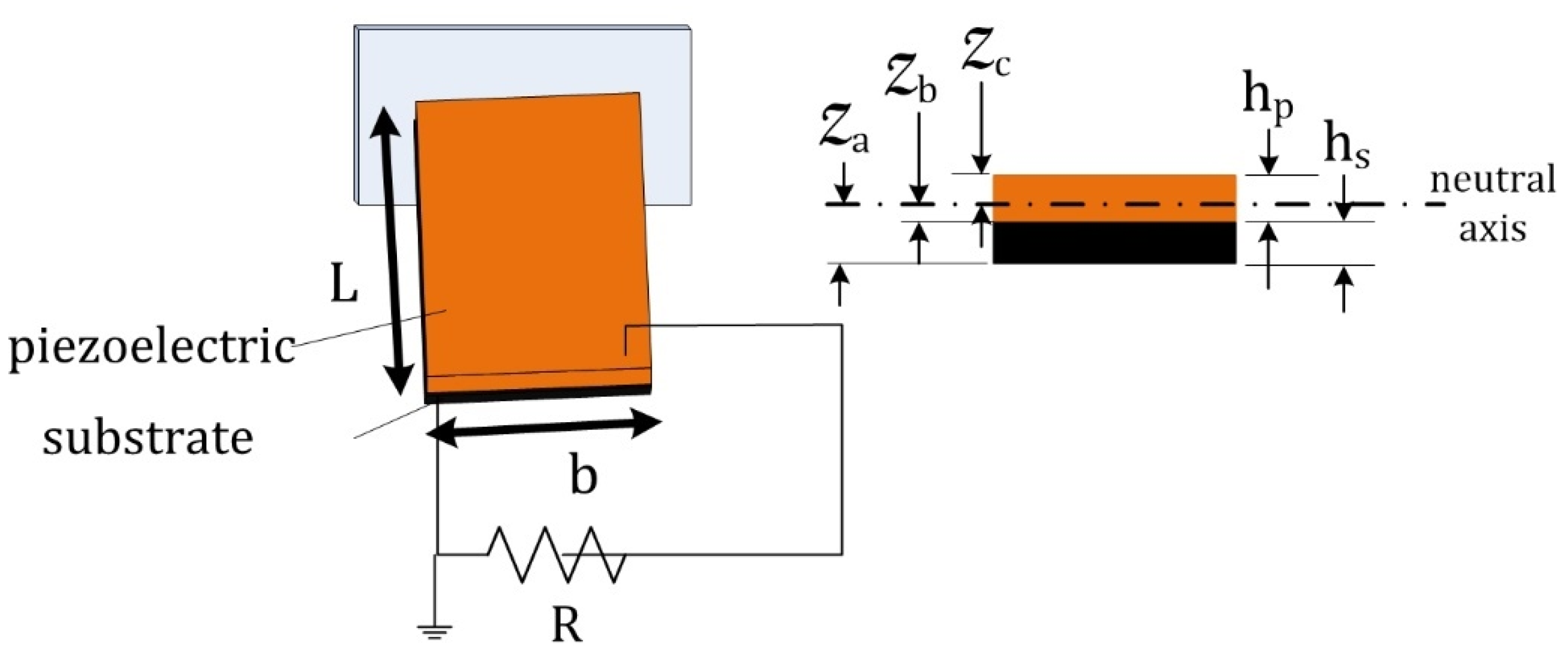
| Definition | Formula | Parameter | ||
|---|---|---|---|---|
| Natural frequency | Beam length ( | |||
| Beam width ( | ||||
| Beam stiffness | Layer thickness ( | |||
| Density ( | ||||
| Mass per unit length | Elastic modulus ( | |||
| Natural frequency coefficient, 1.875, 4.694, 7.885 | Damping coefficient | |||
| Yr | Piezoelectric energy conversion modal coefficient | Permittivity (F/M) | ||
| Electrical load () | ||||
| -distance of neutral axis | ||||
| Piezoelectric reverse energy conversion modal coefficient | -distance: piezo-bottom to neutral axis | |||
| -distance: neutral axis to the top | ||||
| Piezoelectric capacitance | Subscript | Piezoelectric layer | ||
| Harvesting beam mode shapes | Subscript | Substrate layer | ||
| Undamped Natural Frequencies ωr (Hz) | |||
|---|---|---|---|
| Experiment | Current Method (Presented in Section 2) | Error (Hz) | |
| First bending mode | 20.4 | 21.7 | 1.3 Hz |
| Second bending mode | ― | 136.3 | ― |
| Third bending mode | ― | 381.5 | ― |
| Fourth bending mode | ― | 747.7 | ― |
| Fifth bending mode | ― | 1235.9 | ― |
| Experimental Error (%) | Experimental Error (%) | ||||||
|---|---|---|---|---|---|---|---|
| 0.04 | 19.51 | 1.22 | 0.04 | 4.01 | 1.13 | ||
| 0.05 | 38.25 | 1.25 | 0.05 | 6.36 | 0.33 | ||
| 0.075 | 140.68 | 1.20 | 0.075 | 13.73 | 0.55 | ||
| 0.09 | 243.13 | 1.54 | 0.09 | 19.45 | 0.49 | ||
| 0.1 | 344.21 | 1.18 | 0.1 | 24.08 | 1.71 | ||
| 0.12 | 543.71 | 0.29 | 0.04 | 3.01 | 2.75 | ||
| 0.17 | 1104.92 | 0.29 | 0.05 | 4.87 | 0.78 | ||
| 0.2 | 1370.04 | 1.70 | 0.075 | 10.13 | 0.46 | ||
| 0.04 | 6.98 | 1.76 | 0.09 | 14.32 | 0.81 | ||
| 0.05 | 11.45 | 1.05 | 0.1 | 17.44 | 0.47 | ||
| 0.075 | 24.91 | 0.75 | 0.05 | 4.34 | 3.26 | ||
| 0.09 | 35 | 0.82 | 0.08 | 10.65 | 1.78 | ||
| 0.1 | 43.45 | 0.58 | 0.1 | 17.25 | 3.85 | ||
| 0.05 | 3.84 | 2.32 | |||||
| 0.08 | 9.2 | 0.96 | |||||
| 0.1 | 14.12 | 2.99 |
| Index | Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.04 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 19 | 0.1 | 0.05 | 0.05 | 0.08 | 0.05 | 0.08 |
| 2 | 0.04 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 20 | 0.1 | 0.08 | 0.08 | 0.1 | 0.08 | 0.1 |
| 3 | 0.04 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 21 | 0.1 | 0.1 | 0.1 | 0.05 | 0.1 | 0.05 |
| 4 | 0.04 | 0.05 | 0.05 | 0.08 | 0.08 | 0.1 | 22 | 0.1 | 0.05 | 0.05 | 0.1 | 0.1 | 0.1 |
| 5 | 0.04 | 0.08 | 0.08 | 0.1 | 0.1 | 0.05 | 23 | 0.1 | 0.08 | 0.08 | 0.05 | 0.05 | 0.05 |
| 6 | 0.04 | 0.1 | 0.1 | 0.05 | 0.05 | 0.08 | 24 | 0.1 | 0.1 | 0.1 | 0.08 | 0.08 | 0.08 |
| 7 | 0.04 | 0.05 | 0.08 | 0.05 | 0.1 | 0.1 | 25 | 0.1 | 0.05 | 0.1 | 0.08 | 0.05 | 0.1 |
| 8 | 0.04 | 0.08 | 0.1 | 0.08 | 0.05 | 0.05 | 26 | 0.1 | 0.08 | 0.05 | 0.1 | 0.08 | 0.05 |
| 9 | 0.04 | 0.1 | 0.05 | 0.1 | 0.08 | 0.08 | 27 | 0.1 | 0.1 | 0.08 | 0.05 | 0.1 | 0.08 |
| 10 | 0.04 | 0.05 | 0.08 | 0.1 | 0.05 | 0.08 | 28 | 0.1 | 0.05 | 0.1 | 0.1 | 0.08 | 0.05 |
| 11 | 0.04 | 0.08 | 0.1 | 0.05 | 0.08 | 0.1 | 29 | 0.1 | 0.08 | 0.05 | 0.05 | 0.1 | 0.08 |
| 12 | 0.04 | 0.1 | 0.05 | 0.08 | 0.1 | 0.05 | 30 | 0.1 | 0.1 | 0.08 | 0.08 | 0.05 | 0.1 |
| 13 | 0.04 | 0.05 | 0.1 | 0.05 | 0.08 | 0.05 | 31 | 0.1 | 0.05 | 0.08 | 0.05 | 0.08 | 0.08 |
| 14 | 0.04 | 0.08 | 0.05 | 0.08 | 0.1 | 0.08 | 32 | 0.1 | 0.08 | 0.1 | 0.08 | 0.1 | 0.1 |
| 15 | 0.04 | 0.1 | 0.08 | 0.1 | 0.05 | 0.1 | 33 | 0.1 | 0.1 | 0.05 | 0.1 | 0.05 | 0.05 |
| 16 | 0.04 | 0.05 | 0.1 | 0.1 | 0.1 | 0.08 | 34 | 0.1 | 0.05 | 0.08 | 0.08 | 0.1 | 0.05 |
| 17 | 0.04 | 0.08 | 0.05 | 0.05 | 0.05 | 0.1 | 35 | 0.1 | 0.08 | 0.1 | 0.1 | 0.05 | 0.08 |
| 18 | 0.04 | 0.1 | 0.08 | 0.08 | 0.08 | 0.05 | 36 | 0.1 | 0.1 | 0.05 | 0.05 | 0.08 | 0.1 |
| Variable | Degree of Freedom | Mean Square | ||
|---|---|---|---|---|
| frequency) | 1 | = 138,434.3 | = 109.59 | |
| frequency) | 2 | = 4418.2 | = 3.50 | |
| frequency) | 2 | = 5538.2 | = 4.38 | |
| frequency) | 2 | = 4964.7 | = 3.93 | |
| frequency) | 2 | = 507.4 | = 0.40 | |
| frequency) | 2 | = 119.5 | = 0.09 | |
| Residual | = 96 | = 1263.2 |
| Harvester’s Resonant Frequencies | External Excitation Frequencies |
|---|---|
| = 21.7 Hz | = 20.4 Hz |
| = 31.0 Hz | = 40.8 Hz |
| = 136.3 Hz | = 61.2 Hz |
| = 381.5 Hz | = 81.6 Hz |
| = 747.7 Hz | = 102.0 Hz |
| = 1235.9 Hz | = 124.4 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazaee, M. High-Level Vibration for Single-Frequency and Multi-Frequency Excitation in Macro-Composite Piezoelectric (MFC) Energy Harvesters, Nonlinearity, and Higher Harmonics. Micromachines 2023, 14, 1. https://doi.org/10.3390/mi14010001
Khazaee M. High-Level Vibration for Single-Frequency and Multi-Frequency Excitation in Macro-Composite Piezoelectric (MFC) Energy Harvesters, Nonlinearity, and Higher Harmonics. Micromachines. 2023; 14(1):1. https://doi.org/10.3390/mi14010001
Chicago/Turabian StyleKhazaee, Majid. 2023. "High-Level Vibration for Single-Frequency and Multi-Frequency Excitation in Macro-Composite Piezoelectric (MFC) Energy Harvesters, Nonlinearity, and Higher Harmonics" Micromachines 14, no. 1: 1. https://doi.org/10.3390/mi14010001
APA StyleKhazaee, M. (2023). High-Level Vibration for Single-Frequency and Multi-Frequency Excitation in Macro-Composite Piezoelectric (MFC) Energy Harvesters, Nonlinearity, and Higher Harmonics. Micromachines, 14(1), 1. https://doi.org/10.3390/mi14010001







